Sizing of the Drone Delivery Fleet Considering Energy Autonomy
Abstract
:1. Introduction and Literature Review
1.1. The Last Mile Delivery: New Challenges
1.2. Motivation and Target Contribution
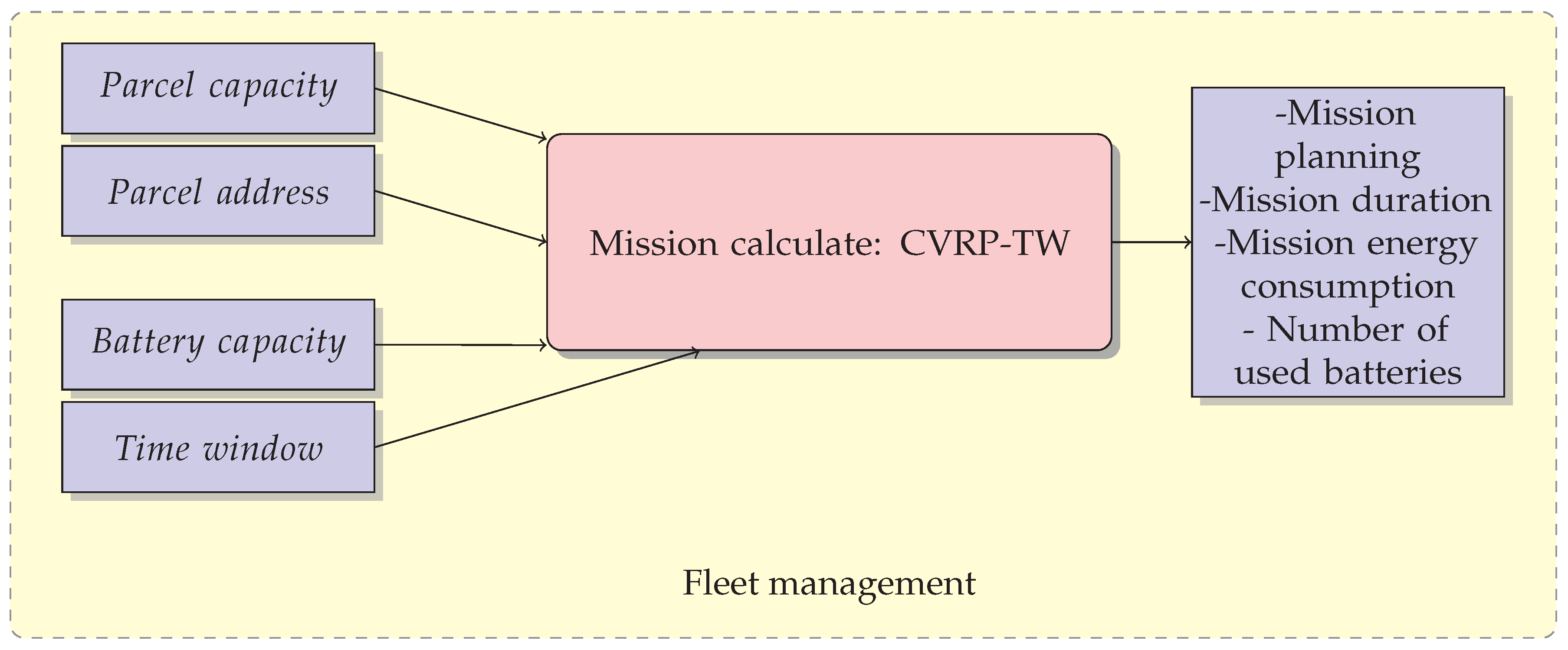
2. Vehicle Routing Problem Approach for Drone Fleet Sizing
2.1. Assumptions and Parameters
- each point i represents a command to deliver;
- the maximum payload is unique for all the fleet;
- the same UAV could do more than one mission per day;
- the service time is the same for each client;
- every mission has a drone with fully-charged battery.
2.2. Mathematical Model
- minimize the distance with []
- minimize the number of used drones []
- minimize the number of used batteries []
3. Case Study: MD4-1000 Drone Fleet
3.1. The Instances Bound
3.2. Numerical Results and Discussions
- A, the minimization of the traveled distance with []
- B, the minimization of the number of the drone used with []
- C, the minimization of the number of the battery used with []
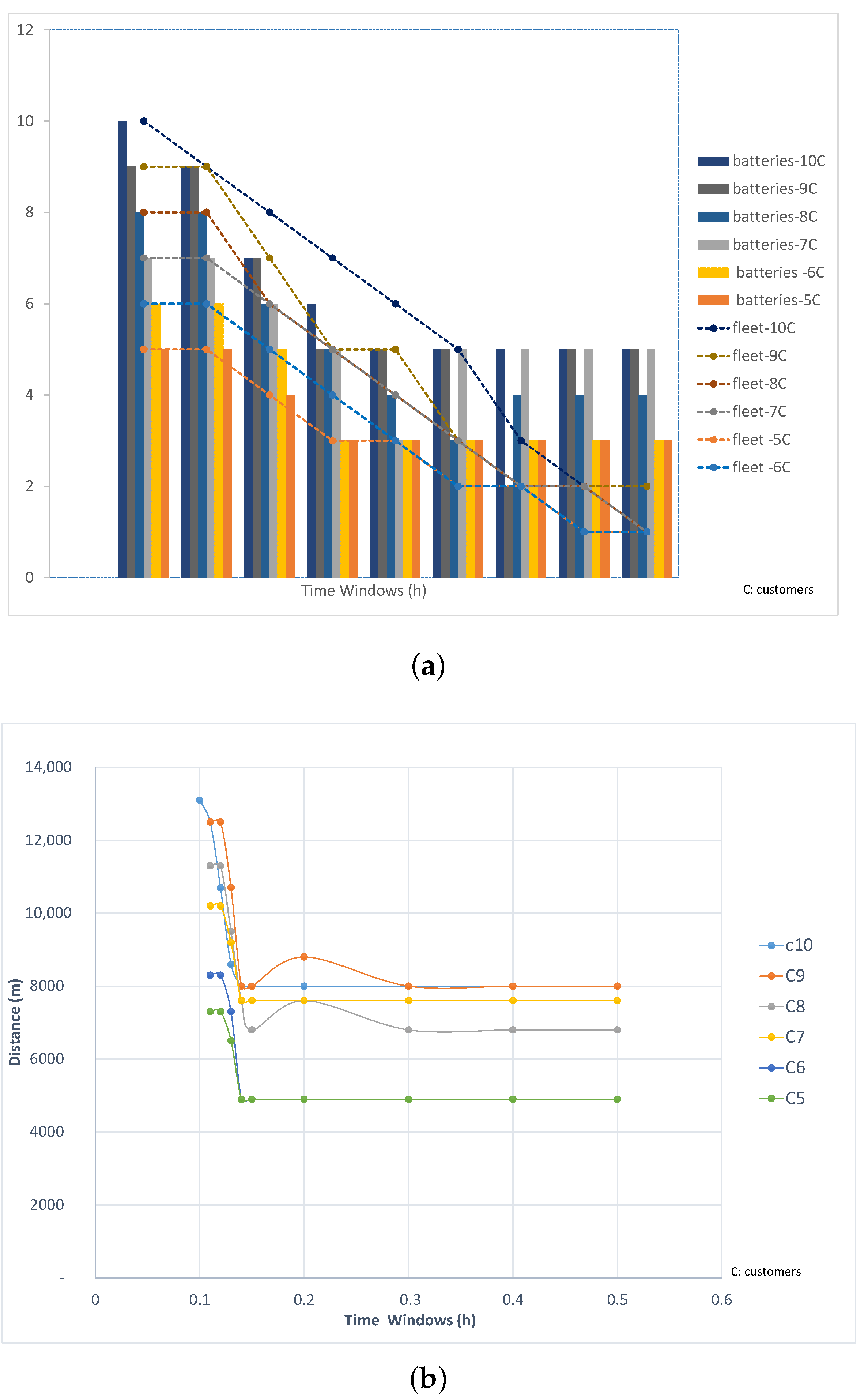
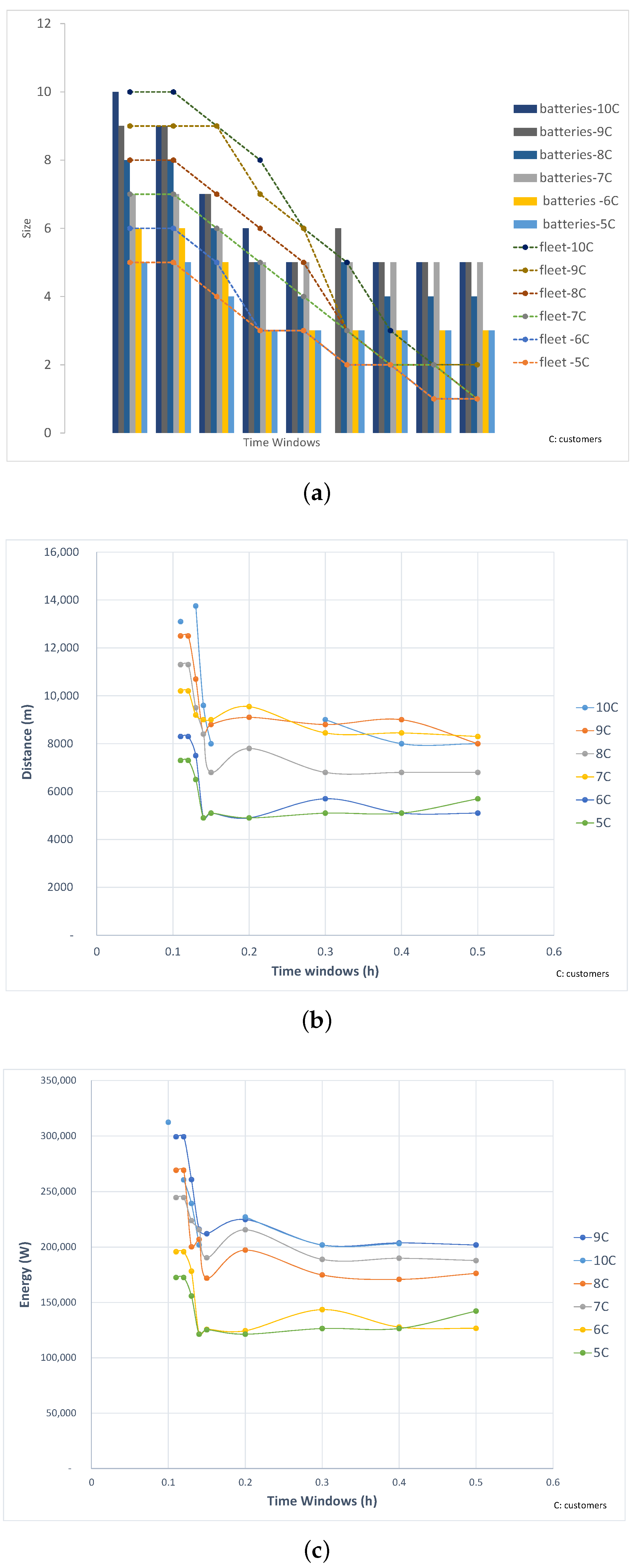
3.2.1. The Impact of the Time Window with the Traveled Distance Minimization (Case A: [, and ])
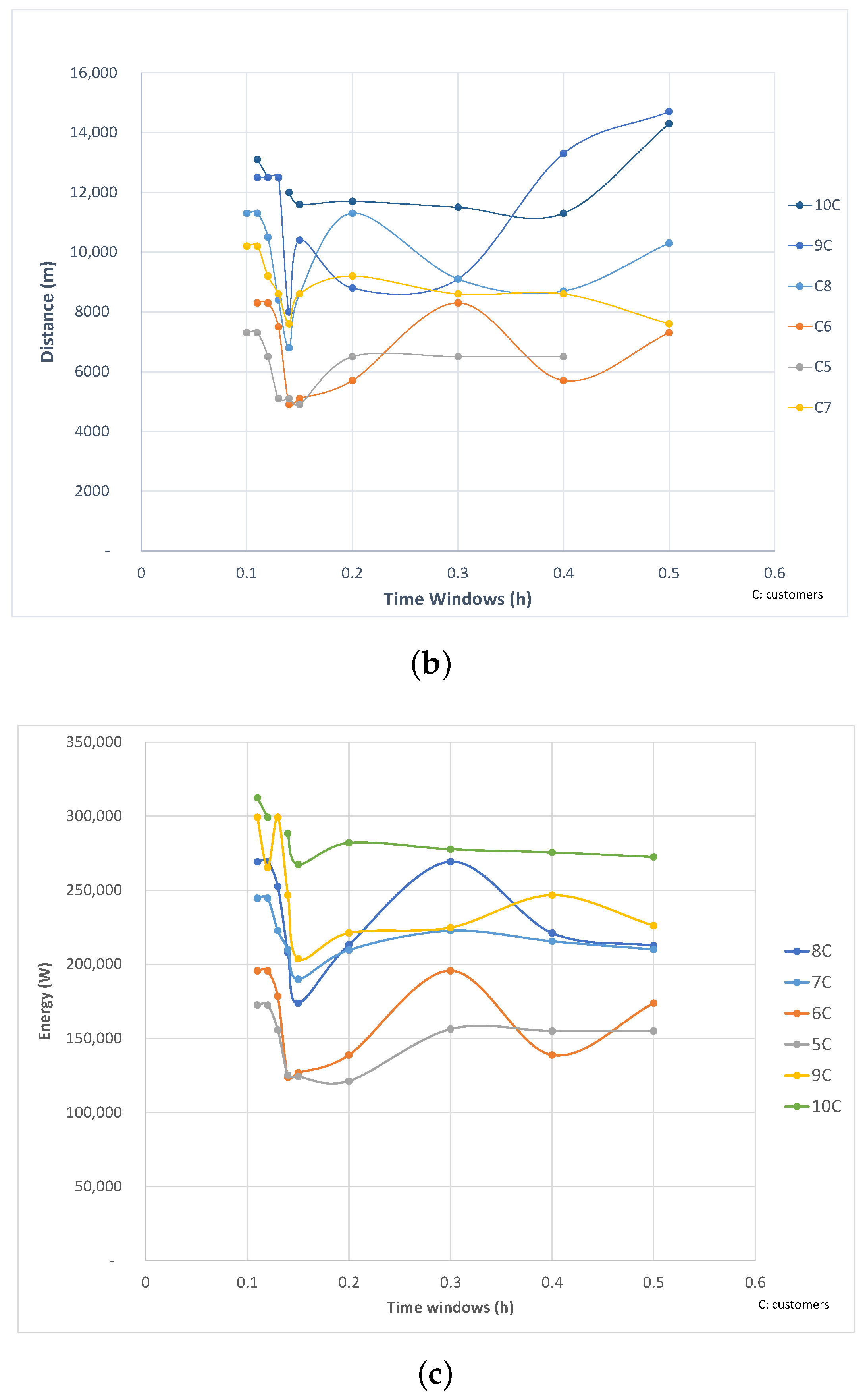
3.2.2. The Impact of the Time Window with Fleet’s Size Minimization (Case B: [, and ])
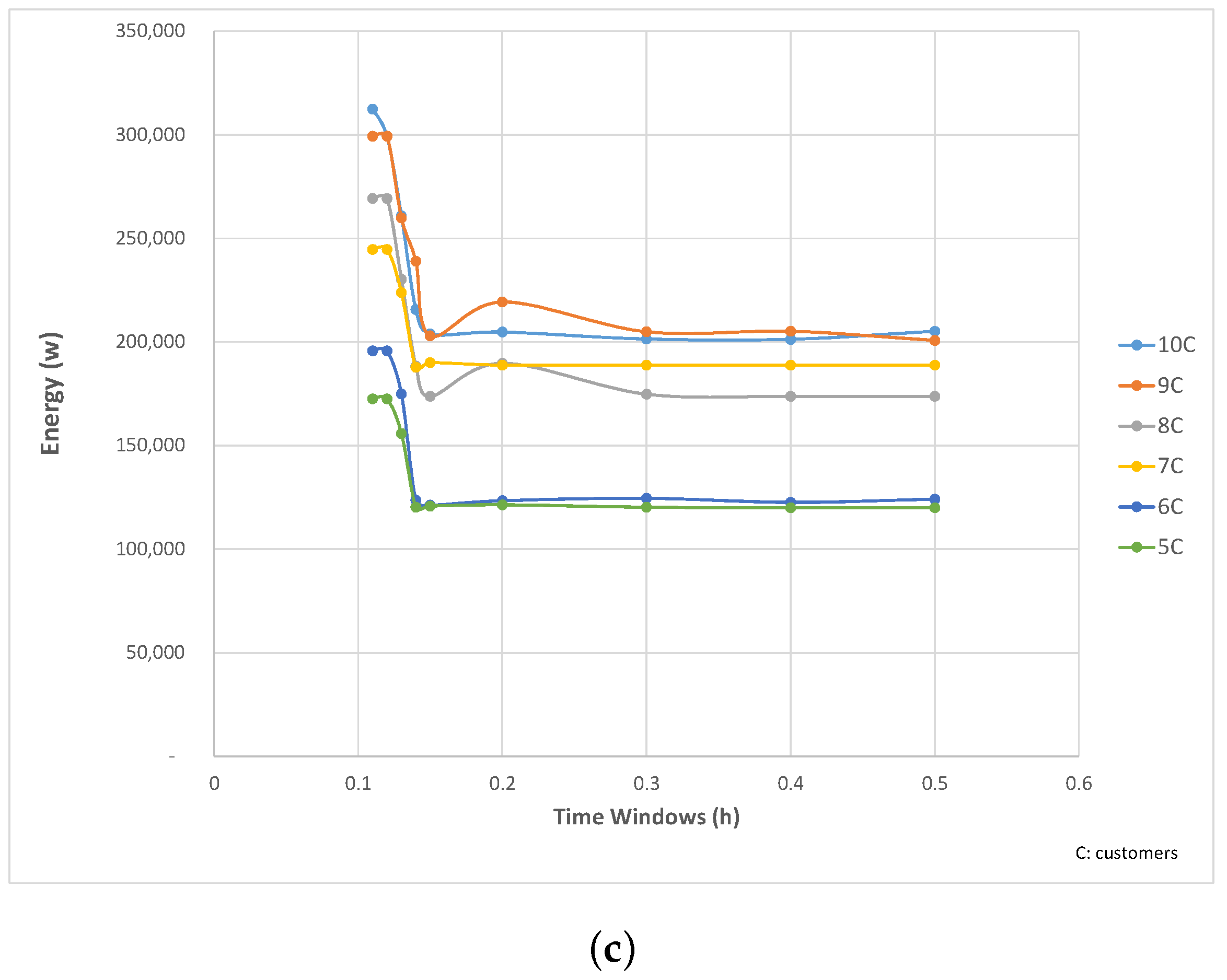
3.2.3. The Impact of the Time Window with Batteries’ Size Minimization (Case C: [, and ])
3.2.4. Classification of the Different Sizing Objectives
4. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Savelsbergh, M.; Van Woensel, T. 50th Anniversary Invited Article—City Logistics: Challenges and Opportunities. Transp. Sci. 2016, 50, 579–590. [Google Scholar] [CrossRef]
- Aerial Transport System Design: Design of an Aerial Transport System for Last Mile Parcel Distribution with Unmanned Aerial Vehicles. Available online: https://repository.tudelft.nl/islandora/object/uuid:9dd1c20f-0de8-4b69-8501-325ae07baeb3 (accessed on 13 February 2017).
- Ducret, R. Parcel deliveries and urban logistics: Changes and challenges in the courier express and parcel sector in Europe—The French case. Res. Transp. Bus. Manag. 2014, 11, 15–22. [Google Scholar] [CrossRef]
- A cost-benefit analysis of Amazon Prime Air. Available online: https://scholar.utc.edu/honors-theses/47/ (accessed on 7 July 2015).
- Patier, D.; David, B.; Chalon, R.; Deslandres, V. A New Concept for Urban Logistics Delivery Area Booking. Proc. Soc. Behav. Sci. 2014, 125, 99–110. [Google Scholar] [CrossRef]
- Oliveira, C.M.D.; Albergaria, D.M.B.R.; Vasconcelos Goes, G.; Schmitz, G.D.N.; D’Agosto, M.D.A. Sustainable Vehicles-Based Alternatives in Last Mile Distribution of Urban Freight Transport: A Systematic Literature Review. Sustainability 2017, 9, 1324. [Google Scholar] [CrossRef]
- Bányai, T. Real-Time Decision Making in First Mile and Last Mile Logistics: How Smart Scheduling Affects Energy Efficiency of Hyperconnected Supply Chain Solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef]
- Ranieri, L.; Digiesi, S.; Silvestri, B.; Roccotelli, M. A Review of Last Mile Logistics Innovations in an Externalities Cost Reduction Vision. Sustainability 2018, 10, 782. [Google Scholar] [CrossRef]
- Morganti, E.; Seidel, S.; Blanquart, C.; Dablanc, L.; Lenz, B. The impact of e-commerce on final deliveries: Alternative parcel delivery services in France and Germany. Transp. Res. Proc. 2014, 4, 178–190. [Google Scholar] [CrossRef]
- Zhang, L.; Matteis, T.; Thaller, C.; Liedtke, G. Simulation-based Assessment of Cargo Bicycle and Pick-up Point in Urban Parcel Delivery. Proc. Comput. Sci. 2018, 130, 18–25. [Google Scholar] [CrossRef]
- Iwan, S.; Kijewska, K.; Lemke, J. Analysis of parcel lockers’ efficiency as the last mile delivery solution–the results of the research in Poland. Transp. Res. Proc. 2016, 12, 644–655. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Ni, L.; Lin, Y. Location-routing problem with simultaneous home delivery and customer’s pickup for city distribution of online shopping purchases. Sustainability 2016, 8, 828. [Google Scholar] [CrossRef]
- Google Tests Drone Deliveries in Project Wing Trials. Available online: https://www.bbc.com/news/technology-28964260 (accessed on 12 November 2015).
- Projet de Drone: Le terminal de Livraison. Available online: https://www.geopostgroup.com/fr/actualites/projet-de-drone -le-terminal-de-livraison (accessed on 13 July 2018).
- Scott, J.; Scott, C. Drone Delivery Models for Healthcare. In Proceedings of the 50th Hawaii International Conference on System Sciences, Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Haidari, L.A.; Brown, S.T.; Ferguson, M.; Bancroft, E.; Spiker, M.; Wilcox, A.; Ambikapathi, R.; Sampath, V.; Connor, D.L.; Lee, B.Y. The economic and operational value of using drones to transport vaccines. Vaccine 2016, 34, 4062–4067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remot. Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Optimization of Drone-Assisted Parcel Delivery. Available online: http://tesi.cab.unipd.it/51947/1/Andrea_Ponza_-_Analisi_e_ottimizzazione_nell’uso_di_droni_per_la_consegna_di_prodotti.pdf (accessed on 13 February 2017).
- Figliozzi, M.A. The time dependent vehicle routing problem with time windows: Benchmark problems, an efficient solution algorithm, and solution characteristics. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 616–636. [Google Scholar] [CrossRef]
- Heuristiques Pour Les Problèmes De Tournées De Véhicules Multi-Attributs. Available online: https://www.cirrelt.ca/DocumentsTravail/CIRRELT-2011-12.pdf (accessed on 23 Janurary 2017).
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Kumar, S.N.; Panneerselvam, R. Survey on the Vehicle Routing Problem and Its Variants. Intell. Inf. Manag. 2012, 4, 66–74. [Google Scholar] [CrossRef]
- Golden, B.L.; Raghavan, S.; Wasil, E.A. The Vehicle Routing Problem: Latest Advances and New Challenges; Springer Science & Business Media: Berlin, Germany, 2008; Volume 43. [Google Scholar]
- Vehicle Routing: Problems, Methods, and Applications. Available online: https://epubs.siam.org/doi/abs/10.1137/1.9781611973594.fm (accessed on 23 January 2016).
- Shetty, V.K.; Sudit, M.; Nagi, R. Priority-based assignment and routing of a fleet of unmanned combat aerial vehicles. Comput. Oper. Res. 2008, 35, 1813–1828. [Google Scholar] [CrossRef]
- Russell, M.A.; Lamont, G.B. A genetic algorithm for unmanned aerial vehicle routing. In Proceedings of the 7th annual conference on Genetic and evolutionary computation, Washington, DC, USA, 25–29 June 2005; pp. 1523–1530. [Google Scholar]
- Savuran, H.; Karakaya, M. Route optimization method for unmanned air vehicle launched from a carrier. Lecture Notes Softw. Eng. 2015, 3, 279. [Google Scholar] [CrossRef]
- Kurdi, H.; How, J. Bio-Inspired Algorithm for Task Allocation in Multi-UAV Search and Rescue Missions. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 5–9 January 2016; p. 1377. [Google Scholar]
- Boone, N.; Sathyan, A.; Cohen, K. Enhanced approaches to solving the multiple traveling salesman problem. In Proceedings of the AIAA Infotech@ Aerospace Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Mathew, N.; Smith, S.L.; Waslander, S.L. Planning Paths for Package Delivery in Heterogeneous Multirobot Teams. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1298–1308. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. Heuristic methods for the Traveling Salesman Problem with Drone. arXiv, 2015; arXiv:1509.08764. [Google Scholar]
- Optimization Approaches for the Traveling Salesman Problem With Drone. Available online: https://www.narcis.nl/publication/RecordID/oai:repub.eur.nl:78472 (accessed on 13 February 2017).
- Sawadsitang, S.; Niyato, D.; Siew, T.P.; Wang, P. Supplier Cooperation in Drone Delivery. arXiv, 2018; arXiv:1805.06803. [Google Scholar]
- Troudi, A.; Addouche, S.A.; Dellagi, S.; El Mhamedi, A. Logistics Support Approach for Drone Delivery Fleet. In Proceedings of the Smart Cities: Second International Conference, Smart-CT 2017, Málaga, Spain, June 14–16 2017; Alba, E., Chicano, F., Luque, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 86–96. [Google Scholar] [CrossRef]
- Soutien Logistique Intégré. Available online: https://www.techniques-ingenieur.fr/base-documentaire/genie-industriel-th6/gestion-des-flux-logistiques-42119210/soutien-logistique-integre-ag5380/ (accessed on 3 April 2015).
- Asma, T.; Addouche, S.A.; Dellagi, S.; Mhamedi, A.E. Post-production analysis approach for drone delivery fleet. In Proceedings of the 2017 IEEE International Conference on Service Operations and Logistics, and Informatics (SOLI), Bari, Italy, 18–20 September 2017; pp. 150–155. [Google Scholar] [CrossRef]
- D’Andrea, R. Guest Editorial Can Drones Deliver? IEEE Trans. Autom. Sci. Eng. 2014, 11, 647–648. [Google Scholar] [CrossRef]


| Paper | Military Use | Civilian Use | Formulation |
|---|---|---|---|
| Russell et al., 2005 | X | GVR | |
| Shetty et al., 2008 | X | mTSP | |
| Kurdi et al., 2016 | X | Multi-UAV task allocation | |
| Murray et al., 2015 | X | FSTSP | |
| Agatz et al., 2015 | X | TSP-D | |
| Ha et al., 2015 | X | Column Generation | |
| Boone et al., 2015 | X | X | MTSP |
| Mathew et al., 2015 | X | HDP/MWDP | |
| Savuran et al., 2015 | X | VRP | |
| Sawadsitang et al., 2018 | x | MIP + merge-and-split algorithm |
| Parameter | Value |
|---|---|
| Speed (m/s) | 13 |
| Range (km) | 1 |
| Structure mass (kg) | 3.35 |
| Maximal take-off mass (kg) | 5.55 |
| Maximal loaded mass (kg) | 1.2 |
| Battery | 22.2 V, 6S2P 13.Ah LiPo |
| Endurance (min) | 70 |
| Traveled Distance | Battery Set Size | Energy Consumption | |
|---|---|---|---|
| Case A | 1 | 1 | 1 |
| Case B | 3 | 3 | 3 |
| Case C | 2 | 2 | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Troudi, A.; Addouche, S.-A.; Dellagi, S.; Mhamedi, A.E. Sizing of the Drone Delivery Fleet Considering Energy Autonomy. Sustainability 2018, 10, 3344. https://doi.org/10.3390/su10093344
Troudi A, Addouche S-A, Dellagi S, Mhamedi AE. Sizing of the Drone Delivery Fleet Considering Energy Autonomy. Sustainability. 2018; 10(9):3344. https://doi.org/10.3390/su10093344
Chicago/Turabian StyleTroudi, Asma, Sid-Ali Addouche, Sofiene Dellagi, and Abderrahman El Mhamedi. 2018. "Sizing of the Drone Delivery Fleet Considering Energy Autonomy" Sustainability 10, no. 9: 3344. https://doi.org/10.3390/su10093344
APA StyleTroudi, A., Addouche, S.-A., Dellagi, S., & Mhamedi, A. E. (2018). Sizing of the Drone Delivery Fleet Considering Energy Autonomy. Sustainability, 10(9), 3344. https://doi.org/10.3390/su10093344




