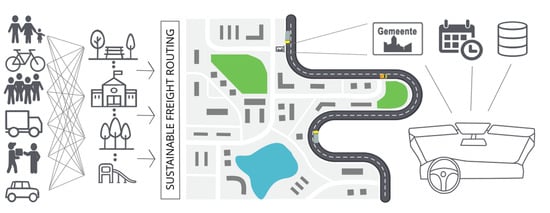
A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics
Abstract
1. Introduction
2. Materials and Methods
2.1. Decision-Making Approach
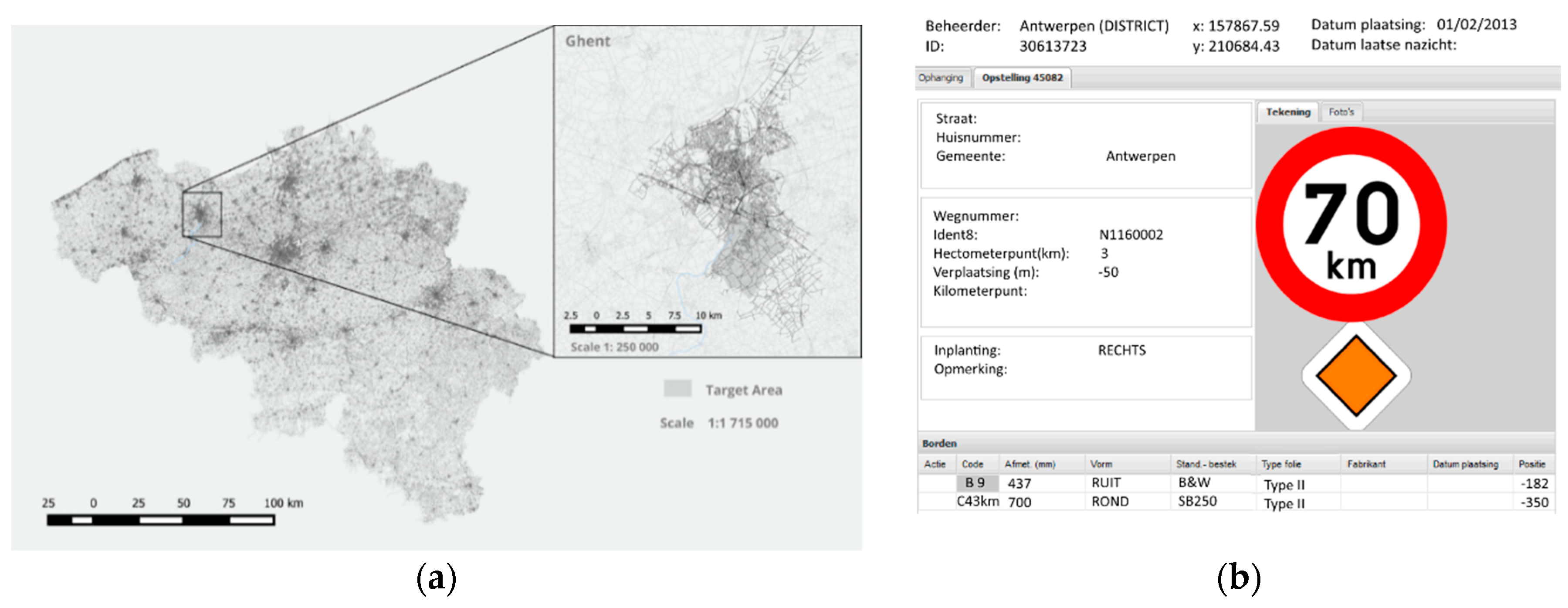
2.2. Study Area
- Nature park areas (e.g., national park or recreation areas where citizens relax, have picnics, or do sport activities);
- Historical areas (monuments and historic locations that might be damaged by traffic-related vibrations or emissions);
- Care facility areas (health-related facilities used for medical treatments and recovery);
- Construction areas (where traffic might cause increased particulate matter presence, like dust);
- Children areas (areas where children gather, play, or go to school).
3. Results
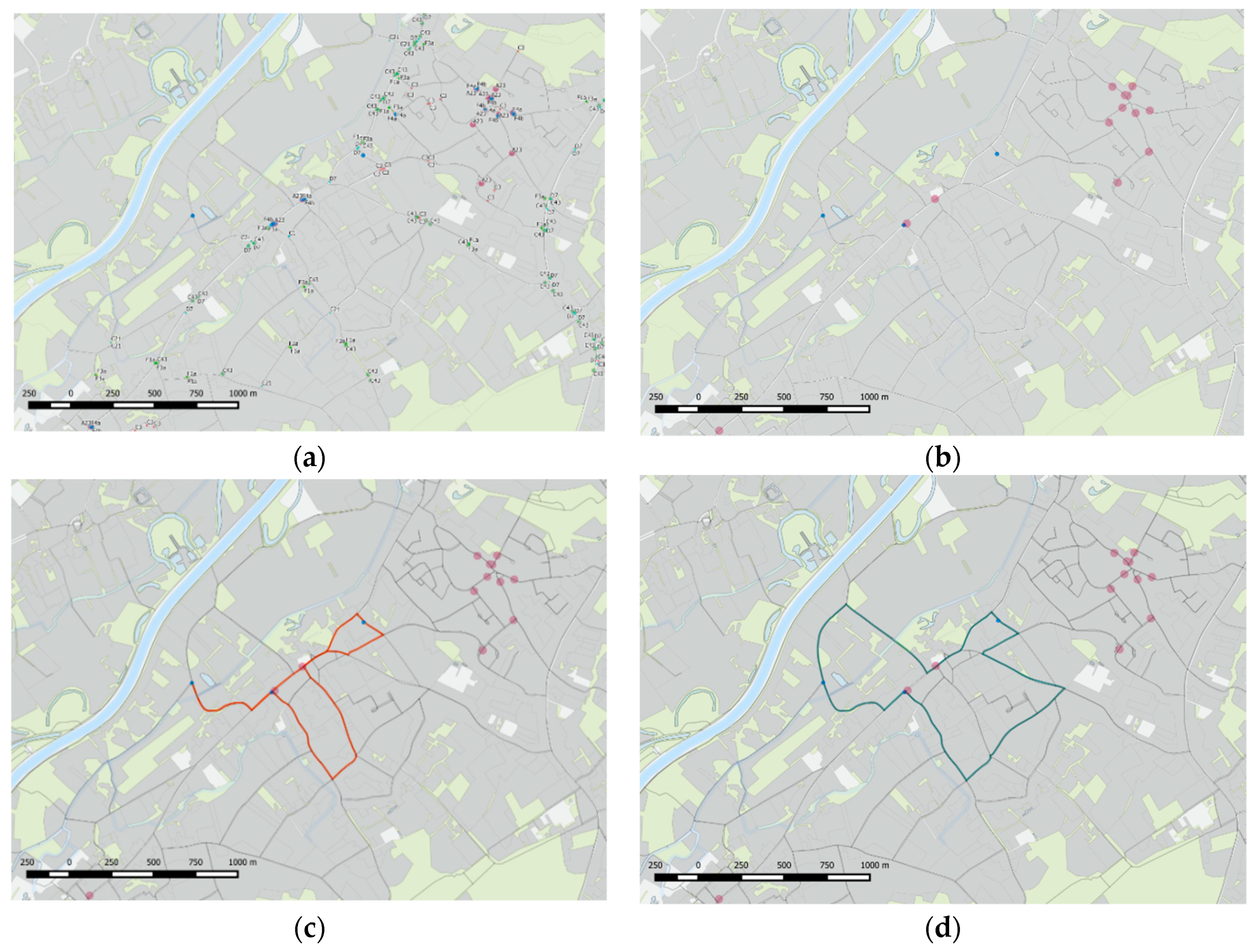
3.1. Integrating Sustainability into the Time-Dependent Route Cost Calculation Based on the Traffic Sign Database
3.2. Sustainable Routing
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UNPFA State of World Population 2007: Unleashing the Potential of Urban Growth. 2007. Available online: https://www.unfpa.org/sites/default/files/pub-pdf/695_filename_sowp2007_eng.pdf (accessed on 15 June 2018).
- Taniguchi, E.; Thompson, R. Innovations in City Logistics; Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Gatta, V.; Marcucci, E. Stakeholder-specific data acquisition and urban freight policy evaluation: Evidence, implications and new suggestions. Transp. Rev. 2016, 1647. [Google Scholar] [CrossRef]
- Holguín-Veras, J. Necessary conditions for off-hour deliveries and the effectiveness of urban freight road pricing and alternative financial policies in competitive markets. Transp. Res. Part A Policy Pract. 2008, 42, 392–413. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Silas, M.; Polimeni, J.; Cruz, B. An investigation on the effectiveness of joint receiver-carrier policies to increase truck traffic in the off-peak hours. Part II: The behavior of carriers. Netw. Spat. Econ. 2008, 8, 327–354. [Google Scholar] [CrossRef]
- Macharis, C.; Melo, S. City Distribution and Urban Freight Transport Multiple Perspectives; Edward Elgar Publishing: Cheltenham, UK, 2011; ISBN 978-1-78347-082-2. [Google Scholar]
- Witkowski, J.; Kiba-Janiak, M. The Role of Local Governments in the Development of City Logistics. Procedia Soc. Behav. Sci. 2014, 125, 373–385. [Google Scholar] [CrossRef]
- Grazia Speranza, M. Trends in transportation and logistics. Eur. J. Oper. Res. 2016, 264, 830–836. [Google Scholar] [CrossRef]
- Castillo-Manzano, J.I.; Castro-Nuño, M.; Fageda, X. Exploring the relationship between truck load capacity and traffic accidents in the European Union. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 94–109. [Google Scholar] [CrossRef]
- Darbyshire, J.L.; Young, J.D. An investigation of sound levels on intensive care units with reference to the WHO guidelines. Crit. Care 2013, 17, R187. [Google Scholar] [CrossRef] [PubMed]
- Hill, J.; LaVela, S. Noise Levels in Patient Rooms and at Nursing Stations at Three VA Medical Centers. HERD Heal. Environ. Res. Des. J. 2015, 9, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Angelelli, E.; Arsik, I.; Morandi, V.; Savelsbergh, M.; Speranza, M.G. Proactive route guidance to avoid congestion. Transp. Res. Part B Methodol. 2016, 94, 1–21. [Google Scholar] [CrossRef]
- Angelelli, E.; Mansini, R.; Vindigni, M. The Stochastic and Dynamic Traveling Purchaser Problem. Transp. Sci. 2016, 50, 363–761. [Google Scholar] [CrossRef]
- Liu, S.; Qu, Q. Dynamic collective routing using crowdsourcing data. Transp. Res. Part B Methodol. 2016, 93, 450–469. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Van Woensel, T.; Bektaş, T.; Laporte, G. The time-dependent pollution-routing problem. Transp. Res. Part B Methodol. 2013, 56, 265–293. [Google Scholar] [CrossRef]
- Franceschetti, A.; Demir, E.; Honhon, D.; Van Woensel, T.; Laporte, G.; Stobbe, M. A metaheuristic for the time-dependent pollution-routing problem. Eur. J. Oper. Res. 2017, 259, 972–991. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Laporte, G.; Van Woensel, T.; Fransoo, J.C. Strategic fleet planning for city logistics. Transp. Res. Part B Methodol. 2017, 95, 19–40. [Google Scholar] [CrossRef]
- Ehmke, J.F.; Campbell, A.M.; Thomas, B.W. Vehicle routing to minimize time-dependent emissions in urban areas. Eur. J. Oper. Res. 2015, 251, 478–494. [Google Scholar] [CrossRef]
- Mensing, F.; Bideaux, E.; Trigui, R.; Tattegrain, H. Trajectory optimization for eco-driving taking into account traffic constraints. Transp. Res. Part D Transp. Environ. 2013, 18, 55–61. [Google Scholar] [CrossRef]
- Fukasawa, R.; He, Q.; Song, Y. A disjunctive convex programming approach to the pollution-routing problem. Transp. Res. Part B Methodol. 2016, 94, 61–79. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; MD Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res. Istraživanja 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Chang, T.; Wang, T. Using the fuzzy multi-criteria decision making approach for measuring the possibility of successful knowledge management. Inf. Sci. (Ny). 2009, 179, 355–370. [Google Scholar] [CrossRef]
- Brnjac, N.; Cavar, I. Example of positioning intermodal terminals on inland waterways. Promet Traffic Transp. 2009, 21, 443–449. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Kavran, Z.; Cavar, I. AHP Model of Selecting Mobile Phones in the Republic of Croatia. In Proceedings of the 15th Mini EURO Conference, Coimbra, Portugal, 22–24 September 2004; pp. 11–14. [Google Scholar]
- Novacko, L.; Cavar, I.; Hozjan, D. Selection of LRT system track gauge using multi-criteria decision-making (City of Zagreb). WIT Trans. Built Environ. 2008, 101, 167–173. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Petrini, M.A.; Rocha, J.V.; Brown, J.C.; Bispo, R.C. Using an analytic hierarchy process approach to prioritize public policies addressing family farming in Brazil. Land Use Policy 2016, 51, 85–94. [Google Scholar] [CrossRef]
- Chaudhary, P.; Chhetri, S.K.; Joshi, K.M.; Shrestha, B.M.; Kayastha, P. Application of an Analytic Hierarchy Process (AHP) in the GIS interface for suitable fire site selection: A case study from Kathmandu Metropolitan City, Nepal. Socioecon. Plann. Sci. 2016, 53, 60–71. [Google Scholar] [CrossRef]
- Kijewska, K.; Torbacki, W.; Iwan, S. Application of AHP and DEMATEL methods in choosing and analysing the measures for the distribution of goods in Szczecin region. Sustainability 2018, 10. [Google Scholar] [CrossRef]
- Stad Gent Belfry Ghent in Statistics Ghent in Statistics. Available online: https://visit.gent.be/en/ghent-statistics?context=tourist (accessed on 22 August 2018).
- Nicholson, B.H. Get on Your Bike in Belgium: The Best Way to See Glorious Ghent? On Two Wheels. Available online: http://www.dailymail.co.uk/travel/article-2508846/Belgium-breaks-The-best-way-glorious-Ghent-On-wheels-.html (accessed on 22 August 2018).
- VIM Vlaams Instituut voor Mobiliteit. 2017. Available online: http://www.vim.be (accessed on 01 September 2018).
- Mobiel Vlaanderen Verkeersbordendatabank. Available online: http://www.mobielvlaanderen.be/verkeersbordendatabank/index.php (accessed on 1 September 2018).

| Preference Factor | Degree of Preference | Explanation |
|---|---|---|
| 1 | Equally | Two factors contribute equally to the objective |
| 3 | Moderately | Experience and judgment slightly to moderately favor one factor over another |
| 5 | Strongly | Experience and judgment strongly or essentially favor one factor over another |
| 7 | Very strongly | A factor is strongly favored over another, and its dominance is shown in practice |
| 9 | Extremely | The evidence of favoring one factor over another is of the highest degree possible of an affirmation |
| 2, 4, 6, 8 | Intermediate | Used to represent compromises between the preferences in weights 1, 3, 5, 7, and 9 |
| Reciprocals | Opposites | Used for inverse comparisons |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
| Type | Description | Type | Description | Type | Description | Type | Description | Type | Description |
|---|---|---|---|---|---|---|---|---|---|
| S34 | Park Area | S31 | Castle | F53 | Nursing Facility/Hospital | A31 | Construction Works | A23 | School |
| S36 | National Park Area | S32 | Ruins | F55 | Aid station/Ambulance | F47 | End of Construction Works | F12a | Start of Living Street zone |
| S33 | Abbey | F12b | End of Living Street zone | ||||||
| S35 | Monument | F4a | Start of zone 30 km/hr | ||||||
| F4b | End of Zone 30 km/hr | ||||||||
| Criteria | ||||
|---|---|---|---|---|
| Pair wise comparison matrix | ||||
| 1.00 | 1.00 | 4.00 | 1.00 | |
| 1.00 | 1.00 | 4.00 | 1.00 | |
| 0.25 | 0.26 | 1.00 | 0.25 | |
| 1.00 | 1.00 | 4.00 | 1.00 | |
| Sum | 3.25 | 3.26 | 13.00 | 3.25 |
| Normalized relative weight | ||||
| 0.308 | 0.308 | 0.308 | 0.308 | |
| 0.308 | 0.308 | 0.308 | 0.308 | |
| 0.077 | 0.077 | 0.077 | 0.077 | |
| 0.308 | 0.308 | 0.308 | 0.308 | |
| Sum | 1.00 | 1.00 | 1.00 | 1.00 |
| Historical areas sub-elements | Normalized principal eigenvector | |||
| 0.308 | ||||
| 0.308 | ||||
| 0.077 | ||||
| 0.308 | ||||
| Sustainable Routing Elements | Pairwise Comparison Matrix | Normalized Principal Eigenvector | |||
|---|---|---|---|---|---|
| Nature park areas | |||||
| 1.000 | 0.143 | 0.125 | |||
| 7.000 | 1.000 | 0.875 | |||
| Historical areas | |||||
| 1.00 | 1.00 | 4.000 | 1.000 | 0.308 | |
| 1.00 | 1.00 | 4.000 | 1.000 | 0.308 | |
| 0.25 | 0.26 | 1.000 | 0.250 | 0.077 | |
| 1.00 | 1.00 | 4.000 | 1.000 | 0.308 | |
| Care facility areas | |||||
| 1.000 | 5.000 | 0.833 | |||
| 0.200 | 1.000 | 0.167 | |||
| Construction areas | |||||
| 1.000 | 1.000 | ||||
| Children areas | |||||
| 1.000 | 4.000 | 9.000 | 0.701 | ||
| 0.250 | 1.000 | 6.000 | 0.243 | ||
| 0.111 | 0.167 | 1.000 | 0.056 | ||
| Criteria | |||||
|---|---|---|---|---|---|
| Nature park areas | 2 | 2.00000 | 0.00000 | 0.00 | 0.0000 |
| Historical areas | 4 | 4.00554 | 0.00185 | 0.90 | 0.0021 |
| Care facility areas | 2 | 2.00000 | 0.00000 | 0.00 | 0.0000 |
| Construction areas | 1 | 1.00000 | 1.00000 | 0.00 | 0.0000 |
| Children areas | 3 | 3.10564 | 0.05282 | 0.58 | 0.0911 |
| Results | Sustainable Routing | Dijkstra | ||||
|---|---|---|---|---|---|---|
| Distance | Sustainability Cost | Overall | Distance | Sustainability Cost | Overall | |
| Cost | 4735.76 | 1182.00 | 5917.76 | 4393.12 | 0 | 4393.12 |
| Percentage | 80.03% | 19.97% | 100.00% | 100% | 0% | 100.00% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semanjski, I.; Gautama, S. A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics. Sustainability 2019, 11, 234. https://doi.org/10.3390/su11010234
Semanjski I, Gautama S. A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics. Sustainability. 2019; 11(1):234. https://doi.org/10.3390/su11010234
Chicago/Turabian StyleSemanjski, Ivana, and Sidharta Gautama. 2019. "A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics" Sustainability 11, no. 1: 234. https://doi.org/10.3390/su11010234
APA StyleSemanjski, I., & Gautama, S. (2019). A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics. Sustainability, 11(1), 234. https://doi.org/10.3390/su11010234