Development of Commute Mode Choice Model by Integrating Actively and Passively Collected Travel Data

Abstract

Travel data collection, which is necessary for travel demand modeling, is always of great concern to modelers due to its huge cost and effort when a large sample is required to achieve satisfactory model precisions. In this paper, travel data collected based on a survey questionnaire and travelers’ active participation are called actively collected data (ACD). It is difficult to guarantee absolute randomness and unbiasedness in a sample when the ACD are collected due to self-selection issues. The aim of this study is to improve the model precision at low cost by using passively collected data (PCD), such as in-vehicle GPS data and transit smart card data, to release sample size restriction and reduce sampling bias of ACD in a commute mode choice model. In an empirical study, a multinomial-logit-based joint model is developed for commute mode choice by integrating ACD and PCD based on the choice-based sampling theory. A comprehensive set of explanatory variables are specified through data integration. Both simulation and empirical results show great improvement in coefficient precisions in the proposed joint model, relative to those in the ACD model and PCD model. In this study, ACD and PCD samples of Shanghai are integrated in the joint model so that several significantly influential level-of-service attributes are identified for auto, rail, and bus modes, and their impacts on commute mode choice probabilities are quantified. The findings can aid in better evaluating the program to improve the existing transit system.

1. Introduction

Massive travel data have been passively generated and continuously stored in the background of some electronic device systems, which are not intentionally collected but can be potentially used for transportation research [1]. For example, transit smart card system records the arrival/departure information of transit users, in-vehicle GPS system records drivers’ behaviors and travel paths ever since the engine starts. The passively collected data (PCD) record travel process of different modes, offering a large sample size and accurate measures over a long-term period. Conventional travel survey data cannot be compared in these respects. With the development of big data technology, travel behavior of every traffic participant could be revived by using passively collected data (PCD), such as mobile phone data [2,3], in-vehicle GPS data [4,5], transit smart card [6,7], loop detector and remote sensor data [8,9,10,11,12], etc.

The features of PCD may enable advanced analysis of travel behavior, meanwhile, limitations are also obvious. Take in-vehicle GPS data and transit smart card data as examples. In-vehicle GPS data provide location and timing of trip departure and arrival while transit smart card data provide information of entry/exit stations and trip timings. In comparison to traditional data sources, much larger samples can be obtained, and behavior can be analyzed over much longer periods [13,14]. Some of the major level-of-service (LOS) attributes of transit and auto modes are contained in PCD and may be utilized to improve the performance of mode choice models. However, personal attributes are lacked in PCD, such as gender, age, income, etc., which need to be enriched by traditional means of data collections [15,16]. Hence, a complementary role may be played by PCD for traditional data collection methods.

In light of the name of PCD, data from revealed preference (RP) survey and stated preference (SP) survey may be called actively collected data (ACD) as per the process of data collection that requires active participation of travelers. RP/SP surveys are still the most widely used data collection approaches for modeling analysis of travel behavior [17,18,19,20]. With a complete set of records on travel modes, ACD provide not only exact trip information of timing, location, and purpose, but also the socioeconomic and demographic attributes of respondents, which are both essential in modeling analysis of travel choices.

The huge cost to collect a large sample of ACD with controlled self-selection bias is always of great concern to transportation researchers and modelers. In RP surveys, sampled individuals will be asked to report their travel behaviors in the past day(s) or upcoming day(s), while SP surveys require respondents to make their travel choices under hypothetical scenarios. The questionnaire surveys usually suffer from high monetary and time costs, particularly when the sample size is large, for estimating a mode choice model with multiple alternative travel modes. The data quality largely depends on the coordination of respondents in the survey. Respondents are sometimes obliged to answer a large number of questions to satisfy the data needs for travel behavior analysis. However, it is not always easy to memorize activities and travels in the past, and respondents may not always be willing to report the exact locations or timings of certain activities or travels. Thus, the behavioral survey based on questionnaire is not always sufficient for the measurement of micro-level travel behavior in space–time dimensions [21].

A potential integration of ACD and PCD may provide a new way to overcome shortcoming of data from a single source. Research has shown the capability of a data integration method to estimate absent behavioral attributes in PCD by using ACD [22,23,24]. The survey-based data directly collect detailed information on travel behavior, but cannot continuously do so over a long-term period among a large portion of population. If covering almost the entire population, PCD can effectively overcome the sample self-selection issue, which is a challenge in ACD. In contrast, PCD provide only fragmentary information on travelers’ behavior, though they can provide a continuous long-term period data from almost the entire population. If the advantages of ACD and PCD are combined for model estimation, the model quality may be substantially improved.

In this paper, a multinomial-logit-based model is developed for commute mode choice by integrating ACD and PCD. The data are integrated based on the choice-based sampling theory of the discrete choice model. The proposed joint modeling method is applied to model commute mode choices in Shanghai, China. The rest of this paper is organized as follows. The second section proposes the methodology to integrate ACD and PCD for developing a joint model. The third section provides results of simulation experiments based on synthetic data. The fourth section introduces the data used for the empirical study and the fifth section discusses estimation results of commute mode choice models. The last section concludes this paper and makes some discussions for future research.

2. Modeling Methodology

This section proposes a choice model estimation method that can integrate ACD and PCD for model precision improvement. The first part presents the basic theory of choice-based sampling method for discrete choice model. Then the second part discusses the model structure and estimation procedure for the joint model.

2.1. Choice-Based Sampling Method

In order to facilitate data acquisition and guarantee data quality, we sometimes collect data directly from travelers using specific travel mode(s) for mode choice analysis. For example, in studying choice of mode for work trips, it is often more convenient to survey transit users at stations and car users at parking lots than to interview commuters at their homes. This method of random sampling in a particular mode is called a choice-based sampling method. Manski and Lerman [25] proposed the exogenous sampling maximum likelihood (ESML) estimation method for multinomial logit models using choice-based samples. If a researcher is using a pure choice-based sample, which means that decision makers are randomly drawn from each group of population who use a specific mode. For example, in a pure choice-based sample of car and rail, car records may come from survey at parking lots while rail records may come from survey at rail stations. Then the logit model estimation produces consistent estimates for all the model parameters except the alternative-specific constants. Furthermore, these constants are biased by a known factor and therefore can be adjusted, so that the adjusted constants are consistent [26]. The formula of ESML to adjust alternative-specific constants is written as:

$$E({\alpha }_k)={\alpha }_k^{*}-ln\left[Q\left(k\right)/H\left(k\right)\right]$$

(1)

where ${\alpha }_k$ is the expectation of estimated constant for alternative k, ${\alpha }_k^{*}$ is the true constant, $Q\left(k\right)$ is alternative k’s mode share in population, and $H\left(k\right)$ is alternative k’s mode share in the choice-based sample.

PCD mostly record travel data of specific mode(s). For example, rail card-swiping data can be considered as a choice-based sample for rail passengers, and GPS data from navigation system as a choice-based sample for car users. Therefore, the ACD and PCD in our study could be integrated through the ESML approach.

2.2. Joint MNL Model Integrating ACD and PCD

Let $U_{ik}^a$ be the utility that individual i associates with alternative k in ACD. The utility equations as well as choice probability equations of ACD are written as:

$$U_{ik}^a=V_{ik}^a+{\epsilon }_k^a={\alpha }_k^a+X_{ik}^a{\theta }_k+{\epsilon }_k^a$$

(2)

$$P_{ik}^a=\frac{\exp \left(V_{ik}^a\right)}{{{\displaystyle \sum }}_{j\in C_i^a}\exp \left(V_{ij}^a\right)}$$

(3)

Based on ESML, the utility $U_{ik}^p$ for PCD can be formulated in a similar way as $U_{ik}^a$. The utilities and choice probabilities of PCD are formulated as:

$$U_{ik}^p=V_{ik}^p+{\epsilon }_k^p={\alpha }_k^p-ln\left[\frac{Q\left(k\right)}{H\left(k\right)}\right]+X_{ik}^p{\mathsf{\delta }}_k+{\epsilon }_k^p$$

(4)

$$P_{ik}^p=\frac{\exp \left(V_{ik}^p\right)}{{{\displaystyle \sum }}_{j\in C_i^p}\exp \left(V_{ij}^p\right)}$$

(5)

In the process of data integration, there will be two cases with inconsistent specification in utility functions, where ACD and PCD are required to complement each other. One case is that the incomplete travel information of PCD causes some attributes to be absent. For example, the access/egress distance of rail passengers is known in survey data but unknown in smart card data. In the joint model, only ACD are used for estimating coefficients of access/egress variables. The other case is, there may exist sampling bias (e.g., self-selection bias, endogenous sampling bias, etc.) in ACD, which may cause unexpected sign of some estimators. The PCD that sometimes cover almost the entire population can avoid the sampling bias. For those coefficients, we only use PCD in model estimation. This complementary method is feasible for variables that are available in either or both of ACD and PCD. Given the low correlation between access/egress distances and other LOS attributes in PCD, the omission of access/egress distances from the utility function is unlikely to cause substantial change in impact estimates for other LOS attributes. However, due to the inconsistent specification in ACD and PCD models, the alternative-specific constants are not expected to be equal and; therefore, specified as two unequal parameters in the maximum likelihood estimation procedure. Since the involvement of PCD, its alternative-specific constant tends to be highly biased, the alternative-specific constant in the ACD model is considered as the alternative-specific constant in the final joint model.

In the cases mentioned above, the attributes absent from the utility will be absorbed into the random component, which leads to unequal standard deviation of ${\epsilon }_k^a$ and ${\epsilon }_k^p$. A scaling factor $m_k$ is introduced to the utility formula of PCD to adjust the distributional deviation, by referring to the joint RP-SP methods [27]. The adjusted utilities and choice probabilities of PCD are written as:

$$U_{ik}^{p^{\prime }}=m_k{V}_{ik}^p+{\epsilon }_k^p$$

(6)

$$P_{ik}^{p^{\prime }}=\frac{\exp \left(m_k{V}_{ik}^p\right)}{{{\displaystyle \sum }}_{j\in C_i^p}\exp \left(m_j{V}_{ij}^p\right)}$$

(7)

In the joint model, the parameter vector $\theta$ is estimated by maximizing the joint log-likelihood function based on equations (3) and (7). The log-likelihood function with respect to the parameter vector $\theta$ for the joint model takes the following form:

$$LL\left(\theta \right)={\displaystyle \sum }_{i=1}^{N_a}\left\{{\displaystyle \sum }_{k\in C_i^a}{y}_{ik}^a ln\left[\frac{\exp \left(V_{ik}^a\right)}{{{\displaystyle \sum }}_{j\in C_i^a}\exp \left(V_{ij}^a\right)}\right]\right\}+{\displaystyle \sum }_{i=1}^{N_p}\left\{{\displaystyle \sum }_{k\in C_i^p}{y}_{ik}^p ln\left[\frac{\exp \left(m_k{V}_{ik}^p\right)}{{{\displaystyle \sum }}_{j\in C_i^p}\exp m_j\left(V_{ij}^p\right)}\right]\right\}$$

(8)

where N_a and N_p represent the sample size of ACD and PCD, respectively.

It should be noted that this modeling framework does not take account of the choice set restriction issue. It becomes an issue because of the lacking personal attributes in the PCD sample. For example, in smart card data, auto ownership is unknown for each user. When smart card data are used in a choice model, we can only assume that all passengers have an opportunity to use auto mode. It is not a serious issue in developed countries with a high level of private auto ownership or developing countries with sophisticated automobile services, such as e-hailing, car-sharing and ride-sharing services, where most commuters do have opportunities to use auto. However, the modeling framework cannot be applied in the areas with obvious restrictions on auto mode choice since it may result in bias in model estimators.

3. Simulation Experiment

In this section, the Monte Carlo simulation technique was applied to test the model performance. This technique has been widely used in modeling methodological research [4,13,28,29]. Our implementation of simulation methods to estimate a multinomial logit (MNL) model is similar to that in [29].

In the Monte Carlo simulation, two million commuters were simulated to make multinomial mode choices among car, rail and bus. Their random utilities were written as below:

$$U_{car}=-0.5x_1-0.1x_2+{\epsilon }_1$$

(9)

$$U_{rail}=-0.5-0.3x_3-0.4x_4+0.8x_5+{\epsilon }_2$$

(10)

$$U_{bus}=-1.5-0.5x_6-0.6x_7-0.4x_8+{\epsilon }_3$$

(11)

where the explanatory variables $X_k$ were randomly generated and followed a uniform distribution between 0 and 10. ${\epsilon }_k$ was the random component following the standard Gumbel distribution.

A total of 45% of commuters had access to rail stations, the rail accessibility was randomly assigned. All the individuals could commute by car and bus. An ACD sample was randomly drawn from the commuter population at a rate of 0.05% so that the sample size was around 1000. For mimicking the structure of PCD used in the empirical study, the simulated PCD consisted of three choice-based subsamples: a private car in-vehicle navigation data sample was randomly drawn from the population using car mode at a rate of 1%, smart card data was a full set of rail records, and bus data came from the ACD since passively collected bus data are not accessible by far. One of explanatory variables in rail utility is intentionally discarded in PCD to mimic the situation with absent attribute(s).

Estimated models are respectively called ACD model, PCD model, and joint model as per the source of data used for model estimation.

Table 1. Estimation results from 100 simulation experiments.

Mode	True Value (Variable Name)	ACD Model			PCD Model			Joint Model			Precision Improvement 2
		Estimate	Estimate S.E.	Sample S.E.	Estimate	Estimate S.E.	Sample S.E.	Estimate	Estimate S.E.	Sample S.E.	Estimate S.E.	Sample S.E.
Car	−0.5 (x1)	−0.50	0.06	0.06	−0.42	0.01	0.01	−0.50	0.06	0.06	1.06	1.03
	−0.1 (x2)	−0.11	0.05	0.05	−0.08	0.01	0.01	−0.10	0.02	0.01	3.03	3.17
Rail	−0.5 (ACD constant)	−0.51	0.67	0.61	—	—	—	−0.42	0.39	0.45	1.72	1.36
	−0.5 (PCD constant)	—	—	—	7.16	0.10	0.08	−2.06	0.11	0.08	—	—
	−0.3 (x3)	−0.31	0.07	0.06	−0.25	0.01	0.01	−0.30	0.04	0.03	1.74	1.85
	−0.4 (x4)	−0.42	0.08	0.07	—	—	—	−0.41	0.07	0.07	1.05	1.01
	0.8 (x5)	0.82	0.12	0.09	0.66	0.01	0.01	0.81	0.10	0.09	1.16	1.04
Bus	−1.5 (ACD constant)	−1.41	0.63	0.65	—	—	—	−1.41	0.66	0.63	0.95	1.03
	−1.5 (PCD constant)	—	—	—	−6.99	0.43	0.41	−0.96	0.44	0.40	—	—
	−0.5 (x6)	−0.54	0.10	0.10	−0.48	0.08	0.08	−0.52	0.10	0.08	1.00	1.19
	−0.6 (x7)	−0.64	0.12	0.11	−0.58	0.09	0.09	−0.61	0.11	0.09	1.11	1.16
	−0.4 (x8)	−0.41	0.08	0.09	−0.39	0.08	0.08	−0.41	0.08	0.08	1.01	1.25
	m1							0.85	0.09	0.10
	m2							0.83	0.10	0.09
	m3							0.95	0.08	0.16

Notes: ¹ The dash “—” refers to missing data. ² The “Precision Improvement” refers to the value of S.E. (Standard Error) of the ACD model divided by S.E. of the Joint model.

displays the average values of coefficient estimators from 100 repeated simulations and estimations. If comparing the estimates of the ACD model and the joint model, one can find that all the coefficient estimators of the joint model are much closer to their true values. It benefits from great reduction in both estimated and sample standard errors of estimators. Estimated standard errors are the average of standard errors computed from the Hessian matrix at convergence, while sample standard errors are standard deviations of estimators from 100 simulation experiments. The absent variable in the PCD model is also complemented by ACD in the joint model but its precision is almost not improved because no additional information is added from PCD. All the adjustment factors “m” were found less than 1.0 and; therefore, scale-up coefficients in the PCD model. In summary, simulation experiments show that the proposed model can greatly improve the precision of model estimates by integrating ACD and PCD. After the model precision is improved, there will be a better opportunity to obtain an estimator being closer to its true value, as demonstrated.

4. Data for Empirical Study

In this section, the data used for empirical study and model development will be discussed in details. In order to meet the model application requirement mentioned above, the choice data of auto mode which contains all types of automobile services like private cars, taxis, e-hailing, etc., was applied in the choice set. With the popularity of emerging mobility services, such as e-hailing, car-sharing, and ride-sharing, coupled with the huge number of private cars and taxis, almost all the commuters will have opportunities to use auto in big cities of China like Shanghai. All the used data are available in the attached Supplementary Materials.

4.1. Web-Based Travel Survey

A web-based travel survey of Shanghai was conducted in May and June 2017. The sample was randomly selected and commute trip data were fed back through the internet. After extensive checking and data integrity screening, the final sample contained 1007 individuals’ commute characteristics. In the survey, the respondents were asked to report their commute habit by completing a series of choice questions. The survey questionnaire consisted of two parts. The first part of the questionnaire collected characteristics of commuting schedules of respondents, including current commute mode choices, travel modes of accessing and egressing public transit stations, commuting trip departure/arrival times, companions, and other errands undertaken during the trip. Intersections defined by two crossroads were collected from respondents to get information of their residential and work locations. In this way, we were not only able to extract reliable coordinates but also to protect the privacy of respondents. The other part collected commuters’ socioeconomic and demographic characteristics, including sex, age, education level, engaged industry, income, marital status, driving license held, residential type, and residence members, etc. 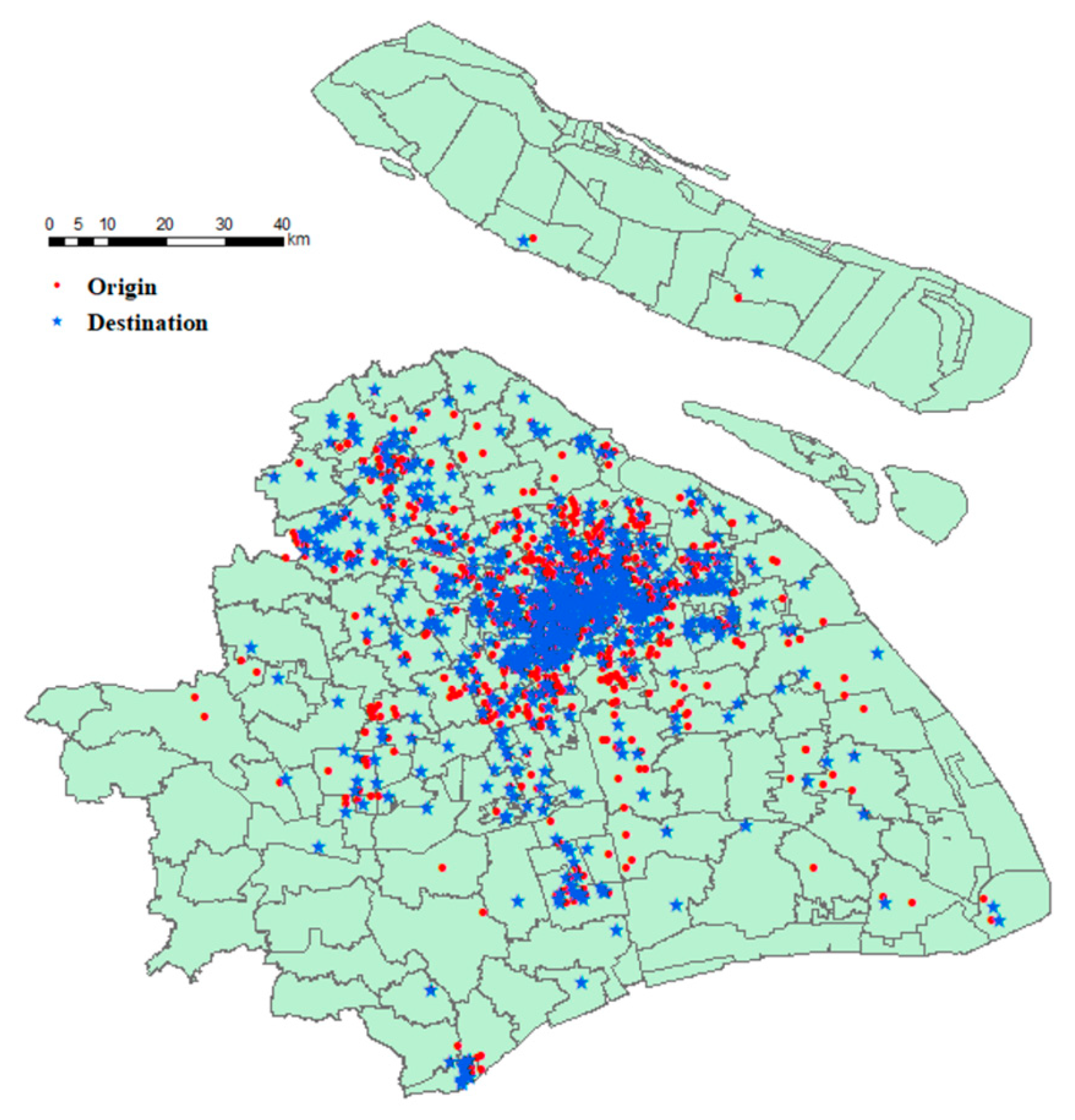Figure 1 shows spatial distributions of commuting trips’ origins/destinations (i.e., home/work locations). As shown, residential and work locations were most densely distributed in the city center and less so in the north and northwest but sparsely distributed in the south. These results were basically in line with the population distribution of the entire city. Most locations were within the metro service area in light of Figure 2.

The answers from the survey questionnaire provided the revealed preference (RP) data of mode choices. We selected the commute trips in the morning whose travel mode was auto (including car, taxi, and e-hailing, etc.), rail (walk-access), or bus. There were a total of 501 trips to form the ACD sample for model estimation. The relevant survey data included: (1) trip information, including home and work locations, commute trip beginning and ending times, commute mode, access/egress mode for rail or bus, etc.; (2) residential information, including type of residence, the number of dwelling members, etc.; and (3) personal information, including gender, age, occupation, education, annual income, driver license, etc.

4.2. Smart Card Data

The smart card data used in this paper is the full sample of rail card-swiping data of April 1, 2015. The original data contain 9,024,322 records. Attributes include card ID, timing, station name, mode, fare, and discount. The pre-process of original data had the following four steps: (1) Eliminating IDs whose number of card-swiping records is odd; (2) reorganizing records into OD format; (3) eliminating trips with unreasonable fare record; (4) combining trips where transfer to another line requires swiping off a station. After all these steps, 4,313,867 trips are obtained for 2,362,628 passengers.

According to the web-survey data, there are mainly four modes that people use to access/egress rail, namely walk, bike, bus and P+R (park and ride). Bus and P+R access/egress modes in smart card data could be identified by time difference of records. By setting threshold values, 23.82% of trips were judged as bus access/egress, and 0.06% trips use P+R. Since the travel distance of walk or bike was less than 3 km in most cases, it was easy to roughly identify the area of origin and destination, which allowed for using other skims. However, the exact origin/destination location could not be identified, access/egress distance was therefore not specified in the PCD model.

In order to identify commute trips from smart card data, we counted card-swiping records on 21 working days in April 2015. The number of records was accumulated during peak hours by every ID. It was assumed that IDs appearing more than 10 times during morning peaks in that month were regular commuters. Finally, 920,787 rail commute trips were selected as a PCD sample for model estimation.

4.3. Car Navigation Data

Car records were collected from in-vehicle navigation systems of 9233 cars in Shanghai. The data were recorded from April 1 to April 30, 2016 and involved totally 89,777,985 GPS records with an interval of 15 s. Each car was identified by a unique ID number in the dataset. Information of car owners includes income level, car make and model, and car emission, etc. It can be realized that all the drivers are workers as per their income level. Attributes of GPS records include car ID, longitude, latitude, time, and speed.

In order to obtain trips from GPS trajectories, it is necessary to identify activity locations from consecutive GPS records. With the in-vehicle GPS identification method by Stopher, Bullock and Jiang [14], activity locations can be judged by time interval and displacement distance. The detailed judgement criteria are given as follows: (1) Time difference with the last GPS record is greater than 300 s; (2) longitude and latitude differences compared with those in the last GPS record are both less than 0.0027; (3) the current speed record is zero. After all these identification processes, totally 600,404 valid activity locations are determined and associated with 600,404 valid trips. The average trip frequency of the 9233 car owners is 2.17 times per day while the average trip length is 33.07 minutes. These statistics are close to those from the Shanghai fifth comprehensive transportation survey.

Since our study is focused on commute mode choice, commute trips are required to be selected. Trip purpose can be identified by classifying activity locations into home, workplace, and other places. We use the cumulative frequency of activity zones within one month as a basis for judgement, referring to the method to identify job and home locations in mobile phone data [30,31]. Activity locations within that month are matched with the 5432 residential zones in Shanghai, by ArcGIS, as activity zones. Cumulative frequency of activity zones is counted for each car ID. According to the lifestyle and travel habits of residents in Shanghai, most trips start from home and end to home, the zone where activities mostly take place is; therefore, deemed as home zone. Since private cars are required to stop in parking spots, and people often choose to park their cars near home or workplace, the work zone should also frequently appear in the monthly records. Additionally, it is unlikely to live and work in the same residential zone since zones are divided into small parts in the urban area of Shanghai. Therefore, the zone with the largest cumulative frequency is identified as home zone, and the zone with the second largest frequency as work zone, other zones as other activity places.

4.4. Zone-to-Zone Network Skims

The transportation networks of Shanghai (as Figure 2) were assembled and integrated in TransCAD based on the GIS data of roads, metro lines and stops, bus lines and stops, and residents’ committees. Based on floating car data, five travel time attributes were added to each link of the road network, corresponding to the travel time before morning peak (before 7:00), in morning peak (7:00 to 9:00), flat period (between 9:00 and 17:00), evening peak (17:00 to 19:00), and after evening peak (after 19:00). Similarly, with different service frequencies in a day, rail, and bus headways of every route were divided into three periods, namely morning peak (7:00 to 9:00), evening peak (17:00 to 19:00), and flat period (other time). Rail fare matrix was also added into the network while bus fare is deemed as flat fare of 2 RMB Yuan, which is the case for mot bus lines in Shanghai.

The 5432 residents’ committees are considered as zones in the system. The zone-to-zone network skims were generated by five time-of-day periods, including in-vehicle travel time of auto, rail, and bus, initial waiting time of rail and bus, station access/egress walk time, and distance of rail and bus, etc. The LOS data were merged into ACD and PCD as per zone ID and trip beginning time period. Due to the absence of origin/destination location information in rail card-swiping data, attributes of rail access/egress walking distance are not available in PCD.

4.5. Sample Description

As stated, there are two types of data used for model development. One is ACD from the web-based travel survey mentioned above. The other is PCD consisting of smart card data and car navigation data.

Rail accessibility (1 refers to the condition that traveler can use rail to travel from origin to destination without transferring to other vehicles, otherwise 0) was specified to identify the choice set of each individual, which was determined by the walking distance between centroid of origin/destination zone and rail station in TransCAD.

There were a total of 501 commute trips in ACD, as well as 920,787 rail commute trips and 2754 car commute trips in PCD. The descriptive statistics of major socio-demographic attributes of the 501 respondents in the travel survey are shown in

Table 2. Descriptive statistics of socio-demographic attributes in ACD (N = 501).

Attribute Characteristics	Type	Percentage	Attribute	Type	Percentage
Age (Years)	<20	0.4%	Gender	Female	57.1%
	20–30	20.8%		Male	42.9%
	31–40	57.2%	Marriage	Married	80.2%
	41–50	18.4%		Unmarried	19.8%
	51–60	2.6%	Driving	yes	78.2%
	>60	0.4%	License	no	21.8%
Income (Yuan/Month)	<2 k	0.8%	Origin inside inner ring road	yes	24.2%
	2 k–4.5 k	7.6%		no	75.8%
	4.5 k–6 k	16.8%	Education	Junior school	0.2%
	6 k–8 k	16.0%		High school	2.4%
	8 k–10 k	20.6%		Technical school	2.0%
	10 k–15 k	21.0%		Associate degree	19.0%
	15 k–20 k	8.8%		Bachelor degree	62.1%
	20 k–30 k	6.0%		Master degree	13.0%
	>30 k	2.6%		Doctoral degree	1.4%

Note: 1 USD = 6.69 Yuan.

. Females account for 57.1%, which is slightly more than males. The average age was 35.7 years old, while the majority are young and middle-aged people among 20 to 50. Their monthly income mainly ranges from 4500 to 10,000 RMB Yuan. Most of them are highly educated and/or married.

Table 3. Descriptive statistics of Level-of-service attributes.

	Attribute	ACD			PCD
		N	Mean	S.E.	N	Mean	S.E.
Auto	In-vehicle time (min)	255	25.12	12.77	2754	24.01	14.18
Rail	In-vehicle time (min)	144	23.58	12.52	920,787	25.29	13.44
	Initial waiting time (min)	144	2.22	0.45	920,787	2.20	0.40
	Transfer waiting time (min)	144	1.82	1.49	920,787	1.54	1.50
	Access distance (km)	144	0.90	0.60	—	—	—
	Egress distance (km)	144	0.63	0.46	—	—	—
Bus	In-vehicle time (min)	102	35.89	26.06	—	—	—
	Access distance (km)	102	0.42	0.29	—	—	—
	Egress distance (km)	102	0.48	0.37	—	—	—
	Number of transfers	102	0.55	0.68	—	—	—

Note: The dash “—” refers to missing data.

shows the descriptive statistics of all LOS attributes involved in the model in both ACD and PCD. ACD provide a commute mode share of 50.9%, 28.7%, and 20.4% for auto, rail, and bus, respectively. The average in-vehicle times of auto and rail are around 25 min. Slight deviations in values between ACD and PCD are caused by different sampling procedures. The average in-vehicle time of bus commuters is about 35.9 min, which is longer than that of auto and rail.

5. Empirical Estimation Results

Model estimation results for the ACD model, the PCD model, and the joint model are shown in

Table 4. Commute mode choice model estimation results.

Mode	Variable	ACD Model			PCD Model			Joint Model			Precision Improvement 3
		Estimates	S.E.	t-statistic	Estimates	S.E.	t-statistic	Estimates	S.E.	t-statistic
Auto	In-vehicle time (min)	−0.106	0.019	−5.571	−0.124	0.004	−33.856	−0.109	0.016	−6.923	1.209
	Living inside inner ring road	−1.376	0.322	−4.279	−1.531	0.084	−18.213	−1.348	0.201	−6.708	1.600
	Age (years)	0.066	0.018	3.639	—	—	—	0.065	0.018	3.658	1.011
	Income dummy (>8000 RMB/month)	0.989	0.324	3.048	—	—	—	0.980	0.322	3.042	1.007
	Number of companions	0.415	0.154	2.698	—	—	—	0.410	0.154	2.658	0.999
	Driving license	2.994	0.436	6.869	—	—	—	2.977	0.436	6.825	1.000
	The commuter engages in IT industry	−1.034	0.385	−2.690	—	—	—	−1.017	0.379	−2.680	1.014
Rail	Constant (ACD)	3.702	1.036	—	—	—	—	3.630	1.024	—	—
	Constant (PCD)	—	—	—	5.130	0.121	—	−1.230	0.120	—	—
	In-vehicle time (min)	−0.031	0.018	−1.726	−0.069	0.003	−24.339	−0.038	0.012	−3.187	1.500
	Initial waiting time (min)	—	—	—	−0.348	0.041	−8.535	−0.197	0.066	−2.994	NA
	Transfer waiting time (min)	−0.142	0.102	−1.389	−0.136	0.018	−7.713	−0.076	0.026	−2.973	3.988
	Access distance (km)	−0.860	0.204	−4.225	—	—	—	−0.877	0.196	−4.481	1.039
	Egress distance (km)	−1.317	0.272	−4.843	—	—	—	−1.291	0.269	−4.803	1.012
	Marriage	1.567	0.477	3.286	—	—	—	1.579	0.478	3.304	0.998
	The commuter engages in the retailing industry	0.926	0.320	2.892	—	—	—	0.934	0.318	2.940	1.008
Bus	Constant (ACD)	4.612	0.883	—	—	—	—	4.761	0.858	—	—
	Constant (PCD)	—	—	—	−3.014	0.272	—	−0.722	0.261	—	—
	In-vehicle time (min)	−0.027	0.009	−3.190	−0.037	0.005	−7.190	−0.030	0.005	−5.471	1.574
	Access distance (km)	−1.136	0.451	−2.516	−1.702	0.355	−4.801	−1.349	0.284	−4.741	1.587
	Egress distance (km)	−0.610	0.362	−1.684	−1.134	0.303	−3.747	−0.842	0.222	−3.798	1.633
	Number of transfers	−0.957	0.232	−4.130	−0.956	0.194	−4.939	−0.850	0.163	−5.230	1.426
	Income dummy (>8000 RMB/month)	−0.664	0.322	−2.063	—	—	—	−0.688	0.320	−2.152	1.007
	The commuter engages in retailing industry	0.968	0.480	2.015	—	—	—	1.000	0.474	2.111	1.014
	m1 (auto)							1.137	0.166	6.858
	m2 (rail)							1.813	0.567	3.195
	m3 (bus)							1.200	0.183	6.544
Summary statistic
	Sample size	501			92,3643			924,144
	LL(0)	−508.64			−1,014,178.20			−1,014,686.80
	LL(c)	−478.52			−11,185.92			−11,664.43
	LL($\widehat{\beta }$)	−301.47			−10,748.55			−11,055.64
	${\rho }_0^2$	0.407			0.989			0.989
	${\rho }_c^2$	0.370			0.039			0.052

Notes: ¹ We do not report any t-statistics for constant terms because constant terms always need to be specified to adjust market shares. ² The dash “—” refers to missing data. ³ The “Precision Improvement” refers to the value of S.E. of ACD model divided by S.E. of joint model. ⁴ 1 USD = 6.69 RMB Yuan

. The alternative-specific constants in the final joint model are very close to those in the ACD model and reflect market shares in ACD, as expected. In the ACD model, the variable of rail initial waiting time was eliminated due to its unexpected sign and statistical insignificance of the coefficient. Insignificant coefficients also existed for some other variables, such as rail transfer waiting time and bus egress distance. This problem in the ACD model was mainly caused by the small sample size and/or correlation among explanatory variables. Estimation results of the PCD model were all of expected sign of coefficients at a high significance level thanks to the large sample size; however, attributes of rail walking access/egress distance and all socio-demographic attributes were lacking in the data. Thus, in the joint model, coefficient of rail initial waiting time was estimated by PCD, and coefficients of lacked attributes in PCD were estimated by ACD. The large sample size of PCD was utilized to improve the significance level and precision of model coefficients, while ACD filled the gap caused by incomplete information in PCD.

With the joint model, a more comprehensive variable set is obtained by integrating ACD and PCD, and all the parameters have expected signs and appear highly significant. Relative to those in the ACD model, the standard deviations of all LOS variables’ estimators in the joint model greatly decreased. The standard deviation of the coefficient for rail transfer waiting time even decreased by nearly four times. With ACD only, the sample size needs to be expanded by more than 15 times to reach the same level of precision in this estimator. The standard deviation for the number of companions and marriage slightly increases, mainly because these socio-demographic variables only come from ACD and do not benefit from added PCD. Variables which are not significant in the ACD model, such as bus walking access/egress distance, appear highly significant after the integration with PCD in the joint model. All these improvements in model precision and variable set show the capability of the joint model in releasing the sample size restriction in the ACD model.

In terms of coefficient magnitude difference among models, the key differences occur in rail utility functions. It can be seen that the coefficient for rail in-vehicle time in the ACD model is −0.031 while that in the PCD model is -0.069. After the scaling factor adjustment, the coefficient takes a value of -0.038 in the joint model, which is fairly close to that in the ACD model with consideration of their standard errors. It implies that ACD and PCD provide fairly consistent coefficient estimator for the rail in-vehicle time. Transfer waiting time takes a coefficient of -0.142 in the ACD model, which is more than four and a half times of that for in-vehicle time and is somewhat higher than expectation. However, in the PCD model, the coefficient is -0.136, which is almost two times of that for in-vehicle time and looks more reasonable. In the joint model, one may see that the ratio between these two coefficients have been adjusted to 2. It implies that the ACD might suffer from the self-selection problem or low precision problem due to the small sample size. However, the bias can be adjusted by the involvement of PCD in the joint model. The coefficient of initial waiting time did not appear significant and took a counterintuitive positive coefficient in the ACD model, probably due to self-selection bias or small sample size. In the PCD and joint models, the coefficient takes a significantly negative value. The ratio between coefficients of initial waiting time and in-vehicle time is about 5.2 in the final model, which is very close to the ratio of 5.0 in the PCD model.

If comparing coefficients in three utilities of the joint model, one can easily identify the difference in commuters’ perceptions on travel times in auto, rail, and bus. The travel times in rail and bus seem alike for commuters since the values of coefficients are almost equal. People show more patience to in-vehicle time of transit modes (rail and bus) than that of auto since the coefficient of auto is approximately triple that of rail and bus. Despite crowdedness in carriages, public transit travel offers people more flexible time for relaxation, recreation, or study. While taking a rail or bus in Shanghai, most passengers are staring at their digital screens and/or wearing headphones nowadays. On the other side, since driving a car requires all attention, coupled with road congestions in peak hours, auto users will easily feel bored and anxious on commute way.

In the utility function of rail and bus, some LOS attributes significantly affect the choice probabilities. Rail choice probability decreases with the increase of rail initial waiting time and transfer waiting time, as indicated by negative coefficients. Similarly, bus choice probability reduces as the number of bus transfers increases. Rail headway, which positively affects waiting time, is a significant factor to commuters’ rail choices. Additionally, rail/bus network density influences rail/bus choice probabilities, because accessibility to rail/bus stations is another significant contributor and long access/egress distance to/from stations discourages people to choose public transit.

Explanatory variables other than LOS attributes will be discussed based on the final joint model. People living inside the inner ring road of Shanghai appear to take public transit for their commute more frequently, as indicated by the negative coefficient in the auto utility function. Road congestion and limited availability of parking spots may be the main factors that discourage people from using auto in the busy city center. Meanwhile, the high density of transit stops and lines in central Shanghai, coupled by the low cost, encourages commuters to take rail and/or bus instead.

The socio-demographic attributes also have significant impact on the choice probabilities. The positive coefficient of age in auto utility shows that elder commuters are more likely to use auto for commute. It is undoubted that having a driving license increases auto choice probability since car-driving trips account for the majority of auto sample, as indicated by the positive coefficient in auto utility. The coefficient of marriage in rail utility suggest that married workers are more likely to take rail, possibly because they undertake heavy family burdens and become sensitive to the high price. People with a high monthly income tend to use auto more frequently, but were less likely to choose bus, as shown by a positive coefficient in auto utility but a negative one in bus utility. When there are other people accompanied, commuters tend to travel by auto modes, as shown by the positive coefficient in auto utility. In many families, parents send children to school on the way to work, and couples go to work together if their workplaces are close to each other. In these cases, auto is much more convenient and flexible. It is also found that people working in different industries show different tendency in commute modes. Travelers who engages in IT industry are less likely to choose auto possibly because most IT companies are located in areas with good access to rail. Travelers who engage in the retailing industry show their preference on rail and bus, as indicated by positive coefficients in respective utilities.

6. Conclusions and Discussions

This paper develops a commute mode choice model by integrating ACD and PCD. The model is developed based on the theory of choice-based sampling for discrete choice model, and coefficients are adjusted by a scaling factor in the utility function of PCD. The model estimation results in both simulation experiments and an empirical study show great improvement in the precision of coefficient estimators. A significant advancement from the proposed joint model is that a more complete set of variables can be specified into utility functions. The utility functions in an ACD model often lack some important LOS variables because of unexpected sign or insignificance of coefficients, which may be caused by the limited sample size or sampling bias from the survey. On the other hand, the utility functions of a PCD model also lack some socio-demographic and LOS attributes, which are not observed and cannot be specified into the model. However, the proposed joint model can overcome these problems by integrating advantages from both ACD and PCD.

Nevertheless, it is realized that ACD plus PCD is not a panacea for mode choice model development through this study. In the exploratory process, rail fare was found to take an unexpected sign in both PCD and joint models and; therefore, was excluded from the final model. The phenomena indicate that endogeneity issues might exist in both small sample and big data. Thus, stated preference (SP) survey data collected under designed and hypothetical scenarios are still necessary to estimate the coefficient of fare or willingness-to-pay for alternative travel modes in some occasions. It should be stressed again that the proposed modeling framework is not applicable to the area with serious mode restriction on auto mode, since auto access information is unavailable from transit smart-card data.

In future studies, additional attempts will be made in the following two respects. Firstly, other PCD sources may be added, such as bus swiping-card data, to further improve precision of coefficients in bus utility function. Secondly, only commute trips are considered in this paper, because commute trips can be easily identified in PCD. There is a challenge to identify other trip purposes in PCD. If this challenge can be overcome, the proposed modeling approach can be extended to model mode choices for other trip purposes as well.