An Enhanced Estimation of Distribution Algorithm for Energy-Efficient Job-Shop Scheduling Problems with Transportation Constraints
Abstract
:1. Introduction
2. Problem Description and Method
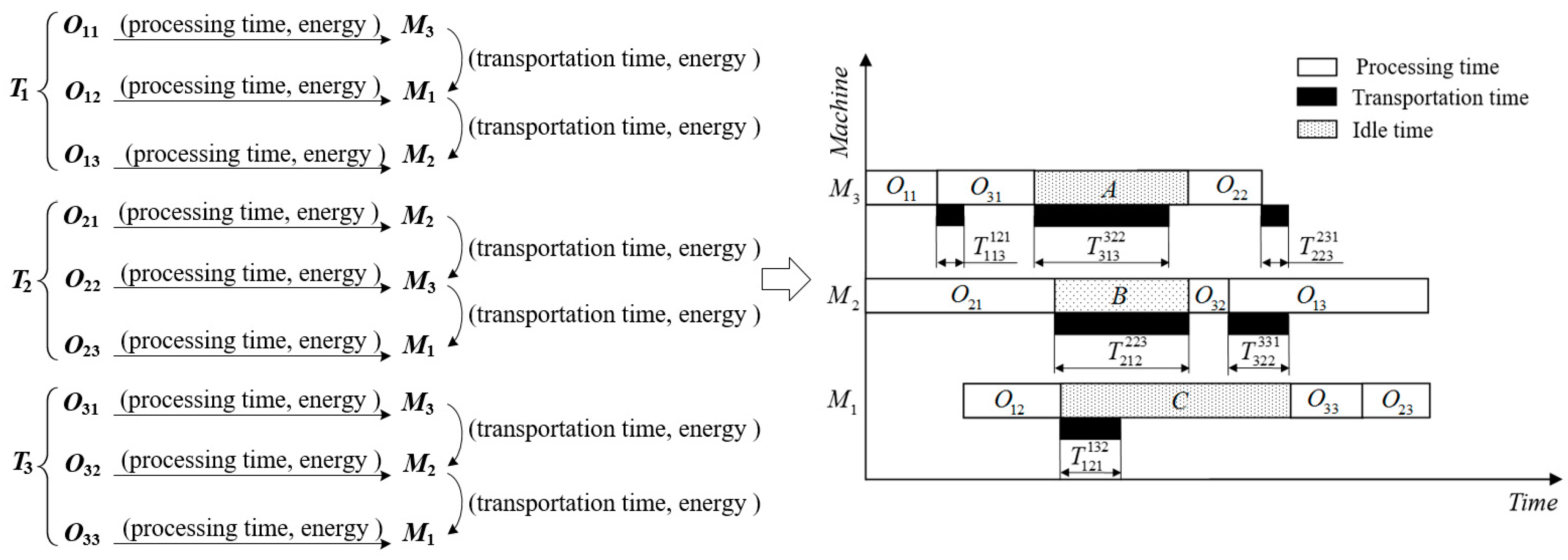
2.1. Problem Description
- (1)
- Each task is available at time zero.
- (2)
- Each machine is available at time zero.
- (3)
- The precedence relationships between operations for each task cannot be changed.
- (4)
- Each machine can only process an operation of one task at a time.
- (5)
- Once an operation begins, the operation cannot be interrupted until it is completed.
- (6)
- There are enough AGVs responsible to move each task.
- (7)
- Handling times of all tasks between machines and AGVs are ignored.
2.2. Enhanced Estimation of Distribution Algorithm (EEDA)
2.2.1. Representation
2.2.2. Estimation of Distribution Algorithm
| Algorithm 1. Estimation of distribution algorithm (EDA) |
| Begin |
| Randomly generate the initial population X(0) |
| Set t = 0 |
| While (the termination condition is not met) do |
| Select a set of candidate individuals (solutions) D(t) to construct the current population X(t) according to the fitness values |
| Construct the probability distribution model of the selected set D(t) |
| Generate a set of new offspring individuals N(t) according to the probabilistic model |
| Create a new population X(t + 1) by replacing some individuals of X(t) by N(t) according to the updating mechanism |
| T = t + 1 |
| End while |
| Report best results |
| End |
2.2.3. Simulated Annealing Algorithm
| Algorithm 2. Simulated annealing algorithm (SAA) |
| Begin |
| Generate the initial schedule Si |
| Initialize the start temperature Ts, the end temperature Te |
| Set T = Ts |
| While (T > Te) do |
| Generate the temporary schedule Sj according to the neighborhood structure |
| Evaluate the improvement of performance criterion function Δ = f(Sj) − f(Si) |
| If (Δ ≤ 0) then |
| Si = Sj |
| Else if (random(0,1) < e−Δ/T) then |
| Si = Sj |
| End if |
| Update new annealing rate function |
| End while |
| Report best results |
| End |
2.2.4. The Procedure of the EEDA
| Algorithm 3. Enhanced Estimation of distribution algorithm (EEDA) |
| Begin |
| Randomly generate the initial population X(0) |
| Initialize the learning rate α, the Hill coefficient n, the start temperature Ts, the end temperature Te |
| Set t = 0, T = Ts |
| While (the termination condition is not met) do |
| Evaluate the fitness value of each individual in X(0) |
| Select a set of candidate individuals (solutions) D(t) to construct the current population X(t) |
| Construct the probability distribution model of the selected set D(t) |
| If (rand ≤ λ) then |
| Generate a set of new offspring individuals N(t) according to the probabilistic model |
| Create a new population X(t + 1) by replacing some individuals of X(t) by N(t) according to the updating mechanism |
| Else |
| While (T >Te) do |
| Generate the temporary individuals N(t) according to the neighborhood structure |
| Evaluate the improvement of the fitness value |
| Update annealing rate function |
| End while |
| End if |
| T = t + 1 |
| End while |
| Report best results |
| End |
3. Model of Energy-Efficient Job-Shop Scheduling Problem (EJSP) with Transportation Constraints
3.1. Notations
| i, i− | Index of tasks |
| j, j− | Index of operations |
| k, w | Index of machines |
| q | Index of position |
| n | Number of tasks |
| m | Number of machines |
| T | Set of tasks, T = {T1, T2, …, Tn} |
| M | Set of machines, M = {M1, M2, …, Mm} |
| Oij | jth operation of task Ti |
| Ni | Number of operations for task Ti |
| Qk | Number of operations processed on machine Mk |
| Ci | Completion time of task Ti |
| Cmax | Completion time of the last task |
| Bkq | Starting time of the operation allocated to the qth position on machine Mk |
| Sijk | Starting time of operation Oij on machine Mk |
| Cijk | Completion time of operation Oij on machine Mk |
| Ci−j−k | Completion time of the preceding operation of operation Oij on machine Mk |
| Tijk | Processing time of operation Oij on machine Mk |
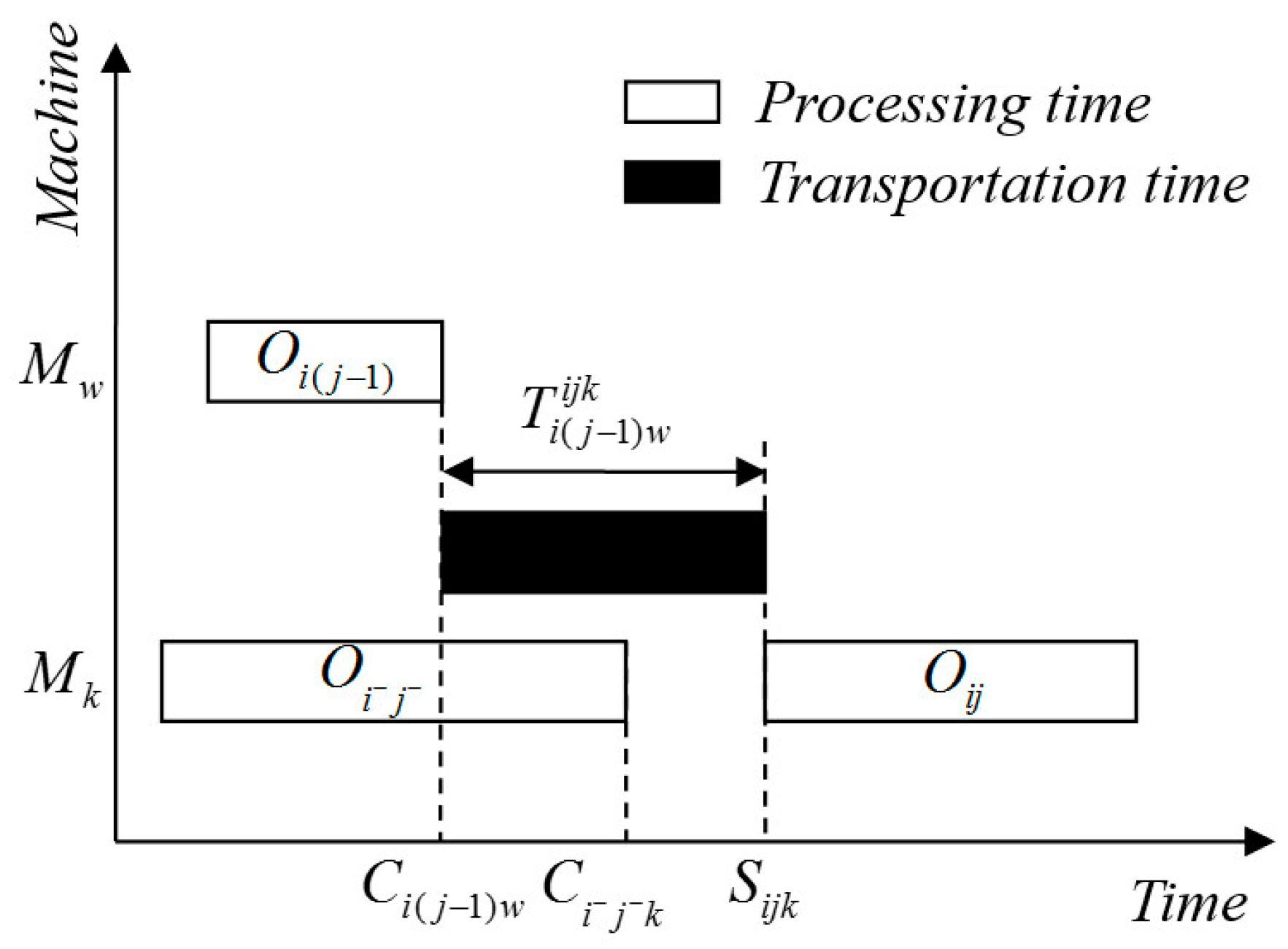
| Transportation time needed to move from machine Mw to machine Mk for two successive operations Oi(j−1) and Oij of task Ti | |
| Pijk | Processing power of operation Oij on machine Mk |
| Pk | Unload power of machine Mk |
| P0 | Transportation power of automatic guided vehicle |
| E | Comprehensive energy consumption for a schedule |
| Ec | Energy consumption module for cutting process |
| Ei | Energy consumption module for idle running process |
| Et | Energy consumption module for transportation process |
| Ea | Energy consumption module for auxiliary process |
| e | Average energy requirement per unit time for auxiliary equipment |
| L | A big positive number |
| Yijkq | Sequencing binary variable that is set to 1 if operation Oij is to be processed in qth position on machine Mk, and 0 otherwise |
3.2. Energy Consumption Model
3.2.1. Energy Consumption Module for a Cutting Process (Ec)
3.2.2. Energy Consumption Module for an Idle Running Process (Ei)
3.2.3. Energy Consumption Module for an Auxiliary Process (Ea)
3.2.4. Energy Consumption Module for a Transportation Process (Et)
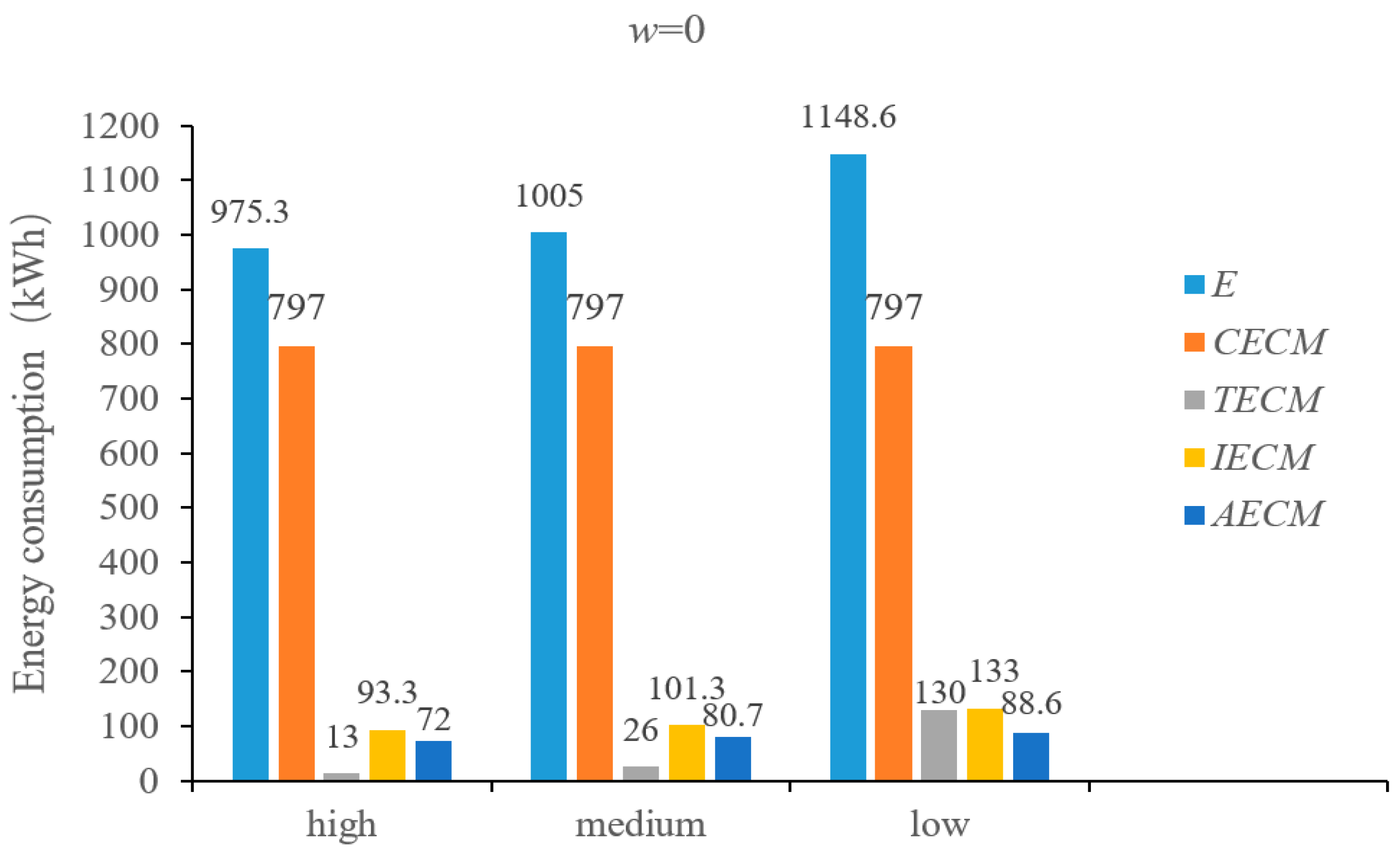
3.2.5. Comprehensive Energy Consumption (E)
3.3. Formulation of the EJSP Optimization Model
4. Experimental Results
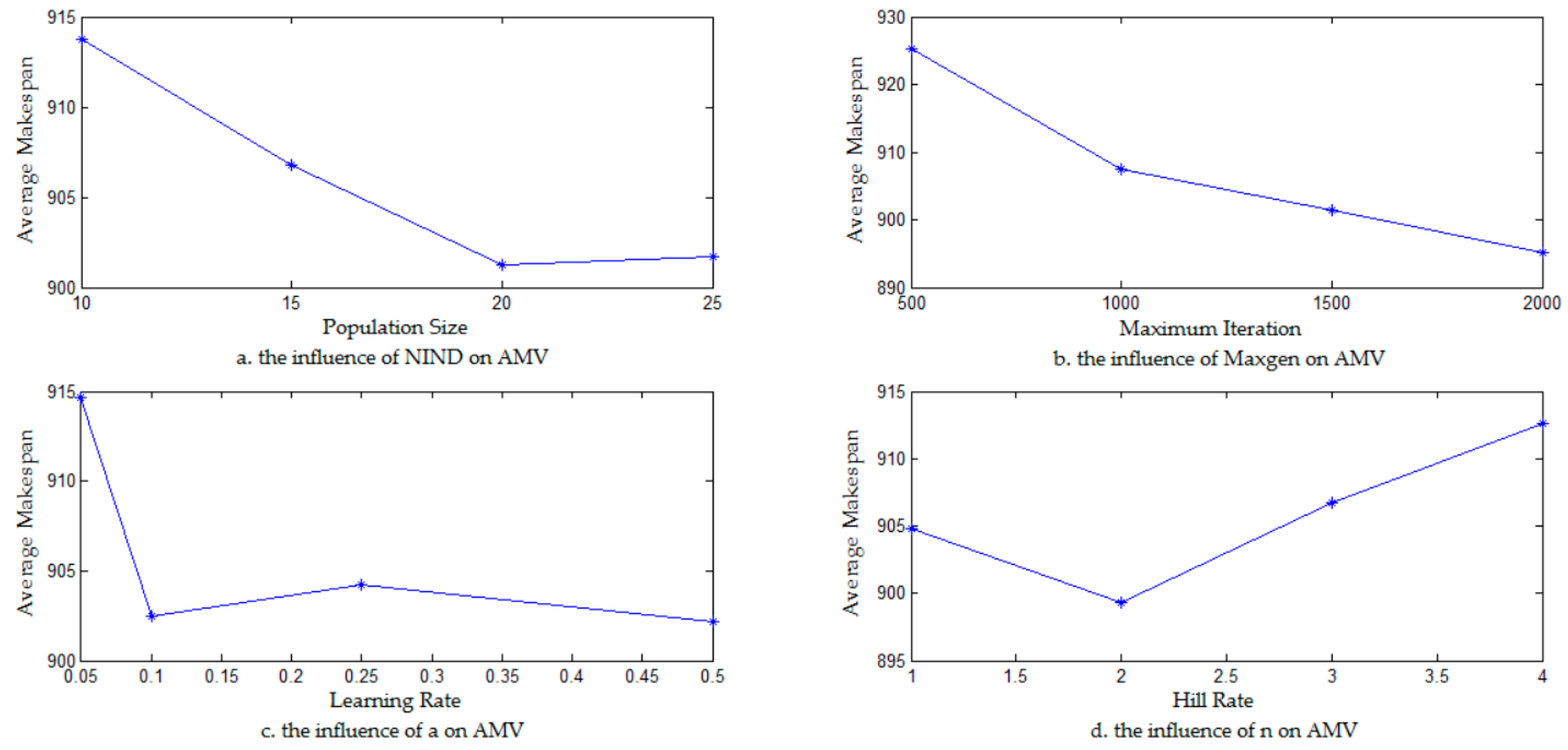
4.1. Sensitivity Analysis of the Algorithm Parameters
4.2. Performance Evaluation
4.3. Case Study
4.3.1. Energy-Efficient Scheduling Analysis
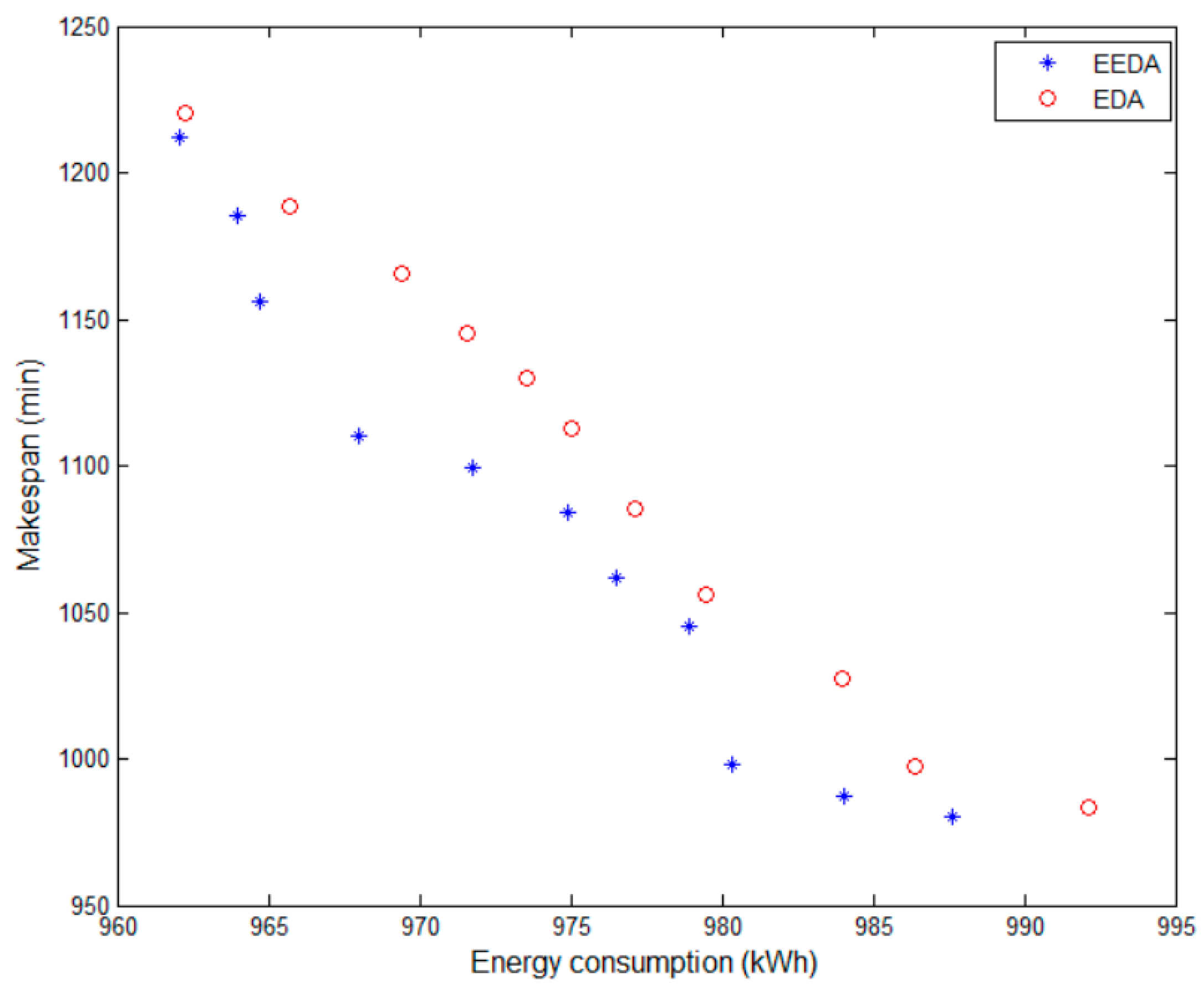
4.3.2. Computational Results on EEDA versus EDA
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, X.; Sun, Y. A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 2018, 172, 3249–3264. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.; Li, S.; Yang, J.; Salido, M.A.; Giret, A.; Zhu, H. An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products. Sustainability 2019, 11, 460. [Google Scholar] [CrossRef]
- Meng, Y.; Yang, Y.; Chung, H.; Lee, P.-H.; Shao, C. Enhancing Sustainability and Energy Efficiency in Smart Factories: A Review. Sustainability 2018, 10, 4779. [Google Scholar] [CrossRef]
- Gahm, C.; Denz, F.; Dirr, M.; Tuma, A. Energy-efficient scheduling in manufacturing companies: A review and research framework. Eur. J. Oper. Res. 2016, 248, 744–757. [Google Scholar] [CrossRef]
- Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37 Pt 1, 126–140. [Google Scholar] [CrossRef]
- Akbar, M.; Irohara, T. Scheduling for sustainable manufacturing: A review. J. Clean. Prod. 2018, 205, 866–883. [Google Scholar] [CrossRef]
- Che, A.; Wu, X.; Peng, J.; Yan, P. Energy-efficient bi-objective single-machine scheduling with power-down mechanism. Comp. Oper. Res. 2017, 85, 172–183. [Google Scholar] [CrossRef]
- Lee, S.; Do Chung, B.; Jeon, H.W.; Chang, J. A dynamic control approach for energy-efficient production scheduling on a single machine under time-varying electricity pricing. J. Clean. Prod. 2017, 165, 552–563. [Google Scholar] [CrossRef]
- Rubaiee, S.; Yildirim, M.B. An energy-aware multiobjective ant colony algorithm to minimize total completion time and energy cost on a single-machine preemptive scheduling. Comput. Ind. Eng. 2019, 127, 240–252. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, J.; Zhang, Y.; Yan, S. Optimization for energy-efficient flexible flow shop scheduling under time of use electricity tariffs. Procedia CIRP 2019, 80, 251–256. [Google Scholar] [CrossRef]
- Li, J.-Q.; Sang, H.-Y.; Han, Y.-Y.; Wang, C.-G.; Gao, K.-Z. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod. 2018, 181, 584–598. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Li, X.; Pan, Q.; Wang, Q. Energy-efficient permutation flow shop scheduling problem using a hybrid multi-objective backtracking search algorithm. J. Clean. Prod. 2017, 144, 228–238. [Google Scholar] [CrossRef]
- Fu, Y.; Tian, G.; Fathollahi-Fard, A.M.; Ahmadi, A.; Zhang, C. Stochastic multi-objective modelling and optimization of an energy-conscious distributed permutation flow shop scheduling problem with the total tardiness constraint. J. Clean. Prod. 2019, 226, 515–525. [Google Scholar] [CrossRef]
- Schulz, S.; Neufeld, J.S.; Buscher, U. A multi-objective iterated local search algorithm for comprehensive energy-aware hybrid flow shop scheduling. J. Clean. Prod. 2019, 224, 421–434. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, H.; Lohse, N.; Petrovic, S.; Gindy, N. An investigation into minimising total energy consumption and total weighted tardiness in job shops. J. Clean. Prod. 2014, 65, 87–96. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, H.; Lohse, N.; Petrovic, S. A multi-objective genetic algorithm for optimisation of energy consumption and shop floor production performance. Int. J. Prod. Econ. 2016, 179, 259–272. [Google Scholar] [CrossRef] [Green Version]
- May, G.K.; Stahl, B.; Taisch, M.; Prabhu, V. Multi-objective genetic algorithm for energy-efficient job shop scheduling. Int. J. Prod. Res. 2015, 53, 7071–7089. [Google Scholar] [CrossRef]
- Zhang, R.; Chiong, R. Solving the energy-efficient job shop scheduling problem: A multi-objective genetic algorithm with enhanced local search for minimizing the total weighted tardiness and total energy consumption. J. Clean. Prod. 2016, 112, 3361–3375. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Giret, A.; Barber, F. A genetic algorithm for energy-efficiency in job-shop scheduling. Int. J. Adv. Manuf. Tech. 2016, 85, 1303–1314. [Google Scholar] [CrossRef]
- Masmoudi, O.; Delorme, X.; Gianessi, P. Job-shop scheduling problem with energy consideration. Int. J. Prod. Econ. 2019, 216, 12–22. [Google Scholar] [CrossRef]
- Mokhtari, H.; Hasani, A. An energy-efficient multi-objective optimization for flexible job-shop scheduling problem. Comput. Chem. Eng. 2017, 104, 339–352. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, C.; Shao, X.; Ren, Y. MILP models for energy-aware flexible job shop scheduling problem. J. Clean. Prod. 2019, 210, 710–723. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot. Comput.-Int. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Lacomme, P.; Larabi, M.; Tchernev, N. Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Econ. 2013, 143, 24–34. [Google Scholar] [CrossRef]
- Nageswararao, M.; Narayanarao, K.; Ranagajanardhana, G. Simultaneous Scheduling of Machines and AGVs in Flexible Manufacturing System with Minimization of Tardiness Criterion. Procedia Mater. Sci. 2014, 5, 1492–1501. [Google Scholar] [CrossRef] [Green Version]
- Saidi-Mehrabad, M.; Dehnavi-Arani, S.; Evazabadian, F.; Mahmoodian, V. An Ant Colony Algorithm (ACA) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs. Comput. Ind. Eng. 2015, 86, 2–13. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Leung, S.Y.S.; Shi, L. A bi-level evolutionary optimization approach for integrated production and transportation scheduling. Appl. Soft. Comput. 2016, 42, 215–228. [Google Scholar] [CrossRef]
- Karimi, S.; Ardalan, Z.; Naderi, B.; Mohammadi, M. Scheduling flexible job-shops with transportation times: Mathematical models and a hybrid imperialist competitive algorithm. Appl. Math. Model. 2017, 41, 667–682. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, S.; Wang, L. Integrated green scheduling optimization of flexible job shop and crane transportation considering comprehensive energy consumption. J. Clean. Prod. 2019, 211, 765–786. [Google Scholar] [CrossRef]
- Tang, D.; Dai, M. Energy-efficient approach to minimizing the energy consumption in an extended job-shop scheduling problem. Chin. J. Mech. Eng. 2015, 28, 1048–1055. [Google Scholar] [CrossRef]
- Hao, X.; Lin, L.; Gen, M.; Ohno, K. Effective Estimation of Distribution Algorithm for Stochastic Job Shop Scheduling Problem. Procedia. Comput. Sci. 2013, 20, 102–107. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, S.; Xu, Y.; Zhou, G.; Liu, M. A bi-population based estimation of distribution algorithm for the flexible job-shop scheduling problem. Comput. Ind. Eng. 2012, 62, 917–926. [Google Scholar] [CrossRef]
- Jarboui, B.; Eddaly, M.; Siarry, P. An estimation of distribution algorithm for minimizing the total flowtime in permutation flowshop scheduling problems. Comput. Oper. Res. 2009, 36, 2638–2646. [Google Scholar] [CrossRef]
- Hauschild, M.; Pelikan, M. An introduction and survey of estimation of distribution algorithms. Swarm. Evol. Comput. 2011, 1, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Xie, J.; Liu, S. A method for predicting the energy consumption of the main driving system of a machine tool in a machining process. J. Clean. Prod. 2015, 105, 171–177. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A.; Li, W.D. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robot. Comput.-Int. Manuf. 2013, 29, 418–429. [Google Scholar] [CrossRef]
- Beasley, J.E. OR-Library: Distributing test problems by electronic mail. J. Oper. Res. Soc. 1990, 41, 1069–1072. [Google Scholar] [CrossRef]
- Fisher, H.; Thompson, G.L. Probabilistic Learning Combinations of Local Job-Shop Scheduling Rules; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Lawrence, S. Resource Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques (Supplement); Graduate School of Industrial Administration, Carnegie Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
- He, X.-J.; Zeng, J.-C.; Xue, S.-D.; Wang, L.-F. In an Efficient Estimation of Distribution Algorithm for Job Shop Scheduling Problem. In Swarm, Evolutionary, and Memetic Computing; Panigrahi, B.K., Das, S., Suganthan, P.N., Dash, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6466, pp. 656–663. [Google Scholar]
- Zhao, F.; Shao, Z.; Wang, J.; Zhang, C. A hybrid differential evolution and estimation of distribution algorithm based on neighbourhood search for job shop scheduling problems. Int. J. Prod. Res. 2016, 54, 1–22. [Google Scholar] [CrossRef]
- Laarhoven, P.J.M.V.; Aarts, E.H.L.; Lenstra, J.K. Job shop scheduling by simulated annealing. Oper. Res. 1992, 40, 113–125. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, D.Z. An effective hybrid optimization strategy for job-shop scheduling problems. Comput. Oper. Res. 2001, 28, 585–596. [Google Scholar] [CrossRef]
- Dorndorf, U.; Pesch, E. Evolution Based Learning in a Job Shop Scheduling Environment. Comput. Oper. Res. 1995, 22, 25–40. [Google Scholar] [CrossRef]
- Park, B.J.; Choi, H.R.; Kim, H.S. A hybrid genetic algorithm for the job shop scheduling problems. Comput. Ind. Eng. 2003, 45, 597–613. [Google Scholar] [CrossRef]


| Operations | (Machine Number, Processing Time/min) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tasks | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| T1 | (3,29) | (10,43) | (2,85) | (1,71) | (4,6) | (8,47) | (6,37) | (5,86) | (7,76) | (9,13) | |
| T2 | (2,78) | (7,28) | (3,51) | (6,81) | (5,22) | (10,2) | (1,16) | (4,46) | (9,69) | (8,85) | |
| T3 | (10,9) | (3,90) | (7,74) | (4,95) | (6,14) | (1,84) | (8,13) | (2,31) | (5,85) | (9,61) | |
| T4 | (2,36) | (1,69) | (10,39) | (3,8) | (7,26) | (4,85) | (9,61) | (5,19) | (6,76) | (8,52) | |
| T5 | (3,49) | (7,75) | (2,33) | (5,99) | (8,69) | (9,6) | (6,35) | (1,32) | (4,26) | (10,90) | |
| T6 | (9,11) | (7,46) | (2,10) | (8,43) | (4,11) | (6,52) | (10,21) | (1,74) | (5,11) | (3,47) | |
| T7 | (1,62) | (2,46) | (10,89) | (7,19) | (3,13) | (4,65) | (9,32) | (5,88) | (6,40) | (8,7) | |
| T8 | (7,56) | (2,72) | (3,12) | (6,25) | (10,49) | (5,25) | (1,30) | (4,36) | (9,79) | (8,45) | |
| T9 | (10,44) | (3,30) | (4,90) | (7,52) | (1,21) | (8,48) | (6,89) | (2,19) | (5,74) | (9,64) | |
| T10 | (1,21) | (9,11) | (7,45) | (4,22) | (6,72) | (10,72) | (8,32) | (2,48) | (5,11) | (3,76) | |
| Variables | Value | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| NIND | 10 | 15 | 20 | 25 |
| Maxgen | 500 | 1000 | 1500 | 2000 |
| α | 0.05 | 0.1 | 0.25 | 0.5 |
| n | 1 | 2 | 3 | 4 |
| Number | NIND | Maxgen | α | n | AMV | ART(s) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 946.4 | 84.76 |
| 2 | 1 | 2 | 2 | 2 | 903.8 | 169.55 |
| 3 | 1 | 3 | 3 | 3 | 902.6 | 255.75 |
| 4 | 1 | 4 | 4 | 4 | 902.2 | 339.42 |
| 5 | 2 | 1 | 2 | 3 | 925.4 | 130.50 |
| 6 | 2 | 2 | 1 | 4 | 918.2 | 262.10 |
| 7 | 2 | 3 | 4 | 1 | 895.8 | 434.90 |
| 8 | 2 | 4 | 3 | 2 | 887.8 | 515.95 |
| 9 | 3 | 1 | 3 | 4 | 924 | 178.05 |
| 10 | 3 | 2 | 4 | 3 | 905.8 | 344.34 |
| 11 | 3 | 3 | 1 | 2 | 900.8 | 503.77 |
| 12 | 3 | 4 | 2 | 1 | 874.4 | 734.28 |
| 13 | 4 | 1 | 4 | 2 | 905 | 238.63 |
| 14 | 4 | 2 | 3 | 1 | 902.4 | 474.98 |
| 15 | 4 | 3 | 2 | 4 | 906.2 | 642.57 |
| 16 | 4 | 4 | 1 | 3 | 893.2 | 840.01 |
| Instance | Size | Sbest | EEDA | EDA [40] | EDA- DE [41] | SA [42] | GA-SA [43] | GA [44] | HGA [45] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P-GA | SBGA- 40 | SBGA- 60 | HGA- Param | HGA-Non-delay | HGA- Active | ||||||||
| FT06 | 6 × 6 | 55 | 55 | 55 | 55 | 55 | 55 | - | - | - | 55 | 55 | 55 |
| FT10 | 10 × 10 | 930 | 930 | 937 | 937 | 930 | 930 | 960 | - | - | 930 | 951 | 945 |
| FT20 | 20 × 5 | 1165 | 1165 | 1184 | 1178 | 1165 | 1165 | 1249 | - | - | 1165 | 1178 | 1173 |
| LA01 | 10 × 5 | 666 | 666 | 666 | 666 | 666 | 666 | 666 | 666 | - | 666 | 666 | 666 |
| LA02 | 10 × 5 | 655 | 655 | - | 655 | 655 | - | 681 | 666 | - | 655 | 665 | 655 |
| LA03 | 10 × 5 | 597 | 597 | - | 597 | 606 | - | 620 | 604 | - | 597 | 604 | 603 |
| LA04 | 10 × 5 | 590 | 590 | - | 590 | 590 | - | 620 | 590 | - | 590 | 590 | 598 |
| LA05 | 10 × 5 | 593 | 593 | - | 593 | 593 | - | 593 | 593 | - | 593 | 593 | 593 |
| LA06 | 15 × 5 | 926 | 926 | 926 | 926 | 926 | 926 | 926 | 926 | - | 926 | 926 | 926 |
| LA07 | 15 × 5 | 890 | 890 | - | 890 | 890 | - | 890 | 890 | - | 890 | 890 | 890 |
| LA08 | 15 × 5 | 863 | 863 | - | 863 | 863 | - | 863 | 863 | - | 863 | 863 | 863 |
| LA09 | 15 × 5 | 951 | 951 | - | 951 | 951 | - | 951 | 951 | - | 951 | 951 | 951 |
| LA10 | 15 × 5 | 958 | 985 | - | 958 | 958 | - | 958 | 958 | - | 958 | 958 | 958 |
| LA11 | 20 × 5 | 1222 | 1222 | 1222 | 1222 | 1222 | 1222 | 1222 | 1222 | - | 1222 | 1222 | 1222 |
| LA12 | 20 × 5 | 1039 | 1039 | - | 1039 | 1039 | - | 1039 | 1039 | - | 1039 | 1039 | 1039 |
| LA13 | 20 × 5 | 1150 | 1150 | - | 1150 | 1150 | - | 1150 | 1150 | - | 1150 | 1150 | 1150 |
| LA14 | 20 × 5 | 1292 | 1292 | - | 1292 | 1292 | - | 1292 | 1292 | - | 1292 | 1292 | 1292 |
| LA15 | 20 × 5 | 1207 | 1207 | - | 1207 | 1207 | - | 1237 | 1207 | - | 1207 | 1207 | 1207 |
| LA16 | 10 × 10 | 945 | 945 | 945 | 956 | 956 | 945 | 1008 | 961 | 961 | 945 | 973 | 947 |
| LA17 | 10 × 10 | 784 | 784 | - | 784 | 784 | - | 809 | 787 | 784 | 784 | 792 | 784 |
| LA18 | 10 × 10 | 848 | 859 | - | 855 | 861 | - | 916 | 848 | 848 | 848 | 855 | 848 |
| LA19 | 10 × 10 | 842 | 842 | - | 852 | 848 | - | 880 | 863 | 848 | 842 | 851 | 852 |
| LA20 | 10 × 10 | 902 | 902 | - | 907 | 902 | - | 928 | 911 | 910 | 907 | 926 | 912 |
| LA21 | 15 × 10 | 1046 | 1060 | 1071 | 1058 | 1063 | 1058 | 1139 | 1074 | 1074 | 1046 | 1079 | 1074 |
| LA22 | 15 × 10 | 927 | 938 | - | 952 | 938 | - | 998 | 935 | 936 | 935 | 950 | 962 |
| LA23 | 15 × 10 | 1032 | 1032 | - | 1038 | 1032 | - | 1072 | 1032 | 1032 | 1032 | 1032 | 1032 |
| LA24 | 15 × 10 | 935 | 948 | - | 973 | 952 | - | 1014 | 960 | 957 | 953 | 970 | 955 |
| LA25 | 15 × 10 | 977 | 989 | - | 1000 | 992 | - | 1014 | 1008 | 1007 | 986 | 1013 | 1014 |
| LA26 | 20 × 10 | 1218 | 1218 | 1257 | 1229 | 1218 | 1218 | 1278 | 1219 | 1218 | 1218 | 1218 | 1237 |
| LA27 | 20 × 10 | 1235 | 1270 | - | 1287 | 1269 | - | 1378 | 1272 | 1269 | 1256 | 1282 | 1280 |
| LA28 | 20 × 10 | 1216 | 1218 | - | 1275 | 1224 | - | 1327 | 1240 | 1241 | 1232 | 1250 | 1250 |
| LA29 | 20 × 10 | 1152 | 1200 | - | 1220 | 1203 | - | 1336 | 1204 | 1210 | 1196 | 1206 | 1226 |
| LA30 | 20 × 10 | 1355 | 1355 | - | 1371 | 1355 | - | 1411 | 1355 | 1355 | 1355 | 1355 | 1355 |
| LA31 | 30 × 10 | 1784 | 1784 | 1789 | 1784 | 1784 | 1784 | - | - | - | 1784 | 1784 | 1784 |
| LA32 | 30 × 10 | 1850 | 1850 | - | 1850 | 1850 | - | - | - | - | 1850 | 1850 | 1850 |
| LA33 | 30 × 10 | 1719 | 1719 | - | 1719 | 1719 | - | - | - | - | 1719 | 1719 | 1719 |
| LA34 | 30 × 10 | 1721 | 1721 | - | 1721 | 1721 | - | - | - | - | 1721 | 1721 | 1721 |
| LA35 | 30 × 10 | 1888 | 1888 | - | 1888 | 1888 | - | - | - | - | 1888 | 1888 | 1888 |
| LA36 | 15 × 15 | 1268 | 1290 | 1292 | 1315 | 1293 | 1292 | 1373 | 1317 | 1317 | 1279 | 1303 | 1313 |
| LA37 | 15 × 15 | 1397 | 1445 | - | 1465 | 1433 | - | 1498 | 1484 | 1446 | 1408 | 1437 | 1444 |
| LA38 | 15 × 15 | 1196 | 1210 | - | 1244 | 1215 | - | 1296 | 1251 | 1241 | 1219 | 1252 | 1228 |
| LA39 | 15 × 15 | 1233 | 1255 | - | 1291 | 1248 | - | 1351 | 1282 | 1277 | 1246 | 1250 | 1265 |
| LA40 | 15 × 15 | 1222 | 1236 | - | 1277 | 1234 | - | 1321 | 1274 | 1252 | 1241 | 1252 | 1246 |
| Algorithms | NIS | ARPD | IR | |
|---|---|---|---|---|
| Others | EEDA | |||
| EDA [40] | 11 | 0.92 | 0.28 | 0.70 |
| EDA-DE [41] | 43 | 0.80 | 0.60 | 0.25 |
| SA [42] | 43 | 0.63 | 0.60 | 0.05 |
| GA-SA [43] | 11 | 0.28 | 0.28 | 0 |
| P-GA [44] | 37 | 4.62 | 0.69 | 0.85 |
| SBGA-40 [44] | 35 | 1.43 | 0.73 | 0.49 |
| SBGA-60 [44] | 20 | 1.97 | 1.14 | 0.42 |
| HGA-Param [45] | 43 | 0.40 | 0.60 | -0.50 |
| HGA-Non-delay [45] | 43 | 1.23 | 0.60 | 0.51 |
| HGA-Active [45] | 43 | 1.12 | 0.60 | 0.46 |
| Operations | (Machine Number, Processing Time) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tasks | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| T1 | (1,1740) | (2,4680) | (3,600) | (4,2160) | (5,3000) | (6,660) | (7,3720) | (8,3360) | (9,2640) | (10,1260) | |
| T2 | (1,2580) | (3,5400) | (5,4500) | (10,660) | (4,4140) | (2,1680) | (7,2760) | (6,2760) | (8,4320) | (9,1800) | |
| T3 | (2,5460) | (1,5100) | (4,2340) | (3,4440) | (9,5400) | (6,600) | (8,720) | (7,5340) | (10,2700) | (5,2580) | |
| T4 | (2,4860) | (3,5700) | (1,4260) | (5,5940) | (7,540) | (9,3120) | (8,5100) | (4,5880) | (10,1320) | (6,2580) | |
| T5 | (3,840) | (1,360) | (2,1320) | (6,3660) | (4,1560) | (5,4140) | (9,1260) | (8,2940) | (10,4320) | (7,3180) | |
| T6 | (3,5040) | (2,120) | (6,3120) | (4,5700) | (9,2880) | (10,4320) | (1,2820) | (7,3900) | (5,360) | (8,1500) | |
| T7 | (2,2760) | (1,2220) | (4,3660) | (3,780) | (7,1920) | (6,1260) | (10,1920) | (9,5340) | (8,1800) | (5,3300) | |
| T8 | (3,1860) | (1,5160) | (2,2760) | (6,4440) | (5,1920) | (7,5280) | (9,1140) | (10,2880) | (8,2160) | (4,4740) | |
| T9 | (1,4560) | (2,4140) | (4,4560) | (6,3060) | (3,5100) | (10,660) | (7,2400) | (8,5340) | (5,1560) | (9,4440) | |
| T10 | (2,5100) | (2,780) | (3,3660) | (7,420) | (9,3840) | (10,4560) | (6,2820) | (4,3120) | (5,5400) | (8,2700) | |
| Machine Number | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 0 | 152 | 170 | 193 | 100 | 112 | 173 | 165 | 142 | 133 |
| M2 | 152 | 0 | 131 | 138 | 152 | 169 | 120 | 170 | 162 | 143 |
| M3 | 170 | 131 | 0 | 160 | 151 | 140 | 132 | 171 | 122 | 140 |
| M4 | 193 | 138 | 160 | 0 | 140 | 140 | 165 | 170 | 140 | 198 |
| M5 | 100 | 152 | 151 | 140 | 0 | 103 | 102 | 170 | 180 | 192 |
| M6 | 112 | 169 | 140 | 140 | 103 | 0 | 142 | 140 | 148 | 150 |
| M7 | 173 | 120 | 132 | 165 | 102 | 142 | 0 | 150 | 162 | 160 |
| M8 | 165 | 170 | 171 | 170 | 170 | 140 | 150 | 0 | 141 | 120 |
| M9 | 142 | 162 | 122 | 140 | 180 | 148 | 162 | 141 | 0 | 153 |
| M10 | 133 | 143 | 140 | 198 | 192 | 150 | 160 | 120 | 153 | 0 |
| Machine Number | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Processing power (kW) | 18 | 15 | 6 | 12 | 10 | 5.5 | 7.5 | 3 | 5.5 | 10 |
| Unload power (kW) | 2.4 | 3.36 | 2.0 | 1.77 | 2.2 | 2.55 | 2.02 | 1.77 | 1.16 | 1.8 |
| w | EEDA | EDA | Solution Gap | ||||||
|---|---|---|---|---|---|---|---|---|---|
| f1 | f2 | F | f1 | f2 | F | Gap- f1 (%) | Gap- f2 (%) | Gap- F (%) | |
| 0 | 980.32 | 987.65 | 0.0588 | 992.14 | 983.42 | 0.1071 | 0.32% | 0.45% | 82.14% |
| 0.1 | 987.45 | 984.05 | 0.0623 | 986.39 | 989.28 | 0.0947 | 1.00% | 0.24% | 52.01% |
| 0.2 | 998.03 | 980.34 | 0.0523 | 987.23 | 1027.17 | 0.0874 | 2.92% | 0.38% | 67.11% |
| 0.3 | 1045.17 | 978.93 | 0.0607 | 979.5 | 1056.36 | 0.0954 | 1.07% | 0.06% | 57.17% |
| 0.4 | 1061.78 | 976.52 | 0.0579 | 977.16 | 1085.4 | 0.0948 | 2.22% | 0.07% | 63.73% |
| 0.5 | 1083.9 | 974.89 | 0.0613 | 975.05 | 1112.73 | 0.0983 | 2.66% | 0.02% | 60.36% |
| 0.6 | 1099.06 | 971.75 | 0.0688 | 973.58 | 1130.22 | 0.0832 | 2.84% | 0.19% | 20.93% |
| 0.7 | 1110.37 | 968.02 | 0.0605 | 971.6 | 1145.52 | 0.1046 | 3.17% | 0.37% | 72.89% |
| 0.8 | 1156.21 | 964.71 | 0.0514 | 969.4 | 1165.42 | 0.0983 | 0.80% | 0.49% | 91.25% |
| 0.9 | 1185.53 | 964.01 | 0.0677 | 965.73 | 1188.23 | 0.0916 | 0.23% | 0.18% | 35.30% |
| 1 | 1212.32 | 962.08 | 0.064 | 962.25 | 1220.28 | 0.1109 | 0.66% | 0.02% | 73.28% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, M.; Zhang, Z.; Giret, A.; Salido, M.A. An Enhanced Estimation of Distribution Algorithm for Energy-Efficient Job-Shop Scheduling Problems with Transportation Constraints. Sustainability 2019, 11, 3085. https://doi.org/10.3390/su11113085
Dai M, Zhang Z, Giret A, Salido MA. An Enhanced Estimation of Distribution Algorithm for Energy-Efficient Job-Shop Scheduling Problems with Transportation Constraints. Sustainability. 2019; 11(11):3085. https://doi.org/10.3390/su11113085
Chicago/Turabian StyleDai, Min, Ziwei Zhang, Adriana Giret, and Miguel A. Salido. 2019. "An Enhanced Estimation of Distribution Algorithm for Energy-Efficient Job-Shop Scheduling Problems with Transportation Constraints" Sustainability 11, no. 11: 3085. https://doi.org/10.3390/su11113085
APA StyleDai, M., Zhang, Z., Giret, A., & Salido, M. A. (2019). An Enhanced Estimation of Distribution Algorithm for Energy-Efficient Job-Shop Scheduling Problems with Transportation Constraints. Sustainability, 11(11), 3085. https://doi.org/10.3390/su11113085






