Macro Asset Allocation with Social Impact Investments

Abstract

Using a unique dataset of 50 listed companies that meet the majority of the OECD requirements for social impact investments, we construct a social impact finance stock index and investigate how investing in social impact firms can contribute to portfolio risk-return performance. We build portfolios with three different methodologies (naïve, Markowitz mean-variance optimization, GARCH-copula model), and we study the performance in terms of returns, Sharpe ratio, utility, and forecast premium based on a constant relative risk aversion function for investors with different levels of risk aversion. Consistent with the idea that social impact investment can improve portfolio risk-return performance, the results of our macro asset allocation analysis show the importance of a large fraction of investor portfolios’ stake committed to social impact investments.

1. Introduction

Social impact investments (SIIs) require that investors strive for financial success while targeting specific social and environmental needs of society at large. This same proposition occurs in a wider spectrum of investment approaches that integrate societal and environmental factors into decision making. In particular, socially responsible investments (SRIs) focus on systematically “screening out” socially undesirable products (such as alcohol, tobacco, weapons, gambling, etc.) in order to mitigate risky practices and protect value. Over time, SRIs have evolved from “negatively screening” harmful products or practices to “pro-actively screening” for environmental, social, and governance (ESG) opportunities by integrating social and environmental factors into their portfolio selection. SIIs go beyond both aforementioned approaches. They are distinct in their focus on investments that are characterized by their deliberative intention to: (i) generate specific positive social impact, and (ii) precisely measure the achievement of their social outcome goals [1].

SIIs have evolved over the past decade. JP Morgan [2] estimates a prospective growth in SIIs between $400 and $100 billion by 2025. The World Economic Forum [3] reports a potential growth of 60% per year in the time span of 2013–2020. Tremendous market forces are driving investors to become serious about impact investing. First, investors want to do more than create financial returns as documented by the large number of investors representing $46 trillion in capital who have signed on to the United Nations Principles for Responsible Investing (UN PRI). Additionally, the millennial generation is expressing a widespread desire to marry profit with purpose when making investments [1]. Second, in the current investment climate, large pools of institutional investors are forced to seek other means of investment with good opportunities of returns and potentially less correlated with traditional assets. In this perspective, SIIs could interest not only investors concerned by their social impact (“impact-first” investors), but also “standard” investors interested by the portfolio risk-return performance (“financial-first” investors, as categorized by Freireick and Fulton [4]). Actually, as this niche of the investment industry is developing, some money managers are starting to treat impact investment as an asset class, often including it within “alternatives” [5].

In this paper, we build on the work of La Torre et al. [6] and perform an investigation of social impact firms’ (SIFs) contribution to portfolio risk and return performance. The dataset used in this paper is based on a sample of internationally listed companies that show potential as SIIs according to the OECD [7] eligibility criteria. We compare the out-of-sample results for portfolios, including our social impact finance stock index among the feasible assets. The comparison is performed in terms of returns, Sharpe ratio, utility, and forecast premium based on a constant relative risk aversion (CRRA) function for investors with different levels of risk aversion. Following Riccetti [8], the portfolios are built with different methodologies: naïve, Markowitz [9] mean-variance optimization, and the GARCH-copula model.

Overall, our macro asset allocation shows the importance of investing a substantial proportion of a portfolio in SIF stocks. More specifically, we find that relatively risk prone investors maximize their utility when the mean-variance allocation is applied to a portfolio that uses the social impact finance index and the bond index, without the overall stock market index, while very risk adverse investors maximize their utility with a naïve allocation including all indices.

Our paper contributes to the empirical literature on SIFs’ impact in portfolio allocation for many reasons. To the best of our knowledge, there is no previous evidence on this topic that: (i) uses quite a large number of stocks of SIFs (50 in our study) selected according to very tightening criteria; (ii) constructs a social impact finance stock index; (iii) applies different methodologies to allocate the portfolio, including the use of copulas, which are able to consider extreme joint price variations of different assets; and (iv) evaluates the performance in terms of utility, in order to understand the different impacts of the SIF stocks for investors with different levels of risk aversion.

The remainder of the article proceeds as follows. The next section performs a literature review on alternative investments, with a focus on social investments (SRIs and SIIs). Section 3 describes our dataset and the empirical research methods that we employ in this study. The main results are presented in Section 4, while Section 5 concludes.

2. Literature Review

2.1. Alternative Investments

Modern portfolio theory [9,10] states the benefits of diversification and demonstrates opportunities for improving portfolio performance by combining assets that are lowly correlated. Alternative investments have been proven to provide such opportunities. There are a number of studies devoted to investigating the characteristics of alternative investments as portfolio components. Typically, alternative investments include real estate, private equity, commodities, or niches of the investment industry, such as fine art. In the real estate market, the evidence about the beneficial adding of real estate investment trusts (REITs) into multi-asset portfolios is widespread. For example, Lee and Stevenson [11] find that REITs play a significant role for diversification over different time horizons and holding periods. In the same vein, Chiang and Ming-Long [12] show that the additional inclusion of REITs enhances the efficient frontier; therefore, REITs have a rightful role in a mixed portfolio.

Private equity is similar to real estate, as both assets are not traded in a permanent marketplace with quoted market prices, and both incorporate low liquidity and asymmetric information. Among studies including private equity in the strategic asset allocation of investors, Lamm and Ghaleb-Harter [13] recommend investing between 19% and 51% in private equity; their result was tested under a variety of alternative conditions and conservative assumptions about future performance. A later study of Chen et al. [14] points out the low correlation coefficient (0.04) between venture capital and stocks, suggesting an allocation of 2% (for the minimum variance portfolio) to 9% (in the maximum Sharpe ratio portfolio) for mixed asset portfolios.

Compared to private equity, investing in commodities is easier, thanks to commodity derivatives, such as traded commodity futures. Given that commodity returns are expected to be almost uncorrelated with traditional bonds’ and equities’ returns, many authors study whether their inclusion in portfolios really improved the diversification and the risk-return performance. Some literature reviews, such as Skiadopoulos [15], concern this topic. Most papers empirically confirm this diversification benefit (see, for instance, [16,17,18]). However, there is no unanimous consensus on this result, with different conclusions drawn, for instance, by Cao et al. [19], Daskalaki and Skiadopoulos [20], Bessler and Wolff [21], and Lombardi and Ravazzolo [22].

In addition, fine art has been investigated as alternative asset class. One study that considers fine art’s potential in strategic asset allocation is proposed by Campbell [23]. This study concludes that although art investments may generate lower returns over time, they deliver superior performance during periods of economic distress/crises, therefore improving portfolio diversification. A similar conclusion is derived in Campbell [24], where a portfolio simulation was run using a mixed asset portfolio composed by stock, bonds, and paintings; results show that mixed portfolios are superior in terms of higher returns and lower volatility.

2.2. SRIs and SIIs as an Alternative Asset Class

Over the last years, investments applying ethical and moral screens to stock selections have become more reputable within the field of alternative asset classes. They employ different strategies and different screens to identify socially responsible investment targets. Negative screens only restrict or prohibit investments in firms that perform poorly on certain attributes (typically screened out firms are those deriving significant revenues from alcohol, tobacco, gambling, nuclear energy, etc.), whereas positive screens over-weight companies, which incorporate environment, social, and governance (ESG) factors into their business activity. Academic interest has also followed the recent growth of the SRI industry. Bello [25] used a sample of socially responsible stock mutual funds matched with randomly selected conventional funds of similar net assets and found no differences in the characteristics of the asset held, portfolio diversification, and investment performance. In contrast, Adler and Kritzman [26] state that some costs are associated with SRIs because they exclude some attractive firms from their portfolio selection. Similarly, Renneboog et al. [27] conclude that investors pay a price for ethics as SRI funds in the US, UK, and in many continental European and Asia-Pacific countries underperform their domestic benchmark by –2.2% to 6.5%. Moreover, performance is worse when the fund has a high number of corporate governance and social screens. However, all previous studies have concentrated their efforts on determining the risk-return profiles of SRI in isolation, without paying attention to the possible diversification attributes of SRI as a portfolio component. To explain the increasing popularity of SRI when it mostly generates similar or lower returns than conventional investments, Nofsinger and Varma [28] postulate that the benefits of SRI arise from holding up better during market crisis periods. Specifically, Nofsinger and Varma [28] find that compared to matched conventional mutual funds, socially responsible funds outperform during periods of market crises, thus adding value for those investors seeking downside risk protection in their portfolio.

SIIs are similar to SRIs in their focus on investments that create additional value for both shareholders and society at large. However, SIIs go beyond this proposition to focus on investments that deliberatively address one or a cluster of pressing social/environmental issues in order to make a positive and measurable social impact. For example, an investment might focus on addressing water scarcity, fostering clean energy, or providing high quality jobs to the long-term unemployed. It is therefore important to distinguish “intent” from actions that might be taken by companies to limit negative externalities from their business activity (for example, limiting gas emission during the productive process). When social intent is an incidental outcome (i.e., whereby a social outcome is attained despite the fact that the target mission is different), there might be room for SRI, but not for SII; to be eligible for SII, the social outcome should represent the target mission of the organization. Furthermore, there should be a strong conjunction among the social target area and the measurement of the social outcome. In the absence of this element, SII is de facto close to more traditional financial investments (such as SRIs). Investments that intentionally create measurable social impact vary in their technical forms and product types [1]. On the one hand, there are situations where a social challenge creates an opportunity for investors through standard investment vehicles. A micro finance structured fund or the most recent social impact fund are two such examples. On the other hand, there are situations where an investment’s delivery of positive social change will require investors to support innovative financial instruments. Private investments into the growing number of social impact bonds (SIBs) around the world, whose business model require cross-sector partnership between the public and private sector [29], are one such example.

The acceptance of SII as a capital investment alternative has lagged behind that of SRI. Reservations about investing in SIIs as an alternative asset class may be caused by several factors. Mainly, despite their fast growth, SIIs are at their early stage of development and there is still a debate on their exact boundaries and, even more importantly, it lacks common regulation at the international level. Moreover, the lack of data aggregators linked with comprehensive transaction information has been critical to backing the theory as well as supporting demand by institutional and individual investors. Actually, some authors point out that the expected growth in SII in the forthcoming years may not be realized if institutional investors are not able to categorize impact investments according to traditional financial standards (e.g., Saltuk et al. [30] and Clark et al. [31]).

Therefore, SIIs’ role as an alternative portfolio component deserves further investigation. Being extremely focused on addressing critical societal needs, SIIs may experience stronger demand during an economic downturn, likely providing superior performance during market crises and lower correlation to traditional investments. Indeed, the Mission Alignment Working Group [5] found that impact investments are anticyclical, differently from most kinds of financial assets and, therefore, SIIs could be useful for portfolio diversification. Few studies investigate the risk-return performance of SIIs and their utility for portfolio allocation. Among the studies offering a financial lens to analyze impact investing, Del Giudice and Migliavacca [32] explore contractual as well as financial characteristics (such as size, maturity, technical form, internal rate of returns, collateral) of a specific kind of SII, i.e., SIBs, and relate these characteristics to the participation of institutional investors. They find that investors are more likely to participate in SIBs with lower information asymmetry and agency problems and confirm the presence of a positive risk–return relationship. However, the financial characteristics of SIBs were investigated in isolation, without any reference to other standard financial drivers, such as the correlation to standard markets. The Asset Allocation Working Group of the G8 Social Impact Investment Taskforce [1] provides a first attempt to propose a portfolio that also includes SII. They conclude that by including an impact allocation, investors may achieve the same financial return while improving portfolio diversification, at the cost of some increase in illiquidity. However, the proposed portfolio is merely illustrative and few details are provided about how the analysis was empirically conducted. La Torre et al. [6] complement previous analyses by investigating SII’s contribution to portfolio risk and performance; by applying Markowitz’s [9,10] and Sharpe’s [33] methodology to alternative samples, including or not the SII, they show that in terms of the Sharpe ratio, non-impact portfolios outperform a SII portfolio, as a consequence of their higher financial returns for the same level of risk. Nonetheless, their conclusion cannot be generalized as the analysis is very market-specific; only eight firms were included in the impact portfolio and were selected among listed companies admitted to the London Social Stock Exchange (SSX). Our innovative approach aims to overcome this gap in the knowledge by specifically analyzing SII with the lens of portfolio management and by using a dataset which is unique with respect to both the number of SIFs considered and the depth of information gathered.

3. Data and Methodology

3.1. Dataset

The existing literature on SII as an alternative asset class that can be used for portfolio allocation is quite limited. The results of those studies are difficult to compare with each other because the datasets used in these empirical analyses are very narrow. The OECD Social Impact Investment Initiative [34], indeed, pointed out the strong need for transparent and standardized data sharing in order to foster social capital market.

We attempt to address the lack of availability of data on SII by creating a unique dataset of SIFs with the following characteristics: (i) relies on independent and publicly available criteria to define impact investments; (ii) is not limited to a specific market nor a geographical area; and (iii) allows for reproducible quantitative analysis of SII. To select our sample of SIFs, we started out with the full list of companies reported on wikipositive.org, a public portal on private and public enterprises that meet the highest financial, social, and environmental standards. This starting sample is ideal for selecting SIFs as it is not limited to a negative screening (e.g., screening out weapons, tobacco, and gambling products), but it includes only those companies with expected positive products and/or services. Moreover, the platform includes a wide range of companies (slightly more than 1000) from different geographical areas.

We further relied on the framework provided by the OECD [7] in order to identify any company included in the wikipositive.org list that might or might not be considered a SIF. This framework helped to operationalize the SII definition during the data collection process, and was previously employed by La Torre et al. [35] and Chiappini [36] to a sample of microfinance vehicles and social impact funds.

According to the OECD [7], the criteria for any investments to be eligible for SII include the following:

(1)

Social target areas: It provides a range of social areas that could potentially be considered SII under various circumstances. There are overall 8 core SII areas that can be eligible, that are: ageing, disability, health, children and families, public order and safety, affordable housing, unemployment, and education and training. In addition, there are 5 other areas, leaning towards the core areas, such as: agriculture, environment and energy, water and sanitation, financial services (including microfinance), and Information and Communications Technology (ICT. The inclusion of these last 5 areas as SIIs depends on the other characteristics of the investments described below.

(2)

Beneficiary context: It relates to who benefits from the firm’s operations. To the extent that a company operates in order to fulfil the needs of populations at risk or those living in underserved or developing areas, the investment might be considered to be SII. More precisely, if the area of business of a company is not among those that are considered as core SIIs, but it provides a benefit to a population that is at risk, then it could be considered as a SII.

(3)

Degree of publicness: It relates to the type of good or service provided by the company. SII eligibility will apply to goods or services within the continuum between the two boundaries (public and private). Indeed, social goods have different characteristics than pure private or public goods insofar as they would not completely exclude benefits accruing to non-target beneficiaries.

(4)

Delivery organization intent: It deals with a verifiable demonstration of the firm’s social intent. Specifically, merely having the intent stated on the mission is not enough to be considered SII as the delivery organization must put sufficient effort into demonstrating that they are committed to the social cause. A strong level of commitment can be demonstrated, for instance, through (i) some form of compulsory reporting of social outcomes to shareholders within the organization’s statutes; (ii) an external certification or label; and (iii) legally binding constraints, which provide the strongest indication of a commitment to social goals.

(5)

Measurability of social impact: It refers to the fact that a firm that does not have any form of social impact measurement cannot be considered as a SII. The assessment of the impact of the investments can be qualitative or quantitative.

Compared to the work of La Torre et al. [35] and Chiappini [36], we excluded two additional requirements, i.e., investor intent and return expectation. Indeed, while the aforementioned studies applied OECD [7] criteria to verify whether existing investment vehicles (specifically microfinance vehicles or social impact funds) are “compliant” to the perimeter of SII, our aim was to select internationally listed firms that show potential as a social impact target company. Therefore, our focus was on those criteria that primarily refer to the investee rather than to the investor.

The analysis of each item was based on various sources of information that met the criteria of transparency and trust worthiness. Specifically, we used several sources of data. From each company’s webpage, we analyzed the company’s overview, mission, article of association, and financial statements in order to clearly identify the social target area, the kind of beneficiaries, the degree of publicness, and the social delivery organization intent. More precisely, we analyzed the delivery intent of the company by further requiring that the company has one of the following: (i) a sustainability report; (ii) an external certification or label, or (iii) legally binding constraints within the article of association. Finally, sustainability reports retrieved from the company’s webpage were used to investigate the effective measurement of the company social impact. Specifically, we required that each company disclosed at least two sustainability reports and that each of them included a measure (i.e., figures or absolute amounts) of the actual social impact of the company’s projects.

To be eligible for inclusion in our sample, a firm in the wikipositive.org website had to be compliant with at least four out of the five criteria outlined by the OECD [7]. Moreover, we asked the firm to be listed on a stock exchange. Overall, these criteria led us to a final sample of 41 SIFs across 13 countries. We further added to the sample 11 SIFs that were admitted to the London Social Stock Exchange (SSX). Therefore, we ended up with 52 SIFs (see Appendix A for more details). Our sample of SIFs is quite different from other datasets (e.g., Asset4, KLD, and CSRHUB), which provide environment, social, and governance (ESG) scores/ratings and other performance indicators in order to assess how well companies manage their ESG risks and opportunities. As explained in Section 2.2, ESG principles and SII are similar in purpose, but different in practice. In our sample, 44.2% (23) of firms are incorporated in Europe, 38.5% (20) are incorporated in the USA and Canada, 15.4% (8) in Asia, and 1 firm in South Africa. With respect to the social investment areas,

Table 1. Social target areas.

SII Areas	Number	Percent
Environment and energy	27	51.9%
Health	8	15.4%
Water and sanitation	5	9.6%
ICT	3	5.8%
Agriculture	4	7.7%
Education and training	3	5.8%
Housing	1	1.9%
Financial services	1	1.9%
Total	52	100.0%

shows that our sample was characterized by a high presence of firms in the environmental and energy sector (51.9%) and in the health sector (15.4%).

In order to construct our social impact finance stock index (that we will call SIFSI hereafter), we gathered the total return index, market capitalization, and free float rate for each SIF included in the sample on a daily basis from January 2002 to September 2018 from Thomson Reuters Datastream. Total returns were calculated on adjusted prices in order to consider corporate events, like, e.g., stock splits, etc.

To perform our portfolio analysis, we further obtained from Thomson Reuters Datastream the daily total return of the following two indexes: Morningstar Global Government Bond Index USD (MGGBI) and MSCI International All Country World Index (ACWI).

3.2. The Social Impact Finance Stock Index

In order to aggregate SIFs’ data and build our SIFSI, we followed the methodology applied by Morgan Stanley Capital International (MSCI) to construct its indices. In particular, we used the MSCI All Country World Index (MSCI ACWI) as a global stock market benchmark, because it takes into account all the countries issuing securities belonging to our SIFSI, including both developed and emerging markets (23 developed and 24 emerging markets). Indeed, the MSCI ACWI is a market capitalization weighted index designed to provide a broad measure of equity-market performance throughout the world.

Due to the availability of the daily data of the aforementioned indices, as underlined in the previous section, the period taken into consideration in the analysis started from January 2002 and finished at the end of September 2018; for the construction of our SIFSI, we used the daily total return index of the selected stocks. Although we started out with 52 possible constituents, we deleted two of them because their price series were overly lacking.

Given the different time of entry in the stock market of each constituent, we followed one of the two MSCI methodologies to update the indices. The first methodology is quarterly reviews (in February and August the so-called quarterly index reviews, and in May and November the so-called semi-annual index reviews) in which new small Initial Public Offerings (IPOs) are included. The second methodology used is ongoing event-related changes in which changes are implemented in the indexes as they occur; more specifically, significantly large IPOs are included in the indexes after the close of the company’s 10th day of trading. We decided to follow the second methodology for all of our securities (also for small IPOs). Therefore, in order to achieve a greater overlap with the MSCI ACWI methodology, we excluded the first 10 days of listing after the IPO. This choice allowed us to make the securities available in the index as soon as possible, thus increasing the descriptive capacity of the index.

The calculation method of the MSCI ACWI imposes that once 99% of the market capitalization is reached, smaller securities are excluded from the index. However, to avoid a reduction in the number of constituents of SIFSI, we decided not to apply this rule.

At the beginning of the analyzed period (January 2002), the SIFSI index was composed of 26 stocks. During the 17 years, another 24 stocks were added and 5 were deleted because of default or delisting. At most, the index included 47 out of the 50 considered constituents at the same time.

3.3. Portfolio Macro Asset Allocation

As already explained, the aim of the paper was to compare the out-of-sample results of portfolios including or not the above mentioned social impact finance stock index among the feasible assets. In particular, the investor (or the asset management company) builds the portfolio using three macro asset classes represented by the three indices mentioned above, all computed in local currencies. We used the three indices in the following combinations:

• Portfolio 1 is composed of the MSCI ACWI and the MGGBI;
• Portfolio 2 can invest in SIFSI and MGGBI;
• Portfolio 3 has no restriction on the feasible assets, therefore it invests in SIFSI, MSCI ACWI, and MGGBI.

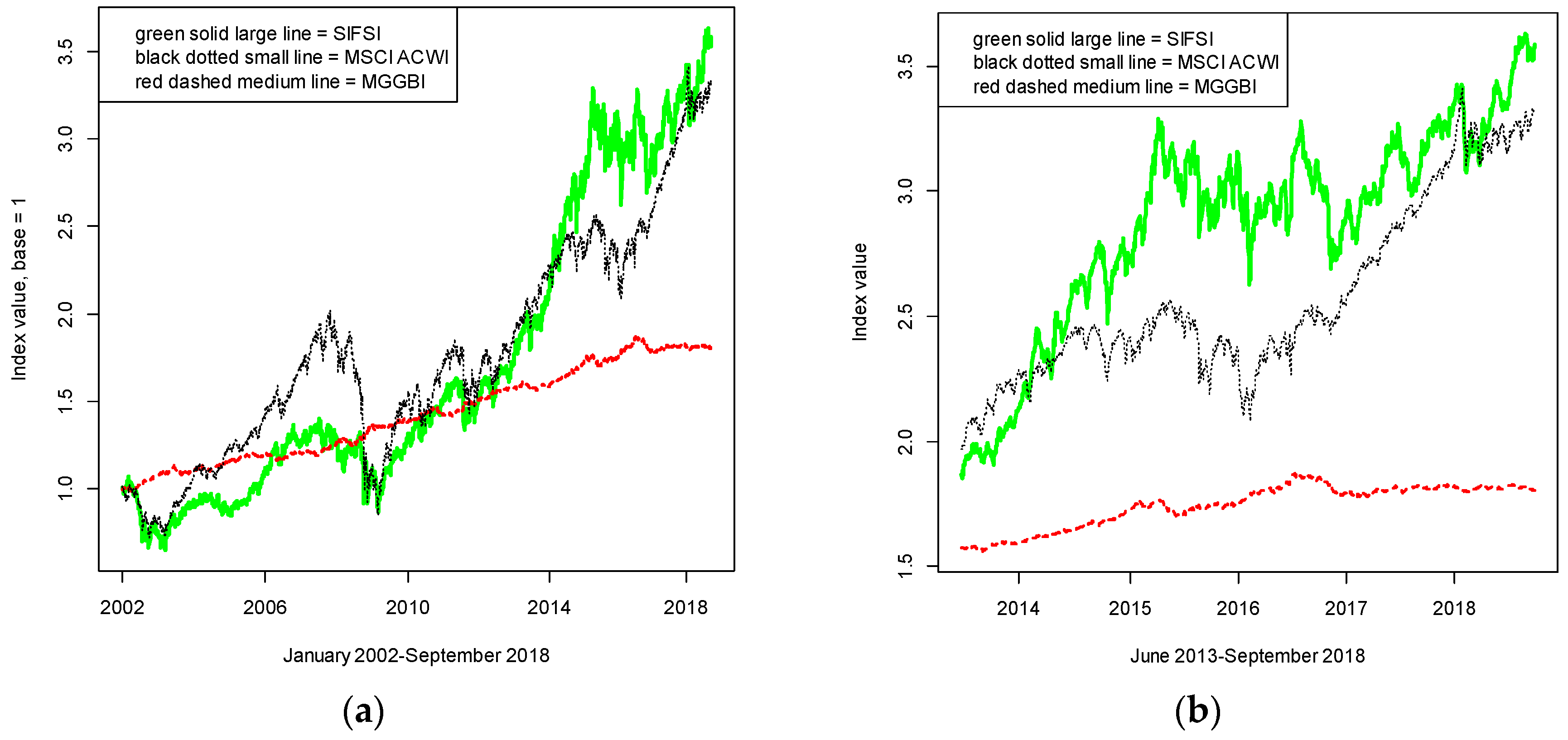
We performed some simplifying assumptions. First, we assumed there are no transaction costs, that is, no costs for portfolio rebalancing or for short-selling. Moreover, we disregarded savings decisions and intermediate consumption: We invested an amount of money at the beginning of the period (for simplicity and without loss of generality, equal to 1) and we did not receive or disinvest anything until the end of the analyzed period. The allocation was done for about five years left out-of-sample, with a monthly portfolio rebalancing. Indeed, assuming that a month is composed by 22 working days, we allocated the portfolio 60 times, every 22 working days. The data, as already said, started from the beginning of January 2002 to the end of September 2018. Therefore, excluding the last 1320 observations (22 × 60), the out-of-sample period starts at the end of June 2013. The time series of the three indices are plotted in Figure 1: The left panel represents the whole time series, while the right panel focuses on the out-of-sample period. The descriptive statistics of the data for the whole sample are reported in

Table 2. Descriptive statistics of the daily compound return (in percentage) of the used indices. SIFSI = social impact finance stock index, ACWI = MSCI All Country World Index, MGGBI = Morningstar Global Government Bond Index. Full data range: 1 January 2002–30 September 2018.

Index	Mean	Std. Deviation	Skewness	Excess Kurtosis
SIFSI	0.035%	1.020%	−0.074	5.808
ACWI	0.033%	0.983%	−0.272	9.115
MGGBI	0.014%	0.169%	−0.096	1.957

. These statistics show that the two stock indices have a similar average and standard deviation of the returns on the whole period, while the bond index shows, as expected, lower levels of return and risk. However, observing also the higher central moments, we can state that the SIFSI performs better than the overall stock market index because it seems to be safer (and even with a slightly higher mean return). Indeed, the former presents a higher skewness and a lower kurtosis. That is, a lower probability of extreme events especially in the negative tail of the distribution or, in other words, a lower probability of crashes.

The left panel of Figure 2 highlights the strong positive correlation (0.67) between the two stock indices, SIFSI and MSCI ACWI. The presence of some joint extreme events could signal the existence of the so-called tail dependence that can be modelled with different kind of copulas.

The other two panels of Figure 2 show, instead, that the bond index is weakly inversely correlated with SIFSI and MSCI ACWI (−0.24 and −0.32, respectively) and, therefore, it is very important for the diversification process of portfolio allocation. Moreover, the range of the axes confirms the very different standard deviations and kurtosis between the two stock indices (with returns also above +5% and below −5%) and the bond index (with return always included between ±1%).

The comparison among the performances of the portfolios was evaluated in terms of:

• Final capitalization (equivalent to overall return);
• Sharpe ratio; that is, the ratio between the mean and standard deviation of returns (Sharpe [33]);
• Utility, based on a constant relative risk aversion (CRRA) for investors with different levels of risk aversion; as stated by Patton [37], “we focus on the CRRA utility because of its prominence in the finance literature”;
• Forecast premium related to the previous CRRA utility function.

In detail, we evaluated the performance of the analyzed portfolios using the Sharpe ratio, following La Torre et al. [6] and Rachev et al. [38]. Even if it proxies the utility analysis with the analysis of only the first two moments (mean and variance) of the return distribution, it has the advantage of not assuming a particular utility function.

Instead, the utility was computed with the CRRA function on monthly returns, as done by many authors, such as Patton [37] and Riccetti [8]:

$$\mathrm{U}\left(\mathsf{\gamma }\right)={\left(1-\mathsf{\gamma }\right)}^{-1}{\left({\mathrm{P}}_0{\mathrm{R}}_{\mathrm{port}}\right)}^{\left(1-\mathsf{\gamma }\right)},$$

(1)

where γ is the risk aversion parameter, R_port is the portfolio capitalization factor (1 plus the portfolio return), and P₀ is the initial investment that we set as equal to 1 (without loss of generality, as already said). The values of the risk aversion parameter, γ, used are 2, 5, 10, and 15, as suggested by Bucciol and Miniaci [39], and as performed in other papers, such as Jondeau and Rockinger [40] and Riccetti [8]. When γ = 2, we are simulating an investor that is relatively risk prone and, for an increasing value of γ, we are simulating a more and more risk averse investor.

However, the utility displays a number that is able to rank the portfolios from the best to the worst, but does not give an economic insight on the strength of the preference. Therefore, we associated to the utility the forecast premium, also called the opportunity cost, because it is the return that needs to be added to the returns obtained by a benchmark portfolio (in our case, the naïve equally divided portfolio that does not use any information and allocation models) so that the investor becomes indifferent to the returns obtained by the analyzed model. Formally:

U (1 + r_e + θ) = U (1 + r_m),

(2)

where r_m is the return obtained by the portfolio allocated using the copula or the mean-variance model, re is the return obtained by the naïve equally divided portfolio, and θ is the forecast premium. Sometimes, the forecast premium is interpreted as a sort of management fee, because it is the maximum amount that the investor would be willing to pay to an asset manager to switch from the benchmark portfolio (in our case, naïve equally divided) to the proposed allocation.

Following Jondeau and Rockinger [40], in the context of a fourth-order Taylor approximation with the CRRA utility function, Equation (2) can be written as follows:

$$\theta = \left(m_m - m_e\right)- \frac{\gamma }{2}\left(m^2{}_m - m^2{}_e\right)+ \frac{\gamma \left(\gamma +1\right)}{3!}\left(m^3{}_m - m^3{}_e\right)-\frac{\gamma \left(\gamma +1\right)\left(\gamma +2\right)}{4!}\left(m^4{}_m - m^4{}_e\right),$$

(3)

where m represents the non-central moments of order i: mⁱ = mean (rⁱ).

We used Equation (3) to calculate the forecast premium. It clearly shows that an investor is willing to pay a forecast premium in order to obtain a portfolio that increases the mean and skewness (odd moments) and decreases the variance and kurtosis (even moments) of the return distribution, as usual for a rational risk averse investor within the expected utility framework (see, for instance, Scott and Horvath [41]).

The returns used for the out-of-sample evaluation were computed monthly, that is, every 22 working days. Even if we rebalanced the portfolio monthly and we evaluated the performance on monthly returns, we used daily returns in our allocation procedure. In this way, we covered quite a long time period without rebalancing (and this reduced the problem of not considering rebalancing costs), but we used more information compared to few monthly returns. Similar procedures were applied, for instance, by Riccetti [8] or by Morana [42], who computed monthly realized betas from daily data. However, to do this procedure, we needed to simulate a path of 22 returns to allocate the portfolio for each out-of-sample month. Now, we will describe the model used for the allocation.

Following Riccetti [8], the portfolios were built with three different methodologies: naïve allocation, the GARCH-copula model, and Markowitz [9] mean-variance optimization.

For the naïve allocation, we did not need a model: We simply equally divided the portfolios among the feasible assets. Therefore, portfolios 1 and 2 show the 50%–50% allocation, while portfolio 3 includes a 33.33% allocation of the investment to each stock index (MSCI ACWI and SIFSI) and a 33.34% allocation to the bond index (MGGBI).

The GARCH-copula model was structured in the following way:

• Means are unconditional. We also attempted to model the returns using ARMA processes, but these models are not theoretically justifiable and, as often happens in these cases, they are effective in-sample, but not useful for the out-of-sample forecast;
• Variances are modelled with a GARCH (1,1), using error terms extracted from a Skewed-t distribution. We chose the GARCH (1,1) because it is the most used GARCH model and, in practice, it often performs better than other (more complex) GARCH models for the out-of-sample forecast. GARCH residuals present negative skewness and excess kurtosis, therefore the error terms were extracted from a skewed-t distribution, following Jondeau and Rockinger [40], Patton [37], and Riccetti [8];
• The joint behavior of the residuals of the indices is modelled by a copula function. We attempted Clayton, normal, and student-t copulas. These copulas possess different tail dependences: The Clayton copula catches the lower tail dependence (high probability that a large negative value of one variable corresponds to a large negative value of the other variable), the student-t copula implies both lower and upper tail dependences (but symmetrical), while the normal copula does not present any tail dependence. We selected the copula presenting the best value of the maximum likelihood. In line with most of the empirical papers applying static copula models, the student-t copula is always preferred and this choice can be confirmed, for instance, by the observation of the left panel of Figure 2 in which the presence of both lower and upper tail dependence is very evident.

The following three steps were used to build the optimal portfolio:

(1)

Estimate using the maximum likelihood the parameters of the explained model;

(2)

Perform a 10,000 times Monte Carlo simulation of the path of assets’ returns on the 22 day investment horizon;

(3)

Choose the optimal weights in order to maximize the investor’s expected utility, assuming that the utility function is represented by the CRRA function, as previously explained.

For the Markowitz [9] mean-variance optimization, we followed a similar method, because in the presence of a CRRA utility function, a simple closed form cannot be derived for the optimal weights. Therefore, we used, as an approximation of the weight for the mean-variance approach, a model that uses GARCH (1,1) for the univariate variances and shocks extracted from a multivariate normal with correlations equal to the in-sample historical ones.

4. Results

Our results depend on the risk aversion level of the simulated investor. We started by analyzing the relatively less risk averse investor simulated with γ = 2. Results are reported in

Table 3. Results for investors with γ = 2.

Panel a—Final amount
Portfolio Assets	Copula Allocation	Mean-Variance Allocation	Naïve Allocation
ACWI + MGGBI	2.2035	Defaulted	1.4006
SIFSI + MGGBI	1.9920	3.8550	1.5029
ACWI + SIFSI + MGGBI	2.0657	3.7695	1.5679
Panel b—Sharpe ratio
Portfolio Assets	Copula Allocation	Mean-Variance Allocation	Naïve Allocation
ACWI + MGGBI	0.2025	Defaulted	0.3758
SIFSI + MGGBI	0.2407	0.2580	0.3143
ACWI + SIFSI + MGGBI	0.1901	0.2228	0.3522
Panel c—Utility
Portfolio Assets	Copula Allocation	Mean-Variance Allocation	Naïve Allocation
ACWI + MGGBI	−0.99017	Defaulted	−0.99451
SIFSI + MGGBI	−0.98997	−0.98351	−0.99348
ACWI + SIFSI + MGGBI	−0.99128	−0.99043	−0.99277
Panel d—Forecast premium compared to the naïve allocation performed on all assets (33.33% ACWI + 33.33% SIFSI + 33.34% MGGBI)
Portfolio Assets	Copula Allocation	Mean-Variance Allocation
ACWI + MGGBI	0.256%	Defaulted
SIFSI + MGGBI	0.280%	0.921%
ACWI + SIFSI + MGGBI	0.148%	0.211%

.

In this case, very often, the weight of the investment on the stock indices is above the 100% of the portfolio and the MGGBI is short sold. In particular, there is a huge overweight of the MSCI ACWI index when it is in the set of feasible assets.

The largely leveraged portfolios make the returns very volatile and, in the case of the portfolio composed of MSCI ACWI and MGGBI and allocated using the mean-variance criterion, the portfolio goes bankrupt. Instead, the return of the two portfolios investing on the SIFSI using the mean-variance criterion is largely above the return of the portfolios allocated with the copula model or in a naïve way (Table 3, panel a). It determines a clear ranking for the risk-return profile of the allocation: The mean-variance criterion builds the riskiest portfolios, the copula model also considering joint tail events is a bit less risky, and the naïve model is much safer.

Even if the return is much lower, the Sharpe ratio (Table 3, panel b) of the naïve allocation is better than the Sharpe ratios of the mean-variance allocations that present very large volatility values. The copula allocations present even lower Sharpe ratios. However, given that the investor is relatively risk prone and, therefore, very focused on the gain and not very scared by volatility risk, the utility of the naïve allocation is the worst (Table 3, panel c).

Given that, among the equally divided portfolios, the portfolio including all the three indices is always the best in term of return and utility (and the related forecast premium) for every kind of analyzed investors (from γ = 2 to γ = 15), we calculated the forecast premium against the naïve allocation 33.33% MSCI ACWI, 33.33% SIFSI, and 33.34% MGGBI, avoiding the comparison with the two other naïve allocations. The forecast premium over the naïve allocation (Table 3, panel d), derived from the utility function, is always positive (obviously except for the defaulted portfolio), confirming that copula and mean-variance allocations are evaluated well by the investor characterized by γ = 2. In particular, the best portfolio is the one including only the SIFSI and MGGBI weighted using the mean-variance criterion. That is, the portfolio with the higher return too. In this case, the forecast premium is very large, close to 1% for each month; annualizing the result, we can say that an asset manager could ask for about 11% of the management fee for this allocation, which almost quadruples the invested amount in the five selected years (final amount equal to 3.855).

Table 4. Results for investors with γ = 5.

Panel a—Final amount
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	1.6013	2.1575		1.4006
SIFSI + MGGBI	1.4892	2.0798		1.5029
ACWI + SIFSI + MGGBI	1.5537	2.2183		1.5679
Panel b—Sharpe ratio
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	0.2461	0.2345		0.3758
SIFSI + MGGBI	0.2809	0.2801		0.3143
ACWI + SIFSI + MGGBI	0.2311	0.2335		0.3522
Panel c—Utility
Portfolio Assets	Copula Allocation	Mean-variance Allocation		Naïve Allocation
ACWI + MGGBI	−0.24454	−0.24552		−0.24489
SIFSI + MGGBI	−0.24463	−0.24231		−0.24427
ACWI + SIFSI + MGGBI	−0.24507	−0.24590		−0.24354
Panel d—Forecast premium compared to the naïve allocation performed on all assets (33.33% ACWI + 33.33% SIFSI + 33.34% MGGBI)
Portfolio Assets	Copula Allocation		Mean-Variance Allocation
ACWI + MGGBI	−0.100%		−0.204%
SIFSI + MGGBI	−0.109%		0.123%
ACWI + SIFSI + MGGBI	−0.152%		−0.243%

reports the results for an investor with a risk aversion parameter, γ, equal to 5. Also, in this case, the weight of the investment on the stock indices is often above the 100% of the portfolio and the MGGBI is short sold, even if it happens less frequently and with lower leverage values compared to the case of γ = 5. This is especially true for the copula model, which is usually safer compared to the mean-variance allocation.

The mean-variance allocation presents a higher return (Table 4, panel a), but, due to the higher level of return volatility, the Sharpe ratio is in line with the copula model and is much lower than the naïve allocation (Table 4, panel b). The mean-variance trade-off is much stronger compared to the case of γ = 2, and the safest naïve allocation with all three assets having the highest utility level except for the portfolio investing in the SIFSI and MGGBI using the mean-variance model (Table 4, panel c). Indeed, the mean-variance criterion does not seem to be useful in terms of utility and the Sharpe ratio when the MSCI ACWI index is a feasible asset: When the riskiest asset is used with the riskiest way to build the portfolio, the return is higher, but the utility is lower even in the case of a not very risk averse investor.

Instead, the portfolio composed of the SIFSI and MGGBI presents a positive forecast premium (Table 4, panel d). The weights of these two indices are represented in Figure 3: The SIFSI has the largest weight with many periods in which the MGGBI is short sold.

Table 5. Results for investors with γ = 10.

Panel a—Final amount
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	1.3984	1.6588		1.4006
SIFSI + MGGBI	1.3350	1.5949		1.5029
ACWI + SIFSI + MGGBI	1.3798	1.6912		1.5679
Panel b—Sharpe ratio
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	0.3116	0.3069		0.3758
SIFSI + MGGBI	0.2745	0.2986		0.3143
ACWI + SIFSI + MGGBI	0.3161	0.2723		0.3522
Panel c—Utility
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	−0.10712	−0.10765		−0.10661
SIFSI + MGGBI	−0.10746	−0.10653		−0.10666
ACWI + SIFSI + MGGBI	−0.10736	−0.10782		−0.10591
Panel d—Forecast premium compared to the naïve allocation performed on all assets (33.33% ACWI + 33.33% SIFSI + 33.34% MGGBI)
Portfolio Assets	Copula Allocation		Mean-Variance Allocation
ACWI + MGGBI	−0.122%		−0.177%
SIFSI + MGGBI	−0.155%		−0.063%
ACWI + SIFSI + MGGBI	−0.145%		−0.194%

and

Table 6. Results for investors with γ = 15.

Panel a—Final amount
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	1.3318	1.4994		1.4006
SIFSI + MGGBI	1.2854	1.4502		1.5029
ACWI + SIFSI + MGGBI	1.3217	1.5225		1.5679
Panel b—Sharpe ratio
Portfolio Assets	Copula Allocation	Mean-variance Allocation		Naïve Allocation
ACWI + MGGBI	0.3581	0.3242		0.3758
SIFSI + MGGBI	0.3098	0.3465		0.3143
ACWI + SIFSI + MGGBI	0.3314	0.3065		0.3522
Panel c—Utility
Portfolio Assets	Copula Allocation	Mean-Variance Allocation		Naïve Allocation
ACWI + MGGBI	−0.06803	−0.06840		−0.06752
SIFSI + MGGBI	−0.06849	−0.06803		−0.06825
ACWI + SIFSI + MGGBI	−0.06817	−0.06850		−0.06745
Panel d—Forecast premium compared to the naïve allocation performed on all assets (33.33% ACWI + 33.33% SIFSI + 33.34% MGGBI)
Portfolio Assets	Copula Allocation		Mean-Variance Allocation
ACWI + MGGBI	−0.058%		−0.096%
SIFSI + MGGBI	−0.104%		−0.058%
ACWI + SIFSI + MGGBI	−0.072%		−0.106%

report the results for a very risk averse investor, that is, an investor with γ = 10 or 15. In these cases, when the MSCI ACWI is not among the feasible assets, weights never exceed 100% and there is no short selling. However, when MSCI ACWI is also present, the short selling of the bond index is very rare, especially if γ = 15 or if the copula model is applied.

The naïve model performs better than the copula and mean-variance models in terms of utility, implying negative forecast premiums. The equally divided allocation also grants higher Sharpe ratios when γ = 10, and the one using all three indices has the best return when γ = 15. Indeed, among the three sets of feasible assets, as already said, the best performance of the naïve model is obtained when all three indices are jointly present.

To summarize our results, we can say that:

• If the investor is relatively risk prone (γ = 2 or 5), the utility is maximized when the mean-variance allocation (that is, the relatively riskiest model for portfolio allocation) is applied to a portfolio that uses the SIFSI and the bond index, avoiding the overall stock market index (that is, the riskiest index in terms of skewness and kurtosis);
• If the investor is very risk averse (γ = 10 or 15), the utility is simply maximized with a naïve allocation including all indices.

Therefore, investing in stocks of social impact finance firms seems to be an effective way to improve the portfolio performance for investors with different levels of risk aversion.

Moreover, it should be noted that this result was obtained from an out-of-sample period (June 2013–September 2018) in which the global financial markets performed well, as shown in the right panel of Figure 1. Hence, this result goes beyond the postulated benefits during a market crisis similarly to other alternative investments that outperform conventional assets during periods of market crises, while they underperform during non-crisis periods (such as art investments or SRI funds, as found by the already cited Campbell [24,25] and Nofsinger and Varma [28])).

4.1. Robustness Check

There is a vast literature on the importance of the method used to estimate inputs of the model; that is, for instance, the expected return. Michaud [43] explains that sample estimators in classical portfolio optimization (e.g., Markowitz [9]) also produce the maximization of some estimation errors, leading managers to “distort” optimal portfolios. In order to circumvent this problem, many authors suggest alternative approaches and different techniques of estimation (see, for instance, Jagannathan and Ma [44], and Ledoit and Wolf [45,46]). DeMiguel et al. [47] performed a good review of the different methods used to estimate expected returns and the variance-covariance matrix, and find that none of the 14 models evaluated across seven empirical datasets “is consistently better than the 1/N naïve rule in terms of Sharpe ratio, certainty-equivalent return, or turnover, which indicates that, out of sample, the gain from optimal diversification is more than offset by estimation error”. Given that, as explained by Brandt [48], “the return modeling step is without doubt the Achilles’ heel of the traditional econometric approach”, we performed a simple robustness check on the means estimation. In the baseline simulation, we used historical unconditional means to forecast the expected return. In this robustness check, we assumed that the asset manager is able to perfectly forecast the expected return. Therefore, we used the real return of the next month as an estimate of the expected return. Indeed, as shown in the stock pricing context by authors, such as Elton [49], and Chava and Purnanandam [50], the results derived with expected returns and realized returns can be different because the expected returns might be computed in many ways and they are a very poor measure of the realized returns (and vice versa). Obviously, the assumption of a perfect mean forecast is only theoretical and it implies the use of large values as inputs for the expected returns. Consequently, portfolios thus have to include excessively large short sales and very extreme returns. However, also in this case, the best out-of-sample performance in terms of returns and utility, for investors with γ = 5, 10, and 15, is shown by the portfolio invested in all three indices, which uses the mean-variance model, that is the model with the largest overweight/short sales. This result is not surprising, but it is interesting to see that on average in the 60 months, the SIFSI is the index with the largest fraction of the portfolio, as reported in

Table 7. Average portfolio fraction invested in the three indices for investors with γ = 5, 10, and 15 and a perfect forecast of expected return.

	SIFSI	ACWI	MGGBI
γ = 5	104.6%	38.3%	−42.9%
γ = 10	55.5%	23.8%	20.6%
γ = 15	37.6%	18.9%	43.4%

. Therefore, we can confirm the importance of a significant portfolio stake committed to SIF investments.

5. Conclusions

Besides their social impact, social impact investments should be considered as an alternative asset class that can be used for portfolio allocation. Indeed, the Mission Alignment Working Group [5] finds that, in contrast to the majority of financial assets, these investments are anticyclical. Therefore, SIIs could improve portfolio diversification. Consequently, SII can interest not only investors concerned by their social impact (“impact-first” investors), but also “standard” investors interested by the risk-return portfolio performance (“financial-first” investors, as categorized by Freireick and Fulton [4]).

However, few studies (see, for instance, La Torre, Chiappini, and Mango [6]) have investigated the risk-return performance of SIIs and their utility for portfolio allocation. Therefore, this paper aimed to fill this gap in the literature. The dataset used in this paper was unique and based on a sample of listed companies that show potential as SIIs according to the framework provided by the OECD [7]. We applied the SII criteria outlined by the OECD [7] to the universe of companies reported on wikipositive.org, a public portal on private and public enterprises that meet the highest financial, social, and environmental standards. This allowed us to build a social impact finance stock index (SIFSI) based on 50 listed SIFs.

We compared the out-of-sample results for portfolios including or not the abovementioned social impact index among the feasible assets. We constructed portfolios with three different methodologies (naïve, Markowitz mean-variance optimization, and the GARCH-copula model), and studied the performance in terms of returns, Sharpe ratio, utility, and forecast premium based on a constant relative risk aversion function for investors with different levels of risk aversion.

We found that relatively risk prone investors maximize their utility when the mean-variance allocation is applied to a portfolio that uses the social impact finance index and the bond index, without the overall stock market index, while very risk adverse investors maximize their utility with a naïve allocation including all indices. In the former case, the weight of the SIFSI was found to be very large (sometimes above the 100% of the value of the portfolio, with a short selling of the bond index), while in the latter case, the weight of the SIFSI was 33.33%, which was much larger than the capitalization of the SIF stocks compared to the whole stock market. Obviously, the capitalization and the liquidity of these stocks would not be enough to absorb a very large demand by the investors, which would probably create a bubble on the price of these stocks. However, our macro asset allocation shows the importance of a significant portfolio stake committed to SIF investments and, consequently, investors should closely monitor SIFs in order to include their stocks in their portfolios.

However, a word of caution and further investigation is needed. As explained in Section 4.1, there is ample literature about the importance of the method used to estimate the inputs of the model. Therefore, many robustness checks of our results might be performed by changing the methods used to estimate the inputs, as well as the dataset (time span and asset classes), utility functions, performance evaluation criteria, and kind of asset allocation strategies, for instance, by introducing short selling constraints. Moreover, prior literature on asset allocation has identified additional issues to be further investigated (for a review on these issues, see, for instance, Brandt [48]). Among the most relevant topics, we can cite the issue of multiperiodal allocation; the presence of frictions, such as transaction costs and taxation; or the problem of intermediate consumption and background risk (for example, in order to reduce transaction costs, investors should decide on the optimal number of assets to use and the optimal time to rebalance, as reported in Jansen and Van Dijk [51] and Gaivoronski et al. [52], respectively). Therefore, our analysis is only a first attempt at shedding light on the overarching theme of SIF stocks as portfolio components and can be interpreted as a promising result warranting further investigation.