Estimation of Soil Respiration by Its Driving Factors Based on Multi-Source Data in a Sub-Alpine Meadow in North China
Abstract
:1. Introduction
2. Materials and Methods
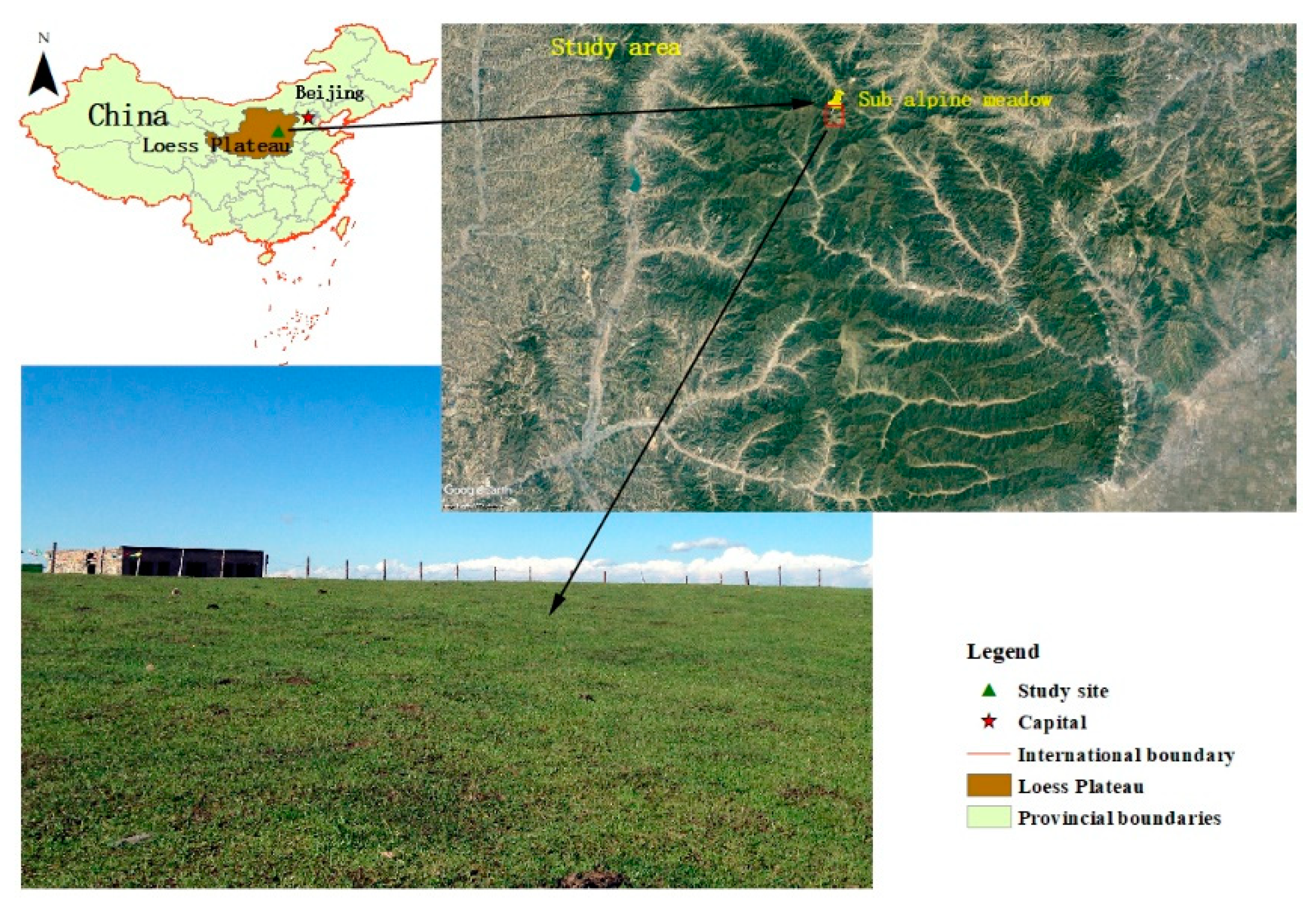
2.1. Overview of the Studying Site
2.2. Experimental Procedures and Measurement of Rs and the Related Environmental Factors
2.3. Modeling Strategy
3. Results
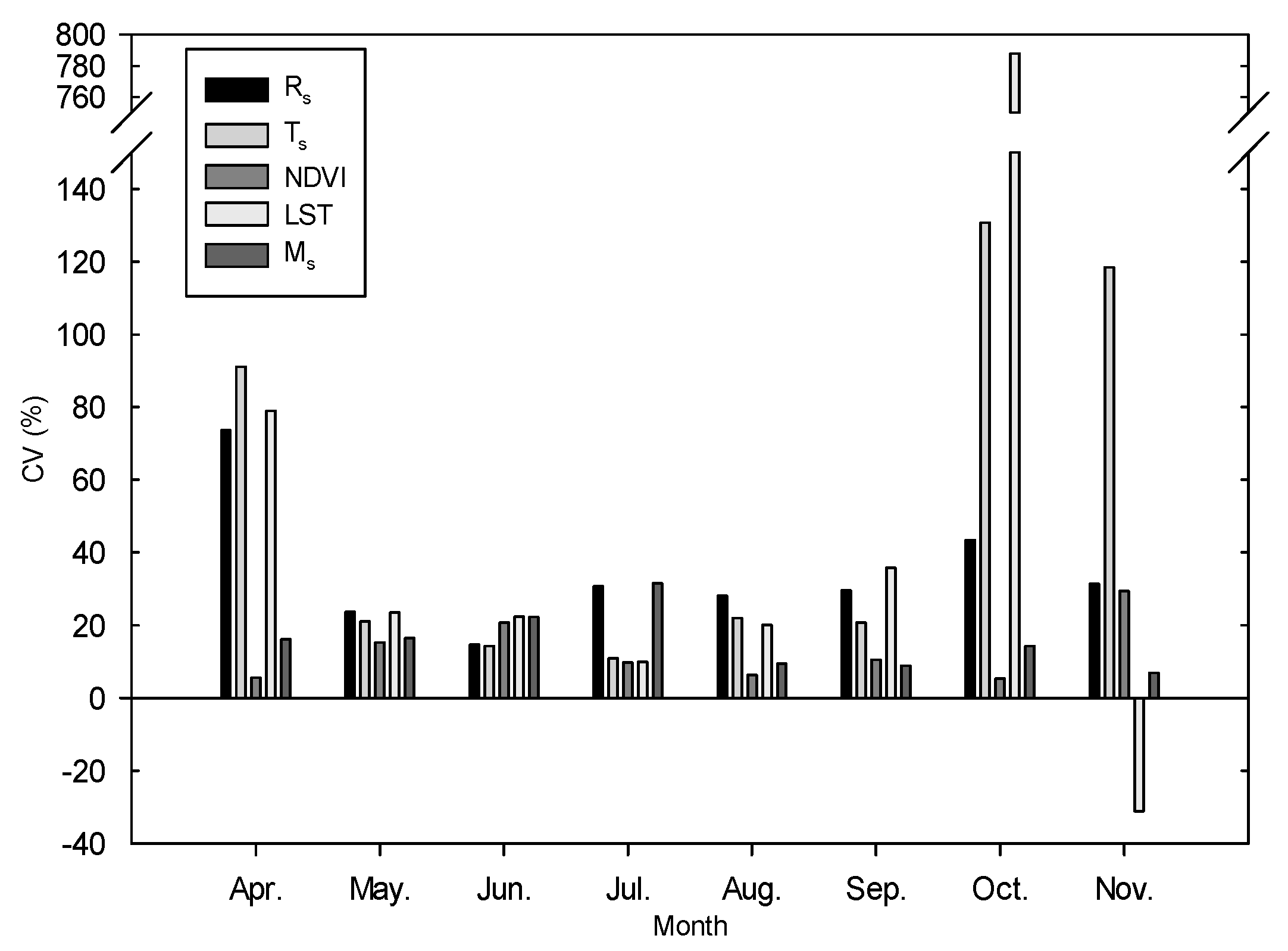
3.1. Seasonal Variations in Rs
3.2. Modeling Rs Seasonal Variations
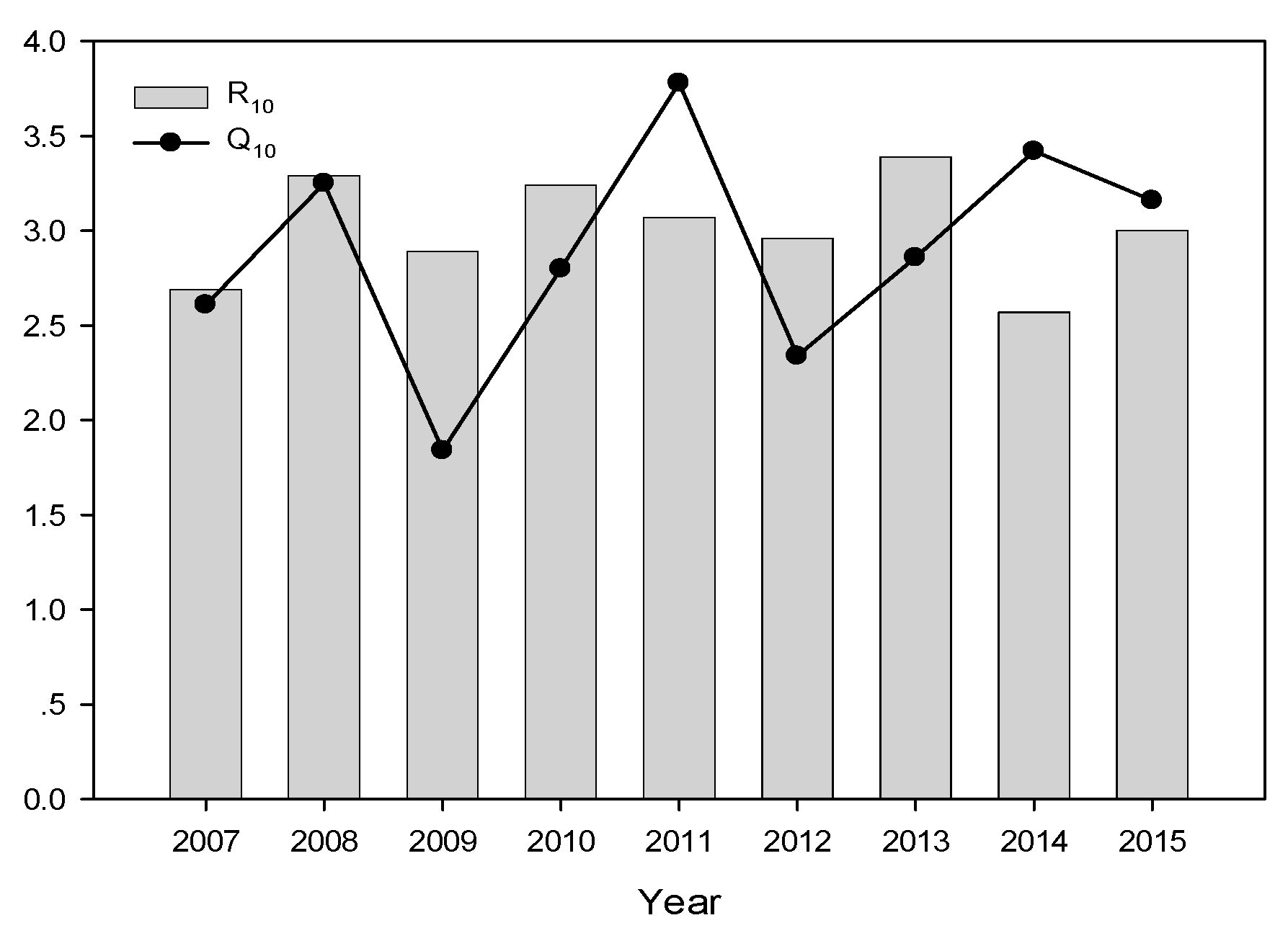
3.3. Temperature Sensitivity of Rs
4. Discussion
4.1. Seasonal Variations in Rs
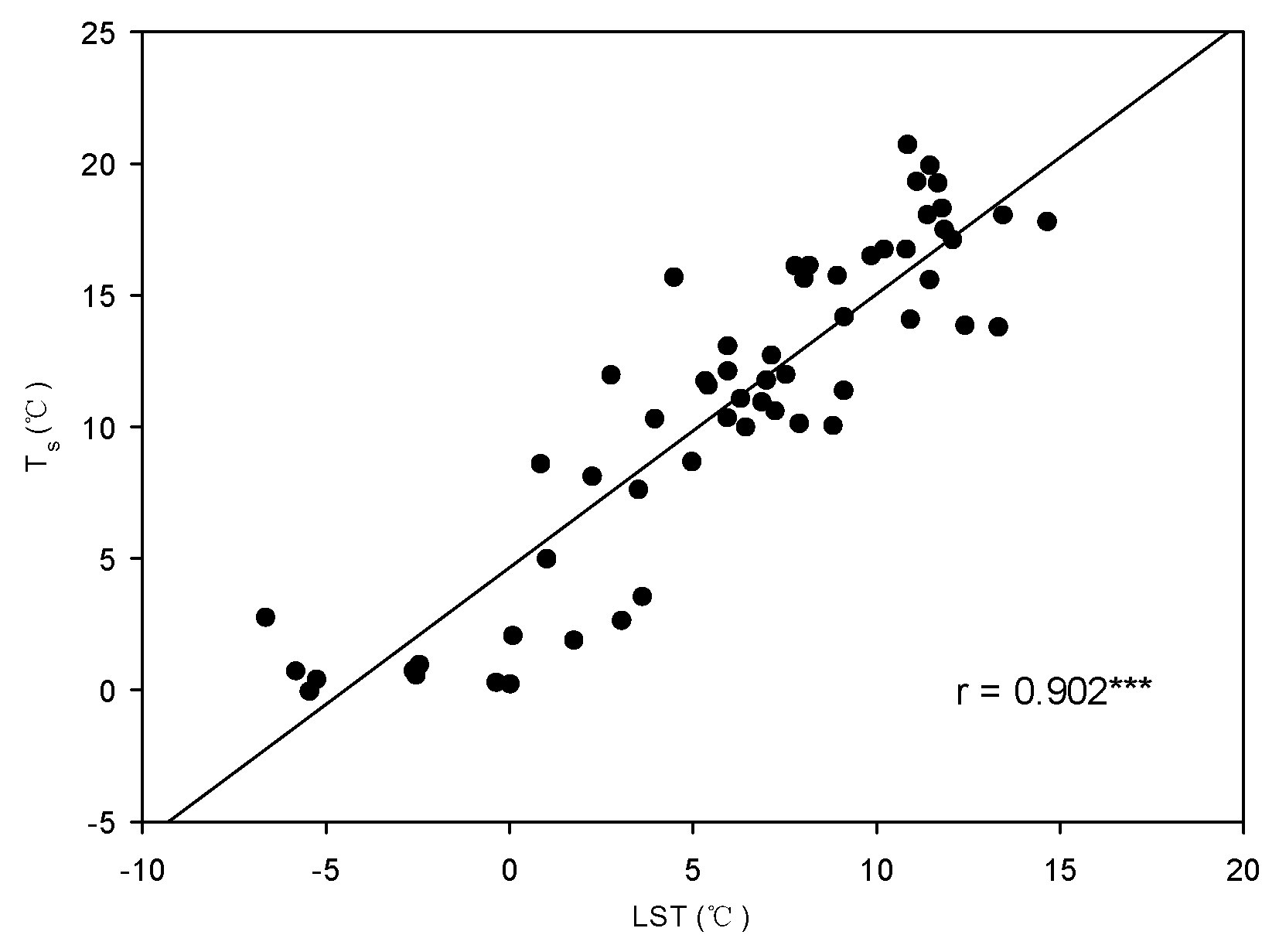
4.2. Factors Affecting the Seasonal Variations of Rs
4.3. Temperature Sensitivity of Rs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, M.G.; Jin, G.Z. Seasonal variations of Q(10) soil respiration and its components in the temperate forest ecosystems, northeastern China. Eur. J. Soil Biol. 2018, 85, 36–42. [Google Scholar] [CrossRef]
- Zhao, K.J.; Dong, B.Q.; Jia, Z.K.; Ma, L. Effect of climatic factors on the temporal variation of stem respiration in Larix principis-rupprechtii Mayr. Agric. For. Meteorol. 2018, 248, 441–448. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Goldberg, S.D.; Xu, J.C.; Harrison, R.D. Spatial and seasonal variation in soil respiration along a slope in a rubber plantation and a natural forest in Xishuangbanna, Southwest China. J Mt. Sci. 2018, 15, 695–707. [Google Scholar] [CrossRef]
- Ohashi, M.; Gyokusen, K. Temporal change in spatial variability of soil respiration on a slope of Japanese cedar (Cryptomeria japonica D. Don) forest. Soil Biol. Biochem. 2007, 39, 1130–1138. [Google Scholar] [CrossRef]
- Wu, C.Y.; Gaumont-Guay, D.; Black, T.A.; Jassal, R.S.; Xu, S.G.; Chen, J.M.; Gonsamo, A. Soil respiration mapped by exclusively use of MODIS data for forest landscapes of Saskatchewan, Canada. ISPRS J. Photogramm. Remote Sens. 2014, 94, 80–90. [Google Scholar] [CrossRef]
- Raich, J.W.; Potter, C.S. Global Patterns of Carbon-Dioxide Emissions from Soils. Glob. Biogeochem. Cycle 1995, 9, 23–36. [Google Scholar] [CrossRef]
- Foti, S.; Balogh, J.; Nagy, Z.; Herbst, M.; Pinter, K.; Peli, E.; Koncz, P.; Bartha, S. Soil moisture induced changes on fine-scale spatial pattern of soil respiration in a semi-arid sandy grassland. Geoderma 2014, 213, 245–254. [Google Scholar] [CrossRef]
- Munoz-Rojas, M.; Lewandrowski, W.; Erickson, T.E.; Dixon, K.W.; Merritt, D.J. Soil respiration dynamics in fire affected semi-arid ecosystems: Effects of vegetation type and environmental factors. Sci. Total Environ. 2016, 572, 1385–1394. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579. [Google Scholar] [CrossRef]
- Zeng, X.H.; Song, Y.G.; Zhang, W.J.; He, S.B. Spatio-temporal Variation of Soil Respiration and Its Driving Factors in Semi-arid Regions of North China. Chin. Geogr. Sci. 2018, 28, 12–24. [Google Scholar] [CrossRef]
- Ahmad, W.; Singh, B.; Dijkstra, F.A.; Dalal, R.C.; Geelan-Small, P. Temperature sensitivity and carbon release in an acidic soil amended with lime and mulch. Geoderma 2014, 214, 168–176. [Google Scholar] [CrossRef]
- Ahmad, W.; Singh, B.; Dijkstra, F.A.; Dalal, R.C. Inorganic and organic carbon dynamics in a limed acid soil are mediated by plants. Soil Biol. Biochem. 2013, 57, 549–555. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Sanchez, M.L.; Ozores, M.I.; Lopez, M.J.; Colle, R.; De Torre, B.; Garcia, M.A.; Perez, I. Soil CO2 fluxes beneath barley on the central Spanish plateau. Agric. For. Meteorol. 2003, 118, 85–95. [Google Scholar] [CrossRef]
- Borken, W.; Xu, Y.J.; Brumme, R.; Lamersdorf, N. A climate change scenario for carbon dioxide and dissolved organic carbon fluxes from a temperate forest soil: Drought and rewetting effects. Soil Sci. Soc. Am. J. 1999, 63, 1848–1855. [Google Scholar] [CrossRef]
- Birch, H.F. The effect of soil drying on humus decomposition and nitrogen availability. Plant Soil 1958, 10, 9–31. [Google Scholar] [CrossRef]
- Ahmad, W.; Singh, B.; Dalal, R.C.; Dijkstra, F.A. Carbon dynamics from carbonate dissolution in Australian agricultural soils. Soil Res. 2015, 53, 144–153. [Google Scholar] [CrossRef]
- Samuelson, L.; Mathew, R.; Stokes, T.; Feng, Y.C.; Aubrey, D.; Coleman, M. Soil and microbial respiration in a loblolly pine plantation in response to seven years of irrigation and fertilization. For. Ecol. Manag. 2009, 258, 2431–2438. [Google Scholar] [CrossRef]
- Li, H.J.; Yan, J.X.; Yue, X.F.; Wang, M.B. Significance of soil temperature and moisture for soil respiration in a Chinese mountain area. Agric. For. Meteorol. 2008, 148, 490–503. [Google Scholar] [CrossRef]
- Zhang, Q.; Katul, G.G.; Oren, R.; Daly, E.; Manzoni, S.; Yang, D.W. The hysteresis response of soil CO2 concentration and soil respiration to soil temperature. J. Geophys. Res. Biogeosci. 2015, 120, 1605–1618. [Google Scholar] [CrossRef]
- Huang, N.; Niu, Z. Estimating soil respiration using spectral vegetation indices and abiotic factors in irrigated and rainfed agroecosystems. Plant Soil 2013, 367, 535–550. [Google Scholar] [CrossRef]
- Huang, N.; Gu, L.H.; Black, T.A.; Wang, L.; Niu, Z. Remote sensing-based estimation of annual soil respiration at two contrasting forest sites. J. Geophys. Res. Biogeosci. 2015, 120, 2306–2325. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.; Gu, L.H.; Niu, Z. Estimating soil respiration using spatial data products: A case study in a deciduous broadleaf forest in the Midwest USA. J. Geophys. Res. Atmos. 2014, 119, 6393–6408. [Google Scholar] [CrossRef]
- Suqing, L.I.; Jintun, Z. Ecological analysis of subalpine meadow in Yunding Mountain, Shanxi. Geogr. Res. 2007, 26, 83–90. [Google Scholar]
- Yan, J.-X.; Li, J.-J.; Li, H.-J.; Zhang, Y.-H. Studies on spatial heterogeneity of soil respiration in a subalpine meadow. Huanjing Kexue 2013, 34, 3992–3999. [Google Scholar] [PubMed]
- Li, H.-J.; Gao, Y.-F.; Yan, J.-X.; Li, J.-J. Spatial heterogeneity of soil respiration in a subalpine meadow at different sampling scales. Huanjing Kexue 2014, 35, 4313–4320. [Google Scholar] [PubMed]
- Wan, Z.M. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Huang, N.; He, J.S.; Niu, Z. Estimating the spatial pattern of soil respiration in Tibetan alpine grasslands using Landsat TM images and MODIS data. Ecol. Indic. 2013, 26, 117–125. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancements and Retrogradation of Natural Vegetation; Texas A & M University, Remote Sensing Center: Greenbelt, MD, USA, 1974. [Google Scholar]
- Mo, W.; Lee, M.S.; Uchida, M.; Inatomi, M.; Saigusa, N.; Mariko, S.; Koizumi, H. Seasonal and annual variations in soil respiration in a cool-temperate deciduous broad-leaved forest in Japan. Agric. For. Meteorol. 2005, 134, 81–94. [Google Scholar] [CrossRef]
- Zhang, Q.; Lei, H.M.; Yang, D.W. Seasonal variations in soil respiration, heterotrophic respiration and autotrophic respiration of a wheat and maize rotation cropland in the North China Plain. Agric. For. Meteorol. 2013, 180, 34–43. [Google Scholar] [CrossRef]
- Widen, B. Seasonal variation in forest-floor CO2 exchange in a Swedish coniferous forest. Agric. For. Meteorol. 2002, 111, 283–297. [Google Scholar] [CrossRef]
- Kato, T.; Tang, Y.H.; Gu, S.; Cui, X.Y.; Hirota, M.; Du, M.Y.; Li, Y.N.; Zhao, Z.Q.; Oikawa, T. Carbon dioxide exchange between the atmosphere and an alpine meadow ecosystem on the Qinghai-Tibetan Plateau, China. Agric. For. Meteorol. 2004, 124, 121–134. [Google Scholar] [CrossRef]
- Hu, Y.G.; Jiang, L.L.; Wang, S.P.; Zhang, Z.H.; Luo, C.Y.; Bao, X.Y.; Niu, H.S.; Xu, G.P.; Duan, J.C.; Zhu, X.X.; et al. The temperature sensitivity of ecosystem respiration to climate change in an alpine meadow on the Tibet plateau: A reciprocal translocation experiment. Agric. For. Meteorol. 2016, 216, 93–104. [Google Scholar] [CrossRef]
- Jenkins, M.E.; Adams, M.A. Respiratory quotients and Q(10) of soil respiration in sub-alpine Australia reflect influences of vegetation types. Soil Biol. Biochem. 2011, 43, 1266–1274. [Google Scholar] [CrossRef]
- Moyano, F.E.; Manzoni, S.; Chenu, C. Responses of soil heterotrophic respiration to moisture availability: An exploration of processes and models. Soil Biol. Biochem. 2013, 59, 72–85. [Google Scholar] [CrossRef]
- Huang, N.; Niu, Z.; Zhan, Y.L.; Xu, S.G.; Tappert, M.C.; Wu, C.Y.; Huang, W.J.; Gao, S.; Hou, X.H.; Cai, D.W. Relationships between soil respiration and photosynthesis-related spectral vegetation indices in two cropland ecosystems. Agric. For. Meteorol. 2012, 160, 80–89. [Google Scholar] [CrossRef]
- Wan, S.; Norby, R.J.; Ledford, J.; Weltzin, J.F. Responses of soil respiration to elevated CO2, air warming, and changing soil water availability in a model old-field grassland. Glob. Chang. Biol. 2007, 13, 2411–2424. [Google Scholar] [CrossRef]
- Huang, G.; Li, Y.; Su, Y.G. Effects of increasing precipitation on soil microbial community composition and soil respiration in a temperate desert, Northwestern China. Soil Biol. Biochem. 2015, 83, 52–56. [Google Scholar] [CrossRef]
- Jiang, J.S.; Guo, S.L.; Zhang, Y.J.; Liu, Q.F.; Wang, R.; Wang, Z.Q.; Li, N.N.; Li, R.J. Changes in temperature sensitivity of soil respiration in the phases of a three-year crop rotation system. Soil Tillage Res. 2015, 150, 139–146. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef]
- Janssens, I.A.; Pilegaard, K. Large seasonal changes in Q(10) of soil respiration in a beech forest. Glob. Chang. Biol. 2003, 9, 911–918. [Google Scholar] [CrossRef]
- Andrews, J.A.; Matamala, R.; Westover, K.M.; Schlesinger, W.H. Temperature effects on the diversity of soil heterotrophs and the delta C-13 of soil-respired CO2. Soil Biol. Biochem. 2000, 32, 699–706. [Google Scholar] [CrossRef]
- Raich, J.W.; Schlesinger, W.H. The global carbon-dioxide flux in soil respiration and its relationship to vegetation and climate. Tellus Ser. B Chem. Phys. Meteorol. 1992, 44, 81–99. [Google Scholar] [CrossRef]
- Vincent, G.; Shahriari, A.R.; Lucot, E.; Badot, P.M.; Epron, D. Spatial and seasonal variations in soil respiration in a temperate deciduous forest with fluctuating water table. Soil Biol. Biochem. 2006, 38, 2527–2535. [Google Scholar] [CrossRef]




| Rs | Rs | Ts | Ms | LST | NDVI | |
|---|---|---|---|---|---|---|
| r | 1.000 | 0.896 ** | −0.183 | 0.834 ** | 0.753 ** | |
| p value | 0.000 | 0.169 | 0.000 | 0.000 |
| Models and Equations | R2 | RSS | RMSE | AIC | |
|---|---|---|---|---|---|
| (1) | 0.803 *** | 56.286 | 0.985 | 2.260 | |
| (2) | 0.842 *** | 4.742 | 0.286 | −141.231 | |
| (1) | 0.816 *** | 52.61 | 0.952 | 0.343 | |
| (2) | 0.850 *** | 4.499 | 0.279 | −142.282 | |
| (1) | 0.695 *** | 87.135 | 1.226 | 27.607 | |
| (2) | 0.762 *** | 7.135 | 0.351 | −117.535 | |
| (1) | 0.568 *** | 123.701 | 1.460 | 47.931 | |
| (2) | 0.605 *** | 11.823 | 0.451 | −88.243 | |
| (1) | 0.718 *** | 80.562 | 1.179 | 25.058 | |
| (2) | 0.782 *** | 6.537 | 0.336 | −120.612 | |
| (1) | 0.817 *** | 52.419 | 0.951 | 2.132 | |
| (2) | 0.854 *** | 4.364 | 0.274 | −142.049 | |
| (1) | 0.748 *** | 72.085 | 1.115 | 20.609 | |
| (2) | 0.819 *** | 5.431 | 0.306 | −129.363 | |
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2007–2015 | |
|---|---|---|---|---|---|---|---|---|---|
| R21 | 0.907 | 0.601 | 0.885 | 0.941 | 0.676 | 0.797 | 0.913 | 0.923 | 0.842 |
| R22 | 0.947 | 0.554 | 0.688 | 0.984 | 0.704 | 0.657 | 0.892 | 0.757 | 0.762 |
| RMSE1 | 0.211 | 0.330 | 0.216 | 0.221 | 0.326 | 0.282 | 0.252 | 0.179 | 0.286 |
| RMSE2 | 0.159 | 0.350 | 0.384 | 0.122 | 0.336 | 0.396 | 0.304 | 0.366 | 0.351 |
| AIC1 | −14.674 | −9.289 | −17.425 | −17.152 | −11.710 | −13.705 | −15.289 | −23.567 | −141.231 |
| AIC2 | −18.054 | −8.614 | −10.461 | −26.477 | −12.352 | −10.040 | −13.730 | −14.391 | −117.535 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Cai, Y.; Yan, J.; Li, H. Estimation of Soil Respiration by Its Driving Factors Based on Multi-Source Data in a Sub-Alpine Meadow in North China. Sustainability 2019, 11, 3274. https://doi.org/10.3390/su11123274
Liang Y, Cai Y, Yan J, Li H. Estimation of Soil Respiration by Its Driving Factors Based on Multi-Source Data in a Sub-Alpine Meadow in North China. Sustainability. 2019; 11(12):3274. https://doi.org/10.3390/su11123274
Chicago/Turabian StyleLiang, Yanan, Yanpeng Cai, Junxia Yan, and Hongjian Li. 2019. "Estimation of Soil Respiration by Its Driving Factors Based on Multi-Source Data in a Sub-Alpine Meadow in North China" Sustainability 11, no. 12: 3274. https://doi.org/10.3390/su11123274
APA StyleLiang, Y., Cai, Y., Yan, J., & Li, H. (2019). Estimation of Soil Respiration by Its Driving Factors Based on Multi-Source Data in a Sub-Alpine Meadow in North China. Sustainability, 11(12), 3274. https://doi.org/10.3390/su11123274




