Application of Multivariate Statistical Analysis to Identify Water Sources in A Coastal Gold Mine, Shandong, China
Abstract
:1. Introduction
2. Materials and Methods
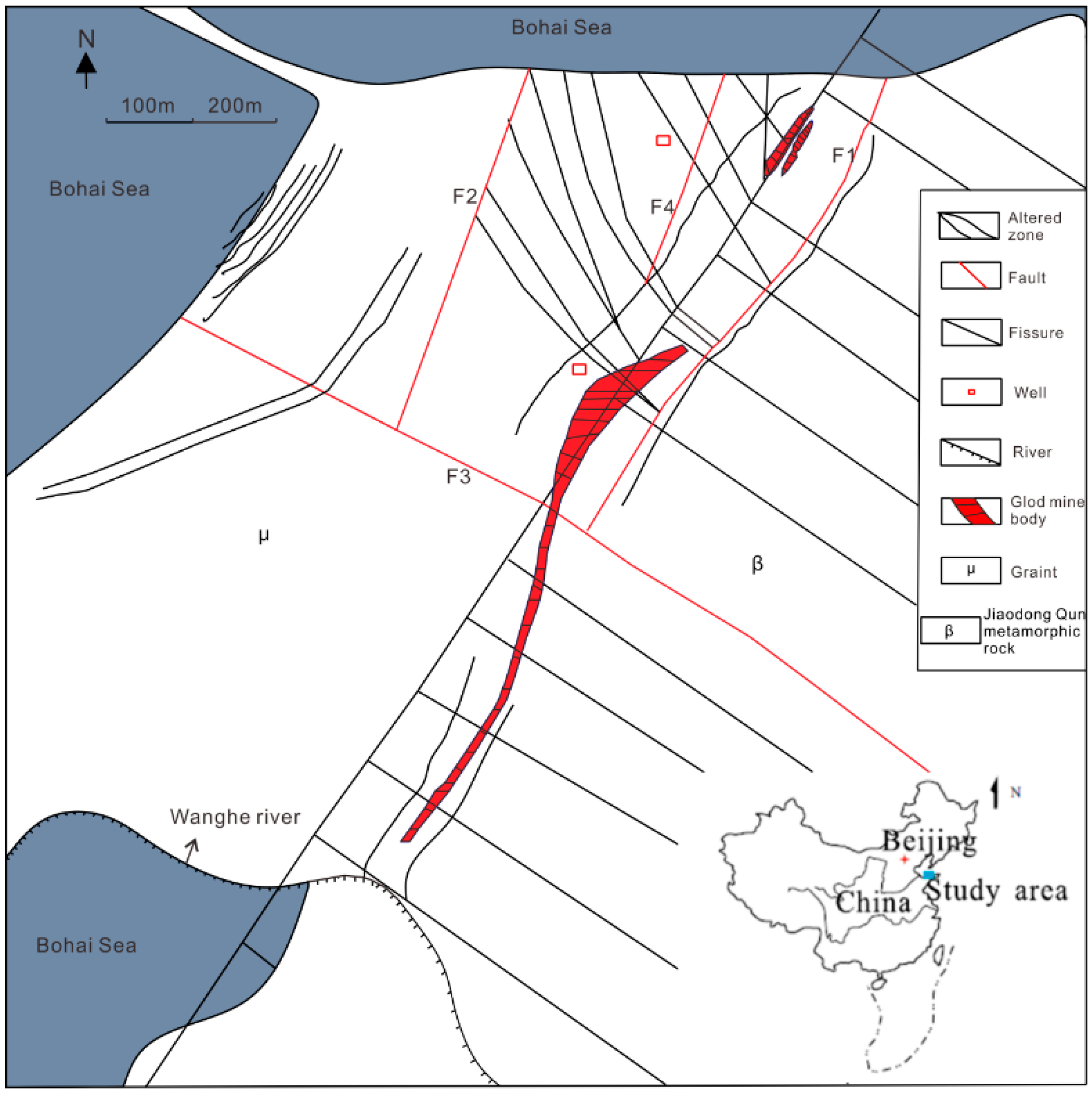
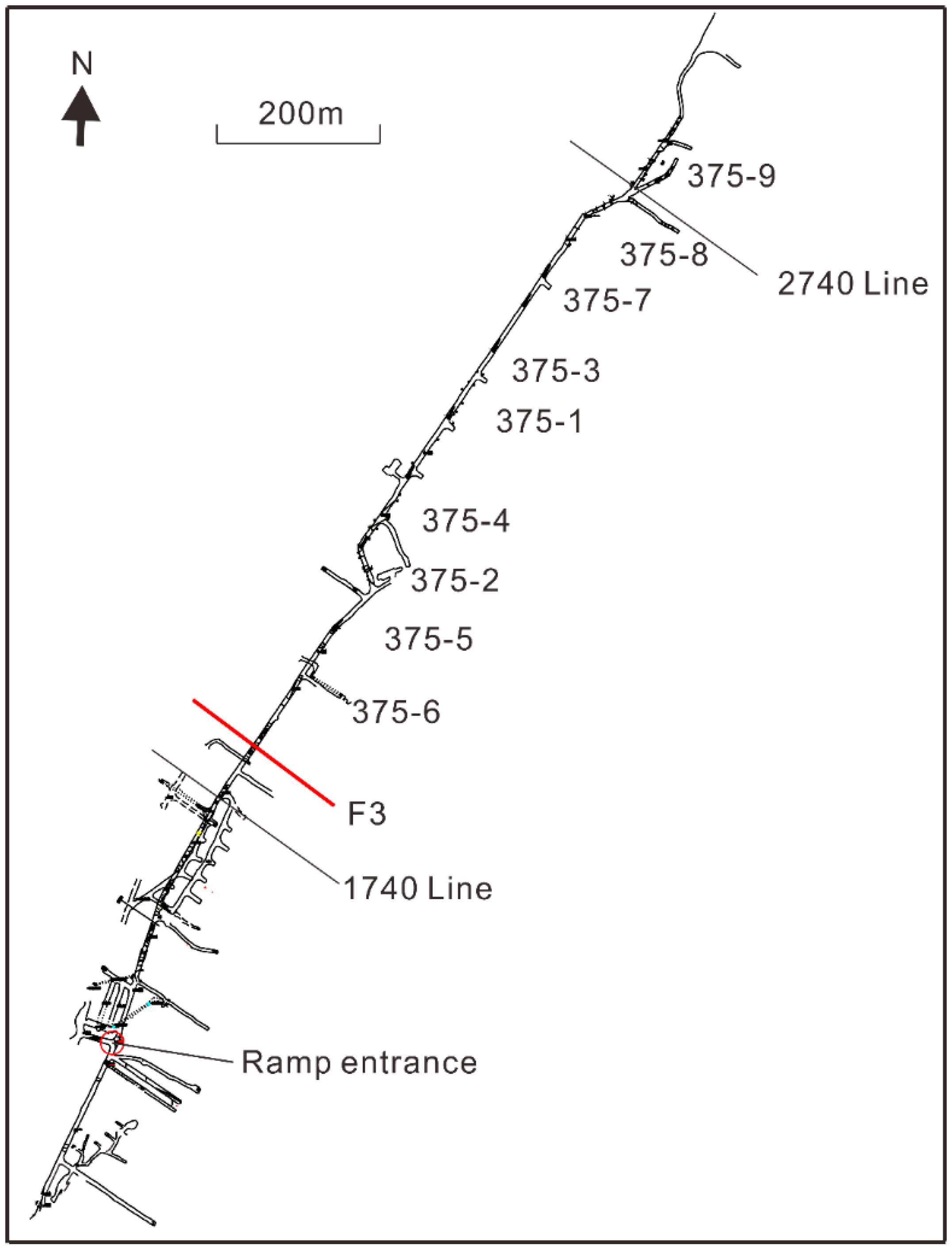
2.1. Geological and Hydrogeological Setting
2.2. Water Sampling and Analysis
2.3. Factor Analysis
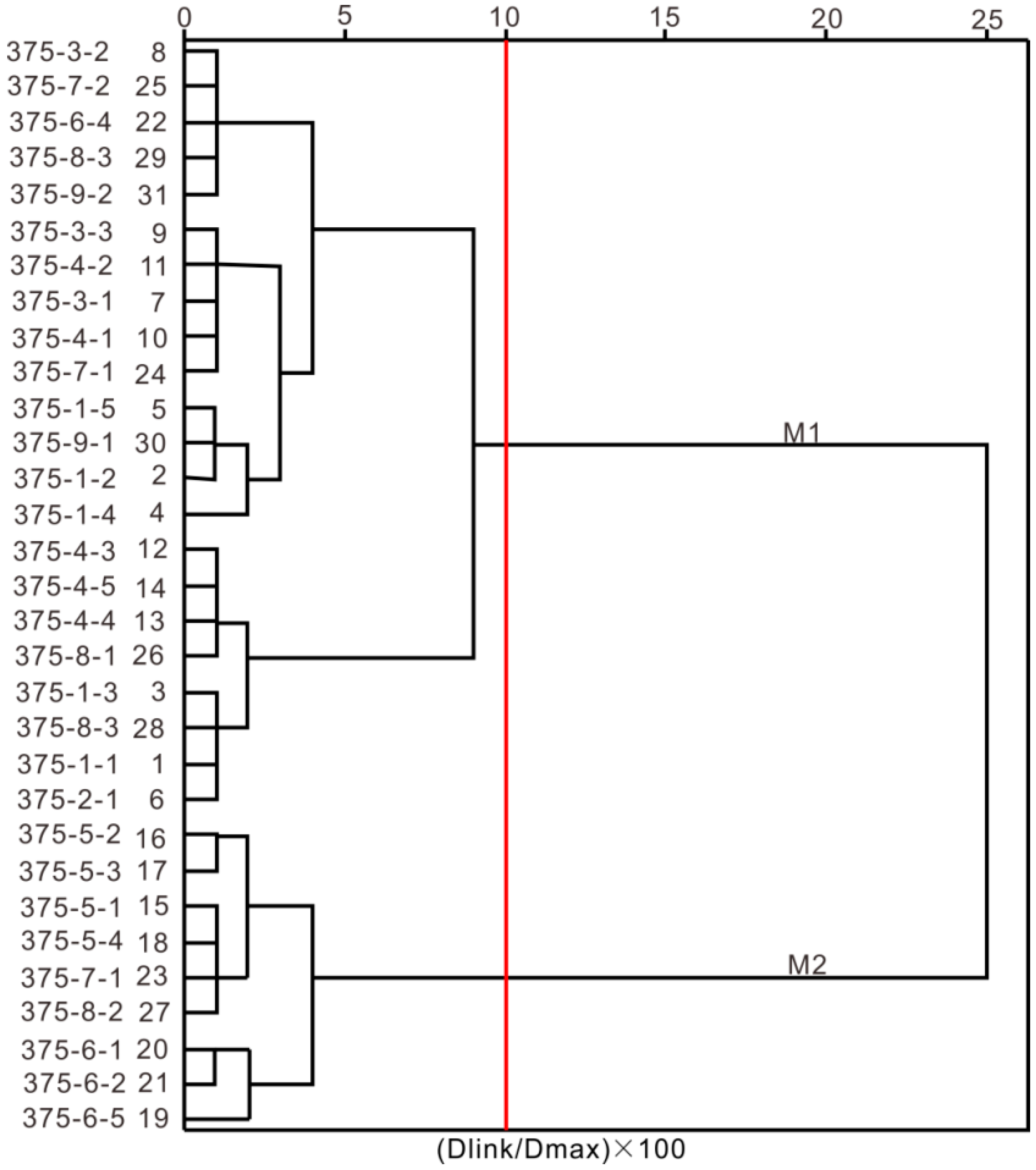
2.4. Clustering Analysis
2.5. Discriminant Analysis
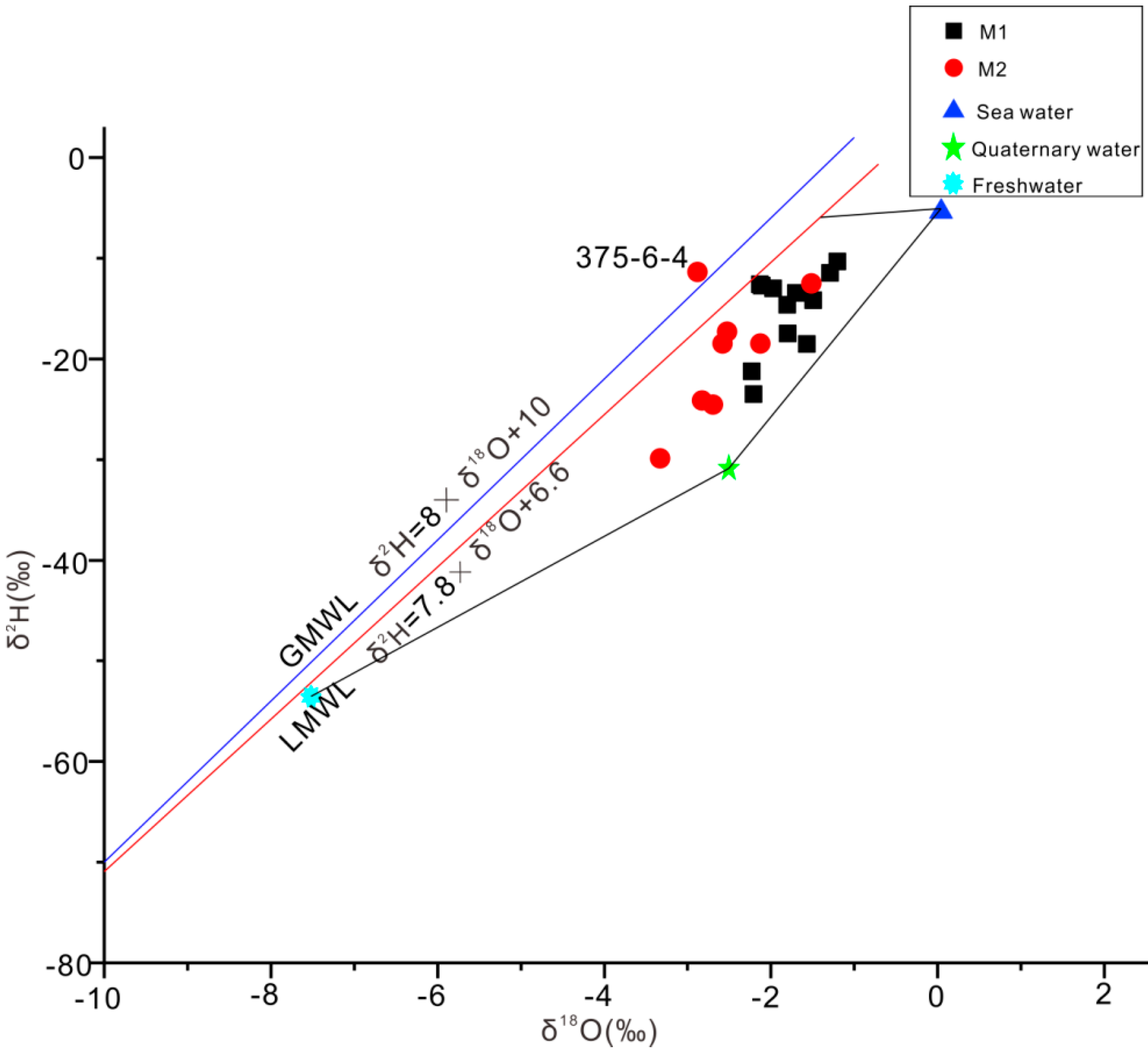
3. Results of Multivariate Statistical Analysis
4. Discussion
5. Conclusions
- (1)
- According to the hydrochemical information of the water samples from Xishan gold mine, the hydrochemical data were preprocessed, and the water samples were divided into M1 and M2 by factor analysis combined with principle component analysis. Among the 31 water samples, three were discriminated incorrectly, and the correct rate of discrimination was 90.3%.
- (2)
- Stepwise discriminant analysis and factor analysis were combined to process the data of seven conventional ions. The Bayes linear discriminant function and function values from the 1740 exploration line to 2740 exploration line in the −375 m sublevel were obtained. The Bayes linear function discriminant results were completely consistent with the results of the factor analysis method, and the two selected discriminant water samples also agreed. The consistency of the discriminant results showed that the factor analysis method and the stepwise analysis method were mutually verified.
- (3)
- A multivariate statistical method was combined to obtain a quantitative Bayes linear discriminant function, which was applied to recognize the source type in the mining area. It was only necessary to know the ion concentration of the corresponding variable, and the water sample type could be determined by substituting the value of the corresponding variable. This method is accurate, fast, and economical.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| ID | δD | δ18O (‰) |
|---|---|---|
| 375-1-1 | −16.907 | −1.458 |
| 375-1-2 | −11.247 | −2.304 |
| 375-1-3 | −17.518 | −1.895 |
| 375-1-4 | −23.531 | −2.076 |
| 375-1-5 | −6.478 | −2.258 |
| 375-2-1 | −15.49 | −1.35 |
| 375-3-1 | −13.573 | −1.215 |
| 375-3-2 | −8.703 | −1.916 |
| 375-3-3 | −21.602 | −2.404 |
| 375-4-1 | −15.387 | −1.33 |
| 375-4-2 | −14.047 | −1.983 |
| 375-4-3 | −14.633 | −1.807 |
| 375-4-4 | −23.488 | −2.207 |
| 375-4-5 | −17.478 | −1.799 |
| 375-5-1 | −24.546 | −2.694 |
| 375-5-2 | −18.458 | −2.583 |
| 375-5-3 | −24.136 | −2.83 |
| 375-5-4 | −29.88 | −3.328 |
| 375-5-5 | −11.362 | −2.88 |
| 375-6-1 | −18.47 | −2.129 |
| 375-6-2 | −17.286 | −2.525 |
| 375-6-3 | −12.475 | −1.515 |
| 375-7-1 | −21.256 | −2.234 |
| 375-7-2 | −13.0051 | −1.97206 |
| 375-7-3 | −11.4324 | −1.28895 |
| 375-8-1 | −12.7097 | −2.11231 |
| 375-8-2 | −18.502 | −1.571 |
| 375-8-3 | −12.581 | −2.135 |
| 375-8-4 | −14.1866 | −1.49238 |
| 375-9-1 | −10.337 | −1.20527 |
| 375-9-2 | −13.4648 | −1.70191 |
| Quaternary water | −32.03 | −3.585 |
| Freshwater | −53.44 | −7.543 |
| Sea water | −5.18 | −0.181 |
References
- Wu, J.; Xu, S.; Zhou, R.; Qin, Y. Scenario analysis of mine water inrush hazard using Bayesian networks. Saf. Sci. 2016, 89, 231–239. [Google Scholar] [CrossRef]
- Epstein, R.; Goic, M.; Weintraub, A.; Catalán, J.; Santibáñez, P.; Urrutia, R.; Cancino, R.; Gaete, S.; Aguayo, A.; Caro, F. Optimizing Long-Term Production Plans in Underground and Open-Pit Copper Mines. Oper. Res. 2012, 60, 4–17. [Google Scholar] [CrossRef]
- Unlu, T.; Akcin, H.; Yilmaz, O. An integrated approach for the prediction of subsidence for coal mining basins. Eng. Geol. 2013, 166, 186–203. [Google Scholar] [CrossRef]
- Meng, Z.; Li, G.; Xie, X. A geological assessment method of floor water inrush risk and its application. Eng. Geol. 2012, 143–144, 51–60. [Google Scholar] [CrossRef]
- Ma, D.; Rezania, M.; Yu, H.S.; Bai, H.B. Variations of hydraulic properties of granular sandstones during water inrush: Effect of small particle migration. Eng. Geol. 2017, 217, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Bai, H.; Ma, D.; Chen, Z. Mechanical behavior of groundwater seepage in karst collapse pillars. Eng. Geol. 2013, 164, 101–106. [Google Scholar] [CrossRef]
- Gu, H.; Ma, F.; Guo, J.; Li, K.; Lu, R. Assessment of Water Sources and Mixing of Groundwater in a Coastal Mine: The Sanshandao Gold Mine, China. Mine Water Environ. 2017, 37, 351–365. [Google Scholar] [CrossRef]
- Janson, E.; Boyce, A.J.; Burnside, N.; Gzyl, G. Preliminary investigation on temperature, chemistry and isotopes of mine water pumped in Bytom geological basin (USCB Poland) as a potential geothermal energy source. Int. J. Coal Geol. 2016, 164, 104–114. [Google Scholar] [CrossRef]
- Wang, J.; Lu, C.; Sun, Q.; Xiao, W.; Cao, G.; Li, H.; Yan, L.; Zhang, B. Simulating the hydrologic cycle in coal mining subsidence areas with a distributed hydrologic model. Sci. Rep. 2017, 7, 39983. [Google Scholar] [CrossRef]
- Liu, Y.; An, S.; Xu, Z.; Fan, N.; Cui, J.; Wang, Z.; Liu, S.; Pan, J.; Lin, G. Spatio-temporal variation of stable isotopes of river waters, water source identification and water security in the Heishui Valley (China) during the dry-season. Hydrogeol. J. 2008, 16, 311–319. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Lei, X.; Wang, H. New approach for point pollution source identification in rivers based on the backward probability method. Environ. Pollut. 2018, 241, 759–774. [Google Scholar] [CrossRef]
- Huang, P.; Chen, J. Recharge sources and hydrogeochemical evolution of groundwater in the coal-mining district of Jiaozuo, China. Hydrogeol. J. 2012, 20, 739–754. [Google Scholar] [CrossRef]
- Christophersen, N.; Hooper, R.P. Multivariate analysis of stream water chemical data: The use of principal components analysis for the end-member mixing problem. Water Resour. Res. 1992, 28, 99–107. [Google Scholar] [CrossRef]
- Doctor, D.H.; Alexander, E.C.; Petrič, M.; Kogovšek, J.; Urbanc, J.; Lojen, S.; Stichler, W. Quantification of karst aquifer discharge components during storm events through end-member mixing analysis using natural chemistry and stable isotopes as tracers. Hydrogeol. J. 2006, 14, 1171–1191. [Google Scholar] [CrossRef]
- Laaksoharju, M.; Skårman, C.; Skårman, E. Multivariate mixing and mass balance (M3) calculations, a new tool for decoding hydrogeochemical information. Appl. Geochem. 1999, 14, 861–871. [Google Scholar] [CrossRef]
- Carrera, J.; Vázquez-Suñé, E.; Castillo, O.; Sánchez-Vila, X. A methodology to compute mixing ratios with uncertain end-members. Water Resour. Res. 2004, 40, 12101–12112. [Google Scholar] [CrossRef]
- Güler, C.; Thyne, G.D. Delineation of hydrochemical facies distribution in a regional groundwater system by means of fuzzy c-means clustering. Water Resour. Res. 2004, 40, 12503–12515. [Google Scholar]
- Li, K.; Ma, F.; Zhang, H.; Li, W.; Lv, Y. Recharge resource identification and evolution Inflowing-water in a sea bed gold mine. J. Eng. Geol. 2017, 25, 180–189. (In Chinese) [Google Scholar]
- Chen, K.; Jiao, J.J.; Huang, J.; Huang, R. Multivariate statistical evaluation of trace elements in groundwater in a coastal area in Shenzhen, China. Environ. Pollut. 2007, 147, 771–780. [Google Scholar] [CrossRef]
- Long, A.J.; Valder, J.F. Multivariate analyses with end-member mixing to characterize groundwater flow: Wind Cave and associated aquifers. J. Hydrol. 2011, 409, 315–327. [Google Scholar] [CrossRef]
- Hao, Z.; Duoxi, Y.; Haifeng, L.; Ningning, Z.; Liang, X. Application of principal component analysis and Bayes discrimination approach in water source identification. Coal Geol. Explor. 2017, 16. [Google Scholar]
- Raiber, M.; White, P.A.; Daughney, C.J.; Tschritter, C.; Davidson, P.; Bainbridge, S.E. Three-dimensional geological modelling and multivariate statistical analysis of water chemistry data to analyse and visualise aquifer structure and groundwater composition in the Wairau Plain, Marlborough District, New Zealand. J. Hydrol. 2012, 436, 13–34. [Google Scholar] [CrossRef]
- Qian, J.; Wang, L.; Ma, L.; Lu, Y.; Zhao, W.; Zhang, Y. Multivariate statistical analysis of water chemistry in evaluating groundwater geochemical evolution and aquifer connectivity near a large coal mine, Anhui, China. Environ. Earth Sci. 2016, 75, 747. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, P.; Bai, Y.; Tian, Z.; Li, J.; Shao, X.; Mustavich, L.F.; Li, B.L. Assessment of surface water quality via multivariate statistical techniques: A case study of the Songhua River Harbin region, China. J. Hydro-Environ. Res. 2013, 7, 30–40. [Google Scholar] [CrossRef]
- Granato, D.; Santos, J.S.; Escher, G.B.; Ferreira, B.L.; Maggio, R.M. Use of principal component analysis (PCA) and hierarchical cluster analysis (HCA) for multivariate association between bioactive compounds and functional properties in foods: A critical perspective. Trends Food Sci. Technol. 2018, 72, 83–90. [Google Scholar] [CrossRef]
- Williams, M.R.; Leydecker, A.; Brown, A.D.; Melack, J.M. Processes regulating the solute concentrations of snowmelt runoff in two subalpine catchments of the Sierra Nevada, California. Water Resour. Res. 2001, 37, 1993–2008. [Google Scholar] [CrossRef]
- Liu, C. The geological analysis and modelling of mining water flow-as an example of San Shan island gold mine. J. Eng. Geol. 1994, 25, 180–189. (In Chinese) [Google Scholar]
- GU, H. A Study of Water Sources and Flow Paths in a Coastal Gold Mine; Institute of Geology and Geophysics; Chinese Academy of Sciences: Beijing, China, 2018. [Google Scholar]
- Ma, F.; Zhao, H.; Guo, J. Investigating the characteristics of mine water in a subsea mine using groundwater geochemistry and stable isotopes. Environ. Earth Sci. 2015, 74, 6703–6715. [Google Scholar] [CrossRef]
- Davis, J.C. Statitics and Data Analysis in Geology, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; p. 536. [Google Scholar]
- Friston, K.J.; Frith, C.D.; Liddle, P.F.; Frackowiak, R.S.J. Functional Connectivity: The Principal-Component Analysis of Large (PET) Data Sets. J. Cereb. Blood Flow Metab. 1993, 13, 5–14. [Google Scholar] [CrossRef]
- Salifu, A.; Petrusevski, B.; Ghebremichael, K.; Buamah, R.; Amy, G. Multivariate statistical analysis for fluoride occurrence in groundwater in the Northern region of Ghana. J. Contam. Hydrol. 2012, 140, 34–44. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
- Otto, M. Multivariate methods. In Analytical Chemistry; Kellner, R., Mermet, J.M., Otto, M., Widmer, H.M., Eds.; Wiley-VCH: Weinheim, Germany, 1998. [Google Scholar]
- Xiang, D.; Li, H.; Liu, X. Applied Multivariate Statistical Analysis; China University of Geosciences Press: Wuhan, China, 2005. (In Chinese) [Google Scholar]
- Gu, H.; Ma, F.; Guo, J.; Zhao, H.; Lu, R.; Liu, G. A spatial mixing model to assess groundwater dynamics affected by mining in a coastal fractured aquifer, China. Mine Water Environ. 2018, 37, 405–420. [Google Scholar] [CrossRef]
- Delsman, J.R.; Essink, G.H.O.; Beven, K.J.; Stuyfzand, P.J. Uncertainty estimation of end-member mixing using generalized likelihood uncertainty estimation (GLUE), applied in a lowland catchment. Water Resour. Res. 2013, 49, 4792–4806. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Qian, J.; Sun, X. Hydrochemical classification and identification for groundwater system by using integral multivariate statistical models: A case study in Guqiao Mine. J. China Coal Soc. 2010, 35, 0141–0144. [Google Scholar]
- Liu, J.; Xue, X.; Shi, Y.; Yu, Q.; Li, L. Application of multivariate statistical analysis model to identification of water inrush source in coal mines. China Coal 2013, 39, 101–104. [Google Scholar] [CrossRef]
- Li, J.; Su, C.; Xie, X.; Wang, Y. Application of multivariate statistical analysis to research the environment of groundwater: A case study at Datong basin, Northern China. Geol. Sci. Technol. Inf. 2010, 29, 94–100. [Google Scholar]


| Location | K+ | Na+ | Ca2+ | Mg2+ | Cl− | SO42− | HCO3− | pH | EC | TDS |
|---|---|---|---|---|---|---|---|---|---|---|
| (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (mg/L) | (μs/cm) | (mg/L) | ||
| 375-1-1 | 248.4 | 104,00 | 761.5 | 1287.9 | 19,852 | 2305.4 | 219.6 | 7.19 | 44,900 | 35,074.8 |
| 375-1-2 | 197 | 9750 | 801.6 | 1222.3 | 18,453.5 | 2334.3 | 233.7 | 7.74 | 39,600 | 32,995 |
| 375-1-3 | 205 | 10,031.2 | 849.7 | 1239.3 | 18,916.1 | 2497.6 | 244.6 | 7.07 | 42,300 | 33,991.5 |
| 375-1-4 | 190.2 | 9800 | 841.7 | 1215 | 19,224.5 | 624.4 | 250.7 | 7.31 | 42,100 | 32,147.5 |
| 375-1-5 | 179.7 | 9875 | 721.4 | 1166.4 | 18,402.1 | 2372.7 | 253.2 | 7.34 | 40,000 | 32,974.6 |
| 375-2-1 | 286 | 10,650 | 697.4 | 1312.2 | 19,852 | 2286.2 | 207.4 | 7.03 | 45,200 | 35,292.8 |
| 375-3-1 | 299.2 | 9445 | 537.1 | 1132.4 | 17,583.2 | 2017.3 | 219.6 | 7.36 | 40,800 | 31,233.8 |
| 375-3-2 | 241 | 8900 | 681.4 | 1040 | 16,705.8 | 2190.2 | 233.7 | 7.56 | 37,000 | 29,992.1 |
| 375-3-3 | 275.8 | 9200 | 753.5 | 1069.2 | 17,579.7 | 2286.2 | 273.3 | 7.45 | 39,800 | 31,437.9 |
| 375-4-1 | 316.8 | 9825 | 641.3 | 1044.9 | 17,583.2 | 2017.3 | 201.3 | 7.49 | 41,100 | 31,629.8 |
| 375-4-2 | 258 | 8900 | 921.8 | 945.3 | 17,014.2 | 2295.8 | 181.2 | 7.46 | 37,200 | 30,516.3 |
| 375-4-3 | 282.5 | 9725 | 1122.2 | 1001.2 | 18,607.7 | 2516.8 | 170.8 | 7.11 | 41,800 | 33,433.8 |
| 375-4-4 | 285.5 | 9900 | 1314.6 | 831.1 | 18,710.5 | 2401.5 | 168.4 | 7.32 | 40,800 | 33,614.5 |
| 375-4-5 | 285.1 | 10,000 | 1154.3 | 916.1 | 18,874.3 | 2401.5 | 170.8 | 7.03 | 40,900 | 33,821.3 |
| 375-5-1 | 260 | 12,050 | 1146.3 | 1020.6 | 21,979 | 2459.1 | 119.6 | 7.29 | 50,400 | 39,052.7 |
| 375-5-2 | 208 | 10,886.2 | 1523 | 972 | 20,818 | 2545.6 | 114.1 | 7.41 | 42,500 | 37,081.6 |
| 375-5-3 | 195 | 10,900 | 1595.2 | 957.4 | 19,738.6 | 2708.9 | 108 | 7.05 | 45,800 | 36,216.5 |
| 375-5-4 | 226.5 | 11,250 | 1643.3 | 823.8 | 21,280.6 | 2603.2 | 85.4 | 7.32 | 44,700 | 37,916.2 |
| 375-5-5 | 252.5 | 11,500 | 1971.9 | 517.6 | 21,471.7 | 2353.5 | 81.8 | 7.03 | 44,700 | 38,156.3 |
| 375-6-1 | 337.5 | 11,450 | 2084.2 | 777.6 | 22,156.3 | 2497.6 | 107.4 | 7.02 | 49,700 | 39,411.6 |
| 375-6-2 | 262 | 11,819 | 2276.5 | 726.6 | 22,411.5 | 2488 | 108 | 7.06 | 44,400 | 40,117.1 |
| 375-6-3 | 257.8 | 9062.5 | 505 | 1142.1 | 17,560.5 | 2315 | 236.1 | 7.64 | 34,500 | 31,080.1 |
| 375-7-1 | 305 | 10,700 | 1723.4 | 923.4 | 21,270 | 2363.1 | 134.2 | 7.17 | 48,100 | 37,424.9 |
| 375-7-2 | 251 | 9562.5 | 521 | 1154.3 | 17,642.4 | 2353.5 | 225.7 | 7.16 | 39,300 | 31,716.5 |
| 375-7-3 | 265.6 | 9187.5 | 481 | 1161.5 | 17,731.7 | 2238.2 | 230 | 7.66 | 34,400 | 31,296.2 |
| 375-8-1 | 290.4 | 10,350 | 1026 | 1078.9 | 18,965.7 | 1729.1 | 158.6 | 7.3 | 44,100 | 33,598.7 |
| 375-8-2 | 294 | 10,937.5 | 2312.6 | 626.9 | 21,794.7 | 2257.4 | 102.5 | 7.66 | 43,900 | 38,344.7 |
| 375-8-3 | 198.1 | 10,438 | 721.4 | 1287.9 | 19,597.1 | 2401.5 | 233.7 | 7.22 | 43,000 | 34,884 |
| 375-8-4 | 281.3 | 9062.5 | 521 | 1154.3 | 17,389.3 | 2353.5 | 230 | 7.54 | 35,000 | 30,992.4 |
| 375-9-1 | 205 | 10,375 | 681.4 | 1268.5 | 18,919 | 2449.5 | 256.2 | 7.63 | 42,500 | 34,154.6 |
| 375-9-2 | 262.5 | 9250 | 521 | 1154.3 | 17,731.7 | 2343.9 | 222.7 | 7.57 | 34,900 | 31,486.7 |
| K+ | Na+ | Ca2+ | Mg2+ | Cl− | SO42− | CHO3− | pH | EC | TDS | |
|---|---|---|---|---|---|---|---|---|---|---|
| K+ | 1.000 | 0.010 | 0.194 | −0.366 | 0.065 | 0.037 | −0.270 | −0.105 | 0.112 | 0.065 |
| Na+ | 1.000 | 0.763 | −0.496 | 0.956 | 0.260 | −0.766 | −0.522 | 0.878 | 0.969 | |
| Ca2+ | 1.000 | −0.860 | 0.842 | 0.254 | −0.880 | −0.398 | 0.640 | 0.854 | ||
| Mg2+ | 1.000 | −0.555 | −0.237 | 0.829 | 0.235 | −0.334 | −0.576 | |||
| Cl− | 1.000 | 0.209 | −0.777 | −0.470 | 0.835 | 0.987 | ||||
| SO42− | 1.000 | −0.328 | −0.152 | 0.117 | 0.345 | |||||
| CHO3− | 1.000 | 0.404 | −0.621 | −0.805 | ||||||
| pH | 1.000 | −0.624 | −0.495 | |||||||
| EC | 1.000 | 0.839 | ||||||||
| TDS | 1.000 |
| Variable | Number | Minimum | Maximum | Mean | Variance |
|---|---|---|---|---|---|
| K+ | 31 | 179.70 | 337.50 | 254.92 | 1704.81 |
| Na+ | 31 | 8900.00 | 12,050.00 | 10,167.16 | 777,901.29 |
| Ca2+ | 31 | 481.00 | 2312.60 | 1066.25 | 308,912.05 |
| Mg2+ | 31 | 517.60 | 1312.20 | 1037.77 | 39,872.52 |
| Cl− | 31 | 16,705.80 | 22,411.50 | 19,219.89 | 2,828,300.73 |
| SO42− | 31 | 624.40 | 2708.90 | 2290.57 | 129,613.43 |
| CHO3− | 31 | 81.80 | 273.30 | 186.53 | 3462.04 |
| pH | 31 | 7.02 | 7.74 | 7.33 | 0.05 |
| EC | 31 | 34,400.00 | 50,400.00 | 41,787.10 | 17,233,161.29 |
| TDS | 31 | 29,992.10 | 40,117.10 | 34,228.60 | 8,749,166.58 |
| Principle Component | Eigenvalues | ||
|---|---|---|---|
| Value | Variance (%) | Cumulative Variance (%) | |
| 1 | 6.048 | 60.476 | 60.476 |
| 2 | 1.331 | 13.311 | 73.787 |
| 3 | 0.972 | 9.715 | 83.502 |
| 4 | 0.829 | 8.290 | 91.792 |
| 5 | 0.500 | 5.003 | 96.794 |
| 6 | 0.137 | 1.370 | 98.164 |
| 7 | 0.110 | 1.099 | 99.263 |
| 8 | 0.059 | 0.591 | 99.854 |
| 9 | 0.015 | 0.146 | 100.000 |
| 10 | 0.000002 | 0.000018 | 100.000 |
| Factor Loadings | Rotated Factor Loadings | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Fa1 | Fa2 | Fa3 | Fa4 | Fa11 | Fa21 | Fa31 | Fa41 | HI2 | |
| K+ | 0.195 | −0.712 | −0.451 | 0.393 | 0.136 | 0.055 | −0.938 | −0.011 | 0.90 |
| Na+ | 0.933 | 0.272 | 0.014 | −0.049 | 0.695 | 0.652 | 0.178 | 0.083 | 0.95 |
| Ca2+ | 0.918 | −0.212 | 0.030 | −0.213 | 0.915 | 0.282 | −0.100 | 0.086 | 0.93 |
| Mg2+ | −0.722 | 0.575 | −0.032 | 0.213 | −0.869 | 0.033 | 0.359 | −0.117 | 0.90 |
| Cl− | 0.945 | 0.185 | −0.024 | −0.136 | 0.770 | 0.578 | 0.135 | 0.022 | 0.95 |
| SO42− | 0.330 | −0.166 | 0.794 | 0.473 | 0.170 | 0.076 | 0.006 | 0.977 | 0.99 |
| CHO3− | −0.900 | 0.273 | −0.059 | 0.096 | −0.865 | −0.289 | 0.185 | −0.179 | 0.90 |
| pH | −0.575 | −0.297 | 0.264 | −0.557 | −0.071 | −0.861 | 0.195 | −0.120 | 0.80 |
| EC | 0.837 | 0.353 | −0.235 | 0.130 | 0.478 | 0.815 | 0.044 | −0.052 | 0.90 |
| TDS | 0.966 | 0.161 | 0.084 | -0.053 | 0.765 | 0.583 | 0.127 | 0.161 | 0.97 |
| Water Samples | Factor Scores | |||
|---|---|---|---|---|
| Fa1 | Fa2 | Fa3 | Fa4 | |
| 375-1-1 | 0.145 | 1.681 | −0.299 | 0.707 |
| 375-1-2 | −4.660 | 0.781 | 1.220 | −1.139 |
| 375-1-3 | −1.536 | 1.969 | 0.566 | 0.858 |
| 375-1-4 | −4.660 | 2.575 | −3.173 | −2.340 |
| 375-1-5 | −3.639 | 1.595 | 0.991 | −0.270 |
| 375-2-1 | 1.180 | 1.388 | −0.940 | 1.441 |
| 375-3-1 | −4.223 | −0.812 | −1.128 | 0.426 |
| 375-3-2 | −6.907 | −1.024 | 0.311 | −0.483 |
| 375-3-3 | −5.205 | −0.758 | −0.156 | 0.309 |
| 375-4-1 | −3.236 | −1.471 | −1.133 | 0.118 |
| 375-4-2 | −4.830 | −1.697 | 0.311 | −0.176 |
| 375-4-3 | 0.083 | −0.688 | −0.063 | 1.154 |
| 375-4-4 | 0.297 | −1.496 | −0.008 | 0.251 |
| 375-4-5 | 0.903 | −0.763 | −0.363 | 1.059 |
| 375-5-1 | 8.111 | 1.430 | −0.023 | 0.119 |
| 375-5-2 | 3.954 | 0.656 | 1.285 | −0.716 |
| 375-5-3 | 4.935 | 1.322 | 1.178 | 0.440 |
| 375-5-4 | 6.717 | 0.252 | 1.057 | −0.463 |
| 375-5-5 | 13.600 | −1.555 | 0.094 | −1.265 |
| 375-6-1 | 10.150 | −0.631 | −0.999 | 1.186 |
| 375-6-2 | 9.644 | 0.187 | 0.185 | 0.061 |
| 375-6-3 | −6.903 | −1.162 | 0.638 | −0.402 |
| 375-7-1 | 6.120 | −0.197 | −0.785 | 0.665 |
| 375-7-2 | −3.798 | 0.163 | −0.005 | 0.873 |
| 375-7-3 | −6.697 | −1.197 | 0.421 | −0.492 |
| 375-8-1 | 0.153 | −0.098 | −1.786 | −0.198 |
| 375-8-2 | 6.550 | −1.847 | 0.027 | −1.430 |
| 375-8-3 | −0.864 | 2.346 | 0.589 | 0.270 |
| 375-8-4 | −6.468 | −1.429 | 0.325 | 0.153 |
| 375-9-1 | −2.916 | 1.540 | 1.098 | −0.542 |
| 375-9-2 | −5.999 | −1.060 | 0.569 | −0.175 |
| Component Score Coefficient | ||||
|---|---|---|---|---|
| Fa1 | Fa2 | Fa3 | Fa4 | |
| K+ | 0.195 | −0.712 | −0.451 | 0.393 |
| Na+ | 0.933 | 0.272 | 0.014 | −0.049 |
| Ca2+ | 0.918 | −0.212 | 0.030 | −0.213 |
| Mg2+ | −0.722 | 0.575 | −0.032 | 0.213 |
| Cl− | 0.945 | 0.185 | −0.024 | −0.136 |
| SO42− | 0.330 | −0.166 | 0.794 | 0.473 |
| CHO3− | −0.900 | 0.273 | −0.059 | 0.096 |
| PH | −0.575 | −0.297 | 0.264 | −0.557 |
| EC | 0.837 | 0.353 | −0.235 | 0.130 |
| TDS | 0.966 | 0.161 | 0.084 | −0.053 |
| Water Site | Values of Bayes Function | Water Site | Values of Bayes Function | ||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | Type | M1 | M2 | Type | ||
| 375-1-1 | 242.550 | 230.420 | M1 | 375-5-2 | 224.880 | 229.530 | M2 |
| 375-1-3 | 237.354 | 219.981 | M1 | 375-5-3 | 223.329 | 228.877 | M2 |
| 375-1-4 | 230.862 | 211.502 | M1 | 375-5-4 | 228.640 | 239.012 | M2 |
| 375-1-5 | 234.482 | 215.157 | M1 | 375-5-5 | 236.673 | 248.785 | M2 |
| 375-2-1 | 247.676 | 238.456 | M1 | 375-6-1 | 243.476 | 251.856 | M2 |
| 375-3-1 | 207.215 | 190.310 | M1 | 375-6-2 | 257.332 | 267.475 | M2 |
| 375-3-2 | 191.816 | 170.268 | M1 | 375-7-2 | 213.624 | 196.477 | M1 |
| 375-3-3 | 216.300 | 190.868 | M1 | 375-7-3 | 201.203 | 181.596 | M1 |
| 375-4-1 | 215.089 | 202.574 | M1 | 375-8-1 | 220.082 | 215.998 | M1 |
| 375-4-2 | 174.071 | 159.663 | M1 | 375-8-3 | 248.722 | 234.864 | M1 |
| 375-4-3 | 201.080 | 192.213 | M1 | 375-8-4 | 196.578 | 176.346 | M1 |
| 375-4-5 | 211.255 | 203.763 | M1 | 375-9-1 | 253.996 | 236.763 | M1 |
| 375-5-1 | 269.800 | 279.520 | M2 | 375-9-2 | 201.048 | 182.746 | M1 |
| Test Site | Values of Bayes Function | ||
|---|---|---|---|
| M1 | M2 | Type | |
| 375-1-2 | 223.266 | 205.968 | M1 |
| 375-4-4 | 206.744 | 199.078 | M1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Ma, F.; Liu, G.; Zhao, H.; Guo, J.; Cao, J. Application of Multivariate Statistical Analysis to Identify Water Sources in A Coastal Gold Mine, Shandong, China. Sustainability 2019, 11, 3345. https://doi.org/10.3390/su11123345
Liu G, Ma F, Liu G, Zhao H, Guo J, Cao J. Application of Multivariate Statistical Analysis to Identify Water Sources in A Coastal Gold Mine, Shandong, China. Sustainability. 2019; 11(12):3345. https://doi.org/10.3390/su11123345
Chicago/Turabian StyleLiu, Guowei, Fengshan Ma, Gang Liu, Haijun Zhao, Jie Guo, and Jiayuan Cao. 2019. "Application of Multivariate Statistical Analysis to Identify Water Sources in A Coastal Gold Mine, Shandong, China" Sustainability 11, no. 12: 3345. https://doi.org/10.3390/su11123345
APA StyleLiu, G., Ma, F., Liu, G., Zhao, H., Guo, J., & Cao, J. (2019). Application of Multivariate Statistical Analysis to Identify Water Sources in A Coastal Gold Mine, Shandong, China. Sustainability, 11(12), 3345. https://doi.org/10.3390/su11123345




