Optimization of Just-In-Sequence Supply: A Flower Pollination Algorithm-Based Approach
Abstract
:1. Introduction
2. Literature Review
2.1. Conceptual Framework and Review Methodology
2.2. Descriptive Analysis
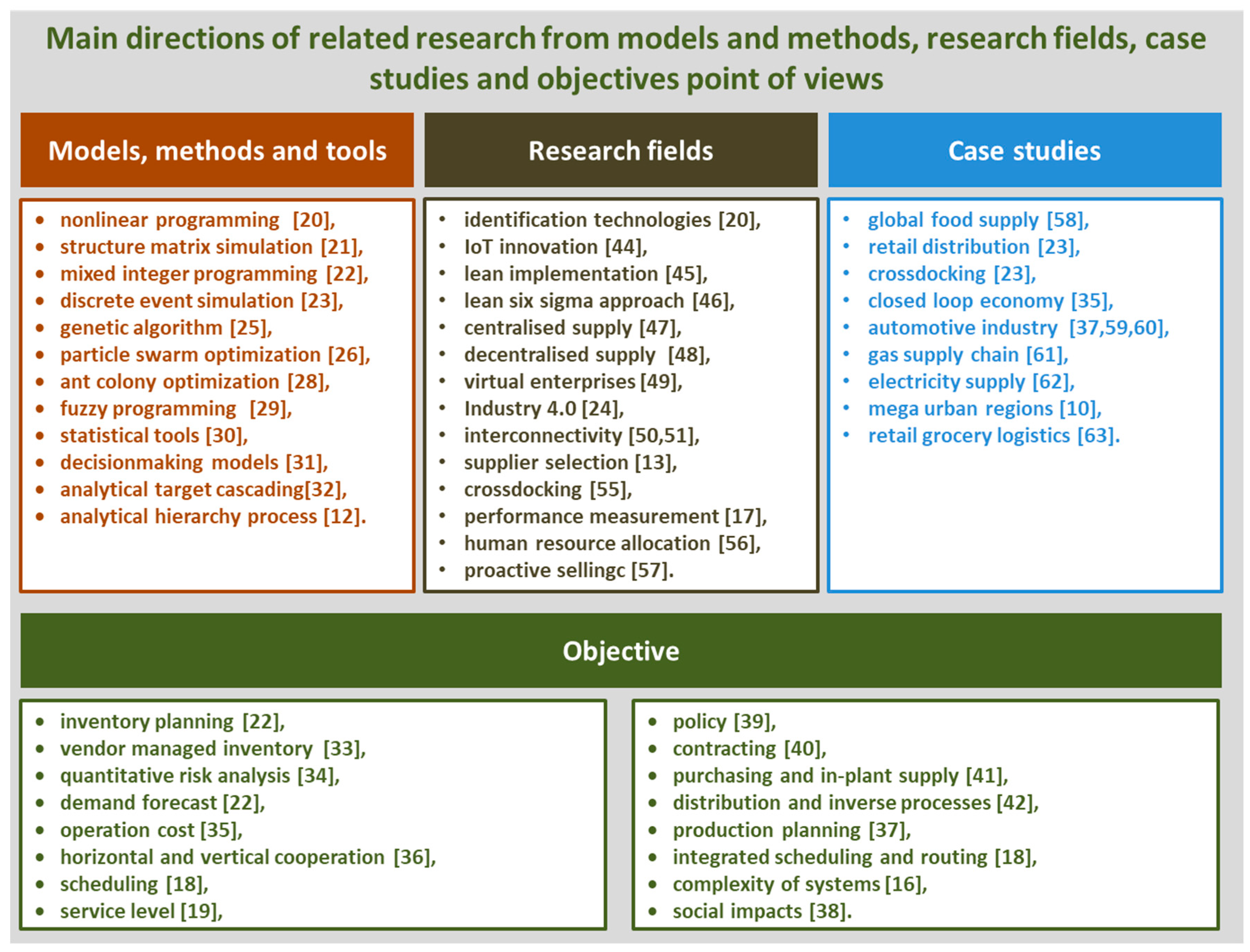
2.3. Content Analysis
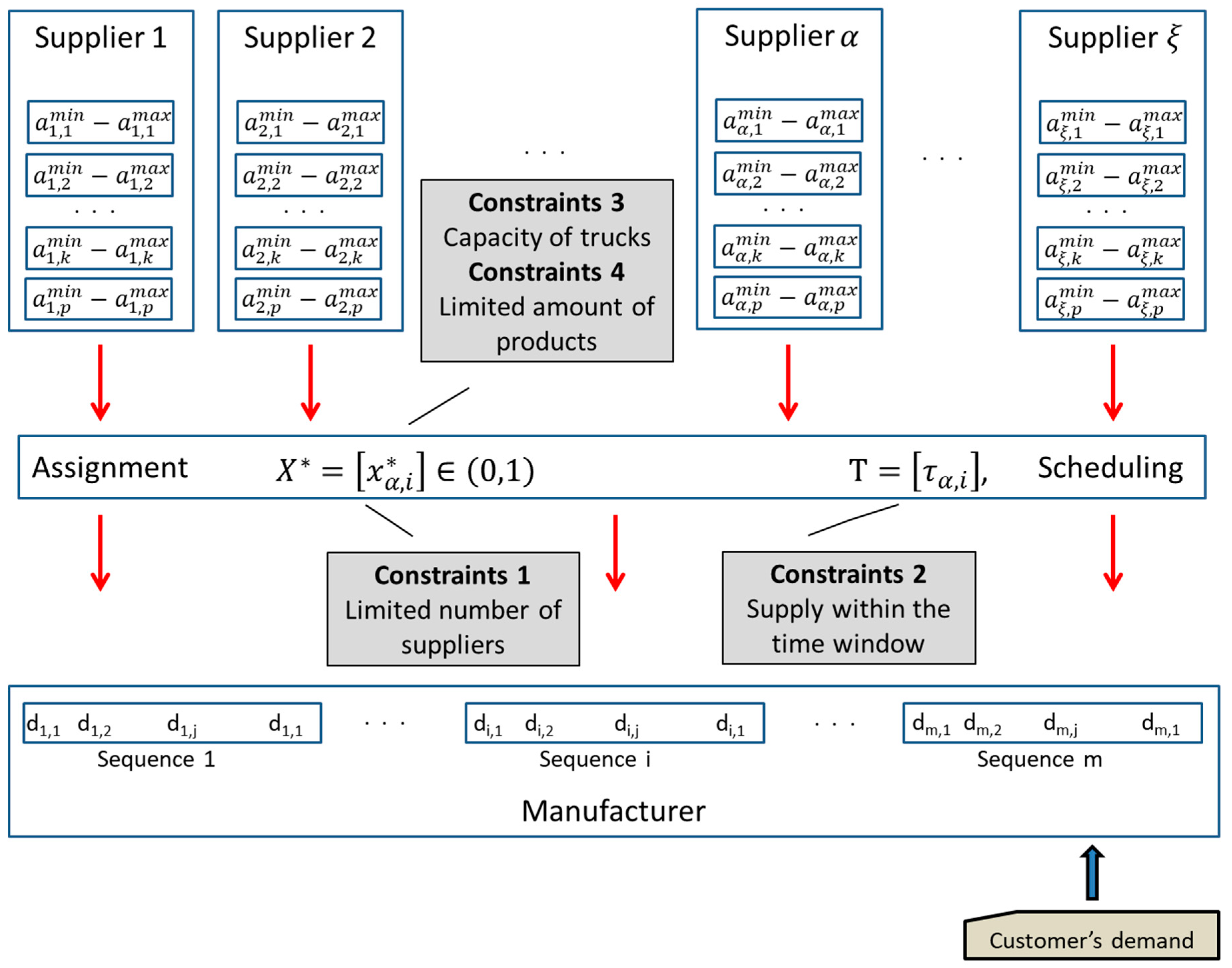
3. Model Framework
- let the number of sequences, where ,
- let the number of orders within sequence i, where ,
- let the number of potential products to order from the potential just-in-sequence suppliers, where ,
- defines the set of products involved in the sequence i,
- let the type of order j in sequence i,
- let the quantity of order j in sequence i,
- let supplier , where ,
- let the lower limit of the quantity of product k at supplier to be supplied to the manufacturer,
- let the available quantity of product k at supplier ,
- defines the set of potential suppliers of product k, where the assignment of suppliers to the potential suppliers of an order can be defined as follows:
- defines the set of potential suppliers of sequence i, where the assignment of suppliers to the potential suppliers of a sequence can be defined as follows:
- let the supply cost of product k from supplier ,
- let the specific energy consumption of supply of product k from supplier ,
- and define the lower and upper limit of delivery time of sequenced demand i to the manufacturer;
- and defines the lower and upper limit of delivery time of sequence i from supplier This lower limit includes all parts of the total order lead time, which means the lead time from customer order received to customer order delivered and includes the following operations: incoming order, manufacturing of ordered components, shipment preparation, check-out, physical delivery, unloading, check-in.
- and are the lower and upper limit of delivery time of components j of sequence i from supplier to the manufacturer;
- is the scheduled transportation time of order j of sequence i from supplier .
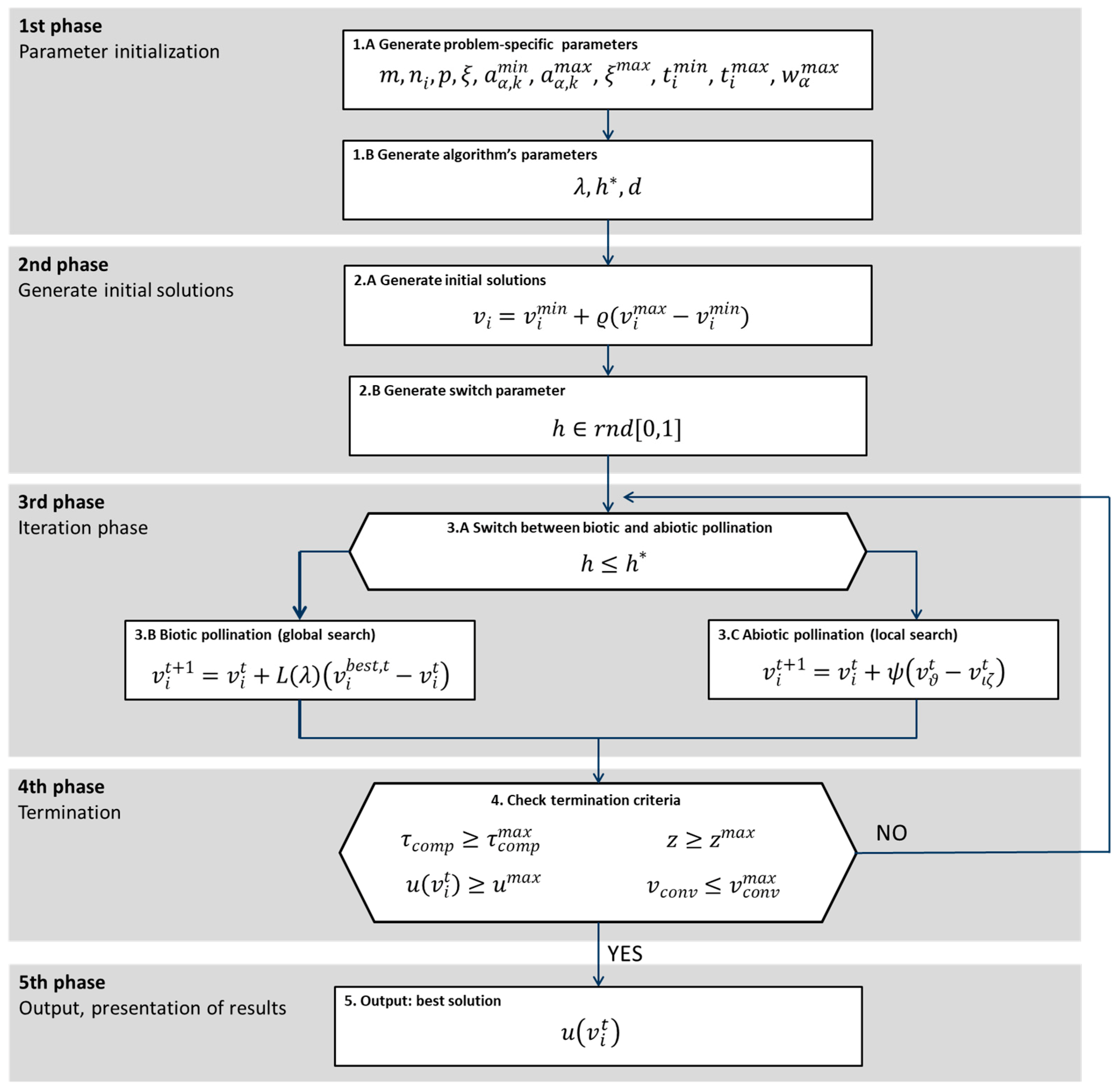
4. Flower Pollination Algorithm-Based Optimization and Its Validation with Test Functions
- the candidate solutions of the optimization problem are represented by pollen grains;
- the global search in the search space is modelled through the biotic pollination via Lévy flight;
- the local search in the search space is modelled by abiotic pollination and self-pollination;
- the global and local search is controlled through a switching probability between biotic, abiotic and self-pollution;
- predefined computational time is reached ();
- number of predefined iteration steps is reached ();
- the predefined value of the best solution is reached ();
- the predefined “lower limit of convergence speed” of the algorithm is reached ().
5. Numerical Analysis of Just-In-Sequence Supply in Interconnected Logistics Systems
5.1. Scenario 1: Just-In-Sequence Supply without Time Frame and without Transportation Capacity Limit
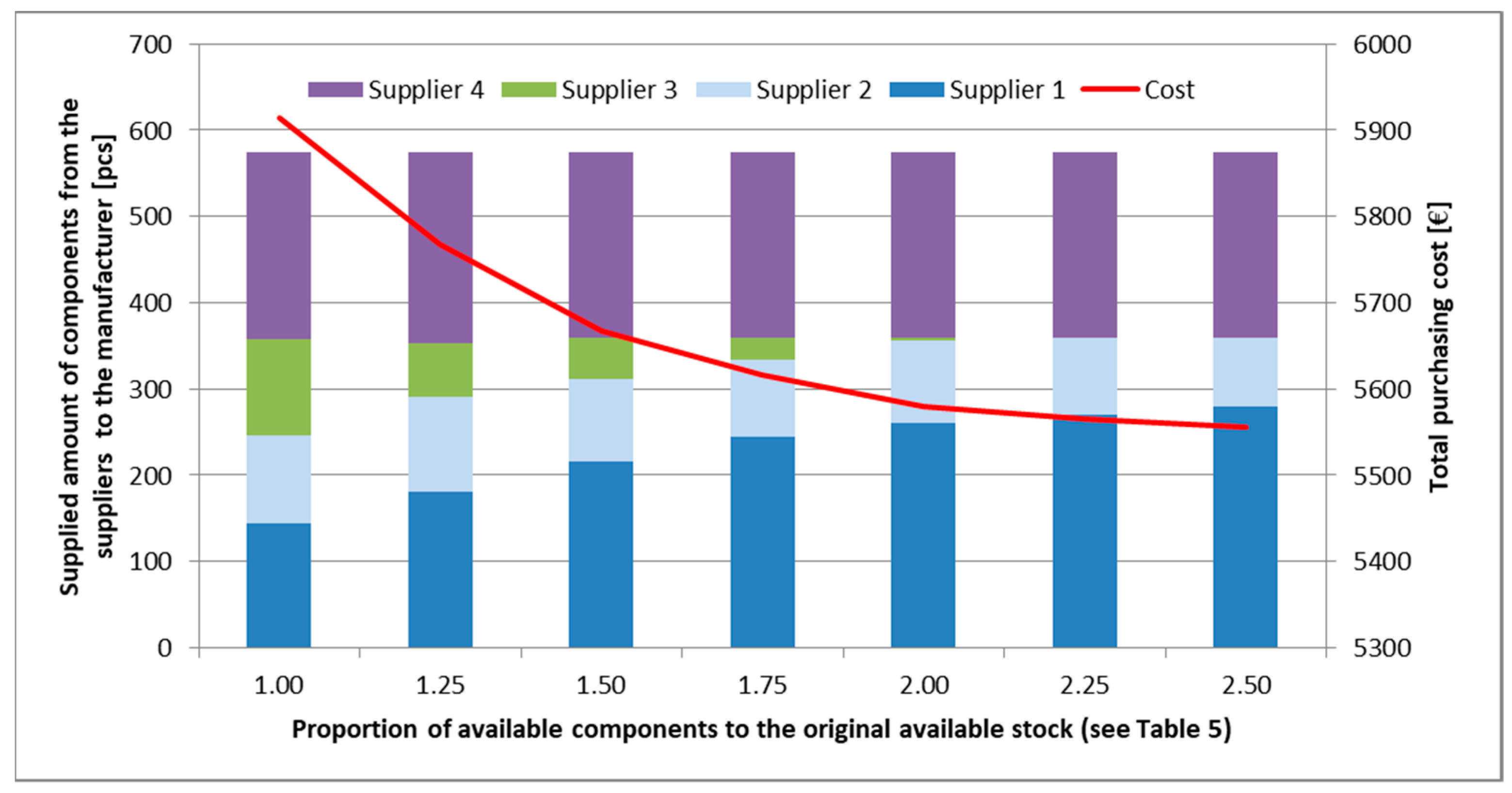
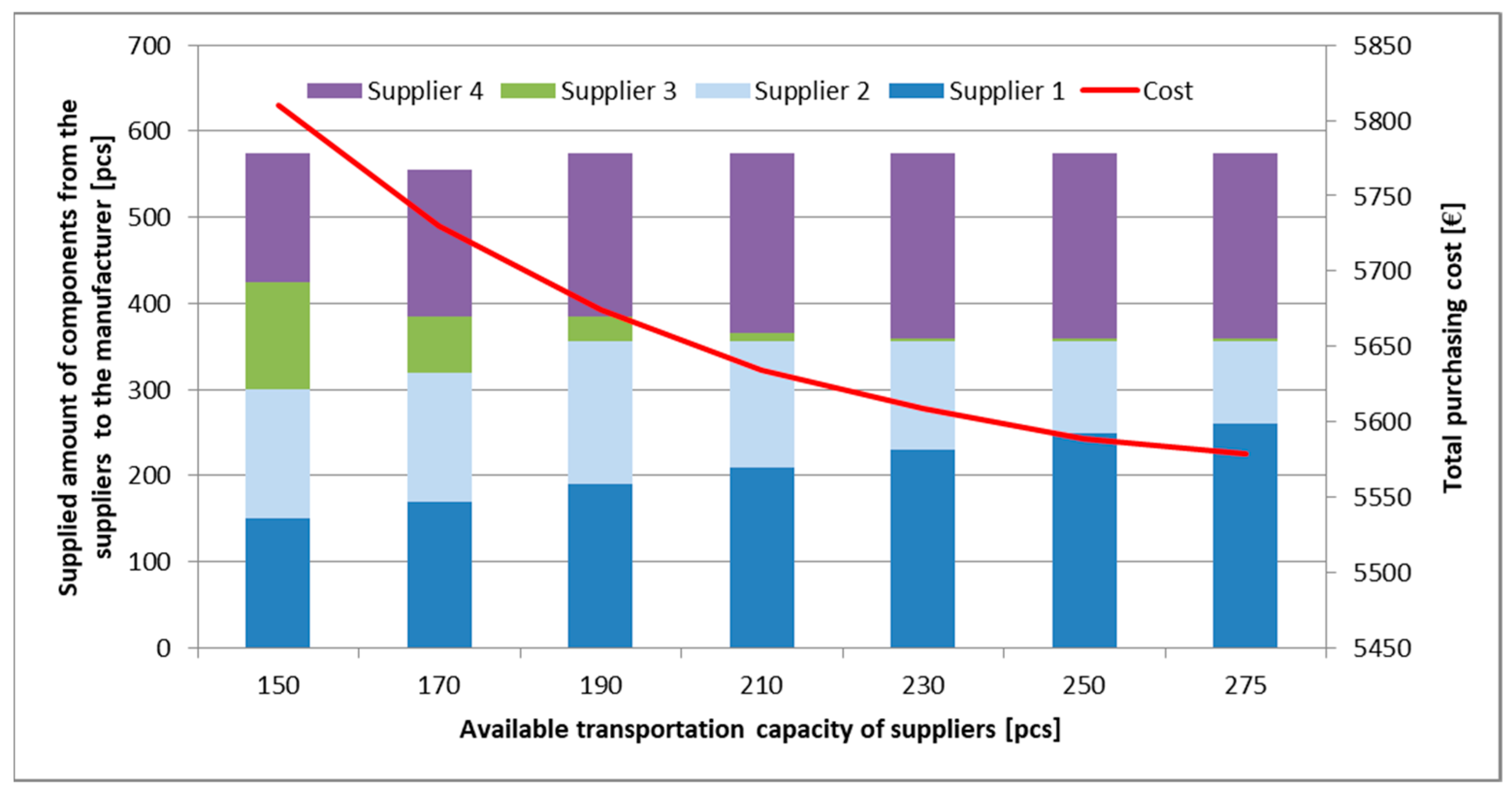
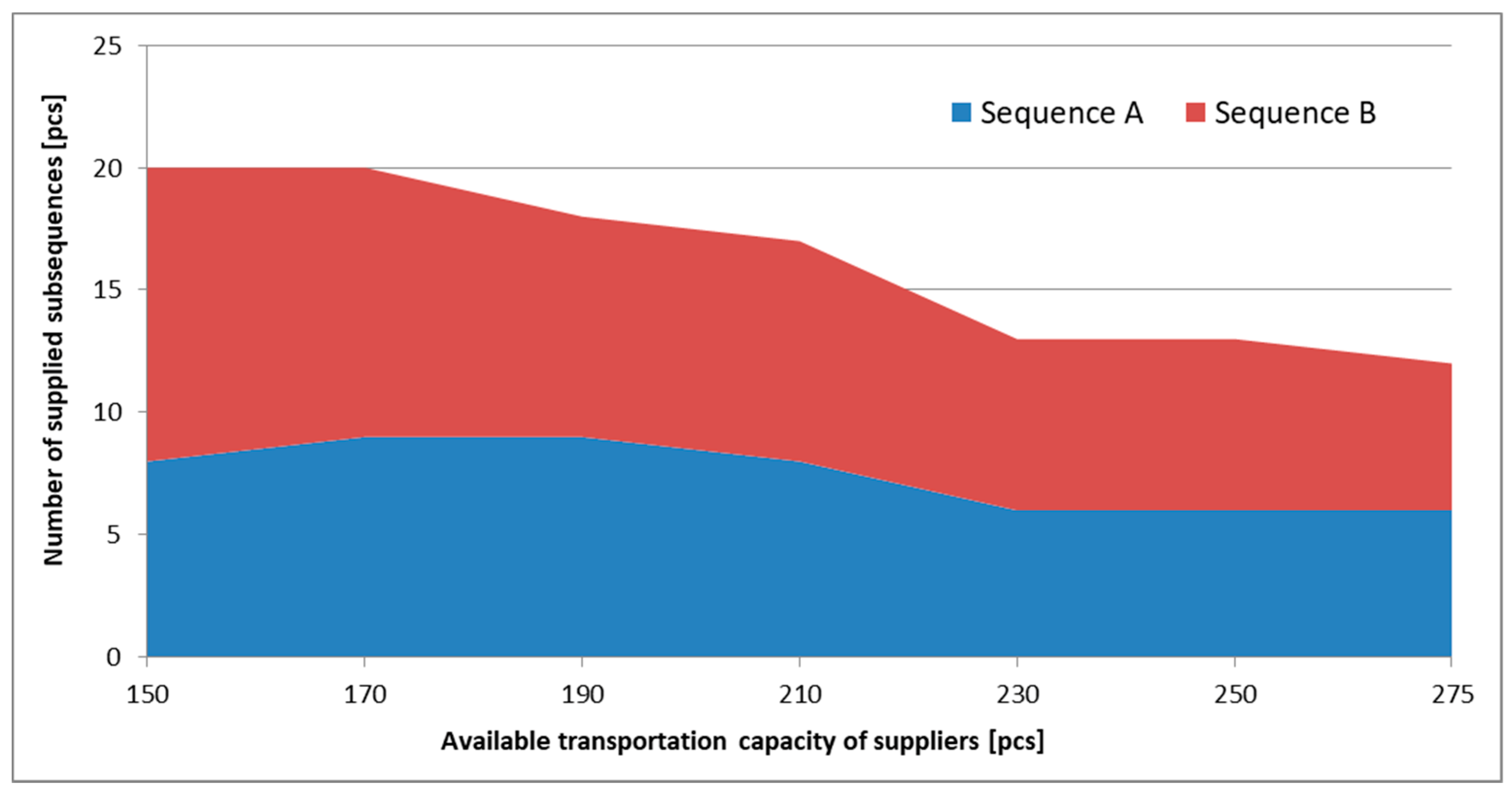
5.2. Scenario 2: Just-In-Sequence Supply without Time Frame and with Transportation Capacity Limit
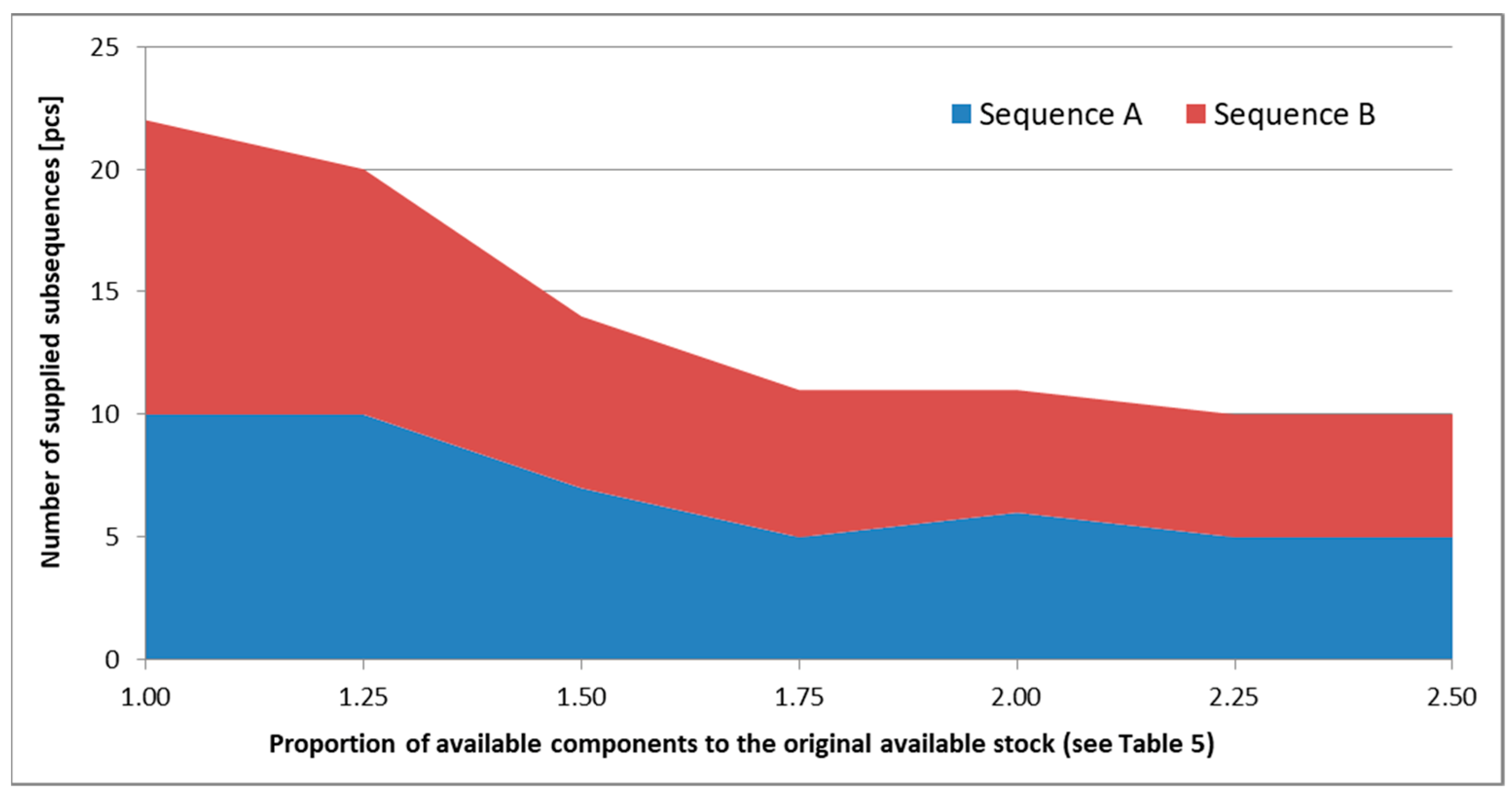
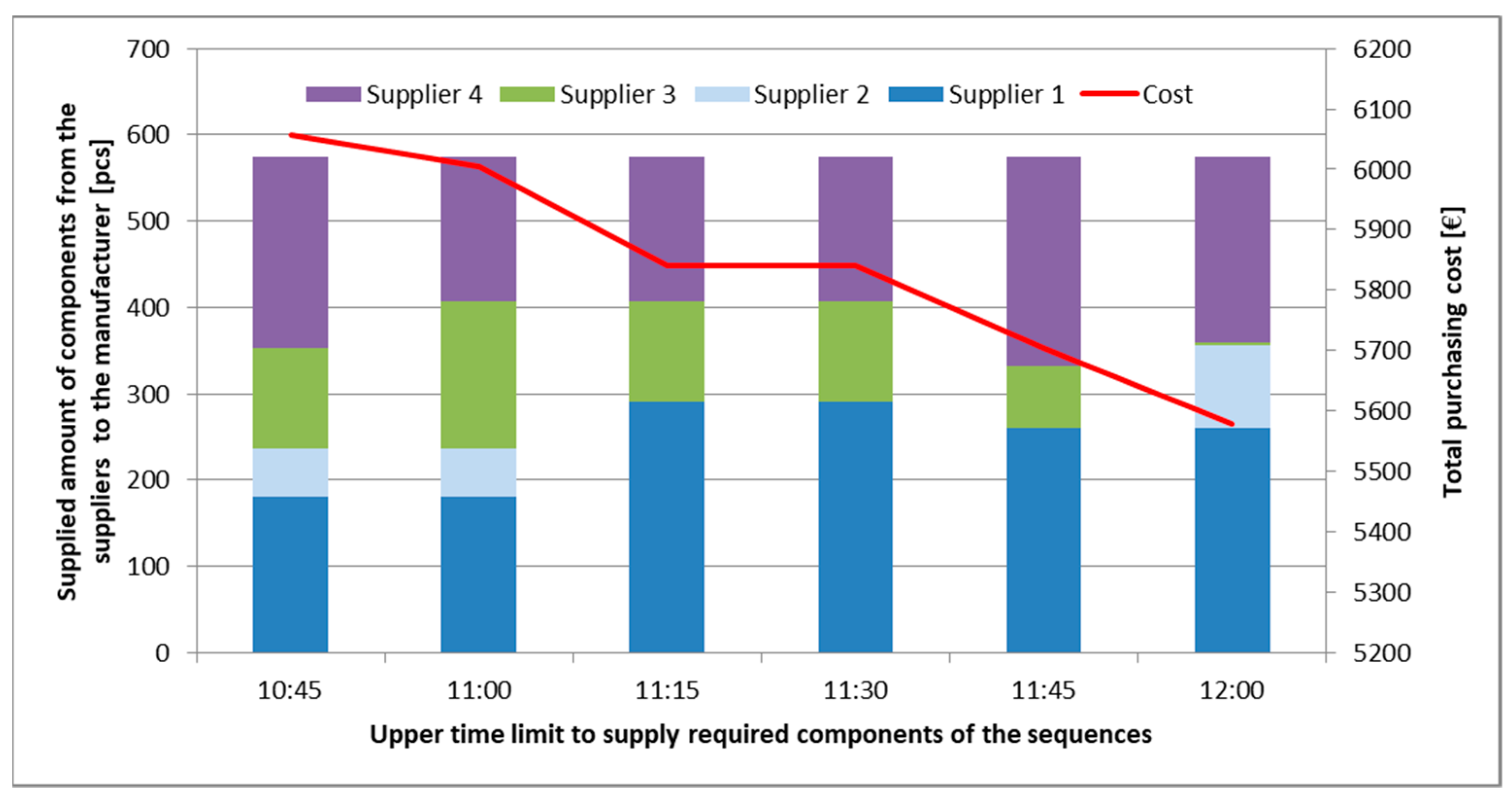
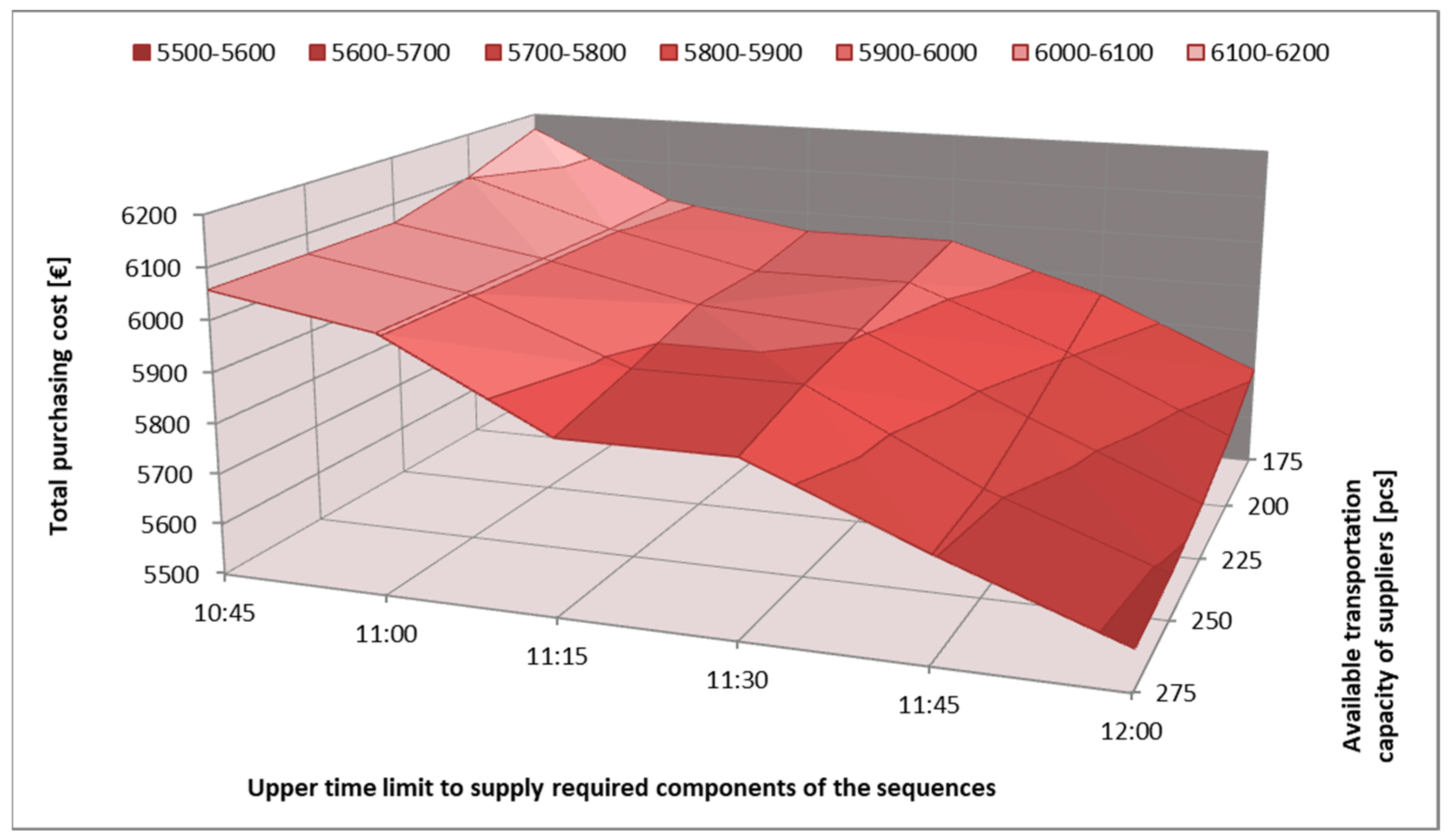
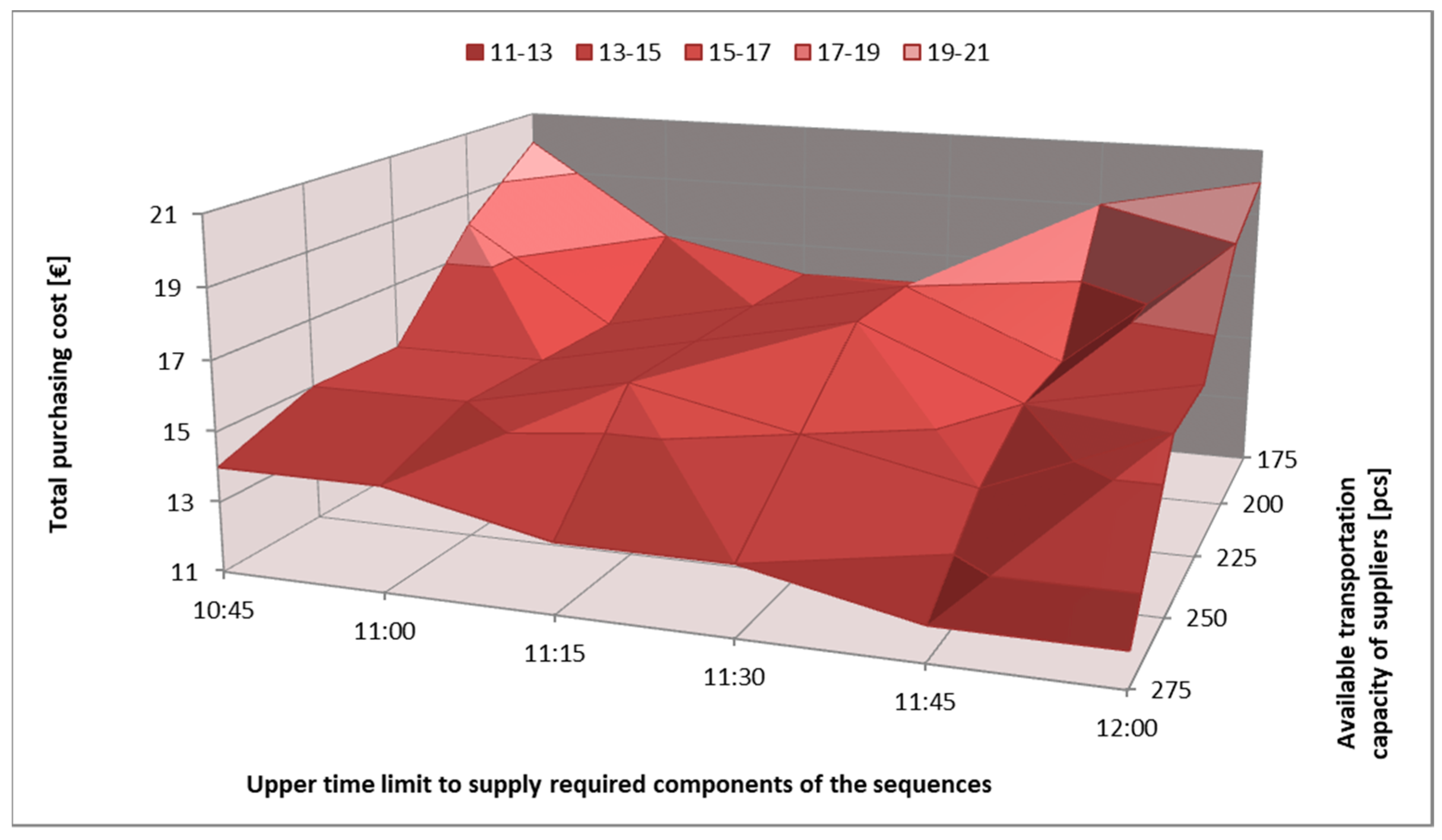
5.3. Scenario 3: Just-In-Sequence Supply with Time Frame and Transportation Capacity Limit
6. Conclusions
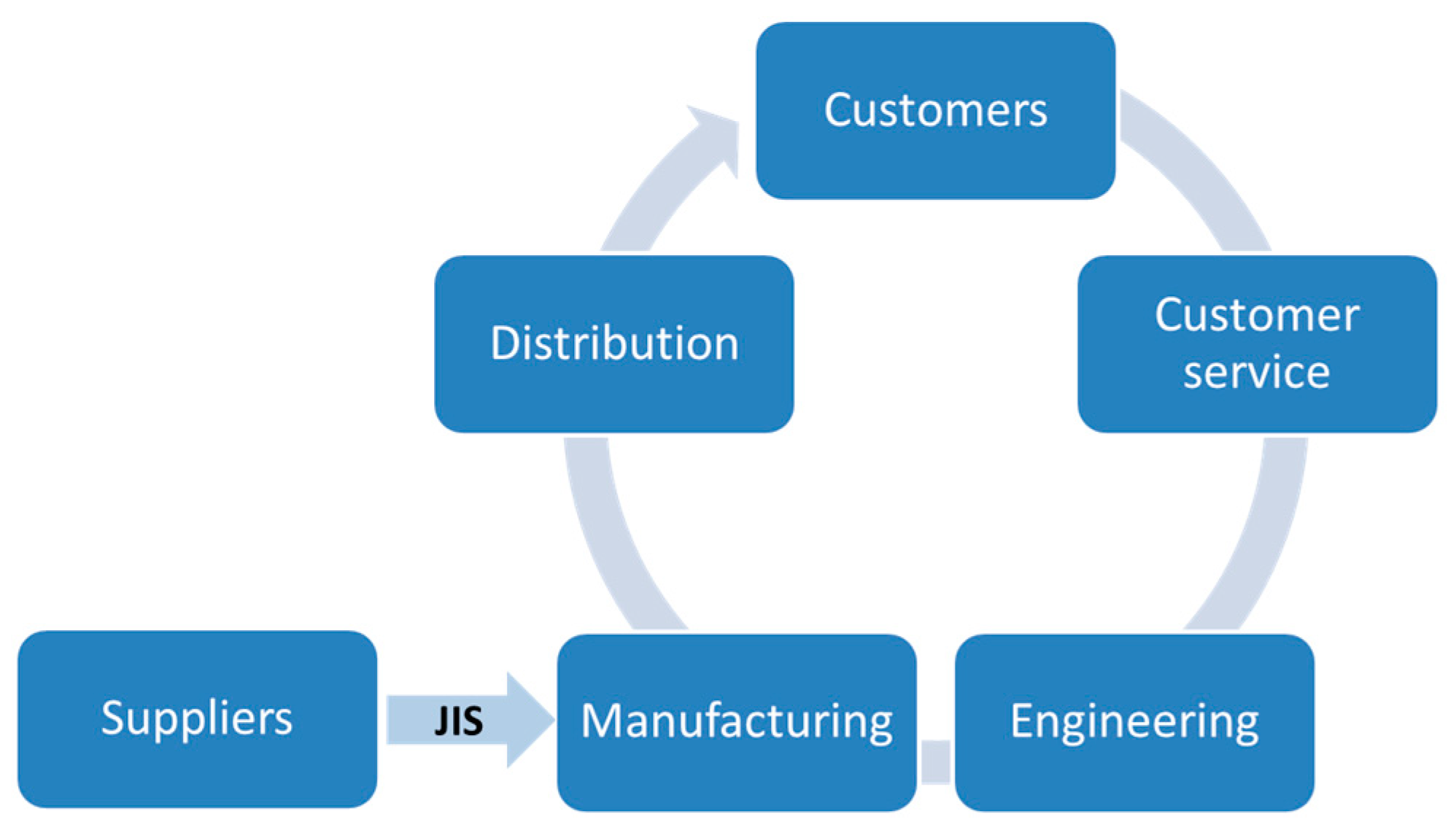
- JIS/JIT solutions are supporting suppliers to focus on their core business.
- The JIS supply philosophy is a core part of lean thinking.
- The aims of the Toyota production system (TPS) are to serve world quality products, reduce operation costs [110], and satisfy customer needs.
- There are several advantages such as controlling costs, reducing risk of supply chain and supporting third-party logistics (3PL).
Author Contributions
Funding
Conflicts of Interest
References
- Bányai, T. Build to sequence supply. Adv. Log. Syst. 2013, 7, 35–40. [Google Scholar]
- Abedi, A.; Zhu, W.H. An optimisation model for purchase, production and distribution in fish supply chain—A case study. Int. J. Prod. Res. 2017, 55, 3451–3464. [Google Scholar] [CrossRef]
- Tamás, P. Decision Support Simulation Method for Process Improvement of Intermittent Production Systems. Appl. Sci. 2017, 7, 950. [Google Scholar]
- Bamana, F.; Lehoux, N.; Cloutier, C. Simulation of a Construction Project: Assessing Impact of Just-in-Time and Lean Principles. J. Constr. Eng. Manag. 2019, 145, 05019005. [Google Scholar] [CrossRef]
- Werner, S.; Kellner, M.; Schenk, E.; Weigert, G. Just-in-sequence material supply—A simulation based solution in electronics production. Robot. Comput. Manuf. 2003, 19, 107–111. [Google Scholar] [CrossRef]
- Plöger, M.; Haasis, H.-D. Equitably taken just-in-sequence supply in production networks. Z. Wirtsch. Fabrikbetrieb 2008, 103, 613–615. [Google Scholar] [CrossRef]
- Tamás, P. Innovative Business Model for Realization of Sustainable Supply Chain at the Outsourcing Examination of Logistics Services. Sustainability 2018, 10, 210. [Google Scholar]
- Lage, M.; Filho, G. Variations of the Kanban system: Literature review and classification. Int. J. Prod. Econ. 2010, 125, 13–21. [Google Scholar] [CrossRef]
- Berry, D.; Naim, M. Quantifying the relative improvements of redesign strategies in a P.C. supply chain. Int. J. Prod. Econ. 1996, 46, 181–196. [Google Scholar] [CrossRef]
- Rodrigue, J.-P.; Rodrigue, J. Freight, Gateways and Mega-Urban Regions: The Logistical Integration of The Bostwash Corridor1. Tijdschr. Econ. Soc. Geogr. 2004, 95, 147–161. [Google Scholar] [CrossRef]
- Chang, T.-S.; Wan, Y.-W.; Ooi, W.T. A stochastic dynamic traveling salesman problem with hard time windows. Eur. J. Oper. Res. 2009, 198, 748–759. [Google Scholar] [CrossRef]
- Korpela, J.; Lehmusvaara, A. A customer oriented approach to warehouse network evaluation and design. Int. J. Prod. Econ. 1999, 59, 135–146. [Google Scholar] [CrossRef]
- Aksoy, A.; Öztürk, N.; Aksoy, A. Supplier selection and performance evaluation in just-in-time production environments. Expert Syst. Appl. 2011, 38, 6351–6359. [Google Scholar] [CrossRef]
- Milgate, M. Supply chain complexity and delivery performance: An international exploratory study. Supply Chain Manag. Int. J. 2001, 6, 106–118. [Google Scholar] [CrossRef]
- D’Amours, S.; Montreuil, B.; Lefrançois, P.; Soumis, F. Networked manufacturing: The impact of information sharing. Int. J. Prod. Econ. 1999, 58, 63–79. [Google Scholar] [CrossRef]
- Vachon, S.; Klassen, R. An exploratory investigation of the effects of supply chain complexity on delivery performance. IEEE Trans. Eng. Manag. 2002, 49, 218–230. [Google Scholar] [CrossRef]
- Chan, F.T.; Qi, H. Feasibility of performance measurement system for supply chain: A process-based approach and measures. Integr. Manuf. Syst. 2003, 14, 179–190. [Google Scholar] [CrossRef]
- Naso, D.; Surico, M.; Turchiano, B.; Kaymak, U. Genetic algorithms for supply-chain scheduling: A case study in the distribution of ready-mixed concrete. Eur. J. Oper. Res. 2007, 177, 2069–2099. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Elahipanah, M. A genetic algorithm to optimize the total cost and service level for just-in-time distribution in a supply chain. Int. J. Prod. Econ. 2008, 111, 229–243. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Linh, V.-T.; Lu, J.-C. Closed-loop supply chain network designs considering RFID adoption. Comput. Ind. Eng. 2017, 113, 716–726. [Google Scholar] [CrossRef]
- Addo-Tenkorang, R.; Helo, P.T.; Kantola, J. Concurrent enterprise: A conceptual framework for enterprise supply-chain network activities. Enterp. Inf. Syst. 2017, 11, 474–511. [Google Scholar] [CrossRef]
- Desport, P.; Lardeux, F.; Lesaint, D.; Di Cairano-Gilfedder, C.; Liret, A.; Owusu, G. A combinatorial optimisation approach for closed-loop supply chain inventory planning with deterministic demand. Eur. J. Ind. Eng. 2017, 11, 303. [Google Scholar] [CrossRef] [Green Version]
- Buijs, P.; Danhof, H.W.; Wortmann, J.C. Just-in-Time Retail Distribution: A Systems Perspective on Cross-Docking. J. Bus. Logist. 2016, 37, 213–230. [Google Scholar] [CrossRef] [Green Version]
- Sarraj, R.; Ballot, E.; Pan, S.; Hakimi, D.; Montreuil, B. Interconnected logistic networks and protocols: Simulation-based efficiency assessment. Int. J. Prod. Res. 2014, 52, 3185–3208. [Google Scholar] [CrossRef]
- Sigari, S. Simulating operations process to achieve a hybrid optimal operational performance in supply chain scheduling: A case study. Int. J. Ind. Syst. Eng. 2016, 23, 254. [Google Scholar] [CrossRef]
- Srinivasan, S.; Sharma, A.K.; Khan, S.H. Modelling and optimization of defective goods supply chain network with heuristics. Int. J. Oper. Quant. Manag. 2016, 22, 177–187. [Google Scholar]
- Ghasimi, S.A.; Ramli, R.; Saibani, N. A genetic algorithm for optimizing defective goods supply chain costs using JIT logistics and each-cycle lengths. Appl. Math. Model. 2014, 38, 1534–1547. [Google Scholar] [CrossRef]
- Euchi, J.; Yassine, A.; Chabchoub, H. The dynamic vehicle routing problem: Solution with hybrid metaheuristic approach. Swarm Evol. Comput. 2015, 21, 41–53. [Google Scholar] [CrossRef]
- Ahmadizar, F.; Zeynivand, M. Bi-objective supply chain planning in a fuzzy environment. J. Intell. Fuzzy Syst. 2014, 26, 153–164. [Google Scholar] [CrossRef]
- Mishra, P.; Sharma, R.K. A hybrid framework based on SIPOC and Six Sigma DMAIC for improving process dimensions in supply chain network. Int. J. Qual. Reliab. Manag. 2014, 31, 522–546. [Google Scholar] [CrossRef]
- Beheshti, H.M. A decision support system for improving performance of inventory management in a supply chain network. Int. J. Prod. Perform. Manag. 2010, 59, 452–467. [Google Scholar] [CrossRef]
- Qu, T.; Huang, G.Q.; Chen, X.; Chen, H.P. Extending analytical target cascading for optimal supply chain network configuration of a product family. Int. J. Comput. Integr. Manuf. 2009, 22, 1012–1023. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X. A One-Vendor Multiple-Buyer Production-Distribution System: The Value of Vendor Managed Inventory. INFOR: Inf. Syst. Oper. Res. 2015, 53, 13–25. [Google Scholar] [CrossRef]
- Mo, H.; Liu, L.; Xu, L. A power spectrum optimization algorithm inspired by magnetotactic bacteria. Neural Comput. Appl. 2014, 25, 1823–1844. [Google Scholar] [CrossRef]
- Jung, K.S.; Dawande, M.; Geismar, H.N.; Guide, V.D.R., Jr.; Sriskandarajah, C. Supply planning models for a remanufacturer under just-in-time manufacturing environment with reverse logistics. Ann. Oper. Res. 2016, 240, 533–581. [Google Scholar] [CrossRef]
- Sepehri, M. Cost and inventory benefits of cooperation in multi-period and multi-product supply. Sci. Iran. 2011, 18, 731–741. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.-Y.; He, Y.-W.; Chen, Z.-X. Production planning model and its implementation technology based on J2EE/Web services. Jisuanji Jicheng Zhizao Xitong Comput. Integr. Manuf. Syst. 2006, 12, 357–363. [Google Scholar]
- Kim, H.Y.; McCann, P. Supply chains and locational adjustment in the global automotive industry. Policy Stud. 2008, 29, 255–266. [Google Scholar] [CrossRef]
- Diponegoro, A.; Sarker, B.R. Operations policy for a supply chain system with fixed-interval delivery and linear demand. J. Oper. Res. Soc. 2007, 58, 901–910. [Google Scholar] [CrossRef]
- Schneeweiss, C.; Zimmer, K.; Zimmermann, M. The design of contracts to coordinate operational interdependencies within the supply chain. Int. J. Prod. Econ. 2004, 92, 43–59. [Google Scholar] [CrossRef]
- Samaranayake, P.; Toncich, D. Integration of production planning, project management and logistics systems for supply chain management. Int. J. Prod. Res. 2007, 45, 5417–5447. [Google Scholar] [CrossRef]
- Munson, C.L.; Rosenblatt, M.J.; Rosenblatt, Z. Use and abuse of power in supply chains. IEEE Eng. Rev. 2000, 28, 81–91. [Google Scholar] [CrossRef]
- Sweeting, R.C.; Spring, M. Empowering customers: Portals, supply networks and assemblers. Int. J. Technol. Manag. 2002, 23, 113. [Google Scholar]
- Links, C. Evolution of the IoT as a service. Microw. J. 2017, 60, 52–60. [Google Scholar]
- Birkie, S.E. Operational resilience and lean: In search of synergies and trade-offs. J. Manuf. Technol. Manag. 2016, 27, 185–207. [Google Scholar] [CrossRef]
- Narahari, Y.; Viswanadham, N.; Bhattacharya, R. Design of synchronized supply chains: A six sigma tolerancing approach. IEEE Int. Conf. Robot. Autom. 2000, 2, 1151–1156. [Google Scholar] [CrossRef]
- Phelps, N. Collaborative buyer-supplier relation and the formation of centralised networks. Geoforum 1996, 27, 393–407. [Google Scholar] [CrossRef]
- Viau, M.A.; Trepanier, M.; Baptiste, P. Integration of inventory and transportation decisions in decentralised supply chains. Int. J. Logist. Syst. Manag. 2009, 5, 249. [Google Scholar] [CrossRef]
- Varela, M.L.R.; Putnik, G.D.; Cruz-Cunha, M.M.; Cruz-Cunha, A.M.M. Web-based Technologies Integration for Distributed Manufacturing Scheduling in a Virtual Enterprise. Int. J. Web Portals 2012, 4, 19–34. [Google Scholar] [CrossRef] [Green Version]
- Sepehri, M.; Fayazbakhsh, K. A multi-period and multi-product optimizer for cooperative supply chains. S. Afr. J. Bus. Manag. 2012, 43, 77–92. [Google Scholar] [CrossRef] [Green Version]
- Wangphanich, P.; Kara, S.; Kayis, B. Analysis of the bullwhip effect in multi-product, multi-stage supply chain systems–A simulation approach. Int. J. Prod. Res. 2010, 48, 4501–4517. [Google Scholar] [CrossRef]
- Centobelli, P.; Converso, G.; Murino, T.; Santillo, L. Flow shop scheduling algorithm to optimize warehouse activities. Int. J. Ind. Eng. Comput. 2016, 7, 49–66. [Google Scholar] [CrossRef]
- Petering, M.E.; Chen, X.; Hsieh, W.-H. Inventory control with flexible demand: Cyclic case with multiple batch supply and demand processes. Int. J. Prod. Econ. 2019, 212, 60–77. [Google Scholar] [CrossRef]
- Memari, A.; Ahmad, R.; Rahim, A.R.A.; Hassan, A. Optimizing a Just-In-Time logistics network problem under fuzzy supply and demand: Two parameter-tuned metaheuristics algorithms. Neural Comput. Appl. 2017, 30, 3221–3233. [Google Scholar] [CrossRef]
- Lim, A.; Miao, Z.; Rodrigues, B.; Xu, Z. Transshipment Through Crossdocks with Inventory and Time Windows. Lect. Notes Comput. Sci. 2004, 3106, 122–131. [Google Scholar]
- Afrazeh, A.; Zarinozv, I. A conceptual framework for presenting and promoting human resource knowledge sharing in the supply chain as a social network. Int. J. Serv. Econ. Manag. 2010, 2, 227. [Google Scholar] [CrossRef]
- Thomas, A. Globalisation presents threats & opportunities. Labels Label. 2003, 4, 81–88. [Google Scholar]
- Wellesley, L.; Preston, F.; Lehne, J.; Bailey, R. Chokepoints in global food trade: Assessing the risk. Res. Transp. Bus. Manag. 2017, 25, 15–28. [Google Scholar] [CrossRef]
- Dinsdale, E.J.; Bennett, D. Benefits; drawbacks and boundaries to deliver JIT: Re-thinking the UK automotive industry operations supply strategy. Benchmarking 2015, 22, 1081–1095. [Google Scholar] [CrossRef]
- Perez, M.P.; Sanchez, A.M. Learning and technological cooperation: The case of the Opel-GM related supply base. Int. J. Automot. Technol. Manag. 2002, 2, 305. [Google Scholar] [CrossRef]
- Manenti, F.; Rovaglio, M. Market-driven operational optimization of industrial gas supply chains. Comput. Chem. Eng. 2013, 56, 128–141. [Google Scholar] [CrossRef]
- Tsigkas, A. Open lean electricity supply communities: A paradigm shift for mass customizing electricity markets. Energy Syst. 2011, 2, 407–422. [Google Scholar] [CrossRef]
- Fernie, J.; Pfab, F.; Marchant, C. Retail Grocery Logistics in the UK. Int. J. Logist. Manag. 2000, 11, 83–90. [Google Scholar] [CrossRef]
- Kisperska-Moroñ, D. Warehousing conditions for holding inventory in Polish supply chains. Int. J. Prod. Econ. 1999, 59, 123–128. [Google Scholar] [CrossRef]
- Hancké, B. Trust or Hierarchy? Changing Relationships Between Large and Small Firms in France. Small Bus. Econ. 1998, 11, 237–252. [Google Scholar] [CrossRef]
- Adrodegari, F.; Bacchetti, A.; Pinto, R.; Pirola, F.; Zanardini, M. Engineer-to-order (ETO) production planning and control: An empirical framework for machinery-building companies. Prod. Plan. Control. 2015, 26, 910–932. [Google Scholar] [CrossRef]
- Rouky, N.; Abourraja, M.N.; Boukachour, J.; Boudebous, D.; Alaoui, A.E.H.; El Khoukhi, F. Simulation optimization based ant colony algorithm for the uncertain quay crane scheduling problem. Int. J. Ind. Eng. Comput. 2019, 10, 111–132. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Hatamlou, A. Solving travelling salesman problem using black hole algorithm. Soft Comput. 2018, 22, 8167–8175. [Google Scholar] [CrossRef]
- Banharnsakun, A. Artificial Bee Colony Algorithm for Solving the Knight’s Tour Problem. Adv. Intell. Syst. 2019, 866, 129–138. [Google Scholar] [CrossRef]
- Mo, J.P.; Cook, M. Quantitative lifecycle risk analysis of the development of a just-in-time transportation network system. Adv. Eng. Inform. 2018, 36, 76–85. [Google Scholar] [CrossRef]
- Kowalski, P.A.; Łukasik, S.; Charytanowicz, M.; Kulczycki, P. Nature inspired clustering—Use cases of krill herd algorithm and flower pollination algorithm. Stud. Comp. Intell. 2019, 794, 83–98. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. Inform. Fokus 2010, 284, 65–74. [Google Scholar]
- Pinto, P.C.; Runkler, T.A.; Sousa, J.M.C. Wasp Swarm Algorithm for Dynamic MAX-SAT Problems. Lect. Notes Comput. Sci. 2007, 4431, 350–357. [Google Scholar]
- Kennedy, J. Thinking is Social—Experiments with the Adaptive Culture Model. J. Conflict Resolut. 1998, 42, 56–76. [Google Scholar] [CrossRef]
- Nasser, A.B.; Zamli, K.Z. Self-adaptive population size strategy based on flower pollination algorithm for T-way test suite generation. Adv. Intell. Syst. 2019, 843, 240–248. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Shawky, L.A. Flower pollination algorithm: A comprehensive review. Artif. Intell. Rev. 2018. [Google Scholar] [CrossRef]
- Binh, H.T.T.; Hanh, N.T.; Van Quan, L.; Dey, N. Improved Cuckoo Search and Chaotic Flower Pollination optimization algorithm for maximizing area coverage in Wireless Sensor Networks. Neural Comput. Appl. 2018, 30, 2305–2317. [Google Scholar] [CrossRef]
- Kabir, M.N.; Ali, J.; Alsewari, A.A.; Zamli, K.Z. An adaptive flower pollination algorithm for software test suite minimization. In Proceedings of the 3rd International Conference on Electrical Information and Communication Technology, Khulna, Bangladesh, 7–9 December 2017; Volume 134453, pp. 1–5. [Google Scholar]
- Bekdaş, G.; Nigdeli, S.M.; Yang, X.-S. Sizing optimization of truss structures using flower pollination algorithm. Appl. Soft Comput. 2015, 37, 322–331. [Google Scholar] [CrossRef]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Multi-level cross entropy optimizer (MCEO): An evolutionary optimization algorithm for engineering problems. Eng. Comput. 2018, 34, 719–739. [Google Scholar] [CrossRef]
- Platt, G. Application of the flower pollination algorithm in nonlinear algebraic systems with multiple solutions. In Engineering Optimization 2014; Informa UK Limited: London, UK, 2014; Volume 115689, pp. 117–121. [Google Scholar]
- Basset, M.A.; Zhou, Y. An elite opposition-flower pollination algorithm for a 0-1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 11, 46. [Google Scholar] [CrossRef]
- Dubey, H.M.; Pandit, M.; Panigrahi, B.K. A Biologically Inspired Modified Flower Pollination Algorithm for Solving Economic Dispatch Problems in Modern Power Systems. Cogn. Comput. 2015, 7, 594–608. [Google Scholar] [CrossRef]
- Kumar, G.V.N.; Suryakalavathi, M. Optimal power flow with static VAR compensator based on flower pollination algorithm to minimize real power losses. In Proceedings of the Conference on Power, Control, Communication and Computational Technologies for Sustainable Growth, Kurnool, India, 11–12 December 2015; Volume 7503934, pp. 112–116. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Tolba, M.A.; Tulsky, V.N. A new hybrid PSOGSA algorithm for optimal allocation and sizing of capacitor banks in RDS. In Proceedings of the 2017 IEEE Russia Section Young Researchers in Electrical and Electronic Engineering Conference, Moscow, Russia, 1–3 February 2017; Volume 7910857, pp. 1496–1501. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Banerjee, S. Optimum power allocation of parallel concatenated convolution turbo code using flower pollination algorithm. In Proceedings of the 2nd International Conference on Control, Instrumentation, Energy and Communication, Kolkata, India, 28–30 January 2016; Volume 7513808, pp. 516–520. [Google Scholar] [CrossRef]
- Rao, M.S.; Babu, A.V.N.; Venkaiah, N. Modified Flower Pollination Algorithm to Optimize WEDM parameters while Machining Inconel-690 alloy. Mater. Today Proc. 2018, 5, 7864–7872. [Google Scholar]
- Zainudin, A.; Sia, C.K.; Ong, P.; Narong, O.L.C.; Nor, N.H.M. Taguchi design and flower pollination algorithm application to optimize the shrinkage of triaxial porcelain containing palm oil fuel ash. IOP Conf. Ser. Mater. Sci. Eng. 2017, 165, 12036. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Basset, M.; El-Shahat, D.; El-Henawy, I.; Sangaiah, A.K. A modified flower pollination algorithm for the multidimensional knapsack problem: Human-centric decision making. Soft Comput. 2018, 22, 4221–4239. [Google Scholar] [CrossRef]
- Rajamohana, S.P.; Umamaheswari, K.; Abirami, B. Adaptive binary flower pollination algorithm for feature selection in review spam detection. In Proceedings of the IEEE International Conference on Innovations in Green Energy and Healthcare Technologies, Coimbatore, India, 16–18 March 2017; Volume 8094094. [Google Scholar] [CrossRef]
- Wang, C.; Sun, H.X.; Yang, J.S.; Zhang, H.; Zong, Y.; Liang, H.P. Calculation of maximum permitted capacity of photovoltaic based on flower pollination algorithm combined with genetic algorithm (GA-FPA) in distribution network. IOP Conf. Ser. Earth Environ. Sci. 2018, 188, 012081. [Google Scholar] [CrossRef]
- Peesapati, R.; Yadav, V.K.; Kumar, N. Flower pollination algorithm based multi-objective congestion management considering optimal capacities of distributed generations. Energy 2018, 147, 980–994. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.; Yang, X.-S. Variants of the Flower Pollination Algorithm: A Review. Stud. Comput. Intell. 2018, 744, 91–118. [Google Scholar] [CrossRef]
- Cui, W.; He, Y. Biological Flower Pollination Algorithm with Orthogonal Learning Strategy and Catfish Effect Mechanism for Global Optimization Problems. Math. Probl. Eng. 2018, 2018, 6906295. [Google Scholar] [CrossRef]
- Digalakis, J.G.; Margaritis, K.G. On benchmarking functions for genetic algorithms. Int. J. Comp. Math. 2007, 77, 481–506. [Google Scholar] [CrossRef]
- Garg, V.; Deep, K. Performance of Laplacian Biogeography-Based Optimization Algorithm on CEC 2014 continuous optimization benchmarks and camera calibration problem. Swarm Evol. Comput. 2016, 27, 132–144. [Google Scholar] [CrossRef]
- Zhou, X.J.; Gao, D.Y.; Yang, C.H. Global solutions to a class of CEC benchmark constrained optimization problems. Optim. Lett. 2016, 10, 457–472. [Google Scholar] [CrossRef]
- Liao, T.; Molina, D.; De Oca, M.A.M.; Stützle, T. A Note on Bound Constraints Handling for the IEEE CEC’05 Benchmark Function Suite. Evol. Comput. 2014, 22, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Liao, T.J.; de Oca, M.A.M.; Stutzle, T. Computational results for an automatically tuned CMA-ES with increasing population size on the CEC’05 benchmark set. Soft Comput. 2013, 17, 1031–1046. [Google Scholar] [CrossRef]
- Bányai, T.; Tamás, P.; Illés, B.; Stankevičiūtė, Ž.; Bányai, Á. Optimization of Municipal Waste Collection Routing: Impact of Industry 4.0 Technologies on Environmental Awareness and Sustainability. Int. J. Environ. Res. Public Heal. 2019, 16, 634. [Google Scholar] [Green Version]
- Larsen, A.W.; Vrgoc, M.; Christensen, T.H.; Lieberknecht, P. Diesel consumption in waste collection and transport and its environmental significance. Waste Manag. Res. 2009, 27, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Cedillo-Campos, M.G.; Ruelas, D.M.; Lizarraga-Lizarraga, G.; Gonzalez-Feliu, J.; Garza-Reyes, J.A. Decision policy scenarios for just-in-sequence (JIS) deliveries. J. Ind. Eng. Manag. 2017, 10, 581. [Google Scholar] [CrossRef]
- Wagner, S.M.; Silveira-Camargos, V. Decision model for the application of just-in-sequence. Int. J. Prod. Res. 2011, 49, 5713–5736. [Google Scholar] [CrossRef]
- Heinecke, G.; Lamparter, S.; Lepratti, R.; Kunz, A. Advanced supply chain information for rule-based sequence adaptions on a mixed-model assembly line with unreliable just-in-sequence deliveries. IFAC Proc. 2013, 46, 1902–1907. [Google Scholar] [CrossRef]
- Hüttmeir, A.; De Treville, S.; Van Ackere, A.; Monnier, L.; Prenninger, J. Trading off between heijunka and just-in-sequence. Int. J. Prod. Econ. 2009, 118, 501–507. [Google Scholar] [CrossRef]
- Gottsauner, B. RFID systems in just-in-sequence production. AutoTechnology 2007, 7, 48–51. [Google Scholar]
- Meissner, S. Controlling just-in-sequence flow-production. Logist. Res. 2010, 2, 45–53. [Google Scholar] [CrossRef]
- Wildemann, H.; Faust, P. Just-in-sequence audits towards partnership-based optimization of processes in the automotive industry. Z. Wirtsch. Fabr. 2004, 99, 157–161. [Google Scholar] [CrossRef]
- Wagner, S.M.; Silveira-Camargos, V. Managing Risks in Just-In-Sequence Supply Networks: Exploratory Evidence from Automakers. IEEE Trans. Eng. Manag. 2012, 59, 52–64. [Google Scholar] [CrossRef]
- Yang, B.; Li, H. A novel dynamic timed fuzzy Petri nets modeling method with applications to industrial processes. Expert Syst. Appl. 2018, 97, 276–289. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, J.; He, T. Automatic Combination Technology of Fuzzy CPN for OWL-S Web Services in Supercomputing Cloud Platform. Int. J. Pattern Recognit. Artif. Intell. 2017, 31, 1759010. [Google Scholar] [CrossRef]
- Kota, L. Optimization of the supplier selection problem using discrete firefly algorithm. Adv. Logist. Syst. 2012, 6, 10–20. [Google Scholar]
- Kota, L. Optimisation of Large Scale Maintenance Networks with Evolutionary Programming. In DAAAM International Scientific Book 2011; DAAAM International: Vienna, Austria, 2011; Volume 11, pp. 495–512. [Google Scholar]
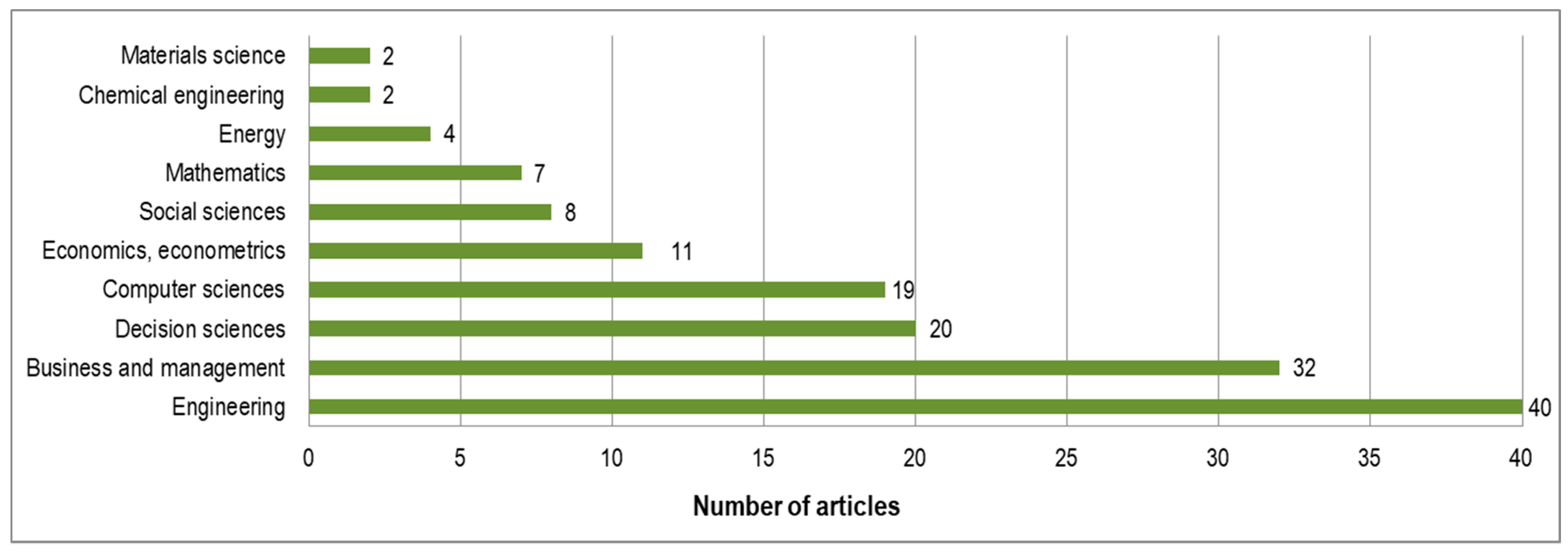

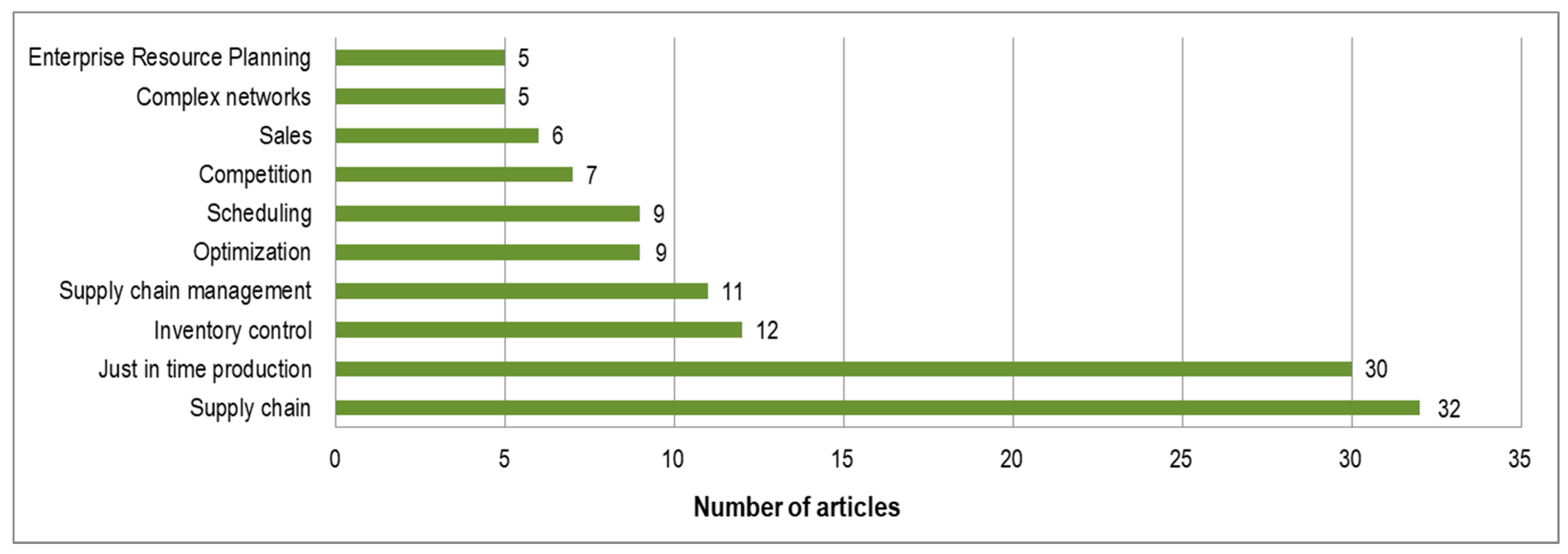


| Scientific Field | Application Examples |
|---|---|
| Computer Science | |
| Engineering | |
| Mathematics | |
| Energy | |
| Physics and Astronomy | |
| Materials Science | |
| Decision Science | |
| Environmental Science |
| Benchmarking Function | BHA | BHA/DSR 1 | SFPA 2 | FPAwFPS 3 |
|---|---|---|---|---|
| 4.24 × 10−4 | 1.48 × 10−5 | 3.12 × 10−5 | 2.49 × 10−5 | |
| 3.24 × 10−2 | 3.24 × 10−2 | 2.01 × 10−3 | 1.41 × 10−3 | |
| 3.56 × 10−9 | 3.56 × 10−3 | 5.61 × 10−4 | 2.90 × 10−6 | |
| 8.96 × 10−9 | 7.01 × 10−9 | 5.50 × 10−9 | 3.58 × 10−9 | |
| 2.45 × 10−6 | 2.32 × 10−6 | 7.44 × 10−7 | 8.61 × 10−7 | |
| 5.50 × 10−6 | 5.44 × 10−6 | 9.72 × 10−7 | 9.65 × 10−7 |
| Benchmarking Function | Problem Size | ||
|---|---|---|---|
| 5 | 10 | 20 | |
| 69% | 100% | 218% | |
| 72% | 100% | 186% | |
| 54% | 100% | 266% | |
| 44% | 100% | 327% | |
| Sequence Order | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Sequence A1 | ToC3 | 1 | 6 | 1 | 4 | 3 | 6 | 1 | 4 |
| RA4 | 10 | 20 | 25 | 25 | 40 | 55 | 75 | 30 | |
| Sequence B2 | ToC | 1 | 2 | 2 | 4 | 5 | 2 | 1 | 3 |
| RA | 30 | 40 | 15 | 60 | 25 | 55 | 40 | 30 | |
| Supplier 1 | Supplier 2 | Supplier 3 | Supplier 4 | |||||
|---|---|---|---|---|---|---|---|---|
| AA1 | EAT2 | AA | EAT | AA | EAT | AA | EAT | |
| Component 1 | 40 | 9:00 | 48 | 11:50 | 36 | 8:40 | 60 | 10:35 |
| Component 2 | 60 | 11:50 | 28 | 9:10 | 40 | 10:50 | 48 | 10:20 |
| Component 3 | 44 | 9:10 | 48 | 10:50 | 52 | 9:20 | 20 | 11:55 |
| Component 4 | 24 | 9:25 | 28 | 10:40 | 36 | 11:20 | 80 | 10:25 |
| Component 5 | 48 | 11:40 | 24 | 10:10 | 48 | 10:50 | 24 | 9:40 |
| Component 6 | 20 | 9:55 | 52 | 12:20 | 22 | 9:50 | 58 | 11:40 |
| Supplier 1 | Supplier 2 | Supplier 3 | Supplier 4 | |
|---|---|---|---|---|
| Component 1 | 1 | 2 | 3 | 4 |
| Component 2 | 9 | 10 | 11 | 12 |
| Component 3 | 17 | 18 | 19 | 20 |
| Component 4 | 24 | 23 | 22 | 21 |
| Component 5 | 16 | 15 | 14 | 13 |
| Component 6 | 8 | 7 | 6 | 5 |
| Supplier 1 | Supplier 2 | Supplier 3 | Supplier 4 | ||
|---|---|---|---|---|---|
| Sequence A | Component 1 | 40 | 26 | 18 | 26 |
| Component 2 | 0 | 0 | 0 | 0 | |
| Component 3 | 22 | 18 | 0 | 0 | |
| Component 4 | 0 | 0 | 18 | 37 | |
| Component 5 | 0 | 0 | 0 | 0 | |
| Component 6 | 0 | 0 | 17 | 58 | |
| Sequence B | Component 1 | 0 | 22 | 18 | 30 |
| Component 2 | 60 | 28 | 22 | 0 | |
| Component 3 | 22 | 8 | 0 | 0 | |
| Component 4 | 0 | 0 | 17 | 43 | |
| Component 5 | 0 | 0 | 1 | 24 | |
| Component 6 | 0 | 0 | 0 | 0 | |
| Routes | Route Length | Emission | |||||
|---|---|---|---|---|---|---|---|
| CO2 | SO2 | CO | HC | NOX | PM | ||
| Specific emissions in g/liter fuel consumption [102] | - | 2629 | 0.08 | 2.2 | 1.2 | 11.9 | 0.1 |
| Route 1 | 103.056 | 86,698 | 2.63 | 72.56 | 39.58 | 392.44 | 3.29 |
| Route 2 | 118.420 | 99,633 | 3.02 | 83.38 | 45.48 | 450.99 | 3.78 |
| Additional routes | 15.360 | 12,935 | 0.39 | 10.82 | 5.90 | 58.55 | 0.49 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bányai, T.; Illés, B.; Gubán, M.; Gubán, Á.; Schenk, F.; Bányai, Á. Optimization of Just-In-Sequence Supply: A Flower Pollination Algorithm-Based Approach. Sustainability 2019, 11, 3850. https://doi.org/10.3390/su11143850
Bányai T, Illés B, Gubán M, Gubán Á, Schenk F, Bányai Á. Optimization of Just-In-Sequence Supply: A Flower Pollination Algorithm-Based Approach. Sustainability. 2019; 11(14):3850. https://doi.org/10.3390/su11143850
Chicago/Turabian StyleBányai, Tamás, Béla Illés, Miklós Gubán, Ákos Gubán, Fabian Schenk, and Ágota Bányai. 2019. "Optimization of Just-In-Sequence Supply: A Flower Pollination Algorithm-Based Approach" Sustainability 11, no. 14: 3850. https://doi.org/10.3390/su11143850
APA StyleBányai, T., Illés, B., Gubán, M., Gubán, Á., Schenk, F., & Bányai, Á. (2019). Optimization of Just-In-Sequence Supply: A Flower Pollination Algorithm-Based Approach. Sustainability, 11(14), 3850. https://doi.org/10.3390/su11143850









