An Optimisation Model to Consider the NIMBY Syndrome within the Landfill Siting Problem
Abstract
:1. Introduction
2. Background
3. Methodology
3.1. Optimisation Model
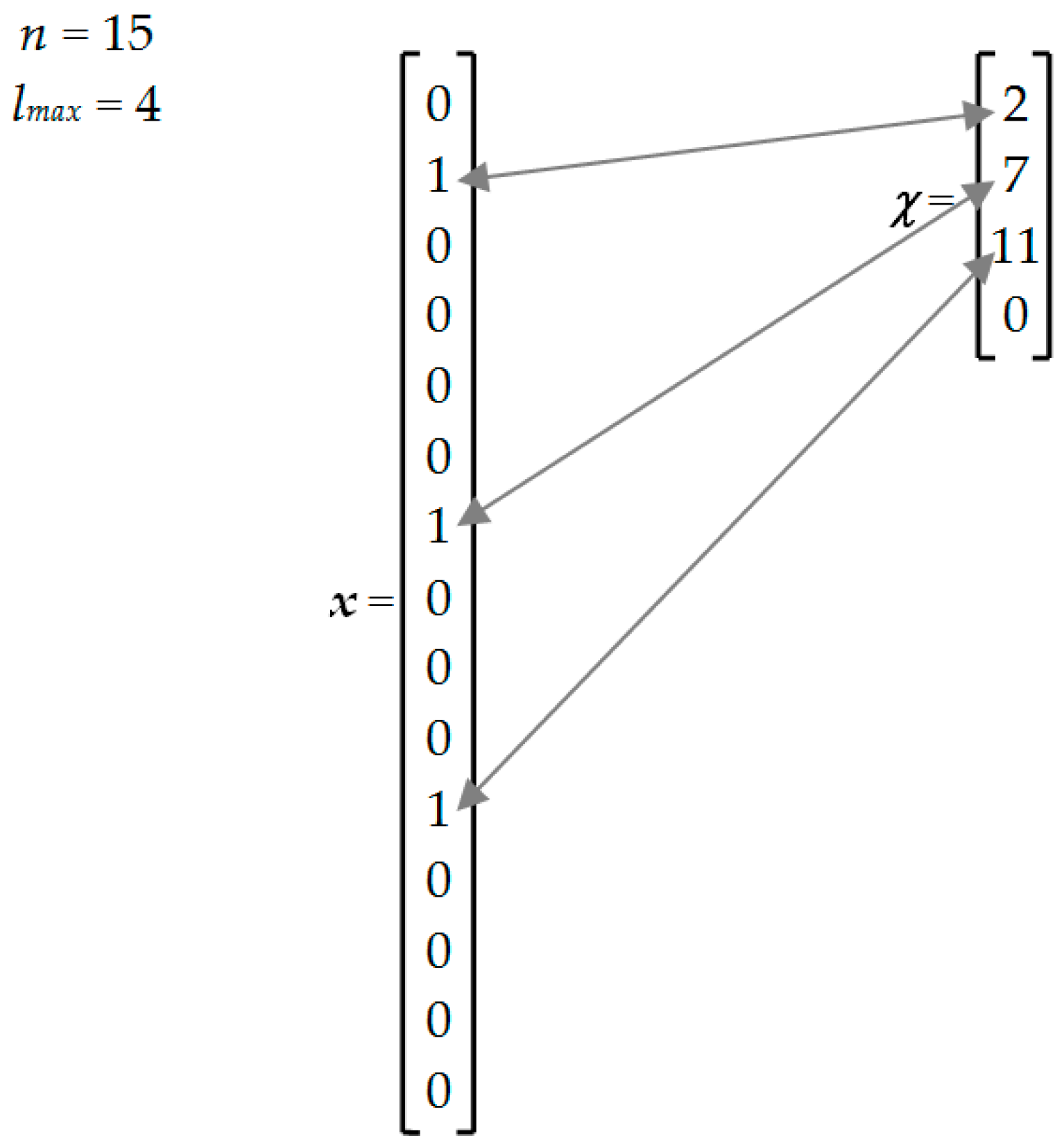
- i indicates an eligible site;
- j indicates a waste source;
- x is the vector of decision variables xi;
- xopt is the optimal solution;
- xi is a binary variable that is equal to 1 if a landfill is located in site i, 0 otherwise;
- wi(x) is the annual waste quantity allocated to site i;
- yci(.) is a function used for calculating the annual cost of the landfill located in site i; it depends on the annual waste quantity to be treated, wi(x);
- dj,min(x) indicates the distance between a waste source j and the nearest landfill;
- wpj indicates the annual production of waste source j;
- ctr indicates the cost per ton-km of transported waste (€/ton-km);
- resi indicates the number of residents that have to be compensated for a landfill located in site i;
- ccomp is the annual compensation cost per ton of waste per resident (€/ton);
- lmax is the maximum number of landfills.
- ai,j(x) is equal to 1 if, under configuration x, site i is the nearest to source j (di,j = dj,min), 0 otherwise, with di,j indicating the distance between site i and source j.
3.2. Solution Algorithm
4. Numerical Results
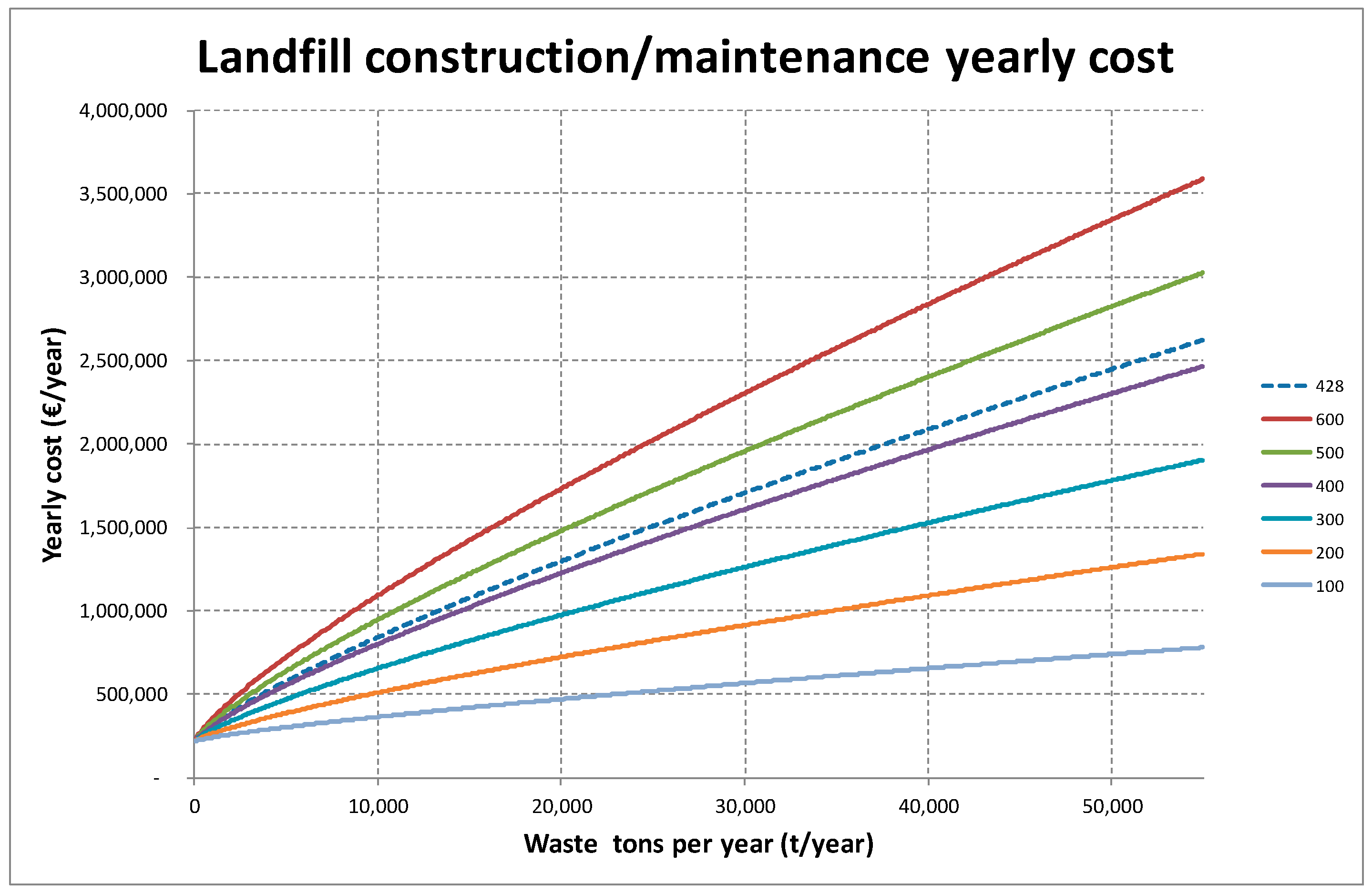
- c0 is a fixed cost of the landfill (€/year);
- c1 is a variable cost per waste ton (€/ton-year), depending on wi for considering the scale economy.
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, H.W.; Yu, Y.H. Social and Economic Factors in the Spread of the NIMBY Syndrome against Waste Disposal Sites in Taiwan. J. Environ. Plan. Man. 1997, 40, 273–282. [Google Scholar] [CrossRef]
- Li, R.Y.M.; Li, H.C.Y. Have Housing Prices Gone with the SmellyWind? Big Data Analysis on Landfill in Hong Kong. Sustainability 2018, 10, 341. [Google Scholar] [CrossRef]
- Jenkins, R.R.; Maguire, K.M.; Morgan, C. Host Community Compensation and Municipal Solid Waste Landfills; Working Paper #02-04; U.S. Environmental Protection Agency, National Center for Environmental Economics (NCEE): Washington, DC, USA, 2002.
- Gallo, M. A model and algorithm for solving the landfill siting problem in large areas. In Optimization and Decision Science: Methodologies and Applications. ODS 2017; Sforza, A., Sterle, C., Eds.; Springer: Cham, Switzerland, 2017; Volume 217, pp. 267–274. [Google Scholar]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems, Part II: The p-medians. SIAM J. Appl. Math. 1979, 37, 539–560. [Google Scholar] [CrossRef]
- ReVelle, C.S.; Eiselt, H.A.; Daskin, M.S. A bibliography of some fundamental problem categories in discrete location science. Eur. J. Oper. Res. 2008, 184, 817–848. [Google Scholar] [CrossRef]
- Daskin, M.S.; Mass, K.L. The p-Median problem. In Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 21–45. [Google Scholar]
- Averbakh, I.; Berman, O.; Drezner, Z.; Wesolowsky, G.O. The Plant Location Problem with Demand-Dependent Setup Costs and Centralized Allocation. Eur. J. Oper. Res. 1998, 111, 543–554. [Google Scholar] [CrossRef]
- Joos, W.; Carabias, V.; Winistoerfer, H.; Stuecheli, A. Social aspects of public waste management in Switzerland. Waste Manag. 1999, 19, 417–425. [Google Scholar] [CrossRef]
- Simsek, C.; Elci, A.; Gunduz, O.; Taskin, N. An improved landfill site screening procedure under NIMBY syndrome constraints. Landsc. Urban Plan. 2014, 132, 1–15. [Google Scholar] [CrossRef]
- Morrisey, A.J.; Browne, J. Waste management models and their application to sustainable waste management. Waste Manag. 2004, 24, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Greco, S.; Ehrgott, M.; Figueira, J.R. Multiple Criteria Decision Analysis. State of the Art Surveys, 2nd ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Department for Communities and Local Government. Multi-Criteria Analysis: A Manual; Communities and Local Government, Eland House: London, UK, 2009.
- Tsolaki-Fiaka, S.; Bathrellos, G.D.; Skilodimou, H.D. Multi-Criteria Decision Analysis for an Abandoned Quarry in the Evros Region (NE Greece). Land 2018, 7, 43. [Google Scholar] [CrossRef]
- Melachrinoudis, E.; Min, H.; Wu, X. A multiobjective model for the dynamic location of landfills. Locat. Sci. 1995, 3, 143–166. [Google Scholar] [CrossRef]
- Hokkanen, J.; Salminen, P. Choosing a solid waste management system using multicriteria decision analysis. Eur. J. Oper. Res. 1997, 98, 19–36. [Google Scholar] [CrossRef]
- Cheng, S.; Chan, C.W.; Huang, G.H. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2003, 16, 543–554. [Google Scholar] [CrossRef]
- Vasiloglou, V.C. New tool for landfill location. Waste Manag. Res. 2004, 22, 427–439. [Google Scholar] [CrossRef] [PubMed]
- Kontos, T.D.; Komilis, D.P.; Halvadakis, C.P. Siting MSW landfills with a spatial multiple criteria analysis methodology. Waste Manag. 2005, 25, 818–832. [Google Scholar] [CrossRef] [PubMed]
- Chang, N.-B.; Parvathinathan, G.; Breeden, J.B. Combining GIS with fuzzy multicriteria decision-making for landfill siting in a fast-growing urban region. J. Environ. Manag. 2008, 87, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Xi, B.D.; Su, J.; Huang, G.H.; Qin, X.S.; Jiang, Y.H.; Huo, S.L.; Ji, D.F.; Yao, B. An integrated optimization approach and multi-criteria decision analysis for supporting the waste-management system of the City of Beijing, China. Eng. Appl. Artif. Intell. 2010, 23, 620–631. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Donevska, K.R.; Mitrovski, C.D.; Frizado, J.P. Integrating multi-criteria evaluation techniques with geographic information systems for landfill site selection: A case study using ordered weighted average. Waste Manag. 2012, 32, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Gbanie, S.P.; Tengbe, P.B.; Momoh, J.S.; Medo, J.; Kabba, V.T.S. Modelling landfill location using Geographic Information Systems (GIS) and Multi-Criteria Decision Analysis (MCDA): Case study Bo, Southern Sierra Leone. Appl. Geogr. 2013, 36, 3–12. [Google Scholar] [CrossRef]
- Al-Jarrah, O.; Abu-Qdais, H. Municipal solid waste landfill siting using intelligent system. Waste Manag. 2006, 26, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Sumathi, V.R.; Natesan, U.; Sarkar, C. GIS-based approach for optimized siting of municipal solid waste landfill. Waste Manag. 2008, 28, 2146–2160. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, M.; Molero, E.; Hurtado, A.; Grindlay, A.; Ramos, A. Evaluation of a municipal landfill site in Southern Spain with GIS-aided methodology. J. Hazard. Mater. 2008, 160, 473–481. [Google Scholar] [CrossRef] [PubMed]
- Chabuk, A.; Al-Ansari, N.; Hussain, H.M.; Knutsson, S.; Pusch, R.; Laue, J. Combining GIS Applications and Method of Multi-Criteria Decision-Making (AHP) for Landfill Siting in Al-Hashimiyah Qadhaa, Babylon, Iraq. Sustainability 2017, 9, 1932. [Google Scholar] [CrossRef]
- Al-Anbari, M.A.; Thameer, M.Y.; Al-Ansari, N. Landfill Site Selection by Weighted Overlay Technique: Case Study of Al-Kufa, Iraq. Sustainability 2018, 10, 999. [Google Scholar] [CrossRef]
- Yousefi, H.; Javadzadeh, Z.; Noorollahi, Y.; Yousefi-Sahzabi, A. Landfill Site Selection Using a Multi-Criteria Decision-Making Method: A Case Study of the Salafcheghan Special Economic Zone, Iran. Sustainability 2018, 10, 1107. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.; Yang, Y.; Hou, Y.; Liu, G.-J.; Zhang, S. Storing E-waste in Green Infrastructure to Reduce Perceived Value Loss through Landfill Siting and Landscaping: A Case Study in Nanjing, China. Sustainability 2019, 11, 1829. [Google Scholar] [CrossRef]
- Chabuk, A.; Al-Ansari, N.; Ezz-Aldeen, M.; Laue, J.; Pusch, R.; Hussain, H.M.; Knutsson, S. Two Scenarios for Landfills Design in Special Conditions Using the HELP Model: A Case Study in Babylon Governorate, Iraq. Sustainability 2018, 10, 125. [Google Scholar] [CrossRef]
- Eiselt, H.A. Locating landfills-Optimization vs. reality. Eur. J. Oper. Res. 2007, 179, 1040–1049. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. A bi-objective model for the location of landfills for municipal solid waste. Eur. J. Oper. Res. 2014, 235, 187–194. [Google Scholar] [CrossRef]
- Guiqin, W.; Li, Q.; Guoxue, L.; Lijun, C. Landfill site selection using spatial information technologies and AHP: A case study in Beijing, China. J. Environ. Manag. 2009, 90, 2414–2421. [Google Scholar]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems, Part I: The p-centers. SIAM J. Appl. Math. 1979, 37, 513–538. [Google Scholar] [CrossRef]
- Hochbaum, D.S. When are NP-hard location problems easy? Ann. Oper. Res. 1984, 1, 201–214. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Sandblom, C.-L. Decision Analysis, Location Models, and Scheduling Problems; Springer: New York, NY, USA, 2004. [Google Scholar]
- Kratica, J.; Tosic, D.; Filipovic, V.; Ljubic, I. Solving the simple plant location problem by genetic algorithm. RAIRO-Oper. Res. 2001, 35, 127–142. [Google Scholar] [CrossRef] [Green Version]
- Jaramillo, J.H.; Bhadury, J.; Batta, R. On the use of genetic algorithms to solve location problems. Comput. Oper. Res. 2002, 29, 761–779. [Google Scholar] [CrossRef]
- Alp, O.; Erkut, E.; Drezner, Z. An Efficient Genetic Algorithm for the p-Median Problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Maric, M. An efficient genetic algorithm for solving the multi-level uncapacitated facility location problem. Comput. Inform. 2010, 29, 183–201. [Google Scholar]
- Fernandes, D.R.M.; Rocha, C.; Aloise, D.; Ribeiro, G.M.; Santos, E.M.; Silva, A. A simple and effective genetic algorithm for the two-stage capacitated facility location problem. Comput. Ind. Eng. 2014, 75, 200–208. [Google Scholar] [CrossRef]
- Murray, A.T.; Church, R.L. Applying simulated annealing to location-planning models. J. Heuristics 1996, 2, 31–53. [Google Scholar] [CrossRef]
- Bornstein, C.T.; Azlan, H.B. The use of reduction tests and simulated annealing for the capacitated plant location problem. Locat. Sci. 1998, 6, 67–81. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Wesolowsky, G.O. Location of Facilities on a Network with Groups of Demand Points. IIE Trans. 2001, 33, 637–648. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Wesolowsky, G.O. The Facility and Transfer Plant Location Problem. Int. Trans. Oper. Res. 2005, 12, 387–402. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, A. Location of congested capacitated facilities with distance sensitive demand. IIE Trans. 2006, 38, 213–221. [Google Scholar] [CrossRef]
- Delmaire, H.; Dìaz, J.A.; Fernandez, E.; Ortega, M. Reactive GRASP and Tabu Search Based Heuristics for the Single Source Capacitated Plant Location Problem. INFOR 1998, 37, 194–225. [Google Scholar] [CrossRef]
- Al-Sultan, K.S.; Al-Fawzan, M.A. A Tabu Search Approach to the Uncapacitated Facility Location Problem. Ann. Oper. Res. 1999, 86, 91–103. [Google Scholar] [CrossRef]
- Mladenovic, N.; Labbé, M.; Hansen, P. Solving the p-center problem with tabu search and variable neighborhood search. Networks 2003, 42, 48–64. [Google Scholar] [CrossRef]
- Ghosh, D. Neighborhood Search Heuristics for the Uncapacitated Facility Location Problem. Eur. J. Oper. Res. 2003, 150, 150–162. [Google Scholar] [CrossRef]
- Sun, M. A tabu search heuristic procedure for the capacitated facility location problem. J. Heuristics 2012, 18, 91–118. [Google Scholar] [CrossRef]
- Ho, S.C. An iterated tabu search heuristic for the Single Source Capacitated Facility Location Problem. Appl. Soft Comput. 2015, 27, 169–178. [Google Scholar] [CrossRef]
- Whitaker, R. A Fast Algorithm for the Greedy Interchange of Large-Scale Clustering and Median Location Problems. INFOR 1983, 21, 95–108. [Google Scholar] [CrossRef]
- Resende, M.G.C.; Werneck, R.F. A Hybrid Heuristic for the p-Median Problem. J. Heuristics 2004, 10, 59–88. [Google Scholar] [CrossRef]
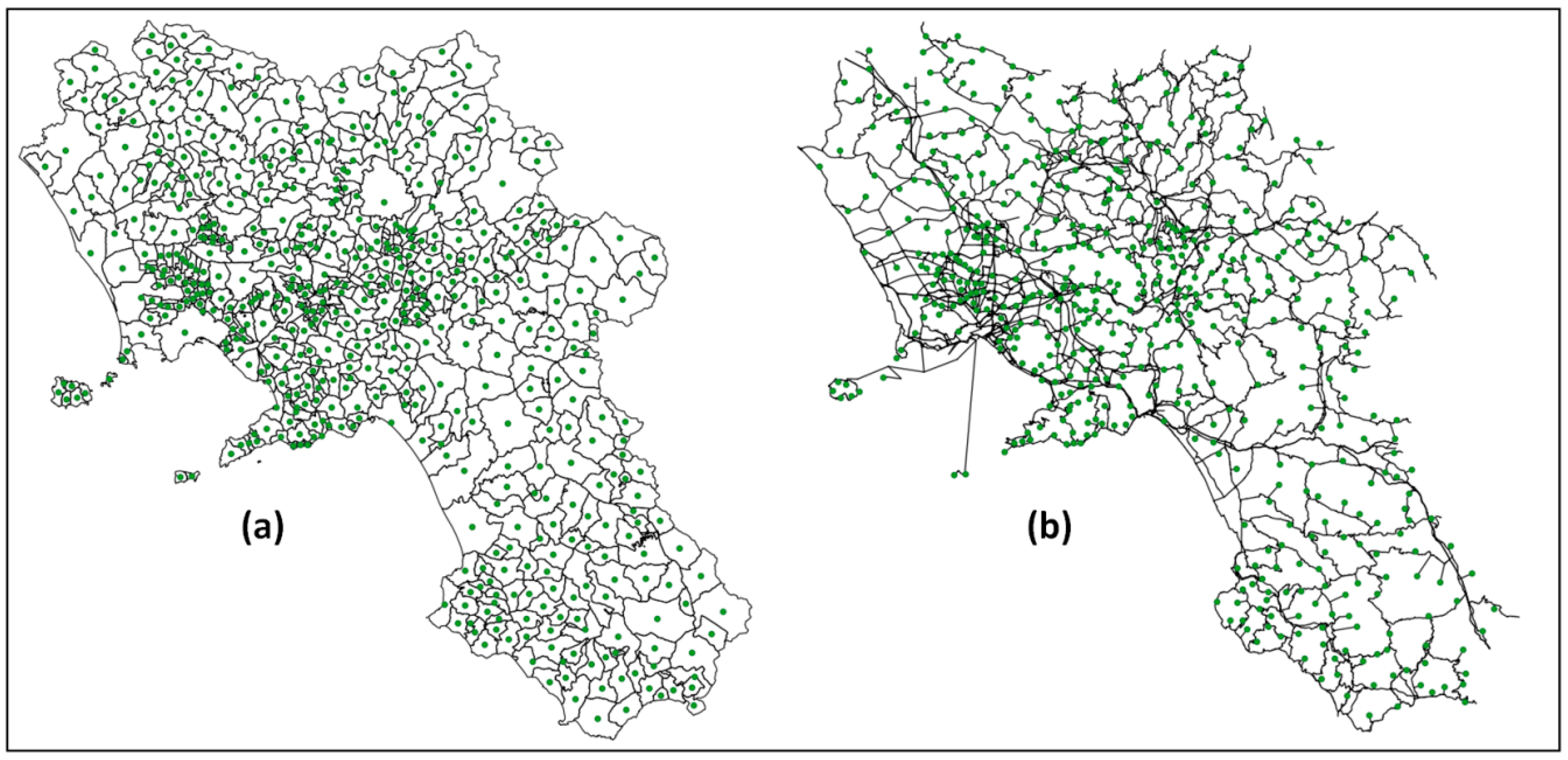
- ISPRA Catasto Rifiuti. Available online: http://www.catasto-rifiuti.isprambiente.it/index.php_?pg=provincia&aa=2015®id=Campania (accessed on 25 February 2019).
- Chan, Y.S.G.; Chu, L.M.; Wong, M.H. Influence of landfill factors on plants and soil fauna—An ecological perspective. Environ. Pollut. 1997, 97, 39–44. [Google Scholar] [CrossRef]
- Caplan, A.; Grijalva, T.; Jackson-Smith, D. Using choice question formats to determine compensable values: The case of a landfill-siting process. Ecol. Econ. 2007, 60, 834–846. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, S.; Gallagher, L. Protest responses and community attitudes toward accepting compensation to host waste disposal infrastructure. Land Use Policy 2010, 27, 638–652. [Google Scholar] [CrossRef]
- Giaccaria, S.; Frontuto, V. Perceived health status and environmental quality in the assessment of external costs of waste disposal facilities. An empirical investigation. Waste Manag. Res. 2012, 30, 864–870. [Google Scholar] [CrossRef] [PubMed]
- Jones, N.; Evangelinos, K.; Halvadakis, C.P.; Iosifides, T.; Sophoulis, C.M. Social factors influencing perceptions and willingness to pay for a market-based policy aiming on solid waste management. Resour. Conserv. Recy. 2010, 54, 533–540. [Google Scholar] [CrossRef]
- Lu, W.; Peng, Y.; Webster, C.; Zuo, J. Stakeholders’ willingness to pay for enhanced construction waste management: A Hong Kong study. Renew. Sustain. Energy Rev. 2015, 47, 233–240. [Google Scholar] [CrossRef]
- Challcharoenwattana, A.; Pharino, C. Wishing to finance a recycling program? Willingness-to-pay study for enhancing municipal solid waste recycling in urban settlements in Thailand. Habitat Int. 2016, 51, 23–30. [Google Scholar] [CrossRef]
- Gallagher, L.; Ferreira, S.; Convery, F. Host community attitudes towards solid waste landfill infrastructure: Comprehension before compensation. J. Environ. Plan. Man. 2008, 51, 233–257. [Google Scholar] [CrossRef]
- Hong, J.; Jung, M.J.; Kim, Y.-B.; Seo, Y.-C.; Koo, J. Analysis of the compensation system at the Environmental-Adverse-Effect Zone of a large-scale waste landfill site. J. Mater. Cycles Waste Manag. 2012, 14, 351–359. [Google Scholar] [CrossRef]
- Liu, J.; Teng, Y.; Jiang, Y.; Gong, E. A cost compensation model for construction and demolition waste disposal in South China. Environ. Sci. Pollut. Res. 2019, 26, 13773–13784. [Google Scholar] [CrossRef]
- Ren, X.; Che, Y.; Yang, K.; Tao, Y. Risk perception and public acceptance toward a highly protested Waste-to-Energy facility. Waste Manag. 2016, 48, 528–539. [Google Scholar] [CrossRef]
- Bathrellos, G.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef] [PubMed]
- Skilodimou, H.D.; Bathrellos, G.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Multi-hazard assessment modeling via multi-criteria analysis and GIS: A case study. Environ. Earth Sci. 2019, 78, 21. [Google Scholar] [CrossRef]
- D’Alisa, G.; Burgalassi, D.; Healy, H.; Walter, M. Conflict in Campania: Waste emergency or crisis of democracy. Ecol. Econ. 2010, 70, 239–249. [Google Scholar] [CrossRef]
- Cantoni, R. The waste crisis in Campania, South Italy: A historical perspective on an epidemiological controversy. Endeavour 2016, 40, 102–113. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, S.P. A political geography of ‘waste wars’ in Campania (Italy): Competing territorialisations and socio-environmental conflicts. Political Geogr. 2018, 67, 46–55. [Google Scholar] [CrossRef]
- Di Nola, M.F.; Escapa, M.; Ansah, J.P. Modelling solid waste management solutions: The case of Campania, Italy. Waste Manag. 2018, 78, 717–729. [Google Scholar] [CrossRef]
- Esposito, F.; Nardone, A.; Fasano, E.; Scognamiglio, G.; Esposito, D.; Agrelli, D.; Ottaiano, L.; Fagnano, M.; Adamo, P.; Beccaloni, E.; et al. A systematic risk characterization related to the dietary exposure of the population to potentially toxic elements through the ingestion of fruit and vegetables from a potentially contaminated area. A case study: The issue of the "Land of Fires" area in Campania region, Italy. Environ. Pollut. 2018, 243, 1781–1790. [Google Scholar]
- Cembalo, L.; Caso, D.; Carfora, V.; Caracciolo, F.; Lombardi, A.; Cicia, G. The “Land of Fires” ToxicWaste Scandal and Its Effect on Consumer Food Choices. Int. J. Environ. Res. Public Health 2019, 16, 165. [Google Scholar] [CrossRef]
- Garofalo, A.; Castellano, R.; Agovino, M.; Punzo, G.; Musella, G. How Far is Campania from the Best-Performing Region in Italy? A Territorial-Divide Analysis of Separate Waste Collection. Soc. Indic. Res. 2019, 142, 667–688. [Google Scholar] [CrossRef]








| With Compensation Costs | Without Compensation Costs | |
|---|---|---|
| Number of landfills | 2 | 2 |
| Municipalities | Massa di Somma; Giungano | Casoria; Battipaglia |
| Total inhabitants | 6702 | 128,440 |
| Transportation costs | 34,274,833 | 30,270,389 |
| Landfill annual costs | 54,311,274 | 55,754,544 |
| Compensation costs | 1,312,718 | − |
| Objective function value | 89,898,825 | 86,024,933 |
| Coeff. | With Compensation Costs | Without Compensation Costs | |
|---|---|---|---|
| 100 | Number of landfills | 5 | 5 |
| Municipalities | Bellizzi; Carinaro; Pietradefusi; San Sebastiano al Vesuvio; Sant’Egidio del Monte Albino | Aversa; Capaccio; Napoli; Pietradefusi; Sant’Egidio del Monte Albino | |
| Total inhabitants | 41,202 | 1,061,188 | |
| Transportation costs | 21,349,521.53 | 19,291,800.69 | |
| Landfill annual costs | 17,018,714.56 | 17,055,619.52 | |
| Compensation costs | 2,168,097.22 | - | |
| Objective function value | 40,536,333.30 | 36,347,420.21 | |
| 200 | Number of landfills | 5 | 5 |
| Municipalities | Capaccio; Carinaro; Pietradefusi; San Sebastiano al Vesuvio; Sant’Egidio del Monte Albino | Benevento; Casavatore; Pompei; Salerno; Vallo della Lucania | |
| Total inhabitants | 50,444 | 247,902 | |
| Transportation costs | 21,206,069.45 | 21,448,200.66 | |
| Landfill annual costs | 32,918,528.70 | 31,482,230.56 | |
| Compensation costs | 2,326,336.09 | - | |
| Objective function value | 56,450,934.24 | 52,930,431.21 | |
| 300 | Number of landfills | 5 | 4 |
| Municipalities | Bellizzi; Carinaro; Celle di Bulgheria; Pietradefusi; San Sebastiano al Vesuvio | Benevento; Casavatore; Salerno; Torre Orsaia | |
| Total inhabitants | 34,215 | 216,131 | |
| Transportation costs | 22,913,058.23 | 24,290,867.40 | |
| Landfill annual costs | 47,126,152.86 | 43,748,060.61 | |
| Compensation costs | 2,173,152.10 | - | |
| Objective function value | 72,212,363.19 | 68,038,928.02 | |
| 400 | Number of landfills | 3 | 3 |
| Municipalities | Giungano; Massa di Somma; Pietradefusi | Battipaglia; Casavatore; Pietradefusi | |
| Total inhabitants | 9072 | 71,795 | |
| Transportation costs | 30,418,540.86 | 26,547,423.82 | |
| Landfill annual costs | 54,645,985.51 | 55,576,136.54 | |
| Compensation costs | 1,239,271.64 | - | |
| Objective function value | 86,303,798.02 | 82,123,560.36 | |
| 500 | Number of landfills | 2 | 2 |
| Municipalities | Giungano; Massa di Somma | Battipaglia; Casavatore | |
| Total inhabitants | 6724 | 69,447 | |
| Transportation costs | 34,274,833.33 | 30,109,769.18 | |
| Landfill annual costs | 63,371,526.24 | 65,128,788.33 | |
| Compensation costs | 1,312,717.53 | - | |
| Objective function value | 98,959,077.10 | 95,238,557.51 | |
| 600 | Number of landfills | 1 | 2 |
| Municipalities | Massa di Somma | Casoria; Agropoli | |
| Total inhabitants | 5444 | 99,123 | |
| Transportation costs | 39,204,346.81 | 32,079,796.38 | |
| Landfill annual costs | 70,697,991.09 | 75,959,521.84 | |
| Compensation costs | 1,397,663.58 | - | |
| Objective function value | 111,300,001.49 | 108,039,318.22 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallo, M. An Optimisation Model to Consider the NIMBY Syndrome within the Landfill Siting Problem. Sustainability 2019, 11, 3904. https://doi.org/10.3390/su11143904
Gallo M. An Optimisation Model to Consider the NIMBY Syndrome within the Landfill Siting Problem. Sustainability. 2019; 11(14):3904. https://doi.org/10.3390/su11143904
Chicago/Turabian StyleGallo, Mariano. 2019. "An Optimisation Model to Consider the NIMBY Syndrome within the Landfill Siting Problem" Sustainability 11, no. 14: 3904. https://doi.org/10.3390/su11143904
APA StyleGallo, M. (2019). An Optimisation Model to Consider the NIMBY Syndrome within the Landfill Siting Problem. Sustainability, 11(14), 3904. https://doi.org/10.3390/su11143904





