An Integrated Variational Mode Decomposition and ARIMA Model to Forecast Air Temperature
Abstract
:1. Introduction
2. Materials and Methods
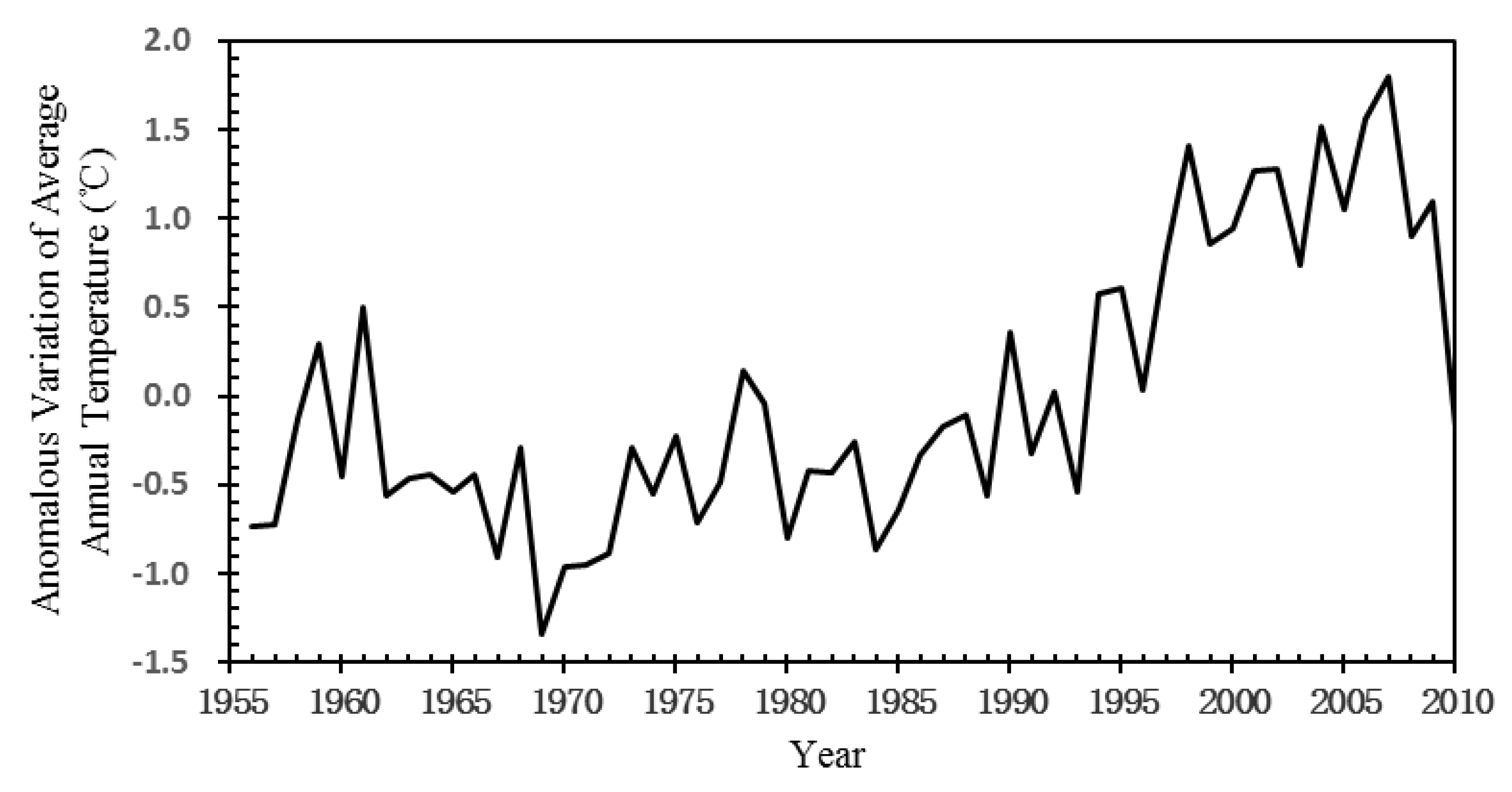
2.1. Study Area and Data Source
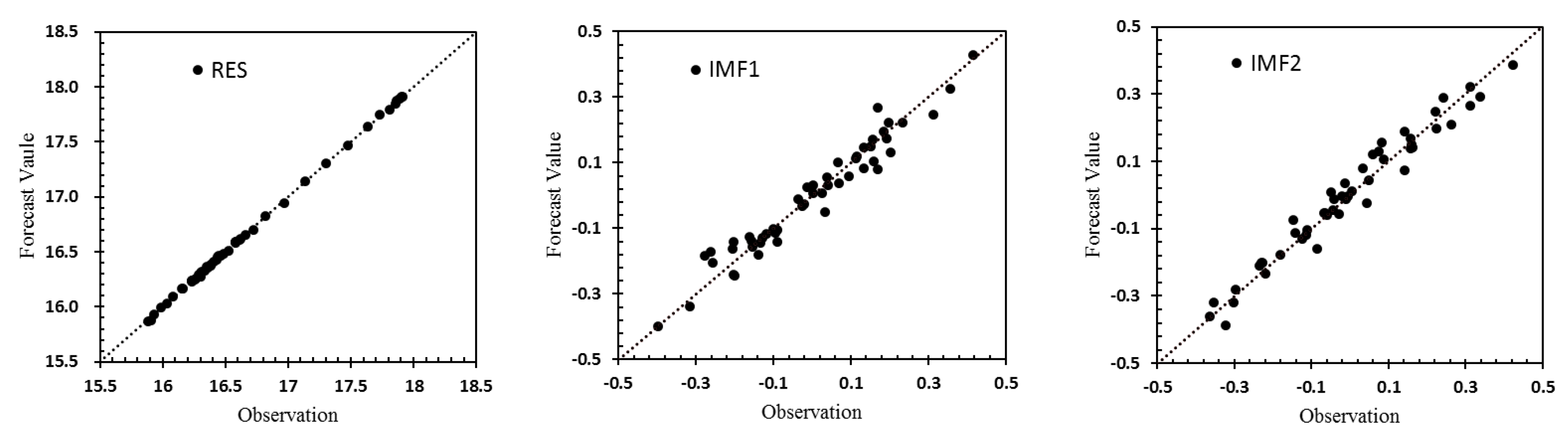
2.2. VMD-ARIMA Model
2.3. Metrics for Comparison
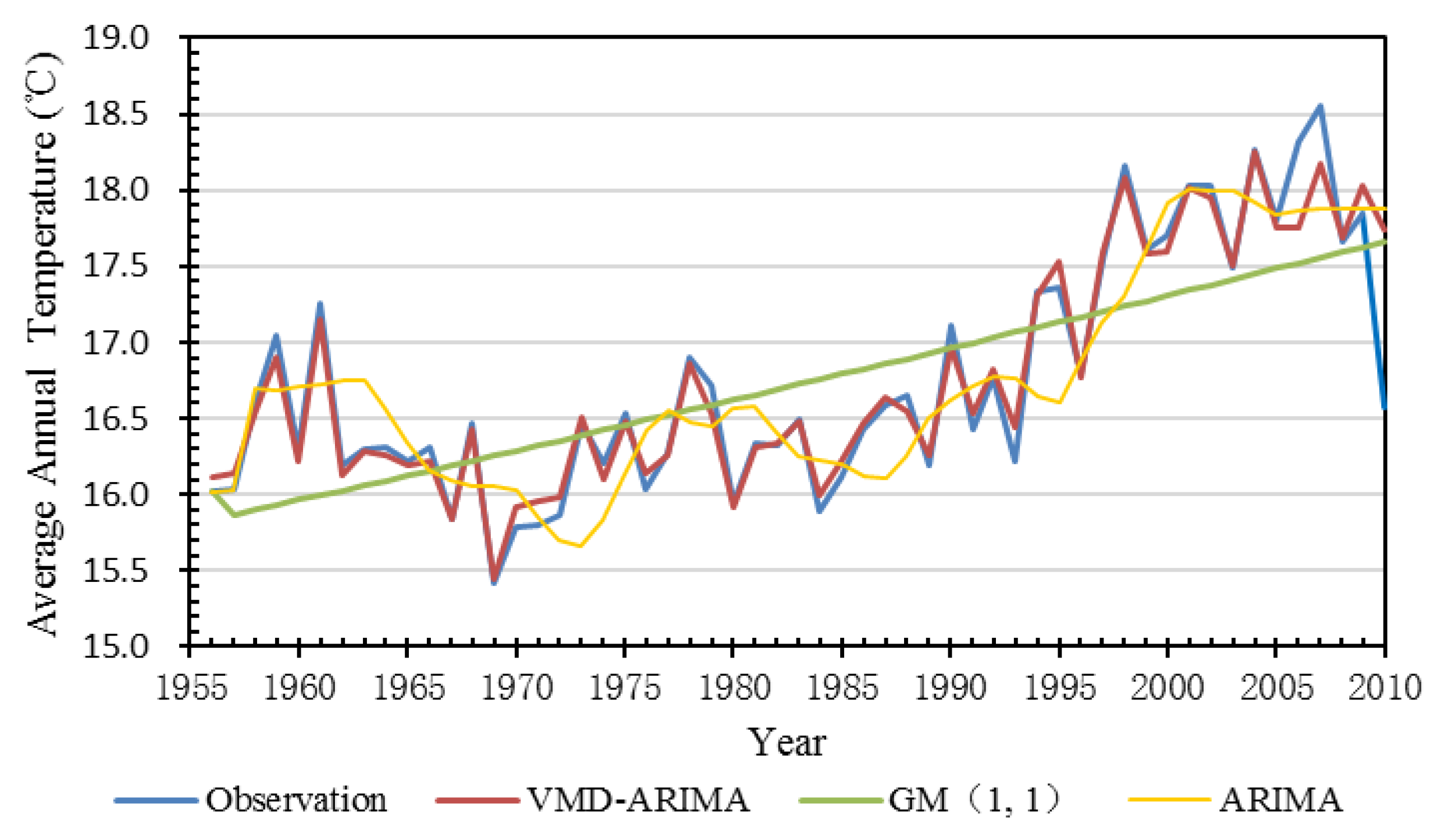
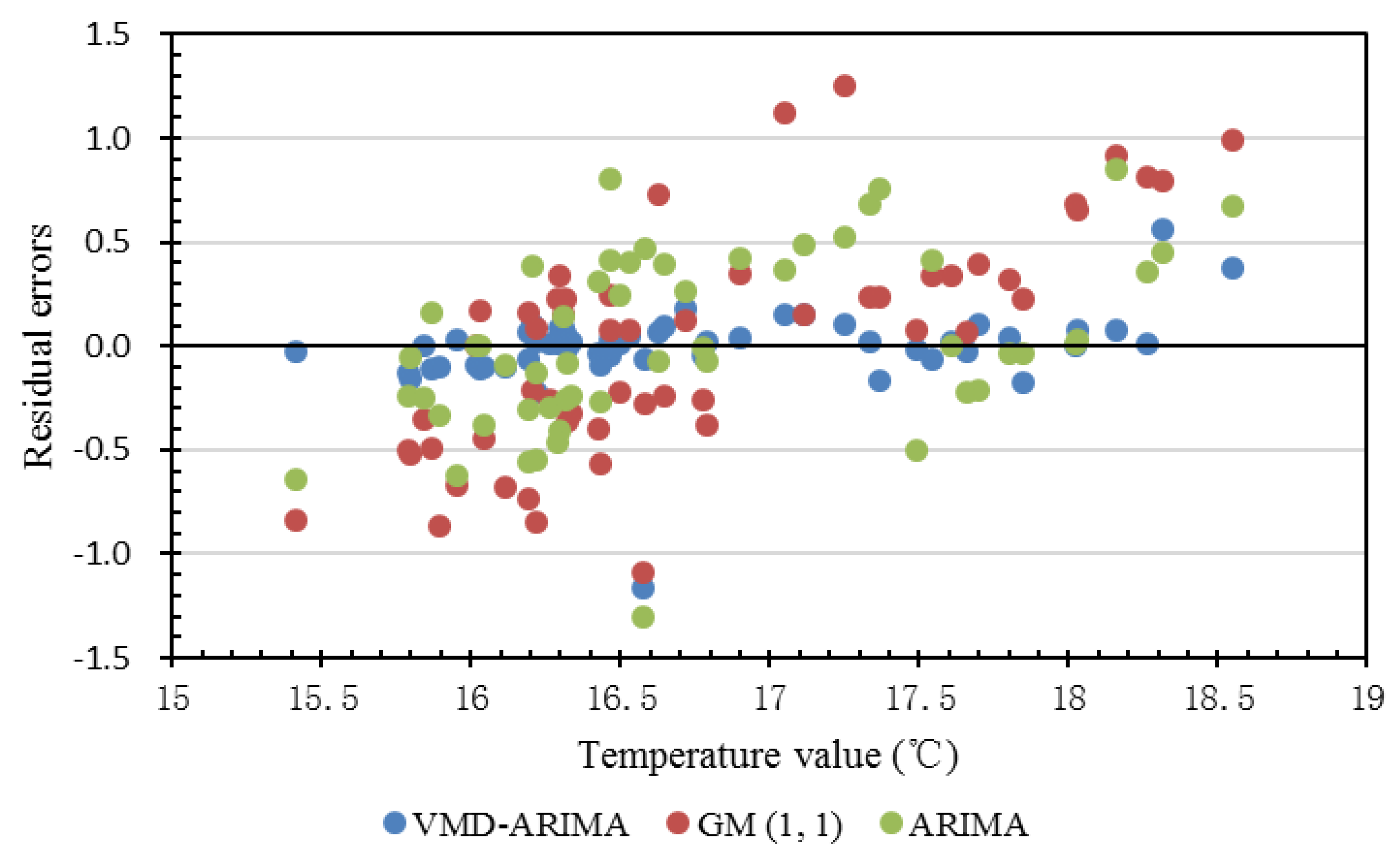
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Clapp, J.; Newell, P.; Brent, Z.W. The global political economy of climate change, agriculture and food systems. J. Peasant. Stud. 2018, 45, 80–88. [Google Scholar] [CrossRef]
- Queiros, A.M.; Huebert, K.B.; Keyl, F.; Fernandes, J.A.; Stolte, W.; Maar, M.; Kay, S.; Jones, M.C.; Hamon, K.G.; Hendriksen, G.; et al. Solutions for ecosystem-level protection of ocean systems under climate change. Glob. Chang. Biol. 2016, 22, 927–3936. [Google Scholar] [CrossRef] [PubMed]
- Watts, N.; Adger, W.N.; Agnolucci, P.; Blackstock, J.; Byass, P.; Cai, W.; Chaytor, S.; Colbourn, T.; Collins, M.; Cooper, A.; et al. Health and climate change: Policy responses to protect public health. Lancet 2015, 386, 1861–1941. [Google Scholar] [CrossRef]
- Kump, L.R. What drives climate? Nature 2000, 408, 651–652. [Google Scholar] [CrossRef] [PubMed]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influences on climate. Rev. Geophys. 2010, 48, 1032–1047. [Google Scholar] [CrossRef]
- Wolf, E.T.; Toon, O.B. The evolution of habitable climates under the brightening Sun. J. Geophys. Res.-Atmos. 2015, 120, 5775–5794. [Google Scholar] [CrossRef]
- Gattuso, J.P.; Magnan, A.; Bille, R.; Cheung, W.W.L.; Howes, E.L.; Joos, F.; Allemand, D.; Bopp, L.; Cooley, S.R.; Eakin, C.M.; et al. Contrasting futures for ocean and society from different anthropogenic CO2 emissions scenarios. Science 2015, 349, aac4722. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; Mcguire, A.D.; Schadel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- He, J.; Winton, M.; Vecchi, G.; Jia, L.; Rugenstein, M. Transient climate sensitivity depends on base climate ocean circulation. J. Clim. 2017, 30, 1493–1504. [Google Scholar] [CrossRef]
- Cai, W.J.; Santoso, A.; Wang, G.J.; Yeh, S.W.; An, S.I.; Cobb, K.M.; Collins, M.; Guilyardi, E.; Jin, F.F.; Kug, J.S.; et al. ENSO and greenhouse warming. Nat. Clim. Chang. 2015, 5, 849–859. [Google Scholar] [CrossRef]
- Kirk-Davidoff, D.B.; Schrag, D.P.; Anderson, J.G. On the feedback of stratospheric clouds on polar climate. Geophys. Res. Lett. 2002, 29, 1556. [Google Scholar] [CrossRef]
- Roundy, J.K.; Ferguson, C.R.; Wood, E.F. Impact of land-atmospheric coupling in CFSV2 on drought prediction. Clim. Dyn. 2014, 43, 421–434. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, M.J.; Sun, M.P.; Wang, B.; Huang, X.Y.; Wang, Q.; Feng, F. Comparison of surface air temperature derived from NCEP/DOE R2, ERA-Interim, and observations in the arid northwestern China: A consideration of altitude errors. Theor. Appl. Climatol. 2015, 119, 99–111. [Google Scholar] [CrossRef]
- Kay, J.E.; Deser, C.; Phillips, A.; Deser, C.; Phillips, A.; Mai, A.; Hannay, C.; Strand, G.; Arblaster, J.M.; Bates, S.C.; et al. The community earth system model (CESM) large ensemble project a community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteorol. Soc. 2015, 96, 1333–1349. [Google Scholar] [CrossRef]
- Morrison, A.L.; Kay, J.E.; Frey, W.R.; Chepfer, H.; Guzman, R. Cloud response to arctic sea ice loss and implications for future feedback in the CESM1 climate model. J. Geophys. Res.-Atmos. 2019, 124, 1003–1020. [Google Scholar] [CrossRef]
- Paulo, A.A.; Ferreira, E.; Coelho, C.; Pereiraa, L.S. Drought class transition analysis through markov and loglinear models, an approach to early warning. Agric. Water Manag. 2005, 77, 59–81. [Google Scholar] [CrossRef]
- Ustaoglu, B.; Cigizoglu, H.K.; Karaca, M. Forecast of daily mean, maximum and minimum temperature time series by three artificial neural network methods. Meteorol. Appl. 2008, 15, 431–445. [Google Scholar] [CrossRef]
- Ortiz-Garcia, E.G.; Salcedo-Sanz, S.; Casanova-Mateo, C.; Paniagua-Tineoa, A.; Portilla-Figuerasa, J.A. Accurate local very short-term temperature prediction based on synoptic situation Support Vector Regression banks. Atmos. Res. 2012, 107, 1–8. [Google Scholar] [CrossRef]
- Ye, L.M.; Yang, G.X.; Van-Rans, E. Time-series modeling and prediction of global monthly absolute temperature for environmental decision making. Adv. Atmos. Sci. 2013, 30, 382–396. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.F.; Zhang, D.D.; Fok, L. Temperature, aridity thresholds, and population growth dynamics in China over the last millennium. Clim. Res. 2009, 39, 131–147. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.R.; Frame, D.J.; Huntingford, C. Warming caused by cumulative carbon emissions towards the trillionth tonne. Nature 2009, 458, 1163–1166. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.P.; Huang, J.J.; Yang, X.N.; Fang, C.L.; Liang, Y.J. Quantifying the seasonal contribution of coupling urban land use types on Urban Heat Island using Land Contribution Index: A case study in Wuhan, China. Sustain. Cities Soc. 2019, 44, 666–675. [Google Scholar] [CrossRef]
- Lei, Y.G.; Lin, J.; He, Z.J.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- McDonald, A.J.; Baumgaertner, A.J.G.; Fraser, G.J. Empirical mode decomposition of the atmospheric wave field. Ann. Geophys. 2007, 25, 375–384. [Google Scholar] [CrossRef]
- Wang, N.; Qin, Q.M.; Chen, L.; Bai, Y.B.; Zhao, S.S.; Zhang, C.Y. Dynamic monitoring of coalbed methane reservoirs using Super-Low Frequency electromagnetic prospecting. Int. J. Coal Geol. 2014, 127, 24–41. [Google Scholar] [CrossRef]
- Mert, A. ECG feature extraction based on the bandwidth properties of variational mode decomposition. Physiol. Meas. 2016, 37, 530–543. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Wang, X.; Dai, D.; Tian, M.; Zhu, G.; Zhang, J. Denoising of UHF PD signals based on optimised VMD and wavelet transform. IET Sci. Meas. Technol. 2017, 11, 753–760. [Google Scholar] [CrossRef]
- Dou, C.; Zheng, Y.; Yue, D.; Zhang, Z.; Ma, K. Hybrid model for renewable energy and loads prediction based on data mining and variational mode decomposition. IET Gener. Transm. Distrib. 2018, 12, 2642–2649. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Series Analysis Forecasting and Control, 1st ed.; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–447. [Google Scholar] [CrossRef]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, S.; Fang, Z. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM (1, 1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Boroojeni, K.G.; Amini, M.H.; Bahrami, S.; Iyengar, S.S.; Sarwat, A.I.; Karabasoglu, O. A novel multi-time-scale modeling for electric power demand forecasting: From short-term to medium-term horizon. Electr. Power Syst. Res. 2016, 142, 58–73. [Google Scholar] [CrossRef]
- Romilly, P. Time series modelling of global mean temperature for managerial decision-making. J. Environ. Manag. 2005, 76, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R.; Lo, K.; Lea, D.W.; Medina-Elizade, M. Global temperature change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.; Sato, M. Regional climate change and national responsibilities. Environ. Res. Lett. 2016, 11, 034009. [Google Scholar] [CrossRef] [Green Version]

| Component | Model Structure | Adjusted R2 | |||
|---|---|---|---|---|---|
| RES | ARIMA (4, 1, 6) | −0.070, −0.435, 0.678, | 2.267, 3.870, 4.378 | −5.771 | 0.975 |
| −0.013 | 3.667, 2.002, 0.861 | ||||
| IMF1 | ARIMA (4, 0, 6) | 0.467, −1.079, 0.378, | 0.076, −0.886, 0.341 | −3.016 | 0.932 |
| −0.521 | 0.737, −0.731, −0.460 | ||||
| IMF2 | ARIMA (3, 0, 2) | −0.975, 0.209, 0.551 | −1.051, 0.088 | −3.496 | 0.959 |
| Model | Training | Forecasting | ||||
|---|---|---|---|---|---|---|
| MRE | MAE | RMSE | MRE | MAE | RMSE | |
| GM (1, 1) | 0.025 | 0.418 | 0.256 | 0.036 | 0.634 | 0.572 |
| ARIMA | 0.020 | 0.332 | 0.157 | 0.031 | 0.538 | 0.484 |
| VMD-ARIMA | 0.004 | 0.070 | 0.008 | 0.027 | 0.461 | 0.369 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, J.; Zhou, H.; Zhao, L.; Yuan, Y. An Integrated Variational Mode Decomposition and ARIMA Model to Forecast Air Temperature. Sustainability 2019, 11, 4018. https://doi.org/10.3390/su11154018
Wang H, Huang J, Zhou H, Zhao L, Yuan Y. An Integrated Variational Mode Decomposition and ARIMA Model to Forecast Air Temperature. Sustainability. 2019; 11(15):4018. https://doi.org/10.3390/su11154018
Chicago/Turabian StyleWang, Huan, Jiejun Huang, Han Zhou, Lixue Zhao, and Yanbin Yuan. 2019. "An Integrated Variational Mode Decomposition and ARIMA Model to Forecast Air Temperature" Sustainability 11, no. 15: 4018. https://doi.org/10.3390/su11154018





