1. Introduction
The influence areas are a critical part of transit-oriented development (TOD), as this is the area around the station where the TOD principles are applied, including high densities, mixed land-uses, mixed income housing and improved infrastructure for non-motorized transport. Andersen and Landex [
1] define the influence area of public transit as a “vicinity of a stop or station of a public transport line” and the “area is where most of the non-transferring passengers at the particular stop or station come from”. The influence area of a transit station, therefore is an area around a transit which serves as the customer base for transit services. It is also the area that receives the maximum benefits of transit. Often these influence areas are based on the distances people are willing to travel to transit in a specified time. These specifications are further based on the various travel modes that are used for last-mile connectivity, often by walking. In the literature, this area has been specified based on access distance, which directly provides the geographic extent of the TOD. A distance of 2000 ft (600 m) was introduced by Calthorpe [
2,
3]. Untermann [
4] and Dittamar and Ohland [
5] determined the distance as 1/2 mi (800 m). These aforementioned distances have been specified based on the walking distance that people prefer to transit [
6,
7,
8]. To determine the extent of the TOD influence areas, some literature refers to a single distance, whereas it is reported that others use a distance range as a basis. Guerra et al. [
8] and Flamm and Rivasplata [
9] emphasized that in the U.S, the radius of influence area can vary between 1/4 and 1/2 mi (400–800 m). Consequently, various cities have adopted different radii for TOD. Guerra et al. [
8] raised doubts about the feasibility of adopting 1/2 mi (800 m) as the de facto standard for TOD in the United States as it is “more an artifact of historical precedent than a statistical or analytical construct”.
In the National TOD Policy of India, the influence area of TOD has been set between 500 m to 800 m [
10]. The capital city of New Delhi is among the pioneers in the country to adopt TOD into its city planning. The Unified Traffic and Transportation Infrastructure (Planning & Engineering) Centre (UTTIPEC) suggested that the influence zones in New Delhi be classified into an intense zone with a radius of 300 m, a standard TOD zone with a radius of 800 m (which corresponds to a 10-min walk), and a TOD transition zone with a radius of 2000 m (which corresponds to a 10-min cycle ride) [
11]. In the Delhi Master Plan 2021, which lays out the specifications for city planning for the coming years, the city authorities have adopted a TOD influence zone of 500 m on both sides of the mass rapid transit system (MRTS) corridor and the Delhi Metro Rail (DMR).
The currently adopted standards are heavily influenced by the TOD standards adopted in developed countries. Quite often, the distances that are used range between approximately 400 m to 800 m considering walking as the last mile mode [
3,
4,
5,
6,
7,
8,
9]. It has been noted that the influence areas for transit vary depending on the type of access mode, the type of main mode, the trip purpose, and the area type [
12]. Walking is undoubtedly the most popular access mode worldwide and has been widely studied by several researchers. In addition, in many cities in developed countries, bicycles are popular as access modes, with many transit agencies allowing bicycles to be taken aboard. The access distances for cyclists have been noted to have a large range (from 1.96 to 4.8 km), varying among studies and cities [
9,
13,
14]. Lee et al. [
14] explored the possibility of introducing a bicycle-based TOD in Seoul, Korea, which could enable the coverage of 74–94% of the area, as compared to the coverage of 30% by walk-only catchment areas. The catchment ranges of feeder buses and cars (kiss and ride) were estimated in the range of 1.24–3.73 miles (approx. 2000–6000 m) and 0.62–4.35 miles (approx. 1000–7000 m) respectively [
15], increasing the influence area of transit services to a larger extent. Therefore, a walk-based TOD is not always necessary; however, it should include other modes of last mile connectivity. The influence of modes other than walking on the catchment areas of transit stations thus, must be thoroughly investigated.
Johar et al. [
16] studied the distances walked by commuters from bus stops to various destinations in New Delhi and found that the mean walking distances (based on lognormal distribution) were 677, 660, 654, and 637 m for shopping, recreation, education, and work trips, respectively. The research shows that commuters walk longer distances to access rail transit than reaching the bus transit [
17,
18,
19]. Therefore, it can be assumed that commuters walk longer distances to reach metro stations in Delhi. Additionally, in Indian cities, modes such as cycle rickshaws, auto rickshaws, mini vans (commonly known as gramin seva in New Delhi) and other forms of informal transport are commonly used for last mile connectivity. Considering the multimodal nature of last mile connectivity in New Delhi, Ann et al. [
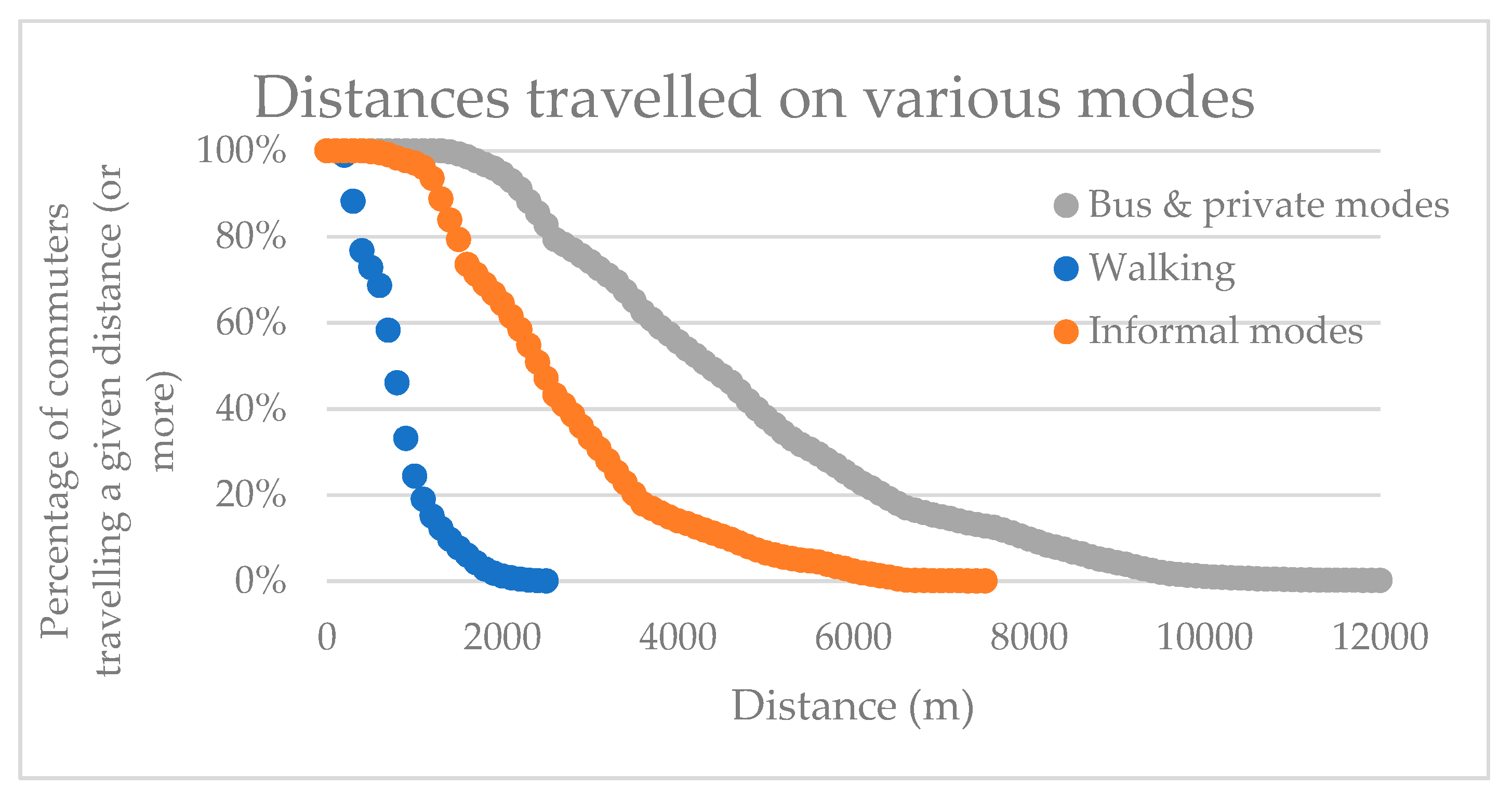
20] estimated the influence zones for DMR stations in New Delhi. In the study, the mean values of the distance for access were estimated to be 700 m for walking, 2900 m for informal transit, 6300 m for buses and private transport. Moreover, using the distance decay function, the 85th percentile distances for access were estimated to be 1400 m for walking, 5600 m for informal transit, 11900 m for private transport and buses. Zhao et al. [
21], El-Geneidy et al. [
22] and Hochmair [
23] have also used the 85th percentile value to establish the catchment areas around transit stations for modes such as walking and cycling. In addition, Ann et al. [
20] found that the threshold distance for access was 1200 m for walking, which is close to the 80-85th percentile values from the decay analysis. These results are considerably different from those in India’s national TOD policy, which specifies the extent of the influence area for walking to be 500–800 m. According to this, the TOD development and associated higher densities and infrastructure will be concentrated within this 500–800 m, limiting the planned development to a limited area without much justification. Moreover, according to the estimated decay curves, the influence area with 500–800 m can only cover 50%–65% of the current transit passengers who walk to stations [
20], excluding the rest from the spatial extent of TOD. Hence, in order to capture the benefits of TOD and extend it to real users of the transit system, the guidelines set for the size of the influence areas and for the extent of influence areas based on ground reality need to be reconsidered. This aspect highlights the need to examine TOD principles and standards based on the mobility characteristics of Indian cities. It has already been shown that commuters to the DMR system in New Delhi, travel much longer distances than 500–800 m. The difference in the last mile connectivity patterns in Indian cities, and cities of the developed world can impact the spatial extent of the TOD influence areas. The multimodal accessibility, if not accounted for in TOD planning, may lead to the exclusion of a certain amount of existing transit users. A brownfield development in such conditions may not be cost effective in developing countries and could also possibly displace several low-income households that may not be able to afford to live in the new developments.
The larger size of the influence areas estimated by Ann et al. [
20] as compared to the size specified in the national TOD policy can help planners and policy makers identify and plan for the real catchment areas of DMR in New Delhi. They need not restrict the development plans for only 500–800 m around stations. Additionally, it can help transit agencies to identify catchment areas and to estimate demand. However, Ann et al. [
20] estimated the influence area with all DMR stations together. They have not considered the station specific characteristics. The locational differences between stations may cause different accessibility patters and traveling preference. Therefore, whether the extent of the influence area differs for individual stations is an aspect worth investigating.
This study focuses on estimating the influence areas for various last mile modes for the individual metro stations in New Delhi. Four stations were chosen from the DMR network: Karkardooma, which is a city station and interchange and urban regional center station; Dwarka Mor, which is a subcity residential area station; Lajpat Nagar, which is an interchange and market station in a central city environment; and Vaishali, which is an outer city station. A questionnaire survey was conducted at these stations to collect information regarding last mile mobility patterns of metro commuters. The methodology for estimation of the sizes of the influence areas was drawn from Ann et al. [
20]. The reported distance data from the surveys revealed considerable heaping and rounding. Thus, the multiple imputation (MI) derived from the work of Heitjan and Rubin [
24], Drechsler and Kiesl [
25] and Yamamoto et al. [
26] was applied to remove the rounding bias before employing the distance decay and receiver operating characteristic (ROC) curves.
The remaining paper is organized as follows:
Section 2 describes the data collection process, and the estimation of the influence areas for the different modes, along with the distance decay analysis and ROC analysis, is described in
Section 3.
Section 4 summarizes the study and presents the derived conclusions.
4. Conclusions
In this study, the focus was on the last mile distances travelled to individual stations of the DMR network in New Delhi. The objective was to compare the last mile distances travelled on different modes among stations, and to establish the TOD influence zones for the metro stations. The results are aimed at influencing the TOD policy in India and helping create TOD policies that are suited to the urban and transport characteristics in India.
In the primary survey carried out for the study, the issues of rounding and heaping were observed, highlighting the issues in the data collection for transportation studies in India, where there is already a dearth of sufficient data. The potential bias in the results of the estimation was removed by creating an imputed dataset, which was subsequently used to perform a distance decay analysis and a ROC analysis for determining the extent of the TOD influence areas.
The bell-shaped curve of the compound power exponential form of distance decay was found to be reliable to investigate the decreasing interaction between the distance from the stations and the percentage coverage of passengers. The estimation result of the decay function provided that the extent of the TOD influence area varies with access modes as well as with the location of the station. The mean and the percentile values of the travel distances increase in the order of walking, the informal modes, and the bus and private modes.
For walking, the difference among stations was not significant implying the willingness to walk does not vary much with the location of stations. Vaishali, the outer city station exhibited slightly higher distances than the other three stations. However, the mean walking distance for Karkardooma, Dwarka mor and Lajpat Nagar indicate an increase of 14%, as estimated for access trips by Ann et al. [
20] for the DMR network. The outer station, Vaishali showed a 29% increase. The threshold distances estimated using the ROC analysis were in agreement with the 80th–85th percentile distances for walking. The threshold walking distance for the four stations lies in the range of 1200–1300 m which is close to the result of the general case across all stations in New Delhi [
20]. These distances also indicate that the size of the influence area (500–800 m) specified in the National TOD policy and the Master Plan for Delhi 2021 is extremely conservative.
In the case of informal modes, there was considerable variation among stations. Vaishali, which is an outer station, corresponded to nearly two times the distance for the other three stations. For Vaishali, the distance was as much as 59% higher than estimated for New Delhi for the mean distance whereas the 85th percentile distance was 30% higher. It means that people who live outside of the city usually travel longer distances on informal modes to reach stations compared those who live inside of the city.
This large variation was also noted when comparing the last mile distances for the bus and private modes. Dwarka Mor (subcity station) and Vaishali (outer city station) corresponded to larger distances compared to those of the other two stations situated in the core urban areas of New Delhi. The mean distances and the 85th percentile distances for Dwarka Mor and Vaishali are nearly twice as much as those for Karkardooma and Lajpat Nagar. Vaishali and Dwarka mor also reported a 26 % increase in the mean distance than the DMR network. The 80th and 85th percentile estimates for Vaishali and Dwarka mor were smaller compared to the estimate for the DMR (access) [
20].
It can thus be concluded that variations are present in the last mile distances among stations. Although the walking distances did not vary considerably among stations, large variations were observed when other modes were compared. The outer city station, Vaishali, exhibited longer distances for informal modes, buses, and private modes, which illustrates that access to such metro stations means commuters tend to travel longer distances on motorized modes. Therefore, when considering multimodal accessibility and multimode-based TOD, these differences in accessibility must be taken into account.
The study provides insights into the last mile patterns for the four DMR stations, and the extent of the influence area for each mode was calculated. The results are not the same across the selected stations, however, they are not considerably different either. Further research needs to be conducted across more station types to arrive at a conclusive remark regarding the size of the influence areas for specific station types.
The estimates of the influence areas for each station can be used to delineate the influence areas for these stations in New Delhi, enabling planners and policy makers to cater to a larger population and maximize the benefits of TOD. The influence areas based on walking should be at least 1200 m based on this study and Ann et al. [
20]. These estimates can be used for a brownfield development (existing stations) and are based on the last mile patterns of existing commuters. Given that informal modes play a very important role in last mile connectivity, the inclusion of informal modes increases the size of the influence areas considerably as shown in this study. The findings from this study can be applied in other cities in India as well as in other developing countries with the presence of informal modes as a preliminary guideline to assess the influence areas and to understand that these areas can extend further than 500–800 m. The methodology can be applied to last mile distances of transit systems and to individual stations. The MI need be applied only in cases where the respondents tend to round the distances.