Optimal Sizing of Irregularly Arranged Boreholes Using Duct-Storage Model
Abstract
:1. Introduction
2. Review of Modified DST Models
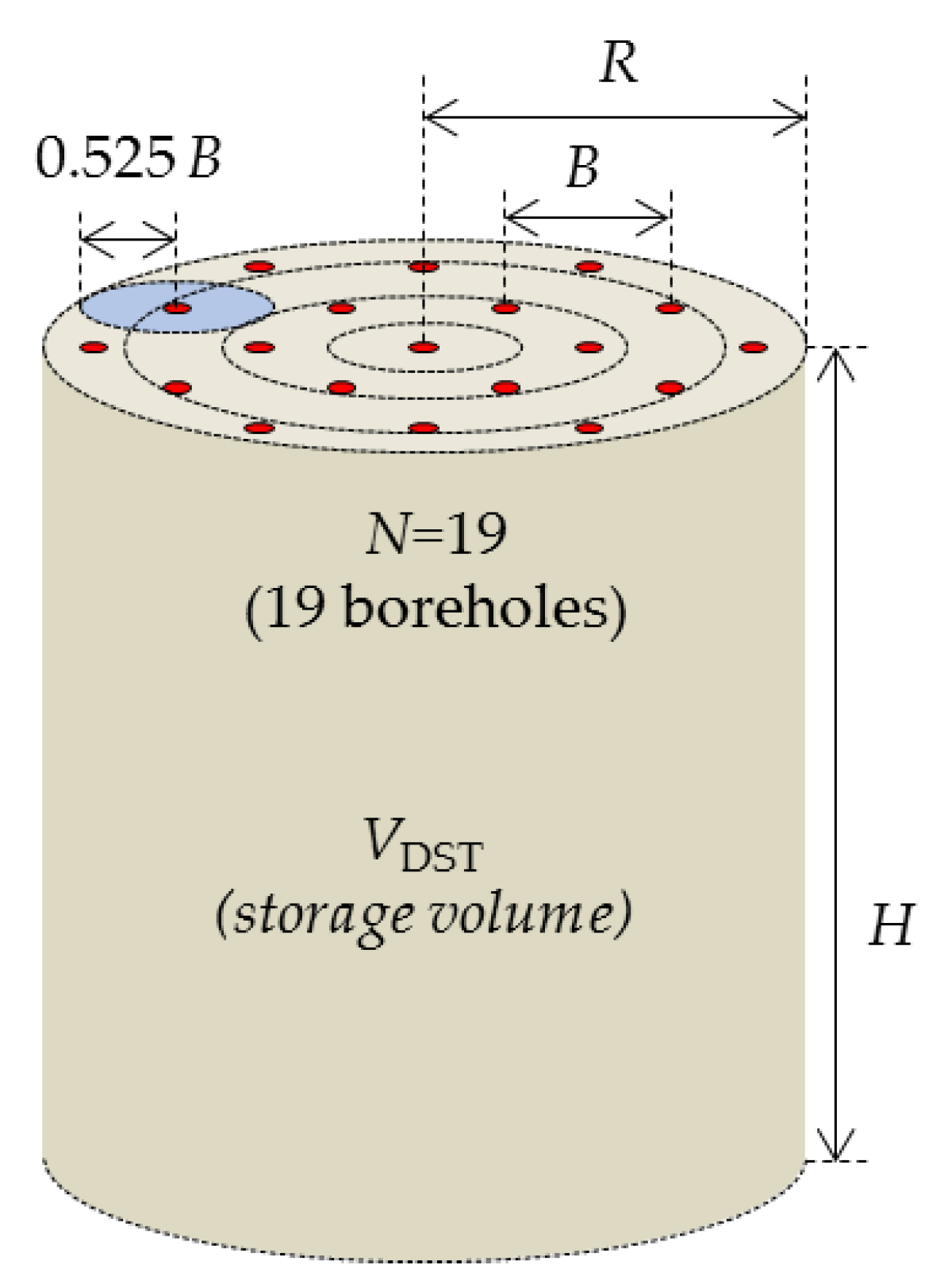
2.1. DST Model
2.2. Modified DST Models
2.2.1. Rule-Of-Thumb Modification
2.2.2. Regression-Based Modification
3. Sizing of BHEs with Optimization
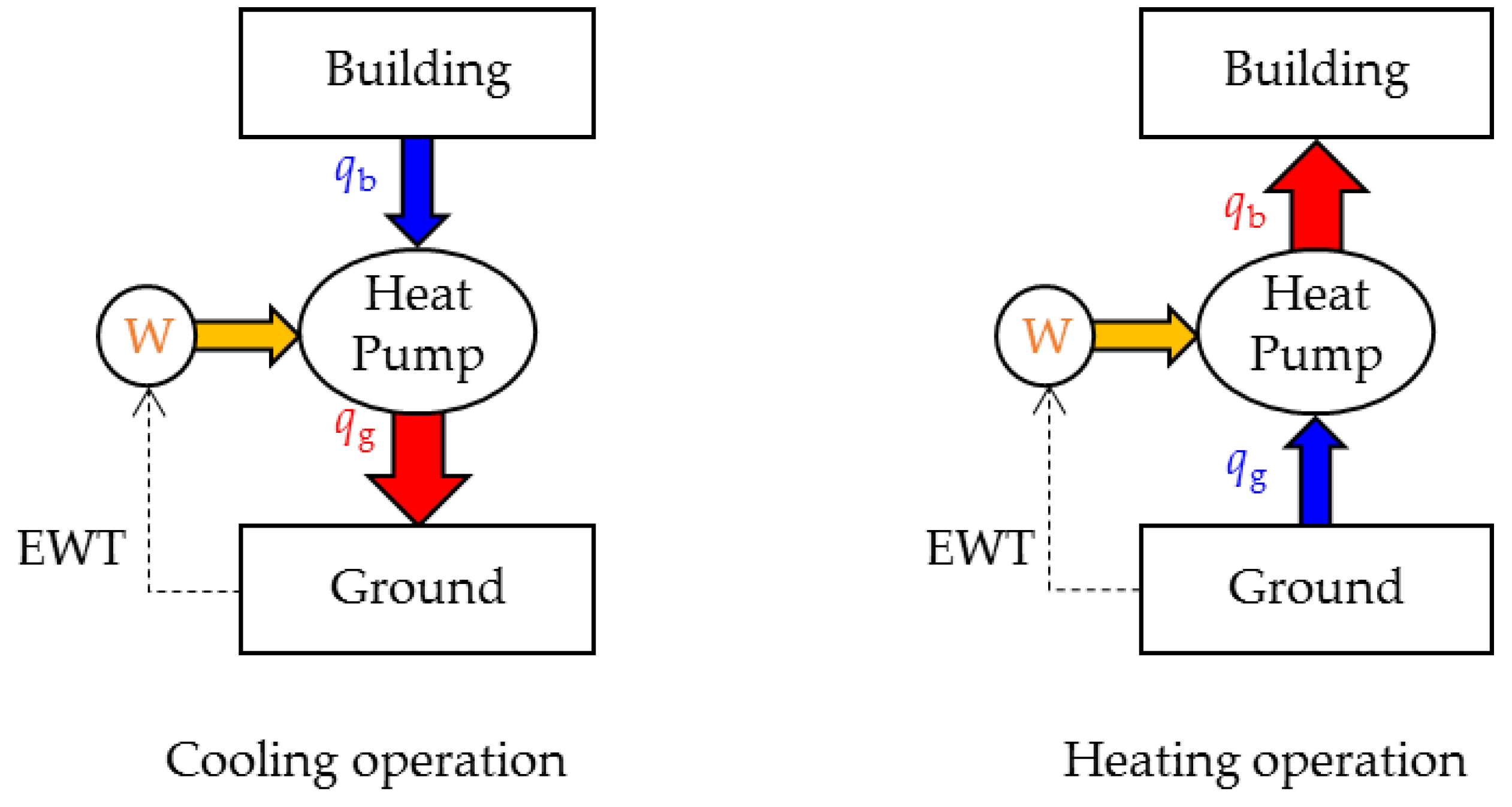
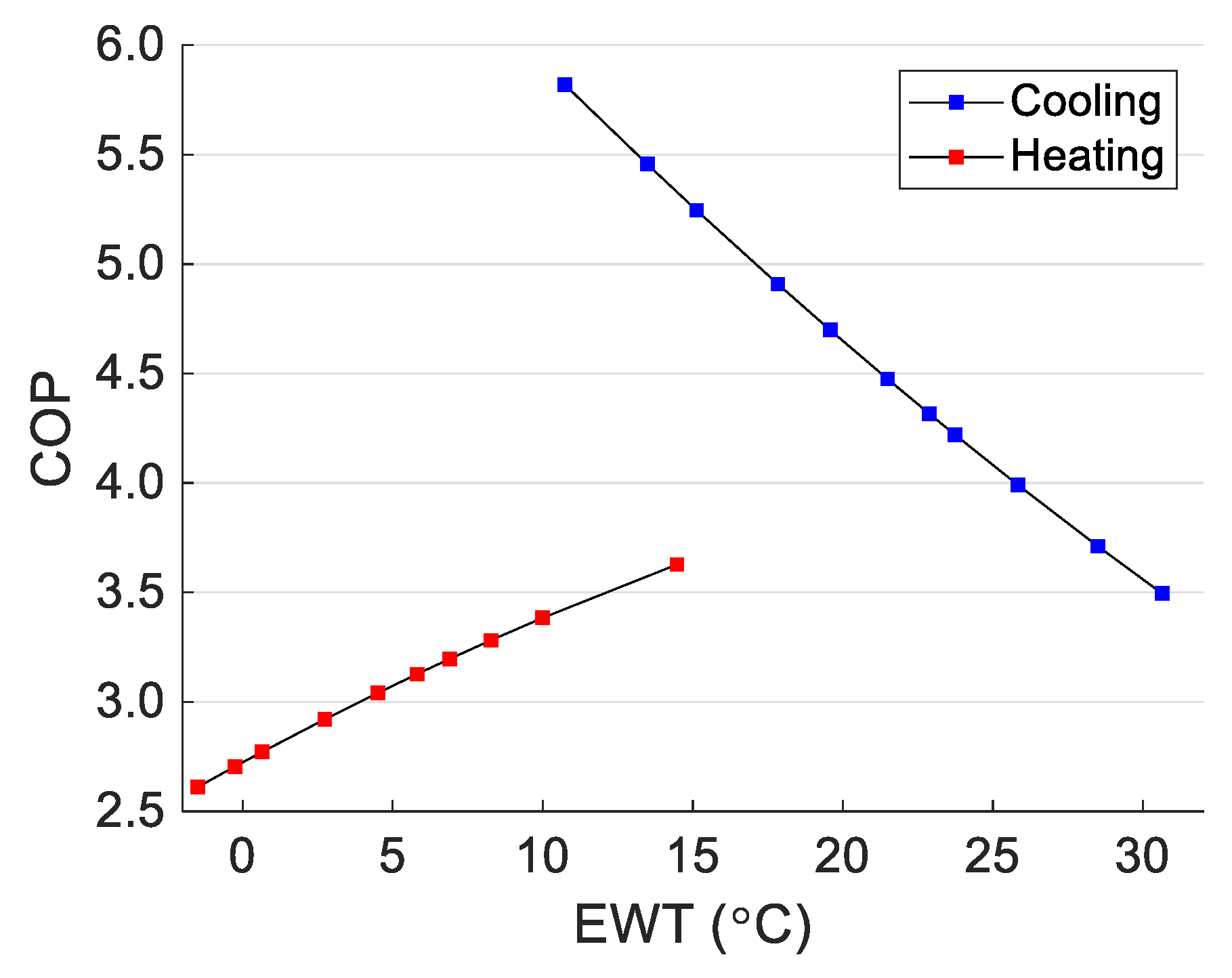
3.1. Design Parameters for BHE Sizing
3.2. Optimization Algorithm for Sizing
where: μ is 106 when (EWTBHE < EWTset, heating or EWTBHE > EWTset, cooling)
μ is 0 when (EWTset, heating ≤ EWT ≤ EWTset, cooling)
4. Test Cases
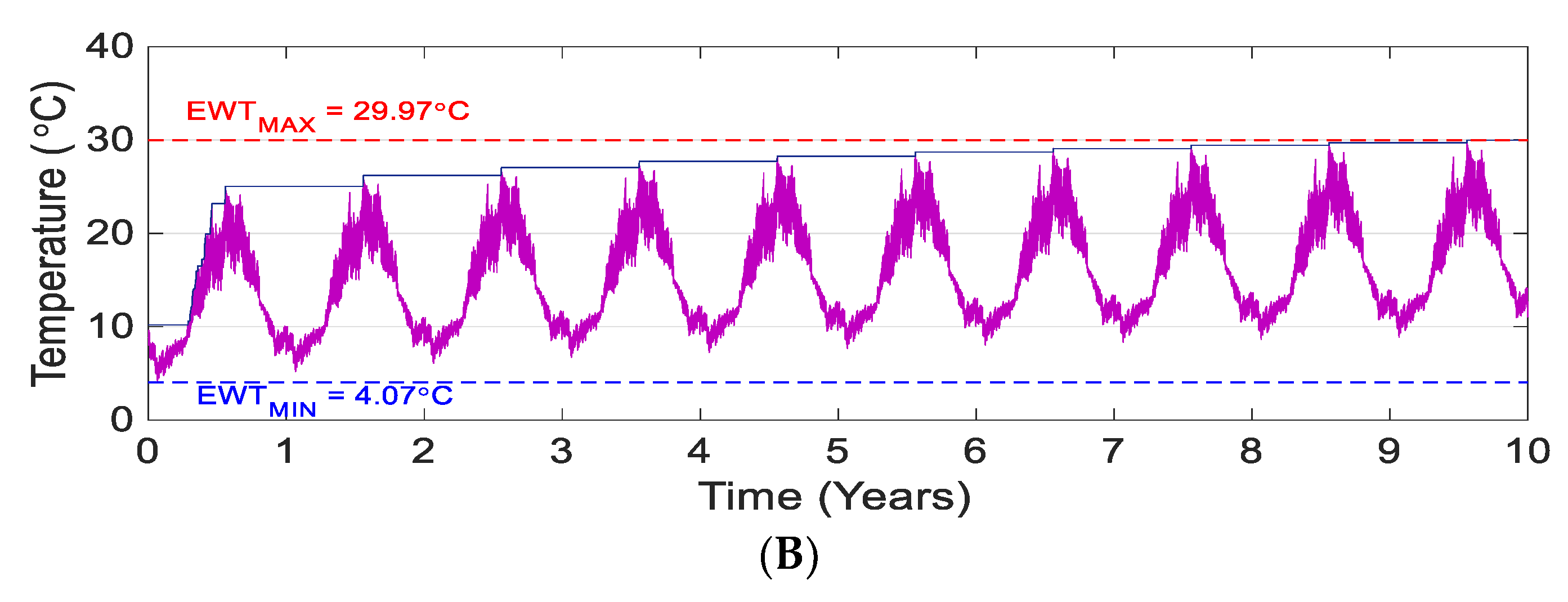
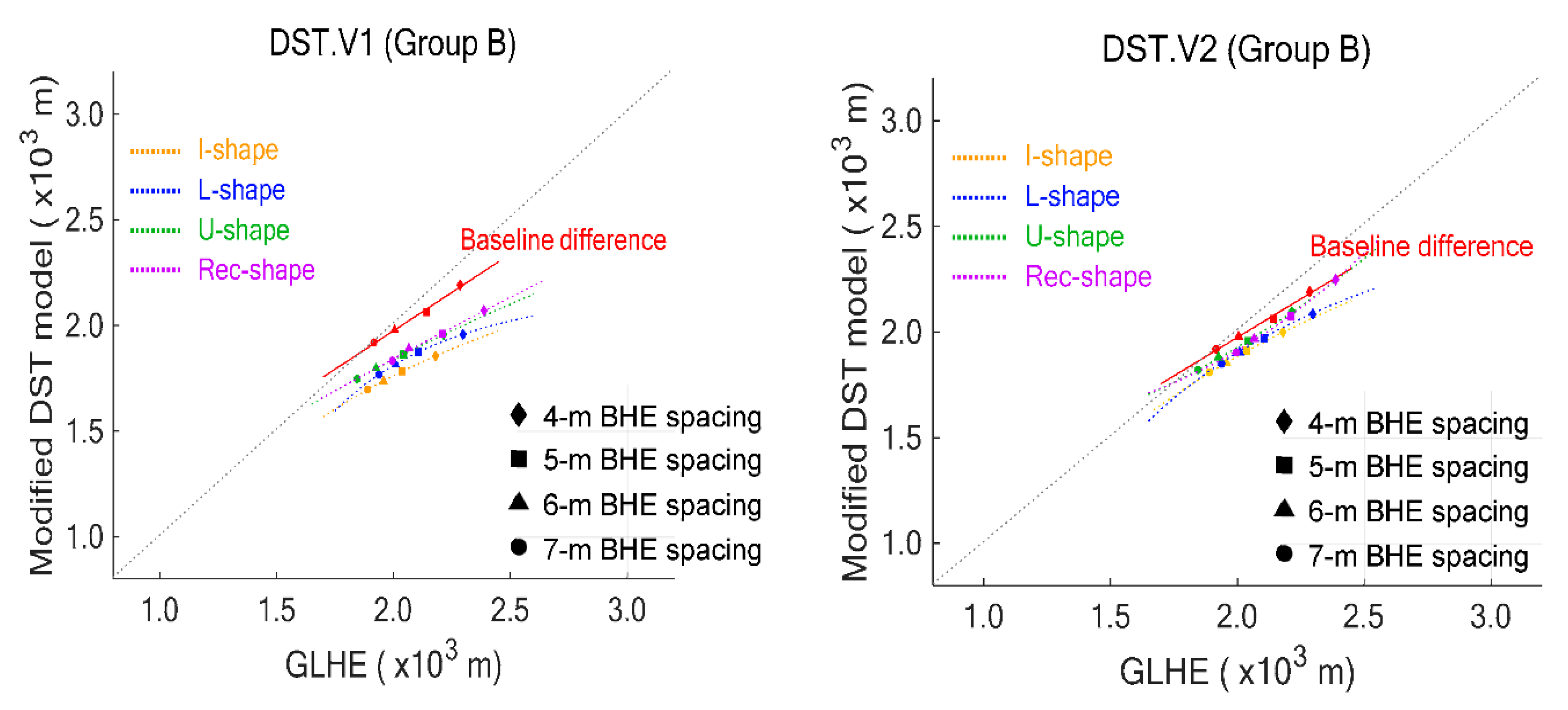
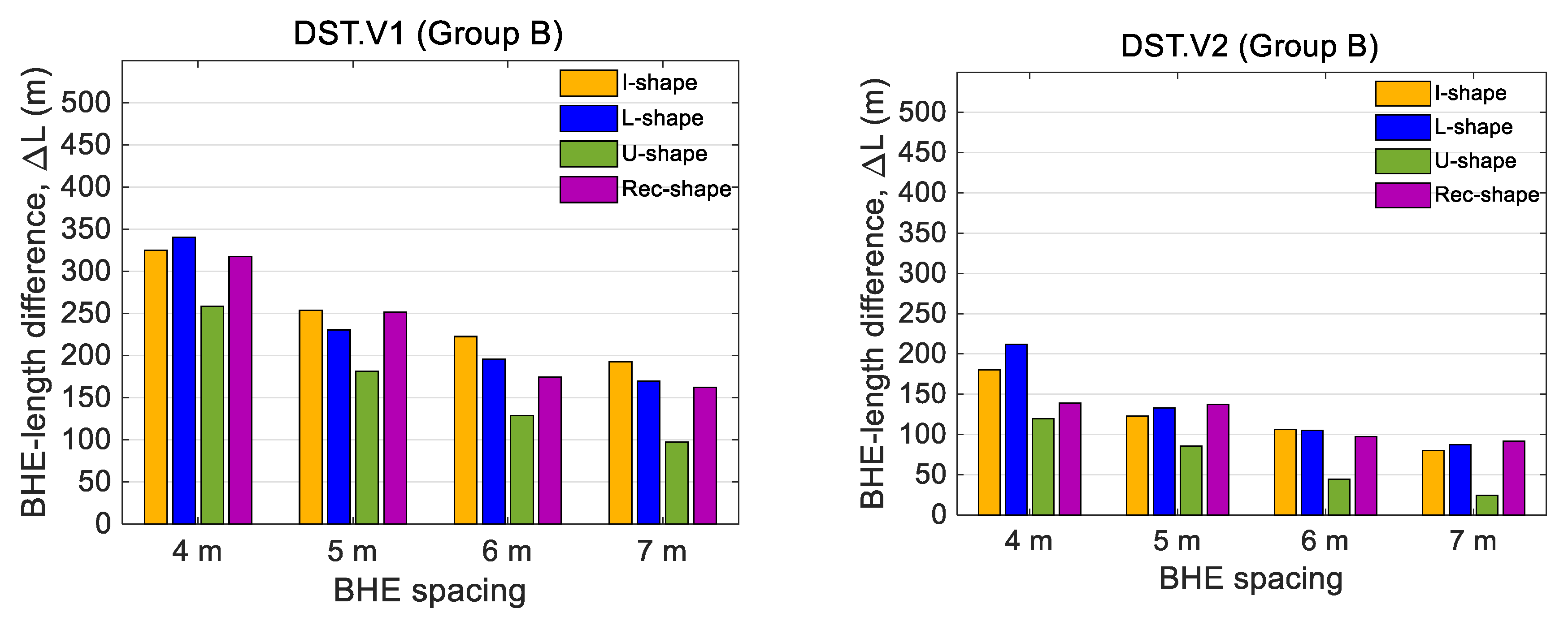
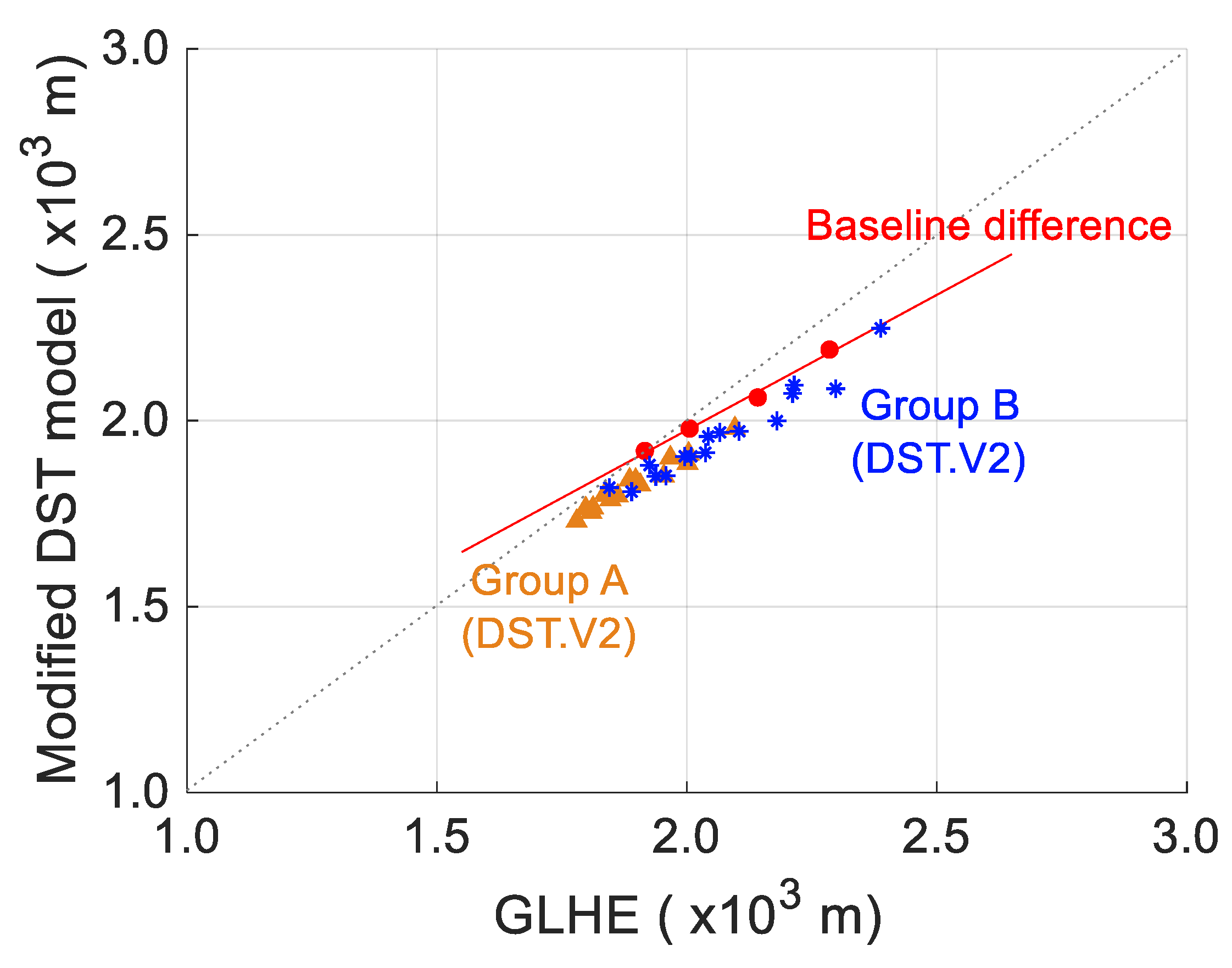
5. Sizing Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| B | Borehole spacing (°C) |
| b | Correlation coefficient (-) |
| B´ | Equivalent or modified borehole spacing (°C) |
| C | Volumetric heat capacity (kJ/m3·K) |
| COP | Coefficient of performance (-) |
| EWT | Entering water temperature (°C) |
| f | Objective function |
| H | Borehole depth (m) |
| N | Number of boreholes (-) |
| N | Number of data (-) |
| q | Heat transfer rate (W) |
| s | Number of I-shaped borefields (-) |
| S | Sum of borehole spacings (m) |
| t | Time (sec) |
| T | Temperature (°C) |
| V | Heat storage volume (m3) |
| W | Work (W) |
| X | Correlation factor (-) |
| Subscript | |
| b | Building |
| BHE | Borehole heat exchanger |
| c | Cooling |
| DST | DST model |
| DST.modif.V1 | DST model with rule-of-thumbs modification |
| DST.modif.V2 | DST model with regression based modification |
| g | Ground |
| GLHE | GLHE software |
| h | Heating |
| I | I-shape borefiled |
| L | L-shape borefiled |
| REC | Hollowed rectangular borefiled |
| set | Set point |
| sf | Steady-flux problem in the DST |
| ℓ | Local to global heat transfer in the DST |
| test | Test borefield configuration |
| U | U-shape borefiled |
| Greek | |
| α | Constant for COP |
| β | Linear coefficient for COP |
| γ | Quadratic coefficient for COP |
| μ | Penalty term |
Appendix A. Detailed BHE Sizing Results for the Modified DST Models (DST.V1, DST.V2) and the GLHE Software
| BHE Spacing | Group A (1-Line Arrangements) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I-Shape (N = 25) | L-Shape (N = 29) | U-Shape (N = 26) | Hollow-Rectangular (N = 30) | |||||||||||||||||
 25 × 1 |  14,1,14 |  8,1,8,1,8 |  6,1,7,1,6,1,7,1 | |||||||||||||||||
| B(m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) |
| 4 | 1954 (78.2) | 1990 (79.6) | –35.5 | 1851 (74.0) | 103.1 | 2001 (69.0) | 1849 (63.8) | 152.0 | 1885 (65.0) | 116.3 | 2004 (77.1) | 1911 (73.5) | 92.8 | 1911 (73.5) | 92.6 | 2096 (69.9) | 1979 (65.2) | 139.2 | 2096 (66.0) | 116.7 |
| 5 | 1862 (74.5) | 1897 (75.9) | –35.5 | 1798 (71.9) | 64.2 | 1907 (65.8) | 1781 (61.4) | 126.2 | 1827 (63.0) | 79.8 | 1897 (73) | 1835 (70.6) | 62.7 | 1840 (70.8) | 57.2 | 1967 (65.6) | 1901 (62.4) | 94.2 | 1967 (63.4) | 66.6 |
| 6 | 1812 (72.5) | 1836 (73.5) | –24.0 | 1766 (70.6) | 46.7 | 1847 (63.7) | 1732 (59.7) | 115.1 | 1788 (61.6) | 59.5 | 1840 (70.8) | 1778 (68.4) | 61.9 | 1799 (69.2) | 40.8 | 1886 (62.9) | 1841 (60.3) | 77.1 | 1886 (61.4) | 44.4 |
| 7 | 1780 (71.2) | 1790 (71.6) | –10.5 | 1730 (69.2) | 49.8 | 1808 (62.4) | 1699 (58.6) | 109.0 | 1755 (60.5) | 53.9 | 1798 (69.1) | 1737 (66.8) | 60.8 | 1764 (67.9) | 33.5 | 1838 (61.3) | 1806 (58.9) | 71.4 | 1838 (60.2) | 31.5 |
| Group B (2-Line Arrangements) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I-Shape (N = 24) | L-Shape (N = 28) | U-Shape (N = 30) | Hollow-Rectangular (N = 28) | |||||||||||||||||
 12 × 2 |  6 × 2, 2 × 2, 6 × 2 |  4 × 2, 2 × 2, 3 × 2, 2 × 2, 4 × 2 |  As shown above | |||||||||||||||||
| B (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) | GLHE L (H) (m) | DST.V1 L (H) (m) | Err (m) | DST.V2 L (H) (m) | Err (m) |
| 4 | 2180 (90.8) | 1855 (77.3) | 325.0 | 2000 (83.3) | 180.5 | 2298 (82.1) | 1957 (69.9) | 340.5 | 2086 (74.5) | 211.7 | 2215 (76.4) | 1956 (67.5) | 258.7 | 2095 (72.3) | 119.5 | 2388 (85.3) | 2070 (73.9) | 317.5 | 2249 (80.3) | 138.9 |
| 5 | 2037 (84.9) | 1783 (74.3) | 253.7 | 1914 (79.8) | 122.9 | 2105 (75.2) | 1874 (66.9) | 230.7 | 1972 (70.4) | 133.0 | 2043 (70.5) | 1862 (64.2) | 181.3 | 1958 (67.5) | 85.6 | 2211 (79.0) | 1960 (70.0) | 251.4 | 2074 (74.1) | 137.5 |
| 6 | 1958 (81.6) | 1735 (72.3) | 222.7 | 1852 (77.2) | 106.1 | 2009 (71.8) | 1813 (64.8) | 195.7 | 1904 (68.0) | 105.0 | 1925 (66.4) | 1797 (62.0) | 128.8 | 1881 (64.9) | 44.7 | 2066 (73.8) | 1892 (67.6) | 174.4 | 1969 (70.3) | 97.4 |
| 7 | 1890 (78.7) | 1697 (70.7) | 192.7 | 1810 (75.4) | 79.9 | 1938 (69.2) | 1768 (63.2) | 169.7 | 1851 (66.1) | 87.1 | 1845 (63.6) | 1747 (60.3) | 97.4 | 1820 (62.8) | 24.4 | 1996 (71.3) | 1833 (65.5) | 162.1 | 1904 (68.0) | 91.6 |
References
- Sanner, B.; Karytsas, C.; Mendrinos, D.; Rybach, L. Current status of ground source heat pumps and underground thermal energy storage in Europe. Geothermics 2003, 32, 579–588. [Google Scholar] [CrossRef]
- Angelino, L.; Dumas, P.; Gindre, C.; Latham, A. EGEC Market Report 2015; European Geothermal Energy Council: Brussels, Belgium, 2016. [Google Scholar]
- Gaia Geothermal. Ground Loop Design Premier 2016 Edition User’s Manual. 2016. Available online: https://www.groundloopdesign.com/downloads/GLD_2016/GLD2016_Manual.pdf (accessed on 10 August 2019).
- Spitler, J.D. GLHEPRO—A design tool for commercial building ground loop heat exchangers. In Proceedings of the Fourth International Heat Pumps in Cold Climates Conference, Aylmer, QC, Canada, 17–18 August 2000. [Google Scholar]
- Blomberg, T.; Claesson, J.; Eskilson, P.; Hellström, G.; Sanner, B. EED v3. 2—Earth Energy Designer; Lund University: Lund, Sweden, 2015. [Google Scholar]
- Hackel, S.; Pertzborn, A. Effective design and operation of hybrid ground-source heat pumps: Three case studies. Energy Build. 2011, 43, 3497–3504. [Google Scholar] [CrossRef]
- Hénault, B.; Pasquier, P.; Kummert, M. Financial optimization and design of hybrid ground-coupled heat pump systems. Appl. Eng. 2016, 93, 72–82. [Google Scholar] [CrossRef]
- Ciani Bassetti, M.; Consoli, D.; Manente, G.; Lazzaretto, A. Design and off-design models of a hybrid geothermal-solar power plant enhanced by a thermal storage. Renew. Energy 2018, 128, 460–472. [Google Scholar] [CrossRef]
- Park, H.; Lee, J.S.; Kim, W.; Kim, Y. Performance optimization of a hybrid ground source heat pump with the parallel configuration of a ground heat exchanger and a supplemental heat rejecter in the cooling mode. Int. J. Refrig. 2012, 35, 1537–1546. [Google Scholar] [CrossRef]
- Salvalai, G. Implementation and validation of simplified heat pump model in IDA-ICE energy simulation environment. Energy Build. 2012, 49, 132–141. [Google Scholar] [CrossRef]
- Klein, S.A.; Beckman, W.A.; Mitchell, J.W.; Duffie, J.A.; Duffie, N.A.; Freeman, T.L.; Mitchell, J.C. Trnsys 17: A Transient System Simulation Program; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]
- Hellström, G. Duct Ground Heat Storage Model Manual for Computer Code; Department of Mathematical Physics, University of Lund: Lund, Sweden, 1989. [Google Scholar]
- Bayer, P.; de Paly, M.; Beck, M. Strategic optimization of borehole heat exchanger field for seasonal geothermal heating and cooling. Appl. Energy 2014, 136, 445–453. [Google Scholar] [CrossRef]
- Huang, S.; Ma, Z.; Wang, F. A multi-objective design optimization strategy for vertical ground heat exchangers. Energy Build. 2015, 87, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Hu, S.; Liu, Y.; Wang, Q. Optimal design of borehole heat exchangers based on hourly load simulation. Energy 2016, 116, 1180–1190. [Google Scholar] [CrossRef]
- Pu, L.; Qi, D.; Xu, L.; Li, Y. Optimization on the performance of ground heat exchangers for GSHP using Kriging model based on MOGA. Appl. Eng. 2017, 118, 480–489. [Google Scholar] [CrossRef]
- Xia, L.; Ma, Z.; Kokogiannakis, G.; Wang, S.; Gong, X. A model-based optimal control strategy for ground source heat pump systems with integrated solar photovoltaic thermal collectors. Appl. Energy 2018, 228, 1399–1412. [Google Scholar] [CrossRef] [Green Version]
- Bertagnolio, S.; Bernier, M.; Kummert, M. Comparing vertical ground heat exchanger models. J. Build. Perform. Simul. 2012, 5, 369–383. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, J.Y.; Jang, Y.S.; Kim, E.J. Development of a multi-objective sizing method for borehole heat exchangers during the early design phase. Sustainability 2017, 9, 1876. [Google Scholar] [CrossRef]
- Park, S.H.; Jang, Y.S.; Kim, E.J. Using duct storage (DST) model for irregular arrangements of borehole heat exchangers. Energy 2018, 142, 851–861. [Google Scholar] [CrossRef]
- Pahud, D.; Fromentin, A.; Hadorn, J.C. The Duct Ground Heat Storage Model (DST) for TRNSYS Used for the Simulation of Heat Exchanger Piles, User Manual; École Polytech & Fédérale Lausanne: Paris, France; Lausanne, Switzerland, 1996. [Google Scholar]
- Chapuis, S.; Bernier, M. Seasonal storage of solar energy in borehole heat exchangers. In Proceedings of the 11th International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009. [Google Scholar]
- Kim, E.J. TRNSYS g-function generator using a simple boundary condition. Energy Build. 2018, 172, 192–200. [Google Scholar] [CrossRef]
- Rad, F.M.; Fung, A.S.; Rosen, M.A. An integrated model for designing a solar community heating system with borehole thermal storage. Energy Sustain. Dev. 2017, 36, 6–15. [Google Scholar] [CrossRef]
- Malmberg, M.; Lindståhl, H. High temperature borehole thermal energy storage—A case study. In Proceedings of the IGSHPA Research Track, Stockholm, Sweden, 18–20 September 2018. [Google Scholar] [CrossRef]
- Panno, D.; Buscemi, A.; Beccali, M.; Chiaruzzi, C.; Cipriani, G.; Ciulla, G.; Di Dio, V.; Lo Brano, V.; Bonomolo, M. A solar assisted seasonal borehole thermal energy system for a non-residential building in the Mediterranean area. Sol. Energy 2018, 1–13. [Google Scholar] [CrossRef]
- Hackel, S.; Nellis, G.; Klein, S. Optimization of hybrid geothermal heat pump systems. In Proceedings of the 9th International IEA Heat Pump Conference, Zürich, Switzerland, 20–22 May 2008. [Google Scholar]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, Department of Mathematical Physics, University Lund, Lund, Sweden, 1987. [Google Scholar]
- Park, S.H.; Jeon, B.K.; Jang, Y.S.; Kim, E.J. Multi-objective Sizing Optimization of Borehole Heat Exchangers. In Proceedings of the 15th IBPSA Conference, San Francisco, CA, USA, 7–9 August 2017. [Google Scholar]
- Kim, E.J.; Bernier, M.; Cauret, O.; Roux, J.J. A hybrid reduced model for borehole heat exchangers over different time-scales and regions. Energy 2014, 77, 318–326. [Google Scholar] [CrossRef]
- Wetter, M. GenOpt-A generic optimization program. In Proceedings of the 7th International IBPSA Conference, Rio de Janeiro, Brazil, 13–15 August 2001. [Google Scholar]
- Spitler, J.D.; Cullin, J.; Bernier, M.; Kummert, M.; Cui, P.; Liu, X.; Fisher, D. Preliminary intermodel comparison of ground heat exchanger simulation models. In Proceedings of the 11th International Thermal Energy Storage Conference, Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Zhang, X.; Zhang, T.; Jiang, Y.; Li, B. Improvement on an analytical finite line source model considering complex initial and boundary conditions: Part 1, model development and validation. Energy Build. 2019, 198, 1–10. [Google Scholar] [CrossRef]




| Authors | GHE Models | Design Variables | Objective Functions |
|---|---|---|---|
| S. Hackel et al. [6] | DST model |
|
|
| S. Huang et al. [14] | DST model |
|
|
| C. Zhang et al. [15] | DST model |
|
|
| L. Pu et al. [16] | DST model |
|
|
| L. Xia et al. [17] | DST model |
|
|
| BHE Configuration | Cylindrical | Rec-Shape | U-Shape | L-Shape | I-Shape | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tested irregular BHEs configurations |  |  |  | 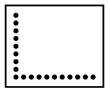 | 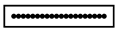 | ||||||
| Borehole spacing | B | ||||||||||
| Equivalent configurations for the DST model |  |  | 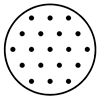 | 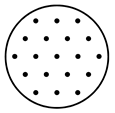 |  | ||||||
| Equivalent borehole spacing | B = B´ | < | B´REC | < | B´U | < | B´L | < | B´I | ||
| i | bi | Xi |
|---|---|---|
| 0 | −6.7140701 | Constant |
| 1 | 1.6921897 | B |
| 2 | −0.0442890 | B2 |
| 3 | 4.6624113 | Stest/SDST |
| 4 | −0.6152736 | (Stest/SDST)2 |
| 5 | 0.1001986 | B × (Stest/SDST) |
| Axisymmetric | Group A (1-Line Arrangements) | |||
|---|---|---|---|---|
| Cylindrical | I-shape | L-shape | U-shape | Rec-shape |
| (N = 19) | (N = 25) | (N = 29) | (N = 26) | (N = 30) |
 Reference DST model |  |  |  |  |
| 25 × 1 | 14,1,14 | 8,1,8,1,8 | 6,1,7,1,6,1,7,1 | |
| Group B (2-line arrangements) | ||||
| I-shape | L-shape | U-shape | Rec-shape | |
| (N = 24) | (N = 28) | (N = 30) | (N = 28) | |
 |  |  |  | |
| 12 × 2 | 6 × 2, 2 × 2, 6 × 2 | 4 × 2, 2 × 2, 3 × 2, 2 × 2,4 × 2 | As shown above | |
| Loads | January | February | March | April | May | June | Jule | August | September | October | November | Deccenber |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| qh,total (MWh) | 24.7 | 19.2 | 11.2 | 2.3 | 0 | 0 | 0 | 0 | 0 | 0.9 | 11.9 | 21.9 |
| qc,total (MWh) | 0 | 0 | 0 | 3.9 | 15.4 | 24.9 | 28.1 | 28.7 | 18.0 | 7.1 | 0 | 0 |
| qh,peak (kW) | 63.2 | 53.6 | 41.1 | 25.9 | 0 | 0 | 0 | 0 | 0 | 13.6 | 43.5 | 55.1 |
| qc,peak (kW) | 0 | 0 | 0 | 39.3 | 79.9 | 88.8 | 96.1 | 92.6 | 76.2 | 42.8 | 0 | 0 |
| Parameter | Value | Unit |
|---|---|---|
| Borehole | ||
| Header depth | 1 | M |
| Borehole radius | 55 | Mm |
| U-tube spacing | 20.1 | Mm |
| U-tube inside diameter | 13 | Mm |
| U-tube outside diameter | 16 | Mm |
| Flow rate per borehole | 0.2 | L/s |
| Borehole thermal resistance | 0.1395 | K/(W·m) |
| Grout heat capacity | 3900 | kJ/(m3·K) |
| Grout thermal conductivity | 2 | W/(m·K) |
| Pipe heat capacity | 1542 | kJ/(m3·K) |
| Pipe thermal conductivity | 2 | W/(m·K) |
| Ground | ||
| Thermal conductivity | 2 | W/(m·K) |
| Heat capacity | 2160.5 | kJ/(m3·K) |
| Initial temperature | 10 | °C |
| Far-field temperature | 10 | °C |
| Fluid | ||
| Density | 1022 | kg/m3 |
| Specific heat | 3960 | kJ/(m3·K) |
| Thermal conductivity | 0.44 | W/(m·K) |
| BHIE Spacing (m) | Base-Line Diff (%) | DST.V1 | DST.V2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | RMSE (%) | Error | RMSE (%) | ||||||||
| I (%) | L (%) | U (%) | Rec (%) | I (%) | L (%) | U (%) | Rec (%) | ||||
| 4 | 4.1 | −1.8 | 7.6 | 4.6 | 6.6 | 5.6 | 5.3 | 5.8 | 4.6 | 5.6 | 5.3 |
| 5 | 3.7 | −1.9 | 6.6 | 3.3 | 4.8 | 4.5 | 3.5 | 4.2 | 3.0 | 3.4 | 3.5 |
| 6 | 1.3 | −1.3 | 6.2 | 3.4 | 4.1 | 4.1 | 2.6 | 3.2 | 2.2 | 2.4 | 2.6 |
| 7 | 0.1 | −0.6 | 6.0 | 3.4 | 3.9 | 4.0 | 2.8 | 3.0 | 1.9 | 1.7 | 2.4 |
| RMSE (%) | 3.0 | 1.5 | 6.6 | 3.7 | 5.0 | 4.6 | 3.7 | 4.2 | 3.1 | 3.6 | 3.7 |
| BHIE Spacing (m) | Base-Line Diff. (%) | DST.V1 | DST.V2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | RMSE (%) | Error | RMSE (%) | ||||||||
| I (%) | L (%) | U (%) | Rec (%) | I (%) | L (%) | U (%) | Rec (%) | ||||
| 4 | 4.1 | 14.9 | 14.8 | 11.7 | 13.3 | 13.7 | 8.3 | 9.2 | 5.4 | 5.8 | 7.4 |
| 5 | 3.7 | 12.5 | 11.0 | 8.9 | 11.4 | 11.0 | 6.0 | 6.3 | 4.2 | 6.2 | 5.8 |
| 6 | 1.3 | 11.4 | 9.7 | 6.7 | 8.4 | 9.2 | 5.4 | 5.2 | 2.3 | 4.7 | 4.6 |
| 7 | 0.1 | 10.2 | 8.8 | 5.3 | 8.1 | 8.3 | 4.2 | 4.5 | 1.3 | 4.6 | 3.9 |
| RMSE (%) | 3.0 | 12.4 | 11.3 | 8.5 | 10.5 | 10.8 | 6.2 | 6.6 | 3.7 | 5.4 | 5.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Kim, E.-J. Optimal Sizing of Irregularly Arranged Boreholes Using Duct-Storage Model. Sustainability 2019, 11, 4338. https://doi.org/10.3390/su11164338
Park S-H, Kim E-J. Optimal Sizing of Irregularly Arranged Boreholes Using Duct-Storage Model. Sustainability. 2019; 11(16):4338. https://doi.org/10.3390/su11164338
Chicago/Turabian StylePark, Seung-Hoon, and Eui-Jong Kim. 2019. "Optimal Sizing of Irregularly Arranged Boreholes Using Duct-Storage Model" Sustainability 11, no. 16: 4338. https://doi.org/10.3390/su11164338





