Optimization of Integrated Inventory Routing Problem for Cold Chain Logistics Considering Carbon Footprint and Carbon Regulations

Abstract

This paper studies the optimization of cold chain integrated inventory routing problem while considering carbon emissions. First, the carbon footprint in inventory and transportation process for cold chain logistics is accurately identified and quantified. Secondly, based on the carbon regulations, which are carbon cap, carbon cap and offset, carbon cap and trade, and carbon tax regulations, four green cold chain inventory routing optimization models that minimize the total cost are constructed, respectively. Subsequently, a genetic simulated annealing algorithm (GASA) is developed in order to efficiently solve the models, which combines the advantages of the two algorithms. The effectiveness of the algorithm and the models is verified by numerical comparison experiments. Further, a set of numerical experiments is conducted to examine in detail the effectiveness of each regulation with the change of cap, carbon price, and unit fuel price in order to investigate the difference of these regulations’ impacts on the cold chain logistics. The research results show that (a) the cap and price plays a relatively important role, for their value setting may even lead to the invalidation of the regulations and the development of the enterprises; (b) carbon cap and carbon tax regulations are more powerful when compared to the other two regulations, which reduce more carbon emissions, but also pose more challenge to the enterprises’ economic development; (c) overall, cap and trade regulation is better than cap and offset regulation, because, when the cap is not sufficient, the two regulations are almost as good, but when the cap is sufficient, the offset policy is invalid; and, (d) unlike the traditional logistics, the increase of unit fuel price will not reduce carbon emissions. Several practical managerial implications for government and enterprises are also provided based on research results.

1. Introduction

Global warming is one of the most serious problems facing the whole world, with the main cause being a large amount of greenhouse gas (GHG) emissions that are generated by human economic activities [1]. Many countries and organizations have issued and implemented corresponding regulations to control the carbon emissions, such as carbon cap, carbon cap and offset, carbon cap and trade, or carbon tax regulation in order to reduce GHG emissions and mitigate the environmental problems. Taking China as an example, the carbon cap and trade regulation is widely accepted and it has launched its pilot emission trading system (ETS) in seven regions in 2013 [2]. Subsequently, in 2017, the National Development and Reform Commission announced the official launch of the national carbon market, and would gradually expand the market coverage [3]. Along with the frequently introduced carbon emission policies and gradually expanded carbon market, the limitation of carbon emissions has become a problem that enterprises must face, especially for high-energy consuming enterprises, such as cold chain logistics [4].

Cold chain logistics is a low-temperature supply chain system that combines refrigeration industry and logistics. In recent years, with the improvement of people’s living standards, it has developed rapidly. According to relevant data, in 2015, the transaction volume of China’s cold chain logistics market was 158.3 billion yuan, which reached 220 billion yuan in 2016 with an increase of 22.3% over 2015 [5]. In 2020, the compound growth rate of China’s cold chain market is expected to reach 17.1% [6]. However, although its development promotes economic development to some certain extent, it also imposes a serious burden on the environment. When compared with normal logistics, the cold chain logistics need to use refrigeration equipment (e.g., refrigerated vehicle) to maintain the freshness of the products, which normal operation will consume enormous energy and produce significant carbon emissions simultaneously [7]. Adekomaya et al. [8] reported that the fossil fuels that are used in transport refrigeration accounted for 15% of world’s energy use and 40% of the global greenhouse effect comes from emissions that are generated from food transportation. Therefore, in the context of stringent governmental carbon regulations and consumers’ increasing expectation for environmental friendliness, it becomes a necessity that the incorporation of carbon emission reduction into the operational decision on logistics management. Afterwards, how to make operational decisions to reduce carbon emissions of cold chain activities and promote sustainable development of enterprises becomes a rough problem that needs to be solved imperatively.

For past few years, there is some research on low-carbon cold chain logistics. Most research focuses on the optimization of operational decision on cold chain network, which significantly contributes to green logistics [9], such as distribution optimization [10,11] and inventory strategy optimization [12] in cold chain logistics. However, although they demonstrated that operation optimization is conducive to reducing carbon emissions, they almost focused on single-stage optimization, few researches studied the holistic optimization of integrated inventory and transportation activities. In fact, firms ought to prefer a holistic optimization whether from an economic or sustainable perspective. According to the relevant report, the total cost of transportation and inventory account for 96% of the logistics costs [13]. As for carbon emissions that are generated from inventory and transportation activities, it negatively contributes to the environment. It is noted that 14% of global greenhouse gas emissions in 2010 came from the transportation sector according to report [14]. With reference to inventory stage, the accompanying warehousing operations that employ special cold warehouse or freezer produce significant carbon emissions [12]. Furthermore, the inventory scheme will also influence the distribution planning decision. Therefore, more attention should be focused on the holistic optimization of integrated inventory and transportation problem in cold chain logistics to accomplish the purpose of both economy and environment.

In addition, considering carbon regulation constraints in optimization models is a good way to reduce the carbon emission from existing research regarding low-carbon cold chain [10,11,15], which can also reflect the effectiveness of the carbon regulation and provide some insights into how to make better decision on carbon regulation formulation [16]. However, most articles doing research only consider one kind of regulation. In fact, in China, or even the world, there are still no specific carbon regulations implemented in cold chain logistics industry. Subsequently, we need to think about some questions: do these carbon policies have the same effect on the carbon emission reduction and economic performance of cold chain logistics? If there js some difference, then what is it? From these points of view, this paper focused on an integrated inventory and transportation problem, namely the inventory routing problem (IRP), of a two-echelon supply chain that includes a supplier and a series of retailers, while simultaneously considering four existing carbon regulations.

The carbon emission regulations that are considered in this paper are carbon cap, carbon tax, carbon cap-and-trade, and carbon cap offset, which have been approved and implemented by some countries or organizations. The carbon cap regulation is one of the policies considered to reduce the carbon emission in the United States (US) by the Congress of the United States, Congressional Budget Office [17]. European countries, like Denmark, Finland, Sweden, Netherlands, and Norway, firstly implemented the carbon tax regulation [18]. As for carbon cap and trade regulation, the carbon emissions are tradable through a trading system, such as the European Union Emissions Trading System (EU-ETS) [19]. The carbon cap offset regulations is often employed by originations who voluntarily decrease their carbon emissions by investing a carbon offset project or activity [20]. From these, we can see that these regulations are very influential and their coverage will expand in the future, so it is valuable to further study these policies in the field of the cold chain logistics. The main purpose of this paper is to reduce the carbon emissions of cold chain by optimizing the operational decision on the inventory control and transportation planning, simultaneously. Our other purpose is to provide some reference for government decision-making on carbon regulation development in cold chain logistics by analyzing the difference of the effect of these carbon policies on the cold chain.

This paper is based on the four existing carbon policies, which are carbon cap, carbon tax, carbon cap-and-trade, and carbon cap offset, investigate the optimization of inventory routing problem in cold chain logistics while considering carbon regulations. Firstly, based on four existing carbon emissions regulations, four optimized green cold chain inventory routing problem models were constructed. Subsequently, the genetic simulated annealing algorithm (GASA) is developed in order to efficiently solve the proposed models. The main advantages of the proposed models are as follows: (1) These models explicitly account for carbon dioxides that are generated not only by transportation sector, but also the inventory stage. (2) This paper systematically analyzes the cost items concerned with cold chain logistics, which includes inventory cost, damage cost, fixed vehicle cost, fuel consumption cost and carbon emission related cost (except the model under carbon cap regulation). (3) According to the rule of each carbon regulation, the corresponding carbon constraints or carbon emission related cost are included in the models. (4) The proposed GASA algorithm combines the genetic algorithm and simulated annealing algorithm, which efficiently enhanced the local search capabilities of the algorithm.

The rest of this paper is structured, as follows: the relevant literature to the problem addressed this paper is reviewed in Section 2. The model formulations are proposed in Section 3. A solution method is described in Section 4. The algorithm experiment and results analysis are shown in Section 5. Finally, conclusions are presented in Section 6.

2. Literature Review

The main purpose of this paper is to obtain optimal planning, including inventory management and routing scheme of each period with consideration of economic and carbon regulation in the inventory routing problem for cold chain logistics. Therefore, we mainly review the related literature in two areas: logistics planning models for cold chain logistics and environmentally conscious inventory routing models.

2.1. Logistics Planning Models for Cold Chain Logistics

We first review the literature on the modeling of logistical operations associated with cold chain logistics since this study targeted at the inventory and the routing problem of cold chain logistics. Unlike normal logistics, cold chain logistics need refrigeration facilities to keep its freshness along every step from its production to final consumption. This, however, significantly increases the cost, energy consumption, and carbon emission because of refrigeration [8,21,22]. Additionally, this intrigues more research on cold chain logistics operational optimization not only considers cost reduction, but also sustainability factors. Bozorgi et al. [23] constructed a new inventory model that considers both cost and emission for cold items. The inventory holding cost and carbon emissions due to the refrigeration of freezer are incorporated in their model. Wang et al. [10] proposed a low-carbon location-routing problem model for cold chain logistics, whereby the objective function incorporated the refrigeration cost, damage cost, and carbon emissions cost. The model explicitly calculates the emissions from distribution center and transportation process. With respect to vehicle routing problem in cold chain logistics, Qin et al. [11] considered cost, customer satisfaction, and carbon emissions simultaneously and proposed a comprehensive cold chain vehicle routing problem optimization model. As for carbon emission, they introduced the carbon trading mechanism to calculate the carbon emissions costs. While considering sustainability in cold supply chain, Hariga et al. [16] presented three models that were targeted at a multi-stage supply chain, which aim to minimize the operational cost, minimize carbon footprint, and minimize the hybrid economic and environmental, respectively. Their research demonstrates that incorporating carbon-related costs through carbon tax regulation may result in a slight increase in operating costs, but can save carbon-related costs. Different from the above literature that considered a deterministic demand, Abdulrahim et al. [7] optimized the replenishment strategy for a firm who is facing a discrete time-varying demand for cold product. They also presented three mathematical models (cost, carbon footprint, and hybrid) and got the conclusion as same as Hariga got. It is noted that both in models of Hariga et al. and Abdulrahim et al., the inventory holding cost are produced mainly due to the freezers using and the carbon emission are mainly generated from electric consumption. Under vendor managed inventory (VMI), Bai et al. [15] studied the supply chain coordination that comprised one manufacturer and two competing retailers and developed an optimization model under the constraint of carbon cap-and-trade regulation.

From the above literature, firstly, it is observed that the incorporation of cargo damage and refrigeration factors in cold chain logistics’ models is necessary [24]. Second, carbon regulations are a strong constraint in controlling the emissions, which were considered in many researches (e.g., carbon tax considered in Wang et al. [10]; Hariga et al. [16]; Abdulrahim et al. [7]; carbon cap and trade considered in Qin et al. [11]; Bai et al. [15]). In summary, the research considering sustainability in cold chain logistics is relatively rich, covering a range of from single to multi-stage supply chain optimization. However, the authors noticed few research studied the integrated inventory and routing problem of cold chain logistics, which plays an important role in supply chain management. Therefore, this paper focuses on inventory routing problem in cold chain logistics with consideration of the multi-attributes of cold chain logistics (cargo damage and refrigeration factors) and different carbon regulations.

2.2. Environmentally Conscious Inventory Routing Models

The inventory routing problem (IRP) addresses the coordination of two components of the supply chain: the inventory management and vehicle routing [25]. The goal is to achieve cost minimization through the joint optimization of these two activities. However, as environmental pressures increase, many researchers begin to consider environmental issues in their research, which is the main goal of our work. Treitl et al. [26] extended the IRP model to include environmental considerations by charging the carbon emissions generated by the company and adding a carbon cap to the total emissions that cannot be exceeded. Similar to Treitl et al., Konur [27] also formulated a carbon cap constraint on the total emissions, but his model considered emission characteristics of various trucks and no more charges for carbon emissions. Chen et al. [28] extended the conventional IRP by considering the environmental impacts and heterogeneous vehicles, and a mixed-integer program with a comprehensive objective, which includes emission cost was constructed. Kuo et al. [29] calculated the carbon footprint while using a totally different method in which product data from different stages of the life cycle are collected to calculate the carbon footprint using life cycle analysis method. As for IRP for perishable products, Shamsi et al. [30] considered the environmental issues by accounting for the cost due to greenhouse emissions into the model. Soyal et al. [31] presented a multi-period IRP model that considered environmental factors by comprehensive evaluation of CO2 emission and fuel consumption. All of the above models are single-objective, which means that carbon emissions must be converted into one of cost item or one of the constraints. However, the question is that the conversion rule is hard to determine, that is, it is difficult to represent the carbon emission in the cost objective function.

Different from the above literature, some researchers developed multi-objective models, which more reasonably reflect the fact. Franco et al. [32] presented a green bi-objective inventory routing problem model, in which the minimization of the CO2 emissions is included and then a multi-objective algorithm that was embedded with the column generation was proposed to solve the model. Muhammad et al. [33] developed a multi-objective mathematical framework for the IRP, where the objectives are (i) minimize the total cost, (ii) minimize the probability of shortage and delivery delays and (iii) minimize the carbon footprint. However, there is still question like that the pareto solution resulting from multi-objective model cannot directly help the decision-makers to make operational decision.

With gradually formulated carbon regulations, the scholars incorporated these regulations into IRP models that can easily solve the above questions, which provides strong carbon constraints and easy to provide suggestions to decision-makers. Under carbon emission regulations, Konur and Schaefer [34] analyzed the integrated inventory routing problem and investigated the economic order quantity model with less-than-truckload (LTL) and truckload (TL) transportation. Similarly, Cheng et al. [35] also studied the IRP problem under different carbon emission regulations. The difference is that Cheng et al. focused on an inbound commodity collection system, while the former scholars considered the extended EOQ model. Through their computational analysis, the impacts of carbon emission regulations on the traditional inventory routing problem were analyzed. In our paper, we also considered four carbon regulations, but our focus is the cold chain inventory routing problem, which has not yet been studied. Furthermore, the cold chain IRP models in this paper comprehensively account for the carbon emissions not only produced by transportation sector, but also inventory stage, which is not explicitly calculated in previous paper. The other difference from inventory routing problem in normal logistics is that the cold chain IRP also concerns the cargo damage and refrigeration factors, which makes the cold chain IRP models more complicated.

In summary, this paper focuses on inventory routing problem for cold chain logistics in a finite planning horizon, while considering four existing carbon regulations (carbon cap, cap and offset, cap and trade, and tax), and construct the cold chain IRP models under the constraints of the carbon emission regulations. The genetic simulated annealing algorithm (GASA) was developed in order to solve the problem more efficiently. Scholars have efficiently demonstrated that the genetic algorithm has gradually developed to be applied in the IRP problem [36,37,38]. However, the genetic algorithm still has the disadvantage of precocity and its local-search ability is weak. Therefore, this paper combines the simulated annealing algorithm, which presents strong hill-climbing ability, to the genetic algorithm, so that the overall performance of the algorithm is improved greatly.

To conclude, the contributions of this paper to the low-carbon cold chain research are as follows: first, we construct a series of cold chain inventory routing models under the constraint of the carbon emission regulations with the purpose of reducing carbon emissions, which accurately identifies and quantifies the carbon footprint generated through inventory and transportation activities and incorporates the multi-attributes of cold chain products. Second, through computational analysis, the impacts of carbon emission regulations on the cold chain IRP were systematically analyzed and several managerial insights were obtained, which provide valuable reference for governments to formulate suitable carbon emission regulation in the cold chain industry. Third, a genetic simulated annealing algorithm (GASA) is designed to obtain high-quality solutions since the IRP problem studied in this problem belongs to NP-hard, which enriches the researches for solving such NP-hard problems.

3. Problem Description and Model Formulation

3.1. Problem Description and Notations

The problem that is studied in this paper is defined on a two-echelon supply chain, which includes a supplier and a series of retailers. The refrigerated central depot that is owned by the supplier is going to distribute fresh products to a set of retailers. During the planning horizon, the supplier only arranges delivery for the retailer at the beginning of each delivery period and stockouts are not permitted. The products are all distributed by one type of refrigerated vehicle, each with capacity Q that is located in the depot. The refrigerated vehicles depart from the depot and deliver products to each retailer and return to the depot at the end. Each vehicle can perform at most one route per time period. Suppose that the demand $q_{it}$ faced by the retailer in each period $t\in$ T is deterministic but variable over periods. With the VMI (Vendor Managed Inventory) management strategy, the ordering cost and order lead time are not considered. In addition, it is assumed that the initial inventory level of each retailer is zero. Therefore, as for the retailer, an inventory holding cost occurs at each period and, due to the perishability of the cold products, the damage cost is also produced in each period. The goal of this question is to determine the delivery amount of each retailer in each period and the distribution route to minimize the total cost under carbon regulations.

The notations are as

Table 1. The notations.

Notations	Description
$V^{\prime }$	set of nodes representing retailers
$V_0$	the node representing the supplier
$T$	set of time periods
$h_i$	the inventory holding cost of retailer i for storing per unit product
$I_{it}$	the inventory level of retailer i at the beginning of the period t
$q_{it}$	the demand of retailer i in period t
$p$	the price of unit product
$\partial$	the spoilage rate of the product
$t_s$	the time duration of a period
${\rho }_o$	the empty load fuel consumption rate (e.g., L/km)
${\rho }^{*}$	the full load fuel consumption rate (e.g., L/Km)
$f_k$	the fixed cost of vehicle k
$u$	the price of unit fuel consumption
$\mathrm{Q}$	the weight capacity of the refrigerated vehicle
$C_i$	the largest inventory capacity of the retailer $i$
$d_{ij}$	the distance between the retailer i and j
$e_0$	the carbon emissions generated by unit fuel consumption
$Q_c$	the total carbon emissions generated during the planning horizon
$Q_q$	the carbon cap allocated by the government
$c_p$	the carbon price
$g$	the carbon emissions generated by per kWh electricity
$p_s$	the energy consumption generated by storing unit product in one period
$Q_{ijkt}$	the load carried by vehicle k from retailer i to j in period t
$D_{it}$	the amount of product delivered to retailer i in period t
$Y_{kt}$	$Y_{kt}=1$ if vehicle k is used to deliver products; 0 otherwise
$x_{ijkt}$	$x_{ij}^{kt}=1$ if vehicle k travels from retailer i to j; 0 otherwise

shows.

3.2. Analysis of Related Factors

3.2.1. Inventory Holding Cost

The average inventory level is used to calculate the inventory cost of each retailer since the retailer’s inventory level is constantly changing. With respect to cold chain products, the inventory costs are generated not only because of the storage of the goods but also the energy consumption to keep the goods in a low-temperature environment. It is also the difference between normal logistics, which has high-level inventory cost due to the refrigeration. Subsequently, the inventory cost can be expressed as:

$$C_1={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}{h}_i\left(I_{it}-\frac{1}{2}{q}_{it}\right)$$

(1)

3.2.2. Damage Cost

The damage cost of the products need to be carefully calculated and incorporated in the model due to the perishability of the cold products. This paper assumes that the products are damaged at the exponential rate when they are stored in the retailer’s warehouse. Afterwards, the formula that was used in Wang et al. [10] and Qin et al. [11] was adopted to calculate the damage cost produced during the inventory process. Subsequently, the damage costs during the inventory process can be expressed as:

$$C_2={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}p\left(I_{it}-\frac{1}{2}{q}_{it}\right)\left(1-e^{-\partial t_s}\right)$$

(2)

3.2.3. Vehicle Fixed Cost

The vehicle fixed cost is generated once a refrigerated truck is dispatched to carry out a distribution task. It includes the driver salary, road maintenance fee, the depreciation expense of the vehicle during use and onboard refrigeration equipment, and so on.

$$C_3={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{f}_k{Y}_{kt}$$

(3)

3.2.4. Fuel Consumption Cost

In this article, we adopt the formula used in Xiao et al. [39] to calculate the fuel that is consumed during the delivery process. Subsequently, the fuel consumption cost can be expressed as:

$$C_4={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{i,j\in V^{\prime }}{x}_{ijkt}\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)u{d}_{ij}$$

(4)

3.2.5. Calculation of Carbon Emissions

For multi-period green cold chain, the carbon emissions are not only generated during the distribution process, but also during the inventory stage.

In the distribution process, since carbon emissions are directly related to fuel consumption, a factor $e_0$ is used to convert fuel consumption into carbon emissions [40]. In the inventory stage, the carbon emissions are generated by the electrical energy consumption of refrigeration equipment, and its electrical energy consumption is directly proportional to the inventory volume. Similarly, a factor $g$, which represents carbon emissions that are generated by per $\mathrm{kWh}$ electricity, is used to convert electrical consumption into carbon emissions. Therefore, the total carbon emissions that are generated in the overall stage can be expressed as:

$$Q_c={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}{\displaystyle \sum }_{j\in V^{\prime }}{e}_0\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}g*p_s\left(I_{it}-\frac{1}{2}{q}_{it}\right)$$

(5)

3.3. Models Formulation

3.3.1. Model Formulation with Carbon Cap Policy

In the carbon cap mechanism, a strict carbon emission limit (cap) is set, and the emissions that are generated through corporate operation must not exceed the limit, otherwise it will be forced to stop production. In cold chain IRP, the carbon emissions that are generated in the transportation process and the inventory storage must lower than or equals to the cap. The cold chain IRP model under carbon cap policy, referred to as $\left(\mathrm{M}\_cc\right)$, can be shown, as follows:

$$\begin{gathered} \mathrm{Min}{Z}_{cc}=C_1+C_2+C_3+C_4 \\ ={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}\left(h_i+p\left(1-e^{-\partial t_s}\right)\right)\left(I_{it}-\frac{1}{2}{q}_{it}\right)+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{f}_k{Y}_{kt} \\ +{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{i,j\in V^{\prime }}u\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij} \end{gathered}$$

(6)

Subject to:

$$I_{i,t+1}-D_{it}=I_{it}-q_{it}-\left(I_{it}-\frac{1}{2}{q}_{it}\right)\left(1-e^{-\partial t_s}\right)$$

(7)

$${\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{j\in V^{\prime }}{x}_{ijkt}=1,\forall i\in V,\forall t\in T$$

(8)

$${\displaystyle \sum }_{i\in V^{\prime }}{D}_{it}{y}_{ikt}\le Q,\forall k\in K,\forall t\in T$$

(9)

$${\displaystyle \sum }_{k\in K}{y}_{ikt}=\{\begin{array}{c}1, i\in V^{\prime }\\ K, i=0\end{array}$$

(10)

$${\displaystyle \sum }_{j\in V^{\prime }}{x}_{ijkt}={\displaystyle \sum }_{j\in V^{\prime }}{x}_{ijkt}\le 1,i=0, k\in K$$

(11)

$${\displaystyle \sum }_{j\in V^{\prime }}{\displaystyle \sum }_{k\in K}{x}_{ijkt}\le K, i=0$$

(12)

$$x_{ijkt}+x_{jikt}\le 1,\forall i,j\in V^{\prime },\forall k\in K,\forall t\in T$$

(13)

$$x_{ijkt},Y_{kt},D_{it}\ge 0$$

(14)

$$I_{it}-q_{it}-\left(I_{it}-\frac{1}{2}{q}_{it}\right)\left(1-e^{-\partial t_s}\right)\ge 0$$

(15)

$${\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}{\displaystyle \sum }_{j\in V^{\prime }}{e}_0\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}g*p_s\left(I_{it}-\frac{1}{2}{q}_{it}\right)\le Q_q$$

(16)

Equation (6) is the objective function of the model that minimizes the total costs of the cold chain IRP. Constraint (7) is the inventory balance equation for each retailer. Constraint (8) imposes that each retailer is only served by one refrigerated vehicle. Constraint (9) represents that the load that is carried by one vehicle cannot exceed the vehicle capacity. Constraint (10) represents that the depot has $K$ vehicles in total and each customer is served by only one truck. Constraint (11) imposes the notion that the path route of each vehicle is closed loop. Constraint (12) shows that the number of routes cannot exceed the quantity of vehicle that is owned by the depot. Constraint (13) is introduced to eliminate the sub-loops. Constraint (14) ensures that the decision variables are non-negative. Constraint (15) represents that stockouts is not permitted. Constraint (16) represents that the carbon emissions that are generated cannot exceed the carbon cap.

3.3.2. Model Formulation with Carbon Cap Offset Policy

In the carbon cap offset mechanism, if the emissions that are generated by the company exceed the carbon cap allocated by the government, the company can compensate for the extra carbon footprint that they have produced. That is, the company can purchase extra carbon credits for their operation through the carbon offset market. Therefore, we extend the $\left(\mathrm{M}\_cc\right)$ to apply to the carbon cap offset policy by adding a cost item, credits purchasing cost. Let the $e^{+}$ represent the carbon credits purchased during the planning horizon, then the credits purchasing cost is $C_5=c_p*e^{+}$. Moreover, the constraint (16) is adapted as Equation (18) shows. Subsequently, the model $\left(\mathrm{M}\_cco\right)$ can be expressed as:

$$\begin{gathered} \mathrm{Min}{Z}_{cco}=C_1+C_2+C_3+C_4+C_5 \\ ={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}\left(h_i+p\left(1-e^{-\partial t_s}\right)\right)\left(I_{it}-\frac{1}{2}{q}_{it}\right)+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{f}_k{Y}_{kt} \\ +{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{i,j\in V^{\prime }}u\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+c_p{e}^{+} \end{gathered}$$

(17)

Subject to (7)–(15) and

$${\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}{\displaystyle \sum }_{j\in V^{\prime }}{e}_0\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}g*p_s\left(I_{it}-\frac{1}{2}{q}_{it}\right)\le Q_q+e^{+}$$

(18)

$$e^{+}\ge 0$$

(19)

The objective of the model $\left(\mathrm{M}\_cco\right)$ is to minimize the total cost of the cold chain IRP, including credits purchasing cost. Constraint (18) denotes that the total carbon emissions that are generated through transportation and inventory stage during the planning horizon cannot exceed the sum of the allocated cap and the purchased carbon credits.

3.3.3. Model Formulation with Carbon Cap-and-Trade Policy

In the carbon cap-and-trade mechanism, the carbon credit is used as a commodity that can be traded through a trading system. The government allocates a certain amount of carbon credits (cap) to the company. If they exceed the cap, they need to buy extra carbon credits; instead, they can sell the remaining carbon emissions to make a profit. Afterwards, the model with carbon cap-and-trade policy $\left(\mathrm{M}\_cct\right)$ can be formulated by extending the model $\left(\mathrm{M}\_cco\right)$ with replacing the credits purchasing cost as carbon trading cost and removing the constraints (18) and (19). The carbon trading cost under carbon cap and trading policy can be expressed as $C_6=c_p\left(Q_c-Q_q\right)$. Subsequently, we get the model $\mathrm{M}\_cct$:

Model $\left(\mathrm{M}\_cct\right)$:

$$\begin{gathered} Min Z_{cct}=C_1+C_2+C_3+C_4+C_6 \\ ={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}\left(h_i+p\left(1-e^{-\partial t_s}\right)\right)\left(I_{it}-\frac{1}{2}{q}_{it}\right)+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{f}_k{Y}_{kt} \\ +{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{i,j\in V^{\prime }}u\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+c_p\left(Q_c-Q_q\right) \end{gathered}$$

(20)

Subject to (5), (7)–(15).

The objective of model $\left(\mathrm{M}\_cct\right)$ is to minimize the total cost of the cold chain IRP, including the carbon trading cost.

3.3.4. Model Formulation with Carbon Tax Policy

Under the carbon tax policy, the company is imposed an emission tax for the unit carbon emissions produced. Here, $c_p$ denotes the tax for unit carbon emission, which is also named carbon price, then the total carbon tax is $C_7=c_p{Q}_c$. The model under carbon tax is $\left(\mathrm{M}\_ct\right)$.

Model $\left(\mathrm{M}\_ct\right)$:

$$\begin{gathered} Min Z_{ct}=C_1+C_2+C_3+C_4+C_7 \\ ={\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{i\in V^{\prime }}\left(h_i+p\left(1-e^{-\partial t_s}\right)\right)\left(I_{it}-\frac{1}{2}{q}_{it}\right)+{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{f}_k{Y}_{kt} \\ +{\displaystyle \sum }_{t\in T}{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{i,j\in V^{\prime }}u\left({\rho }_0+\frac{{\rho }^{*}-{\rho }_0}{Q}{Q}_{ijkt}\right)x_{ijkt}{d}_{ij}+c_p{Q}_c \end{gathered}$$

(21)

Subject to (5), (7)–(15).

The objective of model $\left(\mathrm{M}\_ct\right)$ is to minimize the total cost of the cold chain IRP, including carbon tax cost. The constraints of $\mathrm{M}\_ct$ are the same as $\mathrm{M}\_cct$.

4. Genetic Simulated Annealing Algorithm

IRP belongs to the NP-hard problem [41]. Therefore, it is a wise choice to choose heuristic or metaheuristic methods to obtain high-quality solutions. Recently, genetic algorithm (GA) has been developed to solve IRP to obtain good solutions, such as genetic algorithm-Taguchi based approach, as proposed by Azadeh et al. [38] and new genetic algorithm, which was designed by Abdelmaguid et al. [42].

In this paper, a genetic simulated annealing algorithm (GASA) is developed to solve the cold chain IRP. The simulated annealing algorithm has strong local search ability, which in the GASA just make up the shortcoming of the genetic algorithm. Thus, the GASA can successfully search high-quality solutions with more efficient time. Figure 1 shows the flowchart of the GASA.

4.1. Chromosome Representation and Encoding

This paper defines a chromosome as a two-dimensional matrix which includes the delivery amount and distribution plan information for each period. As Figure 2 shows, the scheme for each period is shown in each row of the matrix, in which the first n columns represent the products amount that need to be delivered and the rest columns represent the vehicle routing of each period.

Firstly, generate a random value of delivery amount $D_{it}\in \left(max\left\{L_{it},0\right\}, U_{it}\right), \forall i,t$ for each retailer. Among them, $L_{it}$ and $U_{it}$ are the lower limit and upper limit for the total amount of products that were delivered to retailer $i$ in period $t$. This will not violate the maximum inventory constraints or it will lead to being out of stock. The calculations of $L_{it}$ and $U_{it}$ are as Equations (22) and (23) shows. After the delivery amounts are determined, each retailer’s inventory level in each period can be easily calculated. Secondly, generate route sequence of each period, that is, randomly sorting the retailers. According to the schedule delivery amounts and route sequence, the vehicle dispatched to serve the customer can be determined according to vehicle load constraint. Take the period 1 as an example, while assuming the vehicle load is 80, then the vehicle 1 serves retailer 3, 4, 1, and the vehicle 2 serves retailer 5, 2, 6. Finally, the routes of each vehicle can be generated while using the nearest neighbor search (NNS) heuristic [37].

$$L_{it}=q_{it}-\left[I_{it-1}-q_{it-1}-\left(I_{it-1}-\frac{1}{2}{q}_{it-1}\right)\left(1-e^{-\partial t_s}\right)\right] \forall i\ne 0$$

(22)

$$U_{it}=C_i-\left[I_{it-1}-q_{it-1}-\left(I_{it-1}-\frac{1}{2}{q}_{it-1}\right)\left(1-e^{-\partial t_s}\right)\right] \forall i\ne 0$$

(23)

NNS heuristic

Step 1

Start from $t=1$;

Step 2

Start from the depot at the given location.

Step 3

Find a non-visited node which is closest to the last visited node.

Step 4

Add this retailer to the route of the current vehicle.

Step 5

Repeat step 2 and 3 until all nodes are visited.

Step 6

Set $t=t+1$;

Step 7

Return to step 2 until $t\le T$.

4.2. Initialization and Fitness Evaluation

According to the population size $\mathrm{N}$, generate $\mathrm{N}$ individuals based on the random method that was described in the previous subsection. As for the fitness value, this paper takes the reciprocal of the individual’s objective function value as its fitness value.

$$F_i=\frac{10000}{Z_i}$$

(24)

4.3. Genetic Operators

1. Selection Operator

This article uses the tournament selection strategy [43], also known as the random league selection, which not only has great solution accuracy, but also solution speed. Moreover, on solving minimization problem, it avoids the trouble of fitness value conversion and achieves better performance.

2. Crossover Operator

Crossover is the core function of GA, as it helps to pass the chromosome fragments of good individuals to the offspring. The crossover operation also plays the role of global search, which can mine unknown space. For the designed chromosome of IRP, the specific crossover operation is as shown in Figure 3. Firstly, randomly choose two individuals as parents. Afterwards, generate two cut-points, representing the retailers that need to crossover the delivery gene and route gene. Next, perform the crossover operation, that is, change the delivery and route gene of the two parents, respectively. Finally, the two new offspring are obtained.

3. Mutation Operator

This paper adopts the delivery exchange procedure to perform mutation on delivery amounts part and uses retailer swap procedure to perform mutation on route part. The specific delivery exchange procedure and retailer swap procedure are as follows.

Delivery Exchange Procedure

Step 1

Randomly choose a period $t$.

Step 2

If the last period is chosen, let $t=t-1$.

Step 3

For the vehicles dispatched to delivery products in period t, choose the vehicle $l$ with the highest remaining capacity.

Step 4

If the last period was chosen, turn to step 6. Else turn to step 6.

Step 5

Randomly choose the retailer $i$ who is included in the path of vehicle l.

Step 6

If $R{C}_{kt}\ge D_{it+1}$, let $D_{it}=D_{it}+D_{it+1}$, $D_{it+1}=0$ and stop. If $R{C}_{kt}<D_{it+1}$, let $D_{it}=D_{it}+R{C}_{kt}$, $D_{it+1}=D_{it+1}-R{C}_{kt}$ and stop.

Retailer Swap Procedure

Step 1

Randomly choose a period $t$.

Step 2

Choose two retailers (each is served by different vehicle) in period $t$ randomly.

Step 3

Exchange the service vehicles of two retailers.

Step 4

Using NNS heuristics to regenerate vehicle routes.

4.4. Simulated Annealing Operators

This paper combines simulated annealing algorithm with the genetic algorithm in order to make up for the shortcomings of poor local search ability of genetic algorithm and produce high quality solutions. The specific steps of the SA in GASA are as follows: The $solu$ is the current solution and $T_i$ is the current temperature;

Step 1

The adjusted new solution is $newsolu$, the objective function value is $newobjv$, and $\Delta f$ is used to represent the increment of the objective function, $\Delta f=newobjv-objv$.Then according to the Metropolis criterion:

$$p=\{\begin{array}{c}exp\left(-\Delta f/T_i\right),\Delta f\ge 0\\ 1, \Delta f\le 0\end{array}$$

(25)

If $\Delta f<0$, accept the new solution with the probability of 1; otherwise, discard the new solution with the probability of $exp\left(-\Delta f/T_i\right)$.

Step 2

Do cooling operation according to the cooling coefficient r, $T_{i+1}=T_i\times r$;

Step 3

If $T_i<T_{end}$, then turn to step 5; Otherwise, turn to step 2.

Step 4

Output the current solution $solu$.

5. Numerical Experiments and Analysis

In this section, the effectiveness of the proposed algorithm GASA is firstly verified through the comparison experiments. Subsequently, a real world case was used to perform a series of numerical experiments to demonstrate the validity of the models and investigate the detailed effects of these carbon regulations on the cold chain logistics. Through experiments, the results are finely concluded and the practical insights and implications from these four regulations are expanded. Finally, the results we attained are well discussed.

5.1. Algorithm Experiment

The instances generation method from Coelho et al. [44] is used in this paper to create randomly instances to perform the numerical tests in order to make up for the shortcomings of poor local search ability of genetic algorithm and produce high quality solutions. With referring to the literature [45,46], the related parameters of the GASA are set as follows: the population size $\mathrm{N}=100$; crossover probability $p_c=0.8$; mutation probability $P_m=0.001$; evolution terminate generation $\mathrm{M}=1000$; the initial temperature $T_0=1000$; and, cooling coefficient $\mathrm{r}=0.9$. The best integer solutions that were obtained by the proposed GASA algorithm with $\mathrm{Matlab}$ R2016a on a PC with Intel core i7 and 1.80 GHz and CPLEX 12.6 are as

Table 2. The results got from CPLEX and GASA.

Instance (n-K-H)		CPLEX			GASA
	Lower Bound	Upper Bound	Gap1 (%)	CPU (s)	Best Objective	Gap2 (%)	CPU (s)
PIRP-10-2-3	28,401.2	28,401.2	0	1	28,401.2	0	1
PIRP-10-2-6	67,252.1	67,252.1	0	3.5	67,252.1	0	2.3
PIRP-10-5-10	81,005.3	81,005.3	0	34	81,005.3	0	4.2
PIRP-20-2-3	60,857.7	60,857.7	0	236	60,857.7	0	6.7
PIRP-20-2-6	133,538	133,538	0	403	133,538	0	7.8
PIRP-20-2-10	197,453	197,453	0	987	197,498	0.02	9.8
PIRP-30-2-3	82,232.3	82,260.3	0.034	3600	82,365.3	0.16	13
PIRP-30-2-6	179,968	179,945	0.013	3600	179,623	0.19	13
PIRP-30-2-10	229,619	229,798	0.077	3600	229,823	0.08	14
PIRP-40-3-3	135,053	136,054	0.74	3600	135,987	0.69	26
PIRP-40-3-6	236,926	239,836	1.22	3600	237,986	0.44	35
PIRP-50-5-3	165,698	172,923	4.36	3600	167,658	1.18	78

shows.

In Table 2, the first column is instances data with different scales, which $n$ represents the number of retailers, $K$ means the number of vehicles owned by depot, and $H$ is the number of periods. The second to fourth columns are the results got from the CPLEX with limited time (3600 s) and the last three columns are the results obtained from GASA.

From Table 2, it can be observed that, in small-sized problems, the optimal solutions that are found by GASA are as good as CPLEX. Moreover, it will be more efficient for GASA to find optimal solutions in medium or large-sized problems than CPLEX. Therefore, the GASA is an effective algorithm to solve such NP-hard problem.

5.2. Instance Data

In this section, the data of the cold chain products distribution from a large-scale cold food company are introduced to perform the numerical experiments. The underlying transportation network consists of one depot from this company and 20 retailers. The depot is responsible for providing cold products to the retailers and

Table 3. The locations and the demands of the retailer.

Number	Location		Demands (Weeks)
	Longitude	Latitude	1	2	3	4
0	114.0128	38.0898	0	0	0	0
1	117.8982	41.0225	0.85	0.4	1	0.7
2	118.6746	40.9883	1.35	1.3	1.6	1.2
3	116.2357	39.9367	0.5	0.6	1.3	0.55
4	116.6488	39.9196	1.1	2.5	0.45	0.5
5	116.4848	39.8603	950	0.9	1.6	1.1
6	116.3491	39.8173	1.3	0.45	0.4	1.5
7	119.1617	39.6918	0.8	0.75	0.5	0.4
8	116.9335	39.6697	2	0.5	0.35	1.3
9	116.9367	38.9113	0.8	0.35	0.7	1.4
10	115.5132	38.8233	1.1	1.5	0.5	0.35
11	114.9987	38.7658	2.55	3.1	2.4	3.1
12	115.4740	38.6443	0.9	0.7	1.3	0.8
13	116.9101	38.4666	1	1.4	1.1	0.75
14	114.4483	38.0677	8.5	1.3	1.1	0.7
15	114.5937	38.0615	1.1	1.2	0.8	1
16	115.7195	37.7211	0.9	0.7	0.8	1
17	114.6036	37.6241	1.3	0.6	0.5	0.6
18	116.8901	37.2072	1.2	0.6	0.5	0.8
19	114.5398	37.0551	1.3	0.8	0.6	0.7
20	114.4925	36.5695	1.4	1.7	1.1	1.6

shows the locations of the depot and retailers. The planning horizon length is four weeks, and each week represents one period. Table 3 shows the real demand of each retailer. With reference to the actual situation and references [10,11], the parameters of corresponding vehicles and models are shown in

Table 4. Vehicle parameters.

Parameters	Parameter Values	Parameters	Parameter Values
Outline dimension	9990 × 2490 × 3850 mm	Container size	7400 × 2280 × 2400
Total mass	16,000 kg	Rated load capacity	9000 kg
Engine type	B19 033	Fuel type	diesel oil

and

Table 5. Relevant parameters of the models.

Parameters	Values
$P$	1000 CNY/t
$h_i$	350 CNY/t
$\partial$	0.002
$t_s$	1 week
$f_k$	100 CNY
$e_0$	2.67 kg/L
${\rho }_0$	0.165 L/km
${\rho }^{*}$	0.377 L/km
$p_s$	0.075 $\mathrm{kW}·\mathrm{h}$
$\mathrm{g}$	$0.997\mathrm{kg}/\mathrm{kW}·\mathrm{h}$

, some of them.

5.3. Numerical Experiments and Analysis

Firstly, we perform the comparison experiments in Section 5.3.1 to evaluate the effectiveness of carbon reduction of these models. Subsequently, in order to further investigate the impacts of the different carbon regulations on the inventory routing problem of the cold chain logistics and explore the different effectiveness of these regulations, the two most important parameters: carbon cap and the carbon price, are chosen to conduct the parameters sensitivity analysis in Section 5.3.2 and Section 5.3.3. In addition, the impact of unit fuel price on the carbon emissions in cold chain IRP has also been investigated in Section 5.3.4 to differentiate our study from the research of the normal IRP. Finally, Section 5.3.5 presents the discussion part.

5.3.1. Model Comparison Experiments

In this Section, a no-considering carbon regulation model ${\mathrm{M}}_{\_ncr}$ for cold chain logistics is used to assess the feasibility of the models under carbon regulations. We can simply get the model ${\mathrm{M}}_{\_ncr}$ by removing the carbon constraints of $\mathrm{M}\_cc$. The objection of $\mathrm{M}\_nrc$ is:$\mathrm{Min}{Z}_{ncr}=C_1+C_2+C_3+C_4$ and it subjects to Equations (7)–(15). The related carbon parameters are set, as follows: the carbon price is 1 CNY/Kg for $\mathrm{M}\_cco$, $\mathrm{M}\_cct$, and $\mathrm{M}\_ct$. The carbon cap for $\mathrm{M}\_cc$, $\mathrm{M}\_cco$, and $\mathrm{M}\_cct$ is 750 Kg. Afterwards, we can get the results with five models, which are shown as

Table 6. The results of the models.

Models	Total Carbon Emission (Kg)	Gap 1	Total Cost (CNY)	Gap 2
$\mathrm{M}\_nrc$	901.2	0	5149.9	0
$\mathrm{M}\_cc$	698.5	−202.7	6274.3	+1097.4
$\mathrm{M}\_cco$	829.3	−71.9	5159.9	+10
$\mathrm{M}\_cct$	828.9	−72.3	5158.5	+8.6
$\mathrm{M}\_ct$	821.5	−79.7	5313.6	+163.7

.

From Table 6, it can be easily observed that the carbon emissions under carbon regulations are smaller than the carbon emissions from the base model, which demonstrates that the models that were constructed this paper are effective. Additionally, it can be seen that the emission reduction effect under different carbon regulations is different, which may be the reason that the different rules of different regulations. Therefore, a series of sensitivity analysis is performed in the following sections in order to investigate the difference of these carbon regulations.

5.3.2. Carbon Cap

In model $\mathrm{M}\_cc$, $\mathrm{M}\_cco$, and $\mathrm{M}\_cct$, we set different cap (from 0 to 600 Kg with step 100 and from 600 to 1100 Kg with step 50) to conduct the experiments and record the results of each experiment. Subsequently, we can draw the changing curve of carbon emissions and total cost under different cap that is shown in Figure 4 to help us analyze the effects of cap on emissions and cost. In three models, the carbon price is set as 1 CNY/Kg. The other parameters’ values are unchanged, which is shown in Section 5.2.

From Figure 4, the following findings and managerial insights can be obtained:

(1)

Overall, as the cap increases, the total cost gradually decreases, but carbon emissions gradually increase.

(2)

When the cap is too small (less than 600), there is no feasible solution under the cap policy. Accordingly, the cap policy is not feasible under this condition, because the companies cannot meet the too harsh requirements of the government. Therefore, if the government adopts the cap policy, it should allocate an appropriate cap to enterprise according to their actual productivity, and the cap should be at least greater than the minimum carbon emission limit of the enterprise. Additionally, the cost curve and the carbon emission curve under the cap offset and cap-and-trade policies almost coincide, which means that the effects of the two policies are the same under this situation.

(3)

When the cap is moderate (between 600 and 850), the carbon emission curve under the cap policy is the lowest, but the cost curve is the highest when compared to the other two policies. Besides, the cost curve and the carbon emission curve under the cap offset and cap-and-trade policies almost coincide. Therefore, the government can choose the appropriate policy based on carbon emission targets or carbon emission pressure. When faced with a relatively high carbon emission pressure, the government can choose the cap policy, but the company must bear certain cost pressure. When the pressure is relatively low, the cap offset policy or cap-and-trade policy will be a good choice.

(4)

When the cap is enough (greater than 850), the cost curve and the carbon emission curve under the cap and cap offset policies almost coincide; the cost of the two achieve to minimum and keep unchanged, but the carbon emission is maximized. In fact, under this circumstance, the cap policy and cap offset policy are ineffective, because the cap allocated to the enterprise is too large. Fundamentally, the two policies do not play a role in carbon emission restrictions. Therefore, for the government, the reasonable setting of the cap is very important, especially for the cap policy and cap offset policy. It is also observed that the trade policy can play a certain role in carbon emission reduction under this situation, in which carbon emissions are smaller than the other two, and the cost is the lowest.

In summary, each policy will show different characteristics with the change of cap. Accordingly, the government must scientifically and effectively select and formulate carbon emission policies according to emission targets and actual business conditions.

5.3.3. Carbon Price (Tax)

In model $\mathrm{M}\_cco$, $\mathrm{M}\_cct$, and $\mathrm{M}\_ct$, we change the carbon price (tax) from 0.5 to 5.5 CNY/Kg with step 0.5 and observe the changes in total costs and carbon emissions. In three models, the carbon cap is set as 750 Kg and other parameters’ values are unchanged, which is shown in Section 5.2. Figure 5 shows the results.

From Figure 5, the following findings and managerial insights can be observed:

(1)

Overall, as the carbon price increases, the total cost gradually increases, and the carbon emissions gradually decrease.

(2)

When compared to the cap offset policy and the cap trade policy, the carbon emission curve under the carbon tax policy is the lowest, but the cost curve is highest. Therefore, the carbon tax policy is the most significant mechanism for reducing emissions. However, it also brings the heaviest cost pressure on enterprises.

(3)

When the carbon price is low (between 0.5 and 1.5), the carbon emission curve and the cost curve of the cap offset policy and the cap trade policy are almost coincident, which means that the effects of the two policies are the same. As carbon prices increase (greater than 1.5), as compared to the cap offset policy, the carbon emission curve and cost curve under the cap trade policy are lower. Hence, overall, the cap trade policy is better than the cap offset policy.

(4)

It is also observed that, when carbon price greater than 4.5, the carbon emissions are basically unchanged. Therefore, we can conclude that higher carbon prices do not always have better environmental benefits. That is, the government should set a reasonable carbon price, so that the effectiveness of carbon emissions reduction is the best.

In summary, the carbon price can serve as leverage for controlling carbon emissions.

5.3.4. Unit Fuel Price

In traditional IRP, the parameter ‘fuel price’ impacts the carbon emissions due to the close relation between fuel consumptions and the carbon emissions from a previous paper [36]. However, in their study, the carbon emissions that were produced in the inventory process are not incorporated, which is really different from cold chain logistics. Therefore, in our study, the impacts of the fuel price on the carbon emissions of the cold chain IRP are essential to investigate. In the four models ($\mathrm{M}\_cc$, $\mathrm{M}\_cco$, $\mathrm{M}\_cct$, $\mathrm{M}\_ct$), we set different unit fuel price (from 5 to 12 CNY/L with step 1) to perform a series of sensitive analysis under four policies. Figure 6 shows the analysis results. The carbon price is set as 1 CNY/Kg and the carbon cap is 700 Kg. Other parameters’ values are unchanged, which is shown in Section 5.2.

From Figure 6, it can be seen that when unit fuel price increases, the total cost presents a continuing growth trend. However, carbon emissions basically keep an unchanged trend. We further analyze the relationship of carbon emission structure in order to investigate the reason for this phenomenon. We take model $\mathrm{M}\_cct$ as an example and further analyze the changing trends of carbon emissions that are generated in the transportation process and the inventory process under different unit fuel price. The result is shown in Figure 7. From Figure 7, we can see that the trends of emissions generated in the transportation and the inventory process are totally opposite. Although a larger unit fuel price will lead to a decrease in carbon emissions that are generated during transportation, the emissions generated during inventory are increasing with the increase of the inventory level, which eventually results in basically unchanged carbon emissions.

Cold chain IRP is different from traditional IRP, and an increase in unit fuel price does not result in changes in total carbon emissions, but result in increases in total cost (in traditional IRP, increase in unit fuel price usually lead to decrease in carbon emissions [35]).

As mentioned above, we can draw the conclusion that, in cold chain IRP, changes in fuel price cannot reduce the carbon emissions, but proper carbon policies can effectively curb the carbon emissions.

5.3.5. Discussion

This paper studied the cold chain inventory routing problem under four carbon regulations. First, the optimized cold chain IRP models were constructed and the impacts of these carbon regulations on the cold chain IRP were then analyzed. Through the experimental results, we observed how existing carbon emission regulations affect the carbon emissions and the total cost of the cold chain logistics enterprises. The key observations are concluded, as follows:

Observation 1: Carbon emission regulation does influence cold chain enterprises’ economic performance and carbon emissions. As the carbon cap decreases or the carbon price increases, the firm tends to reduce the carbon emissions by sacrificing some operational cost. However, the effectiveness of carbon emissions reduction under different carbon emissions regulations or with different settings of carbon cap or price is different.

Observation 2: Under carbon cap and carbon tax policy, the reduction of carbon emission can be significant through appropriate cap allocation and reasonably carbon price settings, respectively. However, there are still things that need to note: for carbon cap policy, the government should allocate appropriate cap to enterprise according to their actual productivity, and the cap should be at least greater than the minimum carbon emission limit of the enterprise. Otherwise, the carbon cap policy will be invalid. For carbon tax policy, the most important and critical link is that the government should set a reasonable carbon price, because the lower price may not lead to good emissions reduction effect while higher carbon prices do not always have better environmental benefits.

Observation 3: the carbon cap-and-trade policy is more efficient than the carbon offset policy. When the carbon cap is tight, the impact of these two regulations on the enterprises’ economic performance and carbon emissions is almost the same. However, when carbon cap is loose, the enterprise can sell unused carbon credits and achieve some profits, such as stronger motivation to reduce carbon emissions. The shapes of the graphs in Figure 5 support this.

Observation 4: unlike the traditional IRP, the increase of unit fuel price will not reduce the carbon emissions. Therefore, formulating a suitable carbon emission policy or regulation and putting it into practice can effectively control the carbon emissions of the cold chain logistics.

When compared with a previous study on traditional IRP, the observations for cold chain IRP are very new and interesting. Based on these, the corresponding suggestions for cold chain enterprises and government were also summarized in the previous section. Especially for the observation 4, the conclusion for cold chain IRP is different from the study of Cheng et al. [36] (traditional IRP), which shows that the characteristic of the cold chain needs to be emphasized when make some carbon reduction strategy.

6. Conclusions

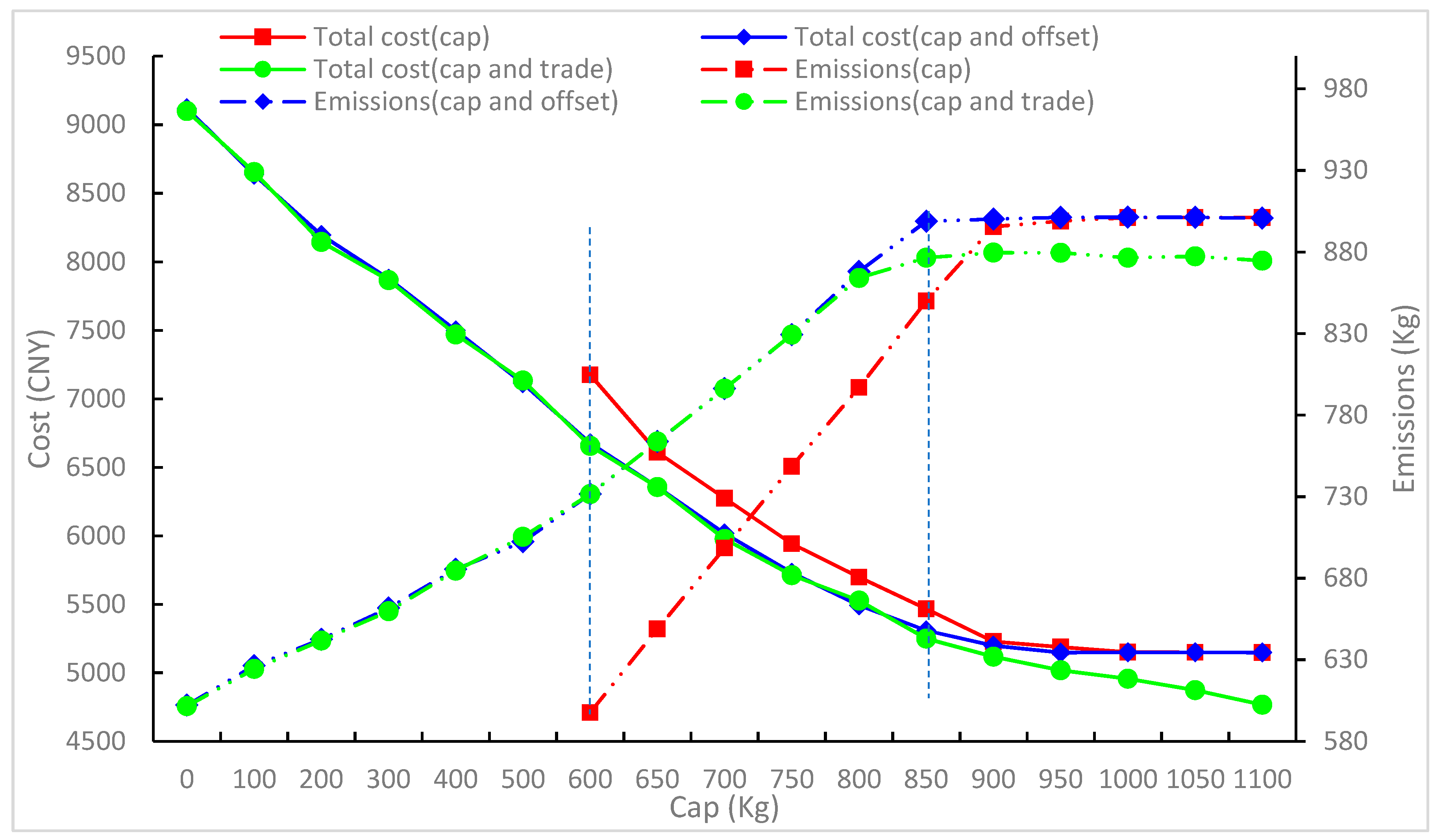
As people become increasingly concerned about environmental issues, many countries have enacted some policies to reduce carbon emissions. As a high emission industry, the cold chain logistics will eventually be affected by carbon emission regulations. However, in China, or even the world, the carbon emission regulation for the cold chain logistics industry is still in the discussion stage. Therefore, this paper focuses on the cold chain inventory routing optimization problem under carbon regulations and systematically analyzes the impacts of carbon emission regulations on cold chain logistics, to provide suggestions for the development of the cold chain enterprises and some valuable reference for government decision-making on carbon emission regulation development. Based on the four existing carbon emission regulations: carbon cap, carbon cap offset, carbon cap-and-trade, and carbon tax policy, four models for cold chain IRP, which jointly minimizes the operational cost, as well as the cost of carbon emissions are constructed. Different from traditional IRP, the cold chain IRP models in this paper comprehensively accounts for the carbon emissions not only produced by transportation sector but also inventory stage, which is not explicitly calculated in previous paper. The cold chain IRP also concerns the cargo damage and refrigeration factors, which makes the cold chain IRP models more complicated but important. Subsequently, a genetic simulated annealing algorithm (GASA) is developed to solve the problem. Through comparison experiments, the effectiveness and efficiency of the GASA was verified. Next, the models and the algorithm are used in an actual instance to carry out a series of sensitivity experiments to analyze the impacts of different carbon policies on the carbon emissions and the total cost. Some interesting phenomena are observed from the parameter sensitivity analyses under different policies. These insights can not only offer advice for companies to balance costs and environmental effects, but also suggest ideas for governments to employ suitable policies and establish reasonable carbon caps and prices.

The limitations of this paper and future work are as follows: this paper focuses on the inventory routing problem for cold chain logistics, without considering the customer satisfaction factor, which may influence the optimal scheme. Therefore, the further in-depth study on the inventory routing problem while considering customer satisfaction is needed.