Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter?
Abstract
:1. Introduction
2. Literature Review
3. Rural Pension System in China
4. Projection Models
4.1. Projection Models for Insured Population
4.2. Actuarial Models for Pension Sustainability
5. Scenarios and Data Assumptions
5.1. Total Fertility Rate Scenarios
5.2. Data Source and Assumption
6. Results Analysis
6.1. Situation 1 (Baseline Scenario): Retaining the One-Child Policy
6.2. Situation 2: Conducting the Two-Child Policy
6.3. Sensitivity Analysis
6.3.1. Parity-Specific Total Fertility Rate at First Birth
6.3.2. Contribution Rate
6.3.3. Retirement Age
6.3.4. Growth Rate of Pension Benefit
7. Conclusions
- The projection results indicate that the NRPP would be challenged by an increasing pension payment burden under the one-child policy. The occurrence of the current and accumulated pension deficits would happen in 2030 and 2042, respectively, which is also supported by previous research findings [9,55]. After that, the pension gap would expand yearly at a faster pace. The current and accumulated pension deficits would arrive at CNY 4.29 trillion and CNY 78.80 trillion at the end of the projection period.
- Fertility scenario analysis shows that a higher proportion of couples desiring to parent a second child would relieve more pension pressure despite a moderate policy effect and a time-lagged effect. This is similar to the conclusions in studies on the impacts of the fertility policy reform on China’s pension schemes for urban employees [6,33,56]. In addition, our simulations reveal the pension trend after the group of the second children retired in 2076 and indicates that the pension gap would be much enlarged thereafter. This outcome is rarely noticed within international academia to the best of our knowledge and deserves close attention by China’s policymakers in their future preparations.
- Sensitivity analysis reveals that, combined with the two-child policy, raising the contribution rate would offer the most help in promoting the sustainable development of the NRPP, compared to delaying retirement and lifting the parity-specific fertility rate at first birth. However, if the annual growth rate increased, the pension deficit would seriously deteriorate and occur 4–12 years earlier than in the baseline scenario. This adverse impact on pension sustainability is far from being offset by the positive effect of the demographic policy reform. Sustainability and adequacy are two sides of the same coin [36,57,58]. However, our sensitivity simulation results indicate that the government chose the former rather than the latter.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A




References
- European Commission. Available online: https://ec.europa.eu/social/main.jsp?langId=en&catId=89&newsId=1194&furtherNews=yes (accessed on 31 July 2019).
- Meier, V.; Werding, M. Ageing and the Welfare State: Securing Sustainability; CESifo Working Paper No.2916; Center for Economic Studies and Ifo Institute: Munich, Germany, 2010. [Google Scholar]
- Barr, N. International Trends in Pension Provision. Account. Bus. Res. 2009, 39, 17–38. [Google Scholar] [CrossRef]
- Alonso-García, J.; Boado-Penas, M.D.C.; Devolder, P. Adequacy, Fairness and Sustainability of Pay-As-You-Go-Pension-Systems: Defined Benefit versus Defined Contribution. Eur. J. Financ. 2018, 24, 1100–1122. [Google Scholar] [CrossRef]
- Zheng, B. China Pension Report 2016, 1st ed.; Economic & Management Press: Beijing, China, 2016; pp. 48–64. ISBN 9787509647141. (In Chinese) [Google Scholar]
- Wang, H.; Huang, J.; Yang, Q. Assessing the Financial Sustainability of the Pension Plan in China: The Role of Fertility Policy Adjustment and Retirement Delay. Sustainability 2019, 11, 883. [Google Scholar] [CrossRef]
- Zhao, Y.; Bai, M.; Feng, P.; Zhu, M. Stochastic Assessments of Urban Employees’ Pension Plan of China. Sustainability 2018, 10, 1028. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, X. Stochastic Forecast of the Financial Sustainability of Basic Pension in China. Sustainability 2016, 8, 46. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, X.; Liu, L. From “Selective Two-Child Policy” to “Universal Two-Child Policy”: Will the Payment Crisis of China’s Pension System be Solved? China Financ. Econ. Rev. 2017, 5, 14. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. Available online: http://www.stats.gov.cn/ (accessed on 20 January 2019).
- National Bureau of Statistics of China. Available online: http://www.stats.gov.cn/tjsj/ndsj/2016/indexch.htm (accessed on 20 January 2019).
- Guo, Y. Pension Policy Reforms in China from 2009 to 2012. China J. Soc. Work 2014, 7, 237–246. [Google Scholar] [CrossRef]
- Shen, C.; Williamson, J.B. China’s New Rural Pension Scheme: Can It Be Improved? Int. J. Sociol. Soc. Policy 2010, 30, 239–250. [Google Scholar] [CrossRef]
- Zeng, Y.; Hesketh, T. The Effects of China’s Universal Two-Child Policy. Lancet 2016, 388, 1930–1938. [Google Scholar] [CrossRef]
- Kitao, S. Fiscal Cost of Demographic Transition in Japan. J. Econ. Dyn. Control 2015, 54, 37–58. [Google Scholar] [CrossRef]
- Godínez-Olivares, H.; Boado-Penas, M.D.C.; Haberman, S. Optimal Strategies for Pay-As-You-Go Pension Finance: A Sustainability Framework. Insur. Math. Econ. 2016, 69, 117–126. [Google Scholar] [CrossRef]
- Castro, G.; Maria, J.R.; Félix, R.M.; Braz, C.R. Aging and Fiscal Sustainability in a Small Euro Area Economy. Macroecon. Dyn. 2017, 21, 1673–1705. [Google Scholar] [CrossRef]
- Lin, B.; Lin, Z.; Zhang, Y.Y.; Liu, W. The Impact of the New Rural Pension Scheme on Retirement Sustainability in China: Evidence of Regional Differences in Formal and Informal Labor Supply. Sustainability 2018, 10, 4366. [Google Scholar] [CrossRef]
- Bongaarts, J. Population Aging and the Rising Cost of Public Pensions. Popul. Dev. Rev. 2004, 30, 1–23. [Google Scholar] [CrossRef]
- Blake, D.; Mayhew, L. On the Sustainability of the UK Pension System in the Light of Population Ageing and Declining Fertility. Procedia Soc. Behav. Sci. 2015, 183, 77–84. [Google Scholar] [CrossRef]
- Stauvermann, P.J.; Kumar, R.R. Sustainability of a pay-as-you-go pension system in a small open economy with ageing, human capital and endogenous fertility. Metroeconomica 2016, 67, 2–20. [Google Scholar] [CrossRef]
- Fanti, L.; Gori, L. Fertility and PAYG Pensions in the Overlapping Generations Model. J. Popul. Econ. 2012, 25, 955–961. [Google Scholar] [CrossRef]
- Stauvermann, P.J.; Kumar, R.R. Demographic Change, PAYG Pensions and Child Policies. J. Pension Econ. Financ. 2018, 17, 469–487. [Google Scholar] [CrossRef]
- Chłoń-Domińczak, A.; Franco, D.; Palmer, E. The First Wave of NDC Reforms: The Experiences of Italy, Latvia, Poland, and Sweden. In Nonfinancial Defined Contribution Pension Schemes in a Changing Pension World; Holzmann, R., Palmer, E., Robalino, D., Eds.; The World Bank: Washington, DC, USA, 2012; pp. 31–85. [Google Scholar]
- Lisenkova, K.; Bornukova, K. Effects of Population Ageing on the Pension System in Belarus. Balt. J. Econ. 2017, 17, 103–118. [Google Scholar] [CrossRef]
- Grech, A.G. What Makes Pension Reforms Sustainable? Sustainability 2018, 10, 2891. [Google Scholar] [CrossRef]
- Moizer, J.; Farrar, S.; Hyde, M. UK State Pension Deferral Incentives and Sustainability. Appl. Econ. 2017, 50, 2356–2368. [Google Scholar] [CrossRef]
- Auerbach, A.J.; Lee, R. Welfare and Generational Equity in Sustainable Unfunded Pension Systems. J. Public Econ. 2011, 95, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Alonso-García, J.; Devolder, P. Optimal Mix Between Pay-As-You-Go and Funding for DC Pension Schemes in an Overlapping Generations Model. Insur. Math. Econ. 2016, 70, 224–236. [Google Scholar] [CrossRef]
- Vidal-Meliá, C.; Ventura-Marco, M.; González, J.M.P.S. Social Insurance Accounting for a Notional Defined Contribution Scheme Combining Retirement and Long-Term Care Benefits. Sustainability 2018, 10, 2832. [Google Scholar] [CrossRef]
- Meneu Gaya, R.; Devesa Carpio, J.E.; Domínguez Fabián, I.; Encinas Goenechea, B.; Alonso Fernández, J.J. The Effects of Recent Spanish Pension Reforms on Sustainability and Pension Adequacy. Appl. Econ. 2018, 50, 2459–2468. [Google Scholar] [CrossRef]
- Coeurdacier, N.; Guibaud, S.; Jin, K. Fertility Policies and Social Security Reforms in China. IMF Econ. Rev. 2014, 62, 371–408. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Zhang, R. Assessing the Impact of Liberalising the One-Child Policy on the Sustainability of China’s Pension System. China J. Soc. Work 2017, 10, 98–119. [Google Scholar] [CrossRef]
- Williamson, J.B.; Fang, L.; Calvo, E. Rural Pension Reform in China: A Critical Analysis. J. Aging Stud. 2017, 41, 67–74. [Google Scholar] [CrossRef]
- Wang, L.; Béland, D. Assessing the Financial Sustainability of China’s Rural Pension System. Sustainability 2014, 6, 3271–3290. [Google Scholar] [CrossRef]
- Salditt, F.; Whiteford, P.; Adema, W. Pension Reform in China. Int. Soc. Secur. Rev. 2008, 61, 47–71. [Google Scholar] [CrossRef]
- Farid, M.; Cozzarin, B.P. China’s Pension Reform: Challenges and Opportunities. Pensions 2009, 14, 181–190. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Research on Fairness of Endowment Insurance System, 1st ed.; Jiangsu People’s Publishing, LTD: Nanjing, China, 2016; pp. 110–114. ISBN 978-7-214-17384-3. (In Chinese) [Google Scholar]
- The Central People’s Government of the People’s Republic of China. Available online: http://www.gov.cn/zwgk/2009-09/04/content_1409216.htm (accessed on 15 May 2019).
- The Central People’s Government of the People’s Republic of China. Available online: http://www.gov.cn/zwgk/2014-02/26/content_2621907.htm (accessed on 15 May 2019).
- Smith, S.K. Accounting for Migration in Cohort-Component Projections of State and Local Populations. Demography 1986, 23, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Land, K.C.; Wang, Z.; Gu, D. Household and Living Arrangement Projections at the Subnational Level: An Extended Cohort-Component Approach. Demography 2013, 50, 827–852. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Chen, N.; Zheng, Q. Evaluation on the Effect of Childbearing Policy Adjuestments in China. Chin. J. Popul. Sci. 2018, 38, 114–125. (In Chinese) [Google Scholar]
- Guo, Z.; Gietel-Basten, S.; Gu, B. The Lowest Fertility Rates in the World? Evidence from the 2015 Chinese 1% Sample Census. China Popul. Dev. Stud. 2018, 2, 1–14. [Google Scholar] [CrossRef]
- Chen, W.; Duan, Y. Recent Levels and Trends of Fertility in China. Popul. Res. 2019, 43, 3–17. (In Chinese) [Google Scholar]
- Lowe, C.R.; McKeown, T. Sex Ratio at Birth. Br. Med. J. 1953, 4831, 339. [Google Scholar] [CrossRef]
- State Council of China. Available online: http://www.gov.cn/zhengce/content/2017-01/25/content_5163309.htm (accessed on 25 October 2018).
- National Bureau of Statistics of China. Available online: http://www.stats.gov.cn/tjsj/ndsj/ (accessed on 2 August 2019).
- Migrant Population Service Center of China’s National Health Commission. Available online: http://www.chinaldrk.org.cn/wjw/#/home (accessed on 2 August 2019).
- Ministry of Human Resources and Social Security of China. Available online: http://www.mohrss.gov.cn/ (accessed on 20 May 2019).
- Ministry of Human Resources and Social Security of People’s Republic of China. Available online: http://www.mohrss.gov.cn/gkml/zcfg/gfxwj/201803/t20180329_291008.html (accessed on 20 May 2019).
- Zhao, Y.; Bai, M.; Liu, Y.; Hao, J. Quantitative Analyses of Transition Pension Liabilities and Solvency Sustainability in China. Sustainability 2017, 9, 2252. [Google Scholar] [CrossRef]
- Fang, L. A Research on the Introduction of a Sustainable Mechanism for Basic Pension Benefit Indexation in China: Lessons from International Cases. Popul. J. 2018, 40, 66–77. (In Chinese) [Google Scholar]
- Calvo, E.; Williamson, J.B. Old-Age Pension Reform and Modernization Pathways: Lessons for China from Latin America. J. Aging Stud. 2008, 22, 74–87. [Google Scholar] [CrossRef] [PubMed]
- Jing, P.; Chen, M.; Hu, Q. The Moderate Benefit and Fiscal Burden of Basic Pension Insurance for Urban and Rural Residents. Public Financ. Res. 2018, 39, 66–78. (In Chinese) [Google Scholar]
- Zeng, Y.; Ling, Y.; Zhang, X. From Selective Two-Child Policy to Universal Two-Child Policy: Can the Sustainability of China’s Basic Pension Insurance Fund for Urban and Rural Residents Be Improved? Public Financ. Res. 2019, 40, 65–79. (In Chinese) [Google Scholar]
- Liu, T.; Sun, L. Pension Reform in China. J. Aging Soc. Policy 2016, 28, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Hu, N.; Yang, Y. The Real Old-Age Dependency Ratio and the Inadequacy of Public Pension Finance in China. J. Popul. Ageing 2012, 5, 193–209. [Google Scholar] [CrossRef]
- Cipriani, G.P.; Pascucci, F. Pension Policies in a Model with Endogenous Fertility. J. Pension Econ. Financ. 2018, 17, 1–17. [Google Scholar] [CrossRef]
- Lugauer, S.; Ni, J.; Yin, Z. Chinese Household Saving and Dependent Children: Theory and Evidence. China Econ. Rev. 2017, 101091. [Google Scholar] [CrossRef]
- Curtis, C.C.; Lugauer, S.; Mark, N.C. Demographics and Aggregate Household Saving in Japan, China, and India. J. Macroecon. 2017, 51, 175–191. [Google Scholar] [CrossRef]
- Curtis, C.; Lugauer, S.; Mark, N.; Curtis, C.C.; Mark, N.C. Demographic Patterns and Household Saving in China. Am. Econ. J. Macroecon. 2015, 7, 58–94. [Google Scholar] [CrossRef]
- Zhao, Q.; Mi, H. Evaluation on the Sustainability of Urban Public Pension System in China. Sustainability 2019, 11, 1418. [Google Scholar] [CrossRef]

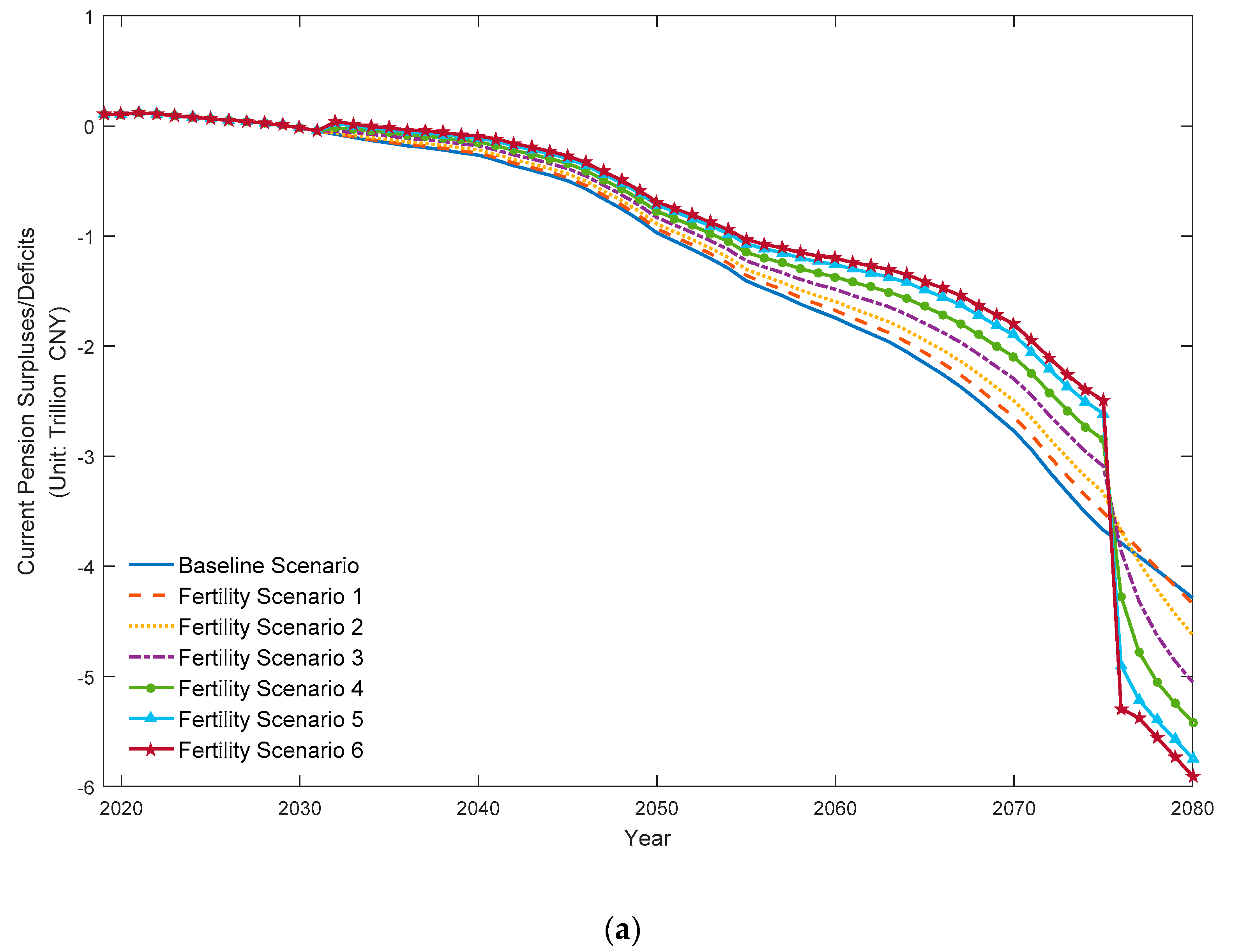

| Year | Pension Income | Pension Expenditure | Current Pension Surplus/Deficit | Accumulated Pension Surplus/Deficit |
|---|---|---|---|---|
| 2019 | 0.43 | 0.33 | 0.10 | 0.85 |
| 2020 | 0.44 | 0.34 | 0.11 | 0.97 |
| 2025 | 0.56 | 0.49 | 0.07 | 1.52 |
| 2030 | 0.70 | 0.71 | −0.02 | 1.75 |
| 2035 | 0.82 | 0.97 | −0.16 | 1.37 |
| 2040 | 0.98 | 1.25 | −0.27 | 0.34 |
| 2042 | 1.03 | 1.39 | −0.36 | −0.33 |
| 2045 | 1.11 | 1.61 | −0.50 | −1.67 |
| 2050 | 1.19 | 2.16 | −0.97 | −5.48 |
| 2055 | 1.32 | 2.73 | −1.41 | −11.55 |
| 2060 | 1.52 | 3.27 | −1.74 | −19.61 |
| 2065 | 1.74 | 3.89 | −2.15 | −29.49 |
| 2070 | 1.93 | 4.70 | −2.77 | −42.02 |
| 2075 | 2.06 | 5.73 | −3.67 | −58.62 |
| 2080 | 2.33 | 6.61 | −4.29 | −78.80 |
| Year | Baseline Scenario (Trillion CNY) | Fertility Scenarios (%) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 2032 | −0.07 | 3.50 | 14.01 | 38.92 | 76.29 | 83.14 | 91.53 |
| 2035 | −0.16 | 6.10 | 19.47 | 40.34 | 60.22 | 78.63 | 87.66 |
| 2040 | −0.27 | 7.19 | 18.28 | 32.21 | 45.57 | 58.85 | 65.49 |
| 2045 | −0.50 | 5.65 | 13.03 | 22.44 | 31.74 | 41.00 | 45.62 |
| 2050 | −0.97 | 3.85 | 8.40 | 14.32 | 20.24 | 26.15 | 29.12 |
| 2055 | −1.41 | 3.48 | 7.51 | 12.92 | 18.39 | 23.89 | 26.64 |
| 2060 | −1.74 | 3.87 | 8.50 | 14.88 | 21.33 | 27.79 | 31.03 |
| 2065 | −2.15 | 4.36 | 9.62 | 16.72 | 23.80 | 30.84 | 34.35 |
| 2070 | −2.77 | 4.57 | 9.95 | 17.13 | 24.31 | 31.50 | 35.10 |
| 2075 | −3.67 | 4.41 | 9.33 | 15.82 | 22.30 | 28.81 | 32.07 |
| 2080 | −4.29 | −1.21 | −7.92 | −17.86 | −26.35 | −34.01 | −37.78 |
| Year | Baseline Scenario (Trillion CNY) | Fertility Scenarios (%) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 2042 | −0.33 | 46.80 | -- | -- | -- | -- | -- |
| 2043 | −0.73 | 24.33 | 66.57 | -- | -- | -- | -- |
| 2044 | −0.73 | 17.31 | 46.50 | 87.99 | -- | -- | -- |
| 2045 | −1.18 | 13.84 | 36.53 | 68.47 | -- | -- | -- |
| 2046 | −1.67 | 11.67 | 30.30 | 56.32 | 82.80 | -- | -- |
| 2047 | −2.24 | 10.11 | 25.87 | 47.71 | 69.90 | 92.53 | -- |
| 2048 | −2.90 | 8.95 | 22.60 | 41.42 | 60.49 | 79.91 | 89.75 |
| 2050 | −5.48 | 7.30 | 17.99 | 32.59 | 47.36 | 62.37 | 69.95 |
| 2055 | −11.55 | 5.37 | 12.64 | 22.50 | 32.44 | 42.51 | 47.59 |
| 2060 | −19.61 | 4.68 | 10.75 | 19.00 | 27.34 | 35.76 | 39.99 |
| 2065 | −29.49 | 4.51 | 10.25 | 18.04 | 25.90 | 33.80 | 37.77 |
| 2070 | −42.02 | 4.51 | 10.13 | 17.74 | 25.38 | 33.06 | 36.91 |
| 2075 | −58.62 | 4.49 | 9.95 | 17.28 | 24.62 | 31.97 | 35.66 |
| 2080 | −78.80 | 3.49 | 6.49 | 9.63 | 12.50 | 15.35 | 16.78 |
| Year | Baseline Scenario | Fertility Scenarios | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||||||
| ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | ⑪ | ⑫ | ⑬ | ⑭ | |
| 2030 | √ | √ | √ | √ | √ | √ | √ | |||||||
| 2042 | √ | √ | ||||||||||||
| 2043 | √ | |||||||||||||
| 2044 | √ | |||||||||||||
| 2046 | √ | |||||||||||||
| 2047 | √ | |||||||||||||
| 2048 | √ | |||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, J.; Sun, S. Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter? Sustainability 2019, 11, 5110. https://doi.org/10.3390/su11185110
Wang H, Huang J, Sun S. Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter? Sustainability. 2019; 11(18):5110. https://doi.org/10.3390/su11185110
Chicago/Turabian StyleWang, Huan, Jianyuan Huang, and Shuangyue Sun. 2019. "Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter?" Sustainability 11, no. 18: 5110. https://doi.org/10.3390/su11185110
APA StyleWang, H., Huang, J., & Sun, S. (2019). Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter? Sustainability, 11(18), 5110. https://doi.org/10.3390/su11185110




