Experimental Research on Deformation Characteristics of Using Silty Clay Modified by Oil Shale Ash and Fly Ash as the Subgrade Material after Freeze-Thaw Cycles
Abstract
:1. Introduction
2. Materials
2.1. Raw Materials
2.2. Preparation of Mixed Samples and Testing Samples
3. Methods of Testing
3.1. Testing Scheme
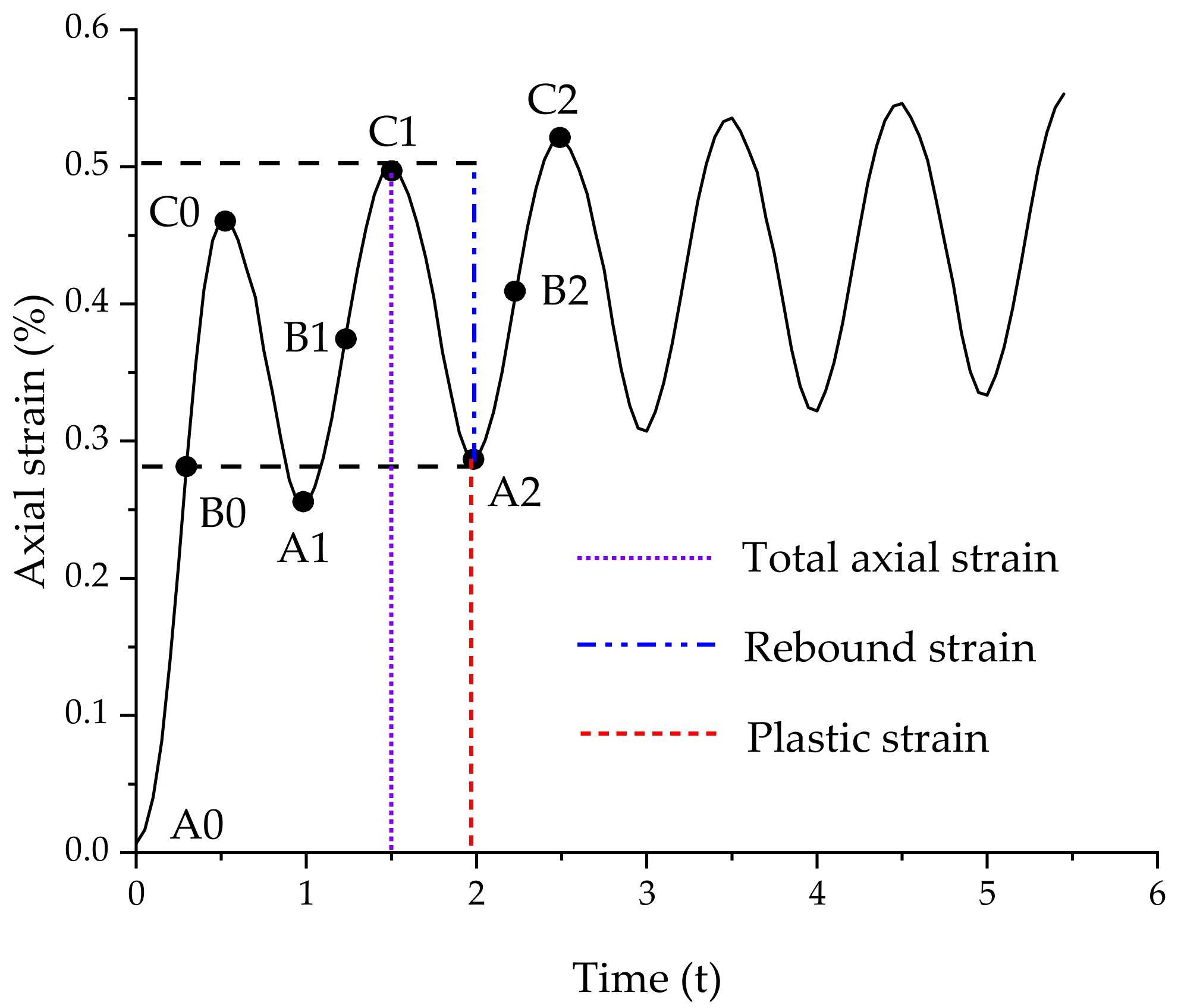
3.2. Data Extraction Criterion
3.3. Failure Criterion
4. Results and Discussion
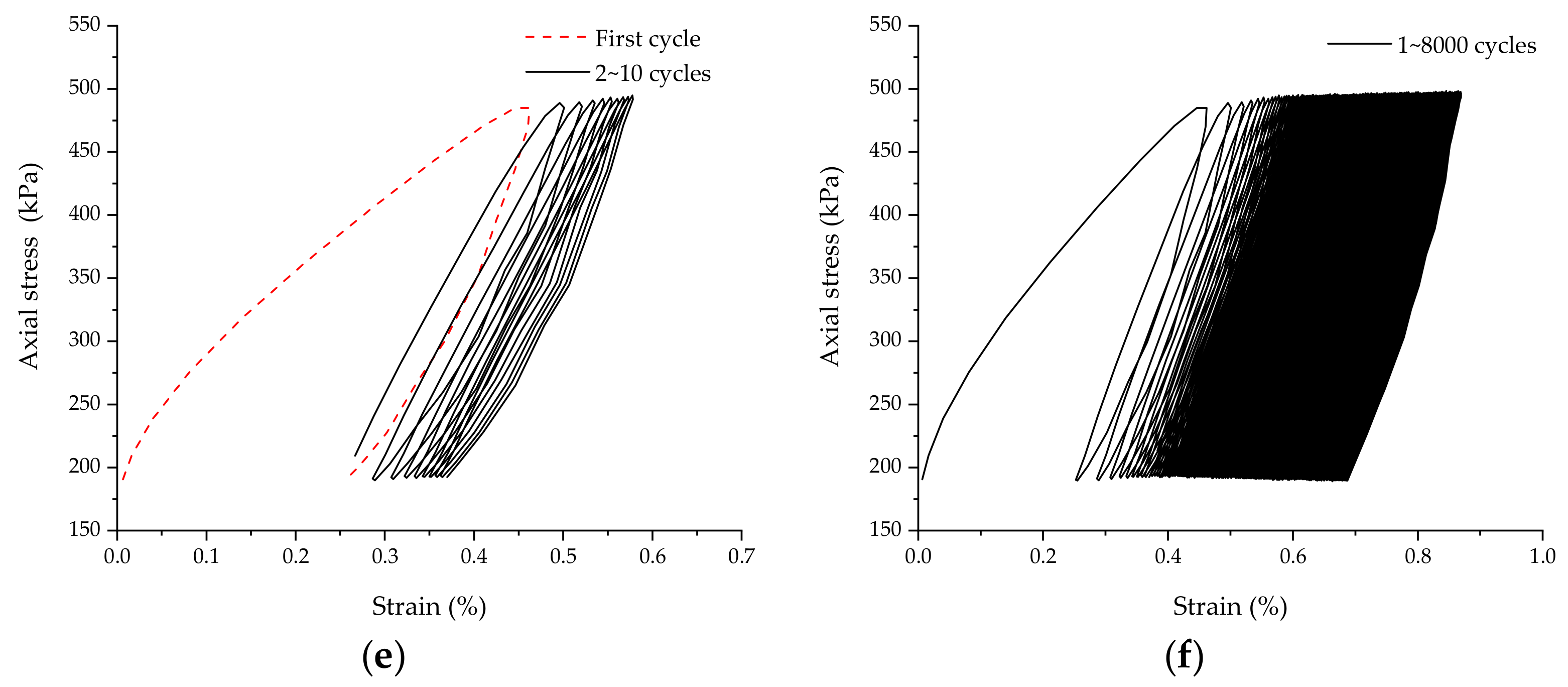
4.1. Shake-Down Analysis on Deformation of MSC
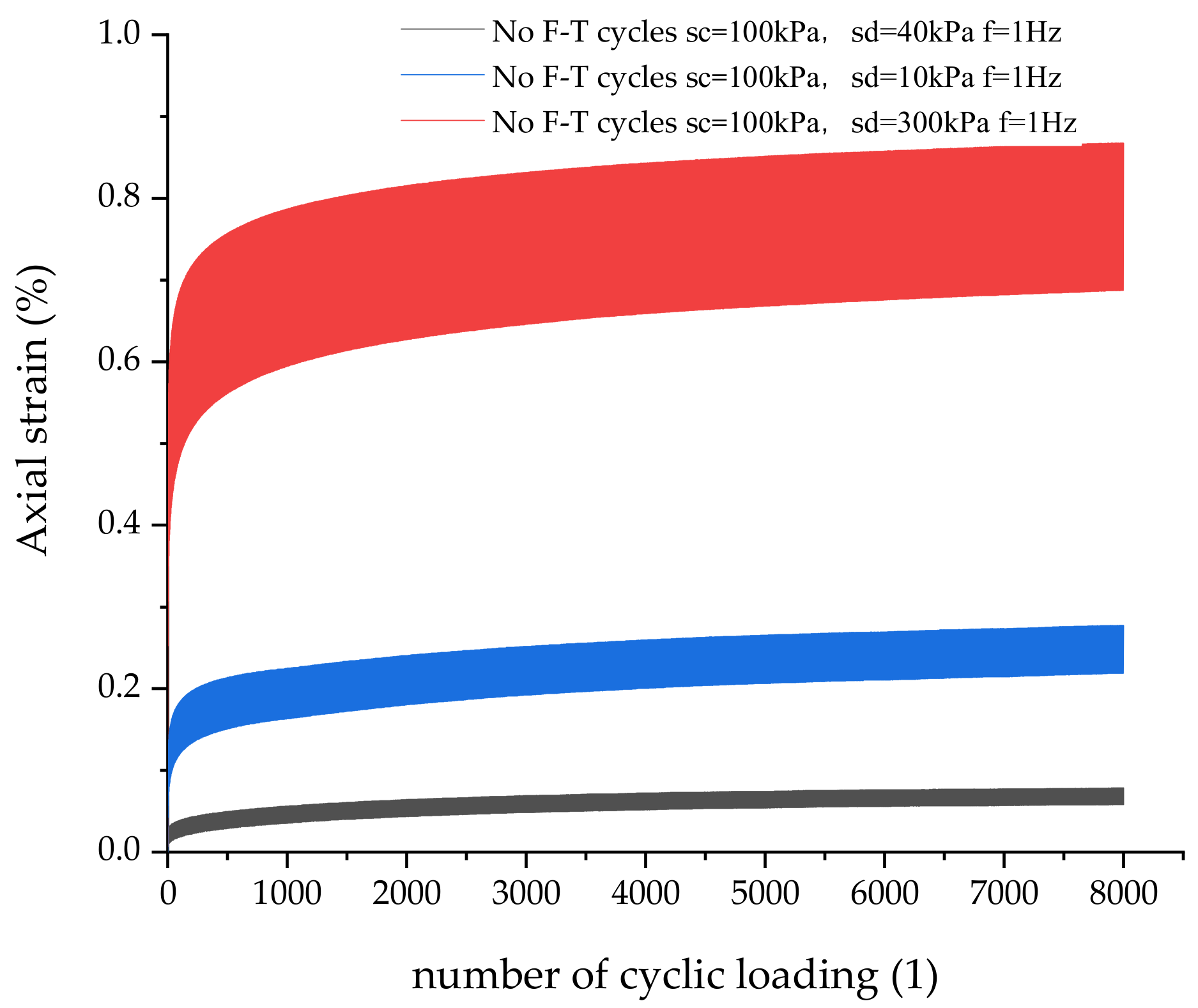
4.2. Axial Strain Characteristics of MSC Undergoing 0~8000 Cycle Loads
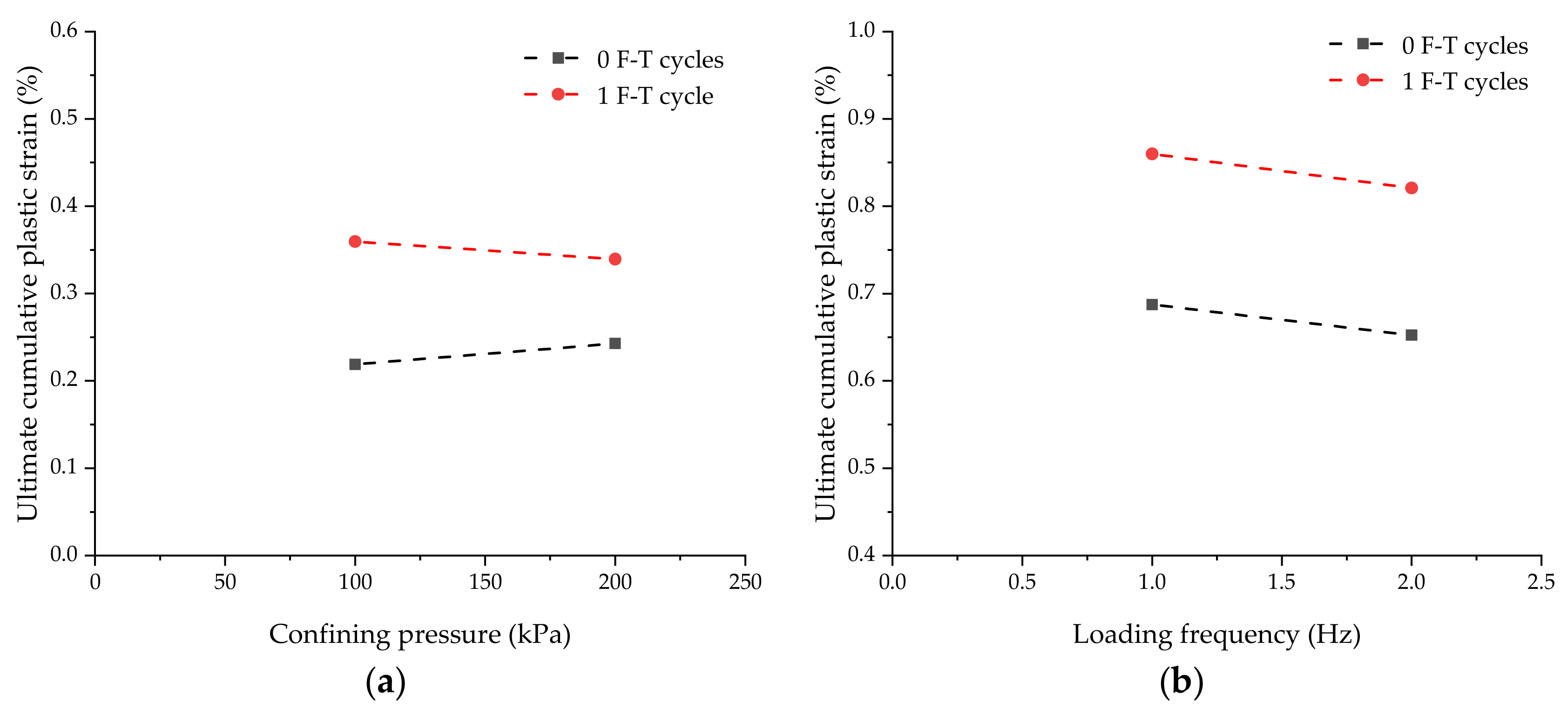
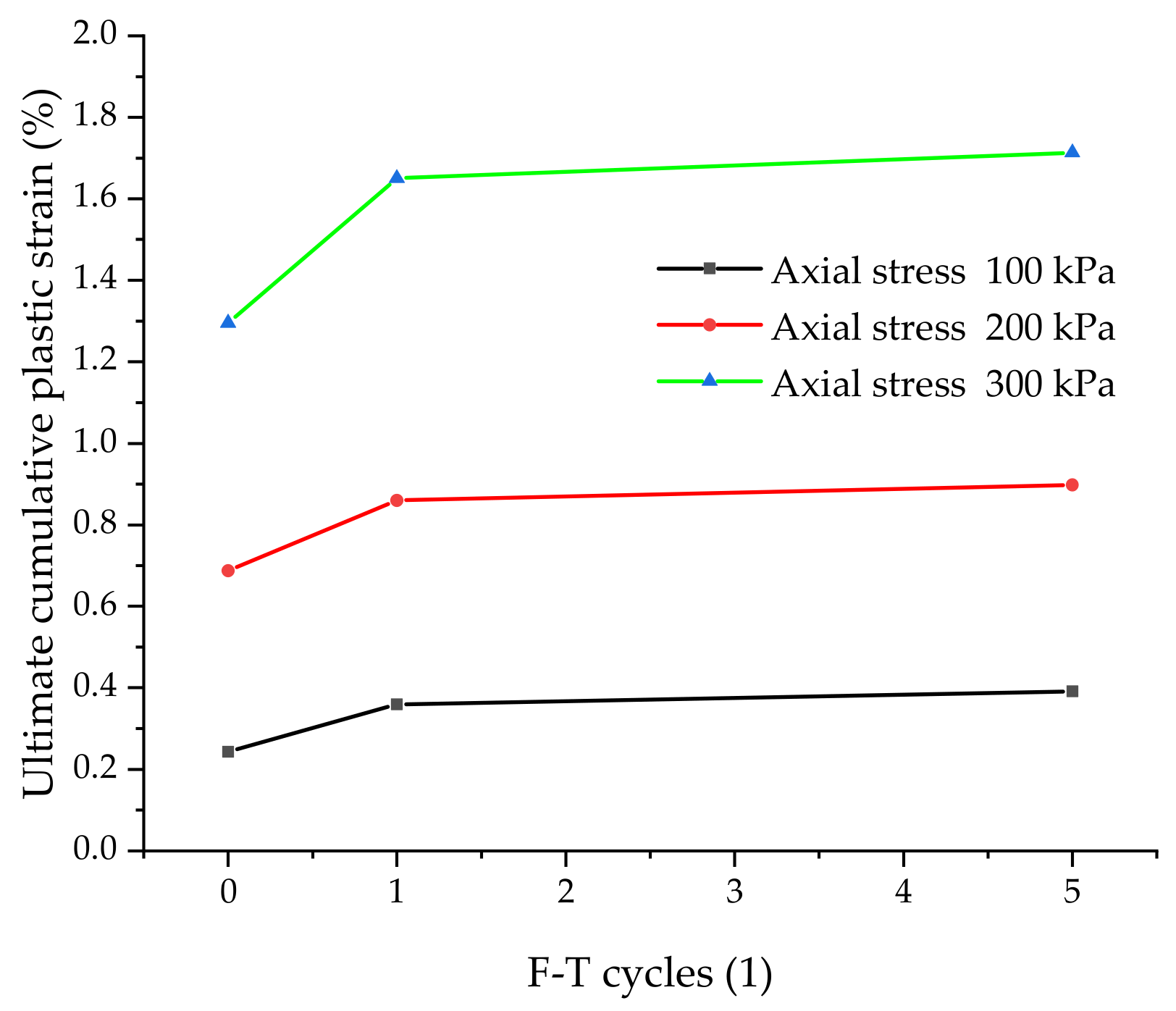
4.3. Plastic Strain Characteristics of MSC after 8000 Cyclic Loads
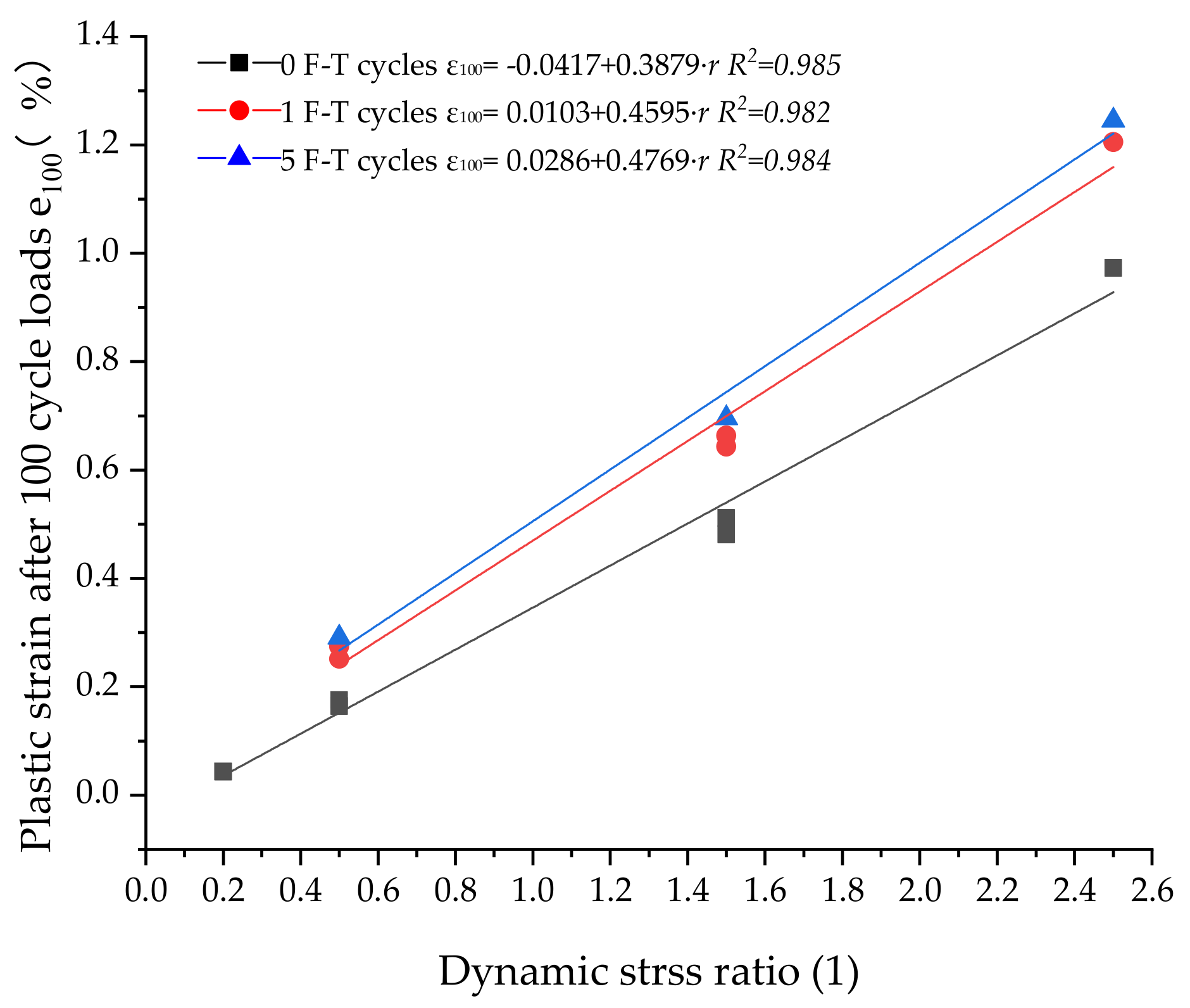
4.4. Prediction Model on the Cumulative Plastic Strain of MSC
4.4.1. Normalized Prediction Model
4.4.2. Logarithmic Prediction Model
4.5. Predict the Value of Cumulative Plastic Strain after a Large Number of Cycle Loads (10 Million Times)
5. Conclusions
- (1)
- As the number of cycle loads increases, the axial strain of MSC begins to increase rapidly, then slowly, and finally tends to be stable. The stress–strain curve of MSC conforms to the shake-down theory of materials. The cumulative plastic strain of MSC after 100 cycle loads occupies for 70.87%~78.39% of that after 8000 cycle loads, indicating that MSC possesses remarkable plastic stability after 100 cycles of cycle loads.
- (2)
- The larger the stress ratio, the larger the axial strain value of MSC under the same number of cycle loads. Under the same low stress ratio, increasing confining pressure and loading frequency have insignificant effect on the cumulative plastic strain of MSC after 8000 loads. The F-T cycles can increase the deformation sensitivity of MSC. Moreover, before and after F-T cycles, the outcomes of dynamic stress ratio and confining pressure operate on MSC are the same.
- (3)
- For the logarithmic prediction model, when the dynamic stress ratio is high (in this study, it is 1.5 and 2.5), there is a linear relationship between the cumulative plastic strain and piecewise function of load number, and the proposed prediction model has a high correlation coefficient with the testing data.
- (4)
Author Contributions
Funding
Conflicts of Interest
References
- Dyni, J.R. Geology and resources of some world oil-shale deposits. Oil Shale 2003, 20, 81–92. [Google Scholar]
- Hou, J.; Ma, Y.; Li, S.; Teng, J. Development and utilization of oil shale worldwide. Chem. Ind. Eng. Prog. 2015, 34, 1183–1190. [Google Scholar]
- Väli, E.; Valgma, I.; Reinsalu, E. Usage of Estonian oil shale. Oil Shale 2008, 25, 101–114. [Google Scholar] [CrossRef]
- Raukas, A.; Punning, J.M. Environmental problems in the Estonian oil shale industry. Energy Environ. Sci. 2009, 2, 723–728. [Google Scholar] [CrossRef]
- Kallemets, K. Economic sustainability of Estonian shale oil industry until 2030. Oil shale 2016, 33, 272. [Google Scholar] [CrossRef]
- Xia, H.; Huang, J.; Kong, G. Ecological restoration of oil shale waste dumps. Acta Ecol. Sin. 2004, 24, 2887–2893. [Google Scholar]
- Haddad, R.H.; Ashteyat, A.M.; Lababneh, Z.K. Producing geopolymer composites using oil shale ash. Struct. Concr. 2019, 20, 225–235. [Google Scholar] [CrossRef]
- Ashteyat, A.M.; Haddad, R.H.; Yamin, M.M. Production of self-compacting concrete using Jordanian oil shale ash. Jordan J. Civ. Eng. 2012, 159, 1–13. [Google Scholar]
- Sharo, A.A.; Ashteyat, A.M.; Alawneh, A.S.; Bany Khaled, B.A. The use of oil shale fly ash to improve the properties of Irbid soil. World J. Eng. 2018, 15, 614–625. [Google Scholar] [CrossRef]
- Turner, J.P. Soil Stabilization Using Oil-Shale Solid Waste. J. Geotech. Eng. 1994, 120, 646–660. [Google Scholar] [CrossRef]
- Mymrin, V.A.; Ponte, H.A. Oil-shale fly ash utilization as independent binder of natural clayey soils for road and airfield base construction. Part. Sci. Technol. 2005, 23, 99–107. [Google Scholar] [CrossRef]
- US EPA. Using Coal Ash in Highway Construction: A Guide to Benefits and Impacts; US EPA: Washington, DC, USA, 2005.
- Benassi, L.; Dalipi, R.; Consigli, V.; Pasquali, M.; Borgese, L.; Depero, L.E.; Clegg, F.; Bingham, P.A.; Bontempi, E. Integrated management of ash from industrial and domestic combustion: A new sustainable approach for reducing greenhouse gas emissions from energy conversion. Environ. Sci. Pollut. Res. 2017, 24, 14834–14846. [Google Scholar] [CrossRef] [PubMed]
- Rosone, M.; Celauro, C.; Ferrari, A. Microstructure and shear strength evolution of a lime-treated clay for use in road construction. Int. J. Pavement Eng. 2018, 1–12. [Google Scholar] [CrossRef]
- Di Sante, M.; Fratalocchi, E.; Mazzieri, F.; Brianzoni, V. Influence of delayed compaction on the compressibility and hydraulic conductivity of soil–lime mixtures. Eng. Geol. 2015, 185, 131–138. [Google Scholar] [CrossRef]
- Tastan, E.O.; Edil, T.B.; Benson, C.H.; Aydilek, A.H. Stabilization of organic soils with fly ash. J. Geotech. Geoenvironmental Eng. 2011, 137, 819–833. [Google Scholar] [CrossRef]
- Athanasopoulou, A. Addition of lime and fly ash to improve highway subgrade soils. J. Mater. Civ. Eng. 2013, 26, 773–775. [Google Scholar] [CrossRef]
- Saravanan, R.; Thomas, R.S.; Joseph, M. A study on soil stabilization of clay soil using fly ash. Int. J. Res. Civ. Eng. Archit. Des. 2013, 1, 33–37. [Google Scholar]
- Prabakar, J.; Dendorkar, N.; Morchhale, R. Influence of fly ash on strength behavior of typical soils. Constr. Build. Mater. 2004, 18, 263–267. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Wang, F.; Che, G.; Li, Q. Experimental Research on Resilient Modulus of Silty Clay Modified by Oil Shale Ash and Fly Ash after Freeze-Thaw Cycles. Appl. Sci. 2018, 8, 1298. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Cui, J.; Han, L.; Li, Z. Engineering and environmental evaluation of silty clay modified by waste fly ash and oil shale ash as a road subgrade material. Constr. Build. Mater. 2019, 196, 204–213. [Google Scholar] [CrossRef]
- Li, Q.L.; Wei, H.B.; Han, L.L.; Wang, F.Y.; Zhang, Y.P.; Han, S.Y. Feasibility of Using Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability 2019, 11, 804. [Google Scholar] [CrossRef]
- Li, Q.; Wei, H.; Zhou, P.; Zhang, Y.; Han, L.; Han, S. Experimental and Numerical Research on Utilizing Modified Silty Clay and Extruded Polystyrene (XPS) Board as the Subgrade Thermal Insulation Layer in a Seasonally Frozen Region, Northeast China. Sustainability 2019, 11, 3495. [Google Scholar] [CrossRef]
- Liu, Z.G.; Xu, F.M.; Cao, G.B. Study on cement concrete pavement treatment methods of common damage diseases. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2015; pp. 307–309. [Google Scholar]
- Li, J.P.; Sheng, Y.; Zhang, J. Study on diseases of cement concrete pavement in permafrost regions. Cold Reg. Sci. Technol. 2010, 60, 57–62. [Google Scholar] [CrossRef]
- Ministry of Housing Urban-Rural Development of Republic of China. Technical Code for Application of Fly Ash Concrete; China Planning Press: Beijing, China, 2014.
- Kuila, U.; Prasad, M. Specific surface area and pore-size distribution in clays and shales. Geophys. Prospect. 2013, 61, 341–362. [Google Scholar] [CrossRef]
- Rhee, I.; Kim, Y.A.; Shin, G.O.; Ji, H.K.; Muramatsu, H. Compressive strength sensitivity of cement mortar using rice husk-derived graphene with a high specific surface area. Constr. Build. Mater. 2015, 96, 189–197. [Google Scholar] [CrossRef]
- Cui, J.H. Research on Stability of Subgrade Soil Modified by Oil Shale Waste Residue and Fly Ash; Jilin University: Changchun, China, 2018. [Google Scholar]
- Ministry of Water Resources of China. Rules of Geotechnical Testing. In SL 237-1999; Ministry of Water Resources of China: Beijing, China, 1999. [Google Scholar]
- Zhao, Y. Mechanical Properties of Plain Soils and Improvwed Soils Subjected to Heavy-Haul Train Load; Harbin Institute of Technology: Beijing, China, 2017. [Google Scholar]
- Rosone, M.; Farulla, C.A.; Ferrari, A. Shear strength of a compacted scaly clay in variable saturation conditions. Acta Geotech. 2016, 11, 37–50. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, Q.; Guo, L.; Juang, C.H.; Wang, J. Permanent deformation characteristics of saturated sand under cyclic loading. Can. Geotech. J. 2014, 52, 795–807. [Google Scholar] [CrossRef]
- Martin, J.B. Plasticity: Fundamentals and General Results; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Jardine, R.; Potts, D.; Fourie, A.; Burland, J. Studies of the influence of non-linear stress–strain characteristics in soil–structure interaction. Geotechnique 1986, 36, 377–396. [Google Scholar] [CrossRef]
- Xu, X.; Lai, Y.; Dong, Y.; Qi, J. Laboratory investigation on strength and deformation characteristics of ice-saturated frozen sandy soil. Cold Reg. Sci. Technol. 2011, 69, 98–104. [Google Scholar] [CrossRef]
- Li, L.L.; Dan, H.B.; Wang, L.Z. Undrained behavior of natural marine clay under cyclic loading. Ocean Eng. 2011, 38, 1792–1805. [Google Scholar] [CrossRef]
- Ling, J.M.; Wang, W.; Wu, H.B. On residual deformation of saturated clay subgrade under vehicle load. J. Tongji Univ. 2002, 30, 1315–1320. [Google Scholar]
- Wang, M.; Meng, S.J.; Wang, X.L.; Yuan, X.M.; Sun, Y.Q. Experimental research on development of vibration excited subsidence of frozen soil under cyclic loading. Chin. J. Geotech. Eng. 2016, 38, 916–922. [Google Scholar]
- Li, D.; Selig, E.T. Cumulative plastic deformation for fine-grained subgrade soils. J. Geotech. Eng. 1996, 122, 1006–1013. [Google Scholar] [CrossRef]
- Lekarp, F.; Dawson, A. Modelling permanent deformation behaviour of unbound granular materials. Constr. Build. Mater. 1998, 12, 9–18. [Google Scholar] [CrossRef]
- Sweere, G.T. Unbound Granular Bases for Roads; University of Delft: Delft, The Netherlands, 1992. [Google Scholar]
- Barksdale, R.D. Laboratory evaluation of rutting in base course materials. In Proceedings of the Third International Conference on the Structural Design of Asphalt Pavements, London, UK, 11–15 September 1972. [Google Scholar]
- Fujikawa, K.; Miura, N.; Beppu, I. Field investigation on the settlement of low embankment due to traffic load and its prediction. Soils Found. 1996, 36, 147–153. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, C.B.; Fu, J.J.; Zhan, Y.X. Research on influence depth of road subgrade induced by vehicle loads. Rock Soil Mech. 2013, 34, 316–321. [Google Scholar]
- Wu, T.; Cai, Y.; Guo, L.; Ling, D.; Wang, J. Influence of shear stress level on cyclic deformation behaviour of intact Wenzhou soft clay under traffic loading. Eng. Geol. 2017, 228, 61–70. [Google Scholar] [CrossRef]
- MOT China. Specifications for Design of Highway Subgrades (JTG D30-2015); China Communications Press: Beijing, China, 2015; p. 7.
- Ministry of Railways of the People׳s Republic of China. Code for Design of Railway Earth Structure; China Railway Publishing House: Beijing, China, 2016.
- Navaratnarajah, S.K.; Indraratna, B. Use of rubber mats to improve the deformation and degradation behavior of rail ballast under cyclic loading. J. Geotech. Geoenvironmental Eng. 2017, 143, 04017015. [Google Scholar] [CrossRef]








| Samples | The Mineral Compositions | ||||
|---|---|---|---|---|---|
| Quartz | Anorthose | Potassium Feldspar | Analcime | Calcitum | |
| SC | 50% | 12% | 2% | / | / |
| FA | 30% | / | / | / | / |
| OSA | 25% | 8% | / | 5% | 10% |
| Kaolinite | Illite/montmorillonite | Mullite | Organic matter | Non-crystalline | |
| SC | 5% | 30% | / | 1% | / |
| FA | / | / | 10% | / | 60% |
| OSA | / | 48% | / | 4% | / |
| Physical Properties | OSA: FA: SC | Reference | ||||
|---|---|---|---|---|---|---|
| 4:3:3 | 3:4:3 | 7:5:8 | 2:1:2 | 9:3:8 | ||
| Plastic Limit (%) | 27.96 | 26.94 | 27.54 | 20.20 | 25.77 | Wei et al. [20] Wei et al. [21] |
| Liquid Limit (%) | 40.51 | 40.17 | 42.70 | 32.6 | 42.60 | |
| Plasticity (%) | 12.55 | 13.23 | 15.16 | 12.4 | 16.83 | |
| CBR Value soaking for 96 h (%) | 17.00 | 13.00 | 31.00 | 40.00 | 33.00 | Cai et al. [29] |
| No. | Number of F-T Cycles | Confining Pressure/kPa | Axial Stress/kPa | Stress Ratio | Loading Frequency/Hz |
|---|---|---|---|---|---|
| 1# | 0 | 100 | 40 | 0.2 | 1 |
| 2# | 100 | 100 | 0.5 | 1 | |
| 3# | 100 | 300 | 1.5 | 1 | |
| 4# | 100 | 300 | 1.5 | 2 | |
| 5# | 100 | 500 | 2.5 | 1 | |
| 6# | 200 | 200 | 0.5 | 1 | |
| 7# | 1 | 100 | 100 | 0.5 | 1 |
| 8# | 100 | 300 | 1.5 | 1 | |
| 9# | 100 | 300 | 1.5 | 2 | |
| 10# | 100 | 500 | 2.5 | 1 | |
| 11# | 200 | 200 | 0.5 | 1 | |
| 12# | 5 | 100 | 100 | 0.5 | 1 |
| 13# | 100 | 300 | 1.5 | 1 | |
| 14# | 100 | 500 | 2.5 | 1 |
| Dynamic Stress Ratio | F-T Cycle Number | Confining Pressure (kPa) | Frequency (Hz) | R after 1 Load Cycles | R after 10 Load Cycles | R after 100 Load Cycles |
|---|---|---|---|---|---|---|
| 0.2 | 0 | 100 | 1 | 29.65% | 50.25% | 72.26% |
| 0.5 | 0 | 100 | 1 | 29.65% | 49.86% | 70.87% |
| 0.5 | 0 | 200 | 1 | 32.38% | 52.12% | 74.37% |
| 0.5 | 1 | 100 | 1 | 32.06% | 51.46% | 72.95% |
| 0.5 | 1 | 200 | 1 | 31.26% | 50.89% | 72.38% |
| 0.5 | 5 | 100 | 1 | 32.58% | 52.12% | 74.37% |
| 1.5 | 0 | 100 | 1 | 33.69% | 52.12% | 74.37% |
| 1.5 | 0 | 100 | 2 | 34.36% | 51.85% | 73.76% |
| 1.5 | 1 | 100 | 1 | 35.31% | 55.59% | 77.16% |
| 1.5 | 1 | 100 | 2 | 34.55% | 53.87% | 78.39% |
| 1.5 | 5 | 100 | 1 | 35.16% | 54.58% | 77.47% |
| 2.5 | 0 | 100 | 1 | 29.81% | 53.90% | 75.14% |
| 2.5 | 1 | 100 | 1 | 29.39% | 52.79% | 73.03% |
| 2.5 | 5 | 100 | 1 | 28.72% | 51.14% | 72.68% |
| Dynamic Stress Ratio | Confining Pressure (kPa) | F-T Cycle Number | Frequency (Hz) | Model (N: Cyclic Load Number) | Correlation Coefficient |
|---|---|---|---|---|---|
| 0.2 | 100 | 0 | 1 | 0.98 | |
| 0.5 | 100 | 0 | 1 | 0.98 | |
| 0.5 | 200 | 0 | 1 | 0.98 | |
| 0.5 | 100 | 1 | 1 | 0.98 | |
| 0.5 | 200 | 1 | 1 | 0.98 | |
| 0.5 | 100 | 5 | 1 | 0.98 | |
| 1.5 | 100 | 0 | 1 | 0.99 | |
| 1.5 | 100 | 0 | 2 | 0.99 | |
| 1.5 | 100 | 1 | 1 | 0.99 | |
| 1.5 | 100 | 1 | 2 | 0.99 | |
| 1.5 | 100 | 5 | 1 | 0.99 | |
| 2.5 | 100 | 0 | 1 | 0.99 | |
| 2.5 | 100 | 1 | 1 | 0.99 | |
| 2.5 | 100 | 5 | 1 | 0.99 |
| Dynamic Stress Ratio | Confining Pressure (kPa) | F-T Cycle Number | Frequency (Hz) | Model (N: 10 Million) | Predicted Results (cm) |
|---|---|---|---|---|---|
| 0.5 | 100 | 0 | 1 | 0.38 | |
| 0.5 | 100 | 5 | 1 | 0.67 | |
| 1.5 | 100 | 0 | 1 | 1.07 | |
| 1.5 | 100 | 5 | 1 | 1.32 | |
| 2.5 | 100 | 0 | 1 | 1.92 | |
| 2.5 | 100 | 5 | 1 | 2.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Li, Q.; Han, L.; Han, S.; Wang, F.; Zhang, Y.; Chen, Z. Experimental Research on Deformation Characteristics of Using Silty Clay Modified by Oil Shale Ash and Fly Ash as the Subgrade Material after Freeze-Thaw Cycles. Sustainability 2019, 11, 5141. https://doi.org/10.3390/su11185141
Wei H, Li Q, Han L, Han S, Wang F, Zhang Y, Chen Z. Experimental Research on Deformation Characteristics of Using Silty Clay Modified by Oil Shale Ash and Fly Ash as the Subgrade Material after Freeze-Thaw Cycles. Sustainability. 2019; 11(18):5141. https://doi.org/10.3390/su11185141
Chicago/Turabian StyleWei, Haibin, Qinglin Li, Leilei Han, Shuanye Han, Fuyu Wang, Yangpeng Zhang, and Zhao Chen. 2019. "Experimental Research on Deformation Characteristics of Using Silty Clay Modified by Oil Shale Ash and Fly Ash as the Subgrade Material after Freeze-Thaw Cycles" Sustainability 11, no. 18: 5141. https://doi.org/10.3390/su11185141
APA StyleWei, H., Li, Q., Han, L., Han, S., Wang, F., Zhang, Y., & Chen, Z. (2019). Experimental Research on Deformation Characteristics of Using Silty Clay Modified by Oil Shale Ash and Fly Ash as the Subgrade Material after Freeze-Thaw Cycles. Sustainability, 11(18), 5141. https://doi.org/10.3390/su11185141





