Free Riding without Dead Weight Losses
Abstract
:1. Introduction
2. Literature Review
2.1. Theoretical Scope
2.2. Review of Recent Studies
2.3. The Distinction of This Study from Existing Studies
3. Free Ride Cases without Market Failure
3.1. Free-Riders’ Influence on the Public Goods
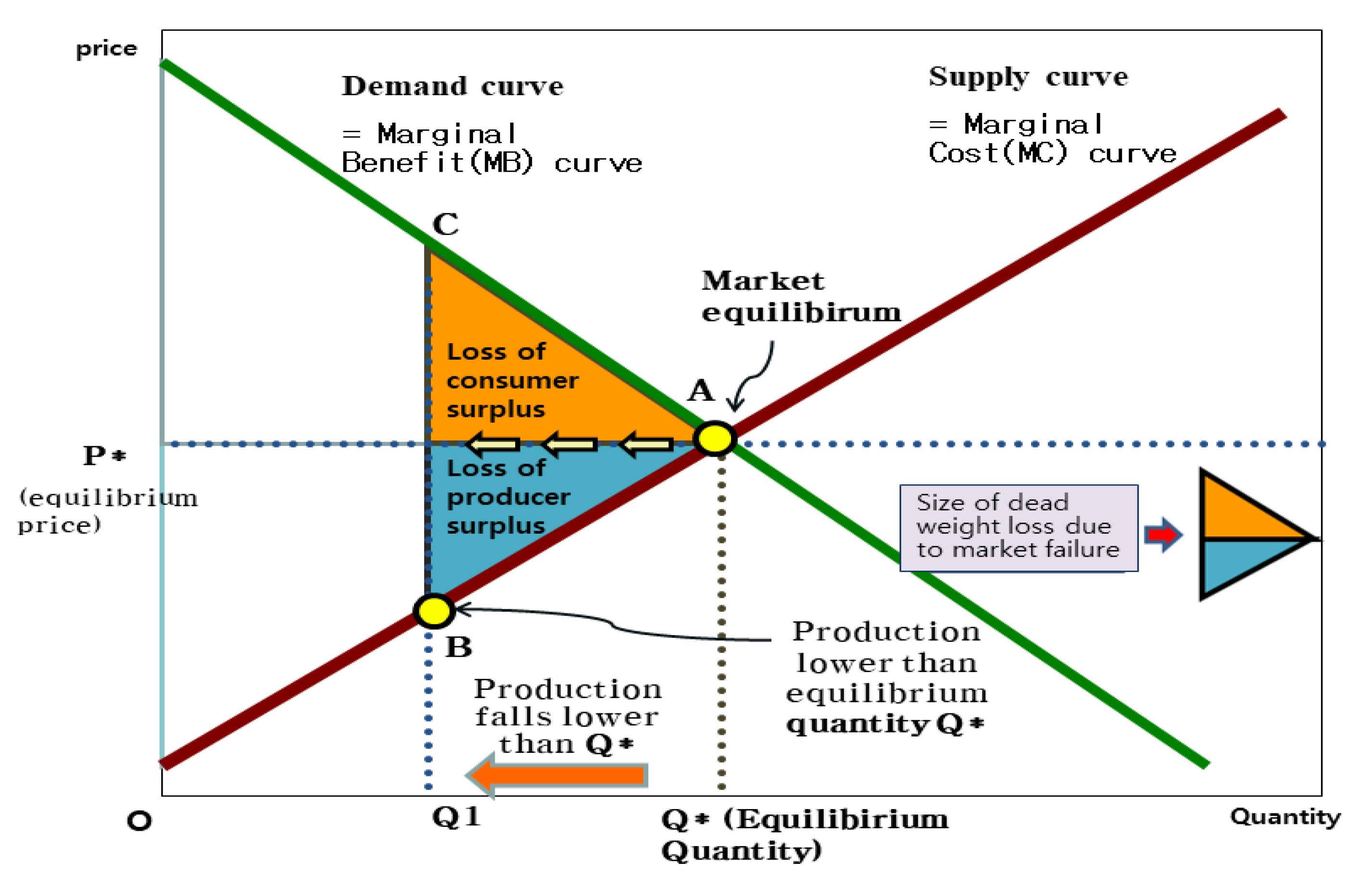
3.2. Welfare Economics Perspective of Free-Riding
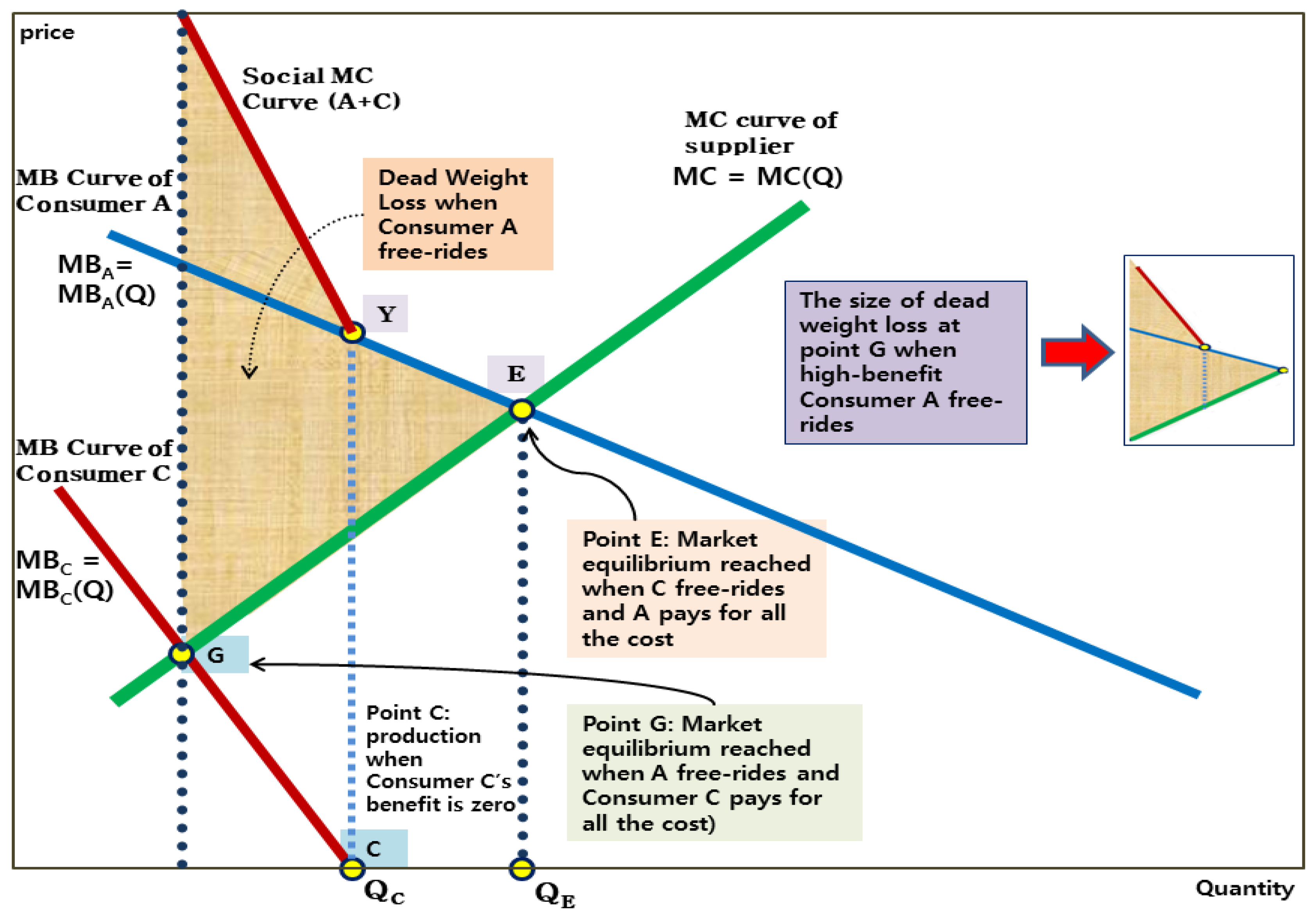
3.3. Why Does Free-Riding Incur Dead Weight Losses?
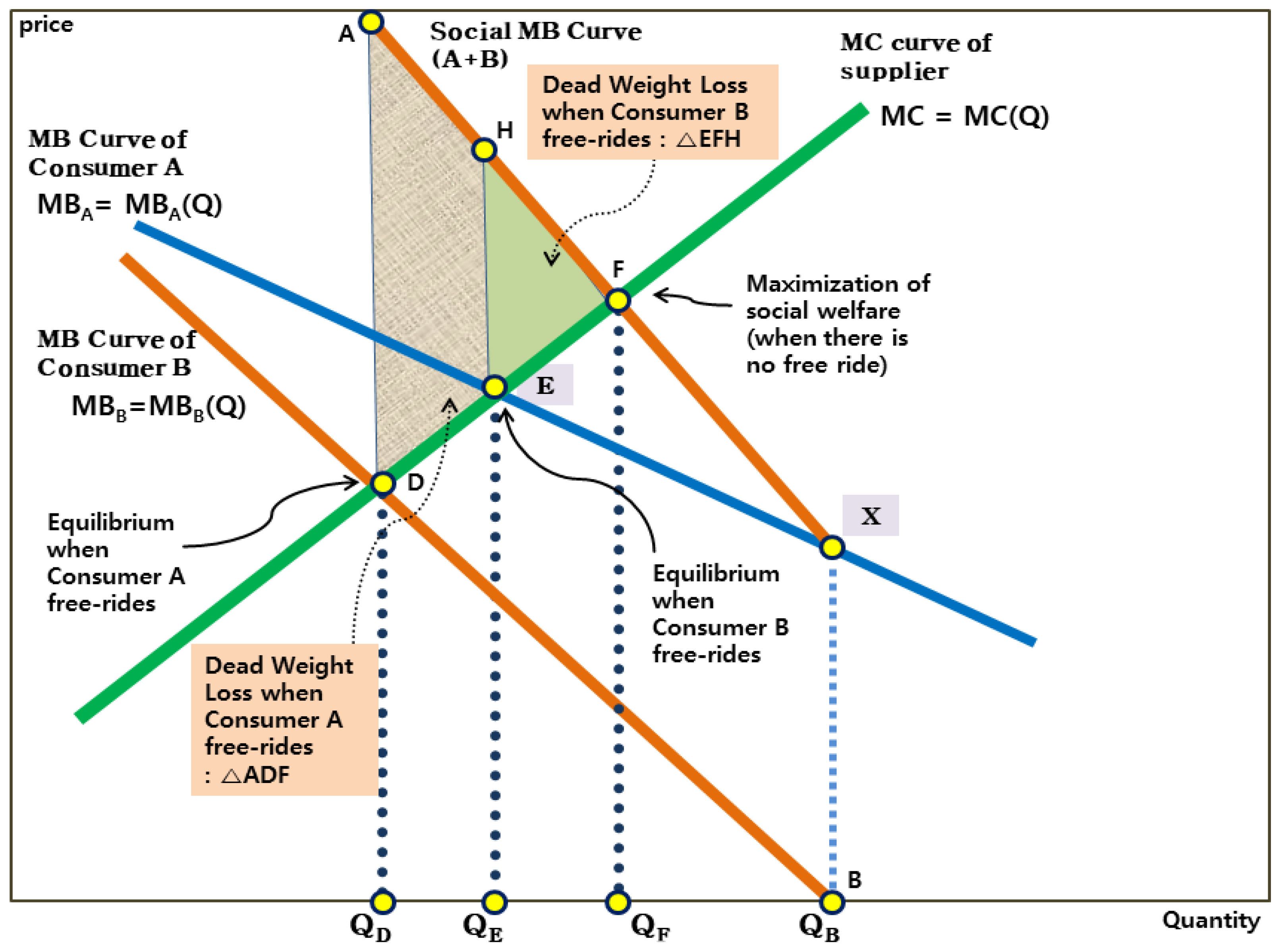
3.4. Possibility of Free Riding without Dead Weight Losses

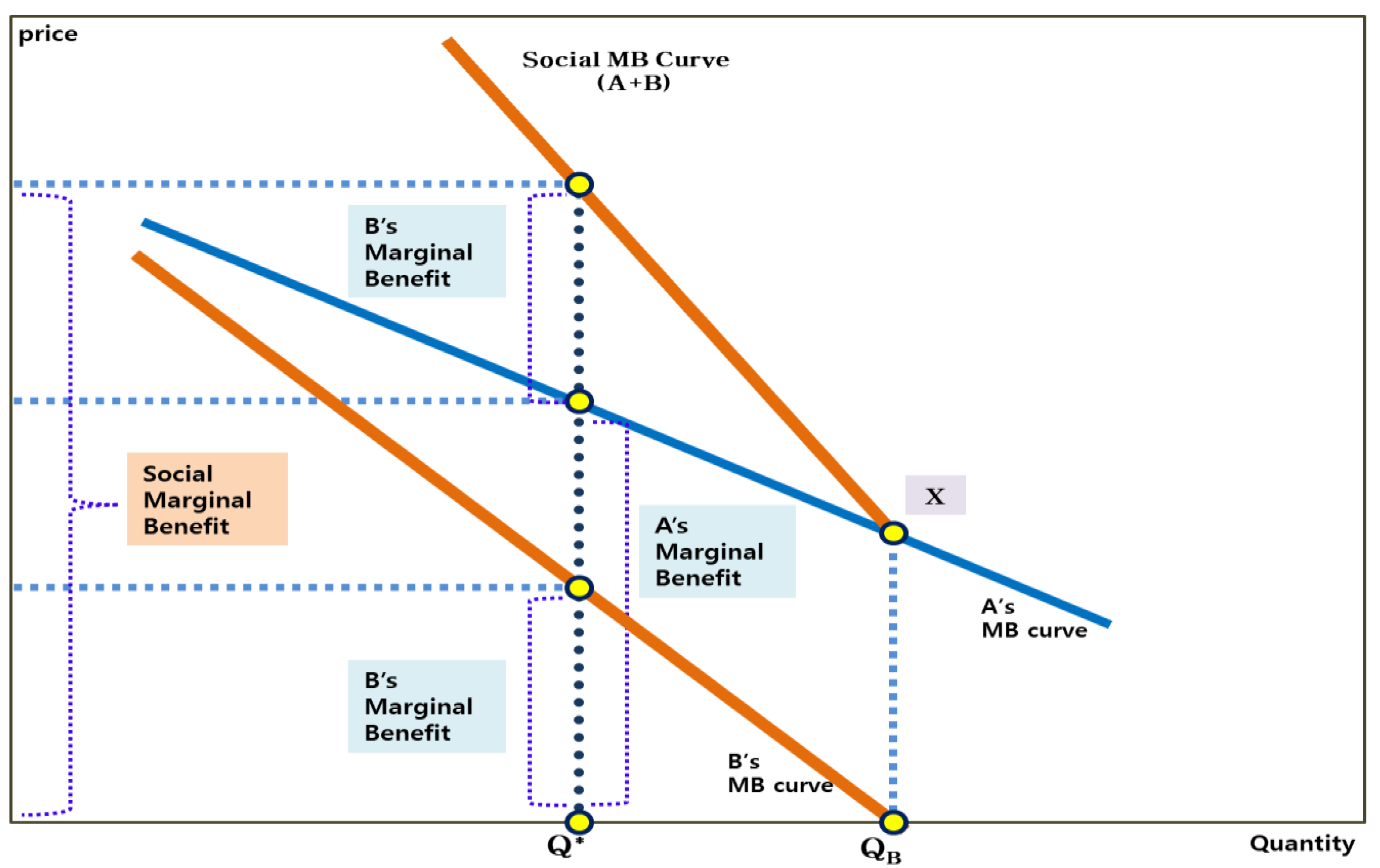
3.5. Free-Rider Problem in the Relationship between Consumer Groups
3.5.1. Assumption 1: Divisibility of Consumer Groups
3.5.2. Assumption 2: Linear Demand Function Moving Down and Right
3.5.3. Assumption 3: Possibility of Allowing Free-Riding by Expressed Preferences and Policy Selection
4. Discussion
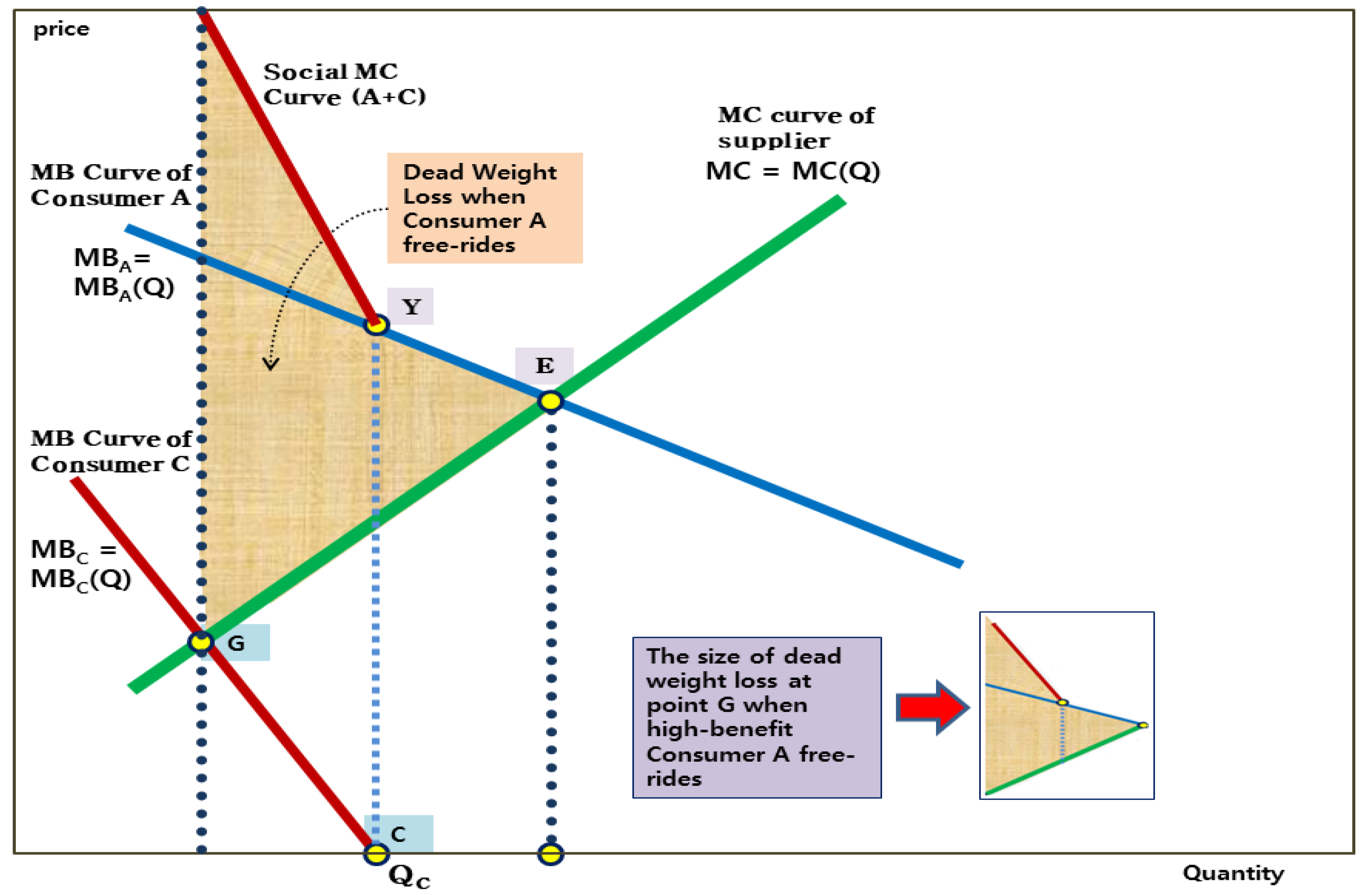
4.1. Possibility of Pursuing the Conflicting Values, Equity and Efficiency, at the Same Time
4.2. Relationship between Income Levels and the Size of Benefits from Public Goods
4.3. Contribution to the Academic Literature and Further Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bowen, H.R. Toward Social Economy; Rinchart: New York, NY, USA, 1948; pp. 176–195. [Google Scholar]
- Case, K.E. Musgrave’s Vision of the Public Sector: The Complex Relationship between Individual, Society and State in Public Good Theory. J. Econ. Financ. 2008, 32, 348–355. [Google Scholar] [CrossRef]
- Groves, T.; Ledyard, J. Optimal Allocation of Public Goods: A Solution to the “Free-Rider” Problem. Econometrica 1977, 45, 783–809. [Google Scholar] [CrossRef]
- Hirschman, A.O. Shifting Involvements: Private Interest and Public Action; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Thompson, D. The Proper Role of Government: Considering Public Goods and Private Goods; The Pennsylvania State University: State College, PA, USA, 2015. [Google Scholar]
- Coase, R. The Problem of Social Cost. J. Law Econ. 1960, 3, 1–44. [Google Scholar] [CrossRef]
- Musgrave, R.A. The Theory of Public Finance: A Study in Public Economy; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Banzhaf, H.S. The Market for Local Public Goods. Case West. Reserve Law Rev. 2014, 64, 1441–1480. [Google Scholar]
- Friedman, M.; Rose, D. Capitalism and Freedom; University of Chicago Press: Chicago, Illinois, United States, 1982. [Google Scholar]
- Tabarrok, A. The private provision of public goods via dominant assurance contracts. Public Choice 1998, 96, 345–362. [Google Scholar] [CrossRef]
- Dilger, R.J.; Beth, R.S. Unfunded Mandate Reform Act: History, Impact, and Issues; Federal Publications: Washington, USA, 2013. [Google Scholar]
- Shin, H.G. Consumer Surplus Analysis for the ‘Tragedy of Free-riding? ’ Korean Policy Stud. Rev. 2016, 25, 221–236. [Google Scholar]
- Jordahl, H.; Liang, C.Y. Merged municipalities, higher debt: on free-riding and the common pool problem in politics. Public Choice 2010, 143, 157–172. [Google Scholar] [CrossRef]
- Nordhaus, W. Climate Clubs: Overcoming Free-riding in International Climate Policy. Am. Econ. Rev. 2015, 105, 1339–1370. [Google Scholar] [CrossRef] [Green Version]
- Thielemann, E. Why Refugee Burden-Sharing Initiatives Fail: Public Goods, Free-Riding and Symbolic Solidarity in the EU. J. Common Mark. Stud. 2018, 56, 63–82. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gachter, S. Social Preferences, Beliefs, and the Dynamics of Free Riding in Public Goods Experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, U.H.; Tyran, J.-R.; Wengström, E. Second thoughts on free riding. Econ. Lett. 2014, 122, 136–139. [Google Scholar] [CrossRef] [Green Version]
- Ellingsen, T.; Paltseva, E. Confining the Coase Theorem: Contracting, Ownership, and Free-Riding. Rev. Econ. Stud. 2016, 83, 547–586. [Google Scholar] [CrossRef]
- Bonroy, O.; Garapin, A.; Hamilton, S.F.; Monteiro, D.M.S. Free-riding on product quality in cooperatives: Lessons from an experiment. Am. J. Agric. Econ. 2019, 101, 89–108. [Google Scholar] [CrossRef]
- Bucciol, A.; Montinari, N.; Piovesan, M. It Wasn't Me! Visibility and Free Riding in Waste Disposal. Ecol. Econ. 2019, 157, 394–401. [Google Scholar] [CrossRef]
- Iida, Y.; Schwieren, C. Contributing for Myself, but Free riding for My Group? Ger. Econ. Rev. 2015, 17, 36–47. [Google Scholar] [CrossRef]
- McDougal, M.K. Unequal and Unfair: Free Riding in One-Shot Interactions. Sociol. Inq. 2018, 88, 494–509. [Google Scholar] [CrossRef]
- Kennedy, M.M.J. Public Finance; PHI Learning Pvt. Ltd.: Delhi, India, 2012; pp. 62–63. [Google Scholar]
- Mankiw, N.G. Principles of Economics, 6th ed.; Cengage Learning: Boston, MA, USA, 2008; pp. 311–313. [Google Scholar]
- Rodrigues, J. Where to Draw the Line between the State and Markets? Institutionalist Elements in Hayek’s Neoliberal Political Economy. J. Econ. Issues 2012, 46, 1007–1033. [Google Scholar] [CrossRef]
- Baron, D. Morally Motivated Self-regulation. Am. Econ. Rev. 2010, 100, 1299–1329. [Google Scholar] [CrossRef]
- Bracht, J.; Figuieres, C.; Ratto, M. Relative Performance of Two Simple Incentive Mechanisms in a Public Goods Experiment. J. Public Econ. 2008, 92, 54–90. [Google Scholar] [CrossRef]
- Burlando, R.; Guala, F. Heterogeneous Agents in Public Goods Experiments. Exp. Econ. 2005, 8, 35–54. [Google Scholar] [CrossRef]
- Nikiforakis, N.; Normann, H. A Comparative Statics Analysis of Punishment in Public-Good Experiments. Exp. Econ. 2008, 11, 358–369. [Google Scholar] [CrossRef]
- Shin, H.G. ‘Prisoner’s Dilemma’ vs. ‘Consumer Surplus’ As an Analysis of Free-riding. Korean Assoc. Policy Dev. 2016, 16, 1–23. [Google Scholar]
- Samuelson, P.A. The Pure Theory of Public Expenditure. Rev. Econ. Stat. 1954, 36, 387–389. [Google Scholar] [CrossRef]
- Lakner, C.; Milanovic, B. Global Income Distribution from the Fall of the Berlin Wall to the Great Recession; Policy Research Working Paper 6719; Oxford University Press: Oxford, UK, 2013. [Google Scholar]

| Independent Variables | Regression Coefficient | t-Value | Significance Probability (P > t) |
|---|---|---|---|
| Gender (male = 1) | 0.315 *** | 4.650 | 0.000 |
| Age | 0.009 *** | 3.390 | 0.001 |
| Marital status (married = 1) | 0.031 | 0.420 | 0.675 |
| Job (employed = 1) | −0.161 ** | −2.330 | 0.020 |
| Middle school graduate | 0.101 | 0.680 | 0.498 |
| High school graduate | −0.111 | −0.920 | 0.357 |
| College graduate | −0.272 * | −1.730 | 0.085 |
| University or higher | −0.076 | −0.580 | 0.562 |
| Self-reported income level | 0.049 ** | 2.410 | 0.016 |
| _cons | 2.003 | 9.250 | 0.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-S.; Jeong, S.-h. Free Riding without Dead Weight Losses. Sustainability 2019, 11, 5168. https://doi.org/10.3390/su11195168
Kim K-S, Jeong S-h. Free Riding without Dead Weight Losses. Sustainability. 2019; 11(19):5168. https://doi.org/10.3390/su11195168
Chicago/Turabian StyleKim, Kwon-Sik, and Seong-ho Jeong. 2019. "Free Riding without Dead Weight Losses" Sustainability 11, no. 19: 5168. https://doi.org/10.3390/su11195168
APA StyleKim, K.-S., & Jeong, S.-h. (2019). Free Riding without Dead Weight Losses. Sustainability, 11(19), 5168. https://doi.org/10.3390/su11195168




