Abstract
The development of microgrids is of great interest to facilitate the integration of distributed generation in electricity networks, improving the sustainability of energy production. Microgrids in DC (DC-MG) provide advantages for the use of some types of renewable generation and energy storage systems, such as batteries. In this article, a possible practical implementation of an isolated DC-MG for residential use with a cooperative operation of the different nodes is proposed. The main criterion is to achieve a very simple design with only primary control in a residential area. This application achieves a simple system, with low implementation costs, in which each user has autonomy but benefits from the support of the other users connected to the microgrid, which improves its reliability. The description of the elements necessary to create this cooperative system is one of the contributions of the work. Another important contribution is the analysis of the operation of the microgrid as a whole, where each node can be, arbitrarily, a consumer or an energy generator. The proposed structures could promote the use of small distributed generation and energy storage systems as the basis for a new paradigm of a more sustainable electricity grid of the future.
1. Introduction
1.1. Evolution of Electrical Networks
For just over 100 years, AC has been the technology that has dominated power systems. Consequently, most electrical loads have been developed in AC [1]. Electrical networks have evolved, from their origin, to the current large interconnected networks. However, there are several factors in current electrical installations that allow proposing an important change in this approach [2].
First, transport networks have been aging and becoming saturated, while the demand for power has not stopped growing [3]. The huge costs required for the construction of large power plants or long transport lines have sparked interest in new structures of smaller size and more flexible [4]. This is how concepts such as microgrids (MGs) emerge.
Secondly, the depletion of fossil resources and climate change favors the development of renewable generation sources [5], many of them characterized as having a small unitary power and using DC in their operation [1].
Third, the development of power electronics facilitates the incorporation of a large number of receivers that work in DC or that include a double conversion of AC/DC/AC power [6].
Consequently, two important concepts have been developed in recent years: The MG and within this, the DC microgrid (DC-MG).
1.2. DC Microgrids
Since its proposal in 2002 [7] the concept of MG has been gaining strength. It can be included in the broader concept of smart grids (SGs) [8]. MGs are conceived as small distribution networks with distributed generation, storage systems, loads and control systems that allow their autonomous operation when the transport network fails [9]. They present potential advantages that make them attractive, such as [9,10]:
- -
- Facilitate the integration of distributed generation (DG) of renewable origin.
- -
- Improve efficiency by bringing generation closer to consumption.
- -
- Enable to reduce the load level of the transmission network.
- -
- Improve reliability by allowing loads to operate during network failures.
Taking into account these advantages, public administrations should facilitate and regulate the creation of these microgrids, which represent a new paradigm in the top-down vision of traditional electricity grids.
MGs can be classified into AC-MG and DC-MG. DC-MGs have been proposed by various researchers since the development of MGs was presented as an alternative to traditional networks [11]. The development of DC-MG can provide advantages over those of AC-MG [12] such as:
- -
- Many renewable generation systems produce energy in DC (e.g., photovoltaic and fuel cells) or use DC in the energy transformation process, as occurs in many small wind generators [1], which use DC generators or permanent magnet synchronous generators, followed by electronic rectifiers.
- -
- Many domestic and industrial loads are of the DC electronic type, or use power electronics with intermediate stages in DC [13].
- -
- As a consequence of the above, avoiding the transition to an AC-MG simplifies and reduces energy transformations with the consequent decrease in losses and associated costs [11]. The convenience of using hybrid systems (photovoltaic, wind, hydro and batteries) in areas without supply from the grid in Sub-Saharan Africa is analyzed in [14].
- -
- Connection to AC networks is simplified because the synchronization of electronic inverters is done very simply and quickly.
- -
- Energy storage systems operate in DC and reduce energy costs [15].
- -
- The stability of the DC network with multiple converters can be improved in an active way [16]. Short-circuit currents can be limited electronically, avoiding high currents [17]. A general scheme of DC-MG protection can be seen in [18].
- -
- The control of DC-MG with multiple generators is much simpler than in an equivalent AC-MG [19].
For all these reasons, it seems attractive, in the near future, to use DC-MG for various applications, beyond the current ones. They can be used for power supply to residential, commercial, educational centers, etc., [19] with the additional possibility of providing high reliability power or improve aspects of power quality [20].
1.3. DC-MG Control
The control of the DC-MG has been addressed by several authors [11,19] in a hierarchical structure, based on the control of conventional transport and distribution networks in AC. Based on this approach, a primary, secondary and tertiary control with different functions is proposed [19].
The primary control must manage the demand between the different DGs in the MG and ensure that the voltage level is within the required limits. For this control, two types of methods have been proposed [11]: The passive control based on the droop concept and its variants (passive control methods), without the need for communication between DGs and the active load sharing method that requires communication links between the nodes of the MG [21].
The droop concept is based on a similar principle to the one used in the primary power-frequency (P-f) control of large AC generators (hydroelectric systems, for example) that adjust the generation level to maintain speed in synchronism with the network. The droop characteristic of a converter in a DC-MG can be established as a linear function between voltage (V) and current (I) or between P and V [22].
This approach allows independent control by each converter in each DG without the need for a communication channel between them. As a disadvantage, the control droop presents an inherent commitment between the regulation of voltage and the distribution of demand among the different DGs [22,23]. To solve this problem, droop control variants have been proposed where the gain (slope of the droop characteristic) is adjusted dynamically [23].
The capacity of the DC systems together with the energy storage systems (ESS) to guarantee an easy control of the networks allows us to propose control strategies for distribution networks with multiple DGs that share resources cooperatively [24]. The possibility of sharing resources, in a hybrid system connected to a MG, and reducing the cost of purchasing power from the distribution network is explored in [25]. In this study, the problem of optimizing the size of resources (EES) and its optimal operation (including the influence of electric vehicles) is formulated. As the MG is connected to a distribution network, the final state of operation is not determinant in the management.
In the use of hybrid systems, such as those proposed for DC-MG, with the use of ESS, many authors have developed control strategies not focused on maintaining voltage, but on the optimal use of available resources [26,27]. In these cases, the aim is to optimize a cost function, for example, by moving the load from one moment to another with a lower price [28] or by facilitating the integration of variable sources such as wind energy [15].
As this paper shows, in a residential grid with an adequate design, a simple structure of primary control can guarantee a proper operating state.
1.4. MG Basic Aspects Background
Throughout the previous sections, several references have been commented on the DC-MG control and strategies for the use of MG resources. The objective of this paper is to describe a possible practical implementation of a DC-MG for residential use with a cooperative operation of the different nodes and the main criterion is to achieve a very simple design. In this section some more specific references that are more related are presented. Authors consider that there are no studies that describe the type of structure proposed here, but some aspects of its functioning have been addressed in the literature.
An autonomous, decentralized control without communication links is proposed. The operation of each node is based on droop control type P–V. Numerous researchers have deepened the analysis of this type of control [11], which can lead to low voltage regulation and difficulties in the distribution of load between the generators. In [21] an average current sharing method is used to deal with these problems, and the feedback signal is sent by a communications network to each generator so that it modifies its set point.
A nonlinear droop function to improve power sharing between sources is proposed in [29]. Nonlinear droop control can increase the gain with strong voltage drops and soften it with the small ones [30]. Adaptive droop control is proposed in [31] to improve the power distribution between the generators. An algorithm developed in [32] is used to improve the functioning of the network. For its operation, each generator communicates with its neighbors through the network and based on the voltages of the nodes an algorithm optimizes the power distribution.
In a hierarchical control structure [19], a second level makes it possible to correct the voltage deviations between the nodes or modify the power distribution. In general, a communication system is used to send the control signals to the generators and to be able to adjust the voltage regulation parameters and the load distribution.
The displacement of the control droop curve (as a secondary control level) is proposed in [33] with the objective of improving the excessive voltage drops that the droop control can cause. Other authors have proposed secondary control schemes to reduce power losses in networks [34].
To improve the resilience of the MGs, the operation of several MGs in a network, with an adequate communication system, would allow the establishment of support policies between them. In this way, energy could be exchanged through the transport network [35], which can constitute a third level of control. A third level of control, within the hierarchical structure, has been proposed by several authors to improve economic aspects or increase the resilience and reliability of networks [36].
The possibility that several microgrids share resources cooperatively has been proposed by several authors [37]. The climatological differences or the diversity in the energy demand can facilitate a cooperative operation of a set of microgrids connected to the electrical network, under the dispatching of a control centre [38].
This cooperative operation of several connected microgrids can also be achieved through a correct economic strategy, which facilitates adopting the correct energy trading criteria to the control centre of each microgrid, without the need for centralized control [39].
Analyzing the data of solar and wind generation from seven sites in Hong Kong [40] demonstrates that the cooperative operation of microgrids in these sites would produce important benefits, taking advantage of the diversity in the generation.
In any case, all the proposed networks have connection to the AC network or several fixed generators, whose operation is to be optimized. The isolated network proposed here has as its main characteristic that each node can be, arbitrarily, a load or a generator, depending on its own parameters. There is no communication system between the nodes, because according to the results that will be shown in the discussion, the third level of control is considered unnecessary. Even, based on the simulations, the second level can be dispensed with, as will be argued.
As justified in the simulations, to achieve an adequate operation with a simple distributed primary control, a node design that guarantees a sufficiently high autonomy will suffice. The required level of autonomy must allow only a percentage of the nodes demanding energy simultaneously. A design of the network that guarantees moderate voltage drops during those possible states of operation is also needed.
The study of generators clusters working in coordination with the structure of a virtual power plant (VPP) is also proposed in the literature. Numerous authors have developed control strategies for the coordinated functioning of these VPP [41]. The optimal coordination of VPPs with renewable sources implies taking into account the generation uncertainty and the influence of weather conditions [42]. The problem of these VPPs is different from the one addressed in this paper, where it is proposed that each node can collaborate to sustain the network according to its own state. There are no fixed generators, but it is considered the collaboration between several nodes to maintain an admissible operating state.
1.5. Contributions and Paper Layout
Despite the practical difficulties that exist for the development of networks in DC (lack of standardization, for example, with an impact on a resource market poorer than that of AC [16]) these structures have aroused considerable interest in the scientific community, especially as an alternative for the energy supply from renewable sources in isolated areas [14,43]. It is not difficult, technically, to create a DC-MG. To facilitate the success of this type of microgrids several requirements must be fulfilled:
- -
- Be safe, reliable and stable electrical distribution systems.
- -
- Be economically profitable for consumers.
- -
- Be dynamic and flexible in its operation and its extension.
In particular, this paper will propose a type of DC-MG easy to control and implement to achieve autonomous operation of a residential area. Each node is, at the same time, a possible load or a possible generator, so that the overall operation is achieved cooperatively between the different participants. This type of structure can be attractive for residential areas, with moderate demand in all nodes, and can facilitate the development of DC-MG.
The analyzed MG is formed by several households, each one equipped with photovoltaic (PV) panels and batteries and linked together through the grid. The use of renewable energy is a sustainable solution for the ever increasing energy consumption worldwide. In particular, PV generation is a viable energy in many isolated areas of the large electricity transmission and distribution networks. PV is characterized by its variable and intermittent production depending on the level of solar radiation. This means that individual PV installations isolated from the electricity grid, even with the battery holder, cannot ensure levels of continuity of supply equivalent to the distribution network of the electricity company [26]. A solution to this problem is the establishment of microgrids that link different consumers and individual generators in an electrical network. The viability of a MG depends on economic factors to be a sustainable option [24].
The type of renewable generator used does not limit the application of the solution proposed in the paper. However, it has been decided to choose PV generators due to its great ease of use in small domestic facilities, its wide diffusion worldwide and the simplicity of its operating model.
The authors have tried to achieve a very simple structure, which can be implemented without limitations. The operation control of the nodes must be autonomous, thus achieving a real operation of the plug and play type. In the proposed network, all the nodes have the same characteristics and participate equally in the operation (peer to peer). Under the operating conditions that will be studied, a relaxation of the control system constraints is possible without affecting the operation of the users. The proposed cooperative microgrid allows us to increase the reliability of energy supply compared to other solutions, with low implementation costs.
In the proposed network, there is no root or slack bus that can represent a critical element in the grid. All nodes respond autonomously to the same signals: Voltage at its point of connection to the network and internal voltage of the node. The operation of each node also depends on the state of charge (SOC) in its storage system. The only critical condition is that, at every moment, the energy demanded by a group of them can be contributed by the others, for which the design of each node is an aspect of great importance. This design should guarantee sufficient autonomy in most of the time. The authors state that no previous approach in any other work related to DC-MG allows such an operation.
The paper is organized as follows; Section 2 describes the basic structure of this type of network, which is called a cooperative residential DC-MG, describing the elements that compose it. In Section 3 the model is developed to analyze the stationary operation of the network based on the power demands of the nodes and the internal state of each one. The application of the operational model of the network to a case is explained in Section 4. Subsequently, the results are analyzed and a discussion of them is carried out in Section 5. Finally, certain conclusions are drawn in Section 6.
2. Description of a Cooperative DC-MG
The proposed concept of a cooperative DC-MG (CoDC-MG) will be applied to a set of interconnected nodes of a DC small electrical network that have autonomous power and can share power between them, so that they can function as loads or as generators depending on the operating state of the network and its own internal energy state. The MG will be assumed isolated from the AC network, because if this connection exists, the mode of operation would be imposed by that network, simplifying all the analysis that will be developed. That any node is purely a load or a generator is not excluded.
To achieve a stable state of operation it is necessary to balance the power provided by the generators and the power demanded by the loads. For this to be possible, the design of the network must satisfy certain rules.
2.1. Structure of Network Nodes
To clarify the concept, we considered an initial CoDC-MG configuration with a small set of dispersed households that must be supplied with electricity according to the following characteristics:
- -
- The energy would come from PV panels. Other resources could be used, but this study started from this solution for simplicity in the subsequent approach.
- -
- Batteries would be used to maintain the electricity supply when there is not enough PV production.
Taking these features into account, it was decided to carry out the distribution with a DC-MG. Initially there were three different alternatives:
- Each household has an independent autonomous installation (there is no MG in this case).
- A centralized generation facility is developed to supply energy to each household.
- Each household has its own installation, but all the houses are interconnected by a CoDC-MG.
The third option was chosen in this study due to:
- -
- The size of the generating and storage facilities is reduced compared to the size of the option 1, benefiting from the diversity of the different consumers’ consumption. That size will be equivalent to the one needed in option 2 but distributed among all the nodes.
- -
- Each consumer can receive support from others if they need more power or energy than the available one in their installation. In the event of a fault in the distribution network, each consumer has his own resource. This fact improves the reliability of the network in comparison with options 1 and 2.
- -
- In option 3, the size of the wiring is, in general, smaller than that required in option 2.
- -
- In conclusion, option 3 improves the sustainability of the system.
The result, therefore, will be a set of Nv households connected by a radial distribution network as shown in Figure 1. All nodes are similar to node 1, with their own energy generation and storage systems.
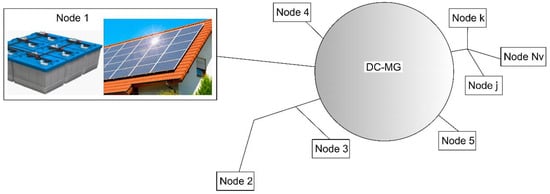
Figure 1.
Cooperative DC-microgrid (CoDC-MG) structure.
The design of the generation and storage facility of each node was made as follows:
- -
- In each household a daily energy consumption Ed (kWh/day) was estimated from the demand curve Pd(t) corresponding to the average value calculated by measurements made in other existing nearby facilities (or of typical statistical values available) [44]).
- -
- With the solar irradiance curve of the region PF(t) (see Figure 2) for the less favorable time of the year (for example, January for latitude 40° N) the power produced by the PV array was calculated as PS(t).
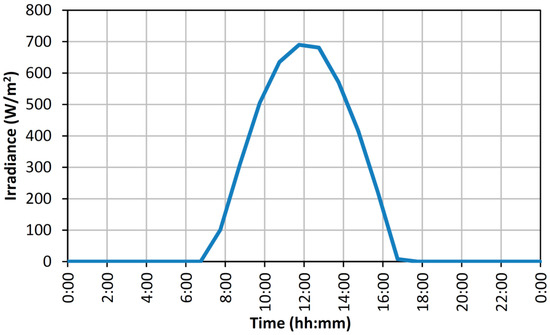 Figure 2. Irradiance in W/m2 for a typical day of January at latitude of 39.735° and longitude of −0.92°, obtained from PVGIS [45].
Figure 2. Irradiance in W/m2 for a typical day of January at latitude of 39.735° and longitude of −0.92°, obtained from PVGIS [45].
From the values PS(t) and Pd(t) the useful energy contributed by the battery in one day was obtained, as depicted in Figure 3. The excess energy produced by the panels, E1, was used to recharge the batteries.

Figure 3.
Useful energy provided by the battery in one day.
- -
- Taking into account the performance of the charging (ηc) and discharging (ηd) operations of the batteries, the energy that must be generated was obtained, based on the installed power Ppeak in the PV panels:
- -
- From the adjustment to the balance of the previous data, the value of Ppeak was specified.
- -
- By admitting a SOC of 80% for example at the end of a discharge cycle for a sunny day, the capacity of the batteries Qb1 is calculated using the expression (6).
- -
- For a set of nc cloudy days, the energy production would be much less than the theoretical one with good weather. For example, admitting that 15% of the theoretical value was obtained, since the irradiance could be between 10% and 20% of what corresponds to a sunny day [46], it would result in:
- -
- E’b is the energy contributed by the battery the nc cloudy days (it has been assumed that Pd(t) > 0.15·PS(t) during all the time those days).
- -
- SOCmin is the minimum admissible value of SOC after those nc days (for example 15%).
- -
- Qb2 is a new value of the necessary capacity in the battery.
Finally, the Qb capacity will be equal to:
After these days it is necessary to recover the normal state of charge in the batteries in a not very long period, for this reason it is necessary to oversize the value Ppeak (for example 20%).
The data used in the examples developed in this work are shown in Section 4. Both the generation and the storage capacity of each node were derived from the real operating data of a group of households, taking as a starting point a consumption level with a probability of 20% of being exceeded.
2.2. Structure of the Cooperative DC-MG
For the design of the DC-MG distribution network the following aspects should be taken into account:
- -
- The power demands are due to some consumers (never to all at the same time). For example, we would assume that 30% of consumers were demanding power from the other nodes.
- -
- The remaining nodes will contribute the demanded power (plus the losses), by sharing this demand between them.
- -
- Any node in the network can be, therefore, a consumer or a power generator.
- -
- The search for hypotheses of the most critical possible operating states allows us to design the wire sections.
- -
- The resulting sections in the cables are always smaller than those that would result if all the demand was distributed to all consumers from a central generator.
In addition, the design of the network must take into account the technical criteria set by the regulations in each country or in international standards [47]. For example, in underground networks it is common to find the limitation S > 6 mm2, where S is the section of the copper underground conductor. Many times, these minimum sections may be sufficient, in a large part of the sections of the network in a suburban DC-MG. The comments made above are also important for the calculation of voltage drops.
Figure 4 shows the elements that make up each node of the cooperative DC-MG.

Figure 4.
Elements in a node of the cooperative DC-MG.
Each node has its PV array with a Ppeak power and a battery with Qb capacity, as indicated above.
The battery has a regulator (battery controller, BC) to control the state of charge and its maximum current, both in charge and discharge. The basic structure is a buck-boost converter [48]. The BC decides the power flows between the PV array, the battery and the internal bus of the node.
Finally, the node is connected to the network with a power flow controller (PFC) and a smart meter (SM) to measure the power flows in both directions.
The PFC decides the transfers of power from the node to the network (power to grid) or from the network to the node (power from grid) depending on the voltages on both sides (grid and internal bus) and the nominal voltage of the network (Vr). This equipment will limit the maximum permissible power flows in each direction.
Three types of loads are frequent in current households:
- -
- Electronic loads that operate in DC at reduced voltages. They have electronic power equipment (currently AC/DC) that would be DC/DC.
- -
- Power loads that can operate directly in DC at the nominal voltage of the network (motors or heating equipment). Currently theses loads are AC but their replacement by equivalent DC devices is simple.
- -
- Power loads that work in AC. For example, the devices mentioned in the previous point that have not been replaced by others in DC. In the future, if DC networks are developed, this type of equipment can be replaced by others in DC that will be offered in the market.
3. Stationary Operation of the CoDC-MG
Each node has an operating regime composed of two stages:
The first stage is the internal operation with respect to the own loads. The battery controller (BC) tries to maintain the internal bus voltage Vi(t) = 1.05·Vr for any power demand of the installation itself.
The BC operates as a voltage source with limited current. To achieve its objective, all the available power of the PV panels Ps(t) was used. In the interval {t1–t2} of Figure 3, there was an excess of generation. Therefore, the voltage Vi would be greater than Vr (Vr ≤ Vi ≤ 1.05 · Vr) and the excess Ps was used to recharge the battery until SOCmax was reached. Outside the interval {t1 − t2} of Figure 3, the power Ps was lower than Pd. The voltage Vi(t) decreased below Vr, and the power provided by the battery Pb(t) was used to try to maintain the value Vr, as long as the Imax established in the equipment was not exceeded.
The power provided by the battery depends on its SOC, a maximum level can be maintained if SOC > 20%. If SOC < 15% the power provided by the battery is zero, to guarantee an adequate duration of the battery. Between 20% and 15% the power delivered can be reduced linearly. The SOCmax can be 100% or 95%, since some types of battery (Li-ion) can suffer a faster deterioration with high values of SOC [49].
If there is an excess of generation with Vi = 1.05 · Vr and the battery has reached SOCmax, the power available in the panels cannot be used. This situation corresponds to a case in which neither the network nor the own loads demand more energy and in addition the battery is charged to SOCmax.
The operation of the battery is indicated in Figure 5.
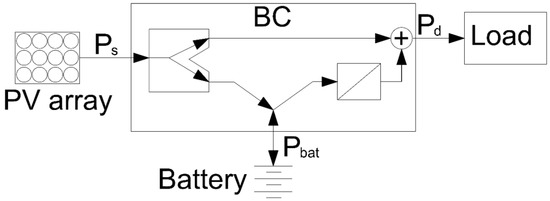
Figure 5.
Battery operation.
The corresponding equations if 20% < SOC ≤ SOCmax are:
If 1 < Vi/Vr ≤ 1.05, Pb < 0 (battery charging):
If 0.97 ≤ Vi/Vr < 1, Pb > 0 (battery discharging):
If 0.7 ≤ Vi/Vr ≤ 0.97, Pb > 0 (battery discharging):
For Vi(t) < 0.7·Vr the battery current should decrease (for example in a linear way) to prevent breakdown situations.
Kc and Kd factors are fictitious resistances according to:
The values of both coefficients could be different from each other, since the maximum charging current can be different from the maximum discharge current.
If the consumption exceeds the power supplied from the BC, the voltage Vi(t) cannot be maintained at its nominal value. In this situation, the voltage Vi(t) decreases rapidly.
The second stage is the operation with respect to the network. In this stage two states can occur:
- -
- If the voltage Vi is greater than 0.97·Vr the node behaves as a generator and injects power to the network depending on the difference 1.05·Vr − Vg. Vg is the voltage of the network at the node connection point.
- -
- If the voltage Vi is less than 0.95·Vr the node becomes a load for the network. This could happen if the power demanded by loads in a node is greater than that allowed by the Imax of the BC or if the battery has reached a low level of SOC in that node.
In both states, the PFC works with a droop control regulation P–V as shown in Figure 6.
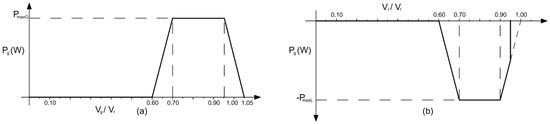
Figure 6.
(a) Node as a generator and (b) node as a load.
The steady state operation of the node is regulated by the following equations:
If Vi ≤ 0.95·Vr, the node receives energy from the network (Pg < 0). The energy delivery is maintained until Vi reaches the value of 0.97·Vr:
If 0.9 ≤ Vi/Vr ≤ 0.97:
If 0.7 ≤ Vi/Vr ≤ 0.9:
If Vi < 0.7·Vr, Pg decreases rapidly to avoid fault situations. The energy delivery is interrupted if Vi < 0.6·Vr. The power received from the grid is limited to the minimum value between PmaxL and the maximum value that the network can provide by keeping Vg in the admissible input voltage range of the PFC.
If Vi ≥ 0.97·Vr the node delivers power to the network (Pg > 0):
If 0.945 ≤ Vg/Vr ≤ 1.05:
If 0.7 ≤ Vg/Vr ≤ 0.945:
If Vg < 0.7·Vr, Pg decreases rapidly to avoid fault situations. The energy delivery is interrupted if Vg < 0.6·Vr. The power supplied to the grid is limited to the minimum value between PmaxG and the available power in the node (Ps + Pbat − Pd).
Factors h1 and h2 (with units of A) are easily obtained from the expressions:
Parameters α1 and α2 took the values 0.1 according to the conditions established by Equations (14) and (16). Later, the influence of these parameters would be analyzed.
The situation Vg < 0.7·Vr or Vi < 0.7·Vr represents a large overload or a fault (short circuit). The power flow is reduced to a very small value (Pres) such that, by eliminating the overload or fault, allows the system to increase the voltage and return to normal operation. Protection elements (breakers) may be necessary to resolve fault situations.
The balance in the network is achieved if:
being:
and the power losses in the network are:
where Rk is the resistance of the conductor of the section k of the network and Ik is the current in that branch.
The nodes close to the load have lower voltages and provide more power than the distant ones, this fact reduces the losses that occur in the network.
Since any node can change from being a load to being a generator or vice versa, the load flows in the network change continuously. The voltage of each node depends on the set of loads and generators in the microgrid, so it is not possible to choose a node as a reference (slack bus).
To analyze the global operation of the network, the power provided by each node depends on the h2 parameter and the existing voltages in the network. If a node has more installed power and PmaxG of the node is increased, its contribution under the same conditions is greater than that of the other nodes if h2 is defined in (19). However, h2 can be a variable parameter according to network performance criteria.
In each billing period, each user must pay the difference between the energy demanded and the energy transferred. Being the price of the demanded energy superior to the one of the transferred energy, this allows covering the cost of the losses and of the control and maintenance of the network. As a guideline value the authors estimate that a sale price between 0.18 and 0.20 €/kWh can be compatible with a 12-year amortization period. The purchase price should be between 0.23 and 0.28 €/kWh. A deeper analysis of these prices should be the subject of further studies.
4. Case Study
4.1. Data of the Network
The steady-state operation of a DC-MG formed by 19 nodes was analyzed. The basic data are shown in Figure 7 and in Table 1. This small network was an adaptation of one of the low voltage sections of the network defined in [50] and has been used in other studies on smart grids. In the aforementioned reference, the data of the impedances of each section of the network can be seen.

Figure 7.
Topology of the study-case network.

Table 1.
Data of the study-case network.
Assuming copper conductors of the types indicated in Table 2, the lengths corresponding to the lines were estimated. Figure 8 shows a possible geographical representation according to these lengths. The line type were selected after applying as a design criterion that the voltage drop in each section did not exceed 5% (which could lead to quite large voltage drops, so a lower value could be used) with a design power that depends on the minimum number of nodes remaining at the two ends of the stretch.

Table 2.
Types of conductor in the analyzed network.

Figure 8.
Geographical representation of the analyzed network (some values from Scenario 1 are shown).
4.2. Data of the Nodes
It was assumed that all the nodes corresponded to households of a neighborhood, all with data equal to those shown in Table 3. The selection of operating data was obtained from the analysis of real data of 12 households during a month, but this was outside the scope of the paper. The voltage Vr was 200 V.

Table 3.
Data of the nodes.
To design the PV generator and the ESS of each household, the Ed(p80) was taken into account, so it was unlikely that many households could demand power from the grid simultaneously. With a greater number of households in the MG, it could be expected that approximately 20% of them may need to receive power from the grid. For the same reason, the total power demanded by these households could be 20% of the total demand of the MG. If each household was independent of the rest, the design of each generator and its ESS should be based on the maximum energy demanded by each household. This led to higher values in Ppeak and Qb, resulting in an excess of produced energy during most of the year, which could not be used. For this reason, we considered that the joint operation of the CoDC-MG was a solution that benefits the energy sustainability of the whole.
4.3. Analysis of the Operation of the Network
Randomly, a group of households was selected to function as loads (Scenario 1), demanding the power indicated in Table 4 (with a negative value). With an algorithm developed in Matlab, according to Equations (16) to (23), the operating state of the network was obtained (power generated (with a positive value) and voltage in each node). No conventional load flow was used since there was no slack bus. Table 4 shows results of Scenario 1 taking α2 = 0.1.

Table 4.
Scenario 1 results.
The PFC had an efficiency ηp (ηp ≈ 95%) that was not reflected in the equations because the power data, both consumed and generated, corresponded to powers measured in the network, at the node connection point. That is, if it was indicated that the node demanded P (kW), in reality the power demanded by the loads would be P·ηp. Otherwise, if P’ (kW) was generated, in reality the power generated in the internal bus would be P’/ηp.
The lines were oriented from a node of origin to the destination node. A negative current indicates that the direction of the current was opposite to that of the line. The reference voltage in the PFCs of the nodes was taken as being equal to 210 V, 5% higher than the rated voltage. There were seven consumer nodes (3, 5, 8, 9, 11, 15 and 17) that demanded altogether a power of 12 kW from the network. Seven households represented 35% of the total households, significantly above the 20% that could be expected in a MG with a greater number of households. The same happened with the value of demanded power (12 kW), greater than what could be expected in the case of many households.
Between the maximum and minimum voltages, the difference was 12.39 V. The lowest voltage occurred in node 9 (189.23 V), so the voltage dropped was 5.38% with respect to the rated voltage of 200 V. The total power losses in the network were 218.7 W.
Another case was also analyzed in which all the loads were concentrated on the same side of the network, which was the most unfavorable case from the point of view of voltage drops (Scenario 2). The results with α2 = 0.1 are shown in Table 5.

Table 5.
Scenario 2 results.
There were eight consumer nodes (0, 1 and 13–18) that demanded altogether a power of 11 kW from the network. Between the maximum and minimum voltage, the difference was 31.3 V. The lowest voltage occurred in node 17 (171.79 V). The voltage drop was 14.1% with respect to the rated voltage of 200 V. The total power losses in the network were 1044.5 W.
This situation represented a very unfavorable case in the operation of the network. This set of eight nodes demanding power at the end of the network produced a great influence on the overall functioning of the grid. The network response was correct, since the neighboring nodes to the area where demand took place (nodes 2 and 3) provided more power without reaching their maximum generation limit. In addition, all the nodes, even the distant ones, provided power and contributed to sustaining the whole grid. However, this situation caused high voltage drops. In the discussion section, possible strategies were proposed to prevent this situation from producing such a large voltage drop.
5. Discussion
The proposed CoDC-MG has a primary autonomous control (P-V droop control), which does not need a communication system to operate. That is one of the imposed requirements and one of the main advantages of this network scheme.
Each node can receive power from the network if needed or generate power to help the operation of the whole. No node is critical. It is an authentic structure of peer to peer nodes. Adding or removing a node does not require modifying anything in others, the nodes are plug and play.
The energy benefit of a cooperative network, such as the proposed one, lies in taking advantage of the diversity of consumption. The values Ppeak and Qb assigned to each node have been proposed based on Ed(p80) from a series of real data. These values are intended to guarantee the self-consumption of each node in most situations. However, taking into account the stochastic nature of energy consumption, there is a small probability that some households exceed the design values and need the support of others.
This support, in fact, is possible in many cases, because for the whole set of households, the average consumption Ed(av) is lower than that used in the design of the facilities.
To guarantee the autonomous operation of an isolated household, it would have been necessary to design the facilities with the maximum registered value of Ed since having only a probability of operation of 0.8 would not be possible. Therefore, Ppeak and Qb values would be higher in the 19 households.
Nonetheless, with these higher values, the probability that the maximum SOC value in the batteries will be reached for many days increases and so a certain amount of energy that would be available in the panels is lost, with a worse overall energy efficiency in the whole microgrid. Hence, the joint operation of the cooperative network improves efficiency, while trying to ensure a reliable operation of the whole, thereby improving global energy sustainability.
As can be observed in the results shown for the very unfavorable scenario 2, depending on the state of the loads, the local voltage in some areas might be noticeably lower than the Vr and the voltage drop might be greater than desired. A secondary control level can correct these deviations [51]. The voltage drops observed in this case are a consequence of the criteria that have been adopted here to design the network (a voltage drop of up to 5% has been allowed in each section of the network). As will be discussed later, with more strict design criteria (less voltage drop in each section) the results shown in scenario 2 could be significantly improved, so that secondary control could be avoided.
To see how some control parameters affect the voltage of nodes, a sensitivity study of the voltage drop was carried out.
The influence of parameter h2 was analyzed for scenario 2. Parameter h2 could vary in three ways, changing the maximum power that each node could provide (PmaxG), changing the reference voltage of the node (Vr) or changing the parameter α2.
Initially the value α2 = 0.1 (that corresponded to was used to obtain the results shown in Section 4. Table 6 shows voltage drops and the losses for several values of α2 (the same value in all the nodes).

Table 6.
Voltage drop and power losses for different values of α2.
Small values of α2 guaranteed lower voltage drops, increasing the power contribution from the nodes closest to the loads, while larger values of the parameter allowed more distribution of the demand among all the nodes of the network. Thus, with larger values of α2 the voltage drops were greater and the losses increased.
By setting α2 = 0.08 (that corresponds to , node 2 saturated the maximum power it could deliver to the network (2 kW). Node 3 increased the power delivered to the network (from 1.56 kW to 1.66 kW). This was because these were the nodes closest to the loads that demand power. If the value of PmaxG in node 2 was increased to 3 kW, parameter h2 increased in that node to a value equal to and the delivered power by this node to the network was 2.94 kW. Delivered power in node 3 decreased to 1.49 kW, the voltage drop decreased from 12.72% to 11.64% and losses in the network decreased from 999 W to 894 W. These results were logical since the proposed control system made the nodes closest to the loads contribute more power and it results in benefits in those two magnitudes.
With other nodes not so close to the loads, the effect was lower. If PmaxG in node 5 was increased to 3 kW, this node went from generating 1.02 kW to 1.44 kW, but the voltage drop was only reduced to 12.48% and the losses would be 993 W.
A similar effect was achieved by varying the parameter α2 of a node, but there were important differences. For example, when changing α2 in node 2 to 0.0533, (same value as the previous case) but the results almost did not change, since the power contributed by the node had reached the maximum. If the same operation was made in node 3, this node saturated. In this case, the voltage drop was slightly improved to 12.37% and the losses decreased to 973 W. However, if the change was made in node 5, the results were the same as if the PmaxG in the node was increased to 3 kW.
Therefore, a secondary control system could act by modifying α2 in all the nodes or in some concrete ones, depending on the voltage profile. The value of PmaxG of some nodes that were saturated could also be varied, although the latter affected the design of each node.
However, this secondary control could be avoided due to the following reasons:
- -
- The load/generation states are variable over time, complicating the requirements of the system and could promote instabilities in the secondary control.
- -
- The correct design of the network can guarantee that in normal operation the voltages remain within the limits Vlim < Vg < 1.05·Vr, being this range an important design factor that the equipment manufacturers should know. The criterion applied in Section 4.1 of this study allowed a wide range of voltage drops, but other more restrictive criteria are possible. In fact, if the sections chosen in each branch can cause voltage drops of up to 5%, the voltage drop of the entire network can be considerably higher. However, choosing as a design criterion a voltage drop of 2% in each section (which results in conductor sections greater than those indicated in Table 1), the results of scenario 2 show a total voltage drop of 4.86%. Thus, the minimum voltage of the network would be 190.3 V at node 17 and the power losses would be 423 W. Bearing in mind that the state of the nodes can arbitrarily change from generation to load and that most of them must operate autonomously, it is not easy with this structure to apply a design criterion based on the voltage drop of the complete network, as it is used in the design of conventional networks.
- -
- Current DC/DC and DC/AC converters support a wide range of input voltages, maintaining the output voltage, with good performance throughout the whole range. Therefore, for the loads fed by this equipment, the fact that the voltage of the network is lower than Vr does not represent a major problem.
- -
- Taking into account that the connection of the nodes to the network is done through PFC that is a smart DC–DC converter, this equipment can admit a wide range of voltages at the input maintaining the output voltage. Therefore, the voltage in the network, within certain limits, does not affect the operating voltage of the internal node, so large voltage drops (20% for example) would be admissible, although the authors proposed to try to limit these voltage drops to lower values.
The possibility of varying the parameter h2 of each node allows varying the power distribution between the nodes, although the final result will always depend on the state of charge/generation.
Regarding the tertiary control is not necessary in this CoDC-MG. The distribution of powers depends on the state of charge/generation of the network, which can vary frequently.
6. Conclusions
In this paper, the authors defined a DC-MG structure with a new approach with respect to other MGs. The operation of the network depends on the collaboration of all the nodes, so the name cooperative DC-MG was proposed.
One of the objectives for CoDC-MG is that the structure must be very simple and the operation must require little or no attention from a control centre and be independent of a communications system. This is intended to simplify the design of this type of networks that can facilitate the use of distributed renewable generation of individual type, but with the support of the network to achieve better guarantees of reliability.
This type of facility could be the basis for future distribution networks, the purpose of which would be to link these facilities together in order to achieve bottom-up network development (from consumers to large networks), in contrast to the classic network structure of electric power systems that develop from top to bottom.
The cooperative DC-MG can operate under variable load-generation situations, as shown in the two examples that have been presented in the paper. Each node can receive power from the network or operate as a generator, depending on the internal energy state and the operating state of the network. Being a DC network, only the voltage is required as a control variable. Each node uses the SOC of his battery, its internal bus voltage and the voltage of the network to which it is connected to establish its mode of operation. The device proposed to perform power transmission between the node and the network (PFC) is a reversible DC/DC smart converter whose general operation was described in the paper.
The developed method allows obtaining the steady state of operation of the MG for any situation of power demand in the nodes (subject to the condition that it can be supplied by the remaining nodes of the MG) without fixing the voltage of any of them as a reference node (there is no root or slack bus). The voltages are self-adjusted to the random loading/generation states of the nodes.
Although an autonomous control system (primary droop control P–V) was proposed for simplicity, a secondary control could be established to improve aspects of the operation of the network. Nevertheless, an adequate design when selecting the branches’ sections could guarantee a correct operation even without this secondary control. The existence in each node of a PFC allows a correct operation of the loads in the node even with large voltage drops in the network (20%).
The development of networks in DC requires further research and important standardization and regulation work is necessary. With the development of this type of networks the individual use of renewable generation would be facilitated. The adaptation of domestic loads (and many industrial loads) to operate in DC is not, today, a major problem.
Author Contributions
Conceptualization and methodology, C.R.-P.; simulation software design C.R.-B.; experiments design and validation, G.E.-E. and E.Q.; formal analysis, C.R.-P.; data curation C.R.-B., G.E.-E. and E.Q.; writing—original draft preparation, C.R.-P.; writing—review and editing, C.R.-B., G.E.-E. and E.Q.; supervision and funding acquisition, C.R.-P.
Funding
This work has been partially supported by funds for research support of the Universitat Politècnica de València.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations were used in this paper:
| AC | Alternating current |
| CoDC-MG | cooperative DC microgrid |
| DC | Direct current |
| DG | distributed generation |
| Eb | daily energy provided by batteries to loads in a sunny day |
| Ed | daily energy consumption |
| Ed(p80) | daily energy consumption with 20% probability of being exceeded |
| Ed(av) | average value of daily energy consumption |
| ESS | energy storage systems |
| E1 | excess energy produced by the PV panels |
| h1, h2 | drop coefficients (A) |
| battery current | |
| Ik | current of the conductor of the section k of the network |
| Imax | BC maximum current value |
| Kc | fictitious conductance for battery charging |
| Kd | fictitious conductance for battery discharging |
| MG | microgrid |
| nc | consecutive cloudy days |
| Nv | Number of households in the MG |
| Pb(t) | power provided by the battery |
| Pd(peak) | maximum demanded power |
| Pd(peak,p80) | maximum power with 20% probability of being exceeded |
| Pd(peak,av) | average value of maximum demanded powers |
| PF(t) | solar irradiance curve |
| PFC | power flow controller |
| Pg | power flow of the grid at one node |
| total power generated in the microgrid | |
| total power demanded in the microgrid | |
| power losses in the microgrid | |
| PmaxL (to load) | maximum power demanded by the household from the grid |
| PmaxG (to grid) | maximum power delivered by the household to the grid |
| Ppeak | rated power installed in PV panels |
| PS(t) | power produced by the PV array |
| PR | PV array performance ratio |
| Qb | battery capacity |
| Rk | resistance of the conductor of the section k of the network |
| S | section of the copper conductor |
| SOC | state of charge of battery |
| SOCmax | maximum admissible value of SOC |
| SOCmin | minimum admissible value of SOC |
| Vg | network voltage at the node connection point |
| Vi(t) | internal bus voltage |
| Vlim | minimum admissible network voltage |
| VPP | virtual power plant |
| Vr | rated network voltage |
| α1, α2 | constant parameters |
| efficiency Li-ion battery | |
| ηc | battery charging efficiency |
| ηd | battery discharging efficiency |
| ηp | PFC efficiency |
References
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J.W. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Brown, R.E.; Willis, H.L. The economics of aging infrastructure. IEEE Power Energy Mag. 2006, 4, 36–43. [Google Scholar] [CrossRef]
- Asmus, P. Microgrids, Virtual Power Plants and Our Distributed Energy Future. Electr. J. 2010, 23, 72–82. [Google Scholar] [CrossRef]
- Raul, A. Barreto, Fossil fuels, alternative energy and economic growth. Econ. Model. 2018, 75, 196–220. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Zhang, B.; Halang, W.A. Power electronics converters: Past, present and future. Renew. Sustain. Energy Rev. 2018, 81 Pt 2, 2028–2044. [Google Scholar] [CrossRef]
- Lasseter, R.H. MicroGrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308. [Google Scholar] [CrossRef]
- Santacana, E.; Rackliffe, G.; Tang, L.; Feng, X. Getting Smart. IEEE Power Energy Mag. 2010, 8, 41–48. [Google Scholar] [CrossRef]
- Hatziargyriou, N. Microgrids: Architectures and Control; Wiley, IEEE Press: Athens, Greece, 2014. [Google Scholar]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Zountouridou, E.I.; Hatziargyriou, N.D. Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 2015, 122, 159–167. [Google Scholar] [CrossRef]
- Paska, J.; Biczel, P.; Kłos, M. Hybrid power systems—An effective way of utilising primary energy sources. Renew. Energy 2009, 34, 2414–2421. [Google Scholar] [CrossRef]
- Salomonsson, D.; Sannino, A. Low-Voltage DC Distribution System for Commercial Power Systems With Sensitive Electronic Loads. IEEE Trans. Power Deliv. 2007, 22, 1620–1627. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Longo, M.; Abegaz, T. Integration and optimization of renewables and storages for rural electrification. Sustainability 2016, 8, 982. [Google Scholar] [CrossRef]
- Khalid, M.; Ahmadi, A.; Savkin, A.V.; Agelidis, V.G. Minimizing the energy cost for microgrids integrated with renewable energy resources and conventional generation using controlled battery energy storage. Renew. Energy 2016, 97, 646–655. [Google Scholar] [CrossRef]
- Mahdavyfakhr, M.; Rashidirad, N.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. Stability improvement of DC grids involving a large number of parallel solar power optimizers: An active damping approach. Appl. Energy 2017, 203, 364–372. [Google Scholar] [CrossRef]
- Lazzari, R.; Piegari, L.; Grillo, S.; Carminati, M.; Ragaini, E.; Bossi, C.; Tironi, E. Selectivity and security of DC microgrid under line-to-ground fault. Electr. Power Syst. Res. 2018, 165, 238–249. [Google Scholar] [CrossRef]
- Salomonsson, D.; Soder, L.; Sannino, A. Protection of Low-Voltage DC Microgrids. IEEE Trans. Power Deliv. 2009, 24, 1045–1053. [Google Scholar] [CrossRef]
- Shuai, Z.; Fang, J.; Ning, F.; Shen, Z.J. Hierarchical structure and bus voltage control of DC microgrid. Renew. Sustain. Energy Rev. 2018, 82 Pt 3, 3670–3682. [Google Scholar] [CrossRef]
- Van den Broeck, G.; Stuyts, J.; Driesen, J. A critical review of power quality standards and definitions applied to DC microgrids. Appl. Energy 2018, 229, 281–288. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed Control to Ensure Proportional Load Sharing and Improve Voltage Regulation in Low-Voltage DC Microgrids. IEEE Trans. Power Electron. 2013, 28, 1900–1913. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.I. Linear Active Stabilization of Converter-Dominated DC Microgrids. IEEE Trans. Smart Grid 2012, 3, 203–216. [Google Scholar] [CrossRef]
- Che, Y.; Zhou, J.; Lin, T.; Li, W.; Xu, J. A Simplified Control Method for Tie-Line Power of DC Micro-Grid. Energies 2018, 11, 933. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, L.; Liu, S.; Wang, G. Cooperation between Two Micro-Grids Considering Power Exchange: An Optimal Sizing Approach Based on Collaborative Operation. Sustainability 2018, 10, 4198. [Google Scholar] [CrossRef]
- González, A.; Riba, J.-R.; Rius, A. Optimal Sizing of a Hybrid Grid-Connected Photovoltaic–Wind–Biomass Power System. Sustainability 2015, 7, 12787–12806. [Google Scholar] [CrossRef]
- Maleki, A.; Rosen, M.A.; Pourfayaz, F. Optimal Operation of a Grid-Connected Hybrid Renewable Energy System for Residential Applications. Sustainability 2017, 9, 1314. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Roldán-Porta, C. Improving the benefits of demand response participation in facilities with distributed energy resources. Energy 2019, 169, 710–718. [Google Scholar] [CrossRef]
- Mao, M.; Jin, P.; Chang, L.; Xu, H. Economic Analysis and Optimal Design on Microgrids with SS-PVs for Industries. IEEE Trans. Sustain. Energy 2014, 5, 1328–1336. [Google Scholar] [CrossRef]
- Elrayyah, A.; Cingoz, F.; Sozer, Y. Construction of Nonlinear Droop Relations to Optimize Islanded Microgrid Operation. IEEE Trans. Ind. Appl. 2015, 51, 3404–3413. [Google Scholar] [CrossRef]
- Meng, L.; Shafiee, Q.; Trecate, G.F.; Karimi, H.; Fulwani, D.; Lu, X.; Guerrero, J.M. Review on Control of DC Microgrids and Multiple Microgrid Clusters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 928–948. [Google Scholar] [CrossRef]
- Huang, H.; Hsieh, C.; Liao, J.; Chen, K. Adaptive Droop Resistance Technique for Adaptive Voltage Positioning in Boost DC–DC Converters. IEEE Trans. Power Electron. 2011, 26, 1920–1932. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed Cooperative Control of DC Microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Wang, P.; Lu, X.; Yang, X.; Wang, W.; Xu, D. An Improved Distributed Secondary Control Method for DC Microgrids with Enhanced Dynamic Current Sharing Performance. IEEE Trans. Power Electron. 2016, 31, 6658–6673. [Google Scholar] [CrossRef]
- Ma, J.; Yuan, L.; Zhao, Z.; He, F. Transmission Loss Optimization-Based Optimal Power Flow Strategy by Hierarchical Control for DC Microgrids. IEEE Trans. Power Electron. 2017, 32, 1952–1963. [Google Scholar] [CrossRef]
- Ren, L.; Qin, Y.; Li, Y.; Zhang, P.; Wang, B.; Luh, P.B.; Han, S.; Orekan, T.; Gong, T. Enabling resilient distributed power sharing in networked microgrids through software defined networking. Appl. Energy 2018, 210, 1251–1265. [Google Scholar] [CrossRef]
- Che, L.; Shahidehpour, M. DC Microgrids: Economic Operation and Enhancement of Resilience by Hierarchical Control. IEEE Trans. Smart Grid 2014, 5, 2517–2526. [Google Scholar] [CrossRef]
- Lasseter, R.H. Smart Distribution: Coupled Microgrids. Proc. IEEE 2011, 99, 1074–1082. [Google Scholar] [CrossRef]
- Fathi, M.; Bevrani, H. Statistical Cooperative Power Dispatching in Interconnected Microgrids. IEEE Trans. Sustain. Energy 2013, 4, 586–593. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Cooperative Planning of Renewable Generations for Interconnected Microgrids. IEEE Trans. Smart Grid 2016, 7, 2486–2496. [Google Scholar] [CrossRef]
- Kasaei, M.J.; Gandomkar, M.; Nikoukar, J. Optimal management of renewable energy sources by virtual power plant. Renew. Energy 2017, 114 Pt B, 1180–1188. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, H.; Zhu, J.; Liang, H.; Li, P. The Optimal Dispatch of a Power System Containing Virtual Power Plants under Fog and Haze Weather. Sustainability 2016, 8, 71. [Google Scholar] [CrossRef]
- Gunasekaran, M.; Mohamed Ismail, H.; Chokkalingam, B.; Mihet-Popa, L.; Padmanaban, S. Energy Management Strategy for Rural Communities’ DC Micro Grid Power System Structure with Maximum Penetration of Renewable Energy Sources. Appl. Sci. 2018, 8, 585. [Google Scholar] [CrossRef]
- Khan, Z.A.; Jayaweera, D. Approach for smart meter load profiling in Monte Carlo simulation applications. IET Gener. Transm. Distrib. 2017, 11, 1856–1864. [Google Scholar] [CrossRef]
- Joint Research Centre. Photovoltaic Geographical Information System. 2014. Available online: http://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 18 December 2018).
- Wang, J.Y.; Qian, Z.; Zareipour, H.; Wood, D. Performance assessment of photovoltaic modules based on daily energy generation estimation. Energy 2018, 165 Pt B, 1160–1172. [Google Scholar] [CrossRef]
- International Electrotechnical Commission, IEC 60364, Electrical Installations of Buildings—Part 5: Selection and Erection of Electrical Equipment. 2009. Available online: https://webstore.iec.ch/publication/1878 (accessed on 1 October 2019).
- Chang, Y.-C.; Chang, H.-C.; Huang, C.-Y. Design and Implementation of the Battery Energy Storage System in DC Micro-Grid Systems. Energies 2018, 11, 1566. [Google Scholar] [CrossRef]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; Wasynczuk, O.; Varigonda, S. Applicability of available Li-ion battery degradation models for system and control algorithm design. Control Eng. Pract. 2018, 71, 1–9. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A.S. Real-Time Coordination of Plug-In Electric Vehicle Charging in Smart Grids to Minimize Power Losses and Improve Voltage Profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).