Multiscale Market Integration and Nonlinear Granger Causality between Natural Gas Futures and Physical Markets

Abstract

This paper comprehensively analyzed the price integration of the U.S. natural gas futures market and its physical markets. The analyses were conducted in the form of graphics using the ensemble empirical mode decomposition (EEMD) method and minimum spanning trees with various horizons. Our findings indicated that the network structures of the minimum spanning trees of the gas futures and physical markets are the same on different time scales. The citygate returns were always the core of the physical gas markets. In addition, the gas futures and physical markets were highly integrated on different time scales. Moreover, our findings showed that at the original data level, unidirectional linear and nonlinear causalities from gas futures to physical returns exist. Specifically, the relationships between futures and physical gas returns were not constant across various time scales. In the long term, futures gas returns had only a linear causality with the citygate, commercial, and industry gas returns, and a unidirectional, nonlinear causality with residential gas returns.

1. Introduction

The integration of the natural gas futures market and the wholesale and end-use gas markets (gas physical markets), and the complex linkage mechanisms between them, have often been the focus of energy policy makers and market participants [1]. Market participants take part in natural gas market activities, and market information is conveyed through the various types of natural gas markets. Changes in the gas futures market could cause changes in the gas physical markets, and price information from the natural gas physical markets could also be fed back to the gas futures market. In addition, price movements in the physical natural gas markets would present price risks for market participants. However, market participants can trade in the natural gas futures market in order to mitigate price risks. Thus, by using this type of information transmission to manage market risk, market participants can create optimal natural gas production or storage plans. Furthermore, by gaining a better understanding of the complex linkage mechanism between the natural gas futures market and the physical markets, related energy policy makers can create effective supply and demand adjustment strategies and long-term policies for the natural gas physical markets.

In this study, a novel approach—the minimum spanning tree model—was used to analyze the integration of natural gas futures and the physical markets. First, the synchronous correlation coefficients of natural gas physical and futures returns were computed. Next, the minimum spanning tree for the natural gas market integration was constructed. To measure the tightness of the minimum spanning trees, the normalized length of the minimum spanning trees was calculated. Thus, the integration between natural gas futures and physical markets could be captured directly in the form of graphics. In particular, the status and the importance of transmitting information about gas futures and physical prices in the network can be identified, thereby providing useful information for related energy policy makers, producers, and dealers.

In addition, as segments in the natural gas markets, the gas futures prices and the upstream and downstream physical gas prices are also impacted by hurricanes, global financial crises, and other significant extreme events related to the crude oil market [2,3,4,5,6]. Moreover, since 2006, the North American shale gas revolution has caused the country’s domestic natural gas production to increase quickly [7,8], which may also change the linkage mechanism between the futures and physical gas markets. The impact of all of these significant shocks on the market may cause the energy markets to undergo structural changes [9,10,11], which also shows that different natural gas markets with different attributes exhibit nonlinear characteristics. Therefore, the nonlinear features of the relationship between the futures and physical markets should be considered. However, previous studies have mainly used a linear model to investigate these issues, making it difficult to capture nonlinear features. Unlike previous studies, this research used the nonlinear Granger test to analyze the nonlinear features of the natural gas markets.

Furthermore, time scales have also been the focus of numerous market participants. The different segments of the natural gas markets with their different attributes are complex systems that have various time scale characteristics [12,13,14]. Consequently, time scales strongly influence the inherent connection mechanisms between natural gas futures and physical markets. For example, differences in the price information transmission mechanisms between the natural gas futures and physical markets may present themselves depending on the time scales considered [15]. Depending on the time scale, the market tactics of market investors, gas producers, suppliers, and consumers will differ. Therefore, the ensemble empirical mode decomposition (EEMD) model proposed by Wu and Huang [16] was employed to construct a new multiscale analysis framework to clarify the integration and complicated relationship between the natural gas physical and futures markets when different time scales are considered. Such information will be beneficial for market participants in developing effective market portfolios and risk aversion strategies on various horizons; in addition, it will help energy policy makers make short-term adjustment strategies or long-term policies.

In the current study, the U.S. natural gas market was chosen as the analysis sample to explore the above issues, due to its maturity. The U.S. natural gas futures market started in 1992, and due to the rapid development of the natural gas futures market, buyers are better able to hedge their options in this market [17]. In the U.S., the natural gas upstream and downstream physical markets have also undergone a series of reforms that started in the 1980s, leading to the gradual liberalization of natural gas physical markets. Unlike previous studies, this study mainly made the following three contributions. First, using a novel approach—the minimum spanning trees—the integration of natural gas futures and physical markets have been directly presented in a graphical form. Second, the nonlinear linkage mechanism between gas futures and physical markets was further tested, providing direct evidence of the differences and similarities with the linear findings. Finally, a multiscale analysis approach was explored to comprehensively analyze the integration and nonlinear relationship between futures and physical gas markets on different time horizons from a new perspective.

The structure of the current paper is organized as follows. The second section reviews the related literature. The third section mainly describes the EEMD model, the minimal spanning tree model, and the linear and nonlinear Granger causality tests and data sources. The fourth section contains the empirical results and the discussion. The last section comprises the conclusion and policy implications.

2. Literature Review

Some scholars have analyzed the integration of the natural gas markets. Siliverstovs et al. [18] investigated the degree of integration between the European, North American, and Japanese natural gas markets between the early 1990s and 2004 and found high integration between the European and Japanese markets, but the European and Japanese markets and the North American markets were still distinct. Renou-Maissant [19] found a strong level of integration between the natural gas markets in continental Europe, while continental European markets and the UK market were not integrated. Dieckhöner et al. [20] found that the increased demand for natural gas developments and major import pipeline commissions had a significant impact on the integration level of the European physical market. Barnes and Bosworth [21] used a gravity model to test whether the liquefied natural gas trade had increased the integration of the global natural gas market, and found that it had played an important role.

Furthermore, some scholars have analyzed the integration and relationship between different market segments in the natural gas markets. Arano and Velikova [22] suggested that there was a long-term co-integration relationship between the natural gas citygate and residential prices in 90% of the U.S. after the FERC636 provisions in 1992. Arano and Velikova [23] studied the integration degree between natural gas citygate and residential gas prices, and the results showed an equilibrium co-integration relationship between these two prices in the long run. Mohammadi [24] analyzed the natural gas upstream and downstream price behavior in the U.S. natural gas industry. Their results showed that supply–demand shock plays an important role in short-term price behavior, and the long-term changes in well prices are mainly because of the impact of changes in residential and power gas prices. Apergis et al. [25] analyzed the co-integration relationship between natural gas citygate and residential retail prices in all U.S. states from January 1989 to December 2012, and revealed a bidirectional linear Granger causality between the citygate and residential retail prices in the short and long term for all states after 1995, further indicating an increase in the integration degree of the natural gas downstream market. Using monthly data from June 1990 to December 2014, Ghoddusi [26] analyzed the relationship between the natural gas futures and physical markets, and showed that a unidirectional Granger causality from natural gas futures to all of natural gas physical prices exists. Ghoddusi and Emamzadehfard [27] analyzed the hedging effect between natural gas futures prices and six different natural gas physical prices for different contract periods. They found that the hedging effect between the natural gas futures and downstream markets was much weaker relative to the natural gas upstream market, and, at the same time, the hedging effect tended to increase as the contract periods rose.

Based on the above literature review, the conclusions that have been drawn regarding the linkage between the natural gas futures and physical gas markets are mixed. Previous literature has analyzed their integration using co-integration methods, and most have also neglected that nonlinear features of natural gas markets exist. Furthermore, most of the previous literature investigated the integration and relationship at the original data level only. To clarify the complex integration and linkage mechanisms between the natural gas futures and physical markets, this study used a novel approach—minimum spanning tree—to intuitively exhibit the integration degree of the gas futures and physical markets. The advantage of the minimum spanning tree is that it can easily unveil the status and the importance of transmitting information about gas futures and physical markets in the network. In addition, this study captured the nonlinear feature of natural gas markets by using nonlinear Granger tests. Furthermore, this study also constructed a new multiscale analysis framework to comprehensively investigate the linkage mechanisms on different time horizons.

3. Methodology and Data Sources

The integration and causalities of the U.S. physical and futures markets have different characteristics on different time scales. Therefore, we constructed a new multi-scale analysis framework. Firstly, the EEMD method was employed to decompose the returns of natural gas futures and physical markets into different time-frequency series. Through the decomposition of the EEMD approach, the high frequency, low frequency, and long trend term decomposed timeseries were obtained, which have different economic implications. Using the decomposition series, the minimal spanning tree model was then employed to construct the minimal spanning tree graphs of natural gas markets on different time scales, in order to explore the integration of natural gas futures and physical markets across the time horizons. Furthermore, using the decomposition series, the linear and nonlinear Granger causality test was used to comprehensively investigate the linear and nonlinear linkages between the natural gas futures and physical markets in the short, medium, and long term.

3.1. EEMD Model

The EEMD method effectively decomposed the price returns of natural gas futures and physical markets into different orthogonal time scale series. Before the decomposition, the returns of the futures and physical markets were calculated for further analysis. If $r_i$ represents the natural gas market return series, then $r_i=\ln (P_i(t))-\ln (P_i(t-1))$ where $P_i(t)$ is the price of the natural gas market $i$ at $t$. By decomposing the original return series $x(t)$, a series of orthogonal intrinsic mode function (IMF) components can be obtained: $c_1,c_2,...,c_n$, and $r_1-c_2=r_2$, $r_2-c_3=r_3$, $...,r_{n-1}-c_n=r_n$. The original target time series $x(t)$ can be represented by the IMFs and one residual term as follows [28]:

$$x(t)={\displaystyle \sum _{i=1}^n{c}_i}+r_n$$

(1)

where $c_i$ represents the IMF, $n$ is the number of IMFs, and $r_n$ represents the residual term of the original target time series $x(t)$.

3.2. Minimal Spanning Tree Model

To investigate the integration of the U.S. physical and futures markets with various horizons, this study used graph theory to construct minimum spanning tree models on multiple time scales. The advantage of the minimum spanning tree approach is that it can overcome the curse of dimensionality based on the pairwise correlation, while other network models, such as connectedness network, are heavily limited by the number of variables [29,30,31,32,33].

First, the synchronous correlation coefficients of natural gas physical and futures returns on multi-time scales were computed as follows [34]:

$${\rho }_{ij}=\frac{\overline{r_i{r}_j}-\overline{r_i}\overline{r_j}}{\sqrt{(\overline{r_i^2}-{\overline{r_i}}^2)(\overline{r_j^2}-{\overline{r_j}}^2)}}$$

(2)

where ${\rho }_{ij}$ is the correlation coefficient, and $r_i$ and $r_j$ correspond to the decomposition time series of the monthly returns for natural gas markets $i$ and $j$, respectively. ${\overline{r}}_i$ is the average of $r_i$ for the whole period; $T$ is the sample length. Thus, the $6\times 6$ matrix of correlation coefficients $C$ can be computed for all pairs $ij$. $C$ is symmetric with ${\rho }_{ij}=1$ when $i=j$.

The minimum spanning tree models for the natural gas market integration was then constructed. However, the correlation coefficient ${\rho }_{ij}$ could not be used as a distance $d_{ij}$ because it did not fulfil the three criteria of Euclidean distance [35]: (1) $d_{ij}=0$ if and only if $i=j$, (2) $d_{ij}=d_{ji}$, and (3) $d_{ij}\le d_{ik}+d_{kj}$. Therefore, the correlation matrix $C$ was transformed into the distance matrix $D$ using the following formula:

$$d_{ij}=\sqrt{2(1-{\rho }_{ij})}$$

(3)

where $d_{ij}$ represents the distance between the monthly gas returns. This distance matrix corresponded to the fully connected graph. If the value of the distance is small, it shows that the degree of integration of the two groups of natural gas markets is high. The minimum spanning tree models of the physical and futures natural gas markets on different time scales were constructed using the algorithm by Kruskal [36].

To measure the tightness of the minimum spanning trees on different time scales, the normalized length of the minimum spanning trees was calculated as follows:

$$L=\frac{1}{N-1}{\displaystyle \sum _{(i,j)\in MST}{d}_{ij}}$$

(4)

where $d_{ij}$ denotes the distance between $i$ and $j$. $N-1$ indicates the number of edges, $MST$ represents the minimum spanning tree, and $L$ represents the normalized length of the minimum spanning tree. If the value of $L$ is small, it shows that the integration degree of the natural gas markets is high.

3.3. Linear Granger Test

First, the stationary characteristics of the original and decomposition series were examined using the unit root test. If all of these characteristics are stationary, the vector autoregressive (VAR) model proposed by Sims [37] can be used to analyze the linear Granger causality between the natural gas futures and physical markets. The bivariate VAR model was constructed as follows:

$$\Delta Y_t=a_1+{\displaystyle \sum _{i=1}^m{b}_{1i}\Delta X_{t-i}}+{\displaystyle \sum _{j=1}^m{c}_{1j}}\Delta Y_{t-j}+{\epsilon }_{1t}$$

(5)

$$\Delta X_t=a_2+{\displaystyle \sum _{i=1}^m{b}_{2i}\Delta X_{t-i}}+{\displaystyle \sum _{j=1}^m{c}_{2j}}\Delta Y_{t-j}+{\epsilon }_{2t}$$

(6)

where $a_1$ and $a_2$ represent the intercept terms, and $b$ and $c$ represent the estimated coefficients. $m$ represents the optimal lag order of the model, which is determined using the Akaike information criterion (AIC). The null hypothesis is that X cannot Granger cause Y in Equation (5), and Y cannot Granger cause X in Equation (6); that is, $b_{1i}=0$ and $c_{2i}=0$ $(i=1,2,...,m)$.

3.4. Nonlinear Granger Test from the GARCH (1,1) Model

First, the GARCH (1,1) model was used to filter the natural gas futures and the physical original and decomposition series to obtain the residual series (considering that the natural gas market returns may have a GARCH effect, this study introduced the GARCH model to capture this dynamic effect) [38]. The standard GARCH (1,1) model was constructed as follows [39]:

$$y_t={\mathbf{x}}_t^{\prime }\mathsf{\gamma }+u_t,u_t\sim N(0,{\sigma }_t^2)$$

(7)

$${\sigma }_t^2=a_0+a_1{u}_{t-1}^2+{\beta }_1{\sigma }_{t-1}^2$$

(8)

where $x_t=(x_{1t},x_{2t},\cdots ,x_{kt}{)}^{\prime }$ is the explanation variable vector, and $\mathsf{\gamma }=({\gamma }_1,{\gamma }_2,\cdots {\gamma }_k{)}^{\prime }$ is the coefficient vector.

The nonlinear Granger causality test proposed by Diks and Panchenko [40] was then performed to uncover the nonlinear causality between the natural gas futures and physical markets by using the GARCH (1,1) filtered residual series, which effectively overcame the over-rejection problem of the method proposed by Hiemstra and Jones [41].

3.5. Data Sources

The natural gas futures (contract 1) and physical prices were derived from the U.S. Energy Information Administration website were obtained from https://www.eia.gov/dnav/ng/NG_PRI_FUT_S1_D.htm; the physical gas prices were obtained from https://www.eia.gov/dnav/ng/ng_pri_sum_dcu_nus_m.htm). Because of the availability of the data, the monthly prices of natural gas futures, citygate, commercial, residential, industrial, and natural power were collected for the period from January 2002 to March 2017. The citygate price of natural gas is the price paid by natural gas retailers when they receive the natural gas through pipelines; the prices of commercial, residential, industrial, and natural power natural gas are the prices paid by service companies, residents, factories, and power companies for using natural gas, respectively. All of the data were adjusted for inflation over the examined period. To construct real oil prices and real gas prices, the nominal prices were deflated by the monthly consumer price index of the U.S., obtained from the Federal Reserve Bank of Saint Louis. Figure 1 shows the movements of the natural gas futures and physical prices from January 2002 to March 2017. Here, it can be seen that the overtrends of the natural gas futures prices and citygate, commercial, industrial, and power prices have always stayed consistent, while the residential prices show obvious seasonal characteristics.

Table 1. Summary statistics of the price series for natural gas futures and physical markets.

	Futures	Citygate	Commercial	Residential	Industry	Power
Mean	5.010	6.149	9.407	12.534	5.810	5.480
Median	4.336	5.730	9.070	12.380	5.280	5.040
Max	13.454	12.480	15.640	20.770	13.060	12.410
Min	1.812	3.220	6.280	7.100	2.880	2.330
Std. dev.	2.320	1.884	1.835	2.818	2.032	2.007
Skewness	1.313	1.010	0.869	0.337	1.138	1.015
Kurtosis	4.968	3.916	3.770	2.409	4.260	4.091
Jarque–Bera	82.099	37.545	27.561	6.119	51.592	40.475
Probability	0.000	0.000	0.000	0.047	0.000	0.000
N	183	183	183	183	183	183

Note: The unit of the price series for natural gas futures and physical markets is USD/Mbtu.

shows the descriptive statistics of the natural gas futures and physical prices. The average prices of commercial and residential gas were significantly higher than those of citygate, industrial, and power. At the same time, the standard deviations of residential gas and futures prices were higher than those of the other kinds of natural gas prices, indicating that residential gas and futures prices fluctuate at significantly higher levels than those of the other kinds of natural gas prices. This is mainly because residential gas prices are susceptible to seasonality, such as in the winter. The seasonal component of the price creates additional noise; thus, the seasonally adjusted data were obtained using the X-12 procedure for further analysis.

4. Empirical Results and Discussion

4.1. Multiscale Analysis

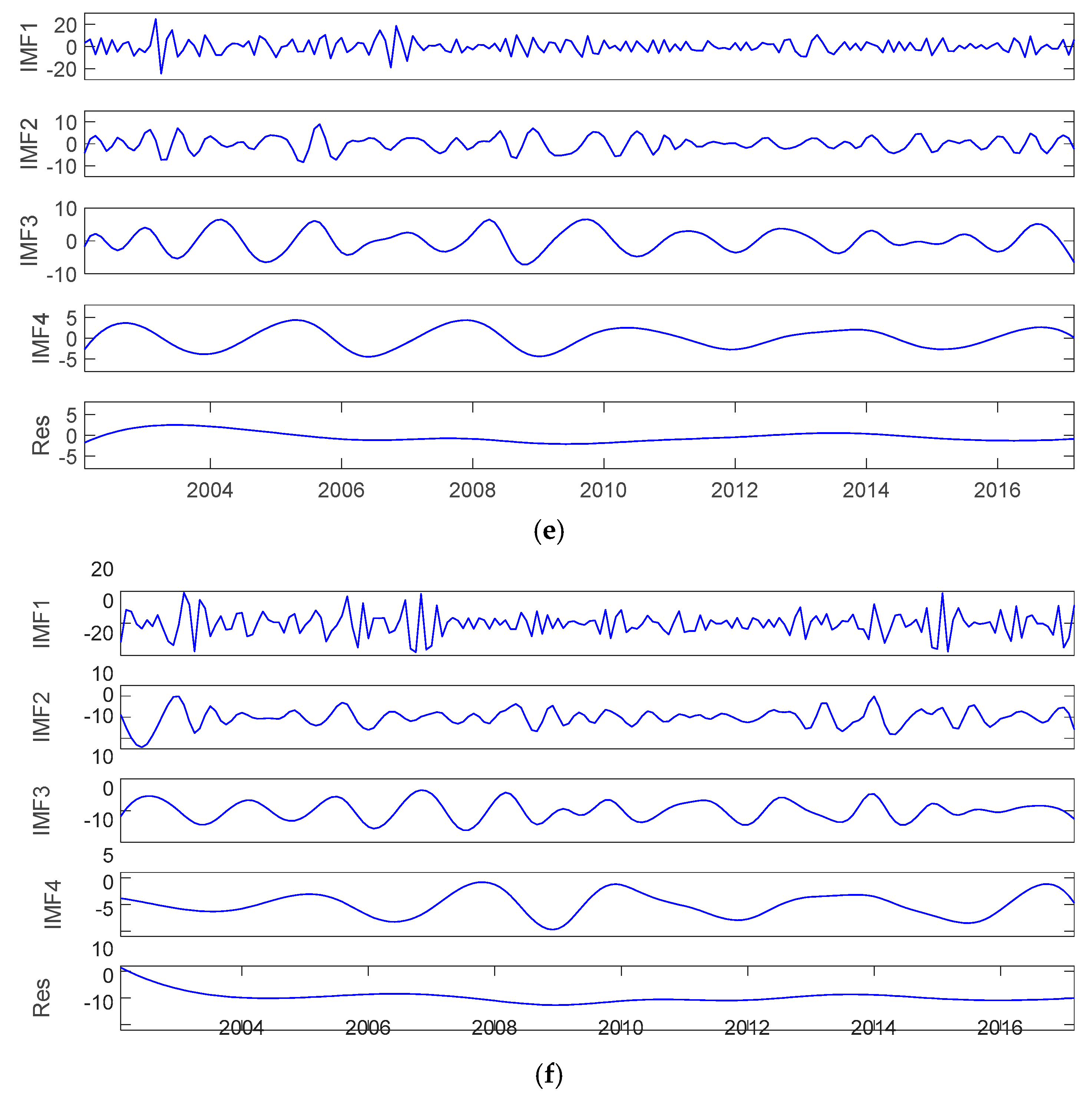
The decomposition results of natural gas futures and physical returns are shown in Figure 2, which shows that four IMFs and one residual term were obtained for all of the original return series. The time scale of each decomposition component was measured, and these results are shown in

Table 2. Measurements of the extracted modes for futures and physical returns.

	Time Scale (Months)	Mode Importance a	Time Scale (Months)	Mode Importance	Time Scale (Months)	Mode Importance
	Futures Returns		Citygate Returns		Commercial Returns
IMF1	2.98	61.77%	3.19	44.85%	3.03	52.89%
IMF2	6.74	14.55%	6.74	28.69%	6.74	17.32%
IMF3	14.00	14.83%	16.55	10.22%	13.00	17.81%
IMF4	36.40	5.52%	36.40	4.56%	36.40	7.11%
Residue	60.67	3.32%	60.67	11.68%	60.67	4.87%
	Residential Returns		Industry Returns		Power Returns
IMF1	3.08	59.14%	3.14	58.50%	2.94	61.07%
IMF2	7.00	21.30%	7.00	15.29%	6.74	18.03%
IMF3	15.17	12.60%	15.17	15.64%	15.17	10.02%
IMF4	36.40	4.50%	36.40	8.53%	36.40	5.43%
Residue	60.67	2.46%	60.67	2.04%	60.67	5.45%

Notes: ^a Mode importance was calculated based on the proportion of the variance of each component that accounted for the total variances of IMFs (intrinsic mode functions) and the residual item.

. The average duration of IMF1 was three months, corresponding to the market fluctuations caused by the short-term market disequilibrium between supply and demand. The duration of this fluctuation effect was relatively short. The duration of IMFs 2–4 was between six months and three years, mainly because of the shock effects of minor or significant events or significant changes in energy policies. Because of the different attributes of the different natural gas markets, the natural gas futures and physical markets are likely to be affected by different factors that have medium-term effects. The residual term reflects the long-term evolution trends of the natural gas markets.

To analyze the contribution of each decomposition series to the total fluctuations of the original series, the proportion of the variance of each decomposition series to the variance of the original series was measured. Based on the results in Table 2, the IMF1 accounted for the largest proportion of the total market fluctuations. In particular, the proportion values of IMF1 accounted for 61.77%, 44.85%, 52.89%, 59.14%, 58.50%, and 61.07% of the natural gas futures, citygate, commercial, residential, industrial, and power returns, respectively. These results show that the short-term market fluctuations contributed most to the behavior of the natural gas futures and physical markets. IMFs 2–4 also accounted for a large proportion, indicating that the impact of minor or significant events can cause large fluctuations in the natural gas futures and physical markets [42,43]. The residual terms contributed relatively little to the fluctuations of the natural gas futures and physical markets. In the different natural gas markets in the U.S., the internal driving mechanisms are basically the same. That is, the U.S. natural gas markets’ fluctuations are mainly caused by short-term disequilibrium between market supply and demand and the shock impact of minor or significant events, while the long-term market trends contribute little to natural gas fluctuations. This is mainly because the pricing of U.S. natural gas is based on the U.S. gas-on-gas pricing system, not on a formula linked to oil prices [44,45,46].

4.2. Analysis of Physical and Futures Gas Market Integration

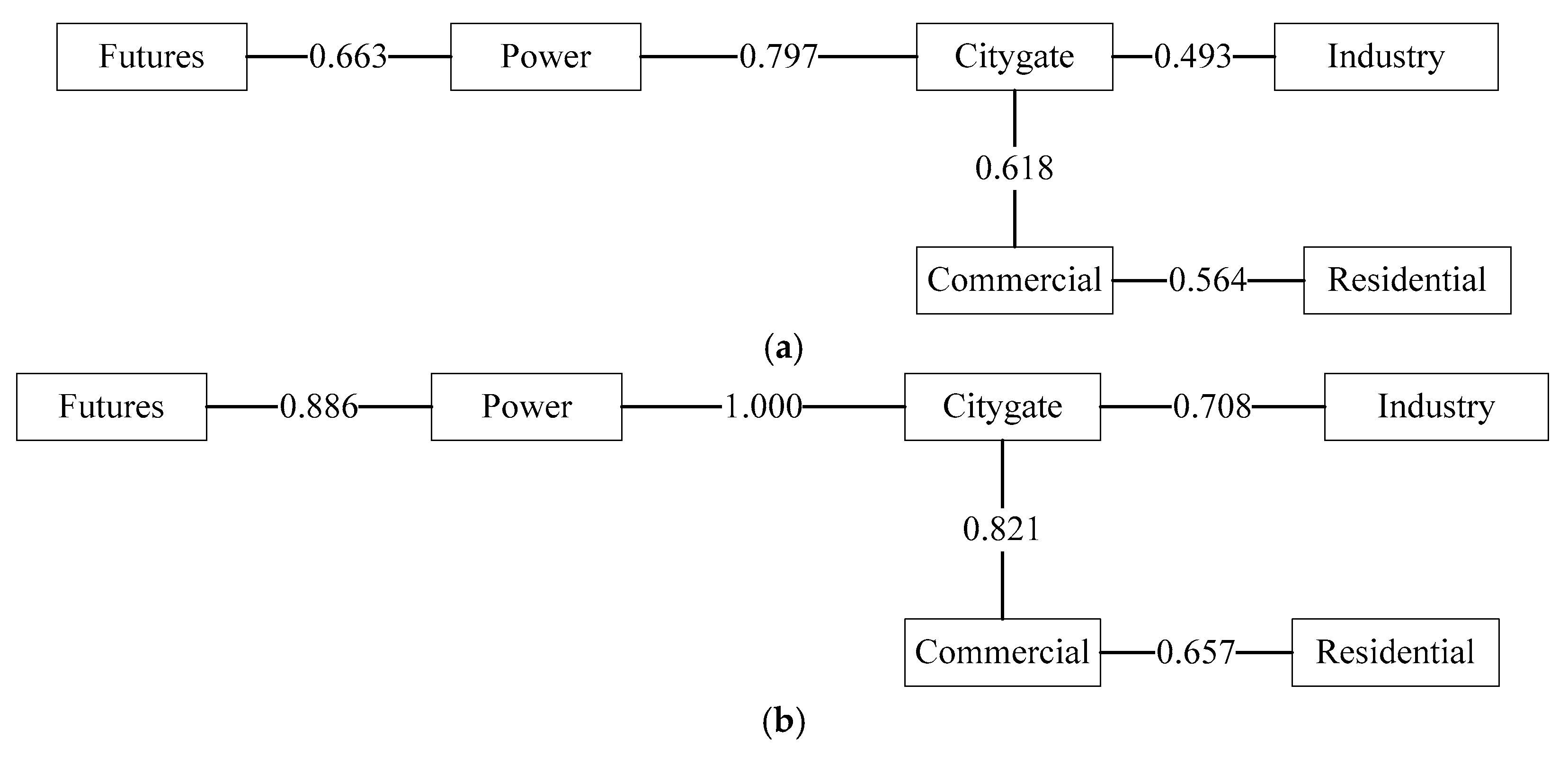
The degree of integration of the futures and physical natural gas markets was analyzed from a multiscale perspective in this study. Figure 3 shows the minimum spanning trees of the return systems of the futures and physical natural gas markets from January 2002 to March 2017 on the original data level and different time scales, where the numbers indicate the distance between the two kinds of natural gas markets. The network structures of the minimum spanning trees were the same on the different time scales. The results show that the linkage between the futures and physical gas markets was similar at various time horizons, and the linkage was stable across different time scales. Specifically, the minimum spanning trees of IMFs for physical gas markets exhibited the same core structures. The citygate returns were always the core of the physical gas markets.

Figure 4 presents the average path length of the monthly minimum spanning tree of the physical and futures gas markets on the original data level and different time scales. Here, the average path length of the minimum spanning trees showed some differences for the different time scales. However, these results did not show an obvious trend. The average path length of the minimum spanning trees ranged from 0.6 to 1, which also shows that the physical and futures natural gas markets are highly integrated on different time scales. This result was also similar to the findings of Arano and Velikova [22], Arano and Velikova [23], Apergis et al. [25], and Ghoddusi [26]. However, these previous studies provided strong evidence of high integration only for the futures, upstream, and downstream gas markets on the original data level. Therefore, this study confirmed new evidence and extended the previous literature on multi-time scales.

4.3. Linear Granger Causality Analysis

The stationary characteristics of the original and decomposition series were tested, and the results of the augmented Dickey–Fuller (ADF) [47] and Phillips–Perron (PP) [48] unit root tests are shown in

Table 3. Unit test results of original futures and physical returns.

	Futures	Citygate	Commercial	Residential	Industry	Power
ADF test	−5.036 ***	−4.650 ***	−4.900 ***	−6.879 ***	−5.333 ***	−5.248 ***
PP test	−12.146 ***	−12.352 ***	−10.171 ***	−12.882 ***	−12.219 ***	−11.729 ***
Zivot–Andrews test	−12.578 **	−12.931 ***	−10.907 ***	−7.151 ***	−7.104 **	−7.014 *
Break point	2005/9	2005/10	2005/10	2006/1	2005/10	2005/10

Notes: *, **, or *** denote the significance at the 10%, 5%, or 1% levels, respectively.

, which suggested that all series are stationary (the results of the unit root test for the IMFs and residual series can be provided upon request). In addition, the structural breaks in the time series may have caused the natural gas price behavior to change, thus affecting the results of the unit root test. In this study, the unit root test allowing for a single exogenous structural break, as proposed by Zivot and Andrews [49], was employed. As shown in Table 3, the results indicated that the original futures and physical returns are stationary, and were not affected by the structural breaks. Meanwhile, most of these structural breaks mainly occurred in 2005/9, 2005/10, and 2006/1, due to the North American shale gas revolution that happened around 2006 [44,46]. Next, the results of the linear Granger causality test between the natural gas futures and physical markets on the multi-time scales are shown in

Table 4. Multiscale linear Granger causality between the futures and physical returns.

Time scale	Series	Lag a	H0: Futures does not Cause End Use		H0: End Use does not Cause Future		Results
			${\mathit{\chi }}^2$	p-Value	${\mathit{\chi }}^2$	p-Value
The Futures and Citygate Returns
Original level	Original	1	263.141	0.000	1.551	0.213	Futures=>Citygate
Short scale	IMF1	2	89.965	0.000	11.866	0.003	Futures<=>Citygate
Medium scale	IMF2	6	40.914	0.000	9.310	0.157	Futures=>Citygate
	IMF3	8	17.498	0.025	13.889	0.085	Futures=>Citygate
	IMF4	7	16.445	0.021	13.627	0.058	Futures=>Citygate
Long scale	Residue	7	16.824	0.019	12.403	0.088	Futures=>Citygate
The Futures and Commercial Returns
Original level	Original	2	320.617	0.000	4.306	0.116	Futures=>Commercial
Short scale	IMF1	2	109.852	0.000	18.250	0.000	Futures<=>Commercial
Medium scale	IMF2	9	37.973	0.000	19.942	0.018	Futures<=>Commercial
	IMF3	7	20.657	0.004	16.983	0.018	Futures<=>Commercial
	IMF4	6	35.171	0.000	11.700	0.069	Futures=>Commercial
Long scale	Residue	7	23.369	0.002	7.301	0.398	Futures=>Commercial
The Futures and Residential Returns
Original level	Original	2	109.293	0.000	1.808	0.405	Futures=>Residential
Short scale	IMF1	4	17.716	0.001	13.255	0.010	Futures<=>Residential
Medium scale	IMF2	13	23.260	0.039	26.269	0.016	Futures<=>Residential
	IMF3	7	10.642	0.155	33.514	0.000	Futures<=Residential
	IMF4	6	26.883	0.000	13.721	0.033	Futures<=>Residential
Long scale	Residue	6	6.574	0.362	2.123	0.908	✕
The Futures and Industry Returns
Original level	Original	3	449.585	0.000	3.016	0.389	Futures=>Industry
Short scale	IMF1	2	112.413	0.000	15.634	0.000	Futures<=>Industry
Medium scale	IMF2	8	59.573	0.000	24.521	0.002	Futures<=>Industry
	IMF3	7	10.169	0.179	10.321	0.171	✕
	IMF4	7	16.898	0.018	8.073	0.326	Futures=>Industry
Long scale	Residue	6	165.127	0.000	9.253	0.160	Futures=>Industry
The Futures and Power Returns
Original level	Original	12	49.706	0.000	9.929	0.622	Futures=>Power
Short scale	IMF1	4	10.807	0.029	12.814	0.012	Futures<=>Power
Medium scale	IMF2	9	12.645	0.179	15.180	0.086	✕
	IMF3	9	11.641	0.234	32.456	0.000	Futures<=Power
	IMF4	6	40.878	0.000	16.918	0.010	Futures<=>Power
Long scale	Residue	7	8.724	0.273	11.681	0.112	✕

Note: ^a The lag number is determined based on the Akaike information criterion (AIC).

. For the original data level, only a unidirectional linear Granger causality from the natural gas futures to all of the physical gas returns was found at the 5% significance level. This result was consistent with the findings of Ghoddusi [26]. Price movements in the natural gas futures market can be expected to cause the change of prices in the wholesale and end-use markets.

For the short time scale, a bidirectional linear Granger causality between natural gas futures and all of the physical gas returns was found at the 5% significance level, showing that short-term market fluctuations can be conducted between the futures and physical markets. For the medium time scale, a unidirectional linear Granger causality from the natural gas futures to citygate returns was found at the 5% significance level. However, a bidirectional linear Granger causality between the natural gas futures and other physical markets was found at the 5% significance level in most cases. For the long-term scale, a unidirectional linear Granger causality was found only from natural gas futures to citygate, commercial, and industry returns, while no evidence was found for a linear Granger causality between natural gas futures and residential and power returns. For the long-term relationship, this result was similar to Ghoddusi [26], who found that futures returns are co-integrated with power, industrial, and citygate returns but not for commercial and residential returns. Both of these results showed that a long-term relationship does not exist between futures returns and residential returns.

In summary, our results extended the findings of Ghoddusi [26] to multiple time scales. Indeed, the time scales have an impact on the linear relationship between futures and physical markets. The relationship between futures and physical gas returns is not constant across various time scales. Due to differences in the market price behavior in the short-term and long-term scales, the linear relationship between futures and physical markets changes on different time horizons. These results also showed that the multi-time scales should be considered when the complex linkage mechanisms between futures and physical markets are explored.

4.4. Results of the Brock, Dechert, and Scheinkman (BDS) Test

To test whether the original return and decomposition series had embedded nonlinear characteristics, the BDS test [50] was employed to explore the time series filtered by the GARCH (1,1) model. If the null hypothesis of the time series as independent and identically distributed was rejected, this would indicate that the time series had nonlinear features. Hence, a nonlinear Granger causality test was needed to capture the nonlinear linkage mechanism.

Table 5. Results of the Brock, Dechert, and Scheinkman (BDS) test from the GARCH (1,1) residuals of futures and physical returns.

Embedding Dimension (m)	Futures	Citygate	Commercial	Residential	Industry	Power
	BDS Statistics
	Panel A: Original Data
2	−0.000242	−0.000194	−0.006822	0.004069	0.002344	0.000862
3	0.002275	0.001693	−0.006713	0.006209	−0.002661	0.009104
4	−0.000154	−0.006946	−0.012462	0.001728	−0.002791	0.010231
5	−0.008789	−0.003270	−0.020357	−0.008917	0.001533	0.002638
6	−0.005726	−0.002051	−0.015795	−0.006580	0.003544	0.001586
	Panel B: IMF1
2	0.009649 **	−0.001624	−0.001430	0.006643	0.005070	0.001176
3	0.014303 **	0.005992	0.014652 **	0.019381 ***	0.017581 **	0.018367 **
4	0.016011 **	0.012205	0.020392 **	0.021703 ***	0.026312 ***	0.025183 ***
5	0.011084	0.006276	0.017401 **	0.014263	0.028664 ***	0.027411 ***
6	0.007941	0.002248	0.010723	0.011620	0.025706 ***	0.021482 **
	Panel C: IMF2
2	0.013157 ***	0.022336 ***	0.014046 ***	0.015443 ***	0.013528 ***	0.032496 ***
3	0.049803 ***	0.052713 ***	0.037088 ***	0.052437 ***	0.050860 ***	0.063068 ***
4	0.080175 ***	0.076892 ***	0.064649 ***	0.089276 ***	0.083164 ***	0.094598 ***
5	0.089173 ***	0.083481 ***	0.078703 ***	0.103173 ***	0.093653 ***	0.105608 ***
6	0.091791 ***	0.087128 ***	0.078959 ***	0.101795 ***	0.096219 ***	0.107025 ***
	Panel D: IMF3
2	0.104119 ***	0.109942 ***	0.100339 ***	0.082090 ***	0.104806 ***	0.112725 ***
3	0.152274 ***	0.158026 ***	0.140181 ***	0.117750 ***	0.151637 ***	0.166554 ***
4	0.174473 ***	0.175693 ***	0.152239 ***	0.137345 ***	0.172999 ***	0.192427 ***
5	0.182647 ***	0.183153 ***	0.153129 ***	0.147097 ***	0.180768 ***	0.208371 ***
6	0.184341 ***	0.184094 ***	0.149664 ***	0.147675 ***	0.180516 ***	0.218008 ***
	Panel E: IMF4
2	0.139982 ***	0.146683 ***	0.138056 ***	0.141213 ***	0.143374 ***	0.136818 ***
3	0.224853 ***	0.232634 ***	0.214129 ***	0.227818 ***	0.224551 ***	0.211520 ***
4	0.267462 ***	0.276486 ***	0.249845 ***	0.271217 ***	0.263199 ***	0.248084 ***
5	0.281226 ***	0.291718 ***	0.258628 ***	0.287203 ***	0.272559 ***	0.262538 ***
6	0.276956 ***	0.288511 ***	0.251665 ***	0.285178 ***	0.262900 ***	0.270274 ***
	Panel F: Residue
2	0.159631 ***	0.159043 ***	0.156567 ***	0.151490 ***	0.165270 ***	0.170011 ***
3	0.255517 ***	0.254679 ***	0.265158 ***	0.266841 ***	0.265031 ***	0.278411 ***
4	0.307311 ***	0.306801 ***	0.329372 ***	0.337955 ***	0.321713 ***	0.341470 ***
5	0.328593 ***	0.329975 ***	0.362891 ***	0.378317 ***	0.360273 ***	0.372463 ***
6	0.329477 ***	0.334311 ***	0.375025 ***	0.397153 ***	0.378444 ***	0.382278 ***

Note: ** or *** denote the significant nonlinear dependencies at 5% or 1% levels of significance, respectively.

shows the results of the BDS test. The results showed that except for the original series of the GARCH (1,1), filtering the residuals for the natural gas futures and physical returns was not significant at the 5% level; all the other series rejected the null hypothesis, indicating that they had embedded nonlinear characteristics.

4.5. Nonlinear Granger Causality Analysis between Futures and Physical Markets from the GARCH (1,1)

This section describes our extension of the previous findings and discusses the results under a nonlinear causality framework. Based on this study’s sample size, according to Diks and Panchenko [40], the lag period was set to 6, the bandwidth parameter was set to 8, the theoretical optimisation rate was set to 2/7, and the optimal bandwidth was set to 1.81 (according to Diks and Panchenko (2006), the bandwidth was calculated by the following: ${\epsilon }_n=\max (C{n}^{-2/7},1.5)$, $C{n}^{-2/7}$ = 1.811502).

Table 6. Multiscale nonlinear Granger causality between futures and citygate returns.

Lx = Ly	H0: Futures does not Cause Citygate	H0: Citygate does not Cause Futures	H0: Futures does not Cause Citygate	H0: Citygate does not Cause Futures
	Tn	Tn	Tn	Tn
	Panel A: Original data		Panel D: IMF3
1	4.837 ***	0.670	0.033	1.956 **
2	4.073 ***	0.893	0.554	1.792 **
3	3.479 ***	0.024	0.505	1.442
4	2.872 ***	−0.382	1.060	1.679 **
5	2.645 ***	−0.188	1.197	1.539
6	2.638 ***	−0.725	1.547	1.752 **
	Panel B: IMF1		Panel E: IMF4
1	3.192 ***	3.025 ***	0.338	1.906 **
2	1.942 **	2.680 ***	0.036	1.723 **
3	1.790 **	1.737 **	0.030	1.411
4	1.683 **	1.670 **	−0.028	1.393
5	0.850	1.324	0.156	1.177
6	0.782	1.569	0.350	1.165
	Panel C: IMF2		Panel F: Residue
1	3.554 ***	2.080 **	−0.630	0.058
2	2.673 ***	0.747	−0.758	−0.115
3	2.133 **	1.050	−0.901	−0.264
4	1.639	1.166	−0.721	−0.153
5	1.776 **	1.589	0.067	−0.182
6	1.712 **	1.874 **	0.379	−0.108

Note: ** or *** denote significance at the 5% or 1% levels, respectively.

,

Table 7. Multiscale nonlinear Granger causality between futures and commercial returns.

Lx = Ly	H0: Futures does not Cause Commercial	H0: Commercial does not Cause Futures	H0: Futures does not Cause Commercial	H0: Commercial does not Cause Futures
	Tn	Tn	Tn	Tn
	Panel A: Original data		Panel D: IMF3
1	5.963 ***	0.522	2.468 ***	−0.312
2	5.009 ***	−0.014	2.409 ***	−0.644
3	4.155 ***	0.941	2.413 ***	−0.034
4	3.647 ***	1.427	1.759 **	1.779 **
5	3.371 ***	1.321	1.425	2.450 ***
6	2.879 ***	1.301	1.042	1.996 **
	Panel B: IMF1		Panel E: IMF4
1	4.292 ***	2.454 ***	1.319 *	−0.001
2	3.361 ***	1.858 **	1.073	−0.124
3	2.613 ***	1.523	1.041	0.009
4	1.776 **	1.265	0.915	0.686
5	1.446	0.951	0.926	1.077
6	1.195	0.467	0.769	1.151
	Panel C: IMF2		Panel F: Residue
1	2.919 ***	2.418 ***	1.155	0.840
2	1.859 **	1.991 **	1.023	0.620
3	2.007 **	1.992 **	1.067	0.255
4	1.856 **	2.329 ***	1.206	0.411
5	1.996 **	2.498 ***	1.308	1.066
6	1.821 **	2.368 ***	1.299	1.380

Note: ** or *** denote significance at the 5% or 1% levels, respectively.

,

Table 8. Multiscale nonlinear Granger causality between futures and residential returns.

Lx = Ly	H0: Futures does not Cause Residential	H0: Residential does not Cause Futures	H0: Futures does not Cause Residential	H0: Residential does not Cause Futures
	Tn	Tn	Tn	Tn
	Panel A: Original data		Panel D: IMF3
1	3.280 ***	−0.820	1.481	−0.478
2	2.555 ***	−0.692	1.151	−0.255
3	2.001 **	−0.760	1.558	0.587
4	1.523	−1.190	0.732	0.901
5	2.124 **	−0.267	0.242	1.297
6	2.207 **	−0.692	0.077	1.300
	Panel B: IMF1		Panel E: IMF4
1	0.947	2.063 **	1.399	−1.424
2	0.484	1.402	1.775 **	−0.867
3	0.823	1.451	1.888 **	−0.379
4	−0.433	1.057	1.906 **	0.268
5	−0.625	−0.322	1.719 **	0.811
6	−0.439	−0.684	1.791 **	0.701
	Panel C: IMF2		Panel F: Residue
1	2.157 **	2.211 **	1.802 **	−0.232
2	0.857	2.069 **	1.690 **	−0.241
3	0.450	1.726 **	1.526	−0.171
4	0.445	2.656 ***	1.474	−0.354
5	0.660	2.262 **	1.661 **	−0.133
6	0.335	2.324 **	1.671 **	−0.115

Note: ** or *** denote significance at the 5% or 1% levels, respectively.

,

Table 9. Multiscale nonlinear Granger causality between futures and industry returns.

Lx = Ly	H0: Futures does not cause Industry	H0: Industry does not cause Futures	H0: Futures does not cause Industry	H0: Industry does not cause Futures
	Tn	Tn	Tn	Tn
	Panel A: Original data		Panel D: IMF3
1	5.937 ***	1.190	1.373	1.409
2	4.202 ***	0.356	1.446	1.582
3	3.894 ***	−0.123	2.196 **	1.679 **
4	3.634 ***	0.499	2.815 ***	1.320
5	3.042 ***	0.296	2.655 ***	1.157
6	2.713 ***	−0.445	2.444 ***	1.180
	Panel B: IMF1		Panel E: IMF4
1	4.595 ***	1.508	1.387	0.961
2	3.408 ***	2.149 **	1.211	1.054
3	3.088 ***	0.744	1.035	1.015
4	2.315 **	−0.453	0.780	0.884
5	1.560	−0.312	0.691	1.004
6	0.957	0.068	1.234	0.970
	Panel C: IMF2		Panel F: Residue
1	4.523 ***	3.418 ***	0.848	0.263
2	3.274 ***	2.072 **	0.820	0.279
3	2.942 ***	2.280 **	0.776	0.199
4	2.983 ***	2.640 ***	0.559	0.103
5	3.316 ***	2.409 ***	0.354	−0.020
6	3.362 ***	2.106 **	0.387	−0.132

Note: ** or *** denote significance at the 5% or 1% levels, respectively.

and

Table 10. Multiscale nonlinear Granger causality between futures and power returns.

Lx = Ly	H0: Futures does not Cause Power	H0: Power does not Cause Futures	H0: Futures does not Cause Power	H0: Power does not Cause Futures
	Tn	Tn	Tn	Tn
	Panel A: Original data		Panel D: IMF3
1	2.211 **	0.954	0.069	1.968 **
2	1.524	0.319	0.597	1.786 **
3	0.906	0.250	1.189	1.776 **
4	0.981	−0.059	1.497	1.993 **
5	0.684	0.137	2.212 **	2.137 **
6	0.678	−0.420	1.999 **	2.109 **
	Panel B: IMF1		Panel E: IMF4
1	0.204	2.852 ***	−1.183	1.802 **
2	−0.153	2.352 ***	−1.049	1.740 **
3	−0.315	2.666 ***	−0.865	1.648 **
4	0.406	2.264 **	−1.209	1.343
5	0.274	1.821 **	−1.181	1.338
6	0.031	1.596	−0.700	1.142
	Panel C: IMF2		Panel F: Residue
1	1.864 **	2.635 ***	1.033	−0.108
2	1.392	2.255 **	1.103	−0.245
3	0.966	2.123 **	1.110	−0.427
4	0.949	1.642	1.052	0.061
5	0.973	1.634	1.140	0.305
6	0.816	1.580	0.948	0.331

Note: ** or *** denote significance at the 5% or 1% levels, respectively.

present the results of the multiscale nonlinear Granger causality test between futures and physical gas markets.

4.5.1. Nonlinear Granger Causality Analysis between Futures and Citygate Returns

On the original data level, only a unidirectional nonlinear causality was found from the gas futures to citygate returns. For the short-term scale, the results for IMF1 showed that a bidirectional nonlinear causality between the gas futures and citygate returns was found at the 5% significance level. For the medium-term scale, the nonlinear Granger causality test indicated that a bidirectional nonlinear Granger relationship existed between them at the 5% significance level for IMF2, but not for IMF3 and IMF4. For the long-term scale, no evidence of nonlinear causality could be found, unlike the linear Granger test, which showed that a unidirectional linear causality was found from the futures to citygate returns.

4.5.2. Nonlinear Granger Causality Analysis between Futures and Commercial Returns

For the original data level, the test showed that only a unidirectional nonlinear causality existed from the futures to commercial returns. For the short-term scale, the results for IMF1 show that a bidirectional nonlinear Granger causality existed between the natural gas futures and commercial returns. For the medium-term time scale, the nonlinear Granger causality test supports that a unidirectional nonlinear Granger causality was significant at the 1% confidence level from the natural gas futures to commercial returns for IMF2 and IMF4. For the long-term scale, the test showed that a nonlinear Granger causality did not exist between the two market returns.

4.5.3. Nonlinear Granger Causality Analysis between Futures and Residential Returns

For the original data level, the test showed that only a unidirectional nonlinear Granger causality existed from the natural gas futures to residential returns. For the short-term scale, the results for IMF1 showed that a unidirectional nonlinear Granger causality existed from the natural gas residential to futures returns. For the medium-term time scale, the nonlinear Granger causality test supported the idea that a bidirectional nonlinear Granger causality was significant at the 5% confidence level between the natural gas futures and commercial returns for IMF2. For the long-term scale, the test showed a unidirectional nonlinear Granger causality from futures to residential returns, which was unlike the results of the linear causality test in which no causality evidence was found between the futures and residential returns on the long-term scale.

4.5.4. Nonlinear Granger Causality Analysis between Futures and Industry Returns

For the original data level, the test showed that only a unidirectional nonlinear Granger causality from the natural gas futures to industrial returns existed. For the short-term scale, a significant bidirectional nonlinear Granger causality was found for IMF1 between the natural gas futures and industrial returns at the 5% confidence level. For the medium-term scale, the nonlinear Granger causality test at the 5% significance level indicated that a bidirectional nonlinear Granger causality existed between the natural gas futures and industrial returns for IMFs 2 and 3. For the long term, the test showed that no nonlinear Granger causality existed between the two market returns.

4.5.5. Nonlinear Granger Causality Analysis between Futures and Power Returns

For the original data level, the test found that a unidirectional nonlinear Granger causality existed from the natural gas futures to power returns. For the short-term scale, the nonlinear Granger causality test results for IMF1 from the power to natural gas futures returns were insignificant at the 5% confidence level. On the medium-term scale, the nonlinear Granger causality test at the 5% significance level indicated a bidirectional nonlinear Granger causality between the natural gas futures and power returns for IMF2. For the long term, the test showed that a nonlinear Granger causality did not exist between the two market returns.

In summary, such nonlinear evidence effectively supplemented the results of the linear causality test, while also providing new evidence to support Ghoddusi [26] and Ghoddusi and Emamzadehfard [27]. On the medium-term scale, the nonlinear test found that bidirectional causality existed between futures and all of the physical returns, while the linear test showed that no evidence of causality between futures and city gate could be found. The nonlinear test also found unidirectional causality from futures to residential returns for the long-term scales. As can be seen, it is indeed important to consider nonlinear features when explaining the complex linkages between futures and physical gas markets. Furthermore, the relationship was strengthened between futures and physical gas returns on the short- and medium-term scales, while it became weak on the long-term time scale.

4.6. Sensitivity Analysis

The natural gas market is an uncertain environment and is often impacted by significant extreme events, such as the North American shale gas revolution or the 2008 Global Financial Crisis. In order to ensure the robustness of the empirical results, a sensitivity analysis was carried out. Thus, this study divided the full sample into two subsamples, and investigated whether the results of the subsamples were consistent with the results of the full sample, considering the impact of the North American shale gas revolution and the 2008 Global Financial Crisis on the full sample. Referring to Geng et al. [44] and Aruga [51], we divided the full sample into two subsamples. The first subsample period ranged from January 2002 to September 2009, and the second subsample period ranged from October 2009 to March 2017.

The minimum spanning trees for natural gas futures and physical markets on the original data level during the two subsample periods are shown in Figure 5. The structure of the minimum spanning trees in the first sample was the same as the one in the second subsample, which was also consistent with the results of the full sample. Furthermore, the linear Granger causality between the futures and physical returns on the original data level during the two subsample periods is shown in

Table 11. Linear Granger causality between the futures and physical returns on the original data level during the two subsample periods.

Series	Lag a	H0: Futures does not Cause End Use		H0: End Use does not Cause Future		Results
		${\mathit{\chi }}^2$	p-Value	${\mathit{\chi }}^2$	p-Value
During the First Subsample Period
Futures and Citygate	4	176.263	0.0000	10.201	0.0372	Futures<=>Citygate
Futures and Commercial	1	232.584	0.0000	1.815	0.1779	Futures=> Commercial
Futures and Residential	4	43.649	0.0000	2.577	0.6310	Futures=> Residential
Futures and Industry	3	193.330	0.0000	5.766	0.1236	Futures=> Industry
Futures and Power	3	36.211	0.000	15.665	0.0013	Futures<=> Power
During the Second Subsample Period
Futures and Citygate	1	52.512	0.0000	0.007	0.9342	Futures=>Citygate
Futures and Commercial	6	87.561	0.0000	8.467	0.2058	Futures=> Commercial
Futures and Residential	12	38.649	0.0010	14.784	0.2534	Futures=> Residential
Futures and Industry	13	216.141	0.0000	16.614	0.2176	Futures=> Industry
Futures and Power	3	10.388	0.0155	6.895	0.0753	Futures=> Power

Note: ^a The lag number was determined based on the AIC.

. Most of the results of the two subsamples were consistent with the results of the full sample. Nonlinear Granger causality results between the futures and physical returns on the original data level during the two subsample periods are shown in

Table 12. Nonlinear Granger causality between the futures and physical returns on the original data level during the two subsample periods.

Y-Variables	$\mathit{X}|\mathit{Y}$	$\mathit{Y}|\mathit{X}$	Y-Variables	$\mathit{X}|\mathit{Y}$	$\mathit{Y}|\mathit{X}$
During the first subsample period			During the second subsample period
Citygate	***		Citygate	***
Commercial	***		Commercial	***
Residential	**		Residential	**
Industry	***		Industry	***
Power	*		Power	*

Note: The test was done in two directions: X means futures returns; X|Y implies variable X Granger-causes variable Y; and Y|X implies variable Y Granger-causes variable X. *, **, or *** denote significance at the 10%, 5%, or 1% levels, respectively.

, which were also consistent with the results of the full sample. Given space limitations, the results of the IMFs and residual series will be provided upon request. These results supported the robustness of the empirical results of the full sample. The results also mean that while the uncertain environment will indeed influence the changes of natural gas prices, it is difficult to affect the integrated relationship between natural gas futures and physical markets.

5. Conclusions and Policy Implications

The minimum spanning tree graphic showed that a unified market has already formed for the futures and physical gas markets. The network structures of the minimum spanning trees were the same on various time horizons. Specifically, the citygate returns were always the core of the physical gas markets. Moreover, high integration always existed for the physical and futures natural gas markets on different time scales. Furthermore, the direction of the causality between the futures and physical markets was comprehensively clarified, showing that the causality direction between the futures and physical gas returns behaves differently across time scales. For the long term, the futures gas returns only had a linear causality with the citygate, commercial, and industry gas returns, and a unidirectional nonlinear causality with residential gas returns.

At various horizons, this study’s findings can provide new information on natural gas futures and physical markets for energy policy makers and market participants. In the short term, policy makers and market participants need to be concerned about potential shock impacts on the physical gas markets regarding the price uncertainty of the futures markets. At the same time, they need to pay more attention to the impact of supply and demand information in the physical gas markets, and how this may affect the natural gas futures market. In the medium term, they should focus on the market conduction effect of the resulting fluctuations of natural gas futures on the physical markets and the variations of the citygate prices. The related medium-term adjusting strategies related to the citygate prices could have a significant impact on the integration of the futures and downstream end-use gas markets. In the long term, policy makers and market participants should focus on the long-term evolution patterns of the futures gas market, because long-term policy of the gas futures market will have an impact on the long-term trends of the natural gas physical markets, with the exception of the power returns.

This study’s findings can be treated as a reference sample when energy policy makers regulate their domestic gas markets or when market participants make investment, production, storage, and consumption plans with various time horizons. Though some differences in the domestic gas markets of different countries exist, this study’s findings also have significant policy implications for other countries. Of course, further analyses of the complex linkage mechanisms in other countries or regions could be a future research avenue, one that can help generalize this study’s findings.