A Fuzzy WASPAS-Based Approach to Determine Critical Information Infrastructures of EU Sustainable Development

Abstract

Critical information infrastructure exists in different sectors of each country. Its loss or sustainability violation will lead to a negative impact on the supply of essential services, as well as on the social or economic well-being of the population. It also may even pose a threat to people’s health and lives. In the modern world, such infrastructure is more vulnerable and unstable than ever, due to rapid technological changes, and the emergence of a new type of threat—information threats. It is necessary to determine which infrastructure are of crucial importance when decision-makers aim to achieve the reliability of essential infrastructure. This article aims to solve the problem of ensuring the sustainable development of EU countries in terms of identifying critical information infrastructures. Integrated multi-criteria decision-making techniques based on fuzzy WASPAS and AHP methods are used to identify essential information infrastructures, which are related to a new type of potential threat to national security. The paper proposes a model for identifying critical information infrastructures, taking into account the sustainable development of countries.

1. Introduction

Sustainability is one of the essential criteria of the well-being of a country’s citizens [1]. Many definitions of the concept of “sustainability” exist. The meaning of most definitions comes down to “continuity through time”, in context-dependent economic, environmental, and social areas [2,3]. The concept of sustainability is very old, and it represents the process itself [4,5,6]. It is synonymous with the concept of “sustainable development” [7]. Critical information infrastructure (CII) has a huge impact on it. CII can impact organizations or separate countries. The growing number of threats poses a real and increasing danger to the process of achieving the persistence and reliability of CII. New vulnerabilities have emerged with the development and application of information technologies in all spheres of life. Therefore, ensuring the development of vital public structures and institutions, including CII, is an essential responsibility of the government in the context of state security and sustainable development. The government must collectively prioritize, formulate clear objectives, and mitigate risks, adapting based on feedback and changing environments to achieve the stable growth of countries and core infrastructure roles. The risks are identified as “the probabilities of harm or loss”. They refer to “a potentially undesirable result that may arise as a result of an incident or undesirable event”. Ensuring the performance of CII at the national level aims to create protective mechanisms for managing the risks to which the country’s CII may be exposed. A collaboration of various sectors within and outside the state helps to achieve these goals. CII sustainability is related to the need to maintain the viability of the environment and society, starting with administration, economic and financial institutions, those of social welfare and health, the military, and civil protection, and ending with supplies of food, water, and energy, transport, communications, etc.

The concept of “infrastructure reliability” can be understood as the ability of the infrastructure, which is in danger, to adapt to the situation and to recover from losses while preserving the functioning of critical structures and elements. Increasing the level of CII reliability is ensured through risk management. The reliability of infrastructure assets, systems, and networks means that they must be flexible and adaptable. To strengthen the reliability of CII, it is important to have accurate, timely, and valid information about threats, and the ability to analyze expected risks, identify mitigation measures, and respond to threats, and, accordingly, the ability to recover.

Thus, the sustainable development of countries can be achieved through the management of risks that are associated with possible significant threats that are aimed at CII. It is necessary to perform a set of activities to:

• identify CII;
• identify, deter, detect, and disrupt threats aimed at CII;
• reduce the vulnerability of CII, and mitigate the potential consequences of the incidents of CII;
• organize the reserves (duplicates) of CII.

The ability to overcome adverse effects is significantly affected by the availability of infrastructure. The protection of CII is based on increasing its sustainability against emergency consequences.

Countries around the world face adverse information security events in the sector of critical infrastructures [8,9,10]. They often lead to numerous and significant losses, the essential disruption of production, and the destruction of the environment, etc. [11,12,13,14].

The problem of CII identification is complicated by the influence on a multitude of factors. It is necessary to assess impacts on various services and areas of activity, on the environment, and on the life and health of the population, etc. CII can affect any area of activity, from government management to engineering, including sustainable development. Therefore, this problem has lots of criteria, and to solve this one, it is acceptable to use the multi-criteria decision-making (MCDM) approach. In our case, the problem is solved by using the fuzzy WASPAS method, which has not been previously used for such tasks [15,16,17]. The WASPAS method actually aggregates two approaches: the WSM (Weighted Sum Model) and the WPM (Weighted Product model).

There are many decision-making approaches that are applied in various fields. For example, the MCDM methods were considered in [18]. Different scientists considered the theory of decision support systems [19,20,21] and their practical applications in many fields of human activity [22,23,24]. Decision-making methods develop dynamically [25,26,27]. Sivilevičius et al. presented an original MADM method, which could be applied to assess different security tools [28]. MCDM has widely used decision-making techniques in science and engineering, as well as in management [29,30,31,32]. Various categories of MCDM approaches solve complicated problems [33,34,35].

In the last few years in the field of information technology, there has been a rise in interest in using analyses that are based on a larger number of criteria, as a decision support tool. Such criteria may include stopping the supply of electricity, natural gas, district heating, drinking water, and electronic communications to settlements and other areas.

Thus, the MCDM methodology is defined as a set of tools that supports and facilitates the decision-making process, as an approach that is based on the use of several criteria, ensuring the correct choice of CII. The use of MCDM in determining CII will ensure its objectivity and transparency in assessing the acceptability of solutions.

2. Methodology of Research and Applied Methods

2.1. Research of the Concept of CII

In the last decade, critical infrastructure study has been directed based on interdependencies from various points. The research is mainly concerned with policies in this field [36,37]. Risk analyses and comments into the existing legal framework have been described in [38,39]. The interdependent essential infrastructures are presented in [40,41,42,43,44]. These works are mainly focused on engineering or computer science, to design better modeling, in order to manage the infrastructure, as well as to protect the vital infrastructure [45,46].

As indicated in the Directive [47], essential infrastructure is a system, asset, or part thereof that is situated in countries, and that is very important for the control of critical societal functions and safety, etc., and the failure or breakdown of which would have a great influence on a country; as consequence of an error in keeping up those functions.

The trends and current geopolitical and geostrategic perspectives expand more and more the concept of “national security” for environmental, financial, information technology and communication, and diplomatic components. Essential infrastructures are usually sensitive to the actions of some internal or external attributes, and they are under a risk of being destroyed or made non-operational [48].

The European Union and other countries use different definitions of critical infrastructure. According to the law of the Republic of Lithuania, CII are electronic communication networks or parts of an information system or a component of a complex of information systems, or a process control system, or part of it, a cyber-incident of which can cause significant damage to national security, state economy and public interests [49]. France notes that vital infrastructure is the structure or equipment that provides critical goods and services in the formation of a society and its lifestyle [50]. The Slovenian national importance of critical infrastructure includes its necessary capabilities and services, the violation of which will have a huge influence on national security, essential social or financial operations, safety, and social security [51]. According to the Canadian National Strategy for Critical Infrastructure, critical infrastructure refers to processes, technologies, etc., that are necessary for the health, safety, or economic well-being of the population, and the impactful operation of a country [52].

Based on relevant state concepts, it can be said that each country has its own perception of critical infrastructure. Identifying critical infrastructure is not sufficient to just rely on the definition. To achieve this goal, various methods and techniques should be used. In this case, the problem of CII identification was solved by applying the MCDM approach.

2.2. Achieving the Sustainability of CII, and Potential Threats to CII

Currently, the problem of natural disasters is considered to be one of the most pressing. In recent years, there have been significant changes in views on the sustainable state and development of natural systems. This is also interrelated with the intensive development of scientific and technical (information technology (IT)) and economic potential, and the industrial development of new territories. Often the cause of environmental disasters and devastating consequences lies in the failure of a critical information resource. For example, a failure in the refining industry may cause tens or hundreds of thousands of tons of crude oil or fuel oil to be released into the marine environment. Such an accident has enormous losses, which are very difficult to estimate due to its magnitude. Accordingly, knowledge of the criticality of information infrastructures that affect natural disasters, the timely development of precautionary measures, and the restoration of destroyed territories and their socio-economic systems and ecosystems is an essential attribute for the sustainable development of systems at various levels of EU countries.

Globalization, rapid technological change, and other factors change the global security situation, and expand the list of traditional threats [53,54,55]. A new type of risk has appeared, such as terrorist attacks, cyber-attacks, cyber wars, etc. [56,57,58].

When the distributed denial-of-service (DDoS) attacks on Lithuanian websites began in 2003. Lithuania recognized that the threat of cyber-attacks is real [59]. It should be noted that by the end of 2016, a list of CII of Lithuania was approved [60]. Other countries have also previously faced cyber threats towards the critical infrastructure. In 2007, Estonia suffered greatly from politically motivated cyber-attacks (the first cyberwar) [61].

In recent years, companies of all types, including those offering critical and emergency services, have been the victims of social engineering attacks [62]. The last most infamous type of cyber threat was the WannaCry ransomware, which was one of the most impactful and propagated malware in 2017. This international wave of cyber threats is reported to have struck over 150 countries worldwide [63]. These events have increased the awareness of potential threats towards critical infrastructure that potentially endanger national security. States began to realize that new types of threats could be directed against national critical infrastructures. This infrastructure is the most sensitive and vulnerable infrastructure, which can entail a huge impact on the state and its environment.

Critical infrastructure plays the main role in countries in with regard to the importance of nationwide, socio-economic, or public security [64]. Potential threats to the critical infrastructure of its countries prompted the EU Member State to take measures to protect the essential infrastructure each country. Identifying essential infrastructure is the first step toward protect the country and the interests of people who depend on critically crucial services. Accurately defining critical infrastructure can defend them against potential threats.

The following characteristics must be considered:

• types of threats;
• threat objects;
• sources of threats.

The main types of threats directed towards sustainability include the violation of the accessibility, integrity, and confidentiality of information.

The objects, which are usually influential to CII work, can be represented as a network, an information or automated system, a process control system, etc.

The sources of key threats affecting the reliability of CII can be of two types:

• External (computer hackers (competitors), carrying out targeted destructive effects, including using computer viruses and other types of malicious codes (human-made, external), terrorists, criminal elements and structures);
• Internal (employees of an organization who are legal participants in information processing and acting outside their authority; employees of an organization who are legitimate participants in information processing and operating within their jurisdiction);
• Common acting of external and internal threats with the aim of affecting CII.

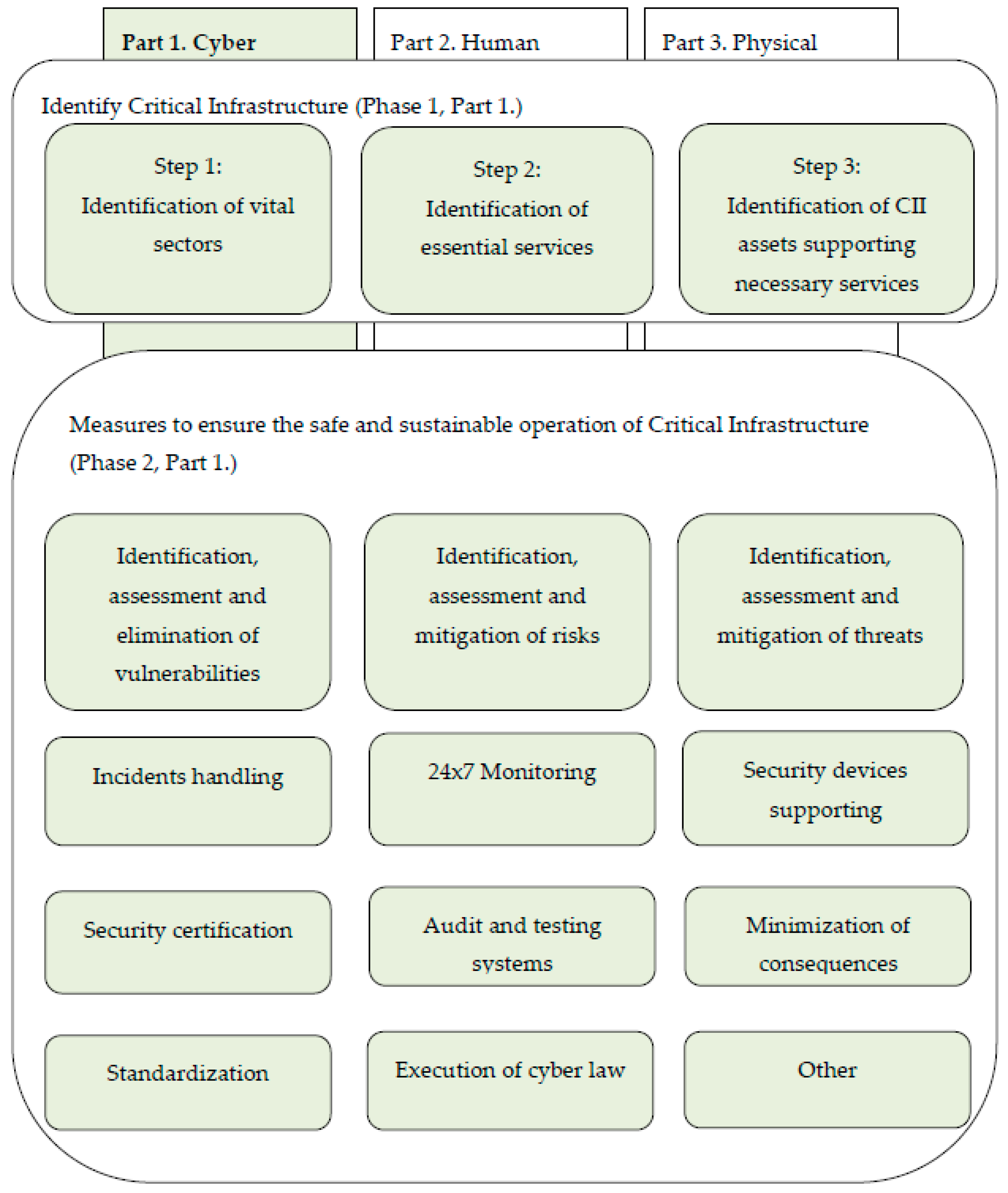
The consequences of the threats can be catastrophic, so that it is essential to take all possible actions to protect and ensure the operation of CII. Figure 1 shows one of the options that are proposed by the authors for providing the process of sustainable functioning of CII.

As can be seen from Figure 1, the identification of CII is the first phase to protect critical infrastructure. Various methods can be used to identify CII.

2.3. CII Identification Models

Various models and methodologies, which were proposed earlier by other researchers and governments, are considered in this paper.

The article by Almeida on the identification of critical infrastructure offers a multi-criteria evaluation model [66]. In the Canadian Critical Infrastructure Assessment Model, Macbeth is proposed to solve the problem, using M-MACBETH software. This method was chosen because it has a social-technical approach to development problems, and it is more convenient for decision-makers. The proposed Macbeth model is improved by the Canadian model, but this is only a theoretical model that has not been tested in practice, and the adequacy of real applicability is not evaluated [66]. Despite this, there are a large number of scientific articles that offer other methods.

Applying the AHP method for a multi-criteria task in determining the level of criticality of the water management system is proposed in [67]. This area is an important sector for all countries, and it is critical infrastructure. The goal is to identify and develop the criteria, and a list of items that will be used to identify the properties of the critical level. The AHP method is the MCDM approach that can help a decision-taker, met with the difficult issue of a multitude of criteria [68]. AHP is an effective tool that can speed up the decision-making process. It is one of the most popular methods with a comprehensive, logical and structured system. Thus, this method was useful in analyzing quantitative information in the water supply industry, and the effectiveness of water management [67].

Izuakor and White [69] continued the analysis of the methods used in relation to critical infrastructures. After research, the novel method to identify essential infrastructure was proposed, and further study in this area is suggested using several criteria of decision theory.

The countries of the European Union apply the Critical service-dependent method, which identifies the most important services. Based on these services, they are trying to identify objects or other assets that belong to the CII. This method consists of three steps, which are shown in Figure 1 [63].

The goal of most of the methods is to determine the essential resources on which governments depend, and tp guarantee that they are adequately detecting faults.

Currently, there are more than 220 identified operators of critical infrastructure. In turn, 1000 critical resources are identified [70].

The different methods to identify CII could be applied. Each of the discussed methods has its advantages and disadvantages, but the government chooses the most appropriate method, taking into account their national characteristics.

The identified critical sectors and subsectors services are shown in

Table 1. Critical sectors, sub-sectors, and services [65].

Critical Sector	Subsector	Essential Services
Energy	Electricity	Generation, transmission/distribution, and the electricity market
	Petroleum	Extraction, refinement, transport, and storage
	Natural gas	Extraction, transport/distribution, storage
Information, Communication Technologies	IT	Web services, data left/cloud, and software services
	Communications	Voice/data communication, Internet connectivity
Water	Drinking water	Water storage, distribution and quality assurance
	Wastewater	Wastewater collection and treatment
Food		Agriculture/food production, supply, distribution, quality/safety
Health		Emergency health- and hospital care, infection/epidemic control, etc.
Financial services		Banking, payment transactions, stock exchange
Public order and safety		Maintenance of public order and safety, judiciary and penal systems
Transport	Aviation	Air navigation services, airports operation
	Road transport	Bus/tram services, maintenance of the road networks
	Train transport	Management or public railway, railway transport services
	Maritime transport	Monitoring and maintenance of shipping traffic, ice-breaking functions
	Postal and Shipping
Industry	Critical industries	Employment
	Chemical and Nuclear Industry	Storage and disposal of hazardous materials Safety of high-risk industrial units
Civil Administration		State functioning
Space		Protection of space-based systems
Civil protection		Emergency and rescue services
Environment		Monitoring and early warning (air and marine pollution, meteorological, groundwater)
Defense		National defense

[65].

The European Commission provides a brief of 11 essential areas: energy; information and communication technologies; water; food; health; financial public order and safety; civil administration; transport; chemical and nuclear industry; space and research [70].

To identify the objects of CII supporting critical services it is essential to determine the main factors that allow determining the degree of influence (

Table 2. The main factors that allow for the determination of the degree of influence [65,71].

Key Factors	Description
Scope or spatial distribution	The geographic zone that can be influenced by the failure or inaccessibility of a essential infrastructure (the international, national, provincial, regional level);
Severity or intensity or magnitude	The results of the interruption of a specific essential infrastructure; It can be measured as zero, minimum, moderate, or heavy. Assessment of the potential values may be used for different criteria.
Effects of time or temporal distribution	The point that the loss of a component can have a severe effect (immediately, several days, one week). The criterion defines when the loss of this part can have a significant impact. Time effects may be measured in different sizes, e.g., directly, for 24–48 hours, one week, or for a longer period.

) [65].

An important criterion is an impact on the population, which indicates the number of people affected, health problems, heavy injuries, etc. Equally important is the economic impact, which reflects the impact on Gross domestic product GDP, the importance of economic losses, as well as products and the deterioration of service quality. Environmental impact testing indicates an impact on a person and the surrounding landscape and takes the main part in assessing the importance of infrastructure. Infrastructure assessment should take into account the interdependence of criteria that show a certain dependence on infrastructure with another critical infrastructure. It may also be subject to political criteria that reflect confidence in the ability of the government [72]. The European Union has, in particular, estimated the destruction of infrastructure or the severity of the consequences of its destruction, based on six criteria: impact on society, economic consequences, environmental effects, political effects, psychological effects, consequences for public health.

Some criteria for the sectoral and sub-sectoral assessment of the Lithuanian critical infrastructure are presented in

Table 3. Some criteria for the evaluation of the services of critical infrastructures in Lithuania [73].

Services	Scores
	3	2	1	0
(K1) Environment, food, health, finance, public security and legal services, industry, government, civil protection, international relations, and security policy sectors	The service would cease to cover more than 145,000 inhabitants, or more than three municipalities, and will last more than 24 h	The service would cease to cover more than 20,000 inhabitants, which will last more than 24 h	The service would cease to cover more than 500 inhabitants, which will last more than 12 h	The service has stopped for less than 12 h
(K1) Services provided by the electricity sub-sector; Services provided by the natural gas subsector; Services provided by the district heating sector	Supply will be cut off for more than 145,000 residents or in more than three municipalities or category I consumers, which will last more than 24 h	Supply will be terminated for more than 20,000 inhabitants or a quarter of the population of the municipality, which will last more than 24 h	Supply will be terminated for more than 500 inhabitants, which will last more than 24 h	Supply will be cut off for less than 500 inhabitants
(K1) Services provided by the oil and petroleum products subsector	Supply of petroleum products will decrease by more than 25% of the average daily consumption	Supply of petroleum products will decrease by 12–25% of the average daily consumption	Supply of petroleum products will decrease by 7–12% of the average daily consumption	Supply of petroleum products will decrease, but not by more than 7% of the average daily consumption in the state

. These criteria indicate the level of impact of the destruction of the particular sector, the object of the subsector, or its inability to manage critical services.

The work is not limited to the criteria for evaluating the sectoral or sub-sectoral criteria. In addition, criteria are included that indicate the significance of the impact of the destruction or damage to the object.

To apply the methodology of the Lithuanian government, the problem of CII identification was solved for three objects. Since the assessment of the critical infrastructure was not publicly available, and this data was not available, the table would be filled with random numbers in the range, from 0 to 3 points. The studied objects provided services for air transport, road transport, rail transport, sea transport, postal subsectors, so the weight of the first criterion was 1. Other results are presented in

Table 4. An example of the matrix for assessing the critical information infrastructure (CII).

CII	Evaluation of Criteria
	K1	K2	K3	K4	K5	K6	K7	K8	K9	K10
Criteria weights	1	1	1	1	1	3	3	1	1	1
Object 1	0	2	3	1	0	0	3	0	0	0
Object 2	0	0	1	2	2	2	1	1	0	0
Object 3	2	0	3	3	0	0	1	2	2	3

.

The number of objects is not limited, but in the example, there are three objects.

The weighted sum method (WSM) is used to calculate the estimates. The results obtained are: Object 1 and Object 2 have 15 scores, and Object 3 has 18 scores. Thus, object 3 has the highest priority, while object 1 and object 2 both share the second priority position. It is impossible to determine which of these objects is more significant, since the importance of the two objects is the same.

Having determined that the WSM method that is used in the above-mentioned method of identifying a CII is currently inappropriate, another MCDM method is further discussed. A methodology should be used to better define the CII, and to solve the problems of the applied WSM model. The use of points from 0 to 3 must be replaced with new ones.

Researchers have proposed different methods for define subjective or objective weights of criteria. The basic idea of assessing the significance of the criterion is that the most critical criterion gains the biggest weight.

An integrated definition of the objective significance of a criterion in the MCDM method is proposed in [74]. In practice, usually, a subjective weight is used, determined by professionals or experts. Many methods have been developed to identify the criteria weights in terms of experts’ assessment of the importance (weights). The most widely used approaches include the Delphi [75], the expert judgment [76], the Analytic Hierarchy Process (AHP) [77,78], the Analytic Network Process, Step-wise weight assessment ratio analysis method (SWARA) [79], and others. For example, criteria weights are determined by applying the AHP method: the weights of the criteria are calculated based on Saaty’s judgment scale and the new original scale, as presented by the authors. The ARAS (Additive Ratio Assessment) method (the MCDM approach) is applied, to solve the problem under investigation. The developed assessment method involves the Leadership in Energy and Environmental Design (LEED) system’s criteria [80].

During the evaluation process, the criteria values, and the degree of domination of each criterion, i.e., the objective weight criteria, could be considered. Unlike their subjective analogues, the objective weights are rarely used in practice. The Entropy method [81,82,83], the LINMAP method [84], the correlation coefficient, and the standard deviation based on the objective value determination method [85], and the prediction algorithm [86] are practical methods that are often used. Combined weighing is based on the integration of both objective and subjective judgments [87,88].

In our case, according to [89], the fuzzy WASPAS method was chosen.

2.4. An MCDM Process to Identify CII

This article presents an MCDM-based model of the applicability of the MCDM method for determining CII.

One of the main stages to determine CII is the design of a mathematical model consisting of:

• a choice of essential variables;
• drawing up restrictions, which are satisfied by variables;
• a compilation of the objective function, which reflects the critical criteria for selecting the assignment of an object to a vital one.

The solution of the problem depends on the set of criteria for classifying objects as critical, as well as on their significance.

The task of classifying an information object is complicated by the presence of incomparable values of criteria, since particular criteria respectively have different units of measure, their scales are not comparable, and therefore, comparing the results that are obtained for each criterion is difficult.

Besides, the scales must be reduced and dimensionless—normalized values of criteria are used. Formally, describing the principle of optimality (the criteria of “correctness of the solution”) is difficult, due to the following reasons:

• The objects considered by the theory of decision-making are so diverse that it is difficult to establish uniform principles of optimality for all classes of problems.
• The goals of the decision-making stakeholders are different and often opposite.
• The criteria for the correctness of the decision depend on the nature of the task, its goals, etc., and also on how correctly they were chosen for a particular country.
• The difficulties in selecting a solution may be hidden in the specific formulation of the problem, if unrealistic results are required.

Alternative objects are characterized by the correctness of the definition of vital criteria and their significances. They have essential meaning. This is possible, by establishing the criticality of information objects and the priority of the compared options. Using international experience and expert assessments, as well as information sources, the values of the criteria are determined [73].

In this paper, the MCDM method performs the following functions:

• The identification of CII among the available information objects;
• The comparison of CII, and the formation of a comparative table.

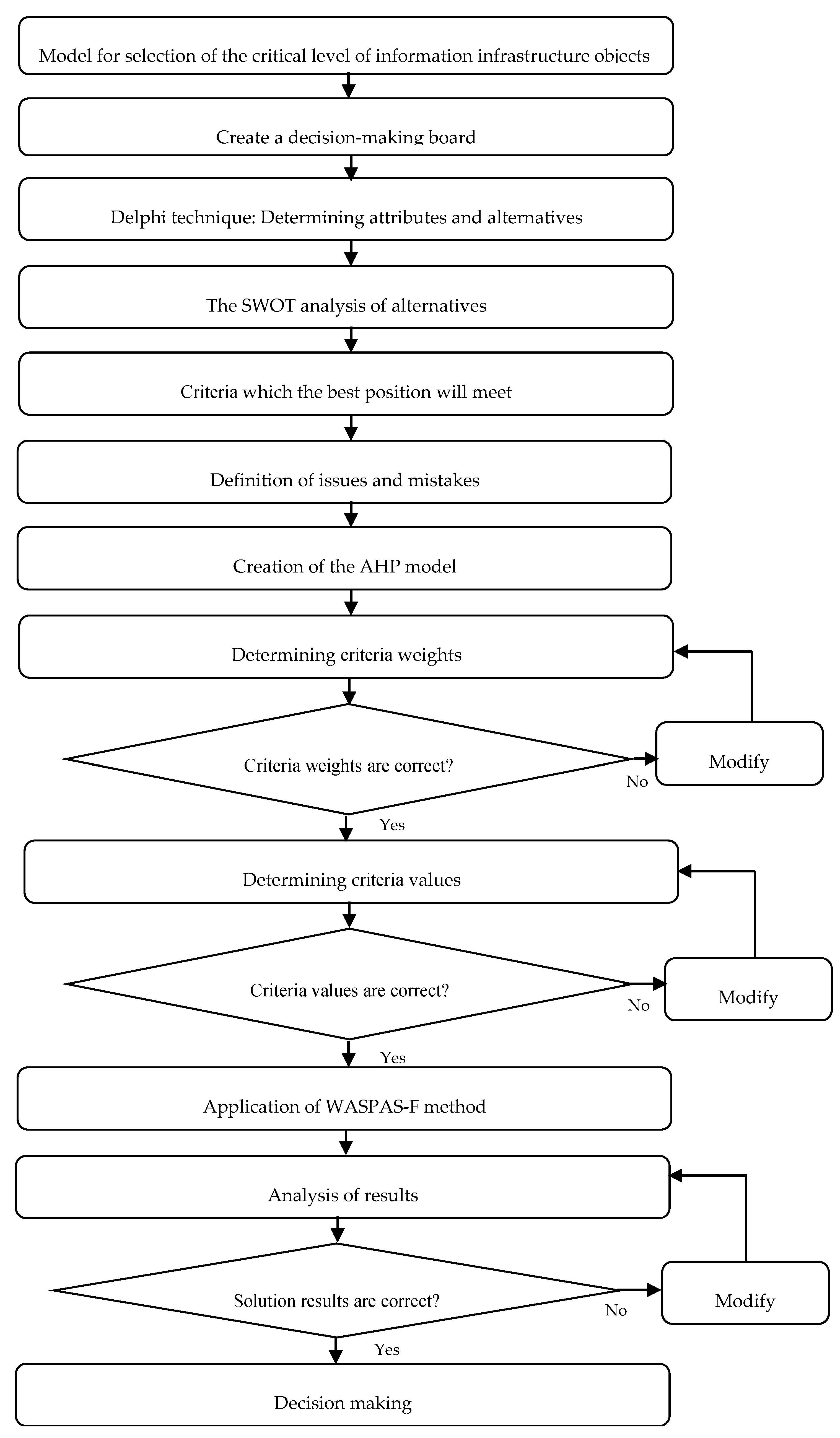
The proposed model and the stages identified for the method for the CII identification structure are shown in Figure 2.

The procedure should concentrate on an essentially imperative task: to identify the decision-taker, and to differentiate it from the issue analysis. Various variants are possible for the criteria optimization, as well as synthesizing all criteria into one criterion of defining the optimum. The criteria are exceedingly conditioned, with the priorities and critical assets being identified. The criteria for the CII evaluation should be identified with a focus on country-critical services. The main stage in forming the criteria involves choosing the basic criteria for CII identification that can be divided into sub-criteria during the procedure. This could be the criteria for the life and health of the population, the criteria for the impact on the economy of the country, the criteria for environmental damage, etc. Criteria groups have various influences on significance.

To form the steps of the MCDM method of CII, we use the model described in the article [90].

Another model, which is used for identifying CII by the MCDM method, is shown in Figure 3.

There are several cases in which different MCDM approaches have various decisions. It might be explained because of the various mathematical artefacts that are used by different MCDM methods. However, the issue of applying a convenient MCDM approach in a specific case still exists. The choice of MCDM methods based on various parameters has already been studied by earlier researchers in [91]. When a particular MCDM method is finally recommended for a particular application, it is observed that its decision accuracy and ranking efficiency strongly depends on the value of its control parameter [92].

The most suitable solution of a problem in different areas, considering a number of criteria, such as environment, engineering, finance, etc., is the use of the MCDM method [67].

The flowchart of the proposed issue is shown in Figure 4.

Often, due to the lack of accurate data, employees spend a lot of time discussing various expert opinions. The problem-solving approach still stands.

The fuzzy set theory is a class of objects with a continuum of membership grades. Here, a fuzzy set A, presented in space $X$, is an ordered set of pairs. The components with 0 degrees can be unlisted:

$$A=\left\{\left(x,{\mu }_A\left(x\right)\right),x\in X\right\},\forall x\in X,\mathrm{and}X\to \left[0;1\right],$$

(1)

where $A$ is described by its function ${\mu }_A:X\to \left[0;1\right]$, which associates with each component $x\in X$, a real number ${\mu }_A\left(x\right)\in \left[0;1\right]$. The function ${\mu }_A\left(x\right)$ at $x$ identifies the grade of membership of $x$ in $A$, and is accounted for by the membership degree to which $x$ belongs to A.

An ordinary subset A of $X$ is presented like a fuzzy set in $X$, with a membership function as its characteristic function:

$${\mu }_A\left(x\right)=\{\begin{array}{l}1,x\in A;\\ 0,x\notin A.\end{array}$$

(2)

If the universe of discourse is discrete and finite with cardinality n, that is $X=\left\{x_1,x_1,\dots ,x_n\right\}$, $A$ is calculated as:

$$A={\displaystyle {\sum }_{i=1}^n\frac{{\mu }_A\left(x_i\right)}{x_i}}=\frac{{\mu }_A\left(x_1\right)}{x_1}+\frac{{\mu }_A\left(x_2\right)}{x_2}+\cdots +\frac{{\mu }_A\left(x_n\right)}{x_n},.$$

(3)

If the universe of discourse $X$ is an interval of real numbers, the A could be shown as follows:

$$A={\displaystyle \underset{X}{\int }\frac{{\mu }_A\left(x\right)}{x}}.$$

(4)

The fuzzy number A is determined to be a fuzzy triangular number, with α- lower, β-modal, and γ-upper values, if its membership function ${\mu }_A\left(x\right)\to \left[0,1\right]$ is defined as:

$${\mu }_A\left(x\right)=\{\begin{array}{ll}\frac{1}{\beta -\alpha }x-\frac{\alpha }{\beta -\alpha },& ifx\in \left[\alpha ,\beta \right],\\ \frac{1}{\beta -\gamma }x-\frac{\alpha }{\beta -\gamma },& ifx\in \left[\beta ,\gamma \right],\\ 0,& otherwise,\\ \alpha \le \beta \le \gamma .& \end{array}$$

(5)

To obtain a crisp output, a defuzzification is implemented, which produces a quantifiable result in fuzzy logic, given the fuzzy sets and their corresponding membership degrees.

The fuzzy number is generally an expert’s given subjective data. Figure 5 presents the ordinary fuzzy set membership function.

Table 5. Main processes on fuzzy triangular numbers [93].

Relations
${\tilde{x}}_1=\left(x_{1\alpha },x_{1\beta },x_{1\gamma }\right),$${\tilde{x}}_2=\left(x_{2\alpha },x_{2\beta },x_{2\gamma }\right)$	(6)	$k{\tilde{x}}_1=\left(\begin{array}{l}k{x}_{1\alpha },\\ k{x}_{1\beta },\\ k{x}_{1\gamma }\end{array}\right)$	(10)
${\tilde{x}}_1\oplus {\tilde{x}}_2=\left(\begin{array}{l}{x}_{1\alpha }+x_{2\alpha },\\ x_{1\beta }+x_{2\beta },\\ x_{1\gamma }+x_{2\gamma }\end{array}\right)$	(7)	${\tilde{x}}_1(÷){\tilde{x}}_2=\left(\begin{array}{l}\frac{x_{1\alpha }}{x_{2\gamma }},\\ \frac{x_{1\beta }}{x_{2\beta }},\\ \frac{x_{1\gamma }}{x_{2\alpha }}\end{array}\right)$	(11)
${\tilde{x}}_1(-){\tilde{x}}_2=\left(\begin{array}{l}{x}_{1\alpha }-x_{2\gamma },\\ x_{1\beta }-x_{2\beta },\\ x_{1\gamma }-x_{2\alpha }\end{array}\right)$	(8)	${\left({\tilde{x}}_1\right)}^{-1}=\left(\begin{array}{l}\frac{1}{x_{1\gamma }},\\ \frac{1}{x_{1\beta }},\\ \frac{1}{x_{1\alpha }}\end{array}\right)$	(12)
${\tilde{x}}_1\otimes {\tilde{x}}_2=\left(\begin{array}{l}{x}_{1\alpha }{x}_{2\alpha },\\ x_{1\beta }{x}_{2\beta },\\ x_{1\gamma }{x}_{2\gamma }\end{array}\right)$	(9)	${({\tilde{x}}_1)}^{{\tilde{x}}_2}=\left(\begin{array}{l}{x}_{1\alpha }^{x_{2\gamma }},\\ x_{1\beta }^{x_{2\beta }},\\ x_{1\gamma }^{x_{2\alpha }}\end{array}\right)$	(13)
A-lower, β-modal and γ-upper values of fuzzy numbers

presents the following basic arithmetic operations for two triangular fuzzy numbers: (6) two triangular fuzzy numbers; (7) addition; (8) subtraction; (9) multiplication; (10) multiplication by constant; (11) division; (12) determining the reciprocal value; (13) the fuzzy power of raising the fuzzy numbers [94].

Experts have determined the weight values $0<{\tilde{w}}_j<1,{\displaystyle \sum _{j=1}^n{w}_j=1}$. It is known that many methods are able to assess weights. Sometimes, some expert data cannot be accurately described by using numerical values. There are four main options that describe various ways of measuring the number of things in quantitative terms: nominal, ordinal, interval, or ratio scales. Likert items were proposed in [95].

Raising a fuzzy triangular number of the power of another fuzzy triangular number, if ${\tilde{x}}_1=\left(x_{1\alpha }\le 1,x_{1\beta }\le 1,x_{1\gamma }\le 1\right)$, and ${\tilde{x}}_2=\left(x_{2\alpha }\le 1,x_{2\beta }\le 1,x_{2\gamma }\le 1,\right)$ this is special for this situation of research.

In the analysis, an initial data matrix is created initially, in which the rows contain alternatives, and in the columns, there are selected significant indicators. Each indicator is assigned to whether it is maximized or minimized.

2.5. The WASPAS Method

The WSM approach calculates the total score of the alternative as a weighted sum of the criteria. The WPM approach was created to prevent alternatives that have poor attributes or criterion values. Zavadskas et al. used the multiplicative exponential weighting method (or WPM) to solve dynamically changing environment problems [27].

The problem solution process by applying the WASPAS-F method is shown below.

Create the fuzzy decision-making matrix by using the values ${\tilde{x}}_{ij}$ and the criteria weights ${\tilde{w}}_j$ as the decision-making matrix entries. Determine the linguistic ratings.

Usually, experts play a main role in identifying the system of criteria, the linguistic values of the qualitative criteria, and the initial criteria weights.

The initial fuzzy decision-making matrix shows the preferences for m reasonable alternatives rated on n attributes:

$$\begin{array}{l}\tilde{X}=\left[\begin{array}{ccccc}{\tilde{x}}_{11}& \cdots & {\tilde{x}}_{1j}& \cdots & {\tilde{x}}_{1n}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{x}}_{i1}& \cdots & {\tilde{x}}_{ij}& \cdots & {\tilde{x}}_{in}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{x}}_{m1}& \cdots & {\tilde{x}}_{mj}& \cdots & {\tilde{x}}_{mn}\end{array}\right];\\ i=\overline{1,m};j=\overline{1,n},\end{array}$$

(14)

where ${\tilde{x}}_{ij}$ is a fuzzy value that presents the performance value of the i alternative in terms of the j criteria. A tilde symbol “~” means a fuzzy set.

The process of normalization of the initial values of all criteria ${\tilde{x}}_{ij}$ eliminates different criteria measurement units. The values of the normalized decision-making matrix $\tilde{\overline{X}}$:

$$\tilde{\overline{X}}=\left[\begin{array}{ccccc}{\tilde{\overline{x}}}_{11}& \cdots & {\tilde{\overline{x}}}_{1j}& \cdots & {\tilde{\overline{x}}}_{1n}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{\overline{x}}}_{i1}& \cdots & {\tilde{\overline{x}}}_{ij}& \cdots & {\tilde{\overline{x}}}_{in}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{\overline{x}}}_{m1}& \cdots & {\tilde{\overline{x}}}_{mj}& \cdots & {\tilde{\overline{x}}}_{mn}\end{array}\right];$$

(15)

are determined as follows:

$$\begin{array}{l}{\tilde{\overline{x}}}_{ij}=\frac{{\tilde{x}}_{ij}}{\underset{i}{\max }{\tilde{x}}_{ij}}if\underset{i}{\max }{\tilde{x}}_{ij}^{}ispreferable;\\ {\tilde{\overline{x}}}_{ij}=\frac{\underset{i}{\min }{\tilde{x}}_{ij}}{{\tilde{x}}_{ij}}if\underset{i}{\min }{\tilde{x}}_{ij}^{}ispreferable;\\ i=\overline{0,m};j=\overline{1,n}.\end{array}$$

(16)

Determine the weighted normalized fuzzy decision-making matrix ${\tilde{\widehat{X}}}_q$ for the WSM:

$$\begin{array}{l}{\tilde{\widehat{X}}}_q=\left[\begin{array}{ccccc}{\tilde{\widehat{x}}}_{11}& \cdots & {\tilde{\widehat{x}}}_{1j}& \cdots & {\tilde{\widehat{x}}}_{1n}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{\widehat{x}}}_{i1}& \cdots & {\tilde{\widehat{x}}}_{ij}& \cdots & {\tilde{\widehat{x}}}_{in}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\tilde{\widehat{x}}}_{m1}& \cdots & {\tilde{\widehat{x}}}_{mj}& \cdots & {\tilde{\widehat{x}}}_{mn}\end{array}\right];\\ {\tilde{\widehat{x}}}_{ij}={\tilde{\overline{x}}}_{ij}{\tilde{w}}_j;i=\overline{1,m};j=\overline{1,n}.\end{array}$$

(17)

Determine the weighted normalized fuzzy decision-making matrix ${\tilde{\widehat{X}}}_p$ for the WPM:

$$\begin{array}{l}{\tilde{\widehat{X}}}_p=\left[\begin{array}{ccccc}{\widetilde{\overline{\overline{x}}}}_{11}& \cdots & {\widetilde{\overline{\overline{x}}}}_{1j}& \cdots & {\widetilde{\overline{\overline{x}}}}_{1n}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\widetilde{\overline{\overline{x}}}}_{i1}& \cdots & {\widetilde{\overline{\overline{x}}}}_{ij}& \cdots & {\widetilde{\overline{\overline{x}}}}_{in}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\widetilde{\overline{\overline{x}}}}_{m1}& \cdots & {\widetilde{\overline{\overline{x}}}}_{mj}& \cdots & {\widetilde{\overline{\overline{x}}}}_{mn}\end{array}\right];\\ {\widetilde{\overline{\overline{x}}}}_{ij}={\tilde{\overline{x}}}_{ij}^{{\tilde{w}}_j};i=\overline{1,m};j=\overline{1,n}.\end{array}$$

(18)

Calculate the multi-attribute utility function values:

The WSM for i alternative:

$${\tilde{Q}}_i={\displaystyle \sum _{j=1}^n{\tilde{\widehat{x}}}_{ij};i=\overline{1,m}},$$

(19)

The WPM for i alternative:

$${\tilde{P}}_i={\displaystyle \prod _{j=1}^n{\widetilde{\overline{\overline{x}}}}_{ij}},i=\overline{1,m}.$$

(20)

The center-of-area is the most practical and easy to use for the defuzzification of the fuzzy performance measurement:

$$Q_i=\frac{1}{3}(Q_{i\alpha }+Q_{i\beta }+Q_{i\gamma }).$$

(21)

$$P_i=\frac{1}{3}(P_{i\alpha }+P_{i\beta }+P_{i\gamma }).$$

(22)

The utility function value K_i of the WASPAS-F method is calculated as follows:

$$K_i=\lambda {\displaystyle {\sum }_{j=1}^n{Q}_i^{}+\left(1-\lambda \right){\displaystyle {\sum }_{j=1}^n{P}_i;\lambda =0,\dots ,1,0\le K_i\le 1,}}$$

(23)

where:

$$\lambda =\frac{{\displaystyle {\sum }_{i=1}^m{P}_i}}{{\displaystyle {\sum }_{i=1}^m{Q}_i}+{\displaystyle {\sum }_{i=1}^m{P}_i}}.$$

(24)

Rank preference orders the alternatives, starting from the highest value, K_i.

A Likert-type 10-point scale was adopted to solve the problem (Figure 6).

A detailed description of the problem-solving process using the AHP and WASPAS-F methods could be found in [93].

3. Results

This article analyzes the problem of identifying the CII of the country.

When solving problems of a MCDM method, first of all, a set of possible alternatives is formed, consisting of the CII. Next, the criteria are selected. A matrix of a set of alternative objects, and the criteria of their criticality are presented in

Table 6. Matrix for CII assessment.

CII	Criteria Criticality
	Criterion 1	Criterion 2	Criterion 3	Criterion 4	…	Criterion n
Object 1	x11	x12	x13	x14	…	x1n
Object 2	x21	x22	x23	x24	…	x2n
Object 3	x31	x32	x33	x34	…	x3n

.

The criteria were identified on the basis of the sectors, which have a large EU counterpart. The list of proposed criteria is as follows:

• The danger to life or health. This criterion is designed to assess how many people will be disturbed if the provision of a particular service stops. This criterion will cover all sub-sectoral and sectoral criteria, since the impacts considered include failure for these sectors or sub-sectors. Many sub-sectoral and sectoral criteria are estimated by the number of injured people, and by general criteria, the population health is also evaluated by their number; therefore, the unit of measure for this criterion is the population of the country.
• The impact on the economy of the country. This criterion is widely used in the methodologies of the respective countries, and is included in the list of criteria that is recommended by the European Union. An economic impact assessment may have several expressions, but the proposed methodology deals with the number of productive working days that are lost. It is being understood as the time at which the destruction, damage, or significant damage to an infrastructure facility stops, or significantly disrupts certain activities. The number of lost production days is defined in terms of the number of lost production days multiplied by the number of employees involved in the work activity that has stopped or failed. When evaluating productive working days, it is necessary to take into account the impact of the destruction, damage, or violation of the estimated infrastructure facility on the productive working days of another infrastructure.
• Environmental damage. The assessment of potential financial damage to the destruction of the environment or infrastructure should be carried out in accordance with the order of the Environmental Protection Law. The measure of environmental damage is the monetary value.
• The impact of other facilities, in order to ensure the supply of basic services and continuous operation. This criterion includes the impact on the operation of another facility, which provides both the most important services, as well as other important services. Measure—the affected facilities that provide a range of important services.
• Influence on public safety. Infrastructure damage or significant disruption can lead to widespread unrest. The impact on public safety is considered as the number of municipalities over which public safety management has been lost.
• Damage to other European Union Member States. The destruction of the CII of one state can lead to negative consequences for other countries. This dependence is one of the important criteria for the EU countries, as its unit of measurement is the impact on the number of countries in the European Union.

Further criteria are determined by the weight, depending on their importance. More significant criteria possess higher weight values (

Table 7. Criteria weights.

	Criterion 1	Criterion 2	Criterion 3	Criterion 4	Criterion n
Criteria weights	Weight 1	Weight 2	Weight 3	Weight 4	Weight n

).

The task of choosing the best alternative, in this case of the creation of a priority sequence of CII, is solved by the previously discussed MCDM methods.

In this case, seven experts were interviewed to assess the critical infrastructure alternatives. Coming both from the information security industry and academia from different European countries, they were invited to ensure the understanding of the European context and deep practical knowledge of the critical infrastructure: one from Poland (academic and industry background), one from Estonia (academic background), one from Sweden (academic background), and four from Lithuania (one of them having academic background and three from an industry background). One of the Lithuanian experts invited is one of the leading information security specialists in Lithuania, with more than 15 years of experience with key competences in critical security control development, a strong background in European knowledge (ENISA and Lithuanian Government advisor on national cybersecurity strategy), keeping CISA (Certified Information Systems Auditor), CRISC (Certified in Risk and Information Systems Control), CISSP (Certified Information Systems Security Professional), and several other security-related certifications. The majority of other experts with practical backgrounds also possessed industry-recognized security related certificates (CISA, CISM (Certified Information Security Manager), CRISC, CEH (Certified Ethical Hacker), CISSP, and others), and have experience in administering critical infrastructure, the organization of CERT (Computer emergency response teams) functions, or performing wide-scale risk assessments.

According to the results of the interview, the data obtained were summarized, and the average estimates of the seven experts were used in the article.

It should also be noted that the assessment of the criticality of the information infrastructure becomes more accurate if the number of experts is greater. Accordingly, it is preferable to take into account the opinion of several experts when assessing criticality.

Materials associated with the CII were collected and defined, and descriptions of the most significant criteria were made. The analysis was implemented. In this study, the SWOT (Strengths, Weaknesses, Opportunities, and Threats) analysis was used. Three information infrastructure alternatives, which are denoted as A₁, A₂, and A₃, were chosen as possible alternatives. The A₁ alternative is the information infrastructure of air transport, which provides both air navigation services and airport operation. A₂ is the information infrastructure of the health sector, which provides emergency and hospital healthcare services. A₃ is the financial information infrastructure, which provides banking, payment transactions, and stock exchange. The AHP approach was used to compare the criteria to each other. As mentioned above, the Likert-type ten-point scale (Figure 6) was used. In addition, a questionnaire about the experts’ evaluation levels toward the CII choices was used. It consisted of 10 various levels—from “not important” (${\tilde{P}}_1$) to “extremely important” (${\tilde{P}}_6$)—on a fuzzy 10-level scale. So, the score of “not important” (${\tilde{P}}_1$) corresponded to a Triangular Fuzzy Number (TFN) of (0, 1, 1), respectively. The comparison matrix set is presented in

Table 8. Determining the linguistic ratings.

Scale		α	γ	Β
Extremely Important	EI	9	10	10
Very Important	VI	7	9	10
Important	I	5	7	9
Medium Important	MI	3	5	7
Low Important	LI	1	3	5
Not Important	NI	0	1	1

.

The experts determined the criteria weights.

Table 9. Pairwise comparisons of the criteria weights for CII.

		x1	x2	x3	x4	x5	x6	w
The danger to life or health	x1	1	3	3	5	3	3	0.38
Impact on the economy of the country	x2	0.33	1	1	3	3	3	0.20
Damage to the environment	x3	0.33	1.00	1	3	1	3	0.17
The influence of other facilities in ensuring the continuous operation of critical services	x4	0.20	0.33	0.33	1	3	3	0.11
Effect on public safety	x5	0.33	0.33	1	0.33	1	3	0.20
Damage to other European Union Member States	x6	0.33	0.33	0.33	0.33	0.33	1	0.06

presents the integrated results of the established weights. The priority weight vector describes the significance level of the criteria in the decision matrix. After obtaining the significance levels of the criteria, the fuzzy WASPAS approach was used to assess the criticality of the information infrastructures.

In this step of the research, fuzzy WASPAS began to establish fuzzy assessments of the alternative information infrastructures (A₁, A₂, and A₃), taking into account the criteria by applying TFNs. This is an initial decision-making matrix (DMM) for ranking alternatives, and it denotes the implementation ratings of the alternatives in accordance with the criteria.

Table 10. The initial Fuzzy Multi-Criteria Decision Making (FDMM) for the CII alternatives.

	A1			A2			A3			max	W
	A	γ	β	A	γ	β	α	γ	β
x1	7	9	10	7	9	10	1	3	5	10	0.38
x2	7	9	10	1	3	5	5	7	9	10	0.20
x3	1	3	5	0	1	1	1	3	5	5	0.17
x4	1	3	5	1	3	5	3	5	7	7	0.11
x5	7	9	10	7	9	10	1	3	5	10	0.20
x6	5	7	9	3	5	7	3	5	7	9	0.06

presents a comparison of the alternatives in accordance with the criteria.

The normalized decision matrix was achieved by applying relation (16) (

Table 11. The normalized FDMM.

	A1			A2			A3			W
	α	γ	β	α	γ	β	α	γ	β
x1	0.7	0.9	1.0	0.7	0.9	1.0	0.1	0.3	0.5	0.38
x2	0.7	0.9	1.0	0.1	0.3	0.5	0.5	0.7	0.9	0.20
x3	0.2	0.6	1.0	0.0	0.2	0.2	0.2	0.6	1.0	0.17
x4	0.1	0.4	0.7	0.1	0.4	0.7	0.4	0.7	1.0	0.11
x5	0.7	0.9	1.0	0.7	0.9	1.0	0.1	0.3	0.5	0.20
x6	0.6	0.8	1.0	0.3	0.6	0.8	0.3	0.6	0.8	0.06

).

Relation (17) was applied to archive the weighted-normalized Fuzzy Multi-Criteria Decision Making (FDMM) for WSM (

Table 12. The weighted normalized matrix for WSM.

	A1			A2			A3
	α	Γ	Β	α	γ	β	α	γ	β
x1	0.3	0.3	0.4	0.3	0.3	0.4	0.0	0.1	0.2
x2	0.1	0.2	0.2	0.0	0.1	0.1	0.1	0.1	0.2
x3	0.0	0.1	0.2	0.0	0.0	0.0	0.0	0.1	0.2
x4	0.0	0.0	0.1	0.0	0.0	0.1	0.0	0.1	0.1
x5	0.1	0.1	0.1	0.1	0.1	0.1	0.0	0.0	0.0
x6	0.0	0.0	0.1	0.0	0.0	0.0	0.0	0.0	0.0
Q			0.8			0.6			0.5
									1.83

), and relation (18) was applied to archive the weighted-normalized FDMM for WPM (

Table 13. The weighted normalized matrix for WPM.

	A1			A2			A3
	α	γ	Β	α	γ	β	α	γ	β
x1	0.9	1.0	1.0	0.9	1.0	1.0	0.4	0.6	0.8
x2	0.9	1.0	1.0	0.6	0.8	0.9	0.9	0.9	1.0
x3	0.8	0.9	1.0	0.0	0.8	0.8	0.8	0.9	1.0
x4	0.8	0.9	1.0	0.8	0.9	1.0	0.9	1.0	1.0
x5	1.0	1.0	1.0	1.0	1.0	1.0	0.8	0.9	0.9
x6	1.0	1.0	1.0	0.9	1.0	1.0	0.9	1.0	1.0
$Q$			5.7			5.1			5.2
								${\displaystyle \sum Q}$	16.0

). Relations (19) and (20), respectively, were applied to determine the values of the optimality function values for WSM and WPM.

The integrated utility function value of the fuzzy WASPAS technique for CII was identified by applying relation (24), as shown in Table 13. A₁ is the most critical information infrastructure in the WSM, WPM, and WASPAS approach (

Table 14. Integrated utility function values of the fuzzy WASPAS approach.

	A1	A2	A3
Qi	0.8	0.6	0.5
Pi	5.7	5.1	5.2
λ			0.90
Ki	0.8	0.6	0.5
Rank	1	2	3

). A₃ is the least critical alternative among all of the CII considered. Usually, the decision-taker recommends information protection measures according to the level of the criticality of information infrastructures.

4. Discussion

There are various MCDM techniques that are widely applied. The WSM, which is now used in the different EU countries, is one of the recently developed and most widely used methods.

The results obtained according to the Lithuanian WSM-based methodology are less accurate than the results obtained by the WASPAS-F approach. The resulting value estimate was an integer. In calculations, it is often difficult to determine the priority of the object, since the results obtained may be the same and repetitive, but this is not the only drawback of this method. Given the fact that the methodology is subject to expert estimates, this limit is not appropriate. The results are subject to significant changes, and for this reason, the importance of the objects can be calculated erroneously.

In this case, CII may be incorrectly assessed, due to the problems mentioned above, as well as due to a misunderstanding of the method. The WSM method has its drawbacks associated with using the same dimensions for different criteria. The application of this approach requires that the assessments of all the criteria have the same magnitude, but the criteria of the critical infrastructure cover very broad areas. The influence is measured by the number of affected populations, the number of affected areas, and other sizes, and this method cannot be applied to solve this problem. The decision to use scores from 0 to 3 does not solve the current problem, since such a scoring system has no mathematical justification. Currently, using this method of identifying the CII, the sum of all criteria weighs from 14 to 16 scores. Such a weighting of criteria is also inappropriate, since, based on the WSM method, the weights of all the criteria must be equal to 1.

To overcome some of the shortcomings of this method, the fuzzy WASPAS method was chosen. The solved problem for identifying and ranking CII shows a more accurate result than the WSM method. The WASPAS-F method joins the advantages of the WSM and WPM approaches.

In this case, the AHP was applied to identify the importance of the criteria, while the fuzzy WASPAS was used to rank the alternative information infrastructures. The AHP method allowed for the effective determination of the weights of the criteria.

Finally, it was found that the described fuzzy WASPAS approach is practical for ranking alternatives.

Thus, the theoretical research and the practical results have demonstrated the effectiveness of using the Fuzzy WASPAS approach to identify CII. This approach can be used to identify the CII of other countries, including EU countries, as well as to solve other problems.

5. Conclusions

The socio-economic development of any country and its sustainable development, in fact, are directly dependent on the correct identification of CII, their reliability, and their safety. The achievement of the sustainable functioning of CII of countries represents for all states the essential elements in developing their strategies, the development of risk management, and the improvement of the ability to respond to information-related incidents and threats.

The stability of national security is a state of well-being of a country’s citizens, because each country can exist only in a safe environment. However, each country often faces different types of threats to national security.

CII, such as the smart grid, gas and water networks, and transportation and communication networks, has a decisive impact on the quality of life and the environment development of EU.

Inaccurate identification of the list of CII may lead to the non-application of appropriate measures to protect them, which may adversely influence the environment, and the economic and political state of the country, etc.

A new model was proposed to solve the problem of identification of the criticality of information infrastructures by applying the WASPAS-F approach. Six main criteria were defined. The weights of the criteria were calculated based on the AHP method. As a result, the most important criteria were “The danger to life or health” and “Impact on the economy of the country”; the medium-important ones were “Damage to the environment” and “The influence of other facilities ensuring the continuous operation of critical services”; and the least important criteria were the “Effect on public safety” and “Damage to other European Union Member States”.

This model is proposed for further use in calculating the criticality of real information infrastructures.