A Multivariate Modeling Analysis of Commuters’ Non-Work Activity Allocations in Xiaoshan District of Hangzhou, China
Abstract
:1. Introduction
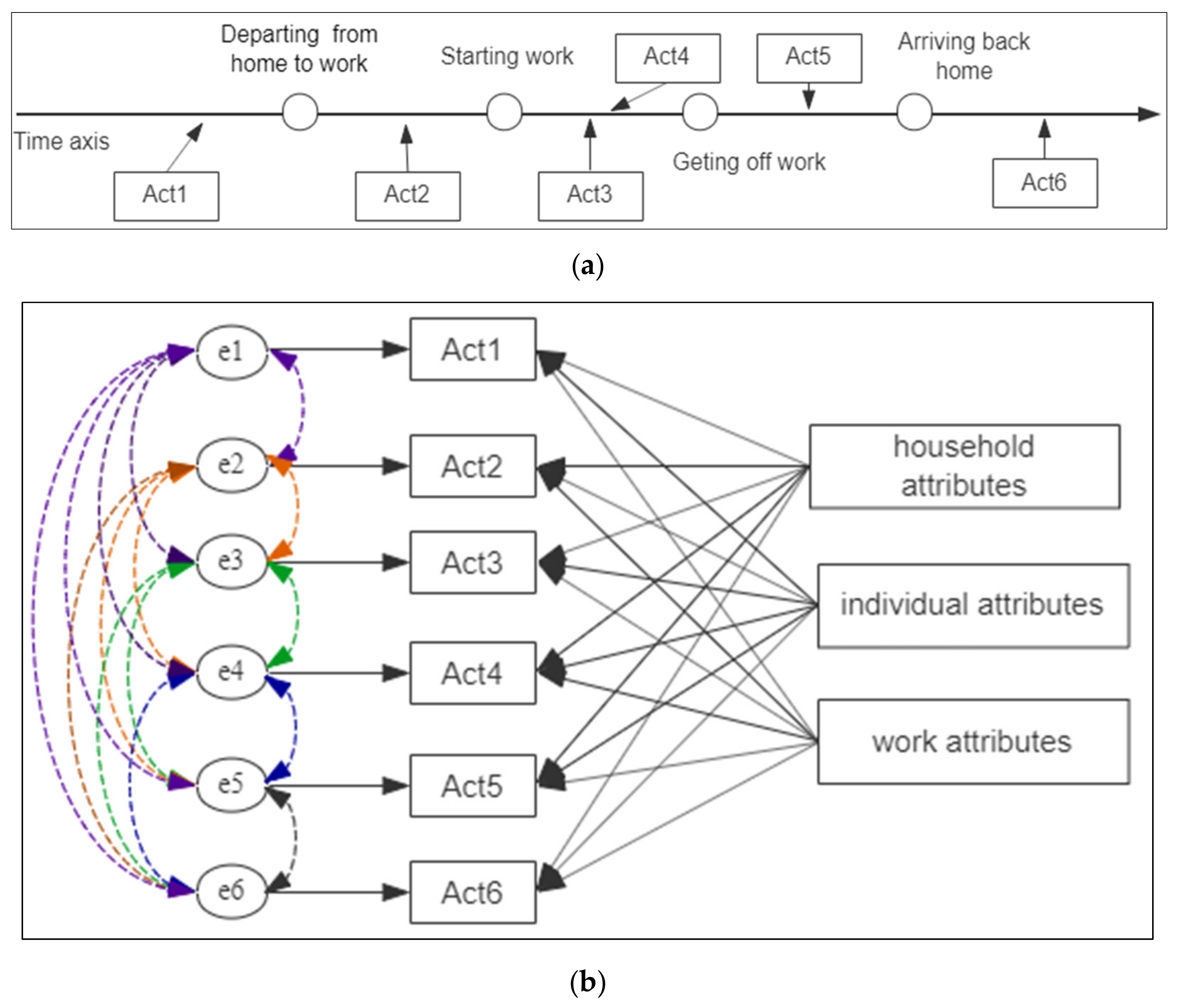
2. Modeling Methodology
3. Data Preparation and Description
3.1. Descriptive Analysis of Sample Data
3.2. Descriptive Analysis of Explanatory Variables and Dependent Variables in the Model
3.3. Distribution Analysis of Purposes of Outdoor Non-Work Activities
4. Empirical Results
4.1. Estimation Results and Elasticity Analysis
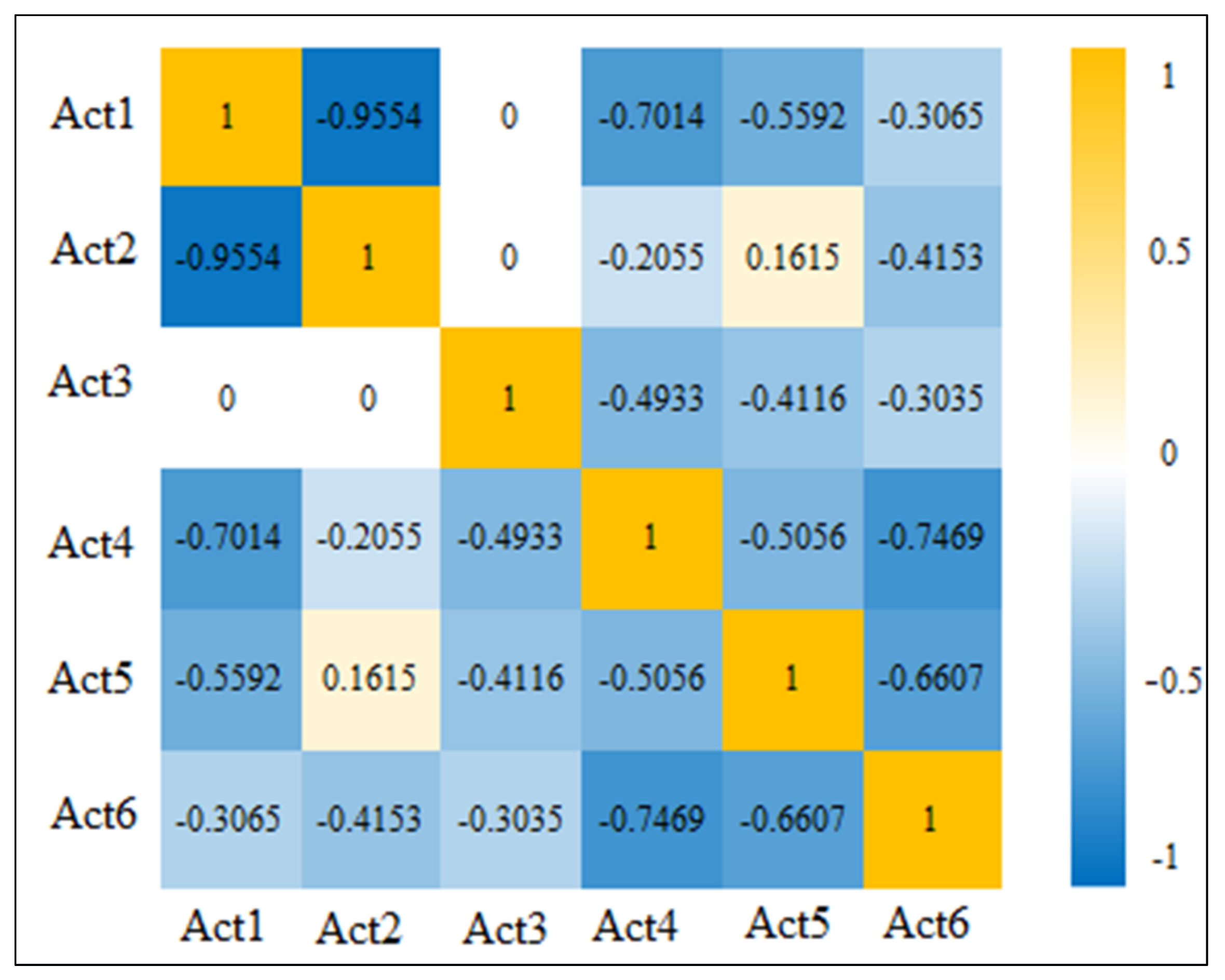
4.2. Discussions on Error Correlation Matrix
5. Conclusions and Discussions
- Daily work time is a highly elastic factor for all types of outdoor non-work activity allocations of commuters. It has a positive effect on midday non-work activities (Act3 and Act4), but a negative effect on morning and evening non-work activities (Act1, Act2, Act5, and Act6). This suggests that increasing the total work hours may shift the demands for non-work activities from morning or evening to noon.
- A work schedule is a combination of times when a commuter starts and finishes his/her work. The starting time for work has a significant impact on non-work activities before work (i.e., Act1 and Act2), while the off-work time has a significant impact on non-work activities after work (i.e., Act5 and Act6).
- The relation between Act2 and Act5 is mutually promotive, and the others are mutually substitutive. Some policies, like encouraging people to participate in activities during off-peak hours, may help to shift travel demand from peak hours to off-peak hours. It should be noted that the magnitude of error correlation depends on the number of significant variables being specified into the model. Model practitioners need to make extensive effort to screen and specify observed variables into the joint model in order to better control their effects and capture correlations among unspecified attributes truly reflecting inherent factors affecting activity or travel behaviours.
- When trip chains become increasingly complex, commuters will be more likely to use motorized private modes, such as automobiles. This indicates that the level of motorization in Xiaoshan District may continue to increase in the future. Local transportation authority should formulate some reasonable policies to prevent traffic congestion.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Shanghai Urban and Rural Construction and Transportation Development Research Institute. The Fifth Comprehensive Traffic Survey in Shanghai; Shanghai Urban and Rural Construction and Transportation Development Research Institute: Shanghai, China, 2015. [Google Scholar]
- Dissanayake, D.; Morikawa, T. Household travel behavior in developing countries: Nested logit model of vehicle ownership, mode choice, and trip chaining. Transp. Res. Rec. 2002, 1805, 45–52. [Google Scholar] [CrossRef]
- Bhat, C.R. Work travel mode choice and number of non-work commute stops. Transp. Res. Part B Methodol. 1997, 31, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Vickerman, R. The demand for non-work travel. J. Transp. Econ. Policy 1972, 6, 176–210. [Google Scholar]
- Maat, K.; Van Wee, B.; Stead, D. Land use and travel behaviour: Expected effects from the perspective of utility theory and activity-based theories. Environ. Plan. B Plan. Des. 2005, 32, 33–46. [Google Scholar] [CrossRef]
- Manoj, M.; Verma, A. Activity-travel behaviour of non-workers belonging to different income group households in Bangalore, India. J. Transp. Geogr. 2015, 49, 99–109. [Google Scholar] [CrossRef]
- Wu, Z.; Ye, X. Joint modeling analysis of trip-chaining behavior on round-trip commute in the context of Xiamen, China. Transp. Res. Rec. 2008, 2076, 62–69. [Google Scholar] [CrossRef]
- Bhat, C. An analysis of evening commute stop-making behavior using repeated choice observations from a multi-day survey. Transp. Res. Part B Methodol. 1999, 33, 495–510. [Google Scholar] [CrossRef] [Green Version]
- Bhat, C.R.; Sardesai, R. The impact of stop-making and travel time reliability on commute mode choice. Transp. Res. Part B Methodol. 2006, 40, 709–730. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Mokhtarian, P.L.; Handy, S.L. Differentiating the influence of accessibility, attitudes, and demographics on stop participation and frequency during the evening commute. Environ. Plan. B Plan. Des. 2008, 35, 431–442. [Google Scholar] [CrossRef]
- Currie, G.; Delbosc, A. Exploring the trip chaining behaviour of public transport users in Melbourne. Transp. Policy 2011, 18, 204–210. [Google Scholar] [CrossRef]
- Portoghese, A.; Spissu, E.; Bhat, C.R.; Eluru, N.; Meloni, I. A copula-based joint model of commute mode choice and number of non-work stops during the commute. Int. J. Transp. Econ. Riv. Internazionale Econ. Trasp. 2011, 38, 337–362. [Google Scholar]
- Susilo, Y.O.; Kitamura, R. Structural changes in commuters’ daily travel: The case of auto and transit commuters in the Osaka metropolitan area of Japan, 1980–2000. Transp. Res. Part A Policy Pract. 2008, 42, 95–115. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Ban, X.; Deng, H.; Shu, H.; Xie, D. Exploring the Relationships between the Non-Work Trip Frequency and Accessibility Based on Mobile Phone Data. Transp. Res. Rec. 2018, 2672, 91–102. [Google Scholar] [CrossRef]
- Mao, Z.; Ettema, D.; Dijst, M. Analysis of travel time and mode choice shift for non-work stops in commuting: Case study of Beijing, China. Transportation 2018, 45, 751–766. [Google Scholar] [CrossRef]
- Brunow, S.; Gründer, M. The impact of activity chaining on the duration of daily activities. Transportation 2013, 40, 981–1001. [Google Scholar] [CrossRef]
- Levinson, D.; Kumar, A. Activity, travel, and the allocation of time. J. Am. Plan. Assoc. 1995, 61, 458–470. [Google Scholar] [CrossRef]
- Hunt, J.D.; Patterson, D. A stated preference examination of time of travel choice for a recreational trip. J. Adv. Transp. 1996, 30, 17–44. [Google Scholar] [CrossRef]
- Sultana, S. Mode and Departure Time Choice Behavior of Non-Work Related Trips. Master’s Thesis, Schulich School of Engineering, Calgary, AB, Canada, 2019. [Google Scholar]
- Khan, S.; Maoh, H.; Lee, C.; Anderson, W. Toward sustainable urban mobility: Investigating nonwork travel behavior in a sprawled Canadian city. Int. J. Sustain. Transp. 2016, 10, 321–331. [Google Scholar] [CrossRef]
- Walle, S.V.; Steenberghen, T. Space and time related determinants of public transport use in trip chains. Transp. Res. Part A Policy Pract. 2006, 40, 151–162. [Google Scholar] [CrossRef]
- Hensher, D.A.; Reyes, A.J. Trip chaining as a barrier to the propensity to use public transport. Transportation 2000, 27, 341–361. [Google Scholar] [CrossRef]
- Ye, X.; Pendyala, R.M.; Gottardi, G. An exploration of the relationship between mode choice and complexity of trip chaining patterns. Transp. Res. Part B Methodol. 2007, 41, 96–113. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; He, R.; Zhang, W. Path optimization of taxi carpooling. PLoS ONE 2018, 13, e0203221. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Liang, J.; Zhang, S.; Huang, H.; Liu, F. Inferring driving trajectories based on probabilistic model from large scale taxi GPS data. Phys. A Stat. Mech. Its Appl. 2018, 506, 566–577. [Google Scholar] [CrossRef]
- Ma, C.; Hao, W.; Wang, A.; Zhao, H. Developing a coordinated signal control system for urban ring road under the vehicle-infrastructure connected environment. IEEE Access 2018, 6, 52471–52478. [Google Scholar] [CrossRef]
- Tang, J.; Liang, J.; Han, C.; Li, Z.; Huang, H. Crash injury severity analysis using a two-layer Stacking framework. Accid. Anal. Prev. 2019, 122, 226–238. [Google Scholar] [CrossRef]
- Zou, Y.; Ash, J.E.; Park, B.-J.; Lord, D.; Wu, L. Empirical Bayes estimates of finite mixture of negative binomial regression models and its application to highway safety. J. Appl. Stat. 2018, 45, 1652–1669. [Google Scholar] [CrossRef]
- Zou, Y.; Zhong, X.; Tang, J.; Ye, X.; Wu, L.; Ijaz, M.; Wang, Y. A Copula-Based Approach for Accommodating the Underreporting Effect in Wildlife‒Vehicle Crash Analysis. Sustainability 2019, 11, 418. [Google Scholar] [CrossRef]
- Zhang, R.; Ye, X.; Wang, K.; Li, D.; Zhu, J. Development of commute mode choice model by integrating actively and passively collected travel data. Sustainability 2019, 11, 2730. [Google Scholar] [CrossRef]
- Ye, X.; Wang, K.; Zou, Y.; Lord, D. A semi-nonparametric Poisson regression model for analyzing motor vehicle crash data. PloS ONE 2018, 13, e0197338. [Google Scholar] [CrossRef]
- Daisy, N.S.; Habib, M.A. Investigating the Role of Built Environment and Lifestyle Choices in Active Travel for Weekly Home-Based Nonwork Trips. Transp. Res. Rec. 2015, 2500, 125–132. [Google Scholar] [CrossRef]
- Parady, G.T.; Chikaraishi, M.; Takami, K.; Ohmori, N.; Harata, N. On the effect of the built environment and preferences on non-work travel: Evidence from Japan. Eur. J. Transport. Infrastruct. Res. 2015, 15, 51–66. [Google Scholar]
- Chib, S.; Greenberg, E. Analysis of multivariate probit models. Biometrika 1998, 85, 347–361. [Google Scholar] [CrossRef] [Green Version]
- Cappellari, L.; Jenkins, S.P. Multivariate probit regression using simulated maximum likelihood. Stata J. 2003, 3, 278–294. [Google Scholar] [CrossRef]
- Börsch-Supan, A.; Hajivassiliou, V.A. Smooth unbiased multivariate probability simulators for maximum likelihood estimation of limited dependent variable models. J. Econom. 1993, 58, 347–368. [Google Scholar] [CrossRef] [Green Version]
- Borsch-Supan, A.; Hajivassiliou, V.; Kotlikoff, L.J. Health, children, and elderly living arrangements: A multiperiod-multinomial probit model with unobserved heterogeneity and autocorrelated errors. In Topics in the Economics of Aging; University of Chicago Press: Chicago, IL, USA, 1992; pp. 79–108. [Google Scholar]
- Hajivassiliou, V.A.; Ruud, P.A. Classical estimation methods for LDV models using simulation. Handb. Econom. 1994, 4, 2383–2441. [Google Scholar]
- Bhat, C.R.; Sidharthan, R. A new approach to specify and estimate non-normally mixed multinomial probit models. Transp. Res. Part B Methodol. 2012, 46, 817–833. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Ye, X.; Shi, C. Development of Multivariate Ordered Probit Model to Understand Household Vehicle Ownership Behavior in Xiaoshan District of Hangzhou, China. Sustainability 2018, 10, 3660. [Google Scholar] [CrossRef]
- Bhat, C.R.; Varin, C.; Ferdous, N. A comparison of the maximum simulated likelihood and composite marginal likelihood estimation approaches in the context of the multivariate ordered-response model. In Maximum Simulated Likelihood Methods and Applications; Emerald Group Publishing Limited: Bingley, UK, 2010; pp. 65–106. [Google Scholar]
- Mothafer, G.I.; Yamamoto, T.; Shankar, V.N. A multivariate heterogeneous-dispersion count model for asymmetric interdependent freeway crash types. Transp. Res. Part B Methodol. 2018, 108, 84–105. [Google Scholar] [CrossRef]
- Bhat, C.R. New matrix-based methods for the analytic evaluation of the multivariate cumulative normal distribution function. Transp. Res. Part B Methodol. 2018, 109, 238–256. [Google Scholar] [CrossRef]
- Godambe, V.P. An optimum property of regular maximum likelihood estimation. Ann. Math. Stat. 1960, 31, 1208–1211. [Google Scholar] [CrossRef]
- Zhao, Y.; Joe, H. Composite likelihood estimation in multivariate data analysis. Can. J. Stat. 2005, 33, 335–356. [Google Scholar] [CrossRef]
| Attribute | Percent | Attribute | Percent |
|---|---|---|---|
| Description of household discrete variables | |||
| Household size | Home ownership | ||
| Mean | 4.01 | Self-owned house | 91.00% |
| 1 | 0.1% | Rented house | 9.0% |
| 2 | 6.4% | Annual household income [RMB Yuan]1 | |
| 3 | 33.0% | ≤100,000 | 30.0% |
| 4 | 26.3% | 100,000–300,000 | 58.5% |
| 5 | 23.7% | 300,000–500,000 | 9.9% |
| 6 | 8.3% | 500,000–1000,000 | 1.4% |
| 7+ | 2.2% | ≥1000,000 | 0.2% |
| The population under the age of 6 | Zone | ||
| Mean | 0.31 | Beigan Street | 14.5% |
| 0 | 71.3% | Chengxiang Street | 24.4% |
| 1 | 26.1% | Ningwei Town | 10.0% |
| 2 | 2.3% | Puyang Town | 0.4% |
| 3+ | 0.3% | Shushan Street | 13.3% |
| Real estate price (RMB Yuan/m2) | Suoqian Street | 2.9% | |
| Mean | 9051 | Wenyan Street | 5.9% |
| ≤10,000 | 49.5% | ETD Zone2 | 4.8% |
| 10,000–15,000 | 46.6% | Xinjie Town | 7.3% |
| 15,000–20,000 | 3.2% | Xintang Street | 16.0% |
| 20,000–30,000 | 0.5% | Yanqian Town | 0.4% |
| >30,000 | 0.2% | ||
| Description of individual discrete variables | |||
| Gender | Licensed commuters | ||
| Female | 45.8% | Have a license | 71.5% |
| Male | 54.2% | Not have a license | 28.5% |
| Profession | Education | ||
| Blue collar worker | 10.2% | Below primary school | 0.7% |
| Clerk | 60.5% | Elementary school | 4.9% |
| Private enterprise head | 3.3% | Junior high school | 13.8% |
| Business service staff | 4.7% | Senior high school | 21.3% |
| Student | 0.3% | Technical secondary school | 13.2% |
| Self-employed | 13.4% | Junior College | 28.8% |
| Public officer | 4.6% | Bachelor | 16.7% |
| Others | 3.0% | Postgraduate | 0.6% |
| Attribute | Mean | S.D. | |
| Description of household continuous variables | |||
| Annual household income (10 thousand RMB Yuan) | 17.52 | 10.66 | |
| Population density3 (10 thousand people/km2) | 0.92 | 1.443 | |
| Description of individual continuous variables | |||
| Average education years of commuters (years) | 12.78 | 2.999 | |
| Commuter household automobile ownership | 1.15 | 0.702 | |
| Commuter household motorcycle ownership | 0.07 | 0.268 | |
| Commuter household electric bicycle ownership | 1.34 | 0.820 | |
| Commuter household human-powered bicycle ownership | 0.32 | 0.574 | |
| Average age of commuters | 36.58 | 8.904 | |
| Description of Explanatory Variables | ||||
|---|---|---|---|---|
| Name | Type | Description | Mean | S.D. |
| Household sociodemographic attributes | ||||
| Self-owned house | Dummy | 1 if the house is self-owned; 0 otherwise. | 0.90 | 0.302 |
| Rented house | Dummy | 1 if the house is rented; 0 otherwise. | 0.09 | 0.283 |
| Real estate price(RMB Yuan/m2) | Categorical | The price of commuter's house. | - | - |
| Household income(10 thousand RMB Yuan) | Continuous | Annual household income converted from discrete variable in household survey data. | 17.71 | 10.775 |
| Population density(10 thousand people/m2) | Continuous | The population density is obtained based on the small zone level (communities) where the commuter is located. | 0.92 | 1.443 |
| Zone: Street/Town | Categorical | The area (11 streets/towns) where the commuter is located in Xiaoshan District. | - | - |
| Individual sociodemographic attributes | ||||
| Gender: Male | Dummy | 1 if the commuter is Male; 0 otherwise. | 0.54 | 0.498 |
| Profession | Categorical | The Profession of commuter based on personal survey data. | - | - |
| Education years of commuters (years) | Continuous | Average education years of commuter based on personal survey data. | 12.78 | 2.999 |
| Trip attributes | ||||
| Commute mode | Categorical | Travel mode used by a commuter to and from work. | - | - |
| One-way commute time (minutes) | Continuous | The time required for commuter from home to work (not stopping halfway) | 22.60 | 12.691 |
| Daily work time (hours) | Continuous | Working hours of commuter | 9.10 | 1.705 |
| Work schedule: start at 7–8 a.m. and end at 4–5 p.m. | Dummy | 1 if the commuter starts working at 7–8 a.m., and ends working at 4–5 p.m.; 0 otherwise. | 0.14 | 0.348 |
| Work schedule: start at 7–8 a.m. and end at 5–6 p.m. | Dummy | 1 if the commuter starts working at 7–8 a.m., and ends working at 5–6 p.m.; 0 otherwise. | 0.26 | 0.438 |
| Work schedule: start at 7–8 a.m. and end at 6–8 p.m. | Dummy | 1 if the commuter starts working at 7–8 a.m., and ends working at 6–8 p.m.; 0 otherwise. | 0.05 | 0.214 |
| Work schedule: start at 8–9 a.m. and end at 4–5 p.m. | Dummy | 1 if the commuter starts working at 7–8 a.m., and ends working at 4–5 p.m.; 0 otherwise. | 0.08 | 0.271 |
| Work schedule: start at 8–9 a.m. and end at 5–6 p.m. | Dummy | 1 if the commuter starts working at 8–9 a.m., and ends working at 5–6 p.m.; 0 otherwise. | 0.24 | 0.425 |
| Work schedule: start at 8–9 a.m. and end at 6–8 p.m. | Dummy | 1 if the commuter starts working at 8–9 a.m., and ends working at 6–8 p.m.; 0 otherwise. | 0.04 | 0.184 |
| Description of Dependent Variables | ||||
| Name | Description | Mean | S.D. | |
| Act1 | Nonwork Trip from Home Before Work | 0.011 | 0.103 | |
| Act2 | Nonwork Trip on Commute Way from Home to Work | 0.018 | 0.134 | |
| Act3 | Going home during work | 0.029 | 0.168 | |
| Act4 | Going out (not going home) during work | 0.092 | 0.289 | |
| Act5 | Nonwork Trip on Commute Way from Work Back Home | 0.155 | 0.362 | |
| Act6 | Nonwork Trip from Home After Work | 0.194 | 0.396 | |
| The Types of Outdoor Non-Work Activities | |||||||
|---|---|---|---|---|---|---|---|
| Act1 | Act2 | Act3 | Act4 | Act5 | Act6 | Total | |
| Shopping and dining | 70.83% | 29.07% | 0.00% | 92.57% | 56.53% | 44.20% | 54.40% |
| Leisure and entertainment | 6.25% | 4.65% | 0.00% | 1.92% | 13.59% | 37.73% | 19.44% |
| Visiting relatives and friends | 0.00% | 4.65% | 0.00% | 1.20% | 10.77% | 10.80% | 7.98% |
| Medical treatment or visiting the sick | 2.08% | 1.16% | 0.00% | 1.20% | 4.71% | 1.59% | 2.43% |
| Companying | 20.83% | 53.49% | 0.00% | 1.68% | 8.48% | 3.64% | 6.85% |
| Going home | 0.00% | 0.00% | 100.00% | 0.00% | 0.00% | 0.00% | 5.68% |
| Others | 0.00% | 6.98% | 0.00% | 1.44% | 5.92% | 2.05% | 3.21% |
| Total | 100.00% (N = 48) | 100.00% (N = 86) | 100.00% (N = 131) | 100.00% (N = 417) | 100.00% (N = 743) | 100.00% (N = 880) | 100.00% (N = 2305) |
| Outdoor Non-Work Activity Type | Act1 | Act2 | Act3 | Act4 | Act5 | Act6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Estimate | T-Test | Estimate | T-Test | Estimate | T-Test | Estimate | T-Test | Estimate | T-Test | Estimate | T-Test |
| Constant | 0.369 | 1.21 | −1.699 | −5.69 | −2.920 | −7.90 | −4.967 | −15.56 | 0.126 | −0.75 | −0.119 | −0.69 |
| Self-owned house | - | - | 0.348 | 1.70 | - | - | - | - | - | - | - | - |
| Rented house | - | - | - | - | 0.596 | 4.71 | - | - | - | - | - | - |
| Real estate price: <10,000 yuan /m2 | - | - | - | - | - | - | - | - | 0.134 | 2.31 | −0.180 | −3.73 |
| Real estate price: >30,000 yuan/m2 | - | - | 1.022 | 1.72 | - | - | - | - | - | - | - | - |
| Household income (10 thousand Yuan) | - | - | - | - | - | - | −0.006 | −1.95 | - | - | - | - |
| Population density (10 thousand people/km2) | - | - | −0.136 | −2.25 | - | - | - | - | −0.079 | −2.78 | - | - |
| Zone: Chengxiang Street | 0.612 | 3.07 | 0.470 | 3.53 | −0.933 | −6.04 | - | - | - | - | - | - |
| Zone: Suoqian Street | 1.561 | 6.01 | 0.490 | 2.18 | 0.502 | 2.61 | - | - | - | - | - | - |
| Zone: Wenyan Street | - | - | 0.529 | 3.09 | −1.227 | −4.07 | - | - | - | - | - | - |
| Zone: Xintang Street | - | - | - | - | −0.468 | −3.10 | - | - | 0.413 | 6.12 | −0.230 | −3.43 |
| Zone: Ningwei Town | - | - | - | - | - | - | - | - | - | - | 0.610 | 8.55 |
| Zone: ETD Zone | - | - | - | - | −1.261 | −3.35 | - | - | 0.374 | 3.41 | - | - |
| Zone: Xinjie Town | - | - | - | - | −0.516 | −2.56 | - | - | 0.402 | 4.51 | - | - |
| Gender: Male | −0.335 | −2.28 | - | - | - | - | - | - | - | - | - | - |
| Profession: Blue collar worker | −0.687 | −1.91 | −0.666 | −1.95 | - | - | - | - | - | - | 0.180 | 2.00 |
| Profession: Clerk | - | - | - | - | −0.202 | −1.88 | - | - | - | - | 0.148 | 2.64 |
| Profession: Business service staff | 0.423 | 1.89 | - | - | - | - | - | - | 0.549 | 4.98 | - | - |
| Profession: Self-employed | - | - | 0.395 | 3.37 | - | - | - | - | - | - | - | - |
| Profession: Public officer | - | - | - | - | 0.356 | 1.67 | 0.344 | 2.62 | - | - | - | - |
| Education years of commuters (years) | −0.134 | −6.66 | - | - | - | - | 0.059 | 4.55 | - | - | −0.027 | −2.91 |
| Commute mode: Private car | - | - | - | - | - | - | 0.201 | 2.81 | 0.174 | 2.54 | −0.145 | −2.51 |
| Commute mode: Motorcycle | - | - | - | - | 0.585 | 1.70 | - | - | - | - | - | - |
| Commute mode: Human-powered bicycle | - | - | - | - | - | - | - | - | - | - | −0.628 | −2.19 |
| Commute mode: Shared bicycle | - | - | - | - | - | - | - | - | - | - | −0.611 | −1.96 |
| Commute mode: Walk | - | - | - | - | - | - | - | - | −0.387 | −2.11 | - | - |
| One-way commute time (minutes) | - | - | −0.008 | −1.87 | −0.018 | −3.49 | 0.013 | 5.42 | - | - | - | - |
| Daily work time (hours) | −0.180 | −6.27 | −0.074 | −2.81 | 0.197 | 6.22 | 0.241 | 10.84 | −0.194 | −11.60 | −0.095 | −6.58 |
| Work schedule: Start at 7–8 a.m. and end at 4–5 p.m. | - | - | - | - | −0.400 | −1.85 | −0.781 | −5.07 | 0.805 | 10.22 | 0.552 | 7.01 |
| Work schedule: Start at 7–8 a.m. and end at 5–6 p.m. | - | - | −0.266 | −1.91 | - | - | −0.240 | −3.28 | 0.431 | 5.42 | 0.352 | 4.81 |
| Work schedule: Start at 7 –8 a.m. and end at 6–8 p.m. | - | - | - | - | - | - | - | - | - | - | −0.313 | −1.91 |
| Work schedule: Start at 8–9 a.m. and end at 4–5 p.m. | - | - | - | - | - | - | - | - | 0.296 | 2.87 | 0.406 | 4.33 |
| Work schedule: Start at 8–9 a.m. and end at 5–6 p.m. | 0.558 | 3.22 | - | - | - | - | - | - | −0.148 | −1.64 | 0.273 | 3.73 |
| Work schedule: Start at 8–9 a.m. and end at 6–8 p.m. | 0.802 | 2.59 | - | - | - | - | 0.242 | 1.77 | - | - | - | - |
| 1 | −25853.518 | |||||||||||
| 2 | −33862.071 | |||||||||||
| 3 | 0.237 | |||||||||||
| 4518 | ||||||||||||
| Variable | Act1 | Act2 | Act3 | Act4 | Act5 | Act6 |
|---|---|---|---|---|---|---|
| Household income (10 thousand Yuan) | - | - | - | −0.125 | - | - |
| Education years of commuters (years) | −2.513 | - | - | 1.247 | - | −0.365 |
| Commute mode: Private car | - | - | - | 0.429 | 0.230 | −0.166 |
| Commute mode: Motorcycle | - | - | 1.514 | - | - | - |
| Commute mode: Human-powered bicycle | - | - | - | - | - | −0.566 |
| Commute mode: Sharing bicycle | - | - | - | - | - | −0.549 |
| One-way commute time (minutes) | - | −0.339 | −0.388 | 0.520 | - | - |
| Daily work time (hours) | −2.625 | −1.346 | 3.378 | 3.774 | −2.301 | −1.277 |
| Work schedule: start at 7a.m.–8 a.m. and end at 4 p.m.–5 p.m. | - | - | −0.532 | −0.688 | 2.283 | 1.227 |
| Work schedule: start at 7 a.m.–8 a.m. and end at 5 p.m.–6 p.m. | - | −0.464 | - | −0.267 | 1.044 | 0.782 |
| Work schedule: start at 8 a.m.–9 a.m. and end at 5 p.m.–6 p.m. | 2.134 | - | - | - | −0.199 | 0.596 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Ye, X.; Shi, C.; Zou, Y. A Multivariate Modeling Analysis of Commuters’ Non-Work Activity Allocations in Xiaoshan District of Hangzhou, China. Sustainability 2019, 11, 5768. https://doi.org/10.3390/su11205768
Guan X, Ye X, Shi C, Zou Y. A Multivariate Modeling Analysis of Commuters’ Non-Work Activity Allocations in Xiaoshan District of Hangzhou, China. Sustainability. 2019; 11(20):5768. https://doi.org/10.3390/su11205768
Chicago/Turabian StyleGuan, Xin, Xin Ye, Cheng Shi, and Yajie Zou. 2019. "A Multivariate Modeling Analysis of Commuters’ Non-Work Activity Allocations in Xiaoshan District of Hangzhou, China" Sustainability 11, no. 20: 5768. https://doi.org/10.3390/su11205768
APA StyleGuan, X., Ye, X., Shi, C., & Zou, Y. (2019). A Multivariate Modeling Analysis of Commuters’ Non-Work Activity Allocations in Xiaoshan District of Hangzhou, China. Sustainability, 11(20), 5768. https://doi.org/10.3390/su11205768





