Mining and Local Economies: Dilemma between Environmental Protection and Job Opportunities
Abstract
1. Introduction
2. Related Literature
3. Model Setup
4. Choices of Agents and Dynamics
5. Dynamic Regimes
- (a)
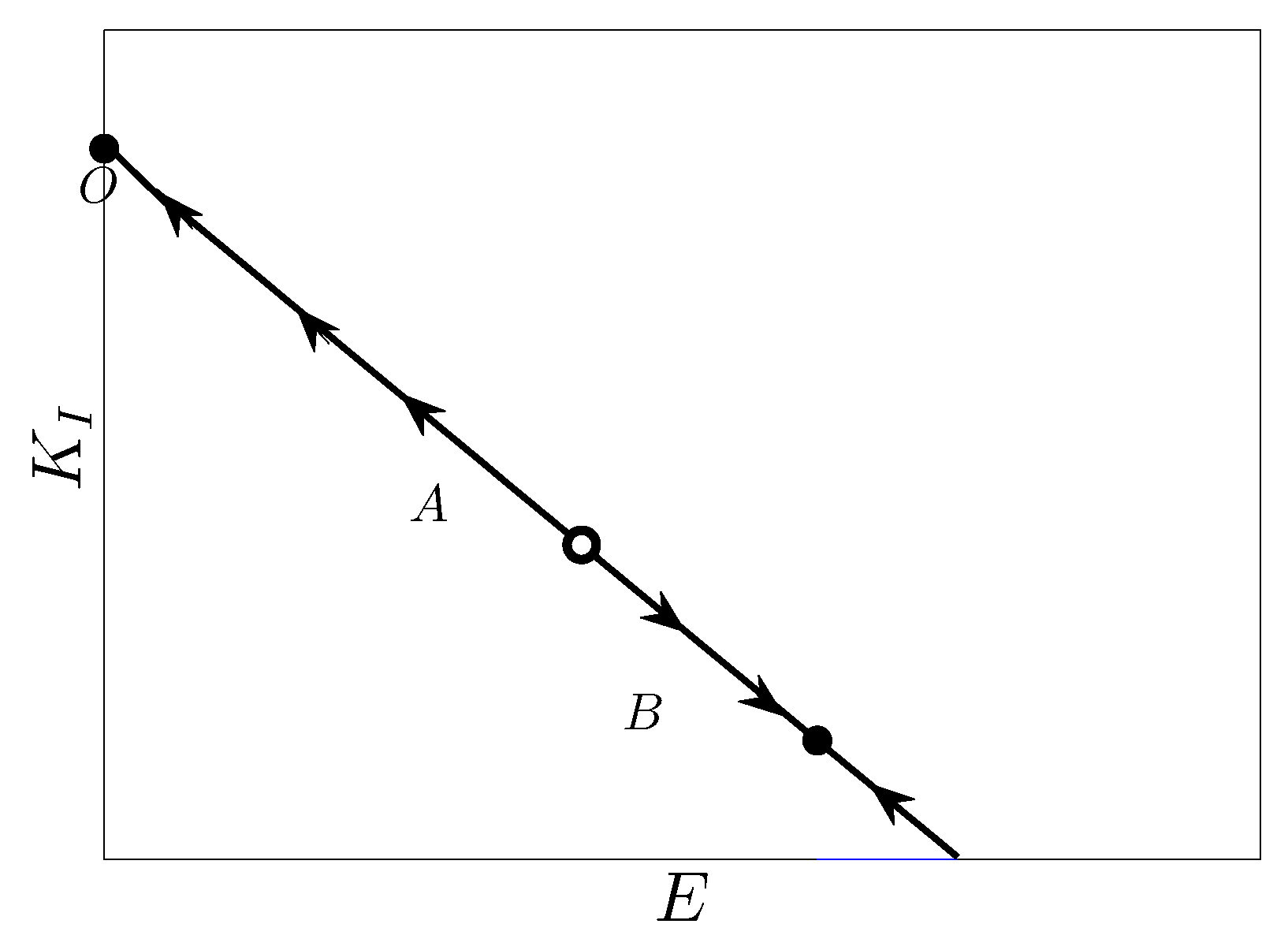
- Dynamic regime illustrated in Figure 1 and Figure 2, where stationary state is globally attractive. In this regime, the trajectory starting from approaches . Thus, opening the economy to mining operations leads to the complete exhaustion of renewable natural resources and the crowding out of the local sector. This dynamic regime is observed when the carrying capacity (measured by parameter ) of the natural resource is very low ( if , if );
- (b)
- Dynamic regimes illustrated in Figure 1b,c and Figure 2b, characterized by the coexistence of two locally attractive stationary states (bistable regimes): stationary state and either stationary state or stationary state . The basins of attraction of the two attractive stationary states are separated by repulsive stationary state . In stationary state , both sectors coexist, while in stationary state , the economy specializes in the local sector. Bistable regimes take place only if carrying capacity of the natural resource is high enough. In this context, the initial condition plays a key role in determining the time evolution of E. The economy, starting from , either remains in or approaches . The former scenario occurs in economies with a very high carrying capacity (, Figure 1c), or high pollution impact of the mining sector ( Figure 2b) which, after the opening up the economy to external capital, remains specialized in the local sector. The latter scenario, namely, the transition towards a diversified economy in which both sectors coexist, is observed in economies with an intermediate level of carrying capacity () and exposed to low-pollution-intensity capital inflows in the mining sector ().
6. Welfare Implications: Root of the Dilemma
6.1. Local Welfare, Environmental Outcomes, and Physical Capital Stock in Attractive Stationary States
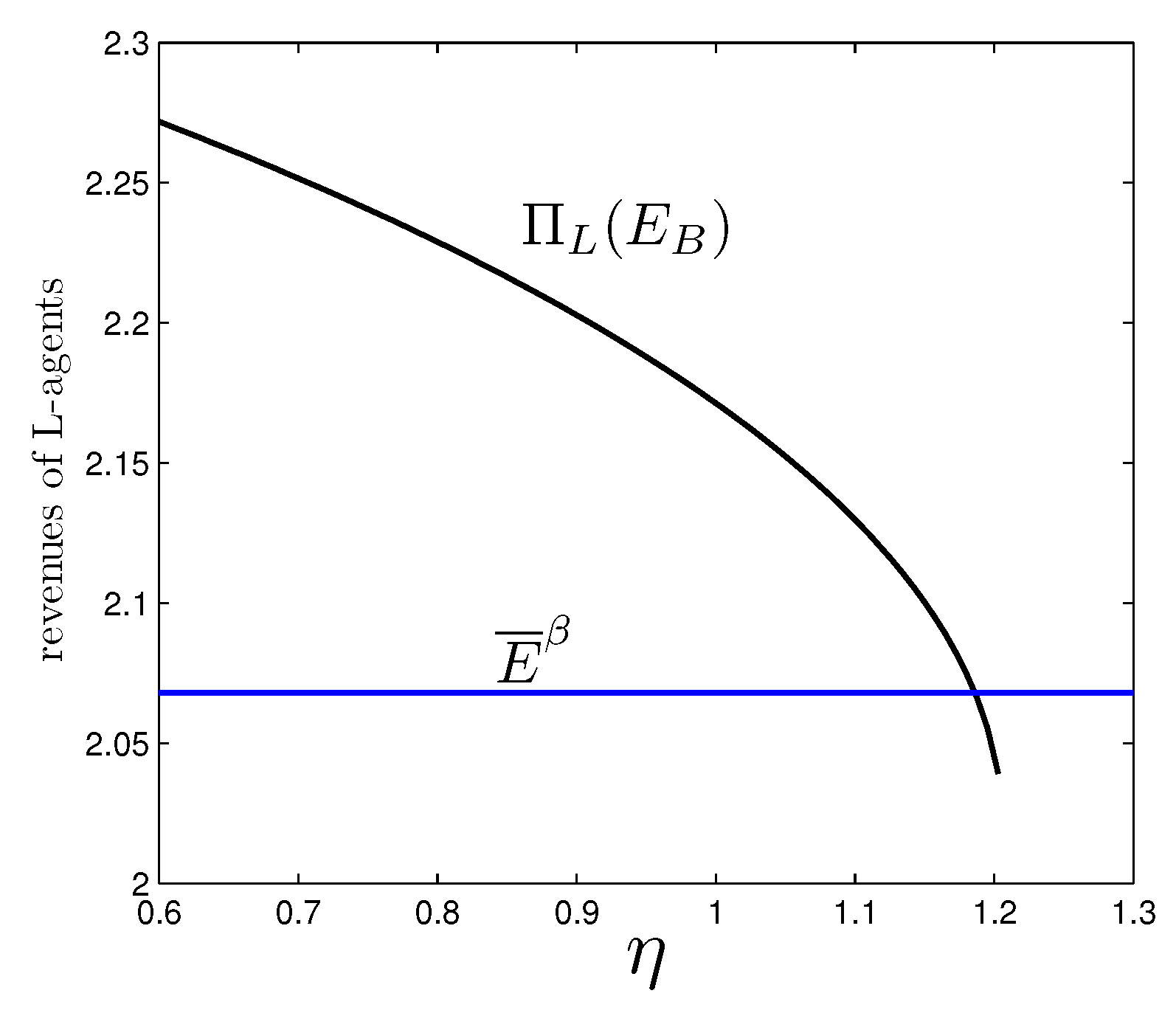
6.2. Openness to Mining Investments: Different Environmental Contexts, Different Welfare Outcomes
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Choice Problem of Agents and Labor-Market Equilibrium
Appendix A.2. Classification of Dynamic Regimes
- (1)
- According to non-negativity constraint , state is always a locally attractive stationary state in that, if stock is low enough, then holds according to Equation (5);
- (2)
- State is a stationary state if and only if . That is, if carrying capacity is higher than threshold value of E that separates the regimes with and without specialization. Furthermore, no stationary state with can exist because always holds for ;
- (3)
- Interior stationary states (that is, those belonging to interval ) coincide with the values of E that annul the right-hand side of Equation (5), in such stationary states, the economy is not specialized (that is, );
- (4)
- Graphs of and can have at most two intersection points; therefore, at most, two interior stationary states exist. The complete taxonomy of possible dynamic regimes is illustrated in the following proposition. The proof is straightforward and therefore omitted.
- (1a)
- If , then a unique interior stationary state exists. This is repulsive and separates the basins of attraction of locally attractive stationary states and (see Figure 1b);
- (1b)
- If , then two interior stationary states and exist, with . Repulsive stationary state separates the basins of attraction of locally attractive stationary states and (see Figure 1b) (in the context of , always holds);
- (1c)
- If , then two stationary state exist, and , and their basins of attraction are, respectively, intervals and ;
- (1d)
- If , then stationary state is globally attractive (see Figure 1a).
- (2a)
- If , then the dynamic regime coincides with that described in Point (1a) of this proposition (see Figure 2b);
- (2b)
- If , then two stationary states exist, and , and their basins of attraction are, respectively, intervals and ;
- (2c)
- If , then stationary state is globally attractive (see Figure 2a).
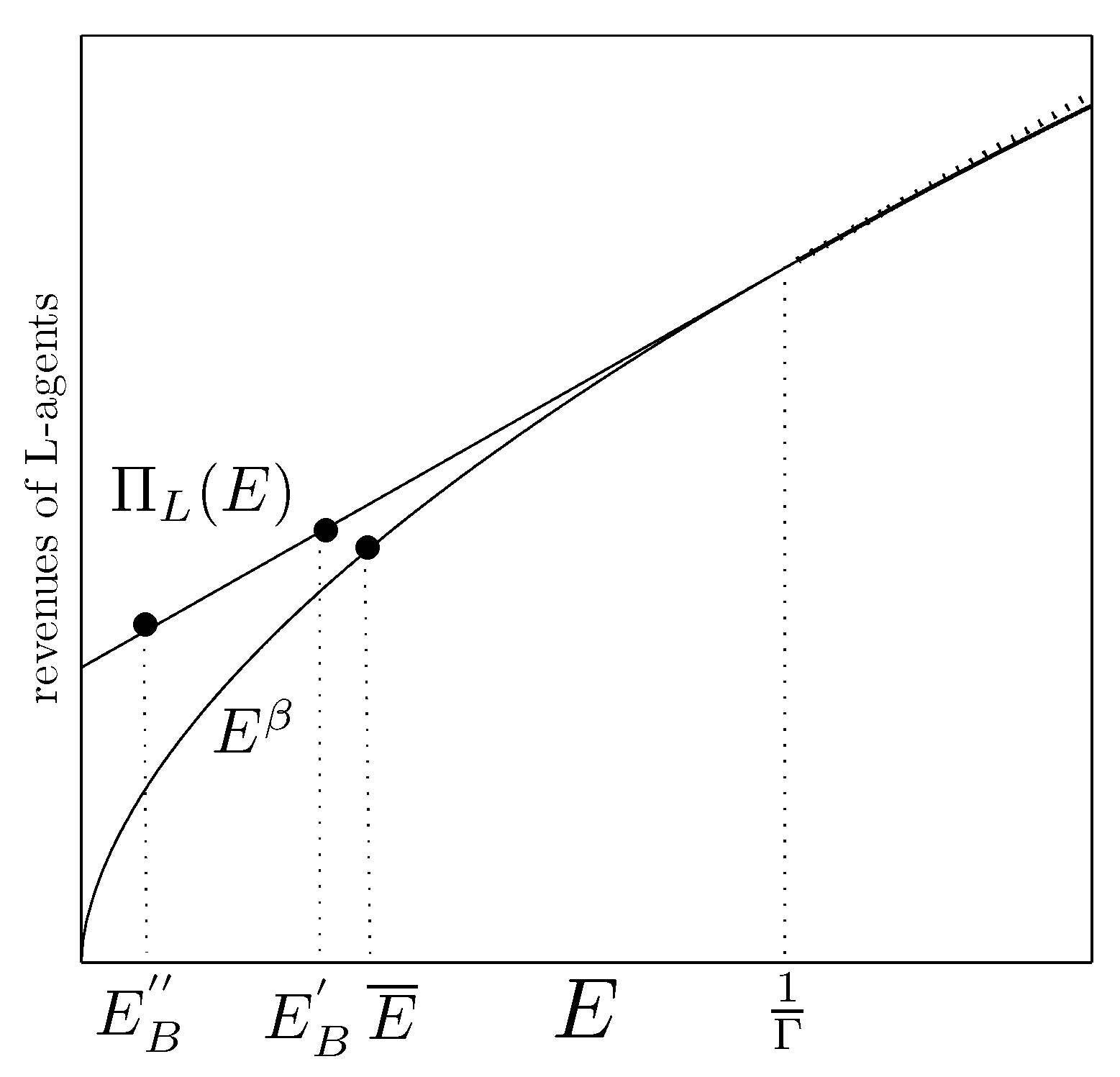
Appendix A.3. Welfare of L-agents
References
- Reichl, C.; Schatz, M. World Mining Data 2019, Federal Ministry Republic of Austria for Sustainability and Tourism, Vienna, Austria. 2019. Available online: www.world-mining-data.info/wmd/downloads/PDF/WMD2019.pdf (accessed on 3 September 2019).
- ICMM. Trends in The Mining and Metals Industry; International Council on Mining & Metals: London, UK, 2012; Available online: http://www.icmm.com/website/publications/pdfs/4441.pdf (accessed on 10 July 2017).
- Andrews, T.; Elizalde, B.; Le Billon, P.; Hoon Oh, C.; Reyes, D.; Thomson, I. The Rise in Conflict Associated with Mining Operations: What Lies Beneath? Canadian International Resources and Development Institute: Vancouver, BC, Canada, 2007. [Google Scholar]
- Environmental Justice Atlas. Available online: http://ejatlas.org/ (accessed on 15 October 2019).
- Temper, L.; del Bene, D.; Martinez-Alier, J. Mapping the frontiers and front lines of global environmental justice: The EJAtlas. J. Political Ecol. 2015, 22, 255–278. [Google Scholar] [CrossRef]
- Acatech—National Academy of Science and Engineering, German National Academy of Sciences Leopoldina, and Union of the German Academies of Sciences and Humanities. Raw Materials for the Energy Transition—Securing a Reliable and Sustainable Supply. Position Paper of the Academies’ Project “Energy Systems of the Future”. Available online: https://energiesysteme-zukunft.de/en/position-paper/raw-materials-for-the-energy-transition/ (accessed on 5 October 2019).
- Parsons, R.; Moffat, K. Constructing the Meaning of Social Licence. Soc. Epistemol. 2014, 28, 340–363. [Google Scholar] [CrossRef]
- EY. Top 10 Business Risks Facing Mining and Metals in 2019-20. 2019. Available online: https://www.ey.com/en_gl/mining-metals/10-business-risks-facing-mining-and-metals (accessed on 5 October 2019).
- Prno, J. An analysis of factors leading to the establishment of a social licence to operate in the mining industry. Resour. Policy 2013, 38, 577–590. [Google Scholar] [CrossRef]
- McMahon, G.; Remy, F. Large Mines and the Community: Socioeconomic and Environmental Effects in Latin America, Canada and Spain; World Bank and the International Development Research Centre: Washington, DC, USA, 2001. [Google Scholar]
- Chuhan-Pole, P.; Dabalen, A.L.; Land, B.C. Mining in Africa: Are Local Communities Better off? Africa Development Forum, World Bank: Washington, DC, USA, 2017. [Google Scholar]
- Katz, J.; Pietrobelli, C. Natural resource based growth, global value chains and domestic capabilities in the mining industry. Resour. Policy 2018, 58, 11–20. [Google Scholar] [CrossRef]
- Mancini, L.; Sala, S. Social impact assessment in the mining sector: Review and comparison of indicators frameworks. Resour. Policy 2018, 57, 98–111. [Google Scholar] [CrossRef]
- Karakaya, E.; Nuur, C. Social sciences and the mining sector: Some insights into recent research trends. Resour. Policy 2018, 58, 257–267. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators; World Bank: Washington, DC, USA, 2007. [Google Scholar]
- World Bank. Poverty and the Environment: Understanding Linkages at the Household Level; The World Bank: Washington, DC, USA, 2008. [Google Scholar]
- Johnston, D.G.; Mellor, J.W. The role of agriculture in economic development. Am. Econ. Rev. 1961, 51, 566–593. [Google Scholar]
- Singer, H. Policy implications of the Lima target. Ind. Dev. 1979, 3, 17–23. [Google Scholar]
- Timmer, C.P. The Agricultural Transformation. In Handbook of Development Economics; Chenery, H., Srinivasan, T.N., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; Volume 1, pp. 275–331. [Google Scholar]
- Vogel, S.J. Structural changes in agriculture: Production linkages and agricultural demand-led industrialization. Oxf. Econ. Pap. 1994, 46, 136–156. [Google Scholar] [CrossRef]
- Ravallion, M.; Datt, G. How important to India’s poor is the sectoral composition of economic growth? World Bank Econ. Rev. 1996, 10, 1–26. [Google Scholar] [CrossRef]
- World Bank. Agriculture for Development; World Development Report 2008; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Bourguignon, F.; Morrisson, C. Inequality and development: The role of dualism. J. Dev. Econ. 1998, 57, 233–258. [Google Scholar] [CrossRef]
- Diao, X.; Hazell, P.; Thurlow, J. The Role of agriculture in African development. World Dev. 2010, 38, 1375–1383. [Google Scholar] [CrossRef]
- Loayza, N.V.; Raddatz, C. The composition of growth matters for poverty alleviation. J. Dev. Econ. 2010, 93, 137–151. [Google Scholar] [CrossRef]
- Valdés, A.; Foster, W. Reflections on the role of agriculture in pro-poor growth. World Dev. 2010, 38, 1362–1374. [Google Scholar] [CrossRef]
- Christiaensen, L.; Demery, L.; Kuhl, J. The (evolving) role of agriculture in poverty reduction: An empirical perspective. J. Dev. Econ. 2011, 96, 239–254. [Google Scholar] [CrossRef]
- Macatangay, R.E. Optimal local content requirement policies for extractive industries. Resour. Policy 2016, 50, 244–252. [Google Scholar] [CrossRef]
- Issabayev, M.; Pelzman, J. A model of FDI spillover in a natural resource rich LDC. Resour. Policy 2019, 64, 101479. [Google Scholar] [CrossRef]
- Issabayev, M.; Rizvanoghlu, I. Optimal choice between local content requirement and fiscal policy in extractive industries: A theoretical analysis. Resour. Policy 2019, 60, 1–8. [Google Scholar] [CrossRef]
- Ghebrihiwet, N.; Motchenkova, E. Relationship between FDI, foreign ownership restrictions, and technology transfer in the resources sector: A derivation approach. Resour. Policy 2017, 52, 320–326. [Google Scholar] [CrossRef]
- Di Corato, L. Profit sharing under the threat of nationalization. Resour. Energy Econ. 2013, 35, 295–315. [Google Scholar] [CrossRef][Green Version]
- Kuramoto, J.R. Las Aglomeraciones Productivas Alrededor de la Minería: el Caso de la Minera Yanacocha S.A.; Grupo de Análisis para el Desarrollo (GRADE) Documentos de Trabajo: Santiago de Chile, Chile, 1999; p. 27. [Google Scholar]
- Aragón, F.M. Natural resources and local communities: Evidence from Peruvian gold mine. Am. Econ. J. Econ. Policy 2013, 5, 1–25. [Google Scholar] [CrossRef]
- Addison, T.; Boly, A.; Mveyange, A. Mining and Economic Development. Did China’s WTO Accession Affect African Local Economic Development? Policy Research working paper; no. WPS 7906; World Bank Group: Washington, DC, USA, 2016. [Google Scholar]
- Fafchamps, M.; Koelle, M.; Shilpi, F. Gold mining and proto-urbanization: Recent evidence from Ghana. J. Econ. Geogr. 2016, 17, 975–1008. [Google Scholar] [CrossRef]
- Kotsadam, A.; Tolonen, A. African mining, gender, and local employment. World Dev. 2016, 83, 325–339. [Google Scholar] [CrossRef]
- Brollo, F.; Nannicini, T.; Perotti, R.; Tabellini, G. The political resource curse. Am. Econ. Rev. 2013, 103, 1759–1796. [Google Scholar] [CrossRef]
- Dube, O.; Juan Vargas, J. Commodity price shocks and civil conflict: Evidence from Colombia. Rev. Econ. Stud. 2013, 80, 1384–1421. [Google Scholar] [CrossRef]
- Maystadt, J.F.; De Luca, G.; Sekeris, P.G.; Ulimwengu, J. Mineral resources and conflicts in DRC: A case of ecological fallacy? Oxf. Econ. Pap. 2014, 66, 721–749. [Google Scholar] [CrossRef]
- Knutsen, C.H.; Kotsadam, A.; Olsen, E.H.; Wig, T. Mining and local corruption in Africa. Am. J. Political Sci. 2017, 61, 320–334. [Google Scholar] [CrossRef]
- Ticci, E.; Escobal, J. Extractive industries and local development in the Peruvian highlands. Environ. Dev. Econ. 2015, 20, 101–126. [Google Scholar] [CrossRef]
- Loayza, N.; Rigolini, J. The local impact of mining on poverty and inequality: Evidence from the commodity boom in Peru. World Dev. 2016, 84, 219–234. [Google Scholar] [CrossRef]
- Addison, T.; Boly, A.; Mveyange, A. The Impact of Mining on Spatial Inequality: Recent Evidence from Africa; Policy Research working paper, no. WPS 7960; World Bank Group: Washington, DC, USA, 2017. [Google Scholar]
- Caselli, F.; Michaels, G. Do oil windfalls improve living standards? Evidence from Brazil. Am. Econ. J.-Appl. Econ. 2013, 5, 208–238. [Google Scholar] [CrossRef]
- Goswami, S.; Goswami, R. Coal mining vis-á-vis agriculture in India: A question of sustainability. Environ. Asia 2015, 8, 24–33. [Google Scholar]
- De Gregori, I.; Fuentes, E.; Rojas, M.; Pinochet, H.; Potin-Gautier, M. Monitoring of copper, arsenic and antimony levels in agricultural soils impacted and non-impacted by mining activities, from three regions in Chile. J. Environ. Monit. 2003, 5, 287–295. [Google Scholar] [CrossRef]
- Briki, M.; Ji, H.; Li, C.; Ding, H.; Gao, Y. Characterization, distribution, and risk assessment of heavy metals in agricultural soil and products around mining and smelting areas of Hezhang, China. Environ. Monit. Assess. 2015, 187, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Wang, Z.; Zhang, R.; Li, S. The ‘golden ten years’: Underground coal mining and its impacts on land use and subsequent social problems: A case study on the Jining city region, China. Int. J. Min. Miner. Eng. 2017, 8, 19–34. [Google Scholar] [CrossRef]
- Ouoba, Y. Economic sustainability of gold mining industry in Burkina Faso. Resour. Policy 2017, 51, 194–203. [Google Scholar] [CrossRef]
- Der Goltz, J.V.; Barnwal, P. The local wealth and health effects of mineral mining in developing countries. J. Dev. Econ. 2019, 139, 1–16. [Google Scholar] [CrossRef]
- Hausermann, H.; Ferring, D.; Atosona, B.; Mentz, G.; Amankwah, R.; Chang, A.; Hartfield, K.; Effah, E.; Asuamah, G.Y.; Mansell, C.; et al. Land-grabbing, land-use transformation and social differentiation: Deconstructing “small-scale” in Ghana’s recent gold rush. World Dev. 2018, 108, 103–114. [Google Scholar] [CrossRef]
- Andersson, M.; Hall, O.; Olén, N.; Tolonen, A. Does Large-Scale Gold Mining Reduce Agricultural Growth? Case Studies from Burkina Faso, Ghana, Mali and Tanzania. In Mining in Africa: Are Local Communities Better Off? Chuhan-Pole, P., Dabalen, A.L., Land, B.C., Eds.; World Bank: Washington, DC, USA, 2017; pp. 147–173. [Google Scholar]
- Aragón, F.; Rud, J.P. Mining, pollution and agricultural productivity: Evidence from Ghana. Econ. J. 2015, 126, 1980–2011. [Google Scholar] [CrossRef]
- Mishra, P.P.; Pujari, A.K. Impact of mining on agricultural productivity: A case study of the Indian State of Orissa. South Asia Econ. J. 2008, 9, 337–350. [Google Scholar] [CrossRef]
- Li, Q.; Stoeckl, N.; King, D.; Gyuris, E. Exploring the impacts of coaling mining on host communities in Shanxi, China-using subjective data. Resour. Policy 2017, 53, 125–134. [Google Scholar] [CrossRef]
- Mtero, F. Rural livelihoods, large-scale mining and agrarian change in Mapela. Limpopo, South Africa, Resour. Policy 2017, 53, 190–200. [Google Scholar]
- Acemoglu, D. Introduction to Modern Economic Growth; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Duraiappah, A.K. Poverty and environmental degradation: A review and analysis of the nexus. World Dev. 1998, 26, 2169–2179. [Google Scholar] [CrossRef]
- Scialabba, N.E.H.; Hattam, C. (Eds.) Organic Agriculture, Environment and Food Security; FAO: Roma, Italy, 2002. [Google Scholar]
- Clark, C. Mathematical Economics; JohnWiley and Sons: New York, NY, USA, 1990. [Google Scholar]
- Barbier, E.B. Poverty, development, and environment. Environ. Dev. Econ. 2010, 15, 635–660. [Google Scholar] [CrossRef]
- Lòpez, R.E. Sustainable economic development: On the coexistence of resource-dependent and resource-impacting industries. Environ. Dev. Econ. 2010, 15, 687–705. [Google Scholar] [CrossRef]
- Cuba, N.; Bebbington, A.; Rogan, J.; Millones, M. Extractive industries, livelihoods and natural resource competition: Mapping overlapping claims in Peru and Ghana. Appl. Geogr. 2014, 54, 250–261. [Google Scholar] [CrossRef]
- Özkaynak, B.; Rodriguez-Labajos, B.; Arsel, M.; Avcı, D.; Carbonell, M.H.; Chareyron, B.; Chicaiza, G.; Conde, M.; Demaria, F.; Finamore, R.; et al. Mining Conflicts Around the World: Common Grounds from Environmental Justice Perspective. EJOLT Report No. 7. Available online: http://www.ejolt.org/2012/11/mining-conflicts-around-the-world-common-grounds-from-an-environmental-justice-perspective/ (accessed on 10 July 2019).
- Bravo-Ortega, C.; Muñoz, L. Mining services suppliers in Chile: A regional approach (or lack of it) for their development. Resour. Policy in press. 2018. [Google Scholar] [CrossRef]
- Arias, M.; Atienza, M.; Cademartori, J. Large mining enterprises and regional development in Chile: Between the enclave and cluster. J. Econ. Geogr. 2014, 14, 73–95. [Google Scholar] [CrossRef]
- Aitken, D.; Rovera, D.; Godoy-Faúndez, A.; Holzapfel, E. Water Scarcity and the Impact of the Mining and Agricultural Sectors in Chile. Sustainability 2016, 8, 128. [Google Scholar] [CrossRef]
- Queirolo, F.; Stegen, S.; Restovic, M.; Paz, M.; Ostapczuk, P.; Schwuger, M.J.; Muñoz, L. Total arsenic, lead, and cadmium levels in vegetables cultivated at the Andean villages of northern Chile. Sci. Total Environ. 2000, 255, 75–84. [Google Scholar] [CrossRef]
- Romero, H.; Meñdez, M.; Smith, P. Mining Development and Environmental Injusticein the Atacama Desert of Northern Chile. Environ. Justice 2012, 5, 70–76. [Google Scholar] [CrossRef]
- Lagos, G. Developing national mining policies in Chile: 1974-96. Resourc. Policy 1997, 23, 51–69. [Google Scholar] [CrossRef]
- Aroca, P. Impacts and development in local economies based on mining: The case of the Chilean II region. Resour. Policy 2001, 27, 119–134. [Google Scholar]
- Lagos, G.; Blanco, E. Mining and development in the region of Antofagasta. Resour. Policy 2010, 35, 265–275. [Google Scholar] [CrossRef]
- Álvarez, R.; García Marín, G.; Ilabaca, S. Commodity price shocks and poverty reduction in Chile. Resour. Policy 2018, in press. [Google Scholar] [CrossRef]
- Akabzaa, T. Mining in Ghana: implications for national economic development and poverty reduction. In Mining in Africa: Regulation and Development; Campbell, B., Ed.; IDRC: Ottawa, ON, Canada, 2009; pp. 25–65. [Google Scholar]
- Ayee, J.; Soreide, T.; Shukla, G.P.; Le, T.M. Political Economy of the Mining Sector in Ghana; World Bank Policy Research Working Paper No. 5730; World Bank: Washington, DC, USA, 2011. [Google Scholar]
- Schueler, V.; Kuemmerle, T.; Schroeder, H. Impacts of surface gold mining on land use systems in Western Ghana. Ambio 2011, 40, 528–539. [Google Scholar] [CrossRef]
- Andrews, N. Land versus livelihoods: Community perspectives on dispossession and marginalization in Ghana’s mining sector. Resour. Policy 2018, 58, 240–249. [Google Scholar] [CrossRef]
- Tuokuu, F.X.D.; Gruber, J.S.; Idemudi, U.; Kayir, J. Challenges and opportunities of environmental policy implementation: Empirical evidence from Ghana’s gold mining sector. Resour. Policy 2018, 59, 435–445. [Google Scholar] [CrossRef]
- Mkodzongi, G.; Spiegel, S. Artisanal Gold Mining and Farming: Livelihood Linkages and Labor Dynamics after Land Reforms in Zimbabwe. J. Dev. Stud. 2019, 55, 2145–2216. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoci, A.; Russu, P.; Ticci, E. Mining and Local Economies: Dilemma between Environmental Protection and Job Opportunities. Sustainability 2019, 11, 6244. https://doi.org/10.3390/su11226244
Antoci A, Russu P, Ticci E. Mining and Local Economies: Dilemma between Environmental Protection and Job Opportunities. Sustainability. 2019; 11(22):6244. https://doi.org/10.3390/su11226244
Chicago/Turabian StyleAntoci, Angelo, Paolo Russu, and Elisa Ticci. 2019. "Mining and Local Economies: Dilemma between Environmental Protection and Job Opportunities" Sustainability 11, no. 22: 6244. https://doi.org/10.3390/su11226244
APA StyleAntoci, A., Russu, P., & Ticci, E. (2019). Mining and Local Economies: Dilemma between Environmental Protection and Job Opportunities. Sustainability, 11(22), 6244. https://doi.org/10.3390/su11226244



