2. Proposed Methods
In this section, we discuss the proposed methods to predict the welfare status of a household. The block diagram depicting the objective of the proposed framework is described in
Figure 2. We predict the welfare status of a household based on three different modalities of data: (a) socio-economic survey data, (b) groundwater levels, and (c) handpump abstraction data.
The different modalities of data survey, groundwater levels and abstraction are represented as and respectively. The abstraction and groundwater levels data are time-series data while the survey data is a fixed set of questions for a particular household.
The problem here is multidimensional, whose inputs are non-Gaussian and may be correlated, with varying degrees of noise and artefacts present in each signal. Therefore, we will model relationships within different modalities of data using a multi-input multi-output neural network, a framework for modeling multi-modal data. The final output of the model is a set of varying probabilistic indices modeling the welfare that incorporate both dynamical trend information and subtle correlations that may exist between the multidimensional data. There are a total of four welfare indices at the output of the model, one for each modality of the data, and one final welfare for the joint model.
The multi-input multi-output framework of the neural network allows the uncertainty in the data to be modeled explicitly, allowing the output of the model to cope with signals that are (a) sampled at different times, and (b) corrupted by varying degrees of artefact and noise. In addition, the proposed method is non-parametric, and therefore can scale to the modeling of very large quantities of big data in a principled manner, where model structure is learned directly from the data, rather than by imposing strong probabilistic modeling assumptions. Furthermore, the welfare status estimated at the output of the model allow the relevant institutions and stakeholders to explore the status and risks being faced by different households and act accordingly.
The block diagram of the proposed framework is shown in
Figure 3. This framework consists of three smaller sub-networks, one for each individual data modality. The different modalities (
) of the data are the inputs to each of the smaller sub-networks, and the output of all networks correspond to welfare label (
y). The embeddings from the penultimate layers of each of the smaller neural network are concatenated and are fed to a series of fully connected layers, with welfare label (
y) as the final output. The resulting multi-input multi-output neural network architecture is jointly trained.
The sub-network for the survey data consists of a one-dimensional CNN (1D-CNN) followed by fully connected layers. A CNN is a sequence of layers, where each layer takes a multidimensional array as input and gives a multidimensional as output. Mathematically, at each of the layer
, where
and
are the input and output arrays respectively and
c is a local function, consisting of translation invariant operators and thus can be considered as a filter. The convolution operation is generally followed by a pooling step which is computed over the input array in small sliding windows. Among different types of pooling functions, e.g., averaging and sum, maxpooling is the one most commonly used. This CNN module is followed by a maxpooling operator. Furthermore, a flattening layer flattens the data before it is fed to a multi-layer FF network with two fully connected layers. The multi-layer FF network consist of a cascade of perceptron layers. The individual perceptron layer is defined as:
where
is the weight vector matrix,
is the input vector,
is the bias, and
is the activation function. The last fully connected layer is connected to a SoftMax layer with two classes.
Since groundwater levels data is a time-series, Long Short-Term Memory networks (LSTM), a type of RNN suitable for time-series data, is used to model the data. The sub-network for groundwater levels data consists of a 1D-CNN followed by a LSTM layer further connected to a series of fully connected layers. 1D-CNN in this sub-network can be considered to be an inbuilt feature extractor. LSTM can learn long term dependencies in the time-series data and have the form of a chain of repeating cells. Each LSTM cell has a forget gate
, input gate
and cell state
. The forget gate decides which information is discarded from the previous cell state. On the contrary, the input gate, based on the current input decides which information is stored in the current cell state. Based on the previous two steps, the cell state stores which information to forget and store. For a given time series
, as input, a LSTM employs following steps:
Finally, an output gate modulated by the cell state computes the hidden layer state as:
where
and
are two activation functions, sigmoid and tanh, respectively.
and
indicates the weight matrices and the biases, respectively, and
t represents the time index. Here * can be
and
c, representing the parameters for forget gate, input gate and the cell state, respectively.
Since abstraction data is also a time-series, a LSTM sub-network, similar to the one used for groundwater levels, is employed for modeling the abstraction data. The outputs of the penultimate layers for survey, groundwater levels, and abstraction data, represented by , and respectively, are concatenated, , and fed to a FF network with two layers. For reference, this entire network is also compared to smaller sub-networks that consider individual datasets separately for welfare prediction, here each individual dataset is modeled by the corresponding sub-network described above.
3. Experimental Setup
This section starts with the detailed description of the dataset along with the problem formulation. Furthermore, we describe the details of various hyper-parameters of the proposed classifiers employed in this work.
3.1. Dataset Description
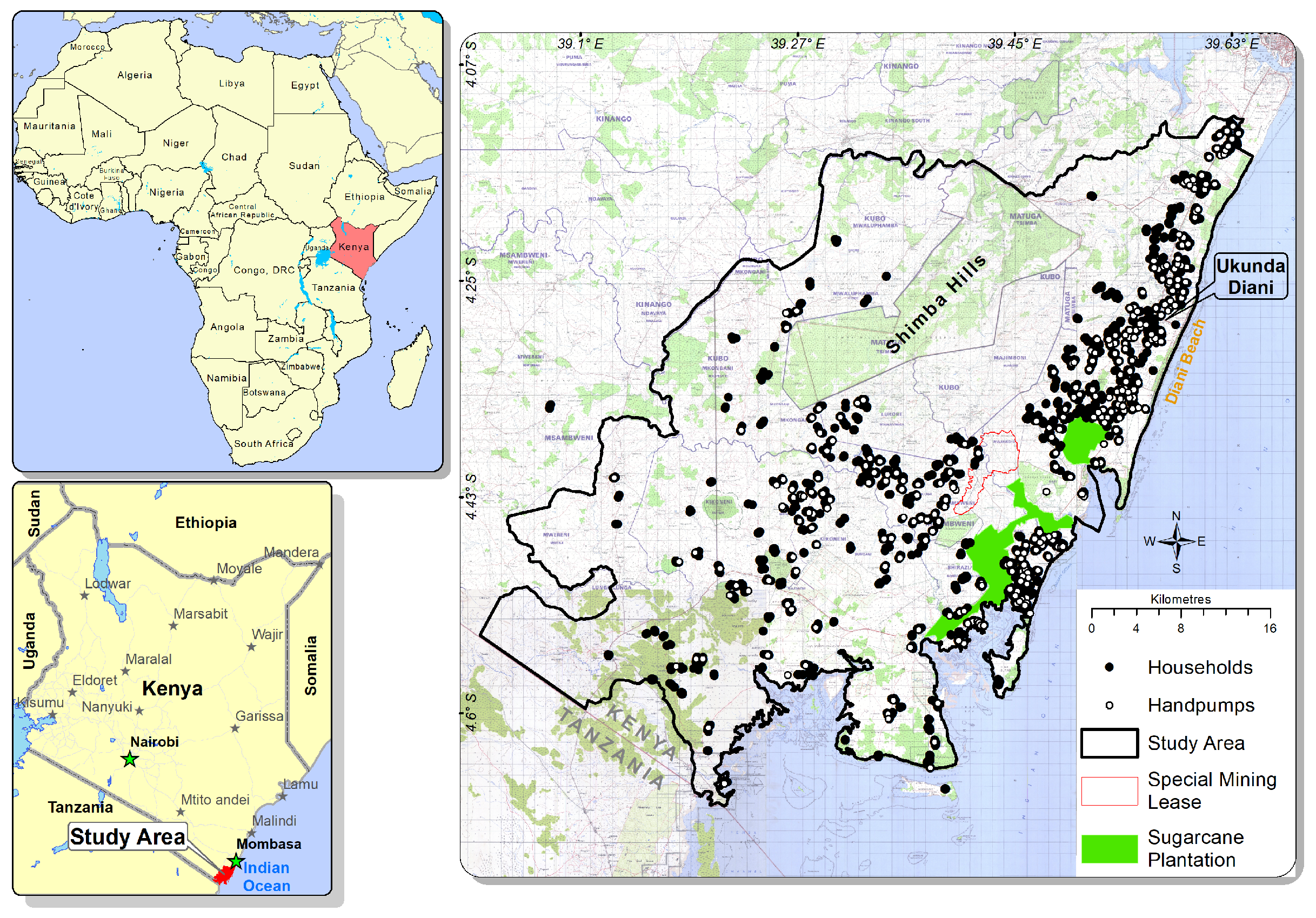
The dataset consists of three modalities: socio-economic survey, abstraction, and groundwater levels. There are challenges to employ these datasets simultaneously in a single model. A detailed description of these datasets and their limitations are as follows.
3.1.1. Socio-Economic Survey Data
The socio-economic data was collected as part of three rounds of longitudinal household surveys between 2013 and 2016 with respect to a sample of 532 handpump locations [
29,
30]. The data collected at each of the longitudinal survey is considered to be data belonging to one year. For each handpump location, an average of six households are randomly selected, generating a sample of 3,500 households. The survey captured information related to household demographics, welfare indicators and household assets, health, drinking water supplies, waterpoint management, and subjective welfare assessments. From these data a set of 29 indicators (
) are used to derive an asset-based multidimensional welfare index with weights defined by principal component analysis (PCA) approach [
29,
31,
32]. This approach differs from income or expenditure measures of poverty where a household would be classified based on one dimension of well-being with a poverty line cut-off which in some cases may be subjectively pre-selected. Welfare is a more inclusive concept acknowledging multiple dimensions such as education, health, assets and other salient indicators.
For this study, the resulting welfare index, normalized between 0 and 1, is used to divide the population into two halves—we consider households with welfare index less than 0.5 to be low-welfare, and the rest high-welfare. These low-welfare vs. high-welfare households are considered to be ground truth labels. A different subset of five questions (
) assumed to represent the how well off a household is, are used as inputs to train the models. Based on wider literature [
29], we select five indicators at the household level: (i) gender of head, (ii) dependency ratio (children over 15 years/total adults), (iii) improved structure (walls are rendered), (iv) own cattle or oxen, (v) subjective perception of being better off. These five questions are different from the 29 questions used to generate the labels to avoid learning a trivial mapping function. The key motivation behind using fewer survey questions to model welfare status is to ensure the proposed framework can be employed in resource-constrained settings, where performing periodic comprehensive surveys may be unfeasible. A potential solution may be asking a small subset of questions by mobile phone survey rather face-to-face interviews.
3.1.2. Groundwater Level Data
A groundwater flow model was developed to characterize the aquifer system of southern coastal Kenya. Following the development of a conceptual model [
18] a numerical model was constructed using Modflow-2005, simulating the period 2010 to 2017 and eight future model scenarios [
24]. As outputs of this model, estimated water levels of the aquifer system for the study area are available at 10-day intervals during 2010–2016. For this study, we assume a time-series of past
intervals of water levels at a household’s location to represent the state of drinking water supply for that household (
). Since we observed that for most of the temporal windows, the change in water levels was very subtle, we use area under the curve as opposed to the raw values. This representation of available water supply has its limitations. The water levels alone do not characterize household water availability, accessibility, and reliability, which are all key factors as defined under sustainable development goals [
33]. A more nuanced approach would be to include additional data such as the distance to the nearest operational handpump, cost (if any) of accessing the pump, quality of water, etc. As one of the aims is to investigate whether a limited data set can provide useful extra information about household welfare, we limit ourselves to using the modeled water levels to represent the state of the water supply.
3.1.3. Abstraction Data
GSM-enabled transmitters were installed on a sample of 300 operational community handpumps to generate daily pump usage data [
19,
34]. For this study, the daily data over 2013-2016 is converted into average weekly data. We assume a time-series of past
weeks of average weekly abstraction (
) represents the water demand of households using that pump. We note there are limitations to this assumption: (1) handpumps abstraction data alone is not representative of the water demand because people also use other sources of water (e.g., river, open wells, rain water, etc.), (2) the data represents average abstraction of the pump which cannot be disaggregated into individual households using the pump, (3) the data cannot be disaggregated into usage by types, i.e., household vs. irrigation vs. livestock activities, and (4) the data has missing values due to many reasons, e.g., pump malfunction, pump not being used temporarily due to availability of other resources (e.g., rainfall, school closures). For this data, it is difficult to overcome the first three limitations but regarding missing data, we propose some potential approaches in
Section 4.2 to alleviate the problem.
Thus, each household specific example is represented by three types of data modalities—
,
, and
, which are the features, along with corresponding welfare label
y. A collection of these examples is used to train the machine learning approaches described in
Section 2. We also use different combinations of these feature to analyze their mutual benefits.
3.2. Model Parameters
In this section, we discuss the experimental setup along with the details of various parameters used in the experiments. The 1D-CNN layers use 16 filter banks with kernel size/stride of 3/1 and all the LSTM layers have 32 nodes. The maxpooling operator is employed with 3 steps and the last two dense layers in each sub-network have 8 and 16 nodes. The concatenated representation is followed by two dense layers with 32 and 16 nodes, respectively. The last fully connected layers of each submodel and joint model are connected to a SoftMax layer with two classes.
All of the networks for this paper are trained using Keras [
35] with Tensorflow [
36] backend. The rmsprop optimizer is used with an initial learning rate of
. All the networks are trained for 100 epochs with a batch size of 32. The loss function used in all the sub-networks and the overall network is binary crossentropy with accuracy as the metric for classification. The overall loss used is weighed by 0.8, 1, 0.5 and 0.5 for the overall network, sub-networks for survey, groundwater levels and abstraction data, respectively. The 1D-CNN layers employ ReLU [
1] as activation and sigmoid is used as activation at the last layer of each of the network. The experiments with individual modalities of data employs each of the respective sub-network. The socio-economic survey data used in all the machine learning experiments
is a set of five questions (
= 5). The data corresponding to past ten time-intervals of groundwater levels data are used as
(
= 10). Similarly, the data corresponding to the average handpump water level abstraction for past eight weeks is used as
(
= 8). All the hyper-parameters and dimensionality of representations corresponding to both the
and
are obtained empirically.
In case of abstraction data, , when the data is missing for two consecutive days, we use the average abstraction level for the following and previous 4 days. If the data for a particular handpump corresponding to the respective household is unavailable, the data belonging to the nearest handpump is used. However, as we vary the distance to the nearest handpump to a household with available data, the number of households available to model varies.
The data corresponding to both and are normalized. The socio-economic survey data is collected over three periods and attempted to cover the same households over time; however, the households from one period to the other does vary. In this work, for most of the experiments, we consider these households to be independent. In all experiments the distance of handpump used for abstraction data is less than 0.5 km, resulting in 3259 households, unless stated otherwise. The year-wise data split for low-welfare/high-welfare households is year one—583/620, year two—263/524 and year three—350/919. We evaluate the performance using classification accuracy (CA) and area under the receiver operating characteristic curve (AUROC) as metrics.
4. Experimental Observations
This section provides a detailed explanation about various experiments starting with the year-wise cross-validation, where the total data belonging to two years of survey is used to train the model and the data belonging to the third year is used for testing. Furthermore, we evaluate the performance of the proposed model when the data from nearby handpumps is used as abstraction data for the households with missing abstraction data. The performance of the welfare prediction model is analyzed for various sections of the geographical locations of households. Finally, a comparison of the proposed method with the traditional machine learning methods is also provided.
4.1. Year-Wise Cross Validation
In this experiment we have employed a combination of two different years of survey data (along with other two input modalities) as training data and the third year as testing. In addition, we have also employed each one of the
,
and
individually and in tandem with each other for the same task. We have also pooled the survey data belonging to three years together for a three-fold cross-validation. The results for these different experiments are shown in the form of CA and AUROC (with 95% confidence interval (CI)) in
Figure 4a,b respectively.
It can be observed that there is complementary information in different modalities as evident from the results for all the data (brown bars). These results are consistent when year one and year two data is used for training and year three is used for testing, except a slight peak in the results for socio-economic survey and groundwater levels data as input.
The results when years two and three are used for training are different from other results, especially for the case of groundwater levels and abstraction data. One possible reason for this could be the temporal information present in the abstraction and groundwater levels data. The testing data here belongs to the previous year as compared to the training data, maybe the lag in temporal dimension of groundwater levels and abstraction data results in bad performance. This observation above is further strengthened by viewing the results using only the socio-economic survey data, here the CI is much smaller for the year-fold validation as opposed to the CI for groundwater levels, abstraction or groundwater levels and abstraction data.
4.2. Missing Abstraction Data
To deal with missing values in abstraction data, whenever household specific handpump abstraction data is unavailable, for that household, we consider data from the next closest representative handpump with available data. The AUROC results with 95% CI for a three-fold stratified cross-validation of the total pooled dataset as we vary the distance (in kms) of closest handpump are shown in
Table 1. We observe that the proposed method performs almost similar in all the cases when this distance is varied. One of the possible reasons could be the similarity between the average weekly abstraction data for different handpumps over a region. It may be the case that the model is able to capture the region-based variations which are not much different. However, in all these cases the use of abstraction and the groundwater levels data improves the performance. This further supports our claim that there is complementary information in the abstraction and groundwater levels data which can assist in welfare prediction for a household.
4.3. Location Based Performance
In an attempt to assess the differential value of the proposed model with respect to geographical location of the study area, we disaggregate the model outputs by specific zones. Although there are no physical boundaries separating these zones, the study area consists of three distinct zones based on geographical characteristics livelihood activities—Ukunda (urban, tourism, some access to piped water), coastal (rural, fishing, water drawn from shallow wells in a karstic coral aquifer), and inland (rural, mining, and commercial irrigation, water from boreholes a sandstone aquifer). The total number of households sampled in coastal, inland and Ukunda regions are 2355, 1361 and 488, respectively. The AUROC (with 95% CI) plots for a three-fold stratified cross-validation, with different modalities of data as input, for different regions are shown in
Figure 5.
The benefits gained from the addition of water level and abstraction data to the socio-economic data varies substantially over the three zones. Inland, the addition of the water level and abstraction data raises the mean AUROC by only 3% (this reduces further if considering the 95% CI). Also, compared to the other two zones the predictive power of the water level data and abstraction data are very different, with the abstraction data being more useful, although still less useful than the socio-economic data. In contrast, the addition of the water level and abstraction data is most beneficial in predicting welfare in the Ukunda region, adding a further 8% to the AUROC.
Given their geography, the inland communities will arguably be more affected by their environment, in particular the state of the aquifer than those in other area. Groundwater is not as easily accessible as it is at the coast, with boreholes drawing water from 30 m to 40 m, as opposed to shallow dug wells less than 10 m deep. Inland households must be more resilient to changes in groundwater levels as if they are not, the consequences will be more deleterious. Similarly, handpump density is much lower making the distance to one’s second water sources much greater than at the coast. Thus, the other measures of welfare may have groundwater levels and abstraction effects built into them. In addition,
Figure 5 shows that for the inland household abstraction alone is a better predictor of welfare than in other areas. Related research in the same study area [
27] showed that handpump use is closely linked to rainfall patterns and that household in this area are more likely to harvest rainwater. This is consistent with there being a closer correlation between handpump abstraction and other welfare-related factors implied by the higher ‘abstraction only’ AUROC in this area relative to the coastal and Ukunda regions. This deserves further investigation beyond the scope of this paper and these datasets.
4.4. Comparison with Other Techniques
The proposed method is also compared with the standard machine learning algorithms as shown in
Table 2. The metrics used for comparison are CA, AUROC, precision and recall, the results are shown with 95% CI for three-fold stratified cross-validation for all the pooled data. The input data used for this experiment consists of all three modalities of data. The methods used for comparison are K-nearest neighbors (KNN), support vector machine (SVM), decision trees (DT), and random forest (RF) [
2,
37]: the number of nearest neighbors chosen for KNN classifier are five; SVM are implemented with a radial basis function (RBF) kernel; the criterion used for the DT is gini impurity with ten minimum samples required for split. The RF classifier fits a number of DT classifiers on various sub-samples of the data and employs averaging to improve the performance.
In addition, we have also employed a standard machine learning classifiers, a multi-layer perceptron (MLP) and 1D-CNN-based deep neural network [
1]. The MLP employed here is a FF network with four layers with 32, 16, 64 and 32 nodes with a dropout of 0.2 after each layer. The 1D-CNN network consists of a 1D-CNN followed by a FF network, the CNN layer have 16 filterbanks with kernel size and stride of 3 and 1, respectively. This is followed by three FF layers with 32, 16 and 32 nodes, a dropout of 0.2 is used here as well. All other hyper-parameters in these networks are similar to the proposed network. It can be observed that the proposed multi-input multi-output neural network outperform the existing machine learning models for our task. It can be observed that the proposed multi-input multi-output neural network is not only outperforming the traditional machine learning methods, but is also better than a standard MLP and CNN-based classifier. In case of AUROC, the proposed method results in a gain of 4.05% as opposed to the 1D-CNN-based model, which is the best performing model among all other models. There could be two possible reasons for better performance: (a) efficient modeling of time-series data in abstraction and groundwater level data using LSTM, and (b) knowledge transfer in the multi-input multi-output deep learning method employed. The proposed model is jointly trained, and hence different modalities will have more interactions during the error backpropagation (in training). Thus, the network may learn hidden representations which contain knowledge that is trained and used by different modalities of data. The hidden representations trained this way will be better than the one estimated in a single model.
5. Conclusions and Discussion
In this work, we have demonstrated that a small set of survey questions along with groundwater level and handpump abstraction data can be used to predict the welfare status of households. Groundwater level and abstraction data alone perform worse as a predictor of welfare, as was expected; however, abstraction is slightly more predictive than water level. Combining abstraction and groundwater levels with survey data improves the performance; however, this gain varies across different regions within the study area, in some areas adding little value. When used in isolation abstraction and groundwater levels may not be what one would choose as an indicator of welfare around which one might design programs and interventions. But the fact that they do have some predictive power demonstrates that, in this locale at least, the water resources and water abstracted are linked to household welfare.
Comprehensive household surveys, rightly so, remain popular tools for determining welfare. Despite providing vital information, a major challenge with their use is that they are time-consuming and resource-intensive. The proposed framework provides an alternative solution by using a relatively small set of survey questions along with complementary available datasets, e.g., from groundwater levels and handpump abstraction data, to estimate the welfare status of households.
We have shown here that, in conjunction with small set of socio-economic survey data, water level and abstraction data provide useful additional information to characterize the welfare status of households. This method may be useful to policymakers, especially when they must allocate scarce resources efficiently, with only limited data available to inform their decision making. In future, other modalities of readily available data can also be employed in this type of a model to further improve the performance.
We draw three main lessons from this work from modeling multiple streams of data in one of the most intensively researched, rural study sites in Africa. First, the data requirements for machine learning methods are large. The groundwater level, daily abstraction data from handpumps and three panels of a large, longitudinal survey do not elicit clear and compelling results despite an extensive portfolio of modeling treatments. Given advances in remote sensing technologies, data resolution and multiple data sources, there is a strong case to conduct further work to validate the findings presented here. The replicability of the field methods applied in this study are unlikely to be available in all but the most strategic locations in Africa.
Second, the modeling has revealed a muted but intriguing signal that welfare may be associated with the patterns of daily water abstraction from handpumps. This partly reflects the notion of accidental infrastructure where one data stream may contain artefacts of useful information for other purposes. There is insufficient evidence to claim any predictive power from handpumps as sentinels of welfare, particularly given the multidimensional nature of welfare and poverty. However, it reflects the spill-over effects of collating data in structured and continuous fashion at the interface between biophysical and social systems.
Third, the interactions between groundwater and human welfare are dynamic and masked by biophysical processes and social practices. Though we have evidence that drinking water is one of four, dominant welfare priorities in the study area [
38], it is ranked below education, energy or sanitation. As we have noted, there are a range of confounding factors which reject any simple causal relationship to hold between groundwater and welfare. The implication that abstraction from rural handpumps is a proxy for the risk status of households may be substantiated by wider work in this study area where it has been shown that dependency and use of handpumps is seasonal and that the majority of the population depends on groundwater in times of dry spells [
29,
39]. The extent to which handpump abstraction is a proxy for risk is therefore plausible and worthy of further exploration to examine unknown aspects of distributional inequalities for different social groups access to and use of handpumps.
In conclusion, we would identify three major limitations to this work which merit consideration in future applications. First, the proposed method involved combining different modalities of data to improve the performance, but it is challenging to combine the varying level of noise and conflicts between modalities. One of the biggest challenges here is learning how to represent and summarize multi-modal data such that the complementary information is emphasized and redundancy is reduced. The multi-modal data is heterogeneous, and the relationship between modalities is open-ended or subjective, which makes it challenging to translate (map) data from one modality to another. Other challenges here include identifying the direct relations between elements and joining information from two or more different modalities. Second, we would also like to point out that there are limitations with the use of PCA-based method employed to generate ground truth labels for our task. Third, our welfare is framed here by five socio-economic variables chosen based on judgement and published literature. There are grounds to test and refine other risk proxies derived from both social and biophysical sources of information in future work.