Effect of Seasonal Characteristics of Temperature and Relative Humidity on Chloride Diffusion Process in Concrete: A Preliminary Theoretical Study
Abstract
:1. Introduction
2. Models and Methods
2.1. Governing Equation
2.2. Analytical Solution
2.3. Numerical Solution
3. Results
3.1. Illustrative Case Study
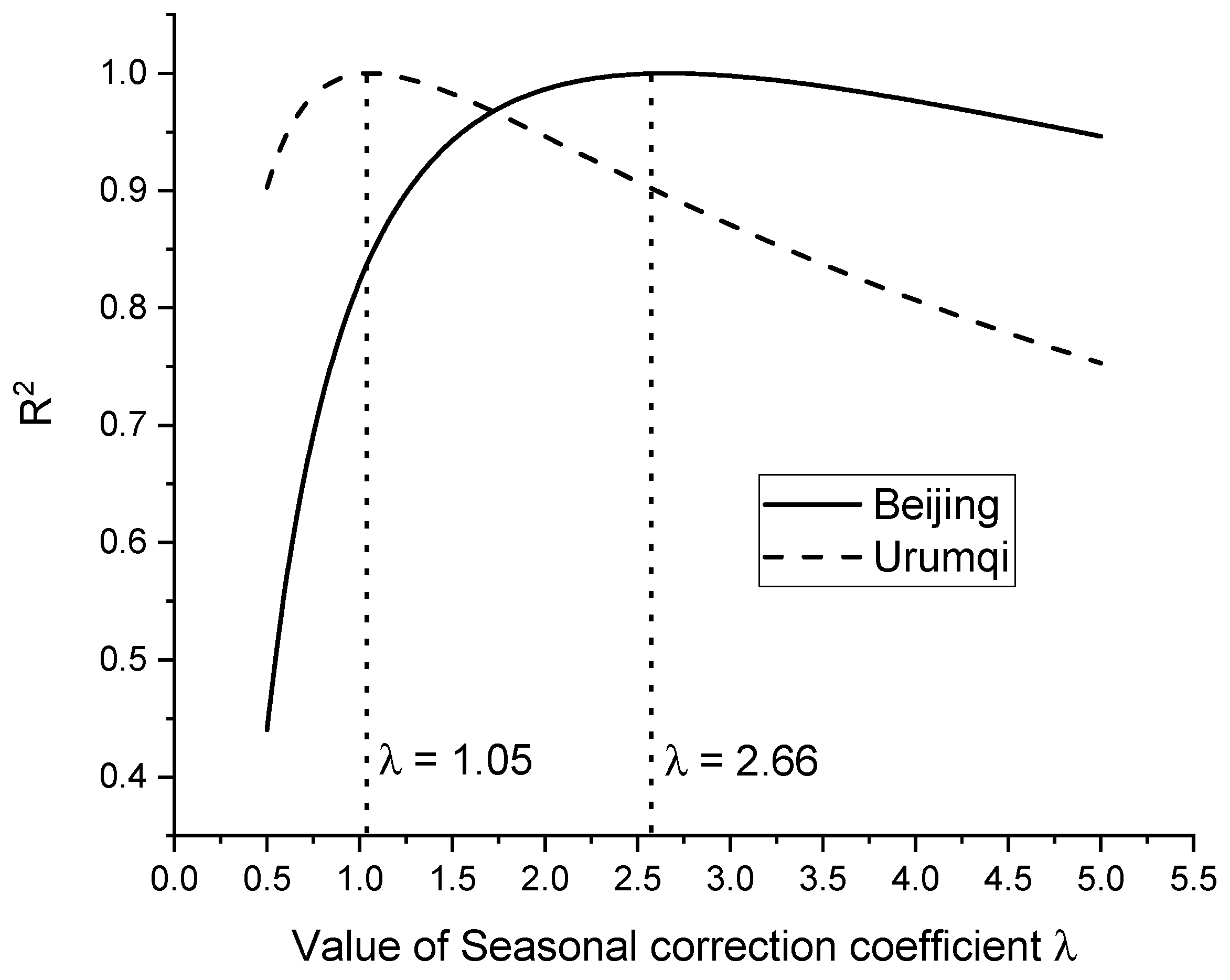
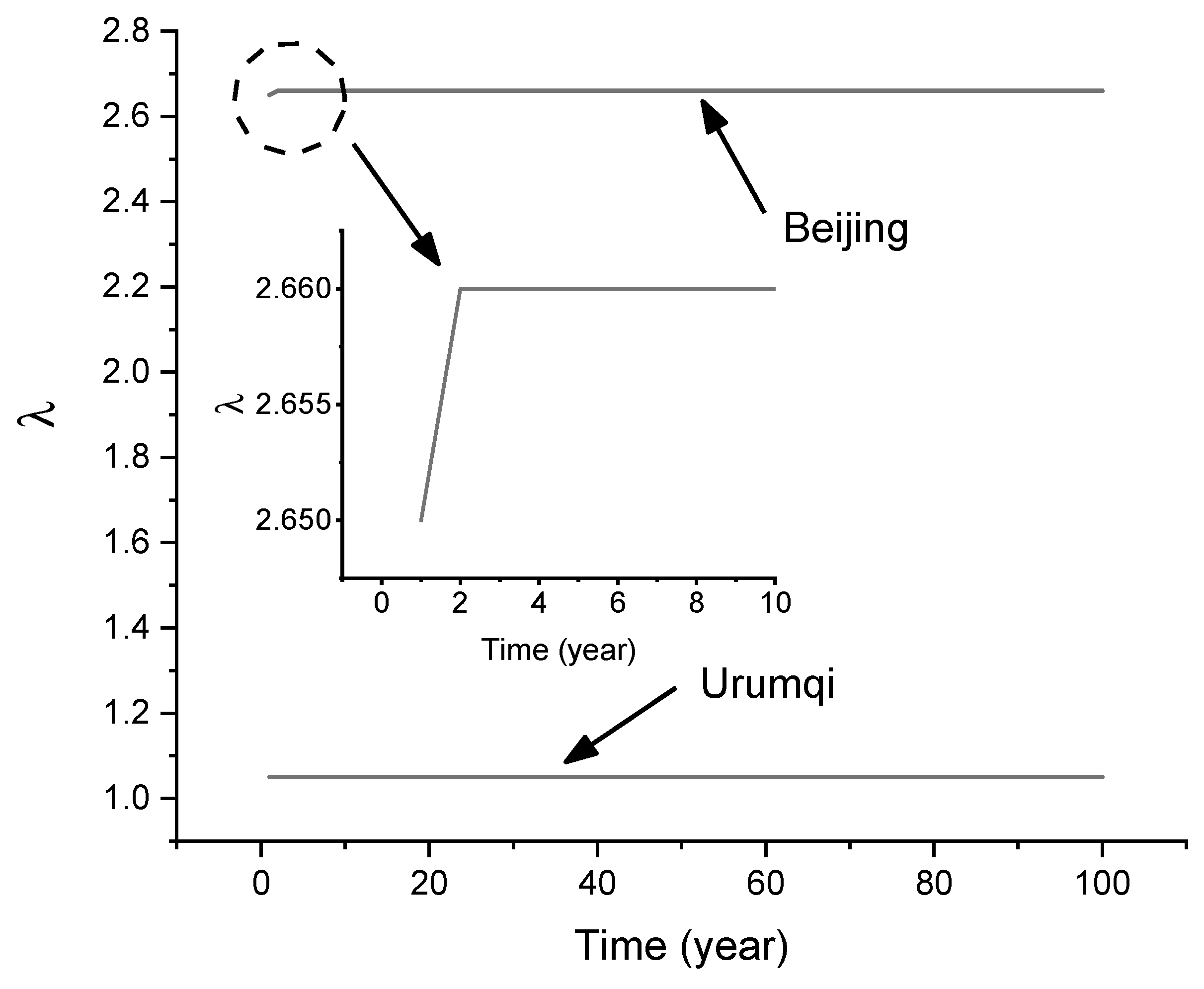
3.2. Seasonal Correction Coefficient
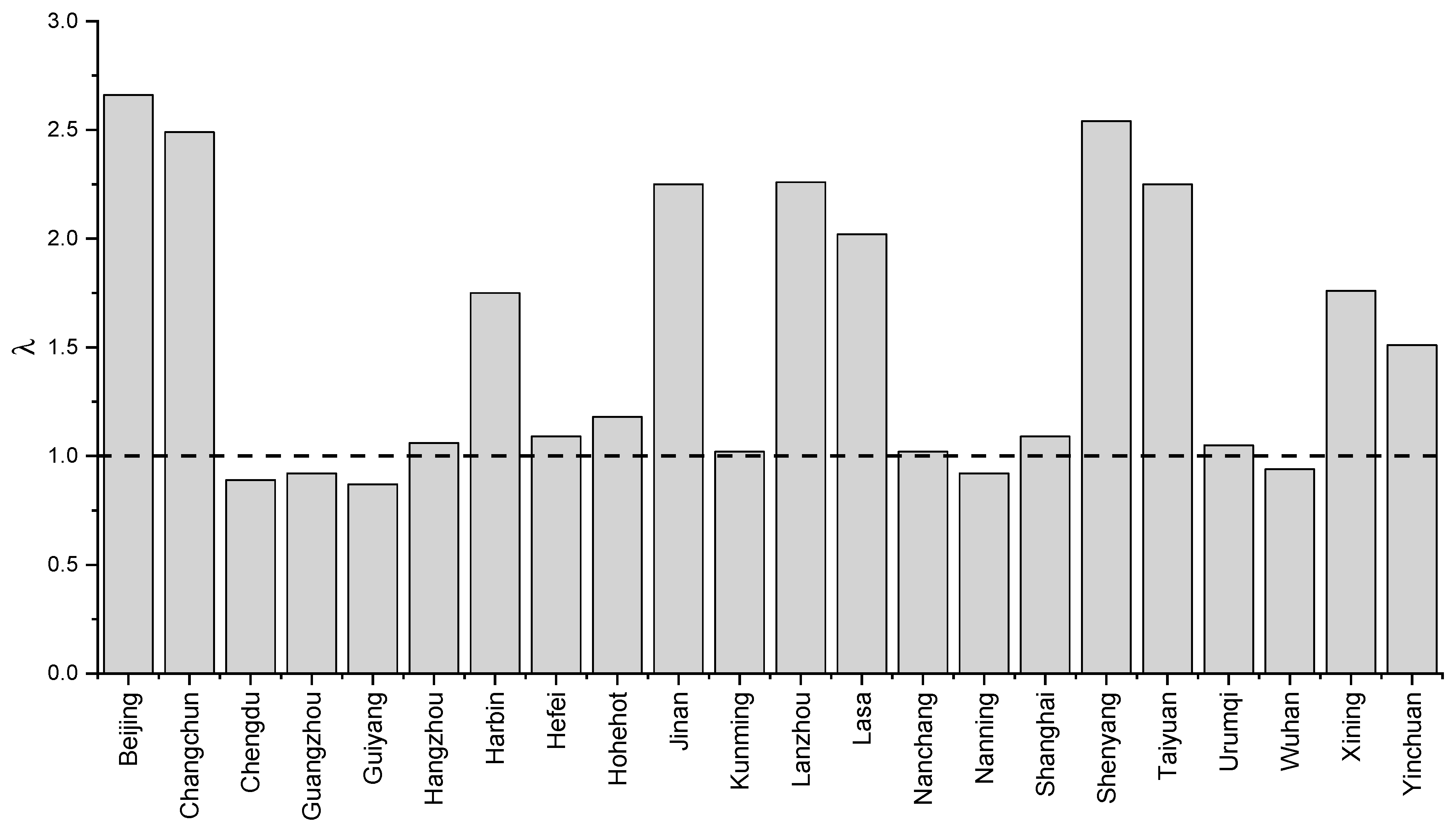
3.3. Nationwide Investigation
4. Discussion
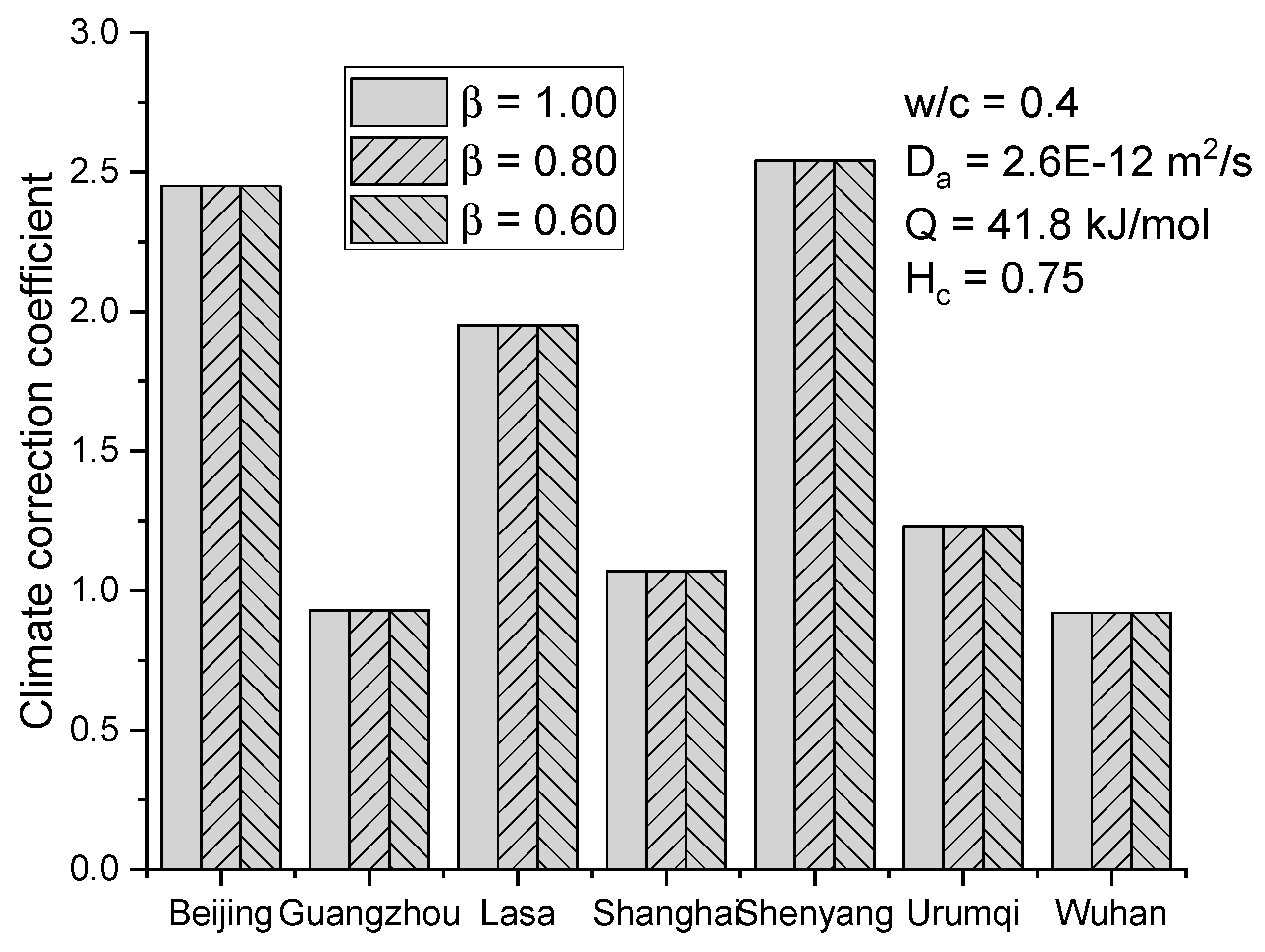
4.1. Effect of Chloride Diffusivity
4.2. Effect of Activation Energy
4.3. Effect of Critical Relative Humidity
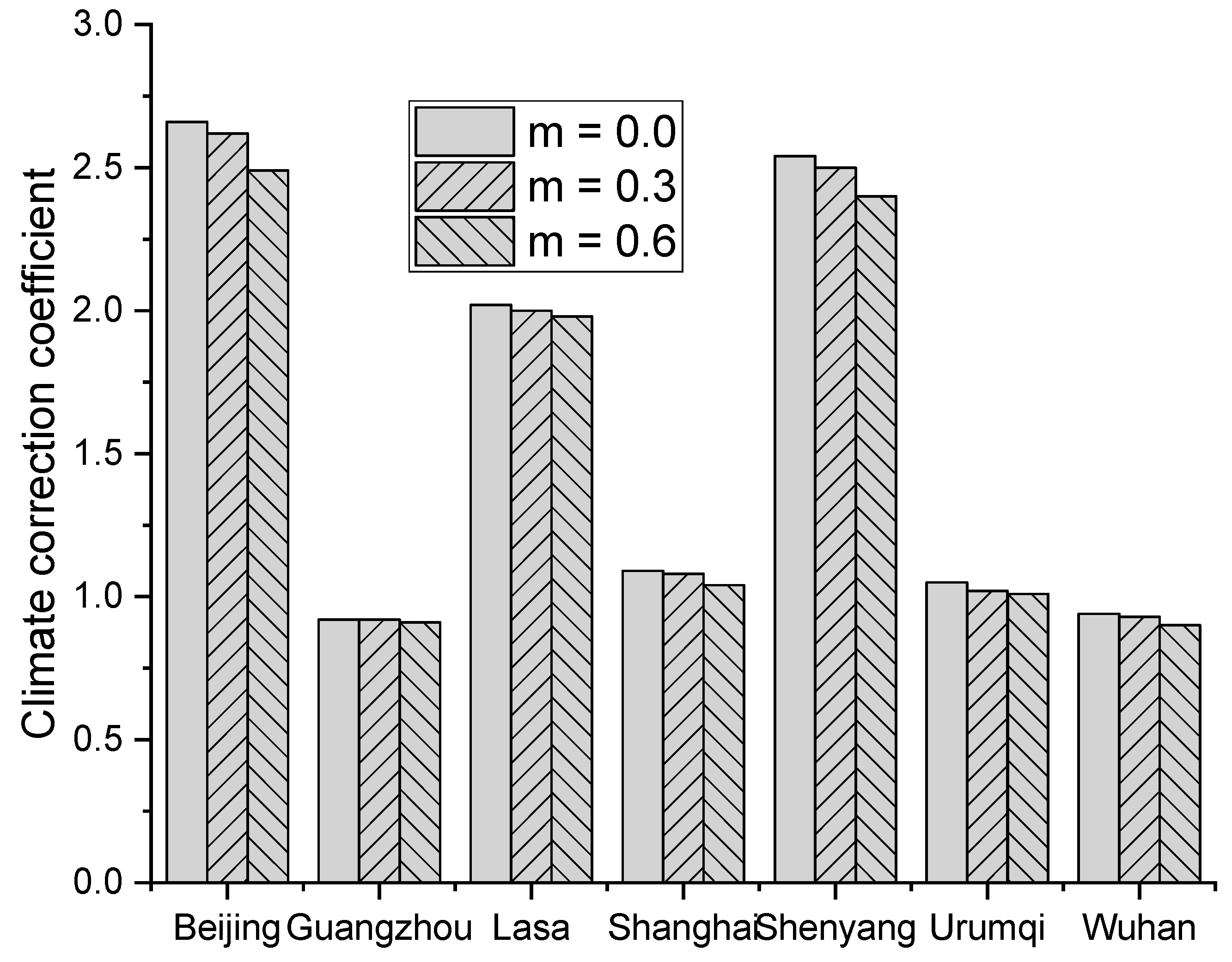
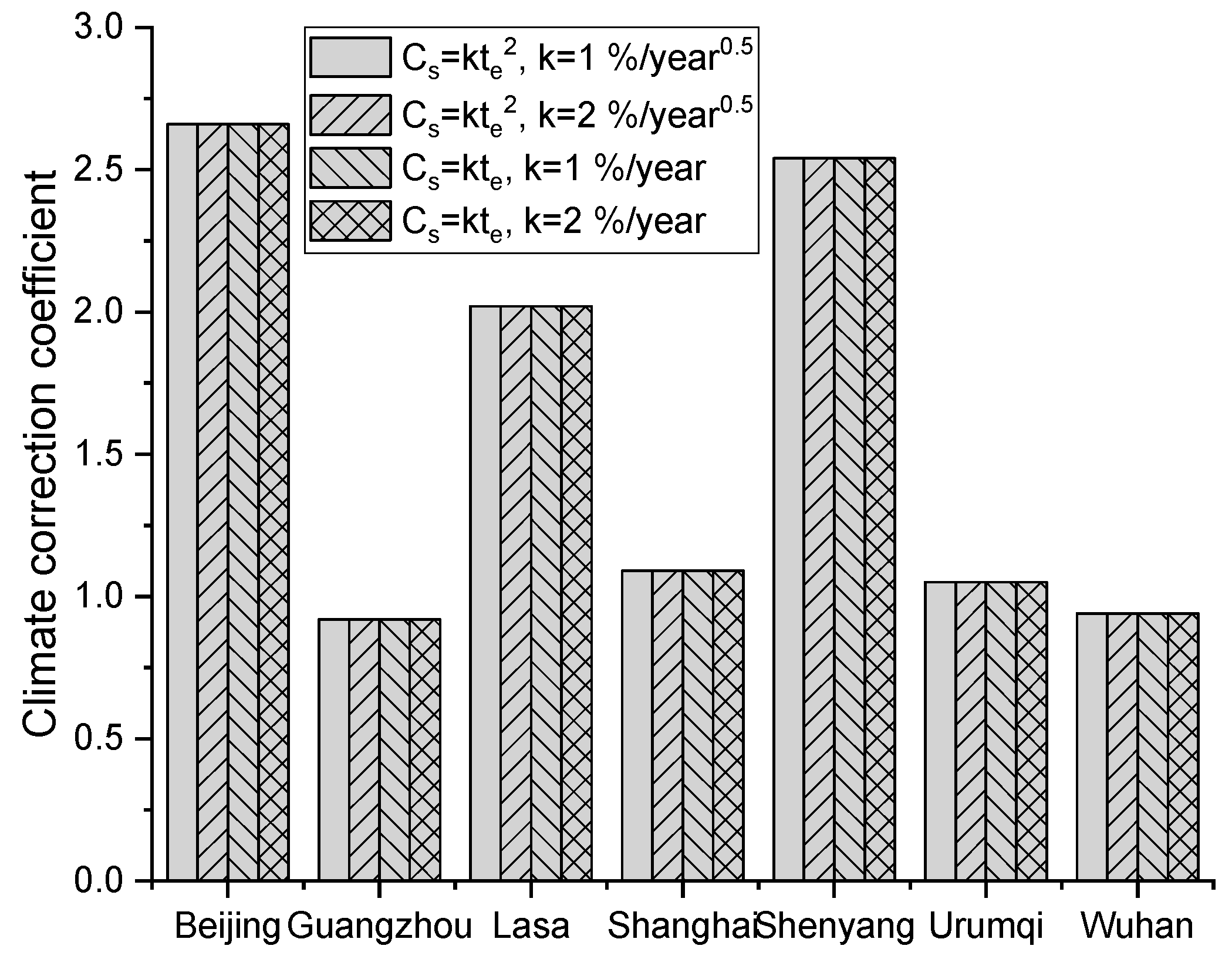
4.4. Effect of Surface Chloride Content
5. Conclusions
- The analytical solution with annual average temperature and relative humidity cannot consider their seasonal variations, which is questionable to calculate chloride profiles for typical cities.
- A seasonal correction coefficient for each city can be introduced to modify the analytical solution to enable its consideration of seasonal characteristics of temperature and relative humidity.
- Based on a parametric study, the seasonal correction coefficient shows a slight difference when the time-dependence of chloride diffusivity is considered.
- The seasonal correction coefficient is independent of how the surface chloride content increases with time and the increase rate.
- Within the common range of water-to-cement ratio for OPC mortar and concrete, the seasonal correction coefficient is affected slightly by the activation energy and greatly by the critical relative humidity in influence functions of temperature and relative humidity, respectively.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| City | Month | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Beijing | −1.7 | 2.3 | 9 | 17.5 | 23.3 | 25.6 | 27.9 | 26.2 | 23 | 12.8 | 4.1 | −0.2 |
| Taiyuan | −2.5 | 0.2 | 5.7 | 13.4 | 21 | 21.9 | 25.6 | 22.7 | 18.9 | 10.5 | 3.1 | −3.1 |
| Hohhot | −9.1 | −5.6 | 0.7 | 10.4 | 17.5 | 20.9 | 24.6 | 20.9 | 16.7 | 7.3 | −3.2 | −8.2 |
| Changchun | −12.2 | −7.7 | 0.6 | 10.7 | 16.6 | 20.2 | 24.8 | 22.1 | 16.4 | 7.7 | −3.1 | −12.4 |
| Harbin | −16.6 | −11 | −1.7 | 9.1 | 16.7 | 19.9 | 24.7 | 22.1 | 15 | 6.2 | −5.7 | −17.1 |
| Shanghai | 6.8 | 6.8 | 10.4 | 17.1 | 21.9 | 24 | 31.9 | 29.4 | 24.6 | 19.3 | 13.6 | 7.1 |
| Hangzhou | 7.3 | 7.8 | 11.3 | 18.7 | 22.8 | 24.1 | 31.6 | 30.3 | 24.9 | 19.1 | 13.7 | 7.4 |
| Hefei | 5.4 | 6.4 | 10.8 | 18 | 23.1 | 25.7 | 30.8 | 28.1 | 23.2 | 16.4 | 11.8 | 5.4 |
| Nanchang | 8.9 | 9.5 | 12.4 | 19.4 | 24.6 | 24.4 | 31 | 29.9 | 26.8 | 20.1 | 14.3 | 8.7 |
| Jinan | 1.1 | 4.7 | 9.3 | 17.5 | 24.3 | 25.8 | 28.2 | 26.7 | 24.1 | 14.7 | 8.9 | 2.5 |
| Wuhan | 6.4 | 7.2 | 11.5 | 17.6 | 22.7 | 25.2 | 30.6 | 28.6 | 23.5 | 16.7 | 12 | 5.4 |
| Guangzhou | 15.4 | 15 | 17.9 | 21.6 | 25.1 | 28.2 | 27.9 | 28.7 | 27.9 | 23.6 | 19.3 | 14.4 |
| Nanning | 15.6 | 15.5 | 17.1 | 22.3 | 25.4 | 27.6 | 27.6 | 27.9 | 28.2 | 23.3 | 18.4 | 14.1 |
| Chengdu | 7.3 | 8.2 | 11.1 | 17.2 | 21.5 | 23.4 | 26.7 | 25.9 | 22.3 | 16.5 | 12.4 | 6.5 |
| Guiyang | 6.6 | 7.5 | 9.2 | 16.5 | 18.8 | 20.1 | 23.5 | 23.6 | 21.7 | 16.4 | 11.4 | 6.5 |
| Kunming | 10.2 | 11.2 | 13.7 | 16.1 | 18.9 | 20.9 | 19.6 | 20.3 | 19.7 | 16.1 | 12.4 | 9.3 |
| Lasa | 0.1 | 4.5 | 5.9 | 10 | 13.4 | 16.1 | 16.6 | 16.4 | 16.2 | 11.6 | 4.5 | 2 |
| Lanzhou | −6.8 | −2.1 | 2.8 | 10.2 | 15.4 | 18.7 | 23.4 | 18.8 | 15.2 | 7.7 | −0.1 | −7.3 |
| Xining | −6.7 | −2.4 | 1.1 | 7.6 | 11.8 | 15.3 | 20.2 | 16.6 | 12.4 | 6.7 | −0.7 | −6.4 |
| Yinchuan | −4.6 | −0.4 | 4.6 | 14 | 19.3 | 23.1 | 25.9 | 22.4 | 19.3 | 9.8 | 2.8 | −4.5 |
| Urumqi | −11.3 | −8 | −2.8 | 11.1 | 18.7 | 23.1 | 26.7 | 22.2 | 17.1 | 7.5 | 1.6 | −6.9 |
| Shenyang | −9.1 | −4.9 | 2.8 | 12.7 | 18.7 | 22.8 | 26.5 | 23.5 | 17.9 | 9.2 | 0.2 | −8.3 |
| City | Month | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Beijing | 50 | 37 | 38 | 36 | 41 | 50 | 70 | 71 | 58 | 70 | 42 | 37 |
| Taiyuan | 55 | 50 | 45 | 47 | 37 | 59 | 67 | 76 | 70 | 81 | 53 | 47 |
| Hohhot | 52 | 47 | 47 | 31 | 29 | 41 | 45 | 51 | 42 | 58 | 42 | 43 |
| Changchun | 65 | 62 | 50 | 38 | 50 | 65 | 75 | 80 | 64 | 51 | 54 | 61 |
| Harbin | 72 | 68 | 62 | 46 | 49 | 68 | 70 | 76 | 70 | 54 | 62 | 67 |
| Shanghai | 73 | 66 | 67 | 64 | 66 | 77 | 66 | 76 | 78 | 75 | 74 | 65 |
| Hangzhou | 74 | 63 | 69 | 63 | 69 | 81 | 66 | 72 | 79 | 76 | 74 | 67 |
| Hefei | 74 | 72 | 70 | 71 | 72 | 76 | 76 | 83 | 85 | 80 | 69 | 67 |
| Nanchang | 71 | 68 | 76 | 70 | 67 | 88 | 70 | 76 | 76 | 73 | 74 | 63 |
| Jinan | 60 | 44 | 43 | 49 | 45 | 54 | 74 | 73 | 60 | 67 | 39 | 44 |
| Wuhan | 78 | 79 | 78 | 79 | 77 | 85 | 75 | 86 | 89 | 88 | 79 | 76 |
| Guangzhou | 81 | 75 | 84 | 83 | 84 | 85 | 85 | 82 | 85 | 75 | 78 | 66 |
| Nanning | 77 | 71 | 85 | 78 | 79 | 86 | 86 | 86 | 85 | 78 | 80 | 67 |
| Chengdu | 81 | 81 | 81 | 76 | 71 | 80 | 81 | 85 | 86 | 90 | 83 | 80 |
| Guiyang | 87 | 79 | 87 | 75 | 73 | 88 | 78 | 80 | 80 | 82 | 78 | 74 |
| Kunming | 71 | 65 | 61 | 67 | 62 | 73 | 83 | 81 | 81 | 83 | 75 | 72 |
| Lasa | 21 | 15 | 22 | 31 | 39 | 49 | 58 | 60 | 48 | 39 | 24 | 23 |
| Lanzhou | 42 | 47 | 50 | 48 | 44 | 62 | 52 | 78 | 75 | 78 | 59 | 53 |
| Xining | 47 | 47 | 52 | 54 | 54 | 60 | 53 | 70 | 76 | 73 | 53 | 48 |
| Yinchuan | 45 | 43 | 44 | 33 | 33 | 45 | 52 | 60 | 55 | 67 | 43 | 49 |
| Urumqi | 79 | 76 | 80 | 56 | 41 | 43 | 37 | 43 | 41 | 55 | 73 | 79 |
| Shenyang | 63 | 59 | 47 | 42 | 50 | 57 | 72 | 81 | 73 | 63 | 48 | 51 |
References
- Jaffer, S.J.; Hansson, C.M. Chloride-induced corrosion products of steel in cracked-concrete subjected to different loading conditions. Cem. Concr. Res. 2009, 39, 116–125. [Google Scholar] [CrossRef]
- Chen, A.; Pan, Z.; Ma, R. Mesoscopic simulation of steel rebar corrosion process in concrete and its damage to concrete cover. Struct. Infrastruct. Eng. 2017, 13, 478–493. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.M.; Takenaka, K. Reliability-based durability design and service life assessment of reinforced concrete deck slab of jetty structures. Struct. Infrastruct. Eng. 2017, 13, 468–477. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.M.; Matsuzaki, H. Life-cycle reliability of RC bridge piers under seismic and airborne chloride hazards. Earthq. Eng. Struct. Dyn. 2011, 40, 1671–1687. [Google Scholar] [CrossRef]
- Angst, U.; Elsener, B.; Larsen, C.K.; Vennesland, O. Critical chloride content in reinforced concrete—A review. Cem. Concr. Res. 2009, 39, 1122–1138. [Google Scholar] [CrossRef]
- Zhou, S. Analytical Model for Square Root Increase of Surface Chloride Concentration and Decrease of Chloride Diffusivity. J. Mater. Civ. Eng. 2015, 28, 04015181. [Google Scholar] [CrossRef]
- Zhou, S. Modeling chloride diffusion in concrete with linear increase of surface chloride. ACI Mater. J. 2014, 111, 483–490. [Google Scholar]
- Meijers, S.; Bijen, J.; De Borst, R.; Fraaij, A. Computational results of a model for chloride ingress in concrete including convection, drying-wetting cycles and carbonation. Mater. Struct. 2005, 38, 145–154. [Google Scholar] [CrossRef]
- Conciatori, D.; Laferrière, F.; Brühwiler, E. Comprehensive modeling of chloride ion and water ingress into concrete considering thermal and carbonation state for real climate. Cem. Concr. Res. 2010, 40, 109–118. [Google Scholar] [CrossRef]
- Ababneh, A.; Benboudjema, F.; Xi, Y.P. Chloride penetration in nonsaturated concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
- Wang, L.; Soda, M.; Ueda, T. Simulation of Chloride Diffusivity for Cracked Concrete Based on RBSM and Truss Network Model. ACT 2008, 6, 143–155. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, C.; Wu, Y.; Sun, L. Random-Walk Algorithm for Chloride Diffusivity of Concrete with Aggregate Shape Effect. J. Mater. Civ. Eng. 2016, 28, 04016153. [Google Scholar] [CrossRef]
- Fu, C.; Jin, X.; Ye, H.; Jin, N. Theoretical and Experimental Investigation of Loading Effects on Chloride Diffusion in Saturated Concrete. J. Adv. Concr. Technol. 2015, 13, 30–43. [Google Scholar] [CrossRef]
- Djerbi Tegguer, A.; Bonnet, S.; Khelidj, A.; Baroghel-Bouny, V. Effect of uniaxial compressive loading on gas permeability and chloride diffusion coefficient of concrete and their relationship. Cem. Concr. Res. 2013, 52, 131–139. [Google Scholar] [CrossRef]
- Abyaneh, S.D.; Wong, H.S.; Buenfeld, N.R. Modelling the diffusivity of mortar and concrete using a three-dimensional mesostructure with several aggregate shapes. Comput. Mater. Sci. 2013, 78, 63–73. [Google Scholar] [CrossRef]
- Page, C.L.; Short, N.R.; El Tarras, A. Diffusion of chloride ions in hardened cement pastes. Cem. Concr. Res. 1981, 11, 395–406. [Google Scholar] [CrossRef]
- Collepardi, M.; Marcialis, A.; Turriziani, R. Penetration of Chloride Ions into Cement Pastes and Concretes. J. Am. Ceram. Soc. 1972, 55, 534–535. [Google Scholar] [CrossRef]
- Nielsen, E.P.; Geiker, M.R. Chloride diffusion in partially saturated cementitious material. Cem. Concr. Res. 2003, 33, 133–138. [Google Scholar] [CrossRef]
- Saetta, A.V.; Scotta, R.V.; Vitaliani, R.V. Analysis of chloride diffusion into partially saturated concrete. ACI Mater. J. 1993, 90, 441–451. [Google Scholar]
- Yang, C.C.; Su, J.K. Approximate migration coefficient of interfacial transition zone and the effect of aggregate content on the migration coefficient of mortar. Cem. Concr. Res. 2002, 32, 1559–1565. [Google Scholar] [CrossRef]
- Caré, S. Influence of aggregates on chloride diffusion coefficient into mortar. Cem. Concr. Res. 2003, 33, 1021–1028. [Google Scholar] [CrossRef]
- Mangat, P.S.; Molloy, B.T. Prediction of Long-Term Chloride Concentration in Concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Bentz, E.C. Probalistic Modeling of Service Life for Structures Subjected to Chlorides. ACI Mater. J. 2003, 100, 391–397. [Google Scholar]
- Pang, L.; Li, Q. Service life prediction of RC structures in marine environment using long term chloride ingress data: Comparison between exposure trials and real structure surveys. Constr. Build. Mater. 2016, 113, 979–987. [Google Scholar] [CrossRef]
- Mustafa, M.A.; Yusof, K.M. Atmospheric chloride penetration into concrete in semitropical marine environment. Cem. Concr. Res. 1994, 24, 661–670. [Google Scholar] [CrossRef]
- Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment—Part I: Main parameters affecting chloride penetration. Mater. Struct. 1999, 32, 252–259. [Google Scholar] [CrossRef]
- Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment—Part II: Prediction of long term chloride penetration. Mater. Struct. 1999, 32, 354–359. [Google Scholar] [CrossRef]
- Meira, G.R.; Andrade, C.; Alonso, C.; Borba, J.C.; Padilha, M. Durability of concrete structures in marine atmosphere zones—The use of chloride deposition rate on the wet candle as an environmental indicator. Cem. Concr. Compos. 2010, 32, 427–435. [Google Scholar] [CrossRef]
- Tang, L.; Nilsson, L.O. Prediction of Chloride Penetration into Concrete Exposed to Various Exposure Environments. In Proceedings of the 9th International Conference on the Durability of Building Materials and Components, Brisbane, Australia, 17–20 March 2002. [Google Scholar]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Li, T.; Ruan, X. Effect of Seasonal Characteristics of Temperature and Relative Humidity on Chloride Diffusion Process in Concrete: A Preliminary Theoretical Study. Sustainability 2019, 11, 6330. https://doi.org/10.3390/su11226330
Pan Z, Li T, Ruan X. Effect of Seasonal Characteristics of Temperature and Relative Humidity on Chloride Diffusion Process in Concrete: A Preliminary Theoretical Study. Sustainability. 2019; 11(22):6330. https://doi.org/10.3390/su11226330
Chicago/Turabian StylePan, Zichao, Tianhua Li, and Xin Ruan. 2019. "Effect of Seasonal Characteristics of Temperature and Relative Humidity on Chloride Diffusion Process in Concrete: A Preliminary Theoretical Study" Sustainability 11, no. 22: 6330. https://doi.org/10.3390/su11226330





