Fuzzy Linear Programming Models for a Green Logistics Center Location and Allocation Problem under Mixed Uncertainties Based on Different Carbon Dioxide Emission Reduction Methods
Abstract
1. Introduction
2. Literature Review
2.1. Review of the Green Logistics Center Location and Allocation Problem
2.2. Review of the Logistics Center Location and Allocation Problem under an Uncertain Environment
2.3. Research Gaps
2.4. Research Works
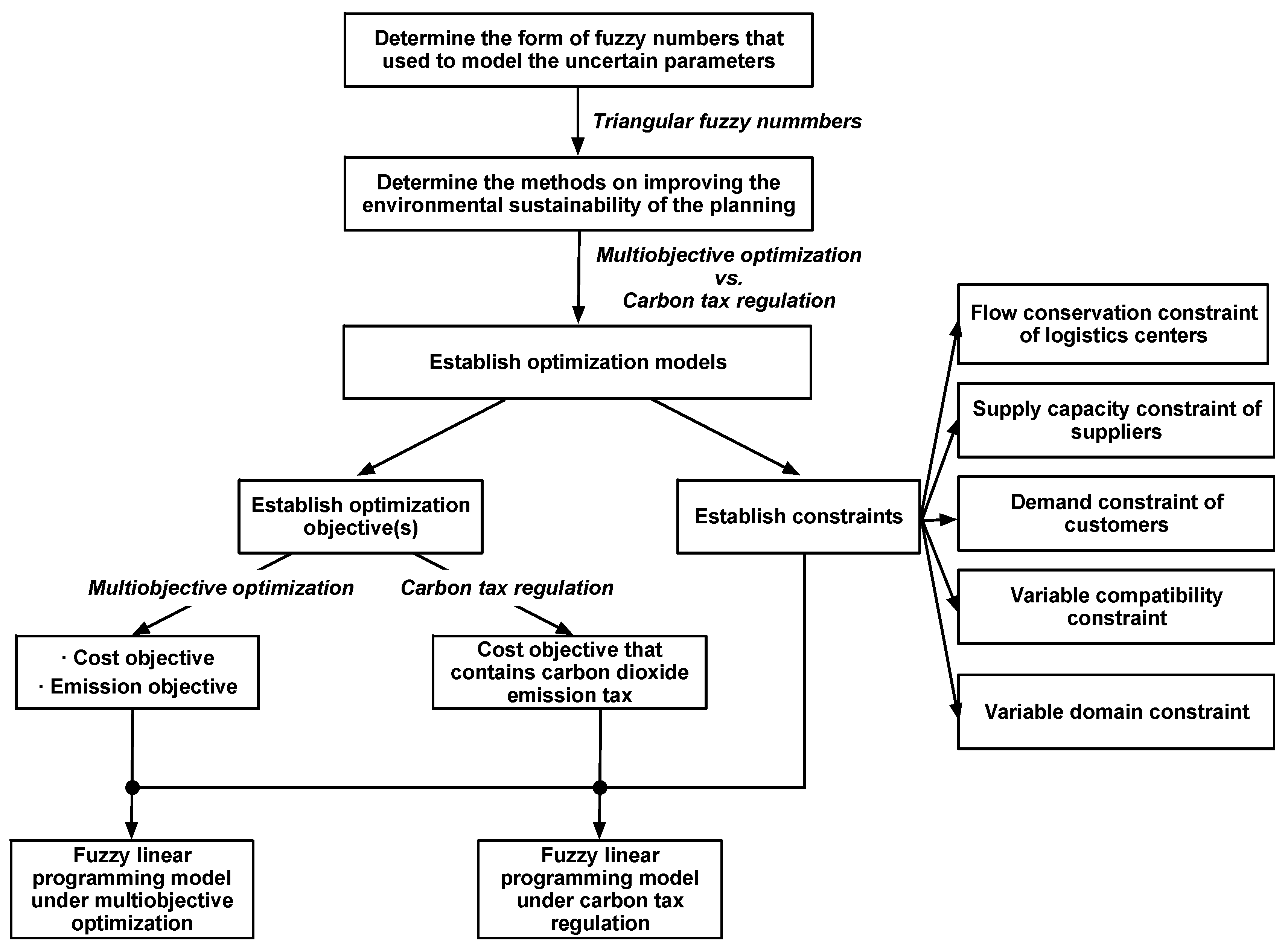
3. Fuzzy Linear Programming Models
3.1. Modeling Mixed Uncertianties
3.2. Notation
- Sets
- : Set of the candidate logistics centers in the logistics network.
- : Set of the suppliers in the logistics network.
- : Set of the customers in the logistics network.
- : Set of the nodes in the logistics, where .
- Indexes
- : Indexes of nodes in the logistics network, where .
- Network Parameters
- : Fuzzy supply capacity in ton per year of supplier , where .
- : Fuzzy operation capacity in ton per year of candidate logistics center , where .
- : Fuzzy demand in ton per year of customer , where .
- : Travel distance in kilometer from node . to node j, where .
- Cost Parameters
- : Travel cost in CNY per ton per kilometer of trucks, where CNY is the abbreviation of Chinese yuan, the Chinese monetary unit.
- : Fixed construction cost in CNY of candidate logistics center , where .
- : Operation cost in CNY per ton per year of candidate logistics center , where .
- : Carbon tax rate in CNY per kilogram.
- Emission Parameters
- Auxiliary Parameter
- : A sufficiently large positive number.
- Decision Variables
- : Non-negative variable that represents the freight volume in ton distributed from node . to node .
- : 0–1 variable. If candidate logistics center is selected, = 1. Otherwise, = 0, where .
3.3. Fuzzy Mixed Integer Linear Programming Models
4. Defuzzification Based on Fuzzy Chance-Constrained Programming
4.1. Step 1: Selection of a Fuzzy Measure
4.2. Step 2: Construction of Fuzzy Chance Constraints
4.3. Step 3: Crisp and Linear Reformations of Fuzzy Chance Constraints
5. Computational Experiments
5.1. Numerical Case Description
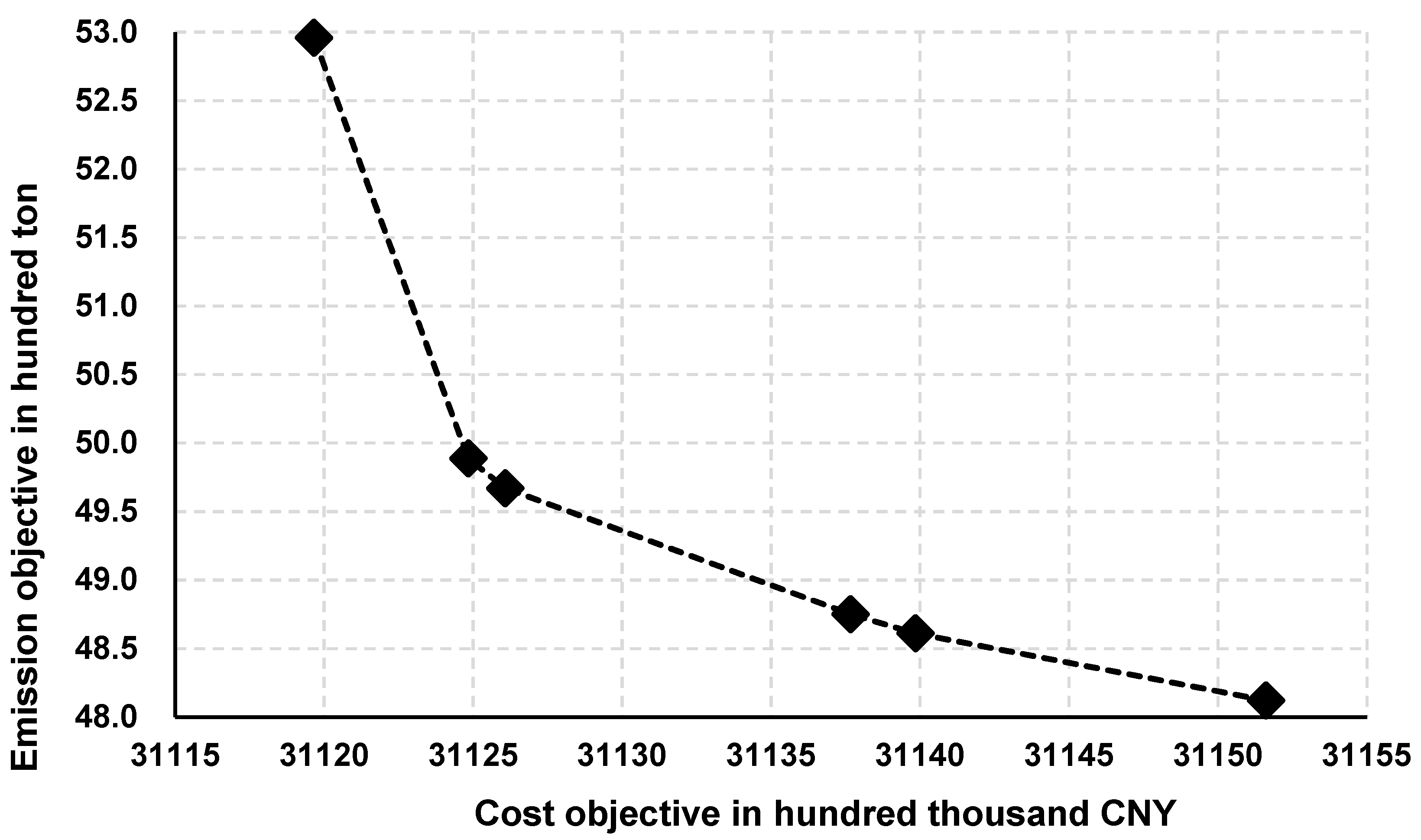
5.2. Multi-Objective Optimization Analysis
5.3. Sensitivity of the Optimization Results with Respect to the Carbon Tax Regulation
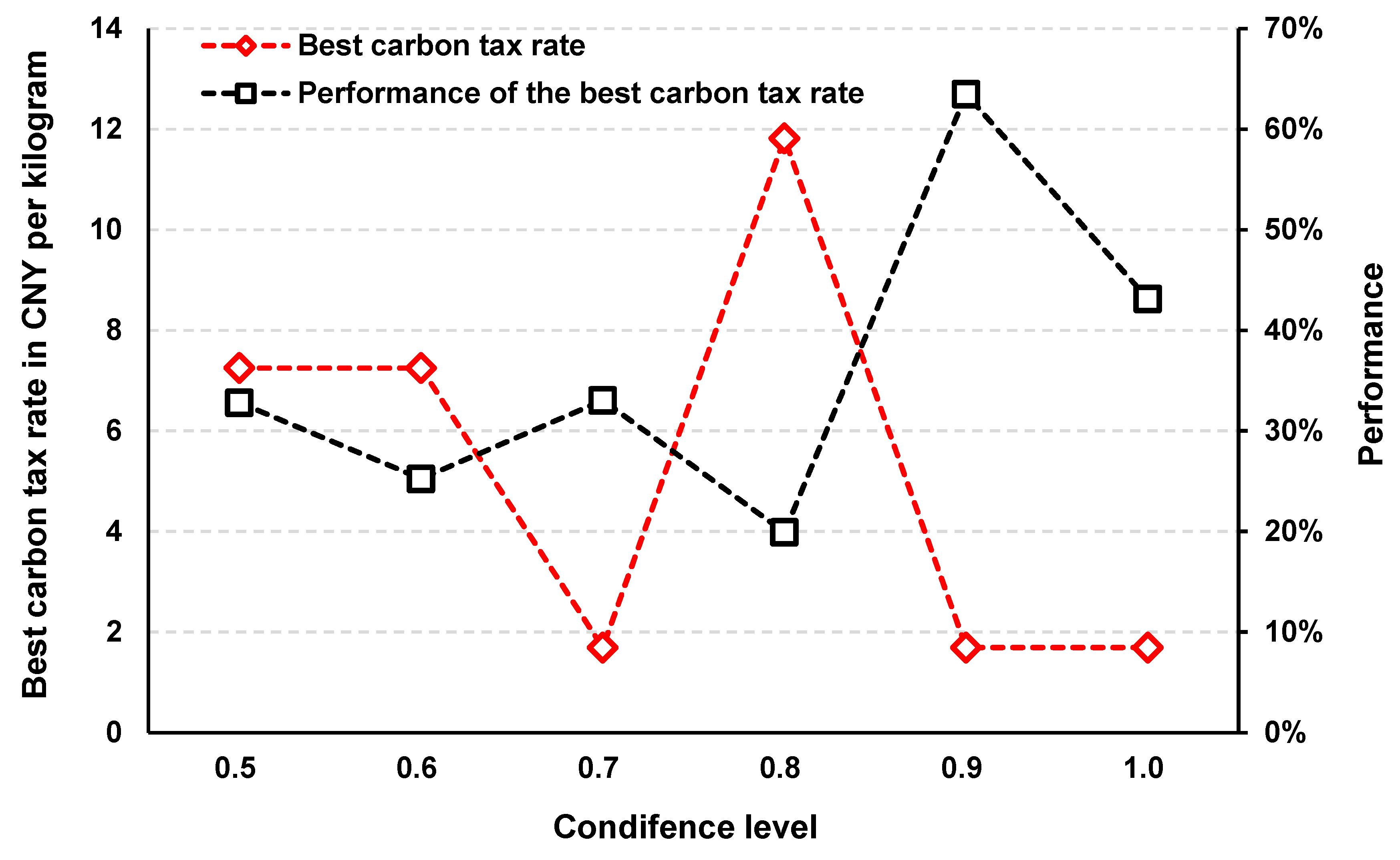
5.4. Sensitivity of the Carbon Tax Regulation with Respect to the Confidence Level
5.5. Comparison between Multi-Objective Optimization and Carbon Tax Regulation
5.6. Sensitivity of the Pareto Solutions with Respect to the Confidence Level
5.7. Fuzzy Simulation to Determine the Best Confidence Level for the Uncertain Problem
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| No. | Supply Capacity of Supplier 1 | Supply Capacity of Supplier 2 | Supply Capacity of Supplier 3 | Operation Capacity of Logistics Center 4 | Operation Capacity of Logistics Center 5 | Operation Capacity of Logistics Center 6 | Demand of Customer 7 | Demand of Customer 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1969 | 2004 | 1276 | 1706 | 2325 | 1336 | 1604 | 1627 |
| 2 | 1857 | 1780 | 1211 | 1603 | 2154 | 1309 | 1543 | 1796 |
| 3 | 1868 | 1912 | 1230 | 1739 | 2134 | 1674 | 1330 | 1795 |
| 4 | 1699 | 1648 | 1346 | 1940 | 2184 | 1472 | 1302 | 2255 |
| 5 | 1734 | 1638 | 1282 | 1711 | 2361 | 1312 | 1350 | 1670 |
| 6 | 1651 | 2043 | 1217 | 1842 | 2034 | 1371 | 1332 | 1796 |
| 7 | 1615 | 1616 | 1210 | 1925 | 2213 | 1352 | 1339 | 1712 |
| 8 | 1617 | 1803 | 1204 | 1932 | 2113 | 1378 | 1392 | 1668 |
| 9 | 1706 | 1709 | 1525 | 1815 | 2231 | 1505 | 1325 | 1775 |
| 10 | 1619 | 1695 | 1240 | 1901 | 2074 | 1395 | 1310 | 1722 |
| 11 | 1611 | 1619 | 1341 | 1909 | 2084 | 1554 | 1445 | 2328 |
| 12 | 1613 | 1665 | 1235 | 1990 | 2208 | 1304 | 1396 | 1939 |
| 13 | 1832 | 1749 | 1241 | 1850 | 2028 | 1322 | 1568 | 1689 |
| 14 | 1916 | 1737 | 1206 | 1828 | 2017 | 1464 | 1350 | 1748 |
| 15 | 1637 | 1826 | 1219 | 1762 | 2287 | 1580 | 1486 | 1715 |
| 16 | 1609 | 1689 | 1426 | 1986 | 2057 | 1343 | 1390 | 1761 |
| 17 | 2005 | 1741 | 1599 | 1708 | 2093 | 1345 | 1413 | 2002 |
| 18 | 1611 | 1787 | 1548 | 1624 | 2231 | 1325 | 1393 | 2008 |
| 19 | 1905 | 1737 | 1224 | 1705 | 2188 | 1302 | 1300 | 1776 |
| 20 | 1727 | 1604 | 1236 | 1682 | 2156 | 1387 | 1321 | 1809 |
References
- Żak, J.; Węgliński, S. The selection of the logistics center location based on MCDM/A methodology. Transp. Res. Procedia 2014, 3, 555–564. [Google Scholar] [CrossRef]
- Wang, B.; He, S. Robust optimization model and algorithm for logistics center location and allocation under uncertain environment. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 69–74. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Farahani, R.Z.; Dullaert, W. A memetic algorithm for bi-objective integrated forward/reverse logistics network design. Comput. Oper. Res. 2010, 37, 1100–1112. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Pasin, F.; Solomon, M.M. An integrated model for logistics network design. Ann. Oper. Res. 2006, 144, 59–82. [Google Scholar] [CrossRef]
- Lee, J.E.; Gen, M.; Rhee, K.G. Network model and optimization of reverse logistics by hybrid genetic algorithm. Comput. Ind. Eng. 2009, 56, 951–964. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, H.; Yu, G.; Ruan, J.; Chan, F.T. A three-stage and multi-objective stochastic programming model to improve the sustainable rescue ability by considering secondary disasters in emergency logistics. Comput. Ind. Eng. 2019, 135, 1145–1154. [Google Scholar] [CrossRef]
- Roscoe, S.; Cousins, P.D.; Lamming, R.C. Developing eco-innovations: A three-stage typology of supply networks. J. Clean. Prod. 2016, 112, 1948–1959. [Google Scholar] [CrossRef]
- Tavana, M.; Santos-Arteaga, F.J.; Mahmoodirad, A.; Niroomand, S.; Sanei, M. Multi-stage supply chain network solution methods: Hybrid metaheuristics and performance measurement. Int. J. Syst. Sci. Oper. Logist. 2018, 5, 356–373. [Google Scholar] [CrossRef]
- Sadic, S.; de Sousa, J.P.; Crispim, J.A. A two-phase MILP approach to integrate order, customer and manufacturer characteristics into Dynamic Manufacturing Network formation and operational planning. Expert Syst. Appl. 2018, 96, 462–478. [Google Scholar] [CrossRef]
- J.-Sharahi, S.; Khalili-Damghani, K.; Abtahi, A.R.; Rashidi-Komijan, A. Type-II Fuzzy Multi-Product, Multi-Level, Multi-Period Location–Allocation, Production–Distribution Problem in Supply Chains: Modelling and Optimisation Approach. Fuzzy Inf. Eng. 2018, 10, 260–283. [Google Scholar] [CrossRef]
- Carter, C.R.; Ellram, L.M. Reverse logistics: A review of the literature and framework for future investigation. J. Bus. Logist. 1998, 19, 85. [Google Scholar]
- Dowlatshahi, S. Developing a theory of reverse logistics. Interfaces 2000, 30, 143–155. [Google Scholar] [CrossRef]
- Sun, Y.; Hrušovský, M.; Zhang, C.; Lang, M. A time-dependent fuzzy programming approach for the green multimodal routing problem with rail service capacity uncertainty and road traffic congestion. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Liao, C.H.; Tseng, P.H.; Lu, C.S. Comparing carbon dioxide emissions of trucking and intermodal container transport in Taiwan. Transp. Res. Part D Transp. Environ. 2009, 14, 493–496. [Google Scholar] [CrossRef]
- IEA. CO2 Emissions from Fuel Combustion 2019; International Energy Agency: Paris, France, 2019; Available online: https://webstore.iea.org/co2-emissions-from-fuel-combustion-2019-overview (accessed on 15 November 2019).
- Rodrigue, J.P.; Slack, B.; Comtois, C. Green logistics. In Handbook of Logistics and Supply-Chain Management; Emerald Group Publishing Limited: Bingley, UK, 2008; pp. 339–350. [Google Scholar]
- Crainic, T.G. Service network design in freight transportation. Eur. J. Oper. Res. 2000, 122, 272–288. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Hong, Z.; Dong, K. How uncertain information on service capacity influences the intermodal routing decision: A fuzzy programming perspective. Information 2018, 9, 24. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Pokharel, S.; Mutlu, F. The Design of Green Supply Chains under Carbon Policies: A Literature Review of Quantitative Models. Sustainability 2019, 11, 3094. [Google Scholar] [CrossRef]
- Wang, F.; Lai, X.; Shi, N. A multi-objective optimization for green supply chain network design. Decis. Support Syst. 2011, 51, 262–269. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Torabi, S.A.; Razmi, J. Credibility-based fuzzy mathematical programming model for green logistics design under uncertainty. Comput. Ind. Eng. 2012, 62, 624–632. [Google Scholar] [CrossRef]
- Govindan, K.; Paam, P.; Abtahi, A.R. A fuzzy multi-objective optimization model for sustainable reverse logistics network design. Ecol. Indic. 2016, 67, 753–768. [Google Scholar] [CrossRef]
- Hang, Y.; Xie, L.; Hang, W.; Cui, X. A robust model for 3PLS to design a remanufacturing logistics network under the uncertain environment. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 367–372. [Google Scholar]
- Zhang, W.; Xu, D. Integrating the logistics network design with order quantity determination under uncertain customer demands. Expert Syst. Appl. 2014, 41, 168–175. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Jolai, F.; Razmi, J. A stochastic optimization model for integrated forward/reverse logistics network design. J. Manuf. Syst. 2009, 28, 107–114. [Google Scholar] [CrossRef]
- Amin, S.H.; Zhang, G. A multi-objective facility location model for closed-loop supply chain network under uncertain demand and return. Appl. Math. Model. 2013, 37, 4165–4176. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Jolai, F. Robust and reliable forward–reverse logistics network design under demand uncertainty and facility disruptions. Appl. Math. Model. 2014, 38, 2630–2647. [Google Scholar] [CrossRef]
- Shimizu, Y.; Matsuda, S.; Wada, T. A flexible design of logistic network against uncertain demands through hybrid meta-heuristic method. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2006; Volume 21, pp. 2051–2056. [Google Scholar]
- Lieckens, K.; Vandaele, N. Multi-level reverse logistics network design under uncertainty. Int. J. Prod. Res. 2012, 50, 23–40. [Google Scholar] [CrossRef]
- Lee, D.H.; Dong, M. Dynamic network design for reverse logistics operations under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 61–71. [Google Scholar] [CrossRef]
- Zeballos, L.J.; Méndez, C.A.; Barbosa-Povoa, A.P.; Novais, A.Q. Multi-period design and planning of closed-loop supply chains with uncertain supply and demand. Comput. Chem. Eng. 2014, 66, 151–164. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, J.; Fu, J. Multi-objective fuzzy location-allocation-routing problem in urgent relief distribution system. J. Transp. Syst. Eng. Inf. Technol. 2014, 14, 160–167. [Google Scholar]
- Bai, Q.; Chen, M. The distributionally robust newsvendor problem with dual sourcing under carbon tax and cap-and-trade regulations. Comput. Ind. Eng. 2016, 98, 260–274. [Google Scholar] [CrossRef]
- Duan, X.; Heragu, S. Carbon Emission Tax Policy in an Intermodal Transportation Network. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015; Volume 30. [Google Scholar]
- Zhang, D.; He, R.; Li, S.; Wang, Z. A multimodal logistics service network design with time windows and environmental concerns. PLoS ONE 2017, 12, e0185001. [Google Scholar] [CrossRef]
- Törnquist, J. Computer-Based Decision Support for Handling Uncertainty in Railway Traffic and Transportation. Ph.D. Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2004. [Google Scholar]
- Sun, Y.; Li, X. Fuzzy Programming Approaches for Modeling a Customer-Centred Freight Routing Problem in the Road-Rail Intermodal Hub-and-Spoke Network with Fuzzy Soft Time Windows and Multiple Sources of Time Uncertainty. Mathematics 2019, 7, 739. [Google Scholar] [CrossRef]
- Zarandi, M.H.F.; Hemmati, A.; Davari, S. The multi-depot capacitated location-routing problem with fuzzy travel times. Expert Syst. Appl. 2011, 38, 10075–10084. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, B. Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 2006, 176, 673–683. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1999, 100, 9–34. [Google Scholar] [CrossRef]
- Liu, X. Measuring the satisfaction of constraints in fuzzy linear programming. Fuzzy Sets Syst. 2001, 122, 263–275. [Google Scholar] [CrossRef]
- Shaocheng, T. Interval number and fuzzy number linear programmings. Fuzzy Sets Syst. 1994, 66, 301–306. [Google Scholar] [CrossRef]
- Özceylan, E.; Paksoy, T. Interactive fuzzy programming approaches to the strategic and tactical planning of a closed-loop supply chain under uncertainty. Int. J. Prod. Res. 2014, 52, 2363–2387. [Google Scholar] [CrossRef]
- Liang, T.F.; Cheng, H.W. Application of fuzzy sets to manufacturing/distribution planning decisions with multi-product and multi-time period in supply chains. Expert Syst. Appl. 2009, 36, 3367–3377. [Google Scholar] [CrossRef]
- Sun, Y.; Liang, X.; Li, X.; Zhang, C. A Fuzzy Programming Method for Modeling Demand Uncertainty in the Capacitated Road–Rail Multimodal Routing Problem with Time Windows. Symmetry 2019, 11, 91. [Google Scholar] [CrossRef]
- Cao, E.; Lai, M. A hybrid differential evolution algorithm to vehicle routing problem with fuzzy demands. J. Comput. Appl. Math. 2009, 231, 302–310. [Google Scholar]
- Gen, M.; Tsujimura, Y.; Ida, K. Method for solving multi-objective aggregate production planning problem with fuzzy parameters. Comput. Ind. Eng. 1992, 23, 117–120. [Google Scholar] [CrossRef]
- Mula, J.; Peidro, D.; Poler, R. The effectiveness of a fuzzy mathematical programming approach for supply chain production planning with fuzzy demand. Int. J. Prod. Econ. 2010, 128, 136–143. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Liang, X.; Zhang, C. A Bi-Objective Fuzzy Credibilistic Chance-Constrained Programming Approach for the Hazardous Materials Road-Rail Multimodal Routing Problem under Uncertainty and Sustainability. Sustainability 2019, 11, 2577. [Google Scholar] [CrossRef]
- NDRC. Available online: http://jgjc.ndrc.gov.cn/Detail.aspx?TId=706&newsId=6894 (accessed on 15 November 2019).
- Schrage, L. LINGO User’s Guide; LINDO System Inc.: Chicago, IL, USA, 2006; Available online: http://www.lindo.com/ (accessed on 15 November 2019).
- Sawik, B. Weighted-sum approach for bi-objective optimization of fleet size with environmental aspects. In Applications of Management Science; Emerald Publishing Limited: Bingley, UK, 2018; pp. 101–116. [Google Scholar]
- Wang, J.; Yan, G.; Jiang, K.; Liu, L.; Yang, J.; Ge, C. The study on China's carbon tax policy to mitigate climate change. China Environ. Sci. 2009, 29, 101–105. [Google Scholar]
- Wang, R.; Yang, K.; Yang, L.; Gao, Z. Modeling and optimization of a road–rail intermodal transport system under uncertain information. Eng. Appl. Artif. Intell. 2018, 72, 423–436. [Google Scholar] [CrossRef]
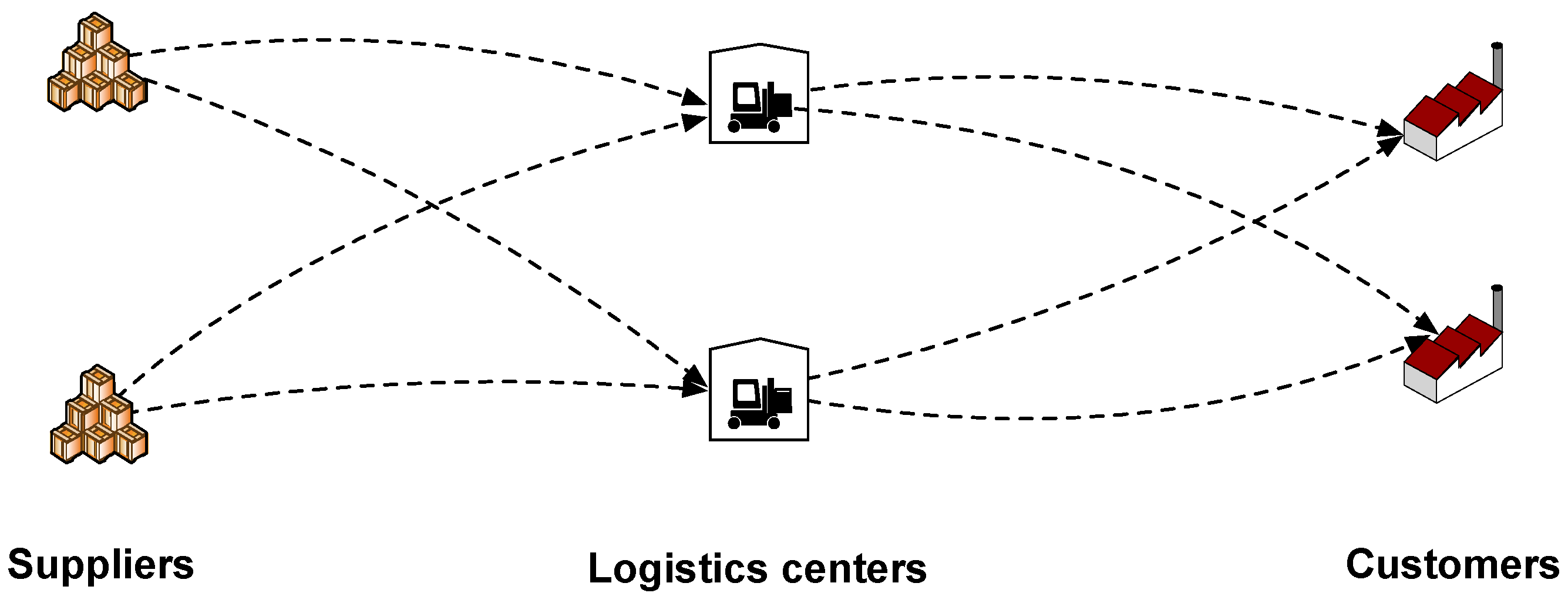





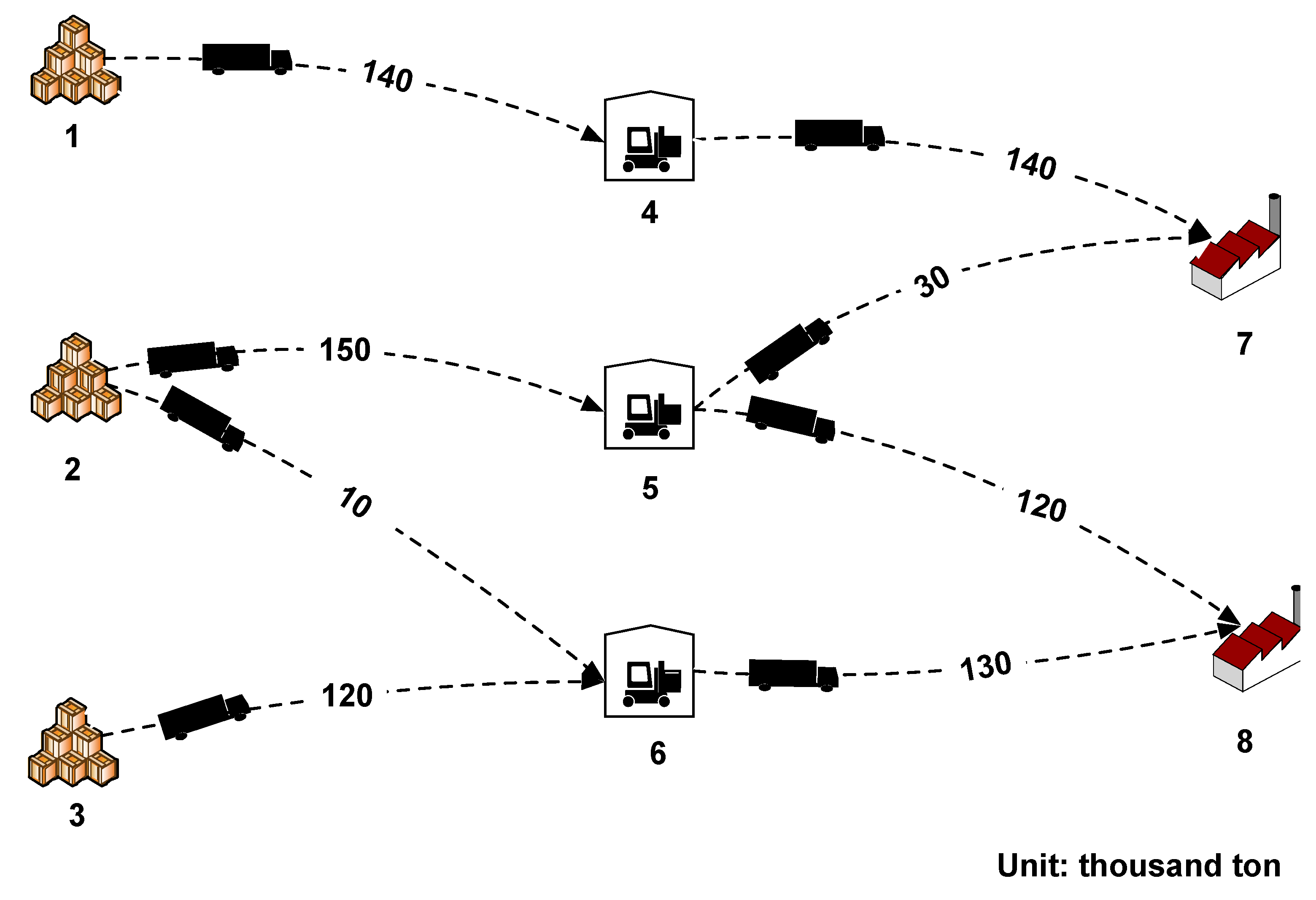
| Transportation Line | Travel Distances in Kilometer | Emission Factors in Kilogram per Ton per Kilometer | Transportation Line | Travel Distances in Kilometer | Emission Factors in Kilogram per Ton per Kilometer |
|---|---|---|---|---|---|
| (1, 4) | 25 | 0.10 | (3, 6) | 30 | 0.08 |
| (1, 5) | 38 | 0.06 | (4, 7) | 35 | 0.08 |
| (1, 6) | 50 | 0.08 | (4, 8) | 50 | 0.07 |
| (2, 4) | 46 | 0.04 | (5, 7) | 45 | 0.04 |
| (2, 5) | 25 | 0.07 | (5, 8) | 30 | 0.10 |
| (2, 6) | 30 | 0.05 | (6, 7) | 60 | 0.06 |
| (3, 4) | 65 | 0.07 | (6, 8) | 40 | 0.04 |
| (3, 5) | 48 | 0.04 |
| Nodes | Fuzzy Supply Capacities in Thousand Ton | Fuzzy Operation Capacities in Thousand Ton | Fuzzy Demands in Thousand Ton | Emission Factors in Kilogram per Ton | Construction Cost in Million CNY | Operation Cost in CNY per Ton |
|---|---|---|---|---|---|---|
| 1 | 160, 190, 210 | 2.50 | ||||
| 2 | 160, 220, 230 | 2.00 | ||||
| 3 | 120, 150, 170 | 1.50 | ||||
| 4 | 160, 210, 230 | 3.00 | 1000 | 7.0 | ||
| 5 | 200, 250, 270 | 4.50 | 1200 | 5.0 | ||
| 6 | 130, 170, 190 | 2.00 | 900 | 6.0 | ||
| 7 | 130, 150, 170 | 3.00 | ||||
| 8 | 160, 180, 250 | 2.50 |
| Confidence Level | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|
| Pareto Solutions to the Problem | (19,108.0, 38.42) | (19,114.8, 41.26) | (21,119.6, 44.47) | (22,113.4, 52.88) | (31,119.7, 52.96) | (31,127.4, 54.01) |
| (19,112.2, 37.84) | (19,118.5, 40.75) | (21,119.6, 44.37) | (22,113.7, 52.77) | (31,124.8, 49.89) | (31,129.5, 52.77) | |
| (19,121.4, 37.00) | (19,130.3, 39.69) | (21,120.7, 43.71) | (22,130.6, 51.34) | (31,126.1, 49.67) | (31,129.9, 52.70) | |
| (21,123.8, 36.78) | (21,127.8, 39.57) | (21,133.4, 42.70) | (22,153.0, 50.38) | (31,137.7, 48.75) | (31,140.9, 51.82) | |
| (31,124.5, 36.65) | (31,134.2, 39.24) | (31,140.3, 42.17) | (22,162.2, 50.29) | (31,139.9, 48.61) | (31,142.2, 51.74) | |
| (31,146.0, 45.15) | (31,151.6, 48.12) | (31,156.6, 51.14) | ||||
| (31,158.0, 51.13) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Lu, Y.; Zhang, C. Fuzzy Linear Programming Models for a Green Logistics Center Location and Allocation Problem under Mixed Uncertainties Based on Different Carbon Dioxide Emission Reduction Methods. Sustainability 2019, 11, 6448. https://doi.org/10.3390/su11226448
Sun Y, Lu Y, Zhang C. Fuzzy Linear Programming Models for a Green Logistics Center Location and Allocation Problem under Mixed Uncertainties Based on Different Carbon Dioxide Emission Reduction Methods. Sustainability. 2019; 11(22):6448. https://doi.org/10.3390/su11226448
Chicago/Turabian StyleSun, Yan, Yue Lu, and Cevin Zhang. 2019. "Fuzzy Linear Programming Models for a Green Logistics Center Location and Allocation Problem under Mixed Uncertainties Based on Different Carbon Dioxide Emission Reduction Methods" Sustainability 11, no. 22: 6448. https://doi.org/10.3390/su11226448
APA StyleSun, Y., Lu, Y., & Zhang, C. (2019). Fuzzy Linear Programming Models for a Green Logistics Center Location and Allocation Problem under Mixed Uncertainties Based on Different Carbon Dioxide Emission Reduction Methods. Sustainability, 11(22), 6448. https://doi.org/10.3390/su11226448






