Stability Control for the Rheological Roadway by a Novel High-Efficiency Jet Grouting Technique in Deep Underground Coal Mines
Abstract
:1. Introduction
2. Time-Dependent Behavior of a Soft Coal Roadway
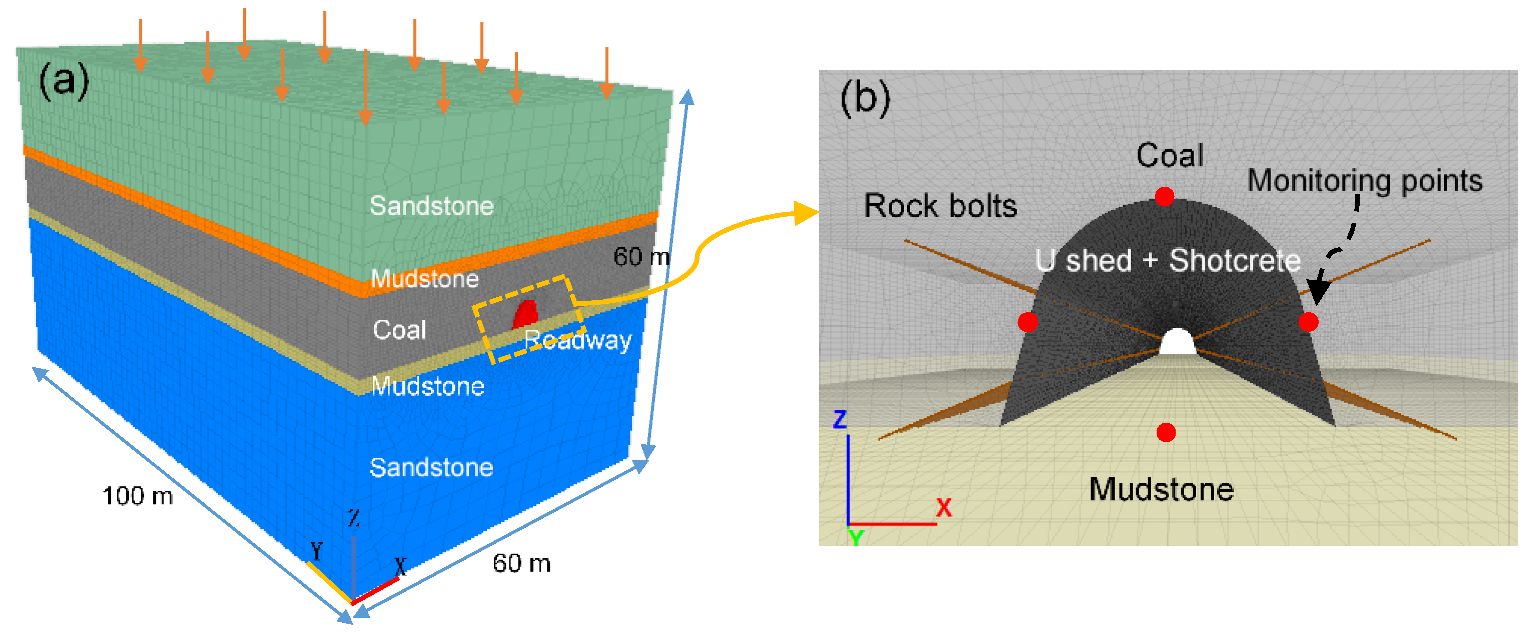
2.1. The Geological Setting
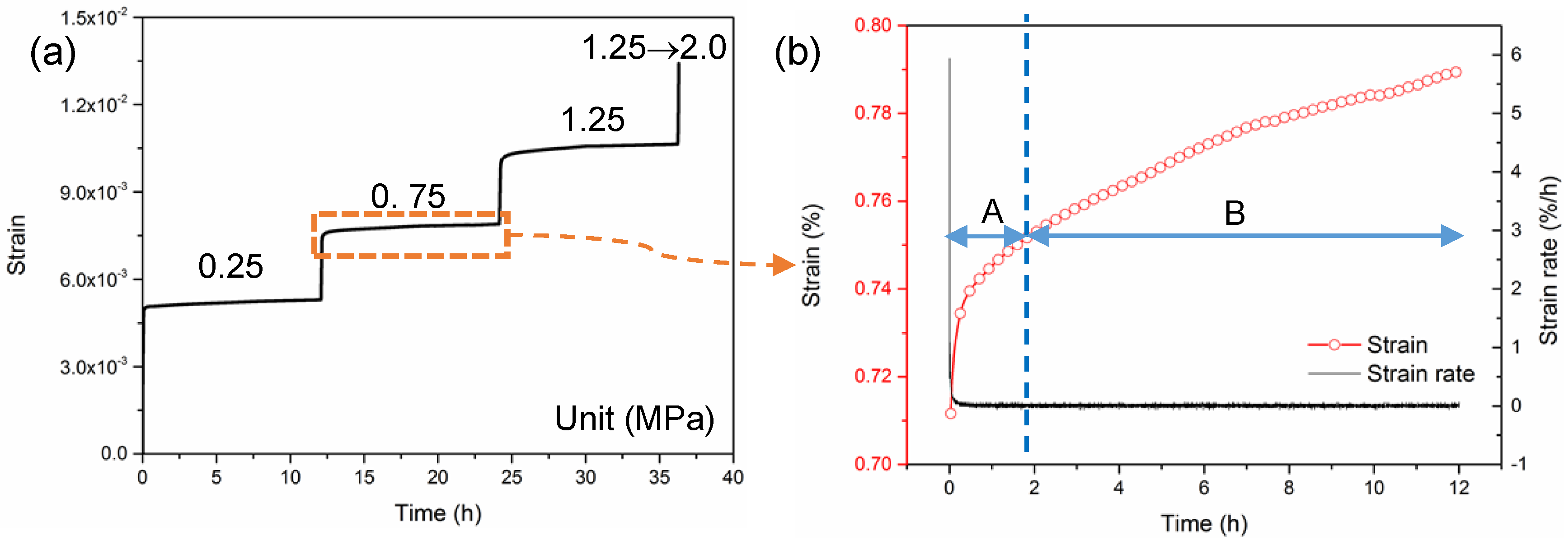
2.2. Creep Behavior of Soft Coal Specimen
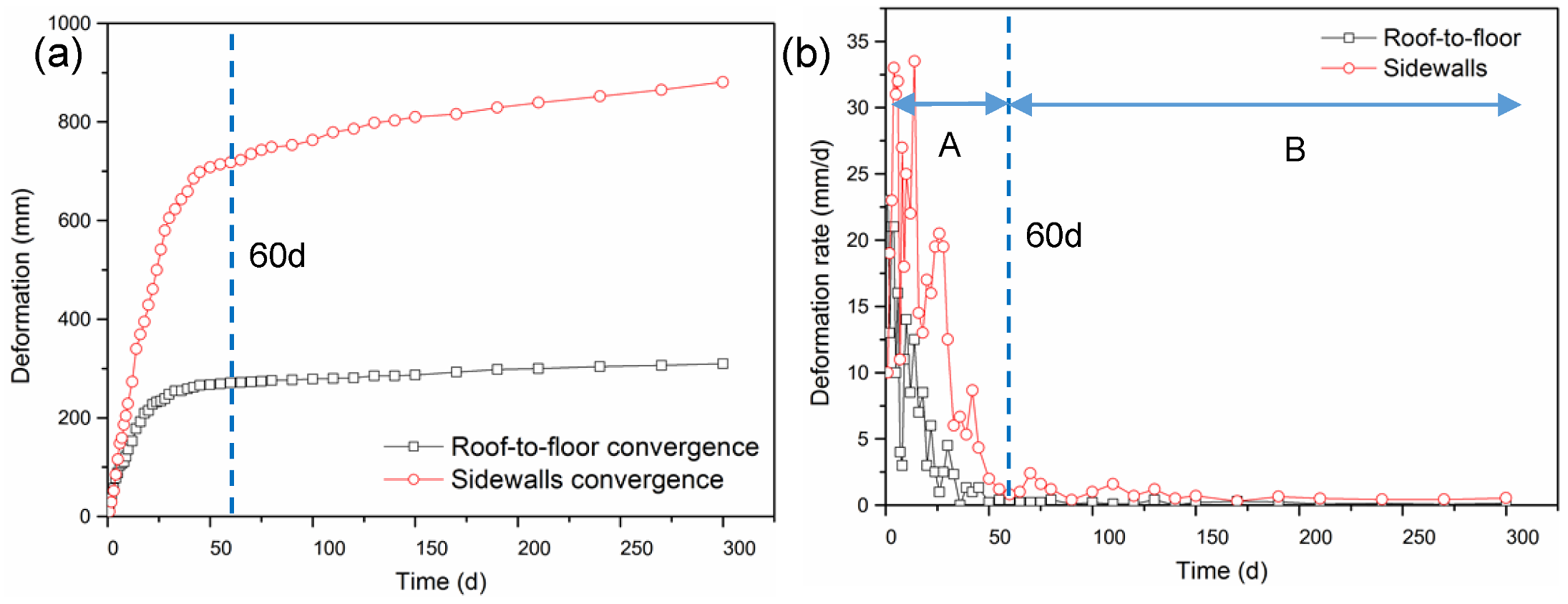
2.3. Field Observation of Roadway Deformation
3. Time-Dependent Numerical Modeling and its Validation
3.1. The Numerical Model of the Roadway by Conventional Support
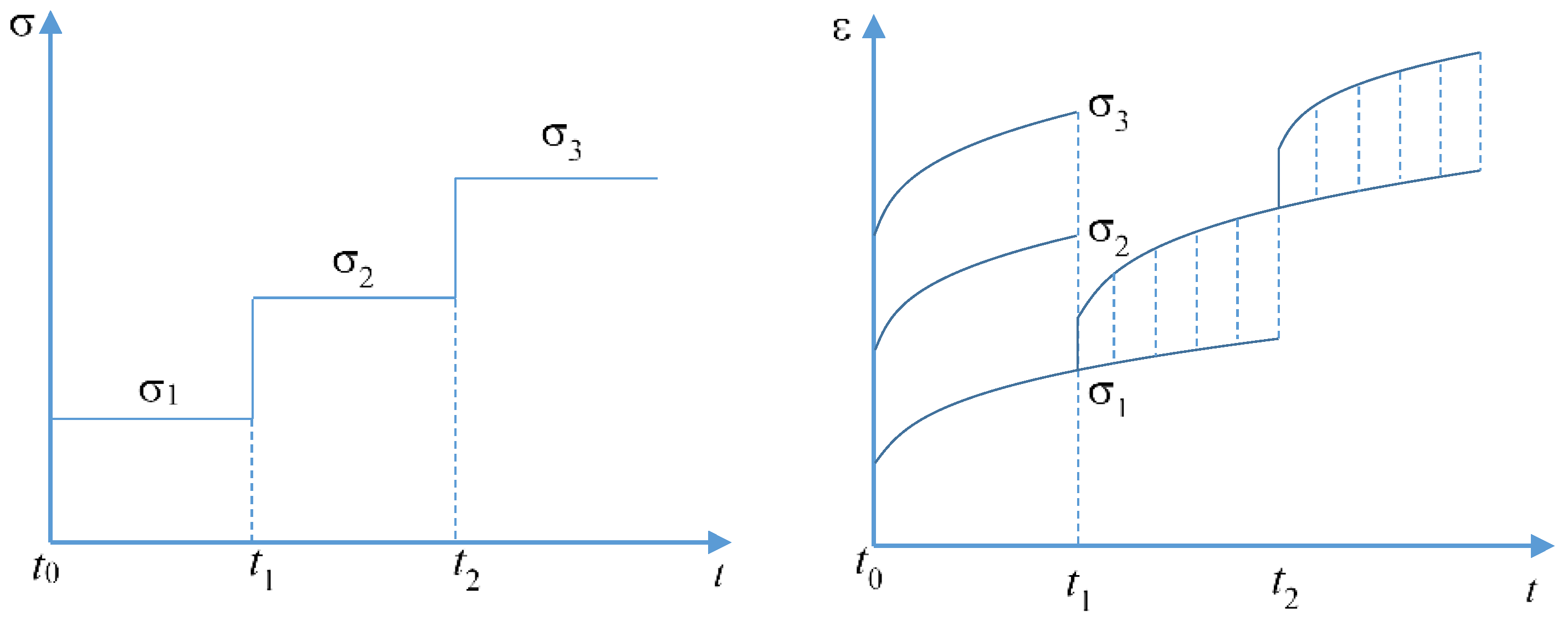
3.2. Burger–Creep Viscoplastic Model (CVISC)
3.3. Properties of the Rock Mass
3.4. The Critical Time-Stepping
3.5. Validation of the Established Model
4. The Numerical Model of the Roadway by JG Support
4.1. The Field Tests of JG
4.2. Mechanical Parameters of Coalcrete
4.3. Numerical Modeling of JG Support
5. Stability Analysis of Rheological Roadway by JG support
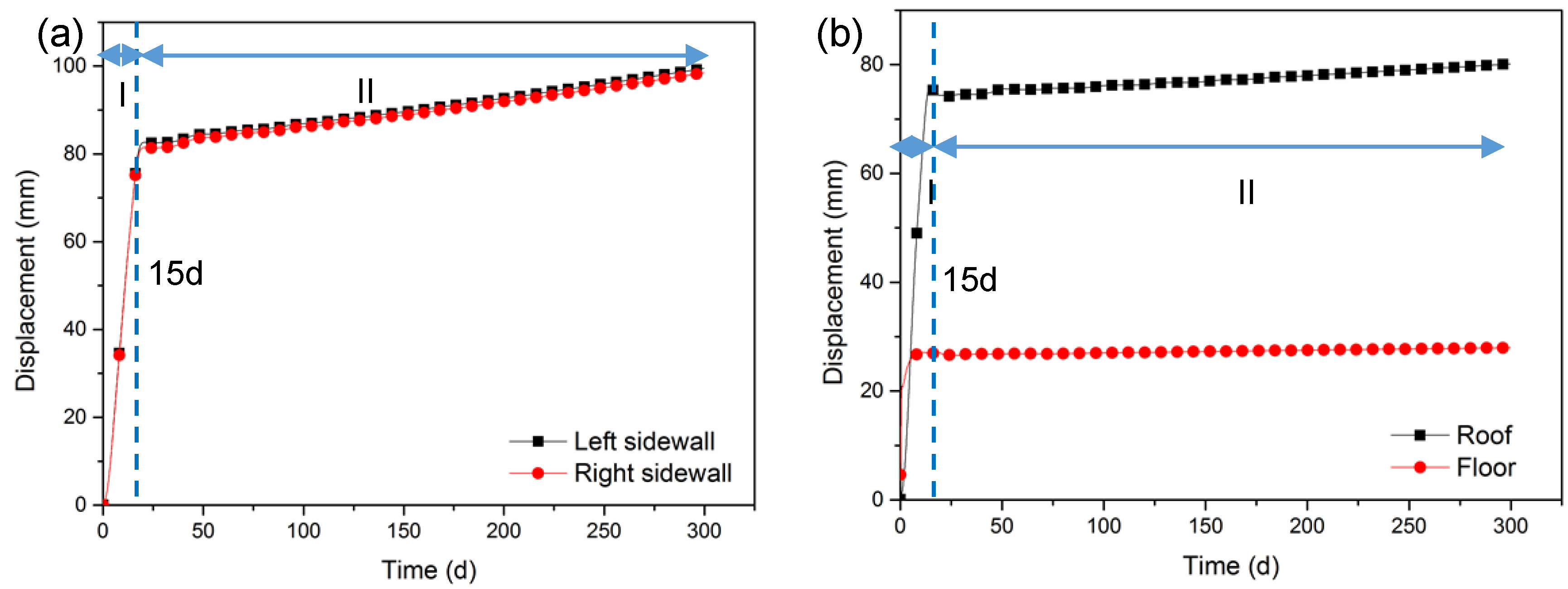
5.1. The Deformation of the Roadway by JG Support
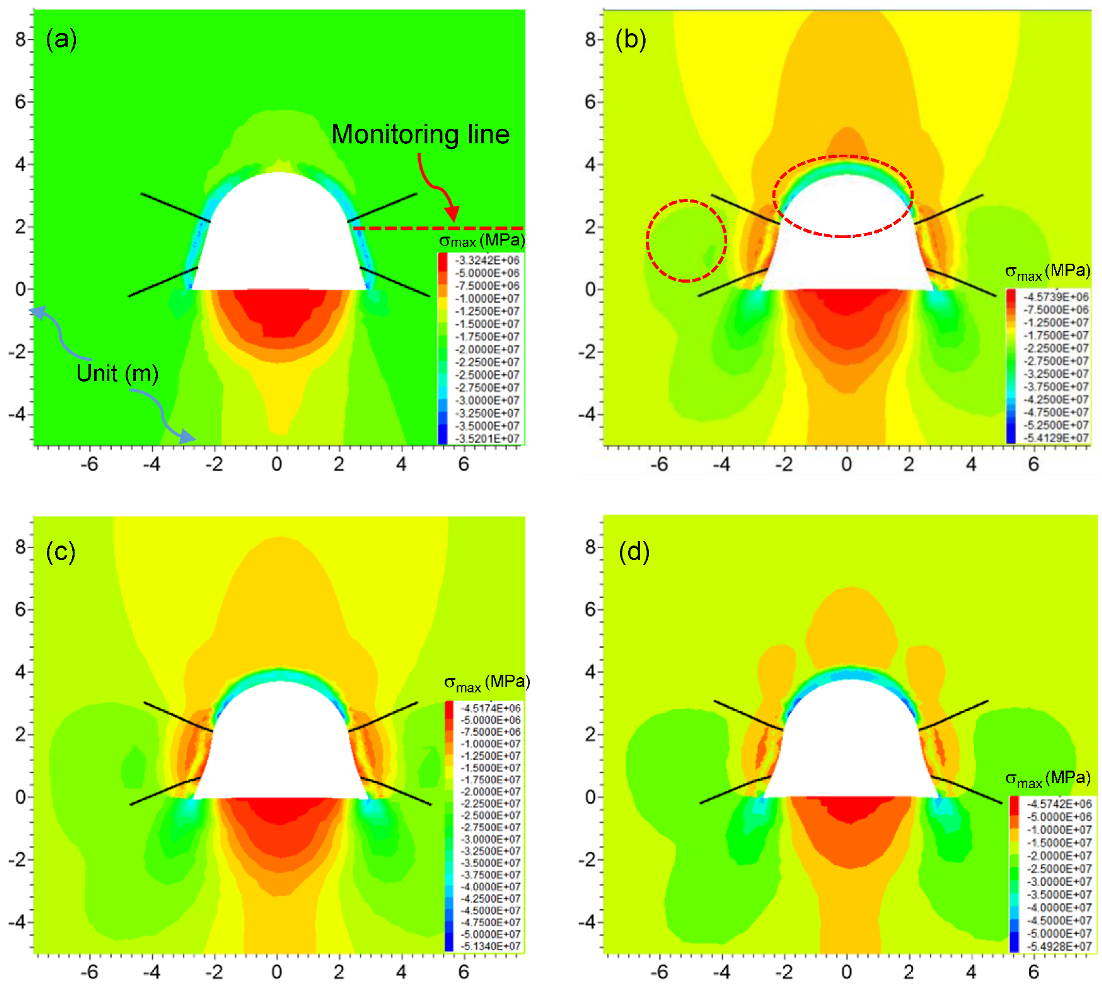
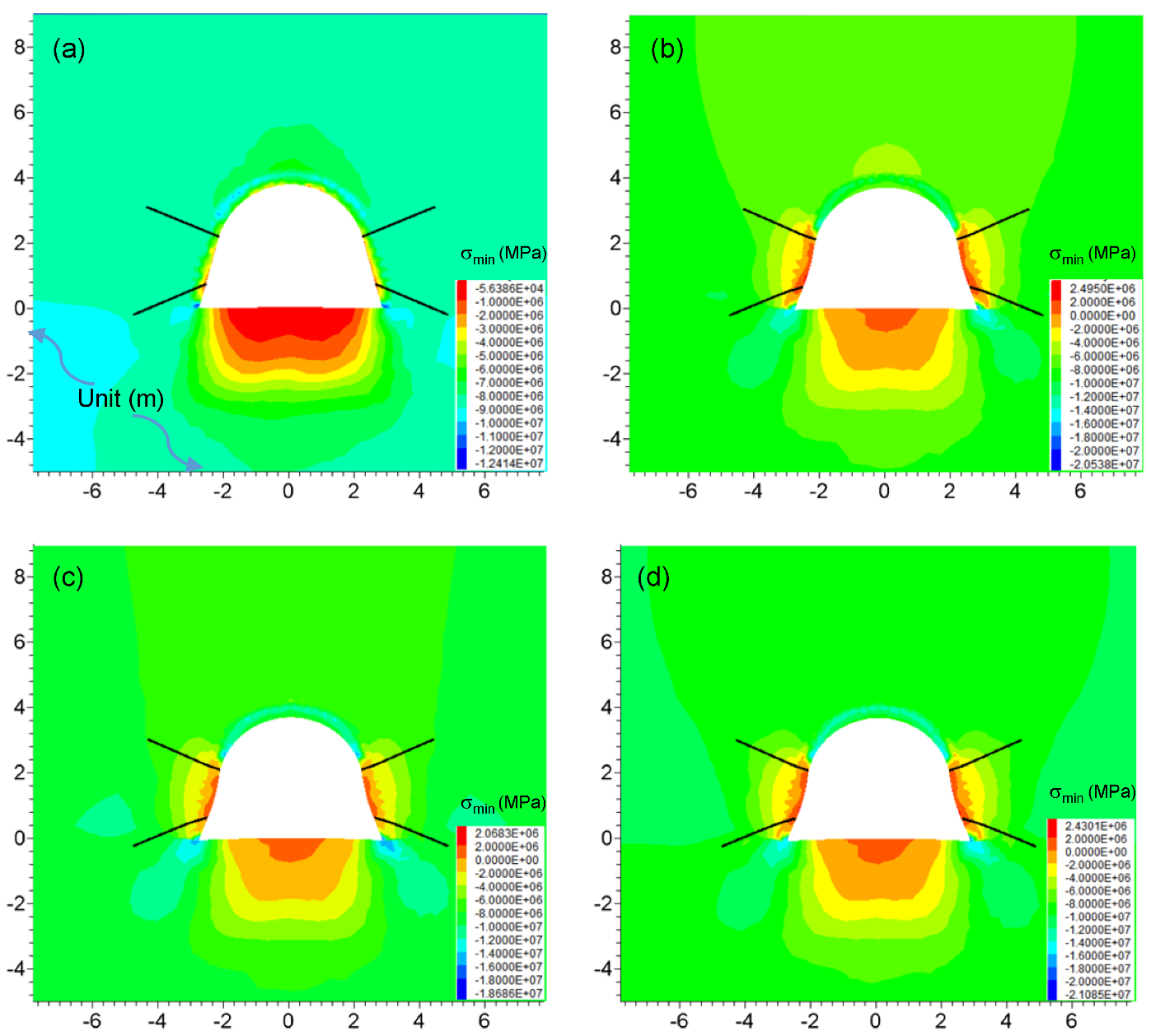
5.2. The Stress States around the Roadway by JG Support
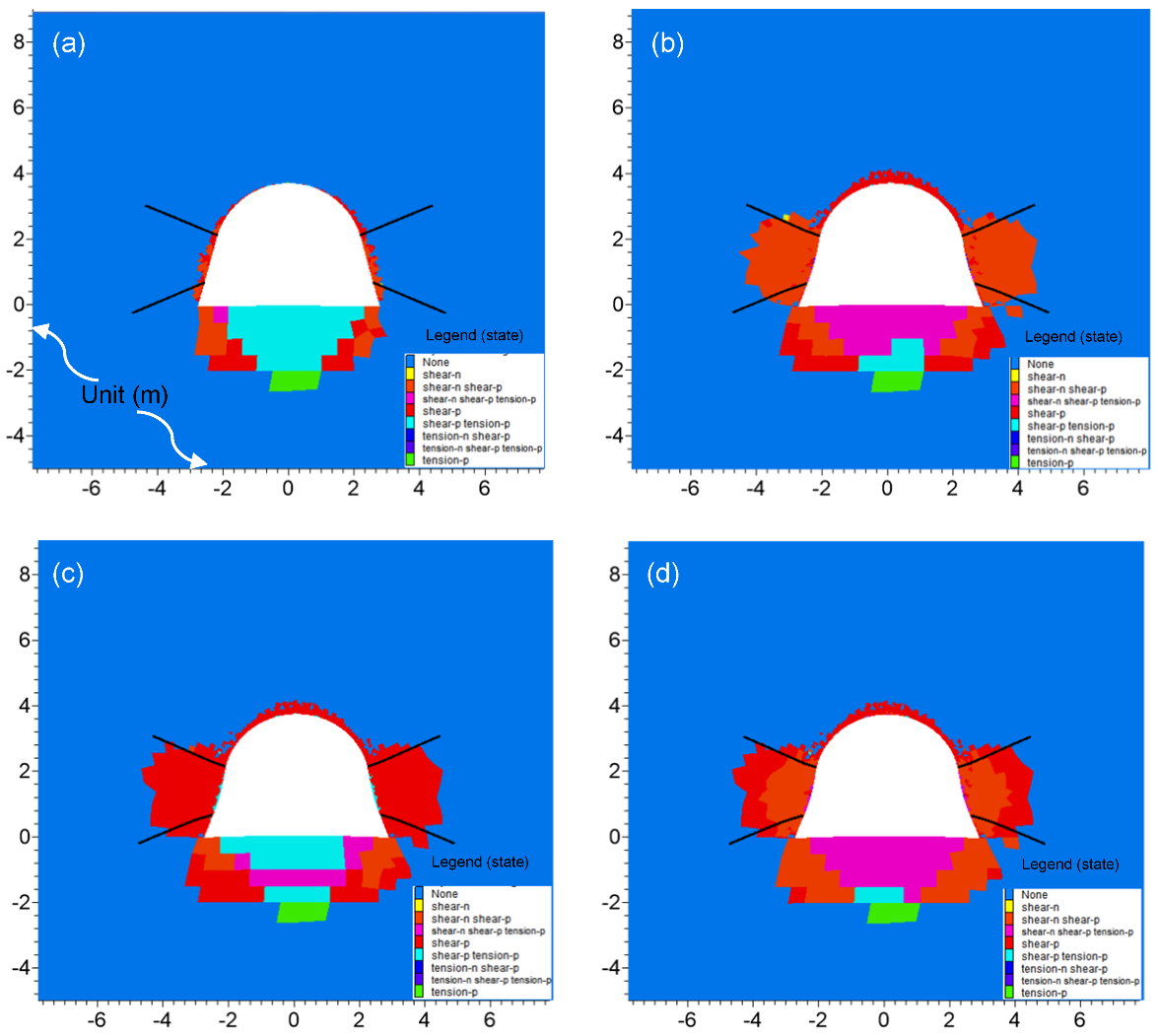
5.3. The Development of Plastic Zones of the Roadway by JG Support
6. Conclusions
- According to the geological setting, the soft coal mass had a negative effect on the roadway stability. The creep test results showed that the soft coal specimen exhibited a two-stage creep behavior, i.e., decelerating creep and uniform creep.
- Based on the in-situ measurements, the roadway deformation also demonstrated two-stage rheological behavior. A large rheological deformation with a large deformation rate occurred, and the conventional support system could not control the stability of the roadway.
- A CVISC model was adopted in a 3D numerical model to simulate the rheological properties of the roadway. Based on the field measurement, the model was validated, confirming that the input parameters and the time-dependent model were reasonable and accurate.
- As per JG tests in the field and laboratory, a numerical model of the roadway with JG support was proposed, and its control effect on roadway stability was systematically analyzed. The results showed that the JG support could efficiently reduce roadway deformation, optimize the stress conditions and reduce the extent of the plastic zone. The rheological properties of soft coal roadways were constrained, and the long-term stability was guaranteed by JG support.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| JG | Jet Grouting |
| σ | Constant loading |
| t | Time |
| ε | Strain |
| ηM | Maxwell viscosity |
| GM | Maxwell shear modulus |
| ηK | Kelvin viscosity |
| GK | Kelvin shear modulus |
| CVISC | Burger-creep visco-plastic model |
| M-C | Mohr-Coulomb |
| RMR | Rock mass rating |
| GSI | Geological strength index |
| mb | Rock mass constants |
| σcm | Uniaxial compressive strength of rock mass |
| σt | Tensile strength |
| D | The disturbance factor |
| c | Cohesion |
| ϕ | Friction angle |
| γ | Unit weight of the rock mass |
| ν | Poisson’s ratio |
| Ei | Intact rock modulus |
References
- Zhang, Z.; Shimada, H.; Sasaoka, T.; Hamanaka, A. Stability control of retained goaf-side gateroad under different roof conditions in deep underground y type longwall mining. Sustainability 2017, 9, 1671. [Google Scholar] [CrossRef]
- Wagner, H. Deep Mining: A Rock Engineering Challenge. Rock Mech. Rock Eng. 2019, 52, 1417–1446. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, C.; Zhou, H.; Liu, N.; Zhang, Y.; Azhar, M.U.; Dai, F. The long-term safety of a deeply buried soft rock tunnel lining under inside-to-outside seepage conditions. Tunn. Undergr. Sp. Technol. 2017, 67, 132–146. [Google Scholar] [CrossRef]
- Szurgacz, D.; Brodny, J. Tests of Geometry of the Powered Roof Support Section. Energies 2019, 12, 3945. [Google Scholar] [CrossRef]
- Szurgacz, D.; Brodny, J. Analysis of the Influence of Dynamic Load on the Work Parameters of a Powered Roof Support’s Hydraulic Leg. Sustainability 2019, 11, 2570. [Google Scholar] [CrossRef]
- Xie, H.; Gao, M.; Zhang, R.; Peng, G.; Wang, W.; Li, A. Study on the Mechanical Properties and Mechanical Response of Coal Mining at 1000 m or Deeper. Rock Mech. Rock Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Sainoki, A.; Tabata, S.; Mitri, H.S.; Fukuda, D.; Kodama, J. ichi Time-dependent tunnel deformations in homogeneous and heterogeneous weak rock formations. Comput. Geotech. 2017, 92, 186–200. [Google Scholar] [CrossRef]
- Lee, C.L.; Shou, K.J.; Chen, S.S.; Zhou, W.C. Numerical analysis of tunneling in slates with anisotropic time-dependent behavior. Tunn. Undergr. Sp. Technol. 2019, 84, 281–294. [Google Scholar] [CrossRef]
- Yang, S.Q.; Chen, M.; Jing, H.W.; Chen, K.F.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; Song, L.; Wang, X.Z.; Coffi Adoko, A. Improvement of the U-shaped steel sets for supporting the roadways in loose thick coal seam. Int. J. Rock Mech. Min. Sci. 2013, 60, 19–25. [Google Scholar] [CrossRef]
- Kang, H.P.; Lin, J.; Fan, M.J. Investigation on support pattern of a coal mine roadway within soft rocks—A case study. Int. J. Coal Geol. 2015, 140, 31–40. [Google Scholar] [CrossRef]
- Yu, W.; Wang, W.; Chen, X.; Du, S. Field investigations of high stress soft surrounding rocks and deformation control. J. Rock Mech. Geotech. Eng. 2015, 7, 421–433. [Google Scholar] [CrossRef]
- Li, S.C.; Wang, H.T.; Wang, Q.; Jiang, B.; Wang, F.Q.; Guo, N.B.; Liu, W.J.; Ren, Y.X. Failure mechanism of bolting support and high-strength bolt-grouting technology for deep and soft surrounding rock with high stress. J. Cent. South. Univ. 2016, 23, 440–448. [Google Scholar] [CrossRef]
- Ghorbani, M.; Sharifzadeh, M. Long term stability assessment of Siah Bisheh powerhouse cavern based on displacement back analysis method. Tunn. Undergr. Sp. Technol. 2009, 24, 574–583. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Tarifard, A.; Moridi, M.A. Time-dependent behavior of tunnel lining in weak rock mass based on displacement back analysis method. Tunn. Undergr. Sp. Technol. 2013, 38, 348–356. [Google Scholar] [CrossRef]
- Nadimi, S.; Shahriar, K. Experimental creep tests and prediction of long-term creep behavior of grouting material. Arab. J. Geosci. 2014, 7, 3251–3257. [Google Scholar] [CrossRef]
- Nadimi, S.; Shahriar, K.; Sharifzadeh, M.; Moarefvand, P. Triaxial creep tests and back analysis of time-dependent behavior of Siah Bisheh cavern by 3-Dimensional Distinct Element Method. Tunn. Undergr. Sp. Technol. 2011, 26, 155–162. [Google Scholar] [CrossRef]
- Mishra, B.; Verma, P. Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks. Int. J. Coal Geol. 2015, 137, 55–65. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Li, Z.; Sun, H. Experimental Study on the Shear Behavior of Regular Sandstone Joints Filled with Cement Grout. Rock Mech. Rock Eng. 2016, 50, 1321–1336. [Google Scholar] [CrossRef]
- Littlejohn, S. The development of practice in permeation and compensation grouting: A historical review (1802–2002): Part 1 permeation grouting. In Proceedings of the Third International Conference on Grouting and Ground Treatment, New Orleans, LA, USA, 10–12 February 2003; pp. 50–99. [Google Scholar]
- Kang, H. Support technologies for deep and complex roadways in underground coal mines: A review. Int. J. Coal Sci. Technol. 2014, 1, 261–277. [Google Scholar] [CrossRef]
- Tinoco, J.; Gomes Correia, A.; Cortez, P. Application of data mining techniques in the estimation of the uniaxial compressive strength of jet grouting columns over time. Constr. Build. Mater. 2011, 25, 1257–1262. [Google Scholar] [CrossRef]
- Ehsanzadeh, B.; Ahangari, K. A Novel Approach in Estimation of the Soilcrete Column’s Diameter and Optimization of the High Pressure Jet Grouting Using Adaptive Neuro Fuzzy Inference System (ANFIS). Open J. Geol. 2014, 4, 386–398. [Google Scholar] [CrossRef]
- Croce, P.; Flora, A.; Modoni, G. Jet Grouting: Technology, Design and Control; CRC Press: Boca Raton, FL, USA, 2014; ISBN 041552640X. [Google Scholar]
- Asteris, P.G.; Roussis, P.C.; Douvika, M.G. Feed-forward neural network prediction of the mechanical properties of sandcrete materials. Sensors 2017, 17, 1344. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhang, J.; Li, G.; Wang, Y.; Sun, J.; Jiang, C. Optimized neural network using beetle antennae search for predicting the unconfined compressive strength of jet grouting coalcretes. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 801–813. [Google Scholar] [CrossRef]
- Basarir, H.; Sun, Y.; Li, G. Gateway stability analysis by global-local modeling approach. Int. J. Rock Mech. Min. Sci. 2019, 113, 31–40. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabashi, Y.; Huang, H. A new rheological model and its application in mountain tunnelling. Tunn. Undergr. Sp. Technol. 2008, 23, 292–299. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabashi, Y. Rheological parameter estimation for the prediction of long-term deformations in conventional tunnelling. Tunn. Undergr. Sp. Technol. 2009, 24, 250–259. [Google Scholar] [CrossRef]
- Hoek, E.; Carter, T.G.; Diederichs, M.S. Quantification of the geological strength index chart. In Proceedings of the 47th US rock mechanics/geomechanics symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Hoek, E.; Marinos, P.G.; Marinos, V.P. Characterisation and engineering properties of tectonically undisturbed but lithologically varied sedimentary rock masses. Int. J. Rock Mech. Min. Sci. 2005, 42, 277–285. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Li, G.; Ma, G.; Huang, Y.; Sun, J.; Wang, Y.; Nener, B. Determination of Young’s modulus of jet grouted coalcretes using an intelligent model. Eng. Geol. 2019, 252, 43–53. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Experimental and numerical investigation on a novel support system for controlling roadway deformation in underground coal mines. Energy Sci. Eng. 2019. [Google Scholar] [CrossRef] [Green Version]


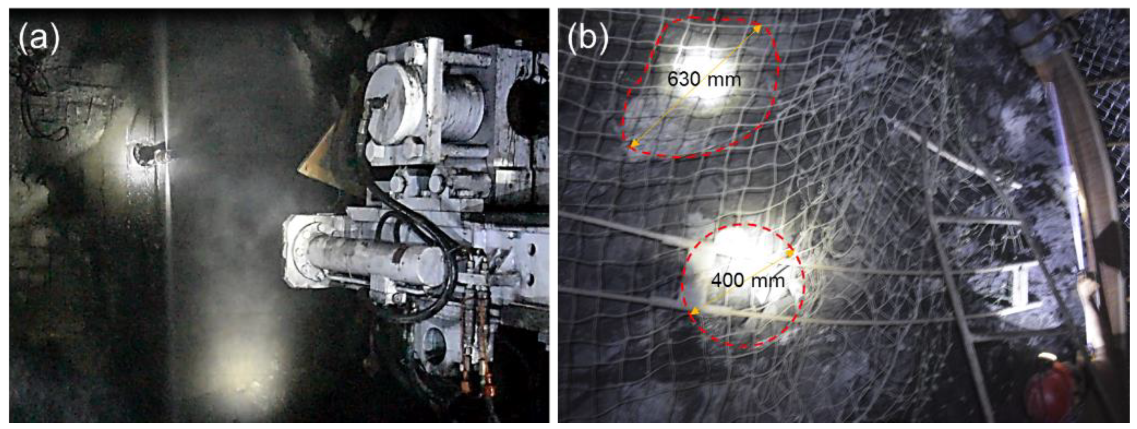

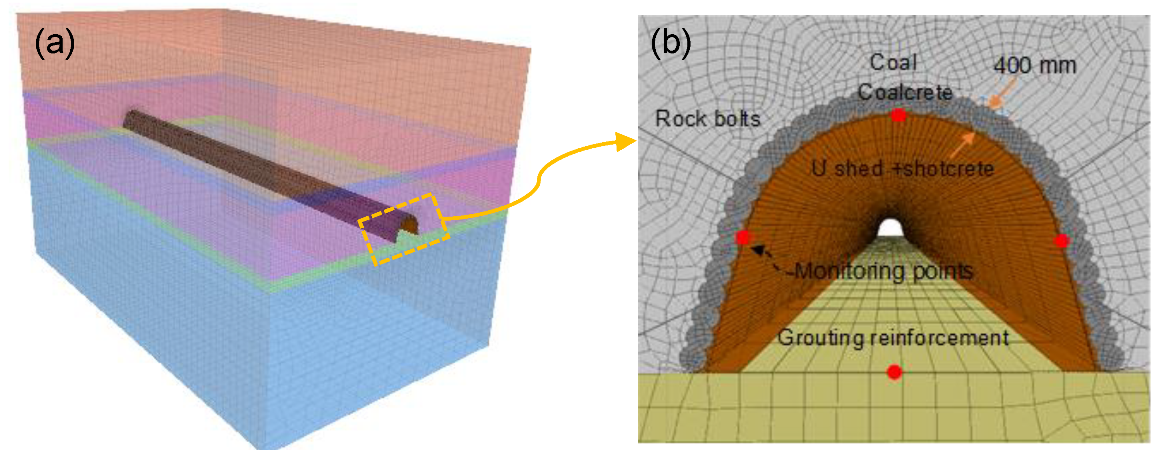
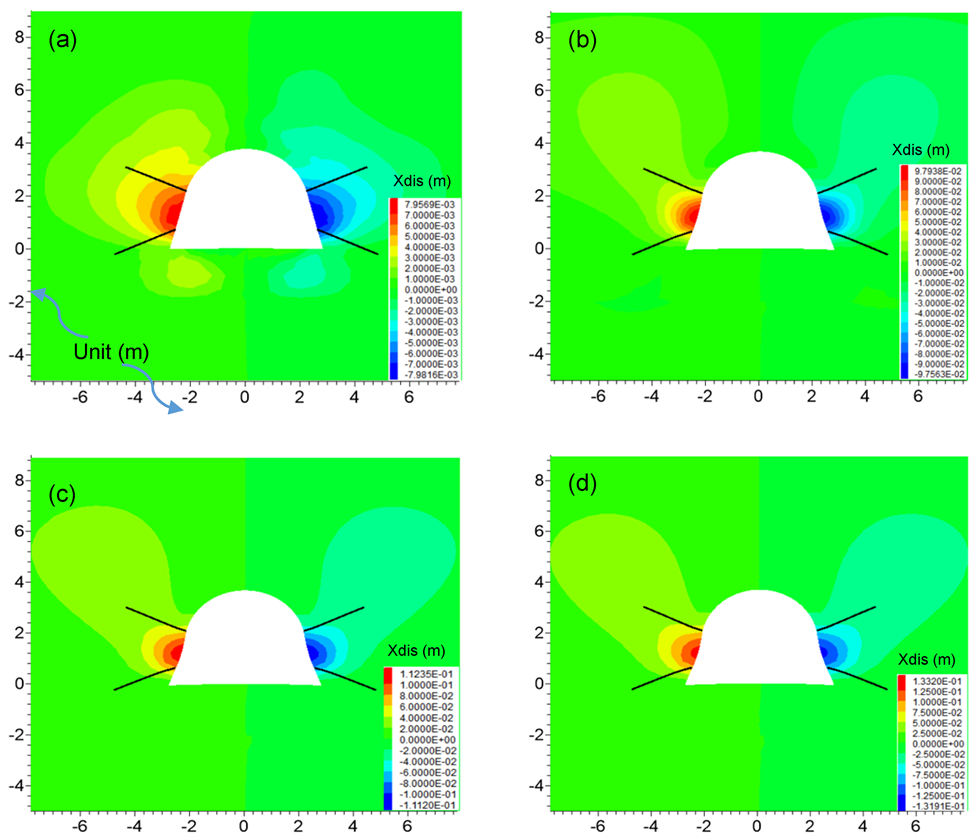
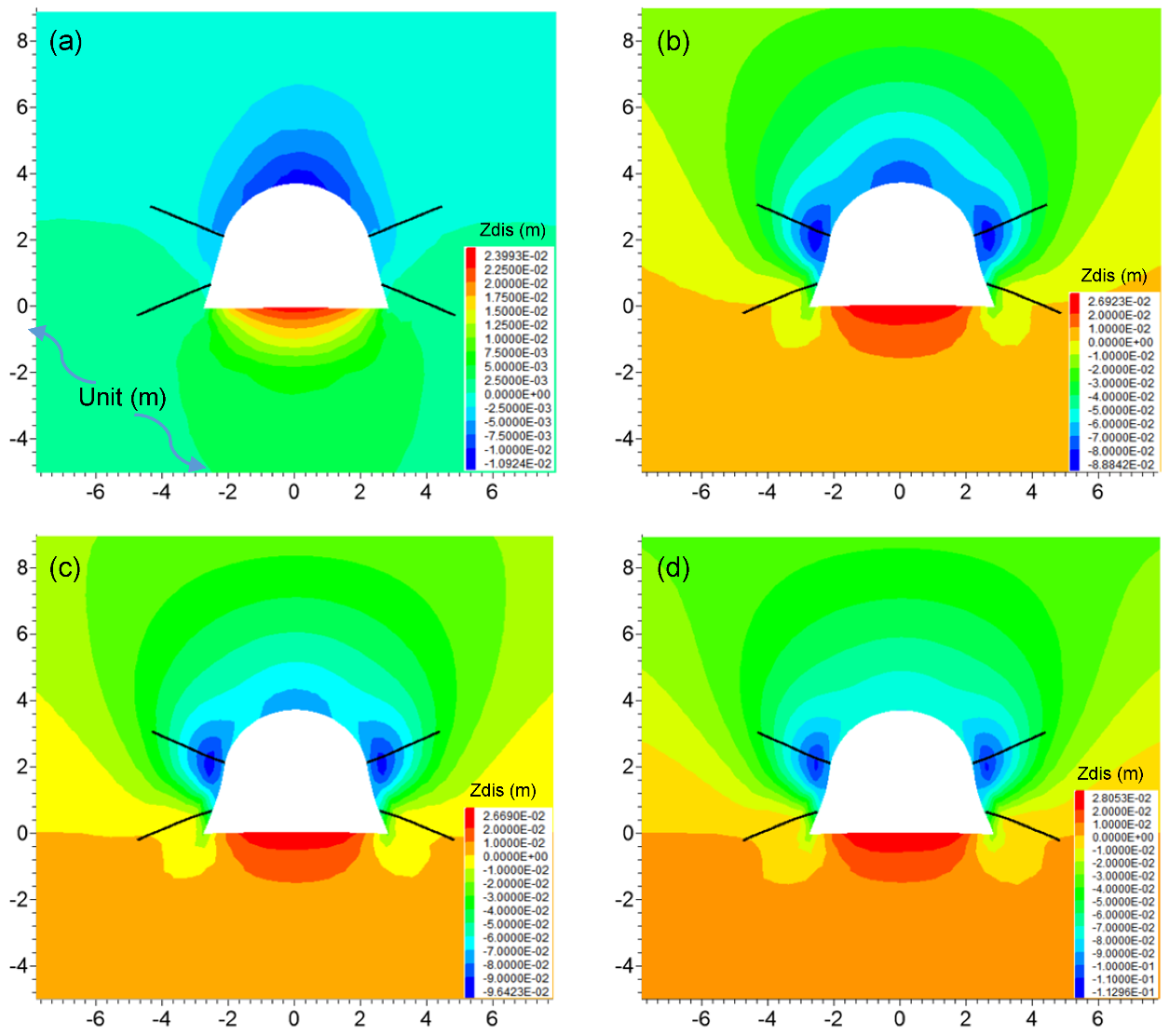

| Parameters, Unit | Rock Bolt | U-shaped Shed | Shotcrete |
|---|---|---|---|
| Elastic modulus, GPa | 200 | 200 | 30 |
| Poisson’s ratio | 0.3 | 0.25 | 0.15 |
| Diameter/thickness, mm | 22 | 15 | 100 |
| Unit weight, kN/m3 | - | - | 24 |
| Length, mm | 2400 | - | - |
| Pre-tensioning, kN | 80 | - | - |
| ηM (MPa.d) | GM (MPa) | ηK (MPa.d) | GK (MPa) |
|---|---|---|---|
| 1.41 × 105 | 1.36 × 102 | 2.54 × 107 | 2.21 × 102 |
| Rock Unit | Rock Material Properties | Rock Mass Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mi | Density, kg/m3 | σci, MPa | Poisson’s Ratio, ν | Ei, GPa | RMR | GSI | c, MPa | ϕ, ° | σt, MPa | Emass, GPa | |
| Sandstone | 9 | 2690 | 85.8 | 0.22 | 18.6 | 72 | 67 | 3.45 | 42 | 0.79 | 12.5 |
| Mudstone | 9 | 2700 | 38.5 | 0.29 | 3.61 | 40 | 35 | 1.24 | 27 | 0.30 | 0.4 |
| Coal | 30 | 1420 | 7.0 | 0.39 | 5.0 | 35 | 30 | 0.98 | 24 | 0.15 | 0.50 |
| Mechanical Parameters | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Values | 3.71 | 30.2 | 4.56 | 2.64 | 0.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Li, G.; Zhang, J.; Qian, D. Stability Control for the Rheological Roadway by a Novel High-Efficiency Jet Grouting Technique in Deep Underground Coal Mines. Sustainability 2019, 11, 6494. https://doi.org/10.3390/su11226494
Sun Y, Li G, Zhang J, Qian D. Stability Control for the Rheological Roadway by a Novel High-Efficiency Jet Grouting Technique in Deep Underground Coal Mines. Sustainability. 2019; 11(22):6494. https://doi.org/10.3390/su11226494
Chicago/Turabian StyleSun, Yuantian, Guichen Li, Junfei Zhang, and Deyu Qian. 2019. "Stability Control for the Rheological Roadway by a Novel High-Efficiency Jet Grouting Technique in Deep Underground Coal Mines" Sustainability 11, no. 22: 6494. https://doi.org/10.3390/su11226494





