Drilling operations are the backbone of the oil and gas industry. They can be very expensive and therefore, they require several economical and safety concerns. Improving oilfield operations requires active monitoring drilling performance to insure minimize drilling costs. Much effort has been excelled to avoid drilling difficulties and enhance the drilling process. Typically, drilling cost is directly related to drilling speed. Therefore, achieving an adequate rate of penetration (ROP) ensures optimal drilling process and accordingly a reduced drilling cost. Thus, various parameters that affect ROP should be optimally controlled.
Rate of penetration (ROP) means how fast the drilling bit is drilling through the formations. It captures the speed or the movement of the drilling bit when it breaks the rocks, and it is identified in field units as ft/h [
1]. Notoriously, in the oil and gas industry, most of the well cost is taken by the drilling operations. Therefore, it is very crucial to drill carefully and improve drilling processes. Nevertheless, it is challenging to predict the influence of every single parameter because most of the drilling parameters depend on each other and altering an individual parameter will have an impact on the rest. Moreover, ROP assists the drilling engineer to define the best drilling parameters to accomplish the lowest cost per foot [
2]. Whereas, many challenges can occur during drilling operations under high ROP such as stuck pipe and poor hole cleaning. Therefore, it is important to select the optimal drilling parameters for ROP that cause no drilling problems [
3].
Many parameters affect ROP such as formation properties, drilling fluid properties, hydraulic and mechanical parameters, and rig efficiency [
4]. Hossain and Al-Majed [
5] categorized these parameters into two groups: environmental and controllable parameters. Environmental factors are those, which are created by nature or drilling conditions that are difficult to change, for example, mud properties are usually difficult to change because of some drilling objectives, which attained only by requiring a specific volume of the mud such as overbalance drilling to prevent the flow of formation fluid. On the contrast, controllable factors are those, which can be altered such as rotary speed, weight on bit and hydraulic parameters.
Many methods propose relationships between different parameters and ROP. Maurer [
6] proposed a theoretical model for roller cone bits based on rotary speed, weight on bit, rock strength, and bit size. He developed his equation based on observation such as the volume of cuttings that created as shown in Equation (1).
where k is drillability constant, N is rotary speed (RPM), W is weight on bit (Klb
f), d
b is the diameter of the bit (in), and S is rock compressive strength (kPa)
Bourgoyne and Young’s [
8] introduced one of the most significant models of predicted ROP using multiple regression analysis of drilling parameters using Equation (3).
where TVD is the true vertical depth (ft), EMW
pore is pore equivalent mud weight (pcf), ECD is the equivalent circulation density (pcf, bound per cubic feet), F
j is impact factor (lb), N is rotation per minute (RPM), W is the bit weight (K
lbf), d
b is the diameter of the bit (in),
is the formation strength effects,
and
are the compaction effects,
is the overbalance effects,
and
are the rotary speed and bit weight effects,
is the tooth wear effects, and
is the bit hydraulic effects. The constants
to
be found for each formation based on local legacy drilling data.
Hareland [
10] modified Warren model by adding a dimensional analysis containing drilling fluid properties and modified impact force and bit wear as shown in Equation (5).
where W
c is wear coefficient, A
abr is relative abrasiveness,
chip hold down function (lb
f),
is mud viscosity (cP),
is fluid specific gravity, F
jm is modified impact force (lb
f), and a, b, c, d are constants.
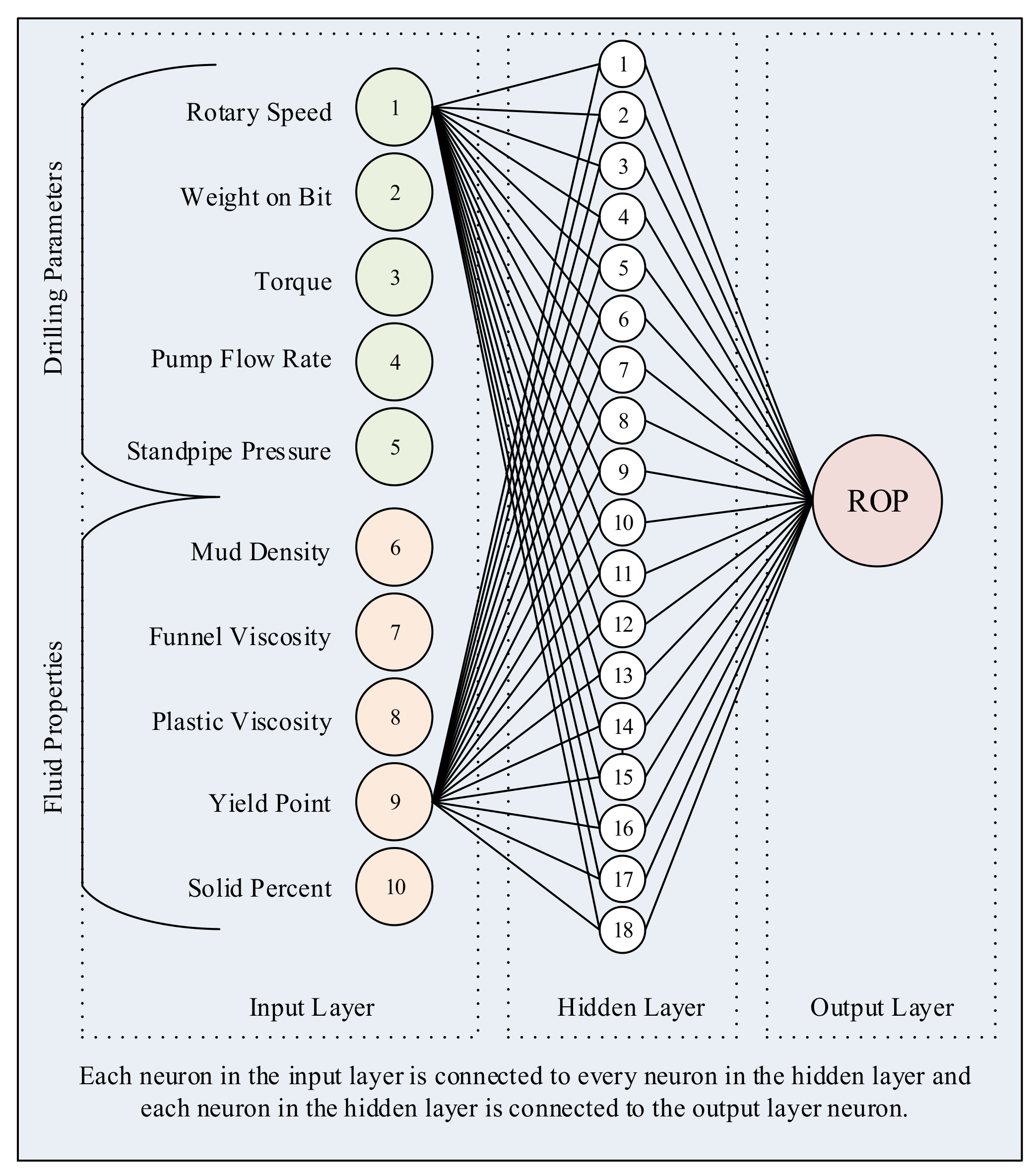
The aim of this study is to introduce a reliable artificial neural network (ANN) predictive model for ROP using drilling data and drilling-mud properties. The outcome attained from the ANN was compared with ROP models to illustrate the model accuracy based on the highest R and the minimum average absolute percentage error (AAPE).
1.3. Application of AI in ROP Prediction
Many mathematical models have been introduced to predict the rate of penetration from different parameters. Nevertheless, no single relationship satisfactory predicts ROP. Mostly because of the complex effect of the parameters describing the ROP and additionally due to incomplete understanding of the relationships between the ROP and some of these parameters. Therefore, many researchers tried to use AI to attain a reliable ROP predictive model.
Bilgesu [
16] used the ANN tool to model ROP and the bit wear for various types of formation and operating parameters. He used 500 dataset records of nine input parameters including RPM, WOB, torque, Q, rotating time, tooth wear, bearing wear, formation abrasiveness and formation drillability. He trained his model using 90% of the data and the remaining 10% for testing. He achieved a correlation coefficient (R) that ranged from (0.902) to (0.982).
Moran [
17] used ANN to study legacy-drilling data and improved the prediction of ROP. He used six input parameters including RPM, WOB, MW, rock strength, abrasion and type of the rock. He achieved a coefficient of determination of R
2 = 0.8 between ANN-predicted ROP and legacy-data ROP.
Jahanbakhshi [
18] used ANN to predict ROP based on offset well data. He used large number of input parameters, 21, which include rotary speed, weight on bit, pump pressure, equivalent circulating density, mud type, yield point, plastic viscosity, mud pH, solid percent, 10 minute gel strength, 10 s gel strength, bit wear, bit type, bit hydraulic power, density of rock, porosity, permeability, formation drillability, differential pressure, hole depth and hole size. He arranged 70% of the data for model training, 15% for model validation and 15% for model testing. He achieved a correlation coefficient of R
2 = 0.916 and mean square error of MSE = 0.015 for the testing data.
Arabjamaloei [
19] used ANN to build a predictive model for ROP. He used 330 data records of ten input parameters including rotary speed, weight on bit, flow rate, mud density, viscosity, depth, bit size, bit hours, bit efficiency and annulus pressure. He achieved a coefficient of determination of R
2 = 0.9402 in model training and R
2 = 0.7401 in model testing.
Bataee [
20] also used ANN to predict ROP and improve drilling parameters. He used a larger dataset, 1810 data records, of five input parameters including RPM, WOB, MW, depth, and bit diameter. He organized data as 60% for model training, 20% for model validation and 20% for model testing.
Amar [
21] used ANN independently to predict ROP and he compared his models with traditional regression. He used seven input parameters including rotary speed, weight on bit, equivalent circulation density, tooth wear, depth, pore gradient and Reynolds number. He achieved an absolute percent relative error (APRE) of 9.6% for ANN.
Xian [
22] compared the results of predicting ROP using ANN and extreme learning machine (ELM). He used a huge dataset of 5000 data records comprising eleven input parameters including rotary speed, weight on bit, pump pressure, mud density, mud viscosity, formation abrasiveness, formation drillability, unconfined compressive strength, bit wear, bit type, and bit size. He arranged 75% of the dataset for model training and 25% for model testing. His ANN model achieved a coefficient of determination of R
2 = 0.91 in model training and R
2 = 0.90 in model testing and a root mean square error of RMSE 1.51 and 3.56 in model training and testing respectively. By using ELM, he achieved a coefficient of determination of
for training and
for testing and a root mean square error of (
) for training and (
) for testing.
Jiang [
23] employed ANN, based on ant colony optimization (ACO), to optimize ROP. He used five input parameters including RPM, WOB, Q, depth, and gamma-ray. He achieved an accuracy of (
).
Manshad [
24] developed a multi-layer ANN to predict ROP. He used a genetic algorithm to optimize the input parameter. He used a dataset of 332 records with ten parameters including rotary speed, weight on bit, flow rate, plastic viscosity, flow area, pump pressure, depth, bit size, drilling interval, and unconfined compressive strength. He trained his mode using 70% of the data and the remaining 30% was divided into 15% validation and 15% testing. His model achieved a correlation coefficient of (
) for training and (
) for testing.
Elkatatny [
4] developed an ANN model to estimate the ROP using a number of mud properties and the mechanical drilling surface parameters. He used a dataset of 3333 records of seven parameters including RPM, WOB, Q, SPP, torque, drilling fluid density and plastic viscosity. He trained his model using 70% of the data and the remaining 30% for testing. His model achieved an accuracy of (
) for training and (
) for testing and AAPE = 3.98 for training and AAPE = 5.6 for testing.
Ahmed [
25] used three techniques of AI to predict ROP using the parameters of hydro-mechanical specific energy. The AI methods are support vector regression (SVR), extreme learning machine (ELM) and artificial neural network (ANN). A dataset of 8869 points from two wells was used in the prediction. The input parameters were depth, flow rate, weight on bit, rotation per minute, torque, standpipe pressure, mud weight, and bit size. The data was divided into 70% training, 15% validation and 15% testing. In well A, they got an RMSE of 14.4 for training and 23.4 for testing using SVR, 27.3 for training and 27.6 for testing using ANN and 23.2 for training and 27.1 for testing using ELM. The correlation coefficients in well A were 0.94 for training and 0.81 for testing using SVR, 0.74 for training and 0.72 for testing using ANN and 0.82 for training and 0.71 for testing using ELM. The results in well B were closed to that in well A.
Bodaghi [
26] applied ANN and support vector regression (SVR) with different algorithms to estimate ROP. 193 datasets were collected from 13 wells including pump rate, tooth wear, mud weight (MW), weight on bit (WOB), pump pressure, well deviation, mud viscosity, lithology, bit size, rotary speed, bit tooth wear, and interval drilled. The data was divided into testing (154 points) and testing (39 points). They achieved high accuracy in terms of correlation coefficient (R) and absolute average relative error (AARE). ANN has average R of 0.95 and AARE of 0.22. SVR with the best algorithm (cuckoo search algorithm (CS)) gave a results of R = 0.96 and AARE = 0.078.
Most of the previous used AI techniques did not select the most important parameters that affect the rate of penetration. Some of them used unrelated parameters that do not have any relation to the ROP. Moreover, most of them did not compare their results with famous ROP models and all of them is a black box that does not provide the model equation to predict the ROP. Also, all of them did not predict the ROP in shale formation.
The main objective of this paper is to develop a new ROP model using the ANN technique based on the drilling parameters and the mud properties for shale formation. In addition, a new empirical equation for ROP based on the optimized ANN model will be developed and compared with the published ROP models.