1. Introduction
Recently, extreme weather has severely affected rainfall patterns and increased the incidents of flooding and other meteorological disasters, which inundated villages and cities and led to the destruction of properties. Prefabricated residential buildings have an advantage in quick installation to become a temporary residence for post-disaster relief of refugees. Prefabricated houses can also be used in coastal areas as vacation homes and other similar purposes with a minimal impact on the environment.
Concrete material has been identified as a major contributor to the greenhouse gas carbon dioxide in the atmosphere. Steel prefabricated houses and wooden houses are both easily corroded and have costly maintenance problems.
As an alternative, fiber reinforced plastic (FRP) composite material has been widely used in the retrofit and repair of buildings and bridges due to its merits of anti-corrosion, light-weight, high strength-to-weight ratio, high elastic modulus, high durability, easy-to-assemble, and great design flexibility. Recently, the FRP composite material was widely used in sporting goods, automotive, aerospace, and civil engineering. FRP composite material can also offer low maintenance cost, low life-cycle cost, and low carbon dioxide emission [
1]. From the research results by Li et al. [
1], the research results show that the total carbon dioxide emission of the GFRP in various stages (production, transportation, and construction stages) is significantly lower than traditional reinforced concrete (RC) and steel pedestrian bridges, which makes GFRP material environmentally friendly. Fabric-reinforced cementitious matrix (FRCM) composites and FRP composite bars as structural members can significantly enhance structural safety and sustainability in the construction industry [
2,
3,
4].
Furthermore, FRP composite materials can be recycled and reused [
5,
6]. Therefore, FRP is a sustainable material for civil engineering usage. Because of the aforementioned advantages, the FRP composite materials can be used for prefabricated houses in mountainous or coastal areas without the worries of being affected by corrosion brought by the harsh environments.
FRP composite material has been used in civil engineering since the 1980s [
7]. The experimental strength tests, such as fatigue and bending tests, and the finite-element analysis were performed on the GFRP composite bridge deck [
8,
9,
10,
11,
12,
13,
14]. The structural behaviors of different sections of GFRP members were investigated, and the results showed that GFRP structural members could be applied to civil engineering [
15,
16,
17]. The mechanical behavior of bolts and the influence of the bolt diameter on the bearing strength of GFRPs were studied experimentally and numerically [
18,
19,
20,
21,
22,
23,
24]. FRP beam-column joint connection methods and their performance were also studied [
25,
26]. Lehman et al. investigated the energy dissipation of four different kinds of bracing joints. Experimental results showed that the four kinds of bracing joints could prevent beam damage better than welded joints [
27].
Related works were also conducted by other researchers. Kapti et al. investigated the effects of preload moment on the bearing strength and failure mode in pin-jointed and bolted carbon–epoxy plates subjected to a traction force [
28]. Davalos et al. used different types of I-section, and box-section members in the three-point and four-point bending tests to examine the mechanics of laminated beams and used a finite element analysis model to predict the deformation and strain of the FRP components [
29]. Masarira performed a finite element modeling of portal frames and established that a consistent relationship exists between the critical load for lateral-torsional buckling of the frame beams and the joint design [
30]. Hejll et al. used a large size mixed ratio of GFRP composite beams in the four-point bending test and conducted a finite element analysis to compare the shear effect with that of the four-point bending test [
31].
Other researchers focused on the numerical analysis of the frame, such as Li et al., who proposed the “equivalent column model” concept to analyze the brick panel inside RC frames. The numerical-analysis results could reasonably predict the lateral force-displacement relationships of these RC frames [
32]. Gray and McCarthy developed a global bolted joint model (GBJM) for bolted composite joints. The GBJM was validated using both three-dimensional finite element models and experiments on both single-and multi-bolt joints [
33]. Balc et al. conducted a finite element analysis of a beam to column end plate bolted connection using ABAQUS finite-element software (ABAQUS Inc., Johnston, RI, USA). The model was simplified by the use of finer mesh in areas of potentially high stress, namely the support regions and the contact areas [
34].
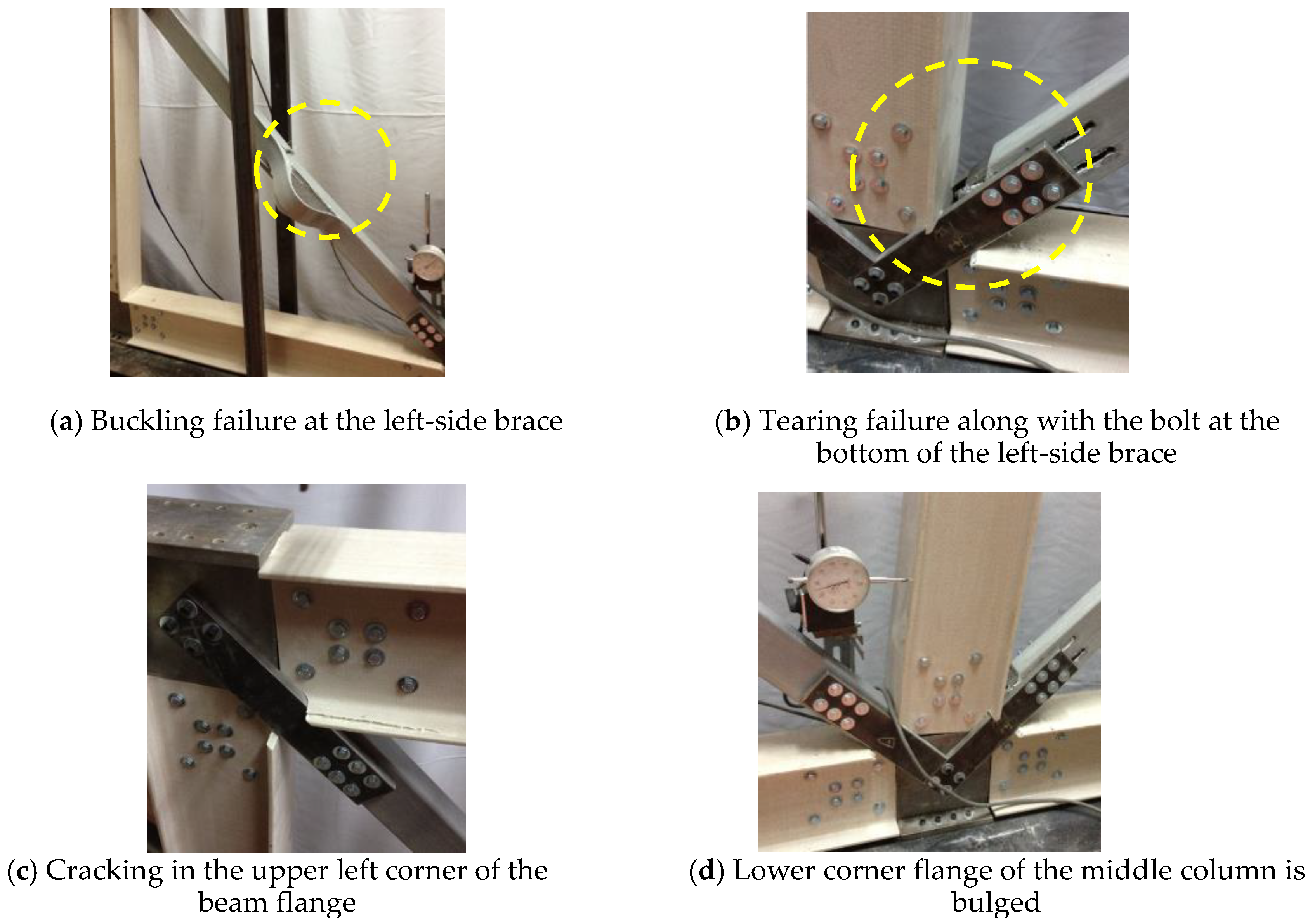
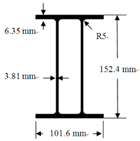
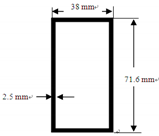
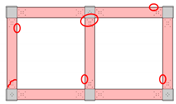
This paper focuses on the mechanical behavior of glass fiber reinforced plastics (GFRP) frames made by assembling GFRP components with steel joints and bolts. A total of six GFRP frames, including single-span and double-span frames with and without diagonal bracing members, were tested using the pushover test to obtain the lateral load-displacement relationships of the GFRP frames. The linear stiffness, maximum load, dissipated energy, and failure modes of the GFRP frames were investigated. Numerical analysis was also performed to obtain the lateral load-displacement relationships of the GFRP frames. The analysis results were compared with the experimental results to show that the numerical-analysis results could reasonably predict the experimental force-displacement relationships of the GFRP frames.
4. Nonlinear Pushover Numerical Analysis
In nonlinear pushover analysis, 2D models of the frames were numerically analyzed using SAP2000 Version 14 [
35]. The model created with the dimensions and material properties of the experimental GFRP frames were analyzed by the software. The left and right lower ends of the frame are assigned fixed supports at the steel joints (also the middle-lower joint in the case of double-span frames). The material parameters of the GFRP components are given in
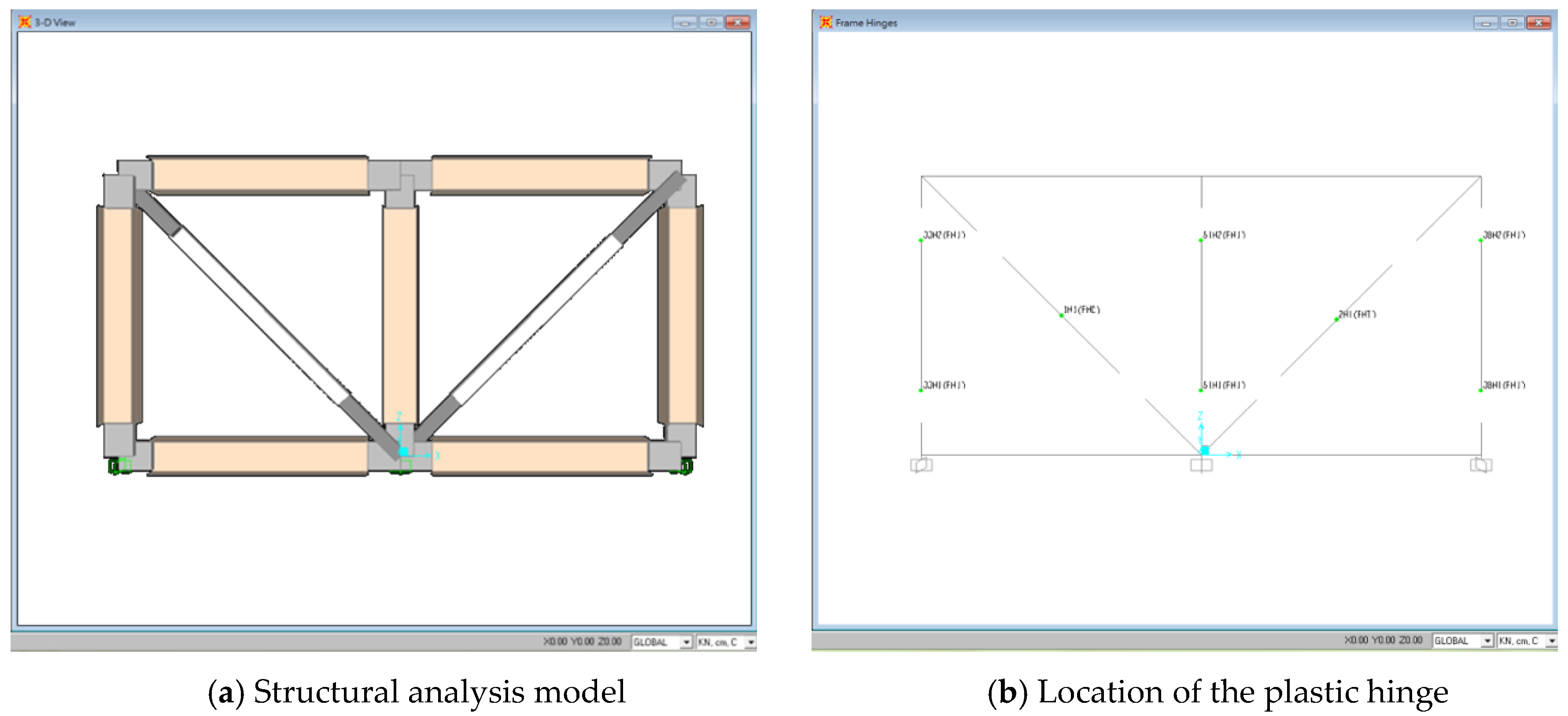
Table 2. Plastic hinges were manually defined for each column member, one in the upper part and one in the lower end. A plastic hinge was also defined in the middle of each bracing member.
The nonlinear nature of the problem requires the use of plastic hinges to simulate the behavior of the frame after yielding. Before yielding, the frame is in an elastic state, and the elastic behavior takes place over the entire length of the member. However, once the yielding point is reached, deformation behavior will be propagated from the hinges. Plasticity may be defined by the force-displacement relationship or moment-rotation relationship. The SAP2000 software; however, limits the negative slope to 10% of the elastic stiffness, so the hinge-overwrite option was used to simulate the force decrease after failure.
The plastic hinge parameters were set by using a single-column force-displacement relationship diagram and converting it into a moment-rotation relationship. Then the moment-rotation relationship was normalized and applied in the software to set the plastic hinge locations. We subtracted the force-displacement relationship of the prototype frame from that of the braced frame to obtain the force-displacement relation of the brace itself [
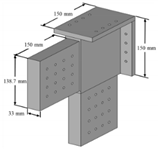
30]. Then, the force-displacement relationship of the bracing was normalized and applied in the software to set the plastic hinge. The span of the frame was set in the x-axis, and the frame height in the z-axis. Using the parameters obtained from the above procedures, “Hinge-overwrites” was set using the built-in commands of SAP2000. When one or more plastic hinges were set, the Hinge-overwrite parameter could be used with location setting between 0 and 1. The illustration figure of the structural analysis model and the locations of the plastic hinge of Frame FP2CT is shown in
Figure 16.
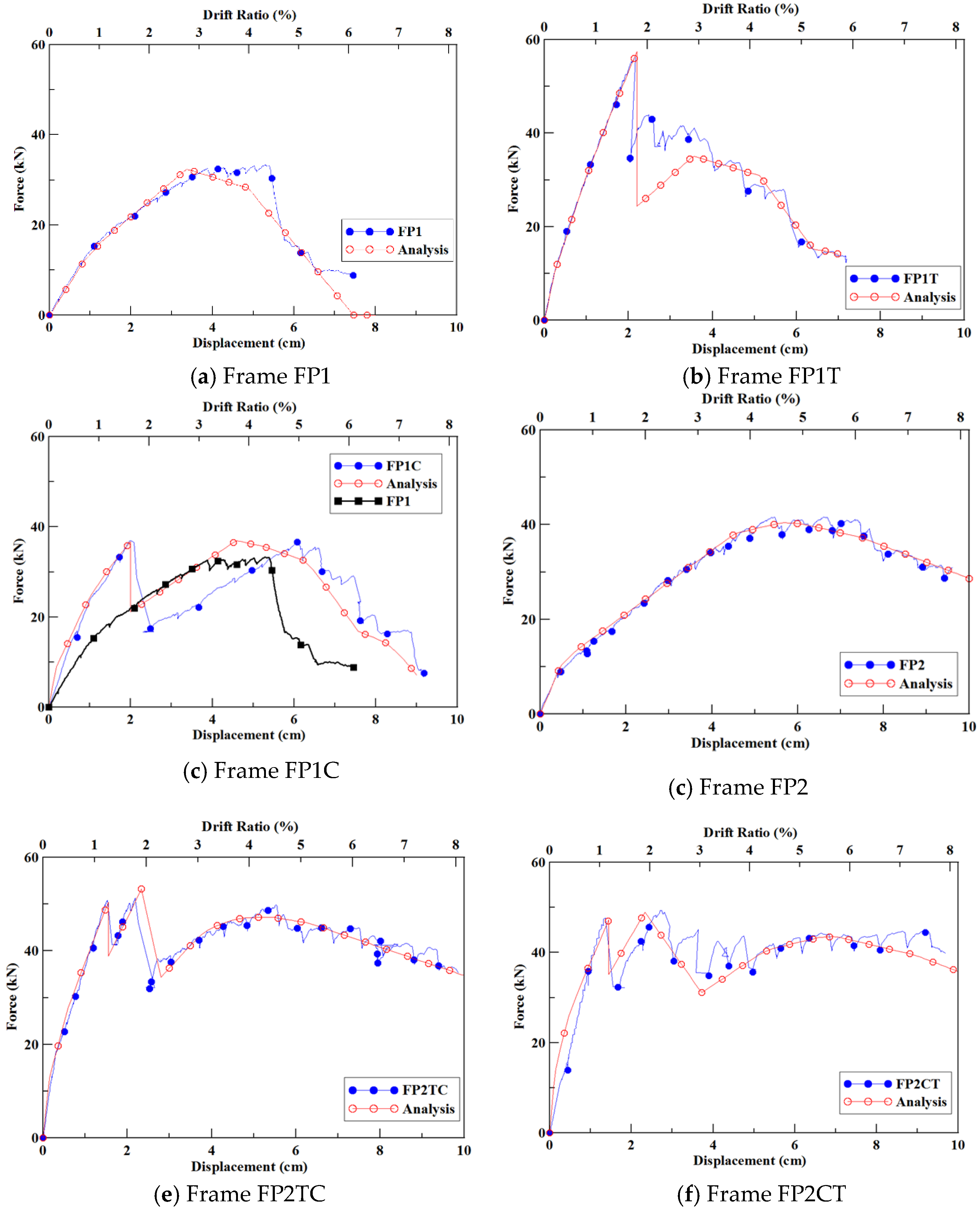
In the case of Frame FP1 shown in
Figure 17, the dotted curve in blue represents the experimental results, and all the other curves were obtained by trial and error of the plastic hinge locations. The parameters were first set without the hinge-overwrite parameter, but the analysis could not simulate the curve at failure. When the plastic hinges were set at 0.9, the strength started to drop after a drift ratio of almost 4%. The hinge locations were varied, and when the value reached 0.2, the numerical-analysis curve (solid triangles in red) had a trend similar to the experimental results. When the parameter was set to 0.1, the analysis showed an unstable curve. Therefore, the hinge-overwrite parameter in Frame FP1 was set using a plastic hinge of 0.2.
The hinge-overwrite settings allow for proper simulation of plastic hinge locations. The plastic hinge allows the transfer of moment, and as such, the analytical behavior of the model can be made to simulate the behavior of the experimental GFRP frames. The hinge overwrites option in this manuscript was adjusted according to the experimental results.
Table 5 gives the recommended hinge-overwrite coefficients to fit the experimental force-displacement curve. For single-span and double-span GFRP frames, the hinge-overwrite coefficients of the column were set as 0.2 and 0.6, respectively. For single-span frames, the hinge-overwrite coefficients of both tension and compression bracings were set as 0.09. For double-span frames, the hinge-overwrite coefficients of tension bracings of FP2TC and FP2CT were set as 0.2 and 0.4, respectively; the compression bracings were set as 0.1. Through more experimental data, we can learn from the big data and conclude the proper values of the hinge-overwrite coefficients for different GFRP structural members. The numerical structural analysis of the GFRP frame depends on the data of the moment versus rotation relationship derived from the experiment and the hinge-overwrite coefficients. The performed structural analysis in this manuscript may not be feasible for different GFRP structural members and systems.
5. The Comparison of the Experimental and Numerical Analysis Results
The force-displacement relationships of the experiments and numerical analysis of GFRP frames were compared, and the findings are discussed below. The detailed comparison results of the six GFRP frames are discussed as follows.
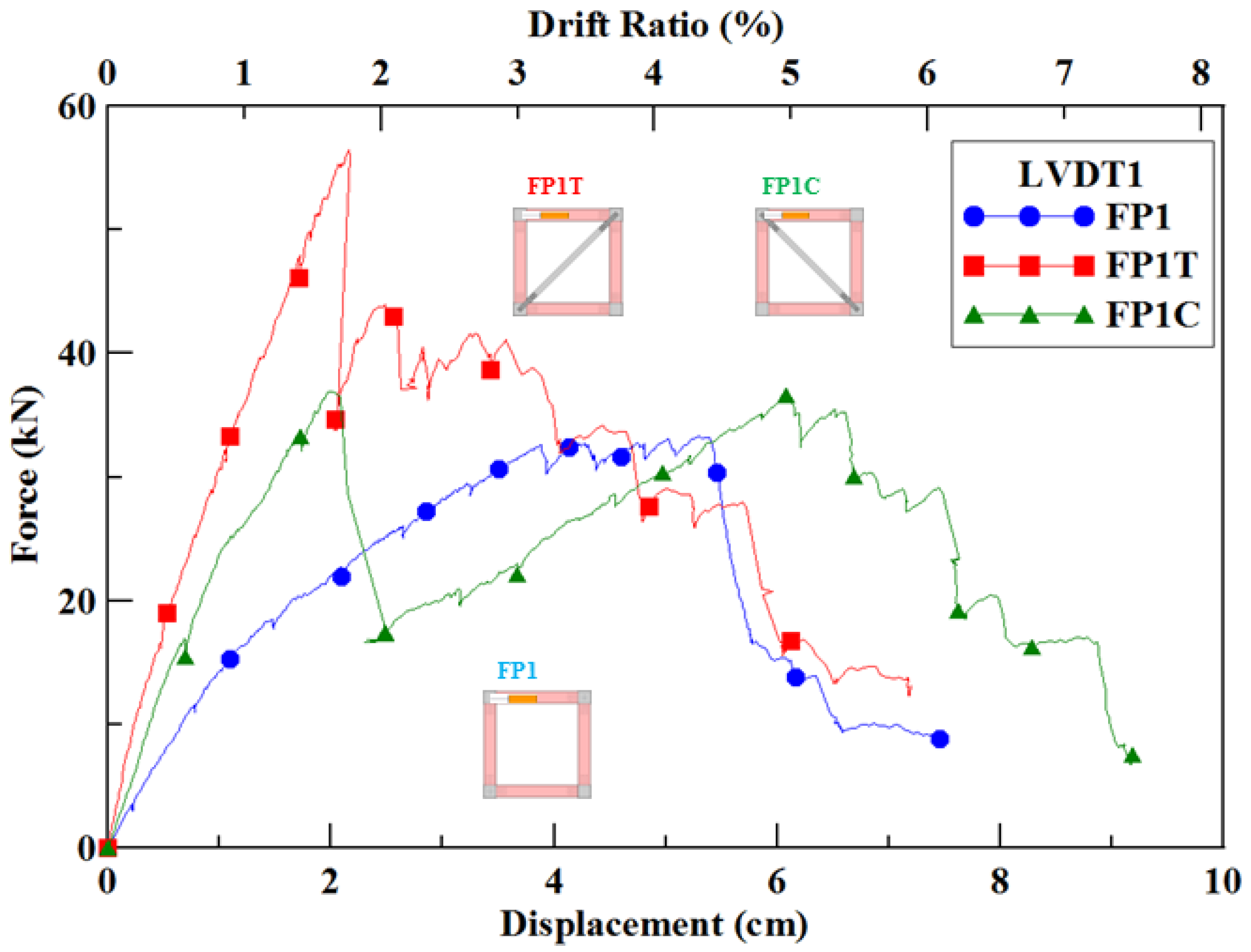
The frame FP1 drift ratio moves from 0 to 3%; the experimental and numerical-analysis curves follow a close trend, as shown in
Figure 18a. The analysis curve’s initial stiffness is similar, but the force is started to decrease after a drift ratio of 3%, while that of the experimental curve decreased after a drift ratio of 4%. The overall trend lines are similar.
The experimental and numerical-analysis trend lines of Frame FP1T are very close at the drift ratio is between 0 and 1.8 %, and the initial stiffness lines are also similar. After a drift ratio of 1.8%, the force in the analysis curve began to decline. The analysis simulated the experiments bracing tension failure. Therefore, the prototype frame was able to sustain the loading after the force decreased so that the force rose again. The numerical-analysis and experimental curves for Frame FP1T are similar, as shown in
Figure 18b.
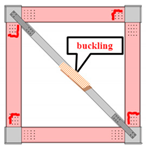
From the drift ratio of 0 to 1.8%, the experimental and numerical-analysis trend lines of Frame FP1C are very close, as shown in
Figure 18c; the bracing buckles and the force decrease after a drift ratio of 1.8%. Comparing the analysis of Frame FP1C with the prototype Frame FP1, it shows that the force decreases in Frame FP1C at the drift ratio of 1.8%, and the loading force is close to that of Frame FP1. This shows that the frame itself is now sustaining the loading directly as Frame FP1 is not braced. However, in the experiment, the force decreased after the drift ratio was greater than 1.8%, which could be attributed to the failure of the load cell to catch up with the frame after the bracing buckled. The recovery numerical-analysis trend of the Frame FP1C, after the bracing buckled, is similar to the experimental curve of Frame FP1.
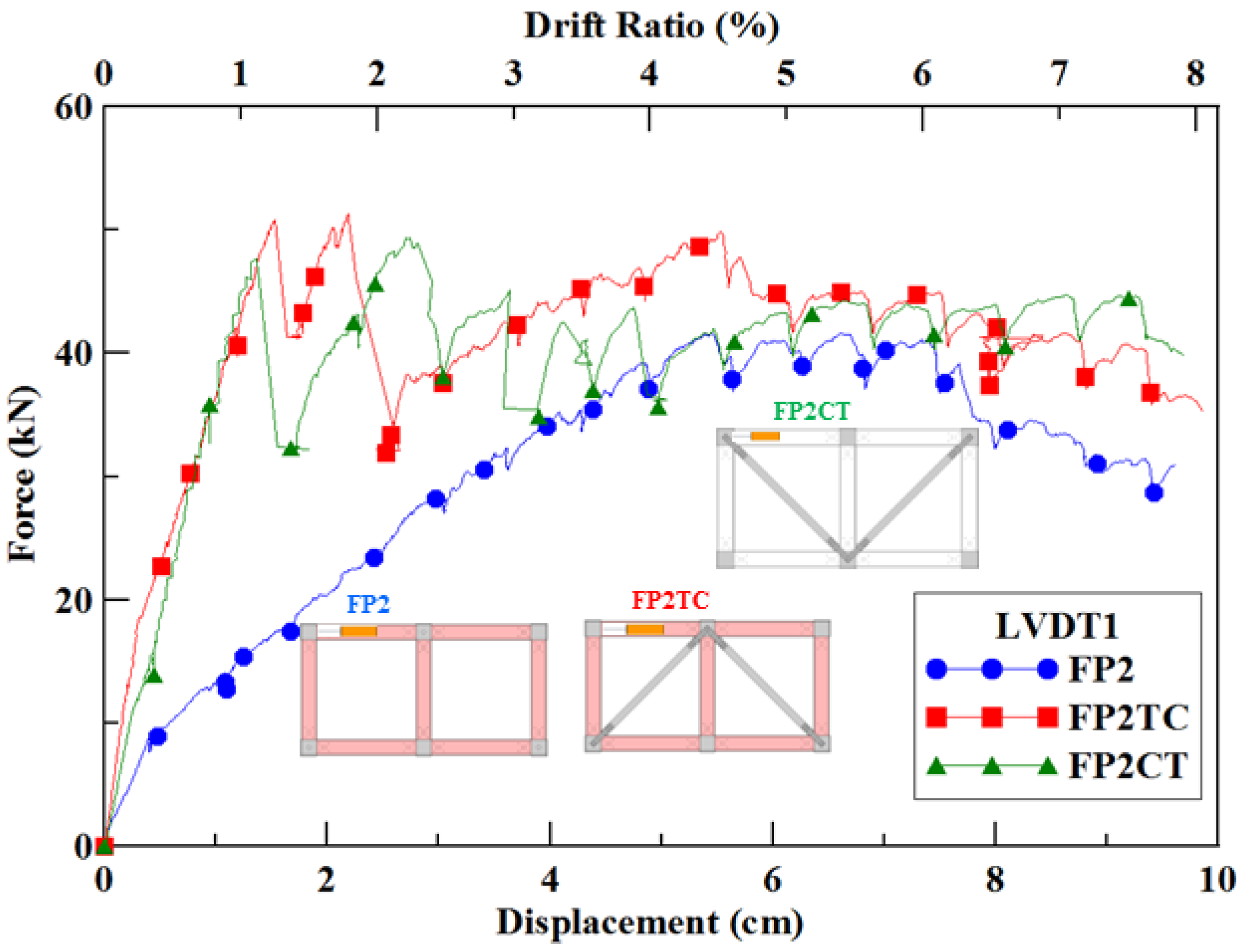
The experimental and numerical-analysis trend lines of Frame FP2 as shown in
Figure 18d. Both trend lines are similar at a drift ratio between 0 and 6%, and the initial stiffness lines are similar, as well. After a drift ratio of 6%, the experimental curve shows a lower force than the analysis curve. Overall, the comparison is very good.
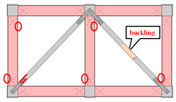
The experimental and numerical-analysis trend lines of Frame FP2TC are very close as shown in
Figure 18e, and the initial stiffness lines are also very similar, which means that the analysis can be used to simulate the experiment effectively. The first failure occurs at the drift ratio of 1.2% when the compression bracing buckles and the force drops. The force increases back up to a drift ratio of 1.8% when the tension bracing also fails, and the force drops again. Finally, the frame takes up the loading, and the force increases slightly. The relationships between the experimental and numerical-analysis force-displacement are identical and follow the same trend with little differences.
The experimental and numerical-analysis trend curves of Frame FP2CT are shown in
Figure 18f. The experimental observation shows that the compression bracing’s first failure occurs at a drift ratio of 1%, causing a drop in force. After the force increases up to a drift ratio of 2%, when the tension bracing also fails. The force then drops again, and as the frame takes up the loading, it increases again. The experimental and numerical-analysis force-displacement relationships are identical and follow the same trend.
The error in the ultimate loads between the experimental and numerical-analysis results are shown in
Table 6. The numerical-analysis results show that the error rate is less than 4% when compared with the experimental results. This numerical-analysis demonstrates that the use of SAP2000 simplifies the work of engineers because the analysis software has an acceptable accuracy and simulation capability.