Forecasting Hourly Power Load Considering Time Division: A Hybrid Model Based on K-means Clustering and Probability Density Forecasting Techniques
Abstract
1. Introduction
2. Literature Review on Load Uncertainty Forecasting
2.1. Interval Forecasting
2.2. Probability Density Forecasting
3. Basic Theory of the Proposed Methodology
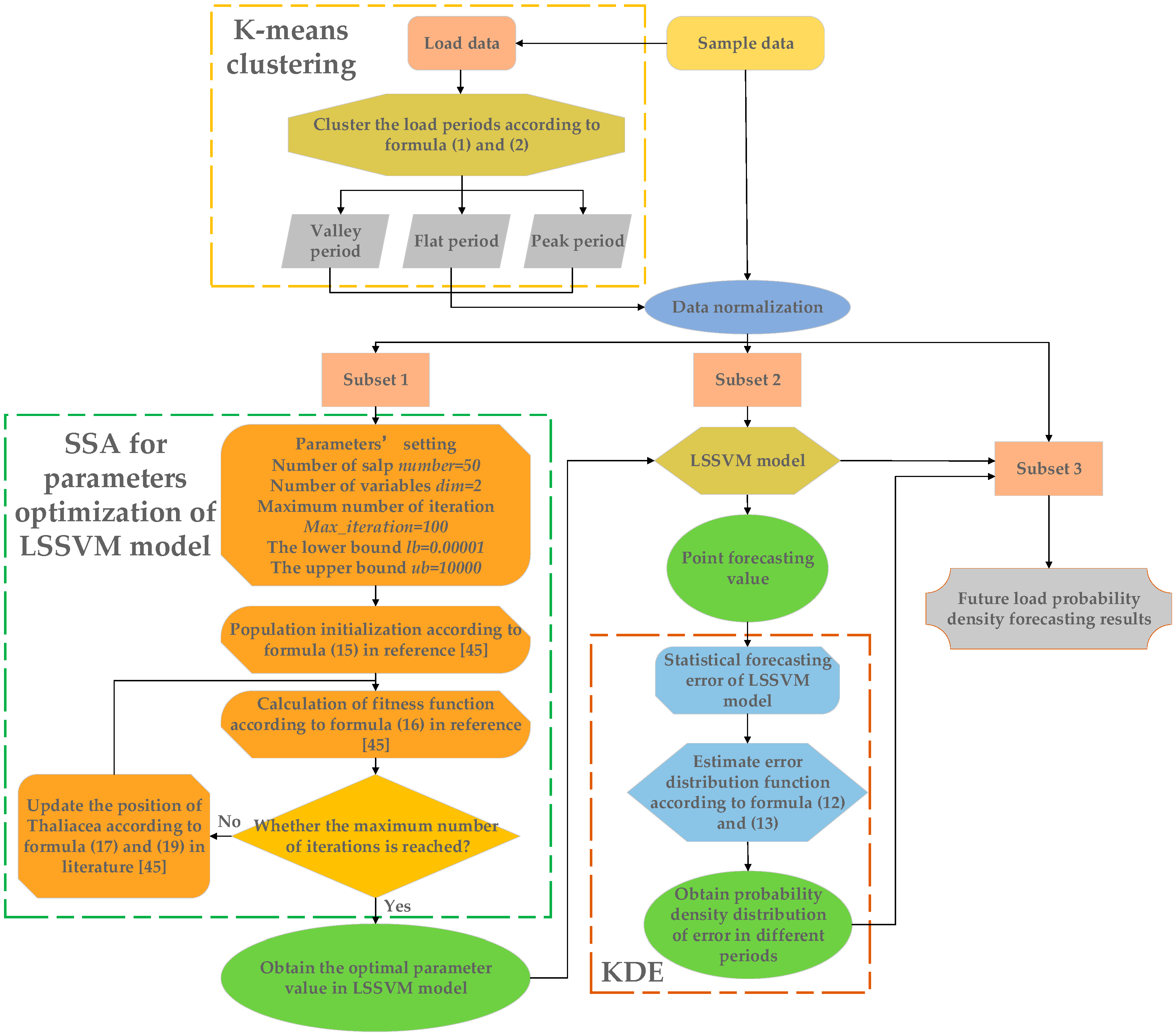
3.1. K-Means Clustering Method
3.2. Deterministic Forecasting Model Based on Salp Swarm Algorithm (SSA)-Least Square Support Vector Machine (LSSVM)
3.3. Kernel Density Estimation Model
4. The Framework of the Proposed Method
5. Empirical Results and Analysis
5.1. Data Sorting and Preprocessing
5.2. K-Means Clustering Results
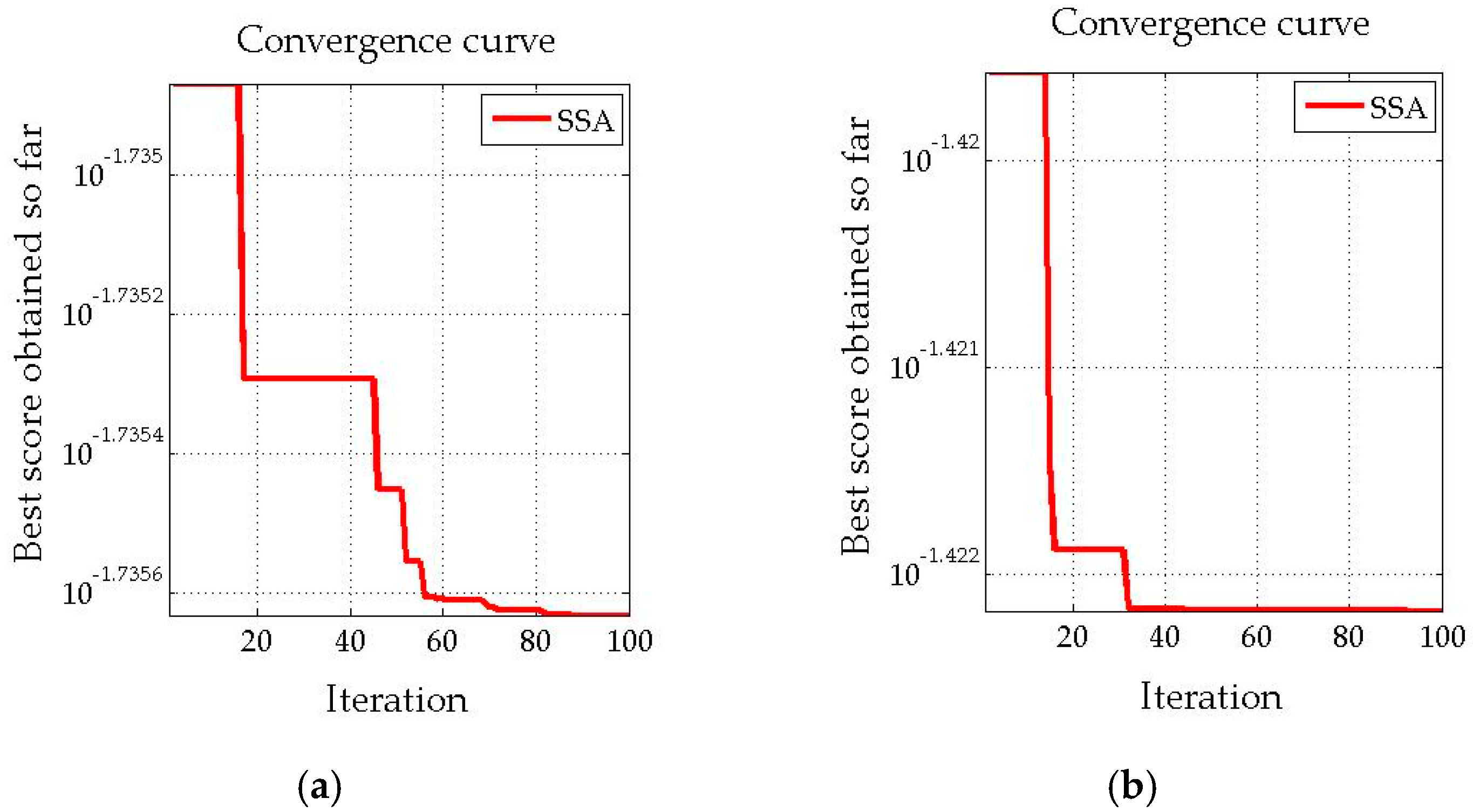
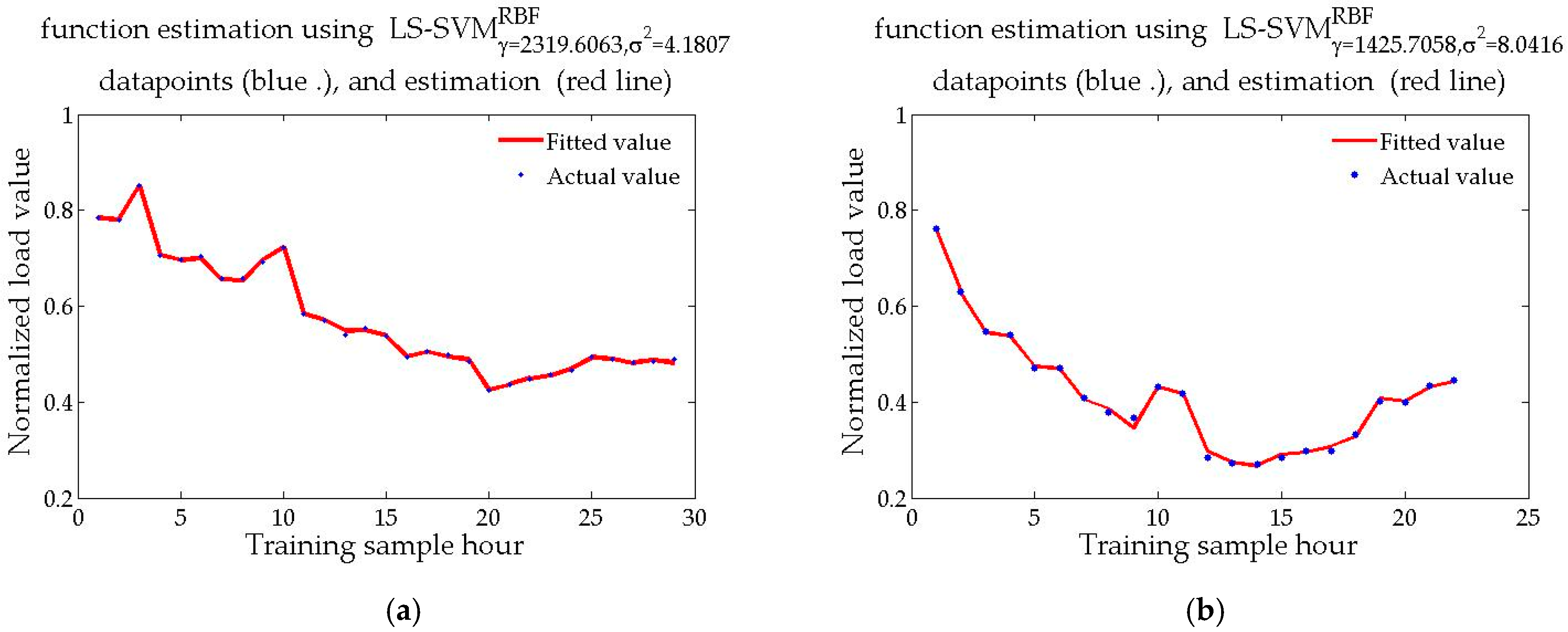
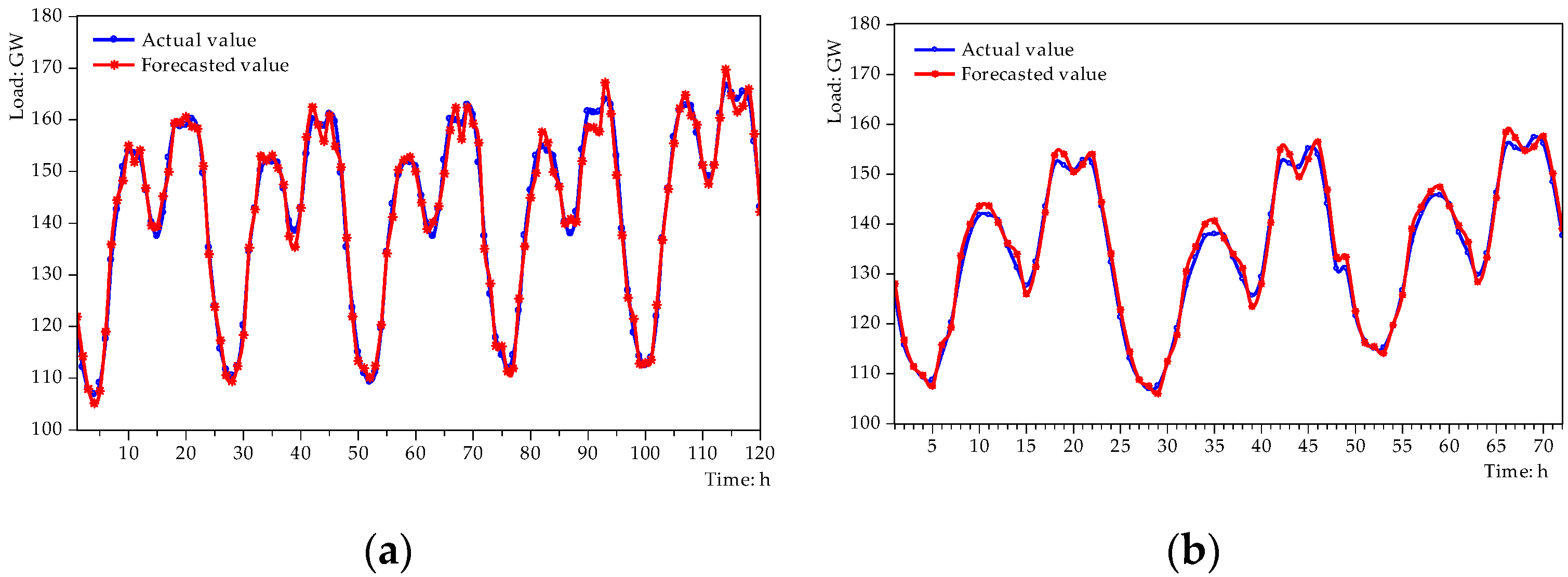
5.3. SSA-LSSVM Forecasting Results
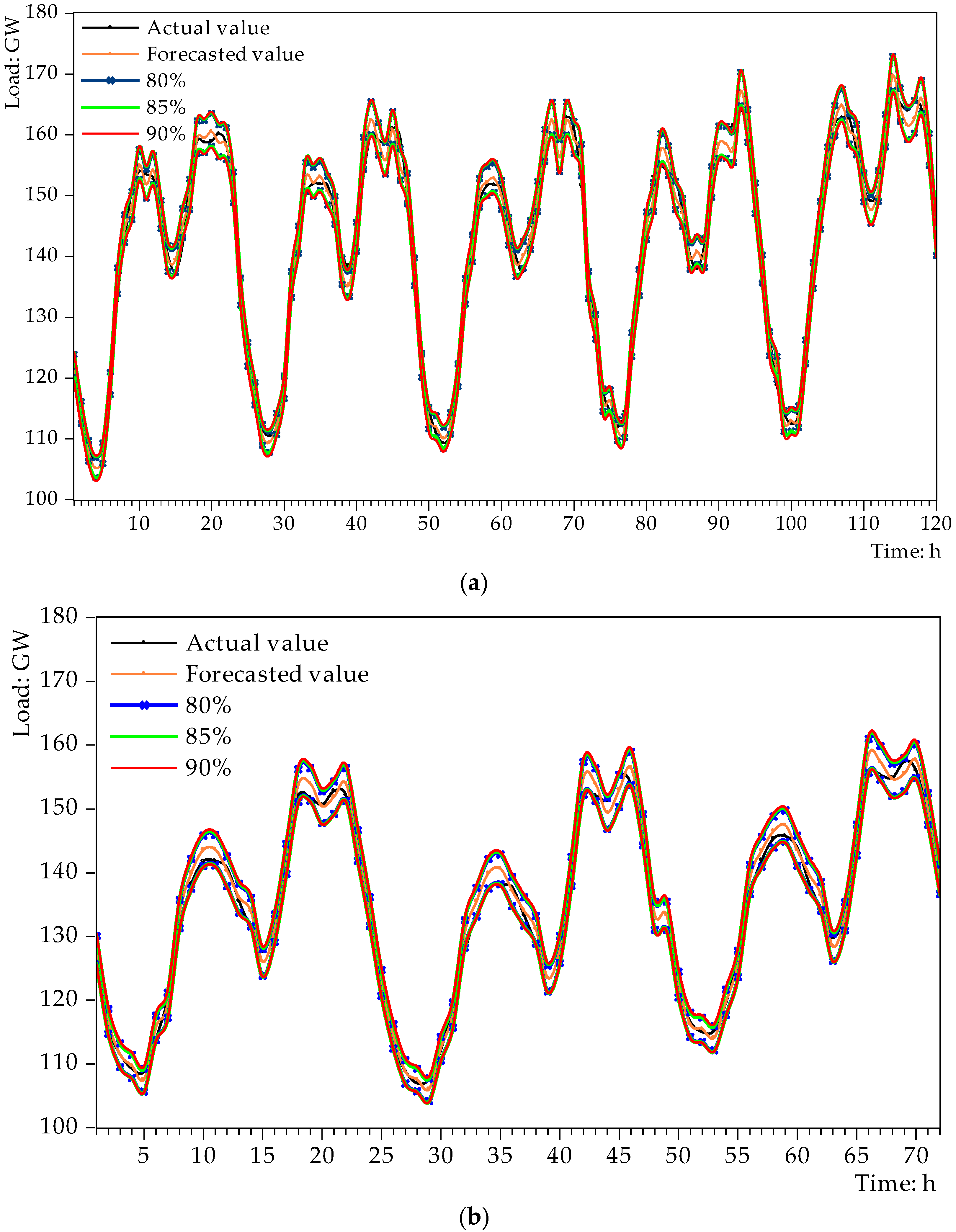
5.4. Probability Density Forecasting Results
5.5. Results and Discussion
- (1).
- By comparing model 1 and model 2, it can be found that the model optimized by SSA algorithm can significantly improve the interval coverage and reduce the interval average width. This is because the optimized model can effectively find the parameter values in the LSSVM model, avoiding the subjectivity of artificially given parameters, and thus improving the model forecasting performance.
- (2).
- By comparing model 1 and model 3, it can be found that, in comparison with the traditional parameter estimation, the non-parametric estimation method can effectively improve the interval coverage and reduce the interval average width. This is because the traditional parameter estimation method needs to make assumptions about the probability density function in advance when estimating the error distribution of point forecasting. In contrast, the non-parametric estimation method can better reflect the true distribution of the error, and the fitting effect is better.
- (3).
- By comparing model 1 and model 4, it can be found that the two models perform similarly on the interval coverage and interval average width. On the interval average width index, model 1 is slightly better than model 4, but the difference is not obvious, indicating that the selection of the kernel function does not show a greater difference in the improvement of the model forecasting performance relative to the improvement of other parts of the model.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qi, L.; Zhen, H.; Sheng, L. Research on power load forecasting based on support vector machine. J. Balk. Tribol. Assoc. 2016, 22, 151–159. [Google Scholar]
- Zhang, Q.; Lu, J.; Yang, Z.; Tu, M. A Deep Learning Based Real-time Load Forecasting Method in Electricity Spot Market. J. Phys. Conf. Ser. 2019, 1176, 062068. [Google Scholar] [CrossRef]
- Yan, Q.; Qin, C.; Nie, M.; Yang, L. Forecasting the electricity demand and market shares in retail electricity market based on system dynamics and Markov chain. Math. Probl. Eng. 2018, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Quan, C.; Wang, X.; Zhang, S. Short-term power load forecasting based on a combination of VMD and ELM. Pol. J. Environ. Stud. 2018, 27, 2143–2154. [Google Scholar] [CrossRef]
- Li, Z.; Yin, X.; Yang, H.; Ma, R.; Shi, G.; Zhao, W. Analysis of seasonal load characteristics based on improved k-means clustering algorithm. Grid Clean Energy 2018, 34, 53–59+64. [Google Scholar]
- Kang, Y.; Yin, S.; Wang, X.; Dong, S.; Deng, X.; Chen, G. Analysis of load characteristics and influencing factors of large urban power grid. Electr. Meas. Instrum. 2016, 53, 51–56. [Google Scholar]
- Li, J.; Sang, C.; Gan, Y.; Pan, Y. Research overview of wind power prediction technology. Mod. Electr. Power 2017, 34, 1–11. [Google Scholar]
- Goodwin, P.; Önkal, D.; Thomson, M. Do forecasts expressed as prediction intervals improve production planning decisions? Eur. J. Op. Res. 2010, 205, 195–201. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Van der Meer, D.W.; Widén, J.; Munkhammar, J. Review on probabilistic forecasting of photovoltaic power production and electricity consumption. Renew. Sustain. Energy Rev. 2018, 81, 1484–1512. [Google Scholar] [CrossRef]
- Yu, X. Research on Ultra-Short-Term Load Forecasting of Micro Power Grid. Master’s Thesis, Jiangnan University, Jiangsu, China, June 2018. [Google Scholar]
- Hernández, J.C.; Ruiz-Rodriguez, F.J.; Jurado, F. Modelling and assessment of the combined technical impact of electric vehicles and photovoltaic generation in radial distribution systems. Energy 2017, 141, 316–332. [Google Scholar] [CrossRef]
- Pinson, P.; Tastu, J. Discussion of “Prediction intervals for short-term wind farm generation forecasts” and “Combined nonparametric prediction intervals for wind power generation”. IEEE Trans. Sustain. Energy 2014, 5, 1019–1020. [Google Scholar] [CrossRef]
- Guan, C.; Luh, P.B.; Michel, L.D.; Chi, Z.Y. Hybrid Kalman filters for very short-term load forecasting and prediction interval estimation. IEEE Trans. Power Syst. 2013, 28, 3806–3817. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Uncertainty handling using neural network-based prediction intervals for electrical load forecasting. Energy 2014, 73, 916–925. [Google Scholar] [CrossRef]
- Li, Z.; Ding, J.; Wu, D.; Wen, F. Integrated limit learning machine method for power load interval prediction. J. North China Electr. Power Univ. Nat. Sci. Ed. 2014, 41, 78–88. [Google Scholar]
- Yu, J.; Bao, Z.; Li, Z. User load interval prediction method based on LSTM. Ind. Control Comput. 2018, 31, 100–102. [Google Scholar]
- Ren, J.; Zhang, L.; Wang, H.; Guo, Q. Prediction of short-term load interval based on IPSO-GPR. Comput. Eng. Des. 2019, 40, 3002–3008. [Google Scholar]
- Meng, Y. Study on Short-Term Load Probability Density Prediction Method Based on Regression Analysis. Master’s Thesis, North China Electric Power University (Beijing), Beijing, China, June 2018. [Google Scholar]
- Liu, R. Prediction Method of Short-Term Power Load Probability Density Based on Support Vector Quantile Regression and Smart Grid. Master’s Thesis, Hefei University of Technology, Anhui, China, June 2017. [Google Scholar]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Chen, L. Short-Term Load Prediction and Confidence Interval Based on Non-Linear Ensemble. Master’s Thesis, Tianjin University, Tianjin, China, June 2016. [Google Scholar]
- Wen, C. Study on Probability Density Prediction Method Based on Neural Network Quantile Regression and Kernel Density Estimation. Master’s Thesis, Hefei University of Technology, Anhui, China, June 2015. [Google Scholar]
- Bracale, A.; Carpinelli, G.; De Falco, P. A Bayesian-based approach for the short-term forecasting of electrical loads in smart grids. Part I: Theoretical aspects. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016. [Google Scholar]
- Bikcora, C.; Verheijen, L.; Weiland, S. Density forecasting of daily electricity demand with ARMA-GARCH, CAViaR, and CARE econometric models. Sustain. Energy Grids Netw. 2018, 13, 148–156. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar] [CrossRef]
- Guo, R. Selection of Conditional Heteroscedasticity Model Based on Density Prediction. Master’s Thesis, Shandong University, Shandong, China, June 2012. [Google Scholar]
- Sun, Z. Analysis and Research on Gas Load Characteristics and Gas Consumption Characteristics of Commercial Users in Chongqing. Master’s Thesis, Chongqing University, Chongqing, China, June 2017. [Google Scholar]
- He, Y.; Liu, R.; Li, H.; Wang, S.; Lu, X. Short-term power load probability density forecasting method using kernel-based support vector quantile regression and Copula theory. Appl. Energy 2017, 185, 254–266. [Google Scholar] [CrossRef]
- Yang, Y.; Li, S.; Li, W.; Qu, M. Power load probability density forecasting using Gaussian process quantile regression. Appl. Energy 2018, 213, 499–509. [Google Scholar] [CrossRef]
- He, Y.; Xu, Q.; Wan, J.; Yang, S. Short-term power load probability density forecasting based on quantile regression neural network and triangle kernel function. Energy 2016, 114, 498–512. [Google Scholar] [CrossRef]
- He, Y.; Wen, C.; Xu, Q. Probability density prediction method of medium power load based on Epanechnikov kernel and optimal window width combination. Power Autom. Equip. 2016, 36, 120–126. [Google Scholar]
- He, Y.; Qin, Y.; Lei, X.; Feng, N. A study on short-term power load probability density forecasting considering wind power effects. Int. J. Electr. Power Energy Syst. 2019, 113, 502–514. [Google Scholar] [CrossRef]
- Sanchez-Sutil, F.; Cano-Ortega, A.; Hernandez, J.C.; Rus-Casas, C. Development and calibration of an open source, low-cost power smart meter prototype for PV household-prosumers. Electronics 2019, 8, 878. [Google Scholar] [CrossRef]
- Li, N.; Wang, L.; Zhang, W.; Wang, Y.; Shu, Y.; Zhang, C. Study on long period peak/valley division model based on high-dimensional data optimization clustering. Mod. Electr. Power 2016, 33, 67–71. [Google Scholar]
- Suykens, J.A.K.; Lukas, L.; Vandewalle, J. Sparse approximation using least squares support vector machines. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems. Emerging Technologies for the 21st Century. Proceedings (IEEE Cat No. 00CH36353), Dalian, China, 26–28 July 2017; Volume 2, pp. 757–760. [Google Scholar]
- Wang, H.; Hu, D. Comparison of SVM and LS-SVM for regression. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2015; Volume 1, pp. 279–283. [Google Scholar]
- Adankon, M.M.; Cheriet, M. Model selection for the LS-SVM. Application to handwriting recognition. Pattern Recognit. 2009, 42, 3264–3270. [Google Scholar] [CrossRef]
- Deo, R.C.; Tiwari, M.K.; Adamowski, J.F.; Quilty, J.M. Forecasting effective drought index using a wavelet extreme learning machine (W-ELM) model. Stoch. Environ. Res. Risk Assess. 2017, 31, 1211–1240. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, H.; Guo, S. Short-term wind electric power forecasting using a novel multi-stage intelligent algorithm. Sustainability 2018, 10, 881. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Li, X.; Li, B.; Zhao, L.; Zhao, H.; Xue, W.; Guo, S. Forecasting the short-term electric load considering the influence of air pollution prevention and control policy via a hybrid model. Sustainability 2019, 11, 2983. [Google Scholar] [CrossRef]
- Jafarizadeh, M.A.; Fouladi, N.; Sabri, H.; Maleki, B.R. A non-parametric estimation approach in the investigation of spectral statistics. Indian J. Phys. 2013, 87, 919–927. [Google Scholar] [CrossRef]
- Han, Q.; Ma, S.; Wang, T.; Chu, F. Kernel density estimation model for wind speed probability distribution with applicability to wind energy assessment in China. Renew. Sustain. Energy Rev. 2019, 115, 109387. [Google Scholar] [CrossRef]
- Yang, N.; Zhou, Z.; Chen, D.; Wang, X.; Li, H.; Li, S. Wind power fluctuation probability density modeling method based on non-parametric kernel density estimation. J. Sol. Energy 2019, 40, 2028–2035. [Google Scholar]
- Liu, C.; Cao, W.; Wang, Z. Short-term interval prediction of wind power based on fuzzy c-means soft cluster condition identification. J. North China Electr. Power Univ. Nat. Sci. Ed. 2019, 46, 83–91. [Google Scholar]
- Li, M.; Lin, X.; Zhang, Z.; Weng, H. Prediction algorithm of ultra-short-term pv output interval and its application. Power Syst. Autom. 2019, 43, 10–18. [Google Scholar]
- Yang, X.; Ma, X.; Kang, N.; Maihemuti, M. Probability interval prediction of wind power based on KDE method with rough sets and weighted Markov chain. IEEE Access 2018, 6, 51556–51565. [Google Scholar] [CrossRef]


| Unit | N | Max. | Min. | Mean | S.D. | |
|---|---|---|---|---|---|---|
| Load | GW | 2040 | 163.9060 | 61.4797 | 112.0106 | 23.5318 |
| Temperature | °C | 2040 | 33.1 | −3.7 | 14.2171 | 7.5424 |
| Humidity | g/m3 | 2040 | 97 | 11 | 50.9137 | 23.6818 |
| Wind speed | m/s | 2040 | 8.6 | 0 | 1.8655 | 1.3130 |
| Air pressure | kPa | 2040 | 1030.8 | 995.5 | 1015.8346 | 6.3951 |
| Rainfall | mm | 2040 | 3.6 | 0 | 0.0153 | 0.1819 |
| Air quality level | / | 2040 | 310 | 9 | 61.1656 | 51.2375 |
| N | Max. | Min. | Mean | S.D. | |
|---|---|---|---|---|---|
| Load | 2040 | 1 | 0 | 0.4933 | 0.2297 |
| Temperature | 2040 | 1 | 0 | 0.4869 | 0.2050 |
| Humidity | 2040 | 1 | 0 | 0.4641 | 0.2754 |
| Wind speed | 2040 | 1 | 0 | 0.2169 | 0.1527 |
| Air pressure | 2040 | 1 | 0 | 0.5761 | 0.1812 |
| Rainfall | 2040 | 1 | 0 | 0.0043 | 0.0505 |
| Air quality level | 2040 | 1 | 0 | 0.1733 | 0.1702 |
| Confidence Level/% | ||||
|---|---|---|---|---|
| Non-Holidays | Holidays | Non-Holidays | Holidays | |
| 80 | 93.33 | 90.28 | 3.5597 | 4.0156 |
| 85 | 96.67 | 95.83 | 3.812 | 4.2932 |
| 90 | 100 | 98.61 | 4.7921 | 5.4212 |
| Model | Confidence Level/% | ||||
|---|---|---|---|---|---|
| Non-Holidays | Holidays | Non-Holidays | Holidays | ||
| Model 1 | 80 | 93.33 | 90.28 | 3.5597 | 4.0156 |
| 85 | 96.67 | 95.83 | 3.812 | 4.2932 | |
| 90 | 100 | 98.61 | 4.7921 | 5.4212 | |
| Model 2 | 80 | 88.33 | 86.11 | 3.7352 | 4.4373 |
| 85 | 94.17 | 91.67 | 4.0689 | 4.7481 | |
| 90 | 95.83 | 93.06 | 4.9857 | 5.8837 | |
| Model 3 | 80 | 87.5 | 83.33 | 4.7498 | 4.9215 |
| 85 | 91.67 | 86.11 | 4.7838 | 4.9375 | |
| 90 | 95.83 | 90.28 | 5.5247 | 6.0786 | |
| Model 4 | 80 | 95.83 | 90.28 | 3.5172 | 3.8225 |
| 85 | 95.83 | 94.44 | 3.9034 | 4.6896 | |
| 90 | 100 | 98.61 | 4.7943 | 5.6759 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhang, S.; Li, W.; Zhao, W.; Li, B.; Zhao, H. Forecasting Hourly Power Load Considering Time Division: A Hybrid Model Based on K-means Clustering and Probability Density Forecasting Techniques. Sustainability 2019, 11, 6954. https://doi.org/10.3390/su11246954
Li F, Zhang S, Li W, Zhao W, Li B, Zhao H. Forecasting Hourly Power Load Considering Time Division: A Hybrid Model Based on K-means Clustering and Probability Density Forecasting Techniques. Sustainability. 2019; 11(24):6954. https://doi.org/10.3390/su11246954
Chicago/Turabian StyleLi, Fuqiang, Shiying Zhang, Wenxuan Li, Wei Zhao, Bingkang Li, and Huiru Zhao. 2019. "Forecasting Hourly Power Load Considering Time Division: A Hybrid Model Based on K-means Clustering and Probability Density Forecasting Techniques" Sustainability 11, no. 24: 6954. https://doi.org/10.3390/su11246954
APA StyleLi, F., Zhang, S., Li, W., Zhao, W., Li, B., & Zhao, H. (2019). Forecasting Hourly Power Load Considering Time Division: A Hybrid Model Based on K-means Clustering and Probability Density Forecasting Techniques. Sustainability, 11(24), 6954. https://doi.org/10.3390/su11246954





