Numerical Study of a New Solar Vacuum Tube Integrating with Phase Change Material
Abstract
:1. Introduction
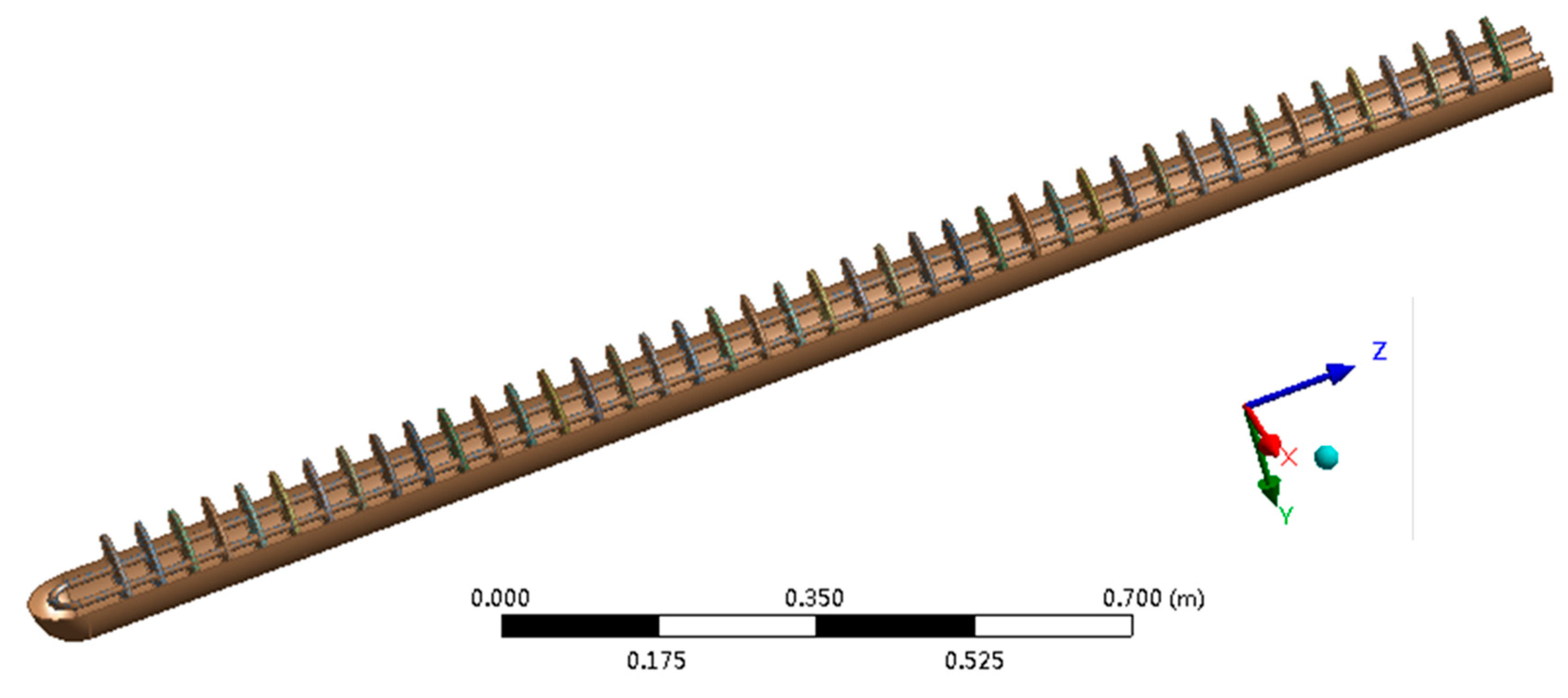
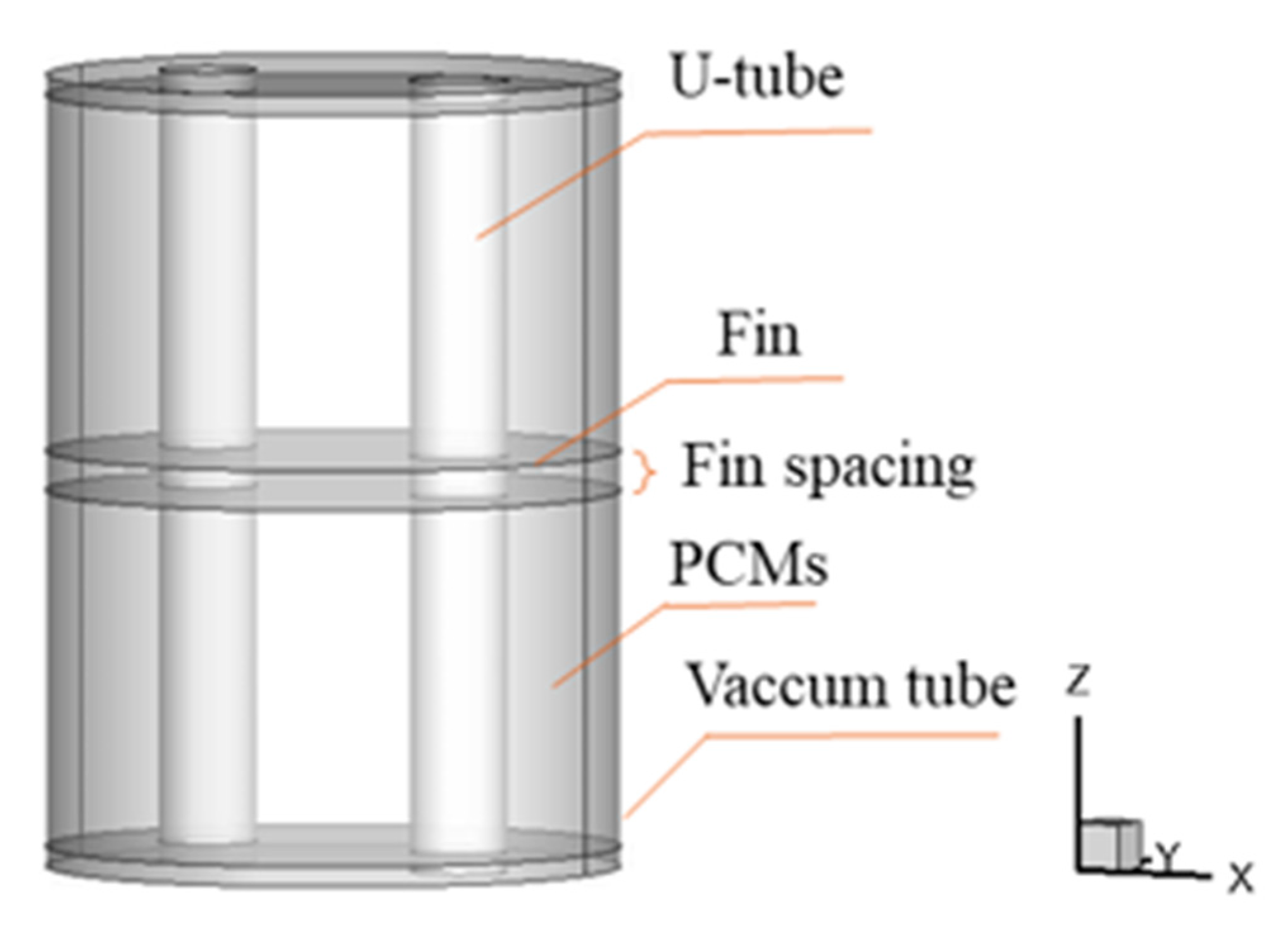
2. Problem Description
3. Macroscopic Governing Equations
3.1. Macroscopic Governing Equations
- (I)
- A mushy zone exists during the melting of paraffin. Therefore, three phase zones exist during the melting of paraffin, which are; solid zone, liquid zone, and mushy zone.
- (II)
- The physical properties of paraffin in the solid phase and the liquid phase are constant. The physical properties of paraffin in the mushy state change linearly with the temperature.
- (III)
- The liquid paraffin is a Newtonian fluid.
3.2. Boundary Conditions
3.3. Parameter Settings
4. Results and Discussion
4.1. Solid-liquid Phase Change Characteristics
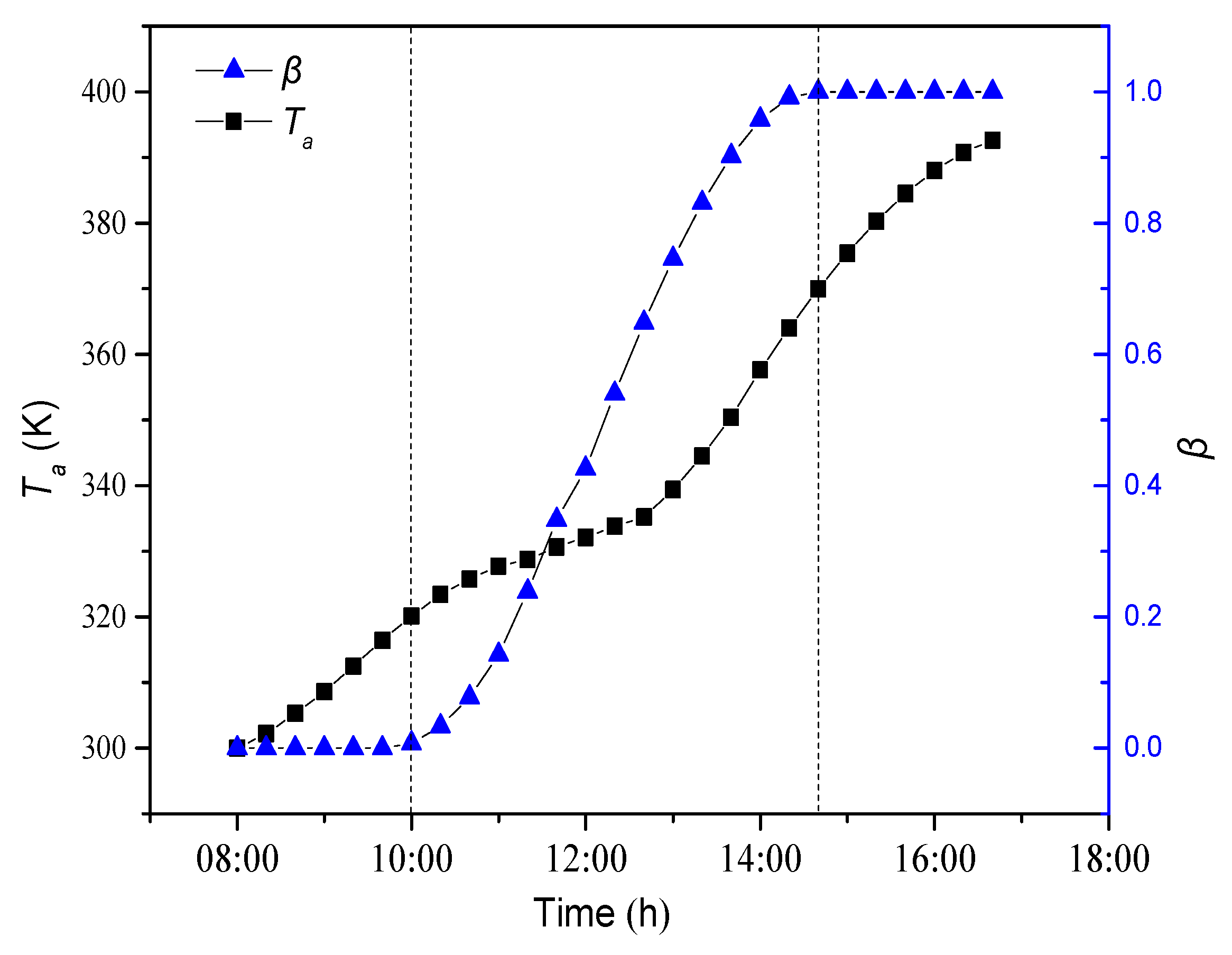
4.1.1. Dynamic Change of Average Temperature and Liquid Fraction
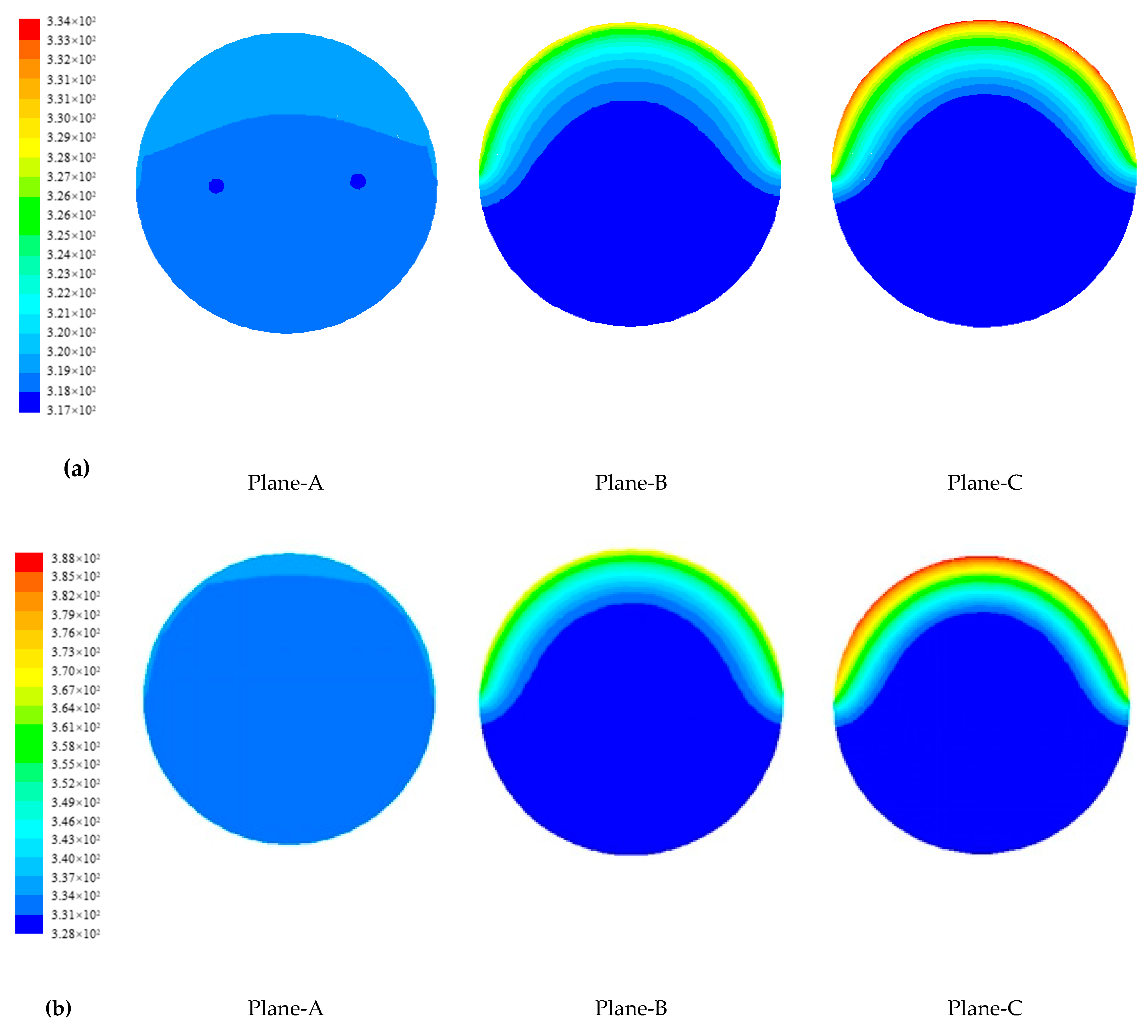
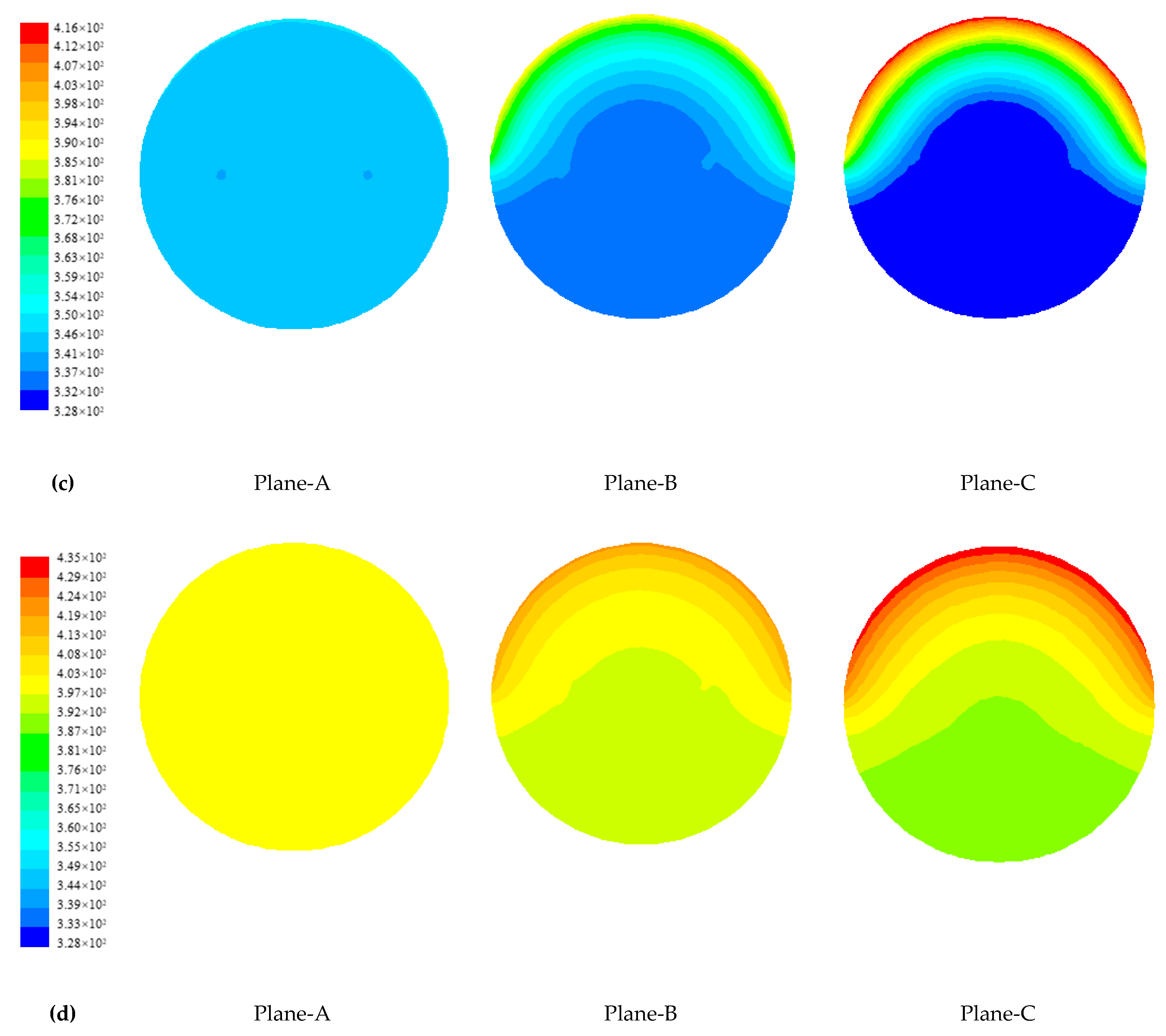
4.1.2. Temperature Distribution of Paraffin
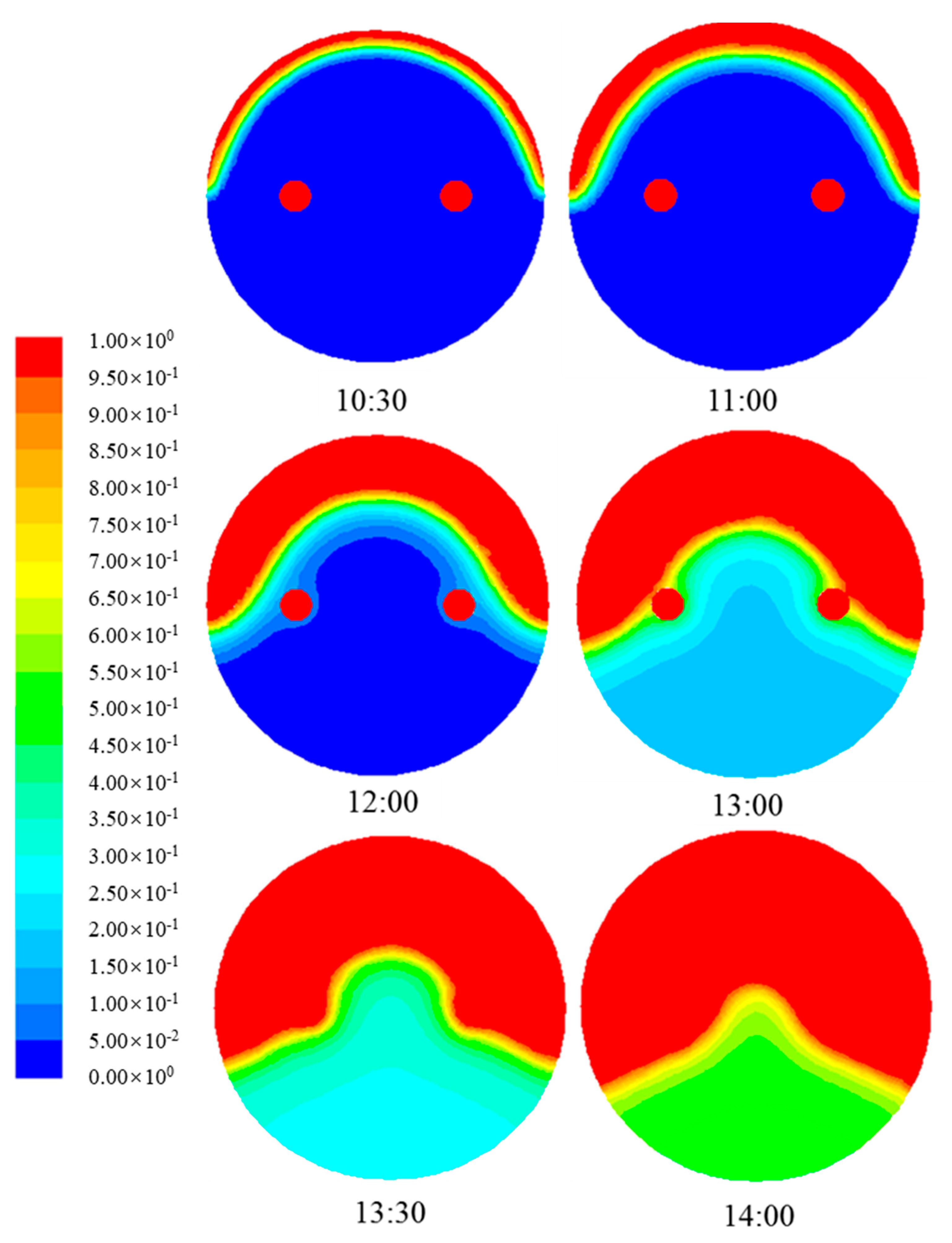
4.1.3. Evolution of Phase Change Interface of Paraffin
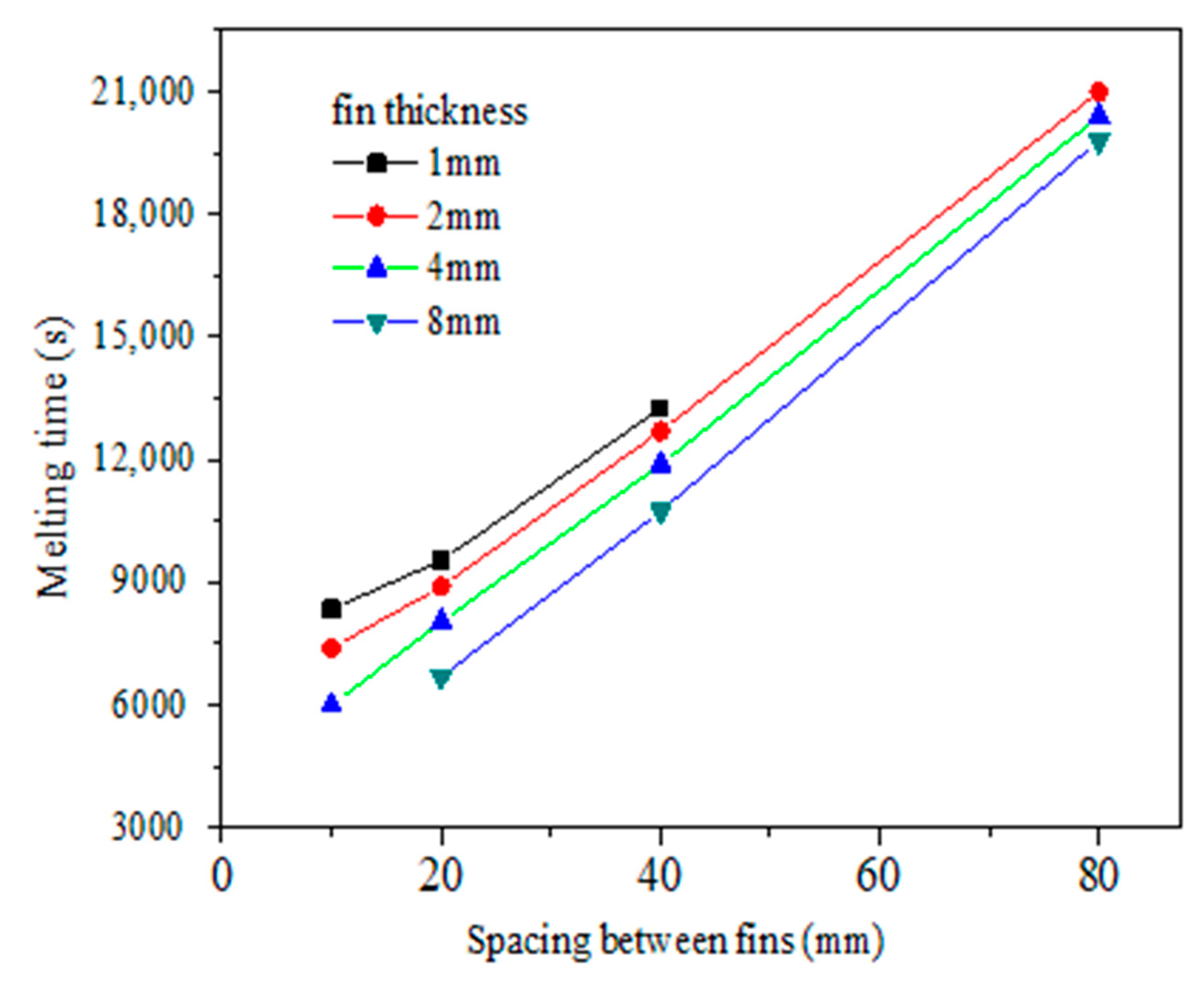
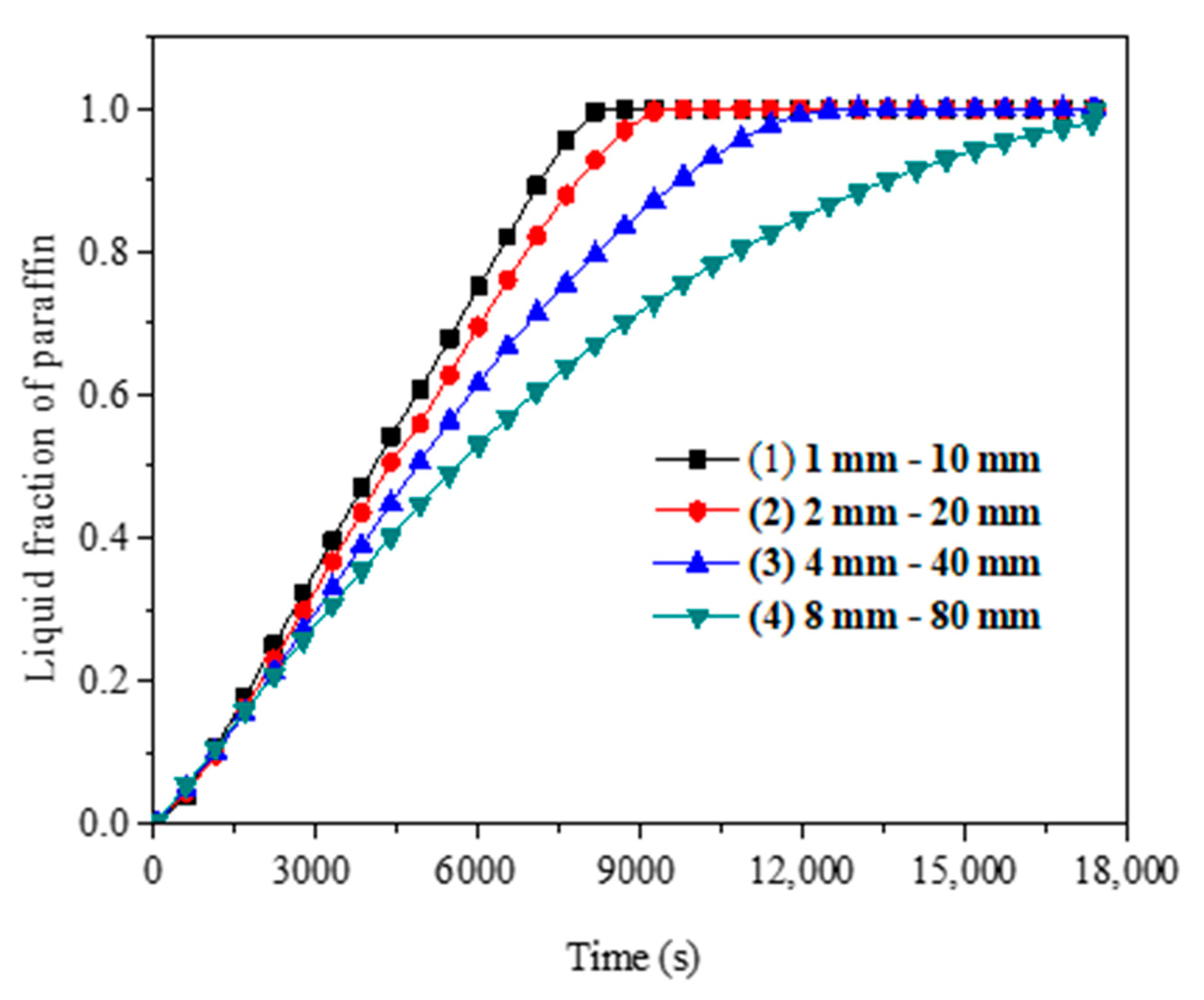
4.2. Optimization Analysis of Fin Structure Parameters in Vacuum Tube
5. Conclusions
- (1)
- As the paraffin gets heat through the daytime, the paraffin experiences a process from solid phase to solid-liquid two phase to liquid phase. Meanwhile, paraffin temperature increases during the daytime. In solid-liquid two phase, paraffin temperature increases slowly as latent heat storage plays an important role during phase change.
- (2)
- The metal fin has a great effect on the phase change heat transfer process of paraffin in SVTs. The closer the paraffin is to the fins, the more uniform the paraffin temperature is and the sooner the paraffin melts.
- (3)
- The metal fin structure and arrangement are major factors that affect the paraffin melting time. The melting time of paraffin decreases with the increase of fin thickness and the decrease of fin spacing. With constant fin volume, it is better to choose a smaller fin thickness and smaller fin spacing.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ρf | Density of the PCM liquid [kg.m−3] |
| g | Gravitational acceleration [m.s−2] |
| Velocity of liquid PCM [m.s−1] | |
| t | Time [s] |
| k | Heat conductivity [W.m−1.K−1] |
| μ | Dynamic viscosity [kg.m−1.s−1] |
| S | Source term in the momentum equation [kg.m−2.s−2.K] |
| β | Ratio of the liquid phase to the whole PCM [kg.kg−1] |
| ε | Small calculation constant to avoid the denominator to be zero [-] |
| Amushy | Constant of mushy zone [-] |
| Sb | Buoyancy term [kg.m−2.s−2.K] |
| α | Volume expansion coefficient of phase change material [-] |
| Tref | Reference temperature [K] |
| H | Enthalpy of PCM [kJ.kg−1] |
| href | Heat enthalpy of PCM at Tref [kJ.kg−1] |
| Tsolid | Low limit level of the mushy zone temperature [K] |
| Tliquid | High limit level of the mushy zone temperature [K] |
| T | PCM temperature [K] |
Appendix A
References
- Sun, L.; Shen, J.; Hua, Q.; Lee, K.Y. Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 2018, 231, 866–875. [Google Scholar] [CrossRef]
- Yin, Z. Development of solar thermal systems in China. Sol. Energy Mater. Sol. Cells 2005, 86, 427–442. [Google Scholar]
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Oró, E.; de Gracia, A.; Castell, A.; Farid, M.M.; Cabeza, L.F. Review on phase change materials (PCMs) for cold thermal energy storage applications. Appl. Energy 2012, 99, 513–533. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Experimental and numerical study of heat transfer performance of nitrate/expanded graphite composite PCM for solar energy storage. Energy Convers. Manag. 2015, 105, 272–284. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Nsofor, E.C. Solidification enhancement of PCM in a triplex-tube thermal energy storage system with nanoparticles and fins. Appl. Energy 2018, 211, 975–986. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Design of effective fins for fast PCM melting and solidification in shell-and-tube latent heat thermal energy storage through topology optimization. Appl. Energy 2017, 208, 210–227. [Google Scholar] [CrossRef]
- Kabeel, A.E.; Khalil, A.; Shalaby, S.M.; Zayed, M.E. Experimental investigation of thermal performance of flat and v-corrugated plate solar air heaters with and without PCM as thermal energy storage. Energy Convers. Manag. 2016, 113, 264–272. [Google Scholar] [CrossRef]
- Al-Hinti, I.; Al-Ghandoor, A.; Maaly, A.; Naqeera, I.A.; Al-Khateeb, Z.; Al-Sheikh, O. Experimental investigation on the use of water-phase change material storage in conventional solar water heating systems. Energy Convers. Manag. 2010, 51, 1735–1740. [Google Scholar] [CrossRef]
- Canbazoğlu, S.; Şahinaslan, A.; Ekmekyapar, A.; Aksoy, Ý.G.; Akarsu, F. Enhancement of solar thermal energy storage performance using sodium thiosulfate pentahydrate of a conventional solar water-heating system. Energy Build. 2005, 37, 235–242. [Google Scholar] [CrossRef]
- Belmonte, J.F.; Izquierdo-Barrientos, M.A.; Molina, A.E.; Almendros-Ibáñez, J.A. Air-based solar systems for building heating with PCM fluidized bed energy storage. Energy Build. 2016, 130, 150–165. [Google Scholar] [CrossRef]
- Veerappan, M.; Kalaiselvam, S.; Iniyan, S.; Goic, R. Phase change characteristic study of spherical PCMs in solar energy storage. Sol. Energy 2009, 83, 1245–1252. [Google Scholar] [CrossRef]
- Amina, B.; Miloud, A.; Samir, L.; Abdelylah, B.; Solano, J.P. Heat transfer enhancement in a parabolic trough solar receiver using longitudinal fins and nanofluids. J. Therm. Sci. 2016, 25, 410–417. [Google Scholar] [CrossRef]
- Eslamnezhad, H.; Rahimi, A.B. Enhance heat transfer for phase-change materials in triplex tube heat exchanger with selected arrangements of fins. Appl. Therm. Eng. 2017, 113, 813–821. [Google Scholar] [CrossRef]
- Kumar, R.A.; Babu, B.G.; Mohanraj, M. Experimental investigations on a forced convection solar air heater using packed bed absorber plates with phase change materials. Int. J. Green Energy 2017, 14, 1238–1255. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Alves, C.L.F.; Modesto, M.S. Numerical and experimental study on the solidification of PCM around a vertical axially finned isothermal cylinder. Appl. Therm. Eng. 2001, 21, 53–77. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Lohrasbi, S.; Ganji, D.D. Response surface method optimization of innovative fin structure for expediting discharging process in latent heat thermal energy storage system containing nano-enhanced phase change material. J. Taiwan Inst. Chem. Eng. 2016, 67, 115–125. [Google Scholar] [CrossRef]
- Lorenzini, G.; Rocha, L.A.O. Constructal design of Y-shaped assembly of fins. Int. J. Heat Mass Transf. 2006, 49, 4552–4557. [Google Scholar] [CrossRef]
- Tiari, S.; Qiu, S.; Mahdavi, M. Discharging process of a finned heat pipe–assisted thermal energy storage system with high temperature phase change material. Energy Convers. Manag. 2016, 118, 426–437. [Google Scholar] [CrossRef]
- Lohrasbi, S.; Miry, S.Z.; Gorji-Bandpy, M.; Ganji, D.D. Performance enhancement of finned heat pipe assisted latent heat thermal energy storage system in the presence of nano-enhanced H2O as phase change material. Int. J. Hydrogen Energy 2017, 42, 6526–6546. [Google Scholar] [CrossRef]
- Tiari, S.; Qiu, S.; Mahdavi, M. Numerical study of finned heat pipe-assisted thermal energy storage system with high temperature phase change material. Energy Convers. Manag. 2015, 89, 833–842. [Google Scholar] [CrossRef]
- Yin, Z.Q.; Harding, G.L.; Collins, R.E. Thermal performance of all glass coaxial vacuum tube solar collector. Sol. Energy Chin. 1997, 2, 19–20. [Google Scholar]
- Xi, W.H.; Wei, Y.K.; Zhang, L.Y. Practical Engineering Technology of Solar Energy; Lanzhou University Press: Lanzhou, China, 2001. [Google Scholar]
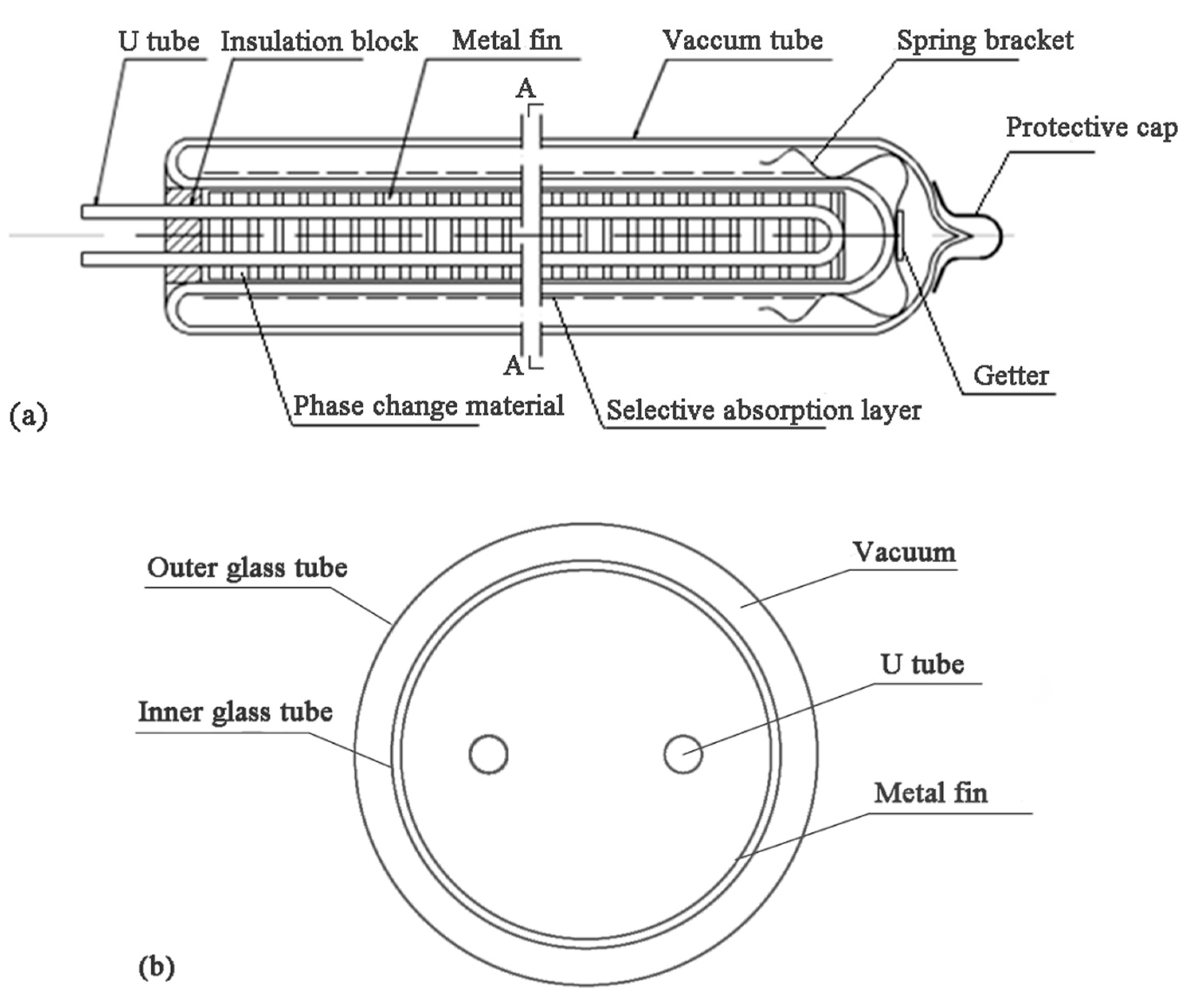

| Items | Paraffin | |
|---|---|---|
| Melting point (K) | 328–334 | |
| Latent heat (kJ·kg−1) | 158.2 | |
| Density (kg·m−3) | Solid phase | 837.7 |
| Liquid phase | 772.2 | |
| Specific heat (J·kg−1·K−1) | Solid phase | 3200 |
| Liquid phase | 2800 | |
| Heat conductivity (W·m−1·K−1) | Solid phase | 0.35 |
| Liquid phase | 0.15 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Xue, H.; Chen, Z.; Sun, L. Numerical Study of a New Solar Vacuum Tube Integrating with Phase Change Material. Sustainability 2019, 11, 6960. https://doi.org/10.3390/su11246960
Shi J, Xue H, Chen Z, Sun L. Numerical Study of a New Solar Vacuum Tube Integrating with Phase Change Material. Sustainability. 2019; 11(24):6960. https://doi.org/10.3390/su11246960
Chicago/Turabian StyleShi, Juan, Hua Xue, Zhenqian Chen, and Li Sun. 2019. "Numerical Study of a New Solar Vacuum Tube Integrating with Phase Change Material" Sustainability 11, no. 24: 6960. https://doi.org/10.3390/su11246960
APA StyleShi, J., Xue, H., Chen, Z., & Sun, L. (2019). Numerical Study of a New Solar Vacuum Tube Integrating with Phase Change Material. Sustainability, 11(24), 6960. https://doi.org/10.3390/su11246960





