Analysis of Walking-Edge Effect in Train Station Evacuation Scenarios: A Sustainable Transportation Perspective

Abstract

Due to the highly developed rail transit over the past decades, the phenomena of complex individual self-organized behaviors and mass crowd dynamics have become a great concern in the train station. In order to understand passengers’ walking-edge effect and analyze the relationship between the layout and sustainable service abilities of the train station, a heuristics-based social force model is proposed to elaborate the crowd dynamics. Several evacuation scenarios are implemented to describe the walking-edge effect in a train station with the evacuation efficiency, pedestrian flow, and crowd density map. The results show that decentralizing crowd flow can significantly increase the evacuation efficiency in different scenarios. When the exits are far away from the central axis of the railway station, the walking-edge effect has little influence on the evacuation efficiency. Obstacles can guide the movement of passengers by channelizing pedestrian flows. In addition, a wider side exit of the funnel-shaped corridors can promote walking-edge effect and decrease the pressure among a congested crowd. Besides providing a modified social force model with considering walking-edge effect, several suggestions are put forward for managers and architects of the train station in designing sustainable layouts.

1. Introduction

Over the past decade, traveling demands have increased rapidly due to world population growth [1]. As an effective mode of transport, especially with the massive construction of high-speed rail, train systems have become very popular and are now the mainstay of transportation in the metropolis [2]. It is reported that more than 58% (35.6 billion people) passengers chose railway as their travel transportation during the Spring Festival of China in 2019 [3]. Mass gathering frequently appears in major train stations. Meanwhile, crowd flows through the train station are typically characterized by high density and rapid movement. In the recent years, several natural or man-made disasters have led to the crowd stampede in some major train stations, resulting in property losses and casualties [4]. For example, on 29 September 2017, a human stampede event occurred at the Elphinstone train station in Mumbai, India, where 39 people were injured and 23 people died [5]. In May 2012, at a railway station in Pretoria, South Africa’s administrative capital, a massive evacuation caused 17 casualties [6]. All the emergency events draw attention to the need for developing protocols for crowd management and sustainable safety design of train stations.

As the station hubs are facing a huge risk in managing great numbers of mass gathering, the study on passenger crowd evacuation modeling and simulation has aroused great attention, for example, the complex nonlinear interaction between individuals, the topographic characteristics of the spaces [7,8], and so forth. Several empirical studies focus on the evacuation progress in the train station. Pedestrian evacuation experiments and surveys are carried out to recognize suitable factors during the evacuation process. Meanwhile, reliable passenger evacuation models are built to present virtual emergency scenarios [9]. In order to provide valuable information for model validation, researchers tend to explore the rule of passengers’ motions [10]. Shiwakoti et al. [11] studied the likely behaviors of train passengers and found that the frequency of herding or symmetry-breaking behavior was not as high as validations of previous mathematical models. In addition, some empirical studies focused on examining operational aspects by employing surveys of passengers in train station. Study by X Shi et al. [12] looked into passengers’ perception of security checks and found that most passengers preferred to trade-off their trip efficiency and privacy in exchange for safety improvement. In some cases, researchers have examined the relationship between safety behaviors and passengers’ psychological factors. Shiwakoti et al. [13] addressed that although most passengers thought it was not difficult to navigate the train station, they lacked perceptions, beliefs, and understanding of evacuation information, tools, and procedure in the emergency situation. Compared with passengers with the competitive and positive beliefs and perceptions, those passengers who were likely to do nothing were less likely to escape safely from the train station [14]. However, there are significant problems of empirical measurements and models because it is not possible to control all the variables (i.e., layouts of station, weather, personality of passengers, etc.) [15].

Though there are several studies conducting controlled laboratory experiments, evacuation drills, and relevant empirical researches, it is difficult to reproduce real passenger crowd evacuation scenarios due to the danger and limitation of experiments [16,17]. Consequently, existing studies on train station evacuation focus mainly on exploring descriptive models and simulations [11]. It is a challenging work to elaborate the complicated movements during passenger evacuation with specific mathematical models. Generally, these descriptive models are classified into three categories (i.e., microscopic, macroscopic, and mesoscopic models), which are widely conducted to analyze the rules of crowd evacuation in the train station. Specifically, microscopic models (i.e., social force model [18], cellular automata model [19]) focus on accurately expressing individual behaviors, while macroscopic models (i.e., continuum model [20], fluid dynamic model [21]) ignore individual differences and regard the crowd as a continuous fluid using average quantities such as the density. Moreover, the modeling basis of mesoscopic models (i.e., lattice gas model [22]) is between microscopic and macroscopic models. These existing models, whether microscopic, macroscopic, or mesoscopic models, are mostly conducted to evaluate the service level of public infrastructures under emergencies, reproduce the fundamental diagram, and describe dynamic characteristics [23]. Such as Tang et al. [24], who found that the service efficiency of ticket barriers and the boarding efficiency played a significant role on complex phenomena occurring in the station hall by using a cellular automaton (CA) model. Wang et al. [25] proposed a modified social force model to simulate how passenger numbers, ticket checking patterns, baggage volumes, and anxiety affect pedestrian flow in a station hall on the background of the Spring Festival in China. Accordingly, several simulation software tools (e.g., EXODUS, EVAC, Pathfinder, Anylogic, etc.) were conducted to model self-organized phenomena and specific emergency situations in train stations. Xuetong et al. [26] found that the number of passengers on the evacuation platform had a negative effect on the evacuation time by utilizing Anylogic software to simulate the evacuation process at Nanjing South Railway Station in China departure platform. Lei and Tai [27] used FDS and EVAC software to quantify the influence of the exits layouts on evacuation process and found that when an exit was located facing the staircases, the occupants flow rate was more stable. Chooramun et al. [28] developed Hybrid Spatial Discretization using EXODUS to simulate an underground rail tunnel station with 2000 agents.

Up to now, social force model has shown great advantage in modeling human motion [29]. Langston et al. [30] represented individuals by three circles shapes to incorporate the rotation of pedestrians, which was a better alternative to describe the projection of human body and collision movements [31]. Yuen and Lee [32] included overtaking behavior, while Hou et al. [33] combined the leadership effect to the social force model. Ma et al. [34] investigated the dual effects of guide-based guidance on evacuation under limited visibility via an extended social force model. Based on surveillance video during rush hours, Liu and Chen [35] extended the social force model to simulate the passengers choosing destinations and planning paths in metro station, considering the estimated distance, queuing number, and convenience. Moussaid et al. [36] proposed a heuristics-based model to search desired velocity with a heuristics intelligent optimum function. Based on the heuristic social force model, this study introduced several new rules and established a modified model to analyze walking-edge effect of passenger motion and evacuation dynamics in the train station hall.

The most important contribution of descriptive models and simulations is to reproduce and explicate the self-organized phenomena and behavioral effect, such as the arching queue, faster-is-slower effect, lane-forming, bandwagon effect, and clogging effects in the crowd evacuation [37,38]. For instance, Hong et al. [38] used the ripple effect and hypothesis of herd behavior to model the self-evacuation of passengers. Rigos et al. [39] explained the cry wolf effect in evacuation by the game-theoretic approach and found that improving the accuracy of thread detection can prevent large inefficiencies. Based on multi-agent simulation, Dossetti et al. [37] concluded that neither fully egotistic nor fully cooperative attitudes were optimal from the point of view of the crowd, which was analogous to the faster-is-slower effect. Besides, walking-along-side effect, imitation effect, and non-optimal effect were tested in outdoor public places [40]. Other researchers investigated how various factors including the capacity of the venue, physical conditions of exits, the level of crow panic, and other underlying causes related to the pedestrian’s behavioral effect [41].

It is important to note that although there are some differences between an evacuation in a train station and a building (i.e., stadium, high-rise building, library [40,41,42,43,44,45]), they may share some rules because of the similar pedestrian dynamic systems. Whereas, there are also significant differences in a train station that need to be considered from a sustainable transportation perspective. For instance, passengers usually walk more carefully in train stations due to special layouts and operation phases such as strict security checks of a station [11]. Therefore, several “safety rules” are proposed to describe the process of passenger crowd evacuation. For example, a passenger wants to escape from the nearest exit; a passenger avoids collision with other passengers and obstacles (walls) by adjusting his/her desired velocity; a passenger tends to walking along the sides, that is, walls, holding handrails, and other familiar facilities. Namely, the walking-edge effect is defined as that a pedestrian is willing to correspondingly adapt his/her actual velocity to desired velocity with a certain characteristic preference of walking along the side. The walking-edge effect is extended to a variable in our study. As mentioned before, a strategy of motion reflecting the passenger behavior cannot be determined by a unique feature within a model. Other aspects should be included, especially the sustainable terms of transportation, in order to evaluate the capability of infrastructures and the attitude of the passenger in conflicts or competitions for spaces. Hence, the study of understanding passengers’ walking-edge effect in a train station evacuation from a sustainable perspective demands specific attention.

The paper is organized as follows. Based on the literature review and analysis, the walking-edge effect factors are introduced to precisely describe the individual motion in train station evacuation scenarios in Section 2. It is then followed by a series of simulations and key results by taking simplified Wuchang Railway Station hall in China as the study object. Section 4 provides some detailed discussions and suggestions for the sustainable design of a train station. Finally, Section 5 presents the conclusions and recommendations for the future research.

2. Materials and Methods

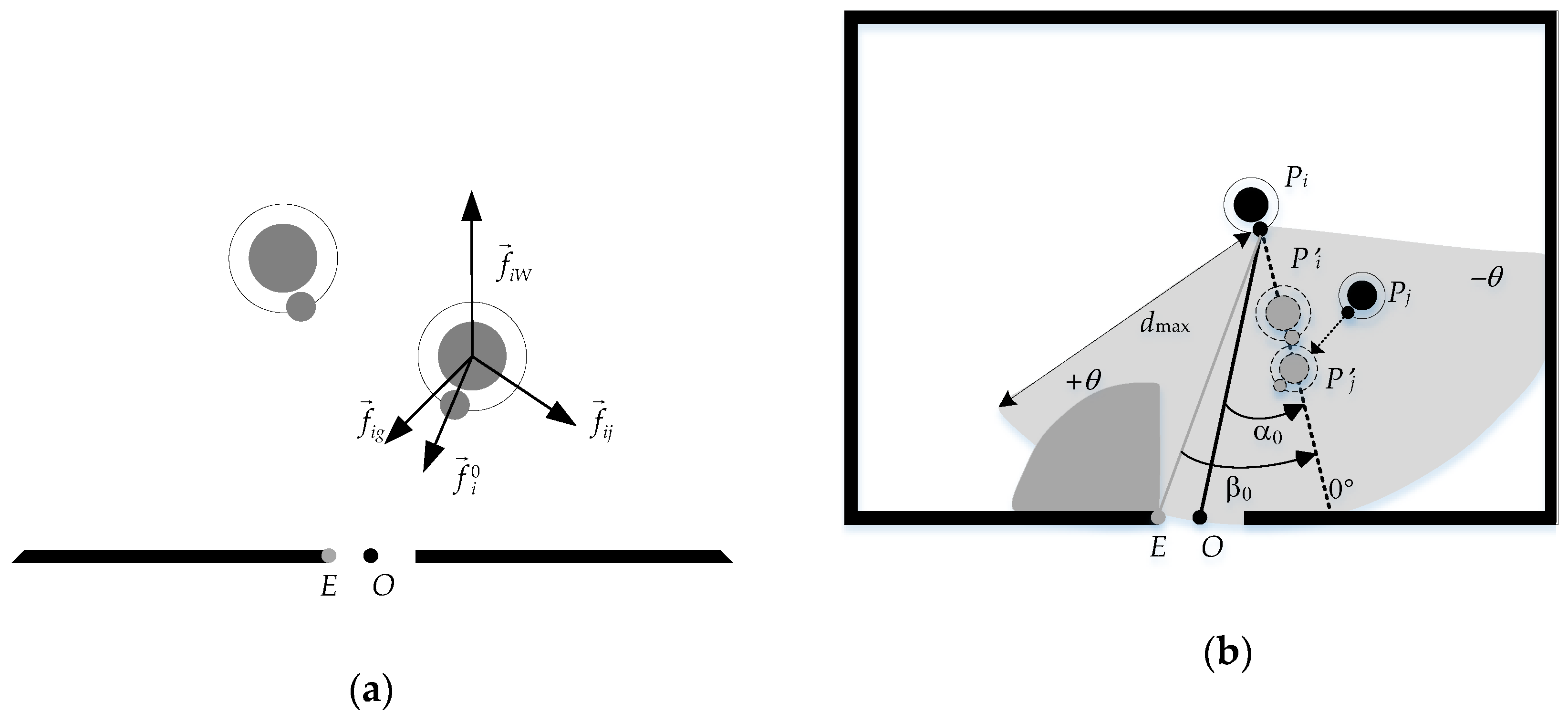
2.1. Evacuation Model

The crowd is a complicated system which is composed of pedestrian–pedestrian and pedestrian–environment interactions [46]. Nonetheless, specific to the individual, the movement behaviors of pedestrians in a crowd are influenced by psychological and physical forces simultaneously. As a well-known microscopic force-based model, the social force model regards pedestrians as self-driven multi-particles and describes pedestrian motions by introducing the self-driven force ${\overrightarrow{f}}_i^0$ and the repulsive effects with pedestrians ${\overrightarrow{f}}_{ij}$ and walls (obstacles) ${\overrightarrow{f}}_{iW}$. Each of N pedestrian $i$ of mass $m_i$ wants to walk with an individual desired speed $v_i^0$ in a certain direction ${\overrightarrow{e}}_i^0$ of the next destination in a 2 dimensional (2D) environment. Deviations of the actual velocity ${\overrightarrow{v}}_i$ from ${\overrightarrow{v}}_i^0=v_i^0{\overrightarrow{e}}_i$ are corrected within a certain characteristic time $\tau \approx 1s$. While each pedestrian moves with ${\overrightarrow{v}}_i$ towards an attractive point, he/she tends to keep a velocity-dependent distance from other pedestrians $j$ and W walls (obstacles). There are some circumstances, though, in which edge motions violating the shortest route principle are considered. In these cases, an enhanced model with walking-edge effect is preferable. In order to account for the walking-edge effect, a modified social force model is built by adding preference force of sideward points ${\overrightarrow{f}}_{ig}$, like attractive force presented by Wan et al. [47]. Hence, a mathematical formulation of enhanced social force model is given by the following acceleration equation:

$$m_i\frac{d{\overrightarrow{v}}_i}{dt}={\overrightarrow{f}}_i^0\left({\overrightarrow{v}}_i,v_i^0{\overrightarrow{e}}_i^0\right)+{\displaystyle \sum _{i(\ne j)}{\overrightarrow{f}}_{ij}\left({\overrightarrow{e}}^0{}_i,{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right)}+{\displaystyle \sum _W{\overrightarrow{f}}_{iW}\left({\overrightarrow{e}}^0{}_i,{\overrightarrow{r}}_i-{\overrightarrow{r}}_W\right)}+\lambda {\displaystyle \sum _g{\overrightarrow{f}}_{ig}({\overrightarrow{e}}^g{}_i,{\overrightarrow{r}}_i-{\overrightarrow{r}}_g)}+{\overrightarrow{\xi }}_i(t)$$

(1)

where ${\overrightarrow{r}}_i$, ${\overrightarrow{r}}_j$, ${\overrightarrow{r}}_W$ and ${\overrightarrow{r}}_g$ represent the position of pedestrians, walls, and sideward points, respectively, while parameter $\lambda \in \left[0,1\right]$ is designed in order to achieve suitable walking-edge effect of different pedestrians. Notably, fluctuation term ${\overrightarrow{\xi }}_i(t)$ denotes random behavioral variations which arise from other self-organized effects or psychological factors. Terms of the right of Equation (1) contain the repulsive forces and attractive forces. Self-driven force ${\overrightarrow{f}}_i^0$ and preference force of sideward points ${\overrightarrow{f}}_{ig}$ are attractive forces that determine pedestrian‘s movement towards his/her target, whereas the repulsive forces ${\overrightarrow{f}}_{ij}$, ${\overrightarrow{f}}_{iW}$ account for short-term corrective motions. These forces are expressed by Equations (2)–(5):

$${\overrightarrow{f}}_i^0\left({\overrightarrow{v}}_i,v_i^0{\overrightarrow{e}}_i^0\right)=m_i{\tau }_i^{-1}(v_i^0{\overrightarrow{e}}_i^0-{\overrightarrow{v}}_i),$$

(2)

$${\overrightarrow{f}}_{ij}\left({\overrightarrow{e}}_i^0,{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right)=A_i\exp (\frac{r_{ij}-d_{ij}}{B_i}){\overrightarrow{n}}_{ij}+k\mathsf{\Theta }(r_{ij}-d_{ij}){\overrightarrow{n}}_{ij}+K\mathsf{\Theta }(r_{ij}-d_{ij})\Delta v_{ij}^t{\overrightarrow{t}}_{ij}$$

(3)

$${\overrightarrow{f}}_{iW}\left({\overrightarrow{e}}_i^0,{\overrightarrow{r}}_i-{\overrightarrow{r}}_W\right)=A_i\exp (\frac{r_i-d_{iW}}{B_i}){\overrightarrow{n}}_{iW}+k\mathsf{\Theta }(r_i-d_{iW}){\overrightarrow{n}}_{iW}+K\mathsf{\Theta }(r_i-d_{iW})(v_i,{\overrightarrow{t}}_{iW}){\overrightarrow{n}}_{iW}$$

(4)

$${\overrightarrow{f}}_{ig}\left({\overrightarrow{e}}_i^g,{\overrightarrow{r}}_i-{\overrightarrow{r}}_g\right)=A_i\exp (\frac{r_i-d_{ig}}{B_i}){\overrightarrow{n}}_{ig}+k\mathsf{\Theta }(r_i-d_{ig}){\overrightarrow{n}}_{ig}+K\mathsf{\Theta }(r_i-d_{ig})\Delta v_{ig}^t{\overrightarrow{n}}_{ig}$$

(5)

where $A_i=2\times {10}^3 N$, $B_i=0.08 m$, $k=1.2\times {10}^5 kg/s^2$, and $K=2.4\times {10}^5 kg/m\cdot s$ are individual parameters and partly based on cultural conventions. $r_{ij}$ denotes the sum of the two pedestrians’ radius, while $d_{ij}$, $d_{iW}$ and $d_{ig}$ means the distance between the individual pedestrian’ center of mass to the other pedestrian, wall, and sideward points respectively. ${\overrightarrow{n}}_{ij}$, ${\overrightarrow{n}}_{iW}$, and ${\overrightarrow{n}}_{ig}$ are the normalized vectors, and ${\overrightarrow{t}}_{ij}$ represents the tangential direction. In cases of overcrowding, notice that when $r-d\le 0$, $\mathsf{\Theta }(x)=0$, otherwise, $\mathsf{\Theta }(x)=r-d$. The designation ${\overrightarrow{f}}_i^0$, ${\overrightarrow{f}}_{ig}$, ${\overrightarrow{f}}_{ij}$, ${\overrightarrow{f}}_{iW}$ and other parameters are shown in Equation (1). The illustration of the social force of pedestrian $i$ is depicted in Figure 1a.

Some researchers have developed a heuristics-based model to modify the traditional social force model with a heuristics intelligent optimum function, which can provide collision prediction [33]. Based on the model, an enhanced model was proposed to calculate the desired velocity ${\overrightarrow{v}}_i^0$ considering walking-edge effect. In Equations (1) and (2), the determination of ${\overrightarrow{v}}_i^0$ is an important content of the model. To make a clear statement of the calculating progress, several notations and assumptions are given as flows: pedestrian $i$ of mass $m_i$ moves at the velocity $v_i^0(0\le v_i^0\le v_i^{\max })$ along the direction of ${\overrightarrow{e}}_i^0(\Vert {\overrightarrow{e}}_i^0\Vert \in \left[-\theta ,\theta \right])$ to his/her destination point $O_i$, namely the place such as the exits, and wants to walk along the side towards sideward points $E_i$. Particularly, the vision field of pedestrian $i$ ranges to the left and to the right by $\theta °$ with respect to horizon distance $d_{\max }$. Pedestrian $i$ will collide with pedestrian $j$ at locations $i^{\prime }$ and $j^{\prime }$ after $\Delta t$ time. Then, $c(\gamma )=v_i^0\Delta t$ is the distance to the first collision with other pedestrian or obstacle along the direction $\gamma$. If no collision occurs, $c(\gamma )$ will set to a default value $d_{\max }$. Empirical evidence indicates that pedestrians tend to walk along the sides and seek an unobstructed walking direction, but avoid deviating too much from the shortest path to their destination. Accordingly, a trade-off has to be developed between avoiding detours and meeting walking-edge effect. The $\Delta t$ can be easily calculated given the location and velocities of pedestrian $i$ and $j$. Then, the value of $c(i)$ is computed through the minimization of the distance $d(\gamma )$ to the destination by two steps:

$$d{(\beta )}^{\ast }=min\left\{d_{max}^2+c{(\gamma )}^2-2d_{max}c(\gamma )cos({\beta }_0-\gamma ),d_{max}\right\}$$

(6)

$$d{(\gamma )}^{\ast }=min\left\{d_{max}^2+c{(\gamma )}^2-2d_{max}c(\gamma )cos({\alpha }_0-\gamma ),d{(\beta )}^{\ast }\right\}$$

(7)

where, ${\alpha }_0$ and ${\beta }_0$ are the direction of the destination and sideward points, respectively. Finally, the optimal velocity direction ${\overrightarrow{e}}_i^0=(cos{\gamma }^{\ast },sin{\gamma }^{\ast })$, where ${\gamma }^{\ast }=argmin\left\{d(\gamma )\right\}$ is the optimal direction. Figure 1b illustrates the calculation.

2.2. Validation

The precisions of models are very important to investigate the characteristics of pedestrian flow in a real case. In order to validate the proposed model, a serious of simulation and experiments were implemented to obtain the flow characteristics and walking-edge effect phenomena. The experiments were conducted in a university classroom (7 m × 6 m) with one single exit (1 m). In the experiments, the mass M of 21 volunteers was roughly distributed in the interval [49 kg, 76.9 kg], the radius r was set to [0.34 m, 0.5 m] (Figure 2a). Based on the real situation, a corresponding simulation model was conducted simultaneously. The simulation results were compared with the observation data.

Walking-edge effect is an important phenomenon in pedestrian flow of rushing for the exit. A snapshot of the experiment was recorded in Figure 2a, there were 21 pedestrians on the classroom, and the phenomenon walking-edge effect was clearly observed. Ten pedestrians chose to evacuate along the side from the classroom. During simulations, the same phenomenon was reproduced. Simulations are based on the configuration of the real experiment, and Figure 2b illustrates the simulation scenario. It turned out that the heuristics-based social force model can reflect the characteristics of pedestrians to some extent. However, this is not enough to prove that the model can reproduce flow characteristics.

According to the extracted data from the video recordings in the experiments, the cumulative number of pedestrians going out of the classroom were calculated for to analyze the details of evacuation process. To validate our model, simulations were conducted, and leaving time of each pedestrian was recorded and compared with video recordings (Figure 3a). It was found that the cumulative flow curves showed an approximately linear relationship with time. The slope of the curves represented the flow rate. Figure 3a shows the similar evacuation process between experimental and simulation scenarios. Therefore, our model could reproduce the observed dynamic flow characteristics. In addition, although the traditional social force model has been verified by ample real cases [33,46,47], our model introduced a special attractive force ${\overrightarrow{f}}_{ig}$ in Equation (1) which needs to be further calibrated. Therefore, under different $\lambda \in \left[0,1\right]$, each simulation scenario was repeated 5 times, and the evacuation time of each simulation was recorded and compared with the experiment (Figure 3b). The simulation parameters are the consistent with the results of experiments. It is found that with the increase of value of $\lambda$, the evacuation time of simulation presented an increasing trend. Particularly, the value of average evacuation time (t = 18.54) was the closest one to the real evacuation time when $\lambda$ is 0.2. Therefore, $\lambda =0.2$ was chosen as the standard parameter of the model.

2.3. Physical Model

Here, we choose Wuchang Railway Station in Wuhan, China as an example. Figure 4a is the aerial photo of Wuchang Railway Station, which was taken by Google Earth in 2019. Wuchang Railway Station is one of the three major railway stations in Wuhan. In 2008, the construction area of Wuchang Railway Station reached 49,000 m² after renovation and expansion, which can accommodate up to 8000 passengers simultaneously [48]. The overall layout of Wuhan Railway Station, which represents the general design of most transportation stations in China, is relatively symmetrical. Based on the actual design size and layout, a simplified station hall Wuchang Railway Station in 2D is constructed without considering stairs and other facilities.

The physical model of the station hall (60 m × 40 m) is mainly divided into the waiting hall (50 m × 20 m) and lobby (50 m × 10 m). There is only one single exit (3 m) in the central axis of the railway station and two service counters (3 m × 2 m), symmetrically distributed on the edge of the lobby. When an emergency occurs, passengers will evacuate from the waiting hall, escape across the lobby, then leave from the only exit. According to the observation and records, there are at least 1000 seats in the waiting hall, and each seat is connected into a seat column, forming an obstacle. Figure 4b illustrates the layout of the station hall.

2.4. Simulation Scenarios

The crowd in the train station hall is always concentrated and follows similar rules. For instance, passengers go to the ticket office to buy or pick up tickets, then arrive in the lobby through the ticket gate after security checking. They will enter their own waiting hall by getting information from the screen in the lobby hereafter, and board the train through the pedestrian bridge. Additionally, some passengers may get help from staff in the service counters. Obviously, exits and facilities in the station hall play an important role in safety evacuation [27,50]. Meanwhile, previous studies conducted controlled experiments on the effect of obstacle layouts on evacuation and found that different obstacle layouts have different influence on pedestrian flow [51,52].

Therefore, in order to better reflect the sustainable transportation perspective and walking-edge effect, four simulation scenarios (SS) were designed. As the control term, SS 1 is a normal train station hall evacuation scenario. SS 2 concentrates on effects of different exit layouts on the passenger evacuation. Three sub-SSs are discussed as follows, containing the different layouts of the exits. Pedestrians randomly choose one of the exits to escape from the station hall, and the service capacity (total length) of the exits is the same to ensure that the total material and economic consumption is equal in all sub-SSs.

• SS 2-1: The two exits (1.5 m) are located at the midpoint of line $a_0{d}_0$ and line $a_0{d}_1$ (i.e., position $b_0$, $c_0$) respectively;
• SS 2-2: Retain the position $a_0$ of original exit (1 m) and add two exits (1 m) at position $b_0$, $c_0$;
• SS 2-3: Retain the position $a_0$ of original exit (1 m) and change two exits’ (1 m) location to the edge position $d_0$, $d_1$.

SS 3 focuses on how the obstacles (service counters, seats) influence the evacuating process considering walking-edge effect. Generally, service counters often distribute between the lobby and waiting hall due to offering more convenient service for passengers. Although there were several simulation models and empirical verification showing beneficial effects of obstacles on the pedestrian flow near an exit, there still exists numerous arguments on the situation on which the beneficial effects of the obstacle could be observed [53]. Thus, the distribution of service counters was considered, particularly under the existing condition which represents the general layouts for station hall. In addition, the number of pedestrians wishing to leave increases with each row of seats that is closer to the edge. Therefore, the evacuation time is not only due to longer escaping distances, but also due to longer waiting times in queues [54]. This will increase anxiety, impatience, and so on in the crowd, particularly in situations considering walking-edge effect, which can cause clogging phenomena or human stampede. Consequently, the widths of egress routes along the side increased in SS 3-3 (Figure 5). Some sub-SS 3 details are showing below:

• SS 3-1: Combine two service counters into one (6 m × 2 m) and set it at the midpoint of line $b_1{c}_1$ (i.e., position $a_0$);
• SS 3-2: Retain the two service counters (3 m × 2 m) and symmetrically set them at position $b_1$, $c_1$;
• SS 3-3: Funnel-shaped side exits of corridors between a number of seats and walls were designed (Figure 5).

2.5. Evacuation Parameter Setting

In the simulation model, all passengers are assumed to be familiar with the exit of the station hall and the position of service counters. According to daily traffic statistics, 800 and 200 passengers are randomly distributed in the waiting hall and lobby, with a total of 1000 people in the entire station hall. Parameters for occupant evacuation simulation of the station hall are showing below:

• Based on the study of Lei et al. [55], the initial response time was uniformly distributed in the interval [0 s, 30 s].
• Combining the research [56] and observation results, the initial speed was uniformly distributed in the interval [0.3 m/s, 0.7 m/s], and the desired speed is approximately Gaussian-distributed with a mean value of 0.8 m/s and a standard deviation of 0.1 m/s.
• According to Xie et al. [57], the radius of passengers was set to [0.125 m, 0.25 m].

3. Simulation Results

The reasonable architectural layouts are important parts of sustainable transportation. Based on the heuristics-based social force model mentioned in Section 2 considering walking-edge effect, different train station hall SSs are simulated in this section. The different layouts of exits and obstacles are discussed in the three main SSs and other sub-SSs. The indicators reflecting the evacuation efficiency and safety are obtained. In addition, in order to promote the stability of the simulation results, every sub-SS was repeated five times to calculate the mean value as the final simulation result. The detailed analysis process and results are described as follows.

3.1. Evacuation Efficiency

In our study, like the result analysis method mentioned in [27], the number of pedestrians who were safely evacuated in the same period of time was employed to illustrate the evacuation efficiency. Then, the slope indicates the number of passengers who safely evacuate, and the evacuation time curve can represent the differences of evacuation efficiency in different sub-SSs. Obviously, a high slope of the curve indicates high evacuation efficiency, that is, the higher the evacuation efficiency, the greater the number of people who safely evacuate from the station hall at the same period in time. The tendency of the flow rate is the change rule of the flow rate with time. The evacuation time of each passenger in different sub-SSs is compared in Figure 6. The simulation results for seven sub-SSs are summarized in

Table 1. Simulation results for SS 1–SS 3.

Time Interval (s)	Number of Safely Evacuated People (p)							Evacuation Efficiency (p/s)
	SS 1	SS 2-1	SS 2-2	SS 2-3	SS 3-1	SS 3-2	SS 3-3	SS 1	SS 2-1	SS 2-2	SS 2-3	SS 3-1	SS 3-2	SS 3-3
0–50	93	161	190	194	96	89	88	1.86	3.22	3.80	3.88	1.92	1.78	1.76
50–100	102	195	239	233	103	91	96	2.04	3.90	4.78	4.66	2.06	1.82	1.92
100–150	114	192	226	192	99	109	116	2.28	3.84	4.52	3.84	1.98	2.18	2.32
150–200	128	186	206	156	117	123	137	2.56	3.72	4.12	3.12	2.34	2.46	2.74
200–250	133	140	107	96	145	132	141	2.66	2.80	2.14	1.92	2.90	2.64	2.82
250–300	111	76	31	68	145	125	109	2.22	1.52	0.62	1.36	2.90	2.50	2.18
300–350	52	48	−	60	152	82	88	1.04	0.96	−	1.20	3.04	1.64	1.76
350–400	117	1	−	−	130	79	74	2.34	0.02	−	−	2.60	1.58	1.48
400–539	149	−	−	−	12	169	150	1.07	−	−	−	0.09	1.22	1.08

.

As shown in Figure 6, the difference in the passenger evacuation among SS 1 (512.36 s), SS 3-2 (538.98 s), and SS 3-3 (508.84 s) is minimal. The evacuation time and evacuation efficiency are almost equivalent. The data analysis of all sub-SSs is presented in Table 1. SS 1, SS 3-2, and SS 3-3 show similar evacuation efficiency. The graph of SS 1, SS 3-2, and SS 3-3 almost share the same slope of the curve. Additionally, SS 3-1 (evacuation time is 413.52 s) shows a similar evacuation efficiency with SS 1, SS 3-2, and SS 3-3 in the early stage, but it shows an excellent evacuation efficiency after 300 s due to the relatively uniform evacuation efficiency at different time intervals. Compared with SS 1 and SS 3, three sub-SSs of SS 2 represent high evacuation efficiency, and the evacuation time of SS 2-2 (282.47 s) is the shortest in all sub-SSs. According to Figure 6a, the points of mean and median value of each pedestrian’s evacuation time almost coincide in their respective box diagrams, showing strong symmetry and stability. Correspondingly, the evacuation efficiency of all sub-SS 2 in different time intervals is higher than that of SS 1 and sub-SS 3 in the corresponding time period. To sum up concisely, in the evacuation of the train station hall considering the walking-edge effect, distribution of obstacles farther away from the exit (such as SS 3-2) has little effect on the evacuation efficiency. But, simply increasing the number of exits (SS 2) can significantly promote the evacuation capacity.

3.2. Pedestrian Flow

Pedestrian flows, which means the number of evacuees passing the exit in per unit time, can be used to monitor the evacuation of mass gathering as well. As shown in Figure 7a, in the evacuation process within the same number of passengers, the maximum and the mean values of pedestrian flow in SS 1 and sub-SSs 3 are almost equal, which indirectly indicates that obstacles keeping a long distance from the exit cannot stimulate walking-edge effect to decrease the pressure of pedestrian flow. It should be noticed that pedestrian flow in SS 3-1 is more balanced and stable. Potentially, the obstacle facing the exit may promote the walking-edge effect, forming standard flow of evacuees along the wall, which evenly shows different crowd distributions in different time periods.

Table 2. Pedestrian flow results for SS 1–SS 3.

Simulation Scenarios	Exit	Flow Rate of Passengers (p/s)
		Mean	Maximum	Minimum	Median	Standard Deviation
SS 1	$a_0$	1620	2560	36	1856	815
SS 2-1	$b_0$	1995	3539	83	2040	1122
	$c_0$	1565	3471	83	1505	944
SS 2-2	$a_0$	1862	3492	12	1836	1115
	$b_0$	1767	3780	12	1728	1053
	$c_0$	1833	3924	168	1896	1016
SS 2-3	$a_0$	2084	5076	72	1800	1451
	$d_0$	1701	2688	120	1824	850
	$d_1$	1591	2556	96	1764	816
SS 3-1	$a_0$	1572	2840	40	1576	907
SS 3-2	$a_0$	1732	2640	52	1916	810
SS 3-3	$a_0$	1626	2704	36	1788	858

shows the results of pedestrian flow near each exit in all sub-SSs.

Considering the multiple exits evacuation, Figure 7b shows the flow rate of passengers in all sub-SSs 2. Compared with SS 1, the maximum pedestrian flow rate of all exits in sub-SSs 2 is higher, because the width of the door is reduced. As to SS 2-1, the two exits are symmetrically distributed at midpoint of line $a_0{d}_0$ and line $a_0{d}_1$ (i.e., position $b_0$, $c_0$), and the overall distribution of pedestrian flow is consistent. However, the mean value of pedestrian flow of Exit $b_0$ is little higher than that of Exit $c_0$. Mainly because the exit $b_0$ is on the right side of $c_0$, while passengers hold the habit of walking on the right. Observing the pedestrian flow in different exits of SS 2-2 and SS 2-3, it can be found that although the three all exits are symmetrically distributed, if the other exits are farther away from the main Exit $a_0$, the clogging pressure at the main exit will increase sharply. This is because although people have the preference of walking along the side, it is not enough to sacrifice the long walking to avoid the congestion. In addition, if the three exits can be evenly distributed at points $a_0$, $b_0$, and $c_0$ (i.e., SS 2-2), it will effectively alleviate the pressure of the main exit, meanwhile, it can balance the pedestrian flow caused by walking-edge effect.

3.3. Density Map

Overcrowding is the direct cause of human stampede. Therefore, the density map is a powerful tool for analyzing the potential risks of mass gatherings. According to [58], the critical population density that causes the crowd stampede is 5.26 person/m², which is conducted as the dangerous density in the simulation. Figure 8 shows seven density maps of all sub-SSs. The whole shape of density map in the sub-SSs including a single exit (SS 1, sub-SSs 3) is funnel-shaped, and the friction among pedestrians near one exit leads to arching queue and clogging effects. Particularly, in addition to the main exit, the front exit of the corridor is a place where congestion occurs as well. Figure 8 compares a sustainable design (SS 3-3) of a train station hall with improved solutions, in which the blocks of seats have a trapeziform rather than a rectangular shape. As a consequence, it shows that the density of the side exit in the end of the funnel-shaped corridors is significantly reduced. Additionally, wake effect shows behind the service counters in SS 3-1 and SS 3-2. Whereas, there are few effects sharing the clogging pressure at the main exit and side exits of the corridors

Overall, multiple exits can more effectively alleviate the congestion pressure than a single exit. But, the different multi-exit distribution indicates the different shunting effects on considering walking-edge effect. When two exits are symmetrically distributed at midpoint of line $a_0{d}_0$ and line $a_0{d}_1$ (i.e., position $b_0$, $c_0$), like analysis results of pedestrian flow in SS 2-1, passengers are more inclined to evacuate from the exit on the right, Exit $b_0$. When there are three exits (SS 2-2 and SS 2-3), the side exit, to a certain extent, can share the congestion pressure. The willingness of walking-edge rarely appears due to more individual effort to detour. On the contrary, the exits which are not distributed on the side (SS 2-2) are better able to alleviate the pressure of the main export congestion.

4. Discussion

Considering the walking-edge effect, the simulation results show that different exits and obstacles layouts bring different levels of risk to train stations. Furthermore, how to combine the policy background of sustainable transportation in the train station with the layout design of a sustainable built environment is discussed henceforth. Several suggestions and policy implications of exits and obstacles layouts in the train station hall are put forward based on the perspective of walking-edge effect and sustainable transportation.

4.1. Effect of the Exit Layouts

Although the government has already implemented the general building code of the train station, it ignores the passengers’ self-organized phenomena in the process of specific implementation. However, due to factors in the different regions, such as the level of economy, regional culture, and geographic features, various types of exit layouts appear in the train station. The concept of sustainable transportation layout to these areas may lead to the different emphasis, as it not only needs to meet the passengers’ safety and regulation of the environment, but also the economic restriction and regional culture.

Similar to the theorem proposed in [59], if every exit is fully used during the evacuation, then evacuation time is reduced and evacuation efficiency is increased. Based on a modified social force model containing passengers’ walking-edge preference and simulation results, results show that decentralizing the crowd flow can increase evacuation efficiency. Specifically, evacuation efficiency in situations of multiple exits is always higher than that of a single exit, but a sustainable exits layout should distribute exits as evenly as possible and avoid designing them too close to the edge. In addition, passengers’ preference of walking on the right should be paid more attention in the railway station crowd management and architectural design. When designing the exit indication, passengers should be guided to use the exits evenly to avoid herd behavior caused by the walking-edge effect. Particular attention is paid to government departments and railway station administration, however, apart from strictly carrying out security inspections, patrols and traffic guidance should be strengthened to ensure that the main exits of railway stations are not blocked by unrelated personnel or goods (such as hawkers, sundries, etc.).

4.2. Effect of the Obstacles Layouts

Obstacles are a double-edged sword. They may hinder passenger motion by obscuring vision and occupying space, but they may guide passengers’ movement by channelizing pedestrian flow. In the situation of considering walking-edge effect, the results in Section 3 suggest that it is more beneficial to pedestrian movement when the obstacle is closer to the main exit. Conversely, obstacles that are farther away from the exits cannot effectively stimulate the walking-edge effect, thus have little effect on relieving the clogging pressure of the main exit. These conclusions were further verified in an experimental study [51]. Although there is no mandatory standard for the width of the corridor exit, appropriately increasing the width of the corridor side exit, while reducing construction materials and costs simultaneously, can obviously improve evacuation efficiency and safety [54].

As a consequence, it would be reasonable to properly design obstacles layouts in the train station. Firstly, train station designers should carefully evaluate the impact of the obstacle location on passenger evacuation because those obstacles (e.g., service counters, columns, seats, etc.) which are properly placed can serve safety functions by optimizing pedestrian flows. Secondly, depending on the design of obstacles layouts, they can provide accessibility to the railway station space and increase orientation, such as putting up evacuation posters on the obstacle. Then, for obstacles like a bench at the railway station, the average width of the side exit should be expanded, so that passengers’ preference of walking along the side is increased. For the train station, it should be encouraged to design funnel-shaped corridors rather than a rectangular shape. In addition, for government departments and legislatures, the impact of obstacle design on crowd evacuation must be rigorously assessed, and sustainable building design should be strengthened through establishing related legislations and regulations.

5. Conclusions

This study proposed a heuristics-based social force model to describe the passenger motion with considering walking-edge effect. In our model, some rules have been introduced to enhance the traditional social force model to represent the features. Additionally, considering the walking-edge effect, the desired velocity was calculated by a heuristics intelligent optimum function, which can be regarded as a so-called walking-edge and collision prediction process.

Then, the proposed model has been applied to simulate train station evacuation scenarios. Several simulation scenarios were conducted considering the layouts of exits and obstacles to analyze the sustainable abilities of the train station. Evacuation simulations of 1000 passengers were implemented to make further analyses on the flow characteristics such as the evacuation efficiency, pedestrian flow, and density map. It was found that decentralizing the crowd flow can increase evacuation efficiency. When the exits are far away from the central axis of the railway station, the walking-edge effect has little influence on the whole evacuation efficiency. According to simulations, obstacles can guide passenger movement by channelizing pedestrian flow, but only when the obstacle is closer to the main exit. Besides, a wider side exit of the funnel-shaped corridors can increase the preference of walking along the side and decrease the pressure in a pushy crowd. Based on simulation results, some suggestions and policy implications of exits and obstacles layouts in the train station hall were put forward.

However, certain limitations still exist in the current work. The parameter setting, relationship between walking-edge effect and scenarios, and mechanism of walking-edge effect rely on further studies. In addition, although an enhanced social force model was developed, more validations needs to be tested in real-life scenarios. Thus, more experiments of the evacuation motion in the train station should be conducted, trying to approach the real emergency situations. Mining parameters related to walking-edge effect and further research are valuable to improve evacuation efficiency.