Assessing the Economic-Environmental Efficiency of Energy Consumption and Spatial Patterns in China
Abstract
:1. Introduction
2. Literature Review
3. Research Method and Data
3.1. The Assessment of Economic-Environmental Efficiency in Energy Consumption
3.1.1. DEA
3.1.2. Indicators and Data
3.2. Spatial Autocorrelation Analysis
3.2.1. Global Spatial Autocorrelation Analysis
3.2.2. Local Spatial Autocorrelation Analysis
4. Results and Discussion
4.1. The Analysis of the Economic-Environmental Efficiency in Energy Consumption
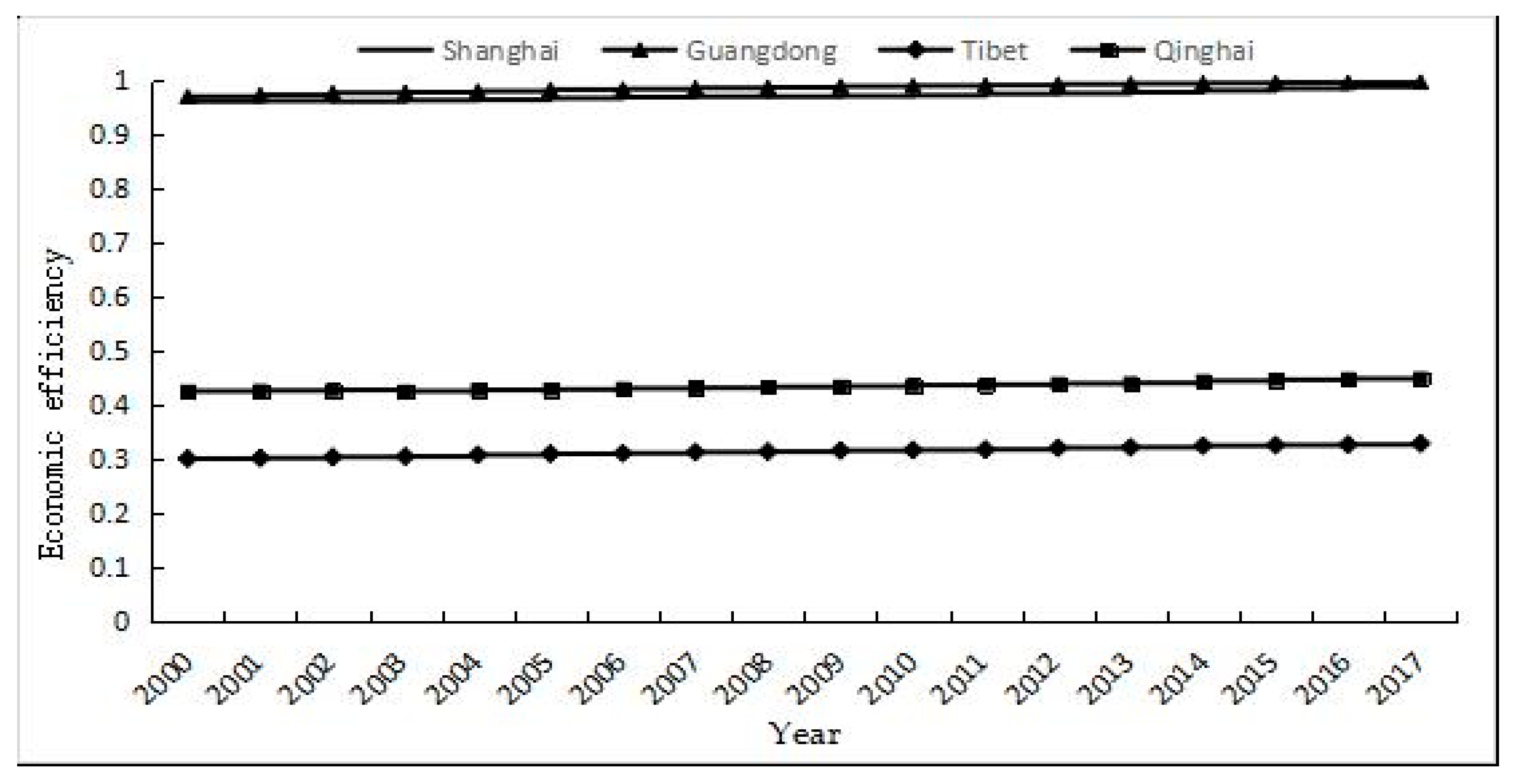
4.1.1. Economic Efficiency in Energy Consumption
4.1.2. Environmental Efficiency in Energy Consumption
4.2. Spatial Autocorrelation Analysis
4.2.1. Economic Efficiency in Energy Consumption
4.2.2. Environmental Efficiency in Energy Consumption
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, X.Y.; Zhao, H.L.; Jiang, L.; Lu, C.Y.; Xue, B. The Influence of Farmers’ Livelihood Strategies on Household Energy Consumption in the Eastern Qinghai–Tibet Plateau, China. Sustainability 2018, 10, 1780. [Google Scholar] [CrossRef]
- Lu, C.Y.; Li, W.L.; Pang, M.; Xue, B.; Miao, H. Quantifying the Economy-Environment Interactions in Tourism: Case of Gansu Province, China. Sustainability 2018, 10, 711. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Wang, K.Y.; Chen, X.P. The relationship between Ecological Efficiency Evolution and Environmental Regulation in China-based on SBM Model and Interprovincial Panel data estimation. Econ. Weky. 2015, 32, 126–131. (In Chinese) [Google Scholar]
- Sheng, C.H.; Cao, Y.; Xue, B. Residential Energy Sustainability in China and Germany: The Impact of National Energy Policy System. Sustainability 2018, 10, 4535. [Google Scholar] [CrossRef]
- Xu, S.T. Spatiotemporal Evolution and Influencing Factors of Energy Ecological Efficiency in China. Ph.D. Thesis, Liaoning Normal University, Dalian, China, 2016. (In Chinese). [Google Scholar]
- Jimenez, R.; Mercado, J. Energy Intensity: A Decomposition and Counterfactual Exercise for Latin American Countries. Energy Econ 2014, 42, 161–171. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. ‘Underlying Energy Efficiency’ in the US, CER-ETH Economics Working Paper Series. 2013; Volume 10, 2139.
- Proskuryakova, L.; Kovalev, A. Measuring energy efficiency: Is energy intensity a good evidence base? Appl. Energy 2015, 138, 450–459. [Google Scholar] [CrossRef]
- Gökgöz, F.; Güvercin, M.T. Energy security and renewable energy efficiency in EU. Renew. Sustain. Energy Rev. 2018, 96, 226–239. [Google Scholar] [CrossRef]
- Simsek, N. Energy Efficiency with Undesirable Output at the Economy-Wide level: Cross Country Comparison in OECD sample. Am. J. Energy Res. 2014, 2, 9–17. [Google Scholar] [CrossRef]
- Borozan, D. Technical and total factor energy efficiency of European regions: A two-stage approach. Energy 2018, 152, 521–532. [Google Scholar] [CrossRef]
- Wrigley, K.; Crawford, R.H. Identifying policy solutions for improving the energy efficiency of rental properties. Energy Policy 2017, 108, 369–378. [Google Scholar] [CrossRef]
- Huang, J.B.; Du, D.; Hao, Y. The driving forces of the change in China’s energy intensity: An empirical research using DEA-Malmquist and spatial panel estimations. Econ. Model. 2017, 65, 41–50. [Google Scholar] [CrossRef]
- Guan, W.; Xu, S.T. Spatial pattern and spatial effect of China’s energy ecological efficiency. J. Geogr. 2015, 70, 980–992. (In Chinese) [Google Scholar]
- Huang, J. Spatial correlation network structure of energy and environmental efficiency in China and its influencing factors. Resour. Sci. 2018, 40, 759–772. (In Chinese) [Google Scholar]
- Suzuki, S.; Nijkamp, P. An evaluation of energy-environment-economic efficiency for EU, APEC and ASEAN countries: Design of a Target-Oriented DFM model with fixed factors in Data Envelopment Analysis. Energy Policy 2016, 88, 100–112. [Google Scholar] [CrossRef]
- Jebali, E.; Hédi, E.; Khraief, N. The analysis of energy efficiency of the Mediterranean countries: A two-stage double bootstrap DEA approach. Energy 2017, 134, 991–1000. [Google Scholar] [CrossRef]
- Wang, T.; Yan, L.; Yi, M. Evaluation of energy ecological efficiency in China. Macroecon. Res. 2017, 7, 149–157. (In Chinese) [Google Scholar]
- Bhat, J.A.; Haider, S.; Kamaiah, B. Interstate energy efficiency of Indian paper industry: A slack-based non-parametric approach. Energy 2018, 161, 284–298. [Google Scholar] [CrossRef]
- Ghiyasi, M. Industrial sector environmental planning and energy efficiency of Iranian provinces. J. Clean. Prod. 2017, 142, 2328–2339. [Google Scholar] [CrossRef]
- Ruizfuensanta, M.J. The region matters: A comparative analysis of regional energy efficiency in Spain. Energy 2016, 101, 325–331. [Google Scholar] [CrossRef]
- Martínez, C.I.; William, H.; Piña, A. Regional analysis across Colombian departments: A non-parametric study of energy use. J. Clean. Prod. 2016, 115, 130–138. [Google Scholar] [CrossRef]
- Xu, H.; Bai, X.Y.; Cheng, S.Q.; Ma, G.Q. Comparative study on total factor energy efficiency of silk road economic belt. Ecol. Econ. 2018, 34, 44–49. (In Chinese) [Google Scholar]
- Zhang, N.; Fang, Z.G. Study on regional differences in total factor energy efficiency and its influencing factors in Xinjiang. Sci. Technol. Manag. Res. 2015, 9, 90–93. (In Chinese) [Google Scholar]
- Sağlam, U. A two-stage data envelopment analysis model for efficiency assessments of 39 state’s wind power in the United States. Energy Convers. Manag. 2017, 146, 52–67. [Google Scholar] [CrossRef]
- Wu, C.Q.; Dong, X. Study on total factor energy efficiency of the Yangtze river economic belt under environmental constraints. China Soft Sci. 2016, 3, 73–83. (In Chinese) [Google Scholar]
- Qin, Q.D.; Li, X.; Chen, X.D.; Li, L. Study on energy efficiency in China’s eastern coastal areas considering unexpected output. Sci. Technol. Manag. Stud. 2016, 36, 54–58. (In Chinese) [Google Scholar]
- Poggi, F.; Firmino, A.; Amado, M. Assessing energy performances: A step toward energy efficiency at the municipal level. Sustain. Cities Soc. 2017, 33, 57–69. [Google Scholar] [CrossRef]
- Mohseni, P.; Borghei, A.M.; Khanali, M. Coupled life cycle assessment and data envelopment analysis for mitigation of environmental impacts and enhancement of energy efficiency in grape production. J. Clean. Prod. 2018, 197, 937–947. [Google Scholar] [CrossRef]
- Raheli, H.; Rezaei, R.M.; Jadidi, M.R. A two-stage DEA model to evaluate sustainability and energy efficiency of tomato production. Inf. Process. Agric. 2017, 4, 342–350. [Google Scholar] [CrossRef]
- Goto, M.; Otsuka, A.; Sueyoshi, T. DEA (Data Envelopment Analysis) assessment of operational and environmental efficiencies on Japanese regional industries. Energy 2014, 66, 535–549. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, H.; Wang, Y.L. Total factor energy efficiency analysis of jiangsu province based on DEA model. Land Nat. Resour. Res. 2018, 1, 59–61. (In Chinese) [Google Scholar]
- Jiang, C. Research on Energy Efficiency Measurement of Resource-Based Cities Based on Full Factor Framework. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2017. (In Chinese). [Google Scholar]
- Imran, M.; Özçatalbaş, O.; Bashir, M.K. Estimation of energy efficiency and greenhouse gas emission of cotton crop in South Punjab, Pakistan. J. Saudi Soc. Agric. Sci. 2018, in press. [Google Scholar] [CrossRef]
- Sun, X.M.; Wang, G.; Dong, H.Z.; Zhang, H. Study on carbon Emission efficiency and influencing factors of Resource-Based cities based on DEA and SE-SBM Model. Res. Sci. Technol. Manag. 2016, 36, 78–84. (In Chinese) [Google Scholar]
- Huang, H.F.; Ge, L.; Wang, M.C. An Analysis of the Energy efficiency of Urban Total element in China. Urban Issues 2015, 8, 53–60. (In Chinese) [Google Scholar]
- Ewertowska, A.; Galán-Martín, A.; Guillén-Gosálbez, G.; Gavaldá, J.; Jiménez, L. Assessment of the environmental efficiency of the electricity mix of the top European economies via data envelopment analysis. J. Clean. Prod. 2016, 116, 13–22. [Google Scholar] [CrossRef]
- Fang, J.C.; Liu, L.X.; Wan, Q. Regional differences in total factor energy efficiency in China. China Mark. 2015, 34, 10–14. (In Chinese) [Google Scholar]
- Yang, T.; Chen, W.; Zhou, K.L.; Ren, M.L. Regional energy efficiency evaluation in China: A super efficiency slack-based measure model with undesirable outputs. J. Clean. Prod. 2018, 198, 859–866. [Google Scholar] [CrossRef]
- Chen, L.; Jia, G.Z. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853. [Google Scholar] [CrossRef]
- Zhu, D.M.; Zhao, H.B. Regional difference analysis of China’s energy environmental efficiency under environmental constraints. Nanjing Soc. Sci. 2016, 4, 15–23. (In Chinese) [Google Scholar]
- Cao, Q.; Fan, M.T. Study on interprovincial energy efficiency rating in China-empirical analysis based on multi-ordered Probit model. Shanghai Econ. Res. 2016, 2, 72–81. (In Chinese) [Google Scholar]
- Huang, Y.Y.; Yan, Q.W.; Zhang, C.R. Spatial–Temporal Distribution Characteristics of PM2.5 in China in 2016. J. Geovis. Spat. Anal. 2018, 2. [Google Scholar] [CrossRef]
- Ghosh, K.G. Analysis of Rainfall Trends and its Spatial Patterns During the Last Century over the Gangetic West Bengal, Eastern India. J. Geovis. Spat. Anal. 2018, 2. [Google Scholar] [CrossRef]
- Zhang, W.; Pan, X.F.; Yan, Y.B.; Pan, X.Y. Convergence analysis of regional energy efficiency in china based on large-dimensional panel data model. J. Clean. Prod. 2017, 142, 801–808. [Google Scholar] [CrossRef]
- Tang, H.B. Study on Spatial Measurement of Regional Energy Economic Efficiency Association and Its Influencing Factors in China. Master’s Thesis, Chongqing Normal University, Chongqing, China, 2017. (In Chinese). [Google Scholar]
- Zhao, N.; Wang, X.R.; Zhu, W.J. Study on convergence of China’s inter-provincial energy efficiency. Stat. Stud. 2015, 32, 29–35. (In Chinese) [Google Scholar]
- Sun, J.S.; Li, G.; Wang, Z.H. Optimizing China’s energy consumption structure under energy and carbon constraints. Struct. Chang. Econ. Dyn. 2018, in press. [Google Scholar] [CrossRef]
- Wang, K.; Yu, S.W.; Zhang, W. China’s regional energy and environmental efficiency: A DEA window analysis based dynamic evaluation. Math. Comput. Model. 2018, 58, 1117–1127. [Google Scholar] [CrossRef]
- Zhao, X.L.; Yang, R.; Ma, Q. China’s total factor energy efficiency of provincial industrial sectors. Energy 2014, 65, 52–61. [Google Scholar]
- Yang, L.; Ouyang, H.; Fang, K.N.; Ye, L.L.; Zhang, J. Evaluation of regional environmental efficiencies in China based on super-efficiency-DEA. Ecol. Indic. 2018, 51, 13–19. [Google Scholar] [CrossRef]
- Song, M.L.; Peng, J.; Wang, J.L.; Zhao, J.J. Environmental efficiency and economic growth of China: A Ray slack-based model analysis. Eur. J. Oper. Res. 2018, 269, 51–63. [Google Scholar] [CrossRef]
- Wu, X.X. Regional differences in energy and environmental efficiency under the pressure of energy conservation and emission reduction and their influencing mechanism. Ecol. Econ. 2018, 34, 49–56. (In Chinese) [Google Scholar]



| Province | Year | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | |
| Beijing | 0.955 | 0.956 | 0.957 | 0.959 | 0.961 | 0.964 | 0.966 | 0.969 | 0.970 |
| Tianjin | 0.822 | 0.826 | 0.830 | 0.833 | 0.839 | 0.844 | 0.845 | 0.847 | 0.847 |
| Hebei | 0.559 | 0.557 | 0.560 | 0.564 | 0.589 | 0.608 | 0.614 | 0.628 | 0.624 |
| Shanxi | 0.517 | 0.526 | 0.531 | 0.539 | 0.562 | 0.571 | 0.570 | 0.581 | 0.583 |
| Inner Mongolia | 0.585 | 0.583 | 0.585 | 0.587 | 0.589 | 0.594 | 0.596 | 0.597 | 0.601 |
| Liaoning | 0.882 | 0.886 | 0.884 | 0.889 | 0.891 | 0.896 | 0.897 | 0.896 | 0.899 |
| Jilin | 0.687 | 0.670 | 0.675 | 0.677 | 0.691 | 0.721 | 0.728 | 0.731 | 0.739 |
| Heilongjiang | 0.721 | 0.726 | 0.727 | 0.735 | 0.739 | 0.742 | 0.751 | 0.759 | 0.767 |
| Shanghai | 0.962 | 0.963 | 0.962 | 0.964 | 0.965 | 0.968 | 0.970 | 0.971 | 0.971 |
| Jiangsu | 0.798 | 0.799 | 0.802 | 0.806 | 0.814 | 0.819 | 0.818 | 0.820 | 0.821 |
| Zhejiang | 0.786 | 0.788 | 0.787 | 0.789 | 0.801 | 0.801 | 0.804 | 0.811 | 0.818 |
| Anhui | 0.688 | 0.689 | 0.692 | 0.694 | 0.699 | 0.702 | 0.709 | 0.716 | 0.721 |
| Fujian | 0.793 | 0.810 | 0.823 | 0.836 | 0.850 | 0.862 | 0.871 | 0.879 | 0.881 |
| Jiangxi | 0.661 | 0.668 | 0.673 | 0.678 | 0.682 | 0.684 | 0.689 | 0.690 | 0.698 |
| Shandong | 0.643 | 0.649 | 0.651 | 0.657 | 0.658 | 0.662 | 0.667 | 0.669 | 0.670 |
| Henan | 0.639 | 0.641 | 0.649 | 0.650 | 0.653 | 0.654 | 0.655 | 0.657 | 0.657 |
| Hubei | 0.628 | 0.629 | 0.629 | 0.631 | 0.632 | 0.634 | 0.636 | 0.641 | 0.644 |
| Hunan | 0.657 | 0.657 | 0.659 | 0.660 | 0.662 | 0.664 | 0.667 | 0.668 | 0.670 |
| Guangdong | 0.971 | 0.974 | 0.978 | 0.979 | 0.981 | 0.984 | 0.985 | 0.987 | 0.988 |
| Guangxi | 0.671 | 0.672 | 0.673 | 0.675 | 0.674 | 0.676 | 0.679 | 0.680 | 0.682 |
| Hainan | 0.898 | 0.899 | 0.901 | 0.907 | 0.909 | 0.913 | 0.914 | 0.916 | 0.919 |
| Chongqing | 0.679 | 0.681 | 0.680 | 0.682 | 0.684 | 0.685 | 0.687 | 0.688 | 0.690 |
| Sichuan | 0.539 | 0.543 | 0.549 | 0.551 | 0.559 | 0.563 | 0.567 | 0.569 | 0.572 |
| Guizhou | 0.473 | 0.474 | 0.476 | 0.477 | 0.476 | 0.479 | 0.480 | 0.482 | 0.483 |
| Yunnan | 0.549 | 0.550 | 0.553 | 0.554 | 0.559 | 0.560 | 0.561 | 0.563 | 0.564 |
| Tibet | 0.301 | 0.302 | 0.304 | 0.305 | 0.308 | 0.310 | 0.311 | 0.313 | 0.314 |
| Shanxi | 0.481 | 0.482 | 0.481 | 0.483 | 0.486 | 0.488 | 0.489 | 0.493 | 0.494 |
| Gansu | 0.460 | 0.461 | 0.463 | 0.468 | 0.469 | 0.471 | 0.472 | 0.475 | 0.476 |
| Qinghai | 0.426 | 0.427 | 0.428 | 0.426 | 0.428 | 0.429 | 0.431 | 0.432 | 0.434 |
| Ningxia | 0.453 | 0.457 | 0.458 | 0.460 | 0.461 | 0.462 | 0.464 | 0.467 | 0.468 |
| Xinjiang | 0.438 | 0.439 | 0.441 | 0.442 | 0.443 | 0.444 | 0.447 | 0.449 | 0.450 |
| Average | 0.6566 | 65.1928 | 65.2260 | 65.262 | 65.299 | 0.6583 | 65.371 | 65.406 | 65.441 |
| Province | Year | ||||||||
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
| Beijing | 0.971 | 0.979 | 0.980 | 0.980 | 0.981 | 0.983 | 0.984 | 0.987 | 0.988 |
| Tianjin | 0.850 | 0.852 | 0.857 | 0.855 | 0.861 | 0.869 | 0.874 | 0.879 | 0.882 |
| Hebei | 0.687 | 0.752 | 0.752 | 0.761 | 0.770 | 0.786 | 0.793 | 0.801 | 0.802 |
| Shanxi | 0.594 | 0.615 | 0.624 | 0.629 | 0.647 | 0.650 | 0.662 | 0.667 | 0.674 |
| Inner Mongolia | 0.614 | 0.627 | 0.630 | 0.638 | 0.647 | 0.658 | 0.663 | 0.671 | 0.710 |
| Liaoning | 0.904 | 0.911 | 0.915 | 0.918 | 0.921 | 0.925 | 0.928 | 0.930 | 0.931 |
| Jilin | 0.747 | 0.753 | 0.759 | 0.766 | 0.770 | 0.738 | 0.824 | 0.828 | 0.830 |
| Heilongjiang | 0.775 | 0.783 | 0.791 | 0.791 | 0.796 | 0.805 | 0.810 | 0.814 | 0.816 |
| Shanghai | 0.972 | 0.973 | 0.976 | 0.977 | 0.979 | 0.982 | 0.986 | 0.989 | 0.991 |
| Jiangsu | 0.824 | 0.825 | 0.829 | 0.830 | 0.835 | 0.841 | 0.849 | 0.850 | 0.851 |
| Zhejiang | 0.826 | 0.837 | 0.841 | 0.848 | 0.856 | 0.864 | 0.872 | 0.876 | 0.878 |
| Anhui | 0.727 | 0.731 | 0.738 | 0.746 | 0.749 | 0.756 | 0.764 | 0.768 | 0.770 |
| Fujian | 0.890 | 0.896 | 0.896 | 0.899 | 0.904 | 0.909 | 0.914 | 0.917 | 0.918 |
| Jiangxi | 0.705 | 0.709 | 0.716 | 0.721 | 0.725 | 0.729 | 0.734 | 0.736 | 0.737 |
| Shandong | 0.673 | 0.678 | 0.680 | 0.684 | 0.689 | 0.711 | 0.724 | 0.725 | 0.728 |
| Henan | 0.659 | 0.663 | 0.669 | 0.671 | 0.675 | 0.681 | 0.685 | 0.688 | 0.690 |
| Hubei | 0.645 | 0.647 | 0.648 | 0.648 | 0.649 | 0.651 | 0.652 | 0.654 | 0.658 |
| Hunan | 0.672 | 0.673 | 0.675 | 0.676 | 0.679 | 0.680 | 0.682 | 0.682 | 0.684 |
| Guangdong | 0.990 | 0.991 | 0.992 | 0.994 | 0.995 | 0.996 | 0.997 | 0.997 | 0.998 |
| Guangxi | 0.683 | 0.685 | 0.688 | 0.689 | 0.691 | 0.692 | 0.695 | 0.696 | 0.698 |
| Hainan | 0.921 | 0.924 | 0.925 | 0.928 | 0.930 | 0.934 | 0.936 | 0.937 | 0.939 |
| Chongqing | 0.691 | 0.692 | 0.694 | 0.698 | 0.710 | 0.718 | 0.724 | 0.732 | 0.736 |
| Sichuan | 0.573 | 0.574 | 0.576 | 0.577 | 0.579 | 0.580 | 0.583 | 0.585 | 0.586 |
| Guizhou | 0.485 | 0.486 | 0.487 | 0.487 | 0.489 | 0.490 | 0.491 | 0.493 | 0.494 |
| Yunnan | 0.566 | 0.569 | 0.570 | 0.571 | 0.572 | 0.573 | 0.577 | 0.579 | 0.580 |
| Tibet | 0.316 | 0.317 | 0.318 | 0.321 | 0.322 | 0.325 | 0.326 | 0.327 | 0.329 |
| Shanxi | 0.495 | 0.497 | 0.498 | 0.499 | 0.501 | 0.504 | 0.505 | 0.507 | 0.508 |
| Gansu | 0.478 | 0.479 | 0.481 | 0.484 | 0.485 | 0.486 | 0.488 | 0.489 | 0.491 |
| Qinghai | 0.435 | 0.437 | 0.438 | 0.440 | 0.441 | 0.445 | 0.447 | 0.449 | 0.450 |
| Ningxia | 0.469 | 0.471 | 0.473 | 0.476 | 0.477 | 0.479 | 0.480 | 0.483 | 0.484 |
| Xinjiang | 0.452 | 0.453 | 0.455 | 0.458 | 0.459 | 0.461 | 0.464 | 0.465 | 0.467 |
| Average | 67.6467 | 0.66 | 67.721 | 0.699 | 67.795 | 67.832 | 0.663 | 67.908 | 0.668 |
| Province | Year | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | |
| Beijing | 0.821 | 0.829 | 0.837 | 0.848 | 0.857 | 0.869 | 0.867 | 0.872 | 0.880 |
| Tianjin | 0.721 | 0.732 | 0.739 | 0.743 | 0.756 | 0.763 | 0.769 | 0.776 | 0.781 |
| Hebei | 0.498 | 0.503 | 0.506 | 0.509 | 0.511 | 0.514 | 0.522 | 0.529 | 0.531 |
| Shanxi | 0.421 | 0.428 | 0.433 | 0.438 | 0.441 | 0.448 | 0.453 | 0.460 | 0.466 |
| Inner Mongolia | 0.563 | 0.570 | 0.576 | 0.581 | 0.587 | 0.594 | 0.599 | 0.563 | 0.568 |
| Liaoning | 0.671 | 0.678 | 0.682 | 0.689 | 0.697 | 0.709 | 0.715 | 0.720 | 0.727 |
| Jilin | 0.642 | 0.649 | 0.657 | 0.660 | 0.668 | 0.674 | 0.679 | 0.686 | 0.691 |
| Heilongjiang | 0.710 | 0.716 | 0.720 | 0.728 | 0.731 | 0.738 | 0.742 | 0.749 | 0.752 |
| Shanghai | 0.913 | 0.917 | 0.924 | 0.928 | 0.932 | 0.938 | 0.943 | 0.949 | 0.953 |
| Jiangsu | 0.791 | 0.794 | 0.796 | 0.799 | 0.804 | 0.808 | 0.811 | 0.813 | 0.816 |
| Zhejiang | 0.698 | 0.699 | 0.672 | 0.675 | 0.679 | 0.682 | 0.687 | 0.691 | 0.694 |
| Anhui | 0.613 | 0.618 | 0.621 | 0.624 | 0.629 | 0.634 | 0.638 | 0.640 | 0.645 |
| Fujian | 0.784 | 0.787 | 0.789 | 0.790 | 0.792 | 0.796 | 0.798 | 0.801 | 0.803 |
| Jiangxi | 0.642 | 0.647 | 0.650 | 0.654 | 0.657 | 0.661 | 0.664 | 0.669 | 0.672 |
| Shandong | 0.629 | 0.632 | 0.633 | 0.635 | 0.639 | 0.641 | 0.643 | 0.644 | 0.648 |
| Henan | 0.625 | 0.628 | 0.629 | 0.631 | 0.635 | 0.638 | 0.640 | 0.643 | 0.644 |
| Hubei | 0.619 | 0.621 | 0.622 | 0.624 | 0.626 | 0.627 | 0.629 | 0.629 | 0.631 |
| Hunan | 0.648 | 0.649 | 0.651 | 0.652 | 0.654 | 0.657 | 0.658 | 0.660 | 0.661 |
| Guangdong | 0.908 | 0.911 | 0.913 | 0.914 | 0.916 | 0.919 | 0.921 | 0.923 | 0.924 |
| Guangxi | 0.664 | 0.665 | 0.668 | 0.669 | 0.671 | 0.672 | 0.674 | 0.675 | 0.678 |
| Hainan | 0.886 | 0.889 | 0.891 | 0.892 | 0.892 | 0.894 | 0.895 | 0.897 | 0.899 |
| Chongqing | 0.583 | 0.585 | 0.586 | 0.588 | 0.591 | 0.596 | 0.597 | 0.599 | 0.602 |
| Sichuan | 0.527 | 0.529 | 0.532 | 0.533 | 0.535 | 0.536 | 0.538 | 0.541 | 0.542 |
| Guizhou | 0.432 | 0.433 | 0.435 | 0.437 | 0.440 | 0.443 | 0.445 | 0.448 | 0.449 |
| Yunnan | 0.537 | 0.539 | 0.542 | 0.546 | 0.548 | 0.549 | 0.551 | 0.552 | 0.554 |
| Tibet | 0.288 | 0.289 | 0.291 | 0.293 | 0.294 | 0.295 | 0.297 | 0.298 | 0.301 |
| Shanxi | 0.478 | 0.479 | 0.482 | 0.483 | 0.484 | 0.486 | 0.489 | 0.491 | 0.491 |
| Gansu | 0.376 | 0.378 | 0.379 | 0.381 | 0.383 | 0.384 | 0.386 | 0.389 | 0.390 |
| Qinghai | 0.424 | 0.425 | 0.427 | 0.428 | 0.429 | 0.431 | 0.433 | 0.434 | 0.437 |
| Ningxia | 0.469 | 0.470 | 0.472 | 0.473 | 0.475 | 0.477 | 0.478 | 0.481 | 0.482 |
| Xinjiang | 0.456 | 0.457 | 0.459 | 0.461 | 0.462 | 0.464 | 0.465 | 0.467 | 0.469 |
| Average | 65.116 | 65.151 | 65.1860 | 65.221 | 65.2576 | 65.293 | 65.328 | 65.362 | 65.397 |
| Province | Year | ||||||||
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
| Beijing | 0.886 | 0.910 | 0.918 | 0.927 | 0.931 | 0.938 | 0.943 | 0.947 | 0.949 |
| Tianjin | 0.786 | 0.792 | 0.791 | 0.794 | 0.796 | 0.802 | 0.811 | 0.816 | 0.820 |
| Hebei | 0.539 | 0.547 | 0.551 | 0.558 | 0.567 | 0.573 | 0.582 | 0.589 | 0.594 |
| Shanxi | 0.471 | 0.479 | 0.482 | 0.487 | 0.490 | 0.496 | 0.501 | 0.508 | 0.513 |
| Inner Mongolia | 0.579 | 0.586 | 0.592 | 0.598 | 0.606 | 0.611 | 0.619 | 0.624 | 0.637 |
| Liaoning | 0.734 | 0.742 | 0.749 | 0.758 | 0.763 | 0.771 | 0.778 | 0.781 | 0.788 |
| Jilin | 0.695 | 0.713 | 0.719 | 0.726 | 0.732 | 0.739 | 0.744 | 0.749 | 0.756 |
| Heilongjiang | 0.760 | 0.768 | 0.776 | 0.781 | 0.785 | 0.788 | 0.792 | 0.799 | 0.807 |
| Shanghai | 0.958 | 0.961 | 0.964 | 0.965 | 0.968 | 0.970 | 0.972 | 0.973 | 0.975 |
| Jiangsu | 0.821 | 0.827 | 0.829 | 0.831 | 0.834 | 0.835 | 0.837 | 0.838 | 0.840 |
| Zhejiang | 0.698 | 0.701 | 0.705 | 0.709 | 0.714 | 0.716 | 0.719 | 0.723 | 0.725 |
| Anhui | 0.649 | 0.652 | 0.658 | 0.663 | 0.666 | 0.671 | 0.676 | 0.681 | 0.689 |
| Fujian | 0.804 | 0.806 | 0.809 | 0.810 | 0.812 | 0.813 | 0.816 | 0.817 | 0.819 |
| Jiangxi | 0.673 | 0.674 | 0.678 | 0.680 | 0.682 | 0.685 | 0.687 | 0.689 | 0.692 |
| Shandong | 0.652 | 0.655 | 0.657 | 0.658 | 0.657 | 0.659 | 0.661 | 0.664 | 0.669 |
| Henan | 0.645 | 0.647 | 0.648 | 0.650 | 0.652 | 0.654 | 0.657 | 0.658 | 0.660 |
| Hebei | 0.633 | 0.636 | 0.638 | 0.639 | 0.642 | 0.644 | 0.648 | 0.649 | 0.651 |
| Hunan | 0.664 | 0.665 | 0.666 | 0.669 | 0.671 | 0.672 | 0.672 | 0.675 | 0.678 |
| Guangdong | 0.927 | 0.929 | 0.932 | 0.934 | 0.935 | 0.937 | 0.938 | 0.941 | 0.943 |
| Guangxi | 0.679 | 0.681 | 0.683 | 0.685 | 0.686 | 0.688 | 0.689 | 0.691 | 0.693 |
| Hainan | 0.902 | 0.908 | 0.909 | 0.911 | 0.913 | 0.917 | 0.919 | 0.921 | 0.922 |
| Chongqing | 0.605 | 0.609 | 0.612 | 0.614 | 0.618 | 0.621 | 0.625 | 0.627 | 0.629 |
| Sichuan | 0.544 | 0.545 | 0.548 | 0.551 | 0.552 | 0.554 | 0.557 | 0.559 | 0.561 |
| Guizhou | 0.451 | 0.452 | 0.454 | 0.457 | 0.458 | 0.461 | 0.463 | 0.464 | 0.466 |
| Yunnan | 0.557 | 0.559 | 0.562 | 0.563 | 0.565 | 0.566 | 0.568 | 0.570 | 0.571 |
| Tibet | 0.304 | 0.309 | 0.310 | 0.312 | 0.313 | 0.315 | 0.316 | 0.317 | 0.318 |
| Shanxi | 0.493 | 0.495 | 0.496 | 0.498 | 0.499 | 0.502 | 0.504 | 0.505 | 0.507 |
| Gansu | 0.392 | 0.393 | 0.395 | 0.396 | 0.398 | 0.401 | 0.402 | 0.403 | 0.405 |
| Qinghai | 0.439 | 0.440 | 0.441 | 0.443 | 0.445 | 0.446 | 0.447 | 0.449 | 0.451 |
| Ningxia | 0.484 | 0.485 | 0.487 | 0.488 | 0.489 | 0.491 | 0.493 | 0.494 | 0.496 |
| Xinjiang | 0.470 | 0.471 | 0.473 | 0.474 | 0.476 | 0.479 | 0.481 | 0.484 | 0.485 |
| Average | 67.598 | 67.636 | 67.672 | 67.709 | 67.745 | 67.782 | 67.818 | 67.854 | 67.891 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| I | 0.234 | 0.248 | 0.262 | 0.281 | 0.294 | 0.334 | 0.329 | 0.332 | 0.389 |
| Z | 1.981 | 2.071 | 2.043 | 2.004 | 1.612 | 1.803 | 1.642 | 1.797 | 2.074 |
| Year | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| I | 0.393 | 0.399 | 0.422 | 0.392 | 0.339 | 0.347 | 0.411 | 0.424 | 0.453 |
| Z | 2.095 | 2.124 | 2.239 | 2.092 | 1.642 | 1.742 | 2.134 | 2.142 | 2.144 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| I | 0.279 | 0.312 | 0.356 | 0.298 | 0.402 | 0.456 | 0.411 | 0.435 | 0.324 |
| Z | 2.085 | 2.135 | 2.056 | 1.988 | 2.901 | 3.125 | 2.856 | 2.963 | 2.657 |
| Year | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| I | 0.419 | 0.431 | 0.368 | 0.345 | 0.439 | 0.402 | 0.325 | 0.420 | 0.311 |
| Z | 3.411 | 3.103 | 2.132 | 2.429 | 3.162 | 3.125 | 2.198 | 3.022 | 2.731 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Meng, P.; Zhao, X.; Jiang, L.; Zhang, Z.; Xue, B. Assessing the Economic-Environmental Efficiency of Energy Consumption and Spatial Patterns in China. Sustainability 2019, 11, 591. https://doi.org/10.3390/su11030591
Lu C, Meng P, Zhao X, Jiang L, Zhang Z, Xue B. Assessing the Economic-Environmental Efficiency of Energy Consumption and Spatial Patterns in China. Sustainability. 2019; 11(3):591. https://doi.org/10.3390/su11030591
Chicago/Turabian StyleLu, Chenyu, Peng Meng, Xueyan Zhao, Lu Jiang, Zilong Zhang, and Bing Xue. 2019. "Assessing the Economic-Environmental Efficiency of Energy Consumption and Spatial Patterns in China" Sustainability 11, no. 3: 591. https://doi.org/10.3390/su11030591
APA StyleLu, C., Meng, P., Zhao, X., Jiang, L., Zhang, Z., & Xue, B. (2019). Assessing the Economic-Environmental Efficiency of Energy Consumption and Spatial Patterns in China. Sustainability, 11(3), 591. https://doi.org/10.3390/su11030591







