1. Introduction
In today’s globalized economic environment, supply chains are more vulnerable to unforeseen disruptions. Supply uncertainty, that exists in many industries, including semiconductors, electronic fabrication and assembly, food processing, bio-pharmaceutical, and resource based industries such as mining and agriculture (Xu and Lu [
1]). These disruptions may be caused by natural disasters, labor strikes, transportation disruptions, storms, etc. Supply disruption will result in the loss of corporate interests and reputation, and decrease reliability of the downstream supply chain, and hence damage the sustainability of the supply chain. For example, Ericsson lost 400 million Euros after his main supplier’s semiconductor plant caught fire in 2000, and Apple missed many customer orders during a supply shortage of Dynamic Random Access Memory(DRAM) chips after an earthquake hit Taiwan in 1999 (Li and Chen [
2]). An unforeseen labor strike occurred in 2002, 29 ports on the West coast of the United States were shut down urgently, which led to the closure of the New United Motor Manufacturing production factory (Baghalian et al. [
3]). Automotive plants worldwide suspended production because of a destructive earthquake and subsequent tsunami in early 2011 in Japan, and Japan-based Toyota was hit particularly hard, with factories on several continents standing still and domestic production plummeting by half. The massive flooding in Thailand in 2011 halted the production of a vast majority of the world’s hard disk manufacturers (Giri and Bardhan [
4]). These examples suggest that supply disruptions pose great challenges to the procurement managers and exert some serious effects on supply chain management, therefore, supply disruption is becoming a major concern in the supply chain management.
In recent years, supply chain management has played an increasingly important role in supply chain design, and have been paid quite a lot of attention from both academics and practitioners. Scholars have obtained a series of impressive and practical results in the study of supply chain management. Interested readers may refer to Tang [
5], Tang and Musa [
6], Xanthopoulos et al. [
7], Fahimnia et al. [
8], Yan et al. [
9], Ro et al. [
10], Kirilmaz and Erol [
11], Reimann et al. [
12], and Akkermans and Wassenhove [
13]. Our paper is mainly motivated by the work of Xanthopoulos et al. [
7], who proposed generic single period inventory models for capturing the trade-off between inventory policies and disruption risks in a dual-sourcing supply chain network under both unconstrained and service level constraints, and the two suppliers have different procurement prices and disruption probabilities. In their model, they regard the actual delivered quantity as a constant percentage of the order quantity, while we view it as a random variable that depends on disruption time and model a dual-sourcing supply chain system containing two suppliers suffering from the risk of random supply disruption.
This paper contributes to the literature containing two parts. First, we build a two-echelon supply chain model, consisting of two unreliable suppliers and one retailer, and the two suppliers are exposed to random supply disruption, then we get the retailer’s optimal order quantity and order policy, and obtain the analytical closed-form solutions. Second, we investigate the effects of disruption time, disruption probability and fill rate on optimal decisions and expected profit of the supply chain by using numerical analysis.
The remainder of this paper is organized as follows:
Section 2 reviews the related literatures.
Section 3 describes the model and introduces some notations and assumptions used in this study. The model is presented in
Section 4.
Section 5 presents some numerical examples to illustrate the model. Finally, in
Section 6, we draw conclusions from our analysis and give some suggestion for the future research directions. All technical proofs are deferred to the appendix for smoothness.
2. Literature Review
Supply uncertainty is usually characterized by three approaches (He et al. [
14]). The first approach is the random yield model in which the delivered quantity by the supplier is a random fraction of the quantity ordered by the retailer. The second approach models the supply uncertainty as the “all-or-nothing”. In this scenario, the supplier can deliver either the entire amount ordered or nothing. The third approach models the supply uncertainty with a stochastic lead-time or a stochastic capacity. This study addresses the problem of identifying the optimal order quantity and expected profit for a dual-sourcing with random yield (random supply disruption). Therefore, our paper relates to the literature on (random) supply disruption, dual-sourcing, and on how to manage the uncertainty and the risks in the supply chains.
The first stream reviews the literature on (random)supply disruption. Weiss and Rosenthal [
15] developed a structure about an optimal policy for
inventory system and presented a procedure model when considering disruption in supply or demand. Anupindi and Akella [
16] derived the optimal ordering policy for the supply process between a buyer and two unreliable suppliers. Tomlin [
17] examined the optimal strategy for a single product system with two suppliers: one is unreliable, cheap and another is reliable but expensive. Schmitt et al. [
18] and Chen et al. [
19] extended the work of Tomlin [
17] to study the system with stochastic demand. Schmitt et al. [
18] studied the common impacts of discrete event uncertainty (disruptions) and continuous sources of uncertainty (stochastic demand or supply yield) on optimal inventory settings. Chen et al. [
19] considered a periodic-review inventory system with two suppliers and determined optimal solutions to particular model. Serel [
20] explored an extension of the single-period (newsboy) inventory problem when supply was uncertain. Qi et al. [
21] investigated a continuous-review inventory problem for a retailer who faces random disruptions both internally and externally (from its supplier). He et al. [
14] investigated two competing manufacturers using these procurement strategies in the presence of supply disruption risks and analyzed the joint pricing and ordering decisions of both manufacturers by using the game theoretic framework. Xu and Lu [
1] studied the joint inventory and pricing decisions before the selling season of firm by considering a price-setting newsvendor model with random yield, and investigated the effect of yield randomness on optimal decisions and expected profit. Li and Li [
22] studied a dual-sourcing problem when facing supply disruption risk and consider the loss-averse behavior of the firm.
The second stream of the literature consists of papers that study the dual-sourcing supply chain. Tomlin and Wang [
23] developed a single period dual-sourcing model with yield uncertainty. Yu et al. [
24] evaluated the impacts of supply disruption risks on the choice between the famous single and dual sourcing methods in a two-stage supply chain with an on-stationary and price-sensitive demand. Iakovou et al. [
25] proposed a single period stochastic inventory decision-making model, that could be employed for capturing the trade-off between inventory policies and disruption risks for an unreliable dual sourcing supply network for both the capacitated and uncapacitated cases, and they obtained some important managerial insights and evaluated the merit of contingency strategies in managing uncertain supply chains. Zhu and Fu [
26] explored the trade-off between ordering policies and disruption risks in a dual-sourcing network under specific (or not) service level constraints, assuming that both supply channels were susceptible to disruption risks. Zhu [
27] studied a dual-sourcing problem of a firm in the face of supply disruptions from two suppliers: local and overseas, and characterized the optimal dynamic policy that simultaneously determines sourcing decisions to minimize the expected total discounted cost under four different scenarios of disruption source and information availability. Xiao et al. [
28] studied a manufacturer marketing a product through a dual-channel supply chain, comprised of an online channel and a brick-mortar retail channel. Chao et al. [
29] invested the joint pricing and inventory replenishment problem for a periodic-review inventory system with random demand and dual suppliers and characterized the firm’s optimal policies. Li [
30] explored the optimal procurement problem for a firm sourcing from two unreliable suppliers with different types of supply risks. One supplier confirms with an “all-or-nothing” type of disruption with a certain probability, the other supplier subjects to a random yield of the firm’s order.
The next stream of literature relates to manage the supply chain and mitigate supply chain risks. Huang et al. [
31] examined the strategic use of dual-sourcing and backup supply options in a two-stage dynamic programming model for one period to mitigate supply risk. Li et al. [
32] combined a penalty term in writing contracts with the provision of financial assistance was carrot and stick used by a manufacturer to deal with supply disruption. Ray and Jenamani [
33] studied a two-echelons supply chain with a risk-averse buyer and multiple unreliable suppliers under newsvendor setting by designing a mean-variance objective function to maximize the buyer’s expected profit while minimizing its variance. Aldaihani and Darwish [
34] considered a newsvendor model which allowed the vendor to place an initial order that satisfied a predetermined fill rate. Fera et al. [
35] analysed and categorized the themes related to the production issues of additive manufacturing technology to reduce the risks in supply chains. Hajmohammad and Vachon [
36] developed a framework for managing supplier sustainability risk by taking a conceptual theory building approach, integrated supply chain disruptions and sustainability, and presented four distinct risk management strategies. Martino et al. [
37] identified risk factors in supply chains by adopting the Analytic Network Process approach(ANP). Fera et al. [
38] defined a system dynamics model to assess competitiveness coming from the positioning of the order in different supply chain locations. Lutz et al. [
39] examined buyer-supplier relationship resilience associated with a psychological contract breach by the buying organization. Ta et al. [
40] examined the critical role of trustworthiness in the financial supply chain relationships in the event of a contract breach. Fera et al. [
41] presented a novel approach to classify and analyze the production of specific products to mitigate supply chain risks by using additive manufacturing or subtractive manufacturing.
Most existing studies assumed that the actual delivered quantity is deterministic (a constant percentage of the order quantity) or one of the two suppliers is subject to random disruption. However, in the actual operation of the supply chain, only when the supply chain is interrupted can we know the exact constant, and at the beginning of the decision cycle, we can’t know the interruption information, therefore, it is hard to determine the constant. In fact, the constant is also a random variable, we can’t even determine its distribution. In the management of supply chain disruption, almost all decisions are made in a random environment. Different from the previous literatures, we introduce a random variable to model the delivered quantity of two suppliers under random demand, and further analyze the order policies of retailer and obtain the optimal quantity.
3. Model Descriptions, Notations, and Assumptions
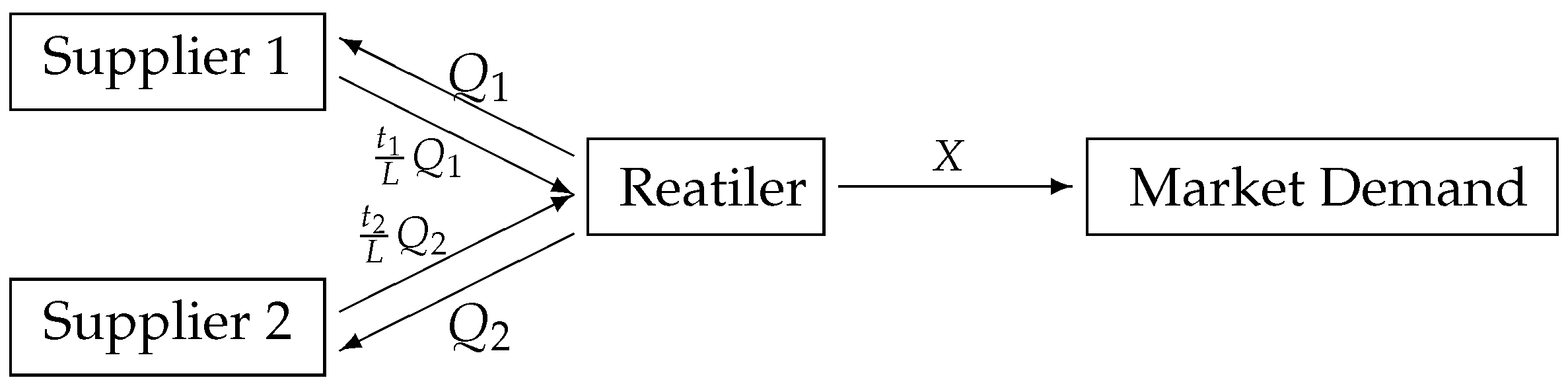
To analyze the impact of disruption time on optimal decisions and expected profit, we consider a dual-sourcing supply chain system consisting of two suppliers and one retailer under a single selling period. The two unreliable suppliers have different disruption probability
, offering the same product to a common retailer who faces random customer demand, and the retailer sells the product to customer with the selling price
s. Assume that the length of the selling period is
L, and disruption time
T is a positive random variable. If there is no disruption, each supplier’s delivery quantity during the selling period is
. When a disruption occurs at
, the actual quantity received by retailer is
, which will be available to satisfy the market demand, and the actual delivered quantity is also a random variable. Denote cumulative distribution function and probability density function of
T by
and
, respectively, and the customer demand,
X, is uncertain, and the cumulative distribution function and probability density function are
and
, respectively. In addition, in our model, goods return, emergency replenishment orders and second purchasing are not allowed. Unit cost of suppliers, unit salvage cost and unit shortage cost are
,
r and
k, respectively, and we assume that
and
. The above model is illustrated in
Figure 1.
Relevant notations and symbols used in our model are explained in
Table 1.
5. Numerical Examples
In this section, we present some examples to further illustrate the implications of obtained results.
Example 1. Assume that the market demand X, disruption time and are uniformly distributed over the intervals , and , respectively, where . The basic parameter values are given as , , , s = 20, k = 10, r = 3, = 6, = 4, = 0.3, = 0.6.
The expected profit function Π
is jointly concave in , as showed in Figure 2, which is consistent with the theoretical result in Proposition 1, and the optimal solutions are , and . When other parameters are fixed, it can be seen from Figure 3 that increases as salvage price r, shortage cost k and selling price s increase, respectively, and increases as the salvage price r increases and decreases as shortage cost k and selling price s increases. In real world, when the shortage cost or selling price is relatively large, the retailer would place more order on the reliable supplier to mitigate supply risks or get more profit. In addition, when the salvage price is relatively large, the retailer will increase the order quantity placed on both suppliers regardless of the impact of cost and disruption probability. When other parameters are constant, while or is changed, Table 2 illustrates the impact of disruption probability on the optimal order quantity and expected profit. The results show that when two suppliers have the same distribution of disruption time, the optimal quantity decreases with the increase in the disruption probability, that means the retailer will prefer the more reliable supplier to mitigate the supply chain risks in this case. When the distribution of disruption time and disruption probability of the two suppliers are same, the retailer would prefer a more cheaper supplier. In addition, an increase in the disruption probability leads to a decrease in the total expected profit of supply chains. This is true because it is more likely to receive nothing from suppliers with a higher disruption probability. The following example illustrates the effect of the disruption time on the supply chain.
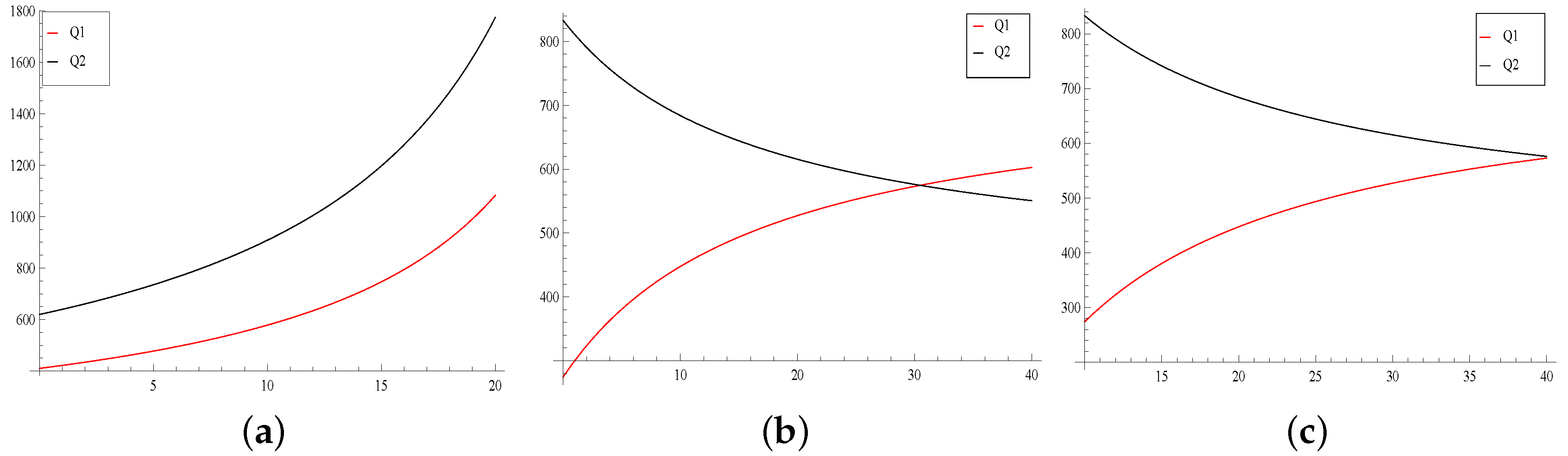
Example 2. Assume that the market demand X is uniformly distributed in the interval , where , disruption time and follow truncated distributions such that Denote = , = , and in the numerical analysis, we take , , , s = 30, k = 9, r = 8, = 0.6, = 0.6, = 13, = 13.
Table 3 shows that the earlier disruption happens at one supplier, the fewer the optimal quantity received by the supplier, and the fewer expected profit obtained by retailer when the two suppliers have the same disruption probability, which shows that the disruption time happened more later in a period will play a small effect on the supply chain system. This observation is intuitive because when a disruption occurs early in one channel, the actual delivered quantity will decrease, and the retailer will increase the order quantity in the other channel to avoid the risk of disruption. To end this section, we present an example to illustrate the effect of fill rate on the optimal order quantity , and the optimal profit .
Example 3. Assume that the market demand X, disruption time and are uniformly distributed over the intervals , and , respectively, where . And , , s = 45, k = 15, r = 10, = 21, = 24, = 0.4, = 0.3, .
The order quantity keeps unchanged when the values of range from to , and there are no feasible , satisfying constraint condition when the values of more than , thus we just list the values of from to in such a setting. It can be seen from Table 4 that the retailer will decrease the quantity placed on the cheaper but less reliable supplier as the fill rate increases, conversely, retailer will increase the order quantity from reliable but expensive supplier. While the expected profit decreases as the fill rate increases. 6. Conclusions
Supply disruption has become a major topic having a drastic effect on supply chains. Also, it presents a real challenge for the risk management of supply disruption. In this paper, we investigate the order strategies of a two-echelon supply chain system under random supply disruption risks. Two models are developed to study the retailer’s ordering decisions. We also get the respective analytical closed-form solutions of the optimal order quantity and maximize the expected profit. Several managerial findings in this note are summarized as follows. First, when the shortage cost or selling price is relatively large, the retailer would prefer the more reliable supplier. Second, the earlier a disruption happens in a selling period, the bigger effect it has on the supply chain, and therefore, the retailer should decrease the quantity placed on the supplier to mitigate the disruption risks. Third, as fill rate increases, the retailer shifts his decisions from the cheaper but less reliable supplier to the more reliable and expensive supplier. The aim of this paper is to help managers of supply chains adjust their order plans in time and effectively protect themselves against the supply disruption risks, so as to achieve a sustainable development.
This work can be extended in several ways in the future research. We just consider single period single product model which can be extended to the case of multiple types of products or multi-period. Multi-sourcing is considered as a common practice to hedge against supply disruption risks, it is interesting to extend the proposed model to the multi-sourcing. In addition, it is also of great interest to explore the different supply chain contracts.