Assessing the Performance of UAS-Compatible Multispectral and Hyperspectral Sensors for Soil Organic Carbon Prediction

Abstract

Laboratory spectroscopy has proved its reliability for estimating soil organic carbon (SOC) by exploiting the relationship between electromagnetic radiation and key spectral features of organic carbon located in the VIS-NIR-SWIR (350–2500 nm) region. While this approach provides SOC estimates at specific sampling points, geo-statistical or interpolation techniques are required to infer continuous spatial information. UAS-based proximal or remote sensing has the potential to provide detailed and spatially explicit spectral sampling of the topsoil at the field or even watershed scale. However, the factors affecting the quality of spectral acquisition under outdoor conditions need to be considered. In this study, we investigate the capabilities of two portable hyperspectral sensors (STS-VIS and STS-NIR), and two small-form multispectral cameras with narrow bands in the VIS-NIR region (Parrot Sequoia and Mini-MCA6), to predict SOC content. We collected spectral data under both controlled laboratory and outdoor conditions, with the latter being affected by variable illumination and atmospheric conditions and sensor-sample distance. We also analysed the transferability of the prediction models between different measurement setups by aligning spectra acquired under different conditions (laboratory and outdoor) or by different instruments. Our results indicate that UAS-compatible small-form sensors can be used to reliably estimate SOC. The results show that: (i) the best performance for SOC estimation under outdoor conditions was obtained using the VIS-NIR range, while the addition of the SWIR region decreased the prediction accuracy; (ii) prediction models using only the narrow bands of multispectral cameras gave similar or better performances than those using continuous spectra from the STS hyperspectral sensors; and (iii) when used in outdoor conditions, the micro hyperspectral sensors substantially benefitted from a laboratory model calibration followed by a spectral transfer using an internal soil standard. Based on this analysis, we recommend VIS-NIR portable instruments for estimating spatially distributed SOC data. The integration of these sensors in UAS-mapping devices could represent a cost-effective solution for soil research and precision farming applications when high resolution data are required.

1. Introduction

Laboratory spectroscopy has proved its reliability for estimating the soil organic carbon (SOC) concentration by exploiting the relationship between electromagnetic radiation and organic carbon spectral features [1]. The key spectral regions affected by SOC content are located in the visible (VIS) region around 664 nm and in the SWIR region from 2100 to 2300 nm [2,3,4]. The accuracy of laboratory spectroscopy is mainly controlled by the technical characteristics of the spectrophotometers: (i) high spectral resolution, (ii) wide spectral range, (iii) stability of the measurement conditions, and (iv) low signal-to-noise ratio (SNR). Laboratory spectroscopy has now become a routine method to estimate SOC and other soil parameters. Although it results in robust and accurate estimates of soil properties, laboratory-based spectroscopy only provides an estimate at the sample point location and geostatistical techniques have to be used to infer continuous spatial information. The use of proximal [5] or remote sensing [6,7,8] could be very useful to provide more information on soil spatial variability at the field or even regional scale. In particular, satellite data are very attractive because of the large spatial coverage and short revisit time, which results in the availability of a larger number of images over the same area. The use of remote sensing data for SOC estimation, despite some promising results obtained with Sentinel-2 multispectral broad-bands [9], is currently hampered by the lack of suitable hyperspectral sensors mounted on the satellite platforms [8,10,11]. Within a few years, six satellites equipped with hyperspectral sensors will be launched [12,13] and the future hyperspectral imagers could provide more reliable data for soil spectroscopy applications. However, the issue related to the low spatial resolution of remote data remains unresolved: most of the current and new satellite sensors have a spatial resolution (10–30 m) that could not allow a sufficient explanation of the short-range variability that characterizes some soil variables, especially if the objective is soil mapping for precision farming. Moreover, fixed revisit times are not optimal for an appropriate temporal coverage, due to the influence of cloud cover, or when dry and bare soil conditions are required. While the spatial resolution of airborne sensors is higher (2–5 m), the high operational costs do not generally allow multi-temporal data to be obtained, which are often necessary to increase the likelihood of collecting remote sensing soil data in an optimal condition, i.e., bare, without harvest residues, low roughness, and low soil moisture [14].

The recent development of Unmanned Aircraft Systems (UAS) [15,16] and lightweight spectrophotometers [17] has allowed the assessment of the spatial and temporal variability of soil properties at a high resolution (<1 m) and at relatively low costs. The advantages in terms of cost, flexibility, and spatial/temporal resolution, compared to aerial and satellite surveys, have been discussed in detail [18,19]. The new generation of hyper-/multi-spectral sensors that have become available during the last few years provides new opportunities for soil science and mapping [20]; UAS-based sensing may provide a very attractive solution for research, particularly where high-resolution spatial data is needed [17].

The technological push toward smaller sensors with a better performance is mainly implemented for precision farming applications with a strong focus on crop performance [4,21,22]. At present, the use of UAS-based applications in soil science is still in an early stage. To our knowledge, only a few authors have dealt with UAS-based multispectral imaging for soil property estimation (e.g., [17,21,23]), and we are not aware of any applications of hyperspectral UAS systems for predicting soil properties.

Most authors that deal with remote or UAS data directly calibrate the sensor signal of a limited number of pixels, i.e., they collect soil samples within bare fields, measure the soil property in the laboratory, and calibrate a multivariate model linking the measured soil property to the spectra extracted from the pixel at its sampling point [24]. Wider applicable estimation models could be calibrated by exploiting existing national or continental or soil spectral libraries [25,26]. Recently, Castaldi et al. [27] used the pan European LUCAS topsoil database [25] to estimate SOC content without applying spectral transfer between the calibration and validation dataset, because both sets of spectra were acquired using the same instrument (FOSS XDS Rapid Content Analyzer; FOSS NIR Systems Inc, Laurel, MD, USA) and no differences between equivalent spectra were detected [25]. The pre-processing procedure (radiometric, geometric, and atmospheric correction) on airborne, satellite, and UAS images introduces uncertainty in the spectra, compromising the comparability of different campaigns and of remote spectra and spectra from soil libraries [27,28]. However, a shorter distance between the UAS sensor and soil surface may result in a more robust acquisition of soil spectra, relative to airborne or satellite sensors. A UAS equipped with an incoming sunlight sensor can also provide a reliable at the surface reflectance, in contrast to satellite or airborne sensors, where the reflectance is calculated using atmospheric correction models. These characteristics make UAS-based soil sensing particularly suitable for spatial continuous mapping.

Here, we present a pilot study to investigate the capabilities of a range of hyper- and multi-spectral sensors that can be mounted on UAS for SOC estimation. The main objective was to compare the influence of spectral resolution and range on SOC prediction accuracy when employing UAS-portable sensors in laboratory and outdoor conditions (where we explicitly consider changing illumination and atmospheric conditions and sensor distance). We acquired reflectance from soil samples at close range (from few cm to 2–3 m), in both laboratory and outdoor conditions, using a range of sensors mounted on a tripod. The performance of multivariate calibration models applied to the spectra acquired by two portable hyperspectral sensors (STS-VIS and STS-NIR from Ocean Optics), and two miniature multispectral cameras (Parrot Sequoia and Tetracam Mini-MCA6), was compared to those obtained with a high-end hyper-spectral sensor (ASD Fieldspec 3 FR). Finally, we analysed the transferability of the prediction models between different measurement setups.

2. Materials and Methods

The experimental design used in this study is summarized in a flowchart (Figure 1). It includes data collection and pre-processing, a comparison of instrument performances, and an evaluation of model transferability. We further detail the design below.

2.1. Soil Datasets

In total, 96 soil samples from one of the Rothamsted long-term field experiments were used. The samples (0–2 cm) were taken from the Hoosfield Spring Barley Experiment, plots 72, 62, and 42 [19,29]. The soil on Hoosfield (Batcombe series; classified as a Chromic Luvisol [30,31]) is a flinty-silty-clay loam overlying clay with flints [32]. The experimental design includes plots that have received different amounts and combinations of mineral fertilizers and organic manures, resulting in plots with very different SOC contents. The plots are ploughed to a depth of 23 cm each year. Consequently, the whole top-soil (0–23 cm) layer is regularly mixed and the C content of the plough layer is relatively homogeneous. The SOC content of the 96 samples used in this study ranged between 8.2 and 46.7 g·kg⁻¹ (mean = 16.56 g·kg⁻¹, sd = 10.82 g·kg⁻¹). Fresh soil samples were oven-dried (72 h 60 °C), ground, and sieved (<2 mm with a sieving machine) prior to analysis. The total carbon content for all samples was obtained in a laboratory by dry combustion (using a VarioMAX CN Analyser Elementar GmbH, Germany). The inorganic carbon content of the soil was measured following the method of Sherrod et al. [33]. SOC was obtained by subtracting the inorganic carbon content from the total carbon content. Each sample was distributed on a petri dish (diameter 6.5 cm) for spectral data acquisition.

2.2. Sensor Equipment

The hyperspectral sensors employed were the STS-VIS and STS-NIR (Ocean Optics Inc., Dunedin, FL, USA). The STS-VIS covers the wavelength range 350–800 nm, while the latter covers the range 650–1100 nm. Both sensors are compact (40 × 42 × 24 mm) and ultra-light (60 g) and provide light intensity values with an output optical resolution of 1.5 nm, resampled at a 0.45 nm data output resolution. Each single spectral acquisition with the STS instruments was performed with an integration time of 0.5 s.

The multispectral sensors employed were the Sequoia (Parrot Drones S.a.s., Paris, France) and Mini-MCA6 (Tetracam Inc., Chatsworth, CA, USA). The Sequoia (Seq) measures 59 × 41 × 30 mm and weighs 72 g. It is a camera equipped with five imaging sensors: one for common RGB images and the other four for spectral bands centred at 550, 660, 735, and 790 nm wavelengths, with a width of 40, 40, 10, and 40 nm respectively. The field of view is 61.9 × 48.5 deg and the image resolution is 1280 × 960 pixels. The Sequoia works in combination with an incident light sensor that provides an image-level correction factor for changing illumination conditions during image acquisition. The Mini-MCA6 (Tc) measures 134 × 93 × 78 mm and weighs 1080 g. It can be customized with a series of band-pass filters. We selected six lenses to filter six spectral windows, centred at 480, 550, 670, 780, 880, and 1000 nm wavelengths, with a width of 10 nm. Nevertheless, only the first five windows were used in this experiment (the window at 1000 nm was malfunctioning). The field of view of the camera is 38.3 × 31.0 deg, while the image resolution is 1280 × 1024 pixels.

The sensor used as the reference was an ASD Fieldspec 3 FR spectro-radiometer sensor (Analytical Spectral Devices Inc.) that provides light intensity data in the VIS-NIR-SWIR region (350–2500 nm) with an optical resolution of 3 nm in the 350–1000 nm region and 10 nm for the 1000–2500 nm region, resampled at a 1 nm data output resolution. Each single spectral acquisition with the ASD instruments was performed with an integration time of 5.4 s.

All sensors and characteristics considered in this study are summarized in

Table 1. Spectral resolution of the sensors used in this study.

Instrument	Type	Wavelength Range (nm)	Output Resolution (nm)	Spectral Windows (nm)
ASD	hyperspectral	350–2500	1	/
STS-VIS	hyperspectral	350–800	0.45	/
STS-NIR	hyperspectral	650–1100	0.45	/
Sequoia	multispectral	/	/	550 ± 20, 660 ± 20, 735 ± 5, 790 ± 20
Mini-MCA6	multispectral	/	/	480 ± 5, 550 ± 5, 670 ± 5, 780 ± 5, 880 ± 5, 1000 ± 5

.

2.3. Spectral Measurements

Radiometric calibration was performed on all raw data acquired from the hyperspectral and multispectral sensors to obtain reflectance data. For the hyperspectral sensors (ASD and STS), the process involved the spectral measurement of a Spectralon white reference surface. Conversion to reflectance was automatically managed by the acquisition software (RS³ software from ASD, OceanView software from OceanOptics). This calibration was repeated every six samples. Radiometric calibration and image correction for the Sequoia were performed by taking a picture of a calibration panel (Parrot Sequoia Calibration Target) and then post-processing the images following the procedure described on the manufacturer’s website [34], using the software R [35]. Radiometric calibration and image correction for the Mini-MCA6 were performed by taking a picture of the Sequoia calibration panel and following the procedure described in Aldana-Jague et al. [19], using the software R.

The spectral measurements of the soil samples were carried out both in laboratory and outdoor conditions. Hyperspectral data with ASD, STS-VIS, and STS-NIR were acquired in both setups, while multispectral acquisitions could only be made outdoors:

• Laboratory setup (“Lab” dataset): all samples were scanned once, by the ASD and the STS sensors, using the ASD contact probe, which is equipped with its own light source (100 W halogen reflectorized lamp), and that allows for a spot size of 10 mm of diameter. Measures were carried out with the probe in contact with the soil sample, in a dark room to minimize sources of disturbance (Figure 2, left).
• Outdoor setup (“Out” dataset): all samples were scanned once, in an open area, to minimize reflection from vertical objects in the surroundings, with stable, clear-sky, natural sunlight conditions for the whole duration of the measurements. In the ASD and STS cases, the sensor head was set at a 10 cm height above the samples, at the nadir position, providing a measuring spot size of 4.4 cm of diameter (Figure 2, right). In the cameras cases, the pictures were taken from a low altitude (c. 2 m) in the nadir position above the samples, resulting in c. [0–9]{1,}–[0–9]{1,} pixels/sample.

2.4. Comparison between Measurement Setups

All STS–VIS and STS–NIR spectra were resampled to match the ASD output resolution of 1 nm. They were then merged in a single continuous spectrum in the VIS-NIR range 450–1050 nm (named “STS” dataset), applying a splice interpolation on the common spectral window to correct for the step between the different sensors. Bandwidths below 450 nm and beyond 1050 nm were removed to eliminate areas with excessive signal noise. ASD spectra were both used in their full spectral range (“ASDfull” dataset, in the 450–2400 nm VIS-NIR-SWIR range, after removing the noisy bands) and cut to the same range of the “STS” (“ASD” dataset) to allow for a comparison. For the “ASDfull” spectra, the noisy bands in the water absorption intervals (1350–1450 and 1800–1950 nm) were removed, in accordance with the ranges used by Castaldi et al. [4]. Both “ASD” and “STS” spectra acquired in outdoor conditions (“Out” dataset) were smoothed with a Savitzky-Golay transformation [36] using a second-order polynomial fit. Then, to facilitate SOC modelling through Partial Least Squares Regression (PLSR), data transformation with 1st derivative (1D), continuum removal (cr), and standard normal variate (snv) were applied and tested. To evaluate the performance of the cameras (respectively “Seq” and “Tc” datasets for Sequoia and Mini-MCA6 cameras), four sub-datasets were extracted from the laboratory and outdoor “ASD” dataset, by resampling to match the spectral windows of Sequoia and Mini-MCA6 (respectively “ASD res Seq” and “ASD res Tc”, for laboratory and outdoor). The data processing was carried out in the software R, using the “prospectr” package [37].

As a preliminary analysis, Pearson’s correlation between SOC and wavelengths was calculated on the full spectral range for both “ASD” laboratory and outdoor setups. Two parameters were calculated in four ranges (450–1050, 1051–1999, 2000–2400, and 450–2400 nm): (i) the Root Mean Squared correlation (RMScorr) and (ii) the percentage of bands with a correlation significantly different from 0 (p < 0.05).

PLSR models were then developed for all groups, i.e., combinations of conditions (Lab and Out), instruments, and data transformations, using the R package “pls” [38]. First, the skewness of the SOC distribution of the calibration datasets was reduced by using a logarithmic transformation. For each group, a PLSR model with up to 25 latent variables and “Leave-one-out” cross validation was built, with the aim of selecting the optimal number of latent variables. The best PLSR model within each group was selected based on the number of latent variables (PLSR components) that provided the first local minimum in the relation between the cross-validated RMSE and the number of components. To evaluate the robustness of the models, a validation was then performed, for each group, splitting the data into a calibration and validation dataset (70% and 30%, respectively), with random selection, for 100 repetitions. The performance of the models was tested on the validation datasets using the mean of 100 simulations of the following metrics: (i) Relative Error percentage (RE%), (ii) Root Mean Square Error of prediction (RMSE), (iii) coefficient of determination (R²), (iv) Ratio of Performance to Deviation (RPD), and (v) Ratio of Performance to Interquartile range (RPIQ) [39]. The significance of the differences between the means of performance indicators, in terms of RMSE, RPD, and RPIQ, was evaluated using a t test for all the comparisons hereby discussed. Furthermore, the importance of the wavelengths relevant for SOC estimation according to the PLSR was identified by the VIP index (Variable Importance for the Projection) [40]. A VIP > 1 was considered as a criterion for the detection of relevant bands, following Chong & Jun [41].

2.5. Model Transferability between Measurement Setups

The dataset was used to test the stability of the spectral measurements collected by ASD and STS-VIS under different acquisition conditions, namely between the laboratory and outdoors. The tests concerned the STS-VIS measurements between 450 and 820 nm (“STS-VIS” dataset) and the ASD data at three spectral ranges: 450–2400 nm (“ASDfull” dataset), 450–1100 nm (“ASD” dataset), and 450–820 nm (“ASDshort” dataset).

The dataset was randomly split 100 times in a calibration (75%) and validation (25%) dataset for each test. The SOC values and the laboratory spectral data of each calibration dataset were then used to build a PLSR model, which was tested on the validation dataset composed of spectral data acquired in outdoor conditions.

We also validated the PLSR models obtained from both ASD and STS-VIS instruments, both under laboratory and outdoor conditions (450–820 nm), on data acquired with the other sensor. For example, the calibration dataset derived from the ASD-VIS laboratory spectra was used to validate the STS outdoor dataset.

All the above-mentioned SOC calibration models were also applied before and after the normalization of the spectra using an internal soil standard [42]. For this purpose, one Australian white sand sample (named Lucky bay) was used as a soil standard. This sand was chosen because: (i) the size and shape of the grains are similar to natural soil, (ii) reiterated spectral measurements are stable across the whole spectral region, (iii) spectral features are negligible, and (iv) the sample is stable because it consists almost entirely of quartz [43]. The Lucky Bay sand sample was scanned using ASD and STS-VIS spectroradiometers, both under laboratory and outdoor conditions. All the sand spectral data were acquired the same day of the soil measurements and using the same protocol described in the previous section. The sand spectra acquired with ASD and STS-VIS (secondary instruments) were compared with the benchmark spectrum, namely the Lucky Bay spectrum acquired with an ASD spectroradiometer (primary instrument) in the Commonwealth Scientific and Industrial Research Organisation (CSIRO) laboratory.

The soil spectral measurements were corrected with a correction factor based on the following equation:

$$C_{\lambda }=1-\left(\frac{{\rho }_{sl, \lambda }-{\rho }_{be,\lambda }}{{\rho }_{sl,\lambda }}\right)$$

(1)

where λ is a given wavelength, ${\rho }_{sl, \lambda }$ is the reflectance of the Lucky Bay sand measured with one of the secondary instruments in laboratory or outdoor conditions, and ${\rho }_{be,\lambda }$ is the Lucky Bay sand reflectance acquired at the CSIRO laboratory (benchmark spectrum).

Then, the correction factor $C_{\lambda }$ is applied to the original soil spectra acquired with the secondary instrument, $R_{so,\lambda }$, obtaining the corrected spectra $R_{sc,\lambda }$ (Equation (2)):

$$R_{sc,\lambda }=R_{so,\lambda }\times C_{\lambda }$$

(2)

The average statistic values (RE%, RMSE, RPD, RPIQ) of the 100 iterations of each test were computed before and after the application of the correction factor based on the Lucky bay sand. The significance of the differences between the means of performance indicators, in terms of RMSE, RPD, and RPIQ, was evaluated using a t test for all the comparisons hereby discussed.

3. Results

3.1. Validated PLSR Models

The correlation plot (Figure 3) between SOC and spectral wavelengths based on the “ASDfull” laboratory dataset showed strongly correlated bands in the range 500–850 nm, and an average RMScorr of 0.53 for the 450–1050 nm spectral region. In total, 78% of wavelengths were significantly correlated to SOC (

Table 2. Root Mean Squared correlation (RMScorr) of the four spectral regions for the “ASDfull” laboratory and outdoor setups.

		Spectral Range (nm)
Setup		450–1050	1051–1999	2000–2400	450–2400
Laboratory	RMScorr	0.53	0.32	0.67	0.48
	% p < 0.05	78	67	93	77
Outdoor	RMScorr	0.49	0.16	0.19	0.28
	% p < 0.05	70	32	37	47

). Almost the same result was obtained when taking into account the full spectrum, with an average RMScorr of 0.48 and 77% of bands significantly correlated; nonetheless, the range between 1000 and 2000 nm was characterized by overall poorly correlated bands (average RMScorr = 0.32), while only the range between 2000 and 2400 nm showed good correlation values (average RMScorr = 0.67, with 93% of bands significantly correlated). For outdoor conditions, the scores for the 450–1050 nm range were just slightly lower than those obtained under laboratory conditions, with an average RMScorr of 0.49% and 70% of wavelengths significantly correlated. On the other hand, the average RMScorr dropped consistently both in the 1050–1999 (RMScorr = 0.16, 32% of wavelengths correlated) and 2000–2400 nm ranges (RMScorr = 0.19, 37% of wavelengths correlated).

The performances of PLSR models built from the “ASD” and “ASDfull” data were first compared to evaluate the possibility of modelling SOC content from the VIS-NIR window only (

Table 3. RE%, RMSE (g·kg⁻¹), RPD, RPIQ, and R² of the validation PLSR performances (data reported represents the mean value over 100 repetitions) for all the instruments and setups: “ASD”, “ASDfull”, “STS”, “ASD res Seq”, “ASD res Tc”, “Seq”, and “Tc”. The number of latent variables (n° comp) used in each model is also reported.

			Laboratory Setup						Outdoor Setup
Dataset	n° Comp	RE%	RMSE	RPD	RPIQ	R2	n° Comp	RE%	RMSE	RPD	RPIQ	R2
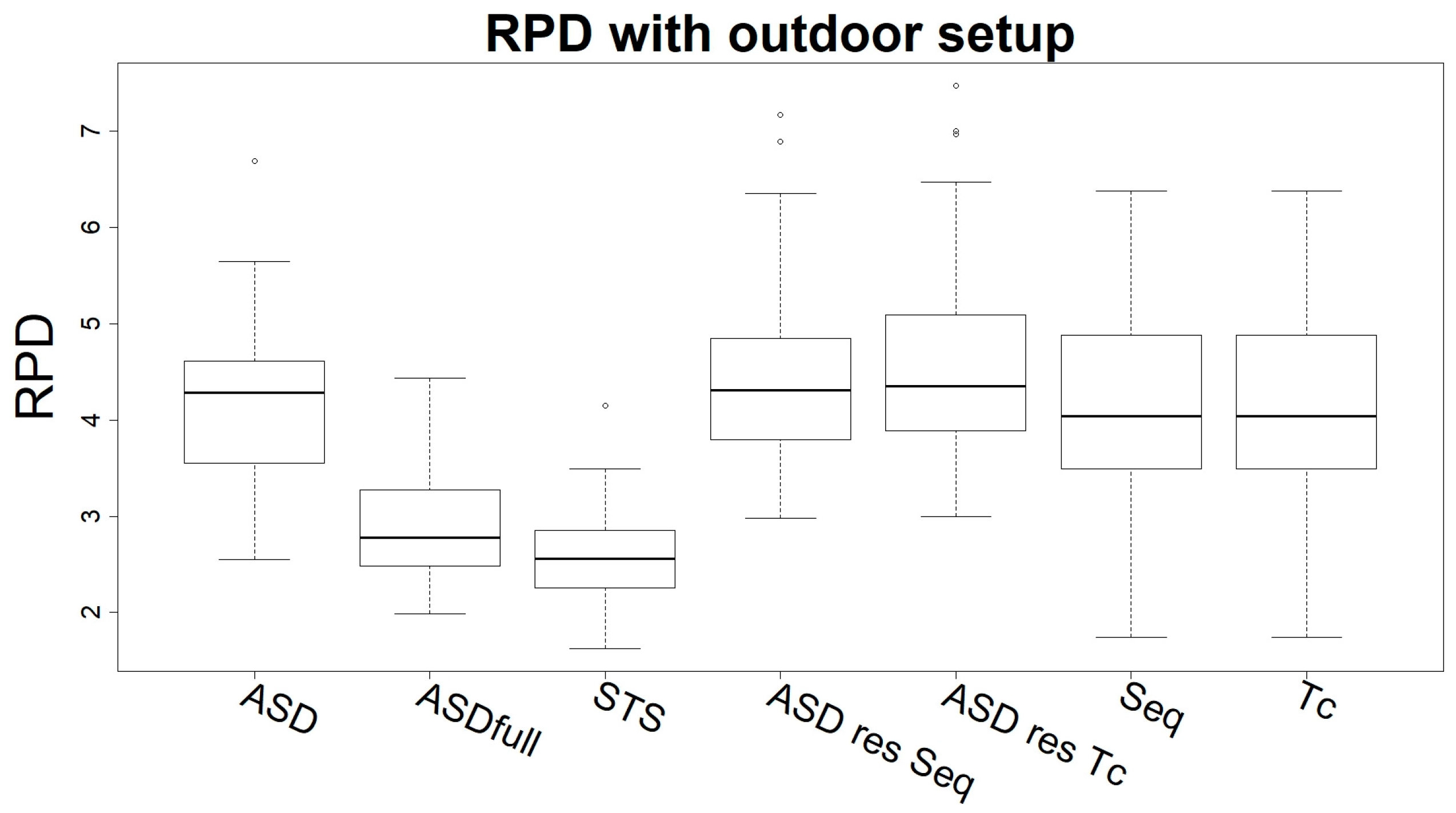
“ASD”	3	0.51	2.2	5.3	6.2	0.96	5	0.8	2.6	4.2	4.9	0.94
“ASDfull”	3	1	2.1	5.4	6.9	0.96	7	2.7	3.9	2.9	3.6	0.89
“STS”	3	2.4	2.9	3.9	4.5	0.94	6	3.1	4.2	2.6	3.0	0.85
“ASD res Seq”	4	0.48	2.4	4.7	5.1	0.95	4	0.45	2.5	4.4	5.6	0.95
“ASD res Tc”	5	0.17	2.6	4.4	5.3	0.95	5	0.79	2.5	4.5	5.2	0.95
“Sequoia”	/	/	/	/	/	/	4	0.82	2.7	4.2	5.1	0.94
“Tc”	/	/	/	/	/	/	5	2.2	3.3	3.5	4.5	0.93

, Figure 4 and Figure 5). First derivative transformation provided the best results in comparison to continuum removal and standard normal variate. Therefore, only the first transformation method was used for the comparisons. Differences in terms of RMSE (2.2 and 2.1 g·kg⁻¹, respectively), RPD (5.3 and 5.4, respectively), and RPIQ (6.2 and 6.9, respectively) were not significant for the laboratory dataset (p > 0.05). Under outdoor conditions, however, the use of the full spectral range caused a significant decrease in performances, i.e., the RMSE increased from 2.6 to 3.9, the RPD decreased from 4.2 to 2.9, and the RPIQ decreased from 4.9 to 3.6.

When comparing the “ASD” and the “STS”, the latter performed ~30% worse for all indices in the laboratory setup (RMSE = 2.9 g·kg⁻¹, RPD = 3.9, RPIQ = 4.5) and even less in the field setup (RMSE = 4.2 g·kg⁻¹, RPD = 2.6 and RPIQ = 3; Table 3, Figure 4 and Figure 5). For the Sequoia and Mini-MCA6 multispectral cameras, we obtained an RMSE of 2.7 and 3.3 g·kg⁻¹ and an RPD of 4.2 and 3.5, respectively. These results were comparable to the performances of the “ASD”, using the VIS-NIR spectral range only, under outdoor conditions. Furthermore, it should be noted that the cameras outperformed the “STS” when used outdoors. We also compared the performance of the cameras and of the laboratory and outdoor “ASD” data resampled on cameras’ spectral windows, to test the effects of size and position of these windows. Laboratory “ASD res Seq” gave an RMSE of 2.4 g·kg⁻¹ and an RPD of 4.7, and laboratory “ASD res Tc” gave an RMSE of 2.6 g·kg⁻¹ and RPD of 4.4. The outdoor “ASD” data resampled on the same windows gave results which were not statistically different from the laboratory resampling (p > 0.05). The average bias estimated with the RE% was low for all models (Table 3).

The plots with the observed versus predicted SOC values from all models used in the comparison of the measuring setups are presented in Figure A1a–l.

The VIP scores calculated for both the “ASD” laboratory and outdoor setups showed a similar trend in the whole VIS-NIR range, highlighting a large single region of interest (VIP > 1) for the PLSR models in the 500–600 nm range (Figure 6). The models built from the cameras were, on the contrary, exploiting all spectral windows except for the one centered on the 550 nm region.

3.2. Evaluation of Model Transferability

The models that were calibrated with the laboratory ASD data, and without applying the correction factor $C_{\lambda }$, were successfully validated with outdoor ASD spectra for all spectral ranges (

Table 4. RMSE (g·kg⁻¹), RPD, RPIQ, and R² of PLSR performances of transferred models, both with and without the application of a spectral correction using an internal soil standard.

Dataset		No Spectral Correction					Spectral Correction
Calibration	Validation	RE%	RMSE	RPD	RPIQ	R2	RE%	RMSE	RPD	RPIQ	R2
Lab “ASDshort”	Out “ASDshort”	−0.4	3.4	3.2	4.0	0.9	0.6	3.4	3.2	3.8	0.9
Lab “ASD”	Out “ASD”	−5.3	3.1	3.5	4.3	0.9	−18.3	5.7	2.3	2.5	0.7
Lab “ASDfull”	Out “ASDfull”	−24.4	4.6	2.5	3.0	0.8	20.9	4.7	2.4	2.6	0.8
Lab “STS-VIS”	Out “STS-VIS”	34.7	7.8	1.4	1.6	0.4	14.6	3.7	2.9	3.2	0.9
Lab “ASDshort”	Out “STS-VIS”	11.5	4.4	2.5	2.9	0.8	−7.8	4.2	2.6	3.1	0.8

). The best estimation accuracies were obtained with a reduced range (“ASDshort” and “ASD”); in these cases, the RPD was higher than 3 and RMSE was 3.1 g·kg⁻¹ for the 450–1100 nm range and 3.4 g·kg⁻¹ for the 450–820 nm range. The use of the full 450–2400 nm spectrum data (“ASDfull”) degraded the estimation accuracy (RMSE = 4.6 g·kg⁻¹; RPD = 2.5; RPIQ = 3.0). After the application of the correction factor, the statistics did not improve for any of the ASD data, while the use of the $C_{\lambda }$ allowed us to align the “STS-VIS” laboratory and “STS-VIS” outdoor spectra. In fact, the RPD after the correction increased from 1.4 to 2.9 (Table 4). The models calibrated using “ASD” laboratory data were successfully tested on “STS-VIS” outdoor data (RMSE = 4.4 g·kg⁻¹; RPD = 2.5; RPIQ = 2.9), and the correction factor allowed us to slightly improve the accuracy.

4. Discussion

The use of spectral sensors that can be mounted on UAS-based platforms for the analysis of soil properties requires optimization. First, UAS payload and battery limitations typically require small and very light sensors. Secondly, their detection capabilities have to be optimized, which is related to the spectral features of the target variable and requires a priori knowledge of the spectral characteristics of all sensed objects for successful applications of any quantitative analysis [44].

The spectral features related to SOC are located along many spectral regions, due to the heterogeneity of its components. Some important features were detected in the NIR and SWIR regions [2,3,4,45,46]. These are mainly related to specific chemical bonds between carbon and hydrogen (C-H) at 1340–1380 nm, the amide nitrogen-hydrogen bond (N-H), and the bond between Oxygen and Hydrogen in the hydroxyl group, both at 1860–1900 nm. Lignin and cellulose influence the reflectance, respectively, between 1600–1800 nm and around 2100 nm [47]. Other features linked to cellulose, lignin, and starch can be found around 2300 nm, close to features related to phenolic, amide, and aliphatic groups [44]. Important correlations between reflectance and organic carbon content were also detected in the VIS region. Although these strong correlation values in the VIS region were mainly reported to be due to the direct relationship between the soil colour and the organic matter abundance [4,47], specific wavelengths and spectral regions were identified. Strong correlations with SOC were found in the VIS region between 550 and 700 nm [48], between 526 and 587 nm [6], and in the 600–800 nm range [49]. Strong correlation between reflectance and SOC was also found within narrower ranges centred at 490 [2], 660 nm [47,50,51], and 750 nm [52]. Melendez-Pastor et al. [6] have already pointed out that the cost-effectiveness of field spectro-radiometers for SOC detection could benefit from their focus on the VIS range and our findings are in line with this statement.

Starting from the analysis of laboratory ASD data, we found regions with a strong average correlation in the 500–850 nm and 2000–2400 nm ranges, but our PLSR models showed that the differences in performance between VIS-NIR and full spectrum (VIS-NIR-SWIR) datasets are not significant (p > 0.05) in terms of SOC prediction accuracy. Since the range between 1050 and 1999 nm was characterized by overall poorly correlated bands, it is therefore possible that this portion of the spectrum is not informative for SOC and its inclusion in PLSR modelling deteriorates overall performances, at least for the specific soil and SOC range we used in this study. When moving from laboratory to outdoor conditions, the model performances decreased when including the SWIR (Table 3, Figure 4 and Figure 5). Indeed, while the correlation for the VIS-NIR range was just slightly lower than the one observed in the laboratory, they dropped both in the 1050–1999 and 2000–2400 nm ranges. This may be due to the lower signal-to-noise ratio of the ASD under outdoor conditions, especially in the 2000–2400 nm range (Figure 7).

The SOC prediction accuracy obtained with the “STS” dataset was lower than that obtained with the “ASD” data. This was most probably due to the presence of important noise in the wavelengths at the start (<500 nm) and at the end (>900 nm) of its spectrum, especially for the outdoor setup (Figure 7, in the zoomed windows). This noise was probably due to the shorter integration time used for data acquisition with the STS instruments (0.5 s), to simulate “in-flight” operational conditions, compared to the ASD one (5.4 s).

The Sequoia and Mini-MCA6 cameras yielded good performances, possibly due to the fact that some of their spectral windows, especially those centred at 550, 660, and 670 nm, match portions of the spectrum that are strongly correlated to SOC (Figure 3). In particular, the Sequoia-based model yielded results similar to those of the ASD in outdoor conditions. The hyperspectral and multispectral resolutions influenced the VIP values in different ways: on the one hand, hyperspectral data exploited the 500–600 nm range that appears to be a very informative region, probably for its slope, (e.g., Bartholomeus et al. [47]). On the other hand, multispectral data mainly exploited the other windows up to 880 nm (Figure 6). The narrow bands used in the Sequoia camera, centred at 660 and 790 nm, cover a spectral range more correlated to SOC than the narrow bands available for our Mini-MCA6 in the same regions (Figure 3). This is supported by the observation that the PLSR performances obtained using the outdoor ASD spectra resampled on the cameras’ windows showed better results when using the Sequoia narrow bands than the Mini-MCA6 ones (Table 3).

The results from the comparison of the validation sets provided some important information on the contribution of different spectral regions and resolutions, and on the influence of setup conditions on SOC prediction accuracy. Nevertheless, it should be noted that the outdoor setup was not fully representing real field conditions. Although the outdoor measurements were made under conditions similar to those in the field (natural sunlight, moist air, and sensor distance), the effects of soil roughness and soil moisture were eliminated in this study. Furthermore, the sensors were not mounted on a drone, but were installed on a tripod, to facilitate the scanning of a range of soil samples with different sensors. In addition, our tests were performed on soils collected from several plots with different SOC contents within a single field experiment and may not fully represent typical ranges of SOC that can be found in real-life conditions. Although new research should be carried out to prove the effectiveness of mapping SOC using UAS-based data under real flight conditions [19], the information obtained here can be used to understand the potential and limitations of different sensor setups.

Another key problem related to SOC mapping is the extrapolation of these empirical models to areas that differ from the ones where the calibration was obtained. This is often very difficult, costly, or just impossible. Consequently, the collection of a specific dataset for each investigated area is necessary in order to obtain an accurate quantitative estimation of the target soil property. Nevertheless, the collection of a calibration dataset requires an extensive sampling and laboratory analysis. However, many large soil spectral libraries covering local to global scales [26,53] already exist. Once the issue of the alignment between datasets is solved, they could be exploited to predict soil properties in another dataset. The alignment between laboratory spectra acquired using two different protocols or instruments is a common practice in soil spectroscopy [54]. This goal can be achieved by applying a spectral transfer function, which is obtained by scanning some soil samples using both instruments. An alternative practice is the alignment by means of an internal soil standard [42]. These techniques could be very attractive to apply predictive models, calibrated with laboratory spectra, to proximal and remote sensing data. However, their use is mainly hampered by the uncertainty of the atmospheric correction, which affects the spectral responses from remote sensing data [27]. For this reason, only a few studies have dealt with the transfer between laboratory and remote spectra [27,28]. Obviously, reducing the distance between the sensor and soil could reduce the issues related to atmospheric correction and UAS-borne sensors could be used for this purpose; however, we are not aware of studies dealing with the alignment between laboratory and UAS spectral data. This is probably due to the large differences between the spectral resolution of laboratory instruments and UAS borne cameras/sensors. Although many light hyperspectral sensors are currently available, their performances for soil properties prediction are still poorly quantified. In this study, we tried to validate laboratory PLSR models for outdoor spectra with and without the alignment by an internal soil standard. Our tests highlighted a good correspondence between the laboratory ASD and outdoor ASD spectra without spectral correction. The worst result with ASD data was obtained using the “ASDfull” range (450–2400 nm), and this is due to the important noise in the SWIR region of the outdoor measurements that increases the difference with the laboratory “ASDfull” (Figure 7). It should be noted that this was also visible in the correlations between reflectance and SOC (Figure 3). The main differences between outdoor ASD and laboratory ASD spectra are in the NIR-SWIR region, while in the VIS, the two spectra have very similar trends and values (Figure 7). The STS-VIS sensor showed a larger difference between laboratory and outdoor spectra, relative to the ASD. In fact, the performance statistics of the validation after the spectral correction consistently increased. However, the “STS-VIS” performance is still lower than the one obtained with the ASD for the same spectral range (“ASDshort” 450–820 nm). These results show that exploiting a predictive model calibrated with laboratory data to outdoor spectra obtained by the same instruments is feasible. However, it should be noted that for the “STS-VIS”, a spectral correction was necessary. The differences between ASD and STS-VIS were mainly due to the high noise in the STS-VIS spectra, especially for the outdoor measurements (Figure 7). In addition, in this case, a satisfactory correspondence between the outputs of the two instruments can be observed (RPD = 2.5), and no significant improvement, in terms of prediction accuracy, was observed when applying $C_{\lambda }$.

5. Conclusions

The UAS-compatible hyperspectral sensors and multi-spectral cameras operating in the VIS-NIR spectral range that were tested in this study are able to provide data with a sufficient quality for developing SOC prediction models in outdoor conditions. SOC prediction modelling based on the narrow bands of the two multispectral cameras (Parrot Sequoia and Tetracam Mini-MCA6) provided better performances than those obtained with the STS hyperspectral sensors. Furthermore, the model built on the Sequoia camera reached the same performance (RMSE = 2.7, RPD = 4.2) as the reference ASD instrument in outdoor conditions (RMSE = 2.6, RPD = 4.2). VIP scores of our PLSR models showed that: i) the spectral region between 500 and 600 nm contains most information for hyperspectral SOC modelling, and ii) the VIS-NIR range up to about 900nm is exploited when using multispectral narrow bands. Validation results indicate that the VIS-NIR range alone may be sufficient for SOC prediction, at least for the conditions encountered in this study. Consequently, the implementation of small-form VIS-NIR portable sensors in UAS systems could be a viable strategy to improve the effectiveness of SOC assessments. Moreover, we showed that it is possible to exploit predictive models calibrated with hyperspectral laboratory data on outdoor spectra obtained by the same portable instruments, applying a correction factor based on an internal soil standard. Together, this shows that UAS-based multispectral and hyperspectral sensors have the potential to estimate soil organic carbon on bare soils with an acceptable accuracy and at a much higher spatial and temporal resolution than existing methodologies.