Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models
Abstract
:1. Introduction
2. Literature Review
2.1. African Energy Research
2.2. Development of Four Methods
- (1)
- Energy demand prediction only depends on single raw data.
- (2)
- The target of prediction is to show the energy demand in the next ten years, and these models can meet the need of long-term prediction.
- (3)
- It is limited data, belonging to a small sample.
3. Methods
3.1. MGM Model
3.2. MECM Model
3.3. ARIMA Model
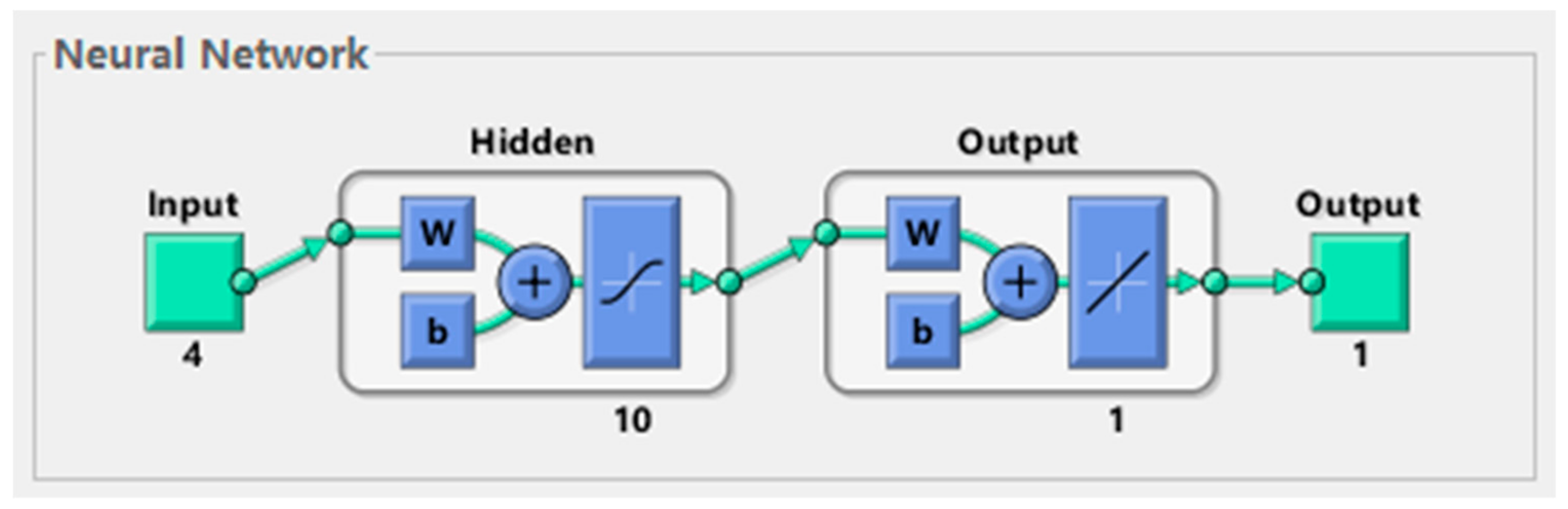
3.4. BP Neural Network
4. Empirical Results and Discussion
4.1. MGM Parameters
4.2. MECM Parameters
4.3. ARIMA Parameters
4.4. BP Neural Network Parameters
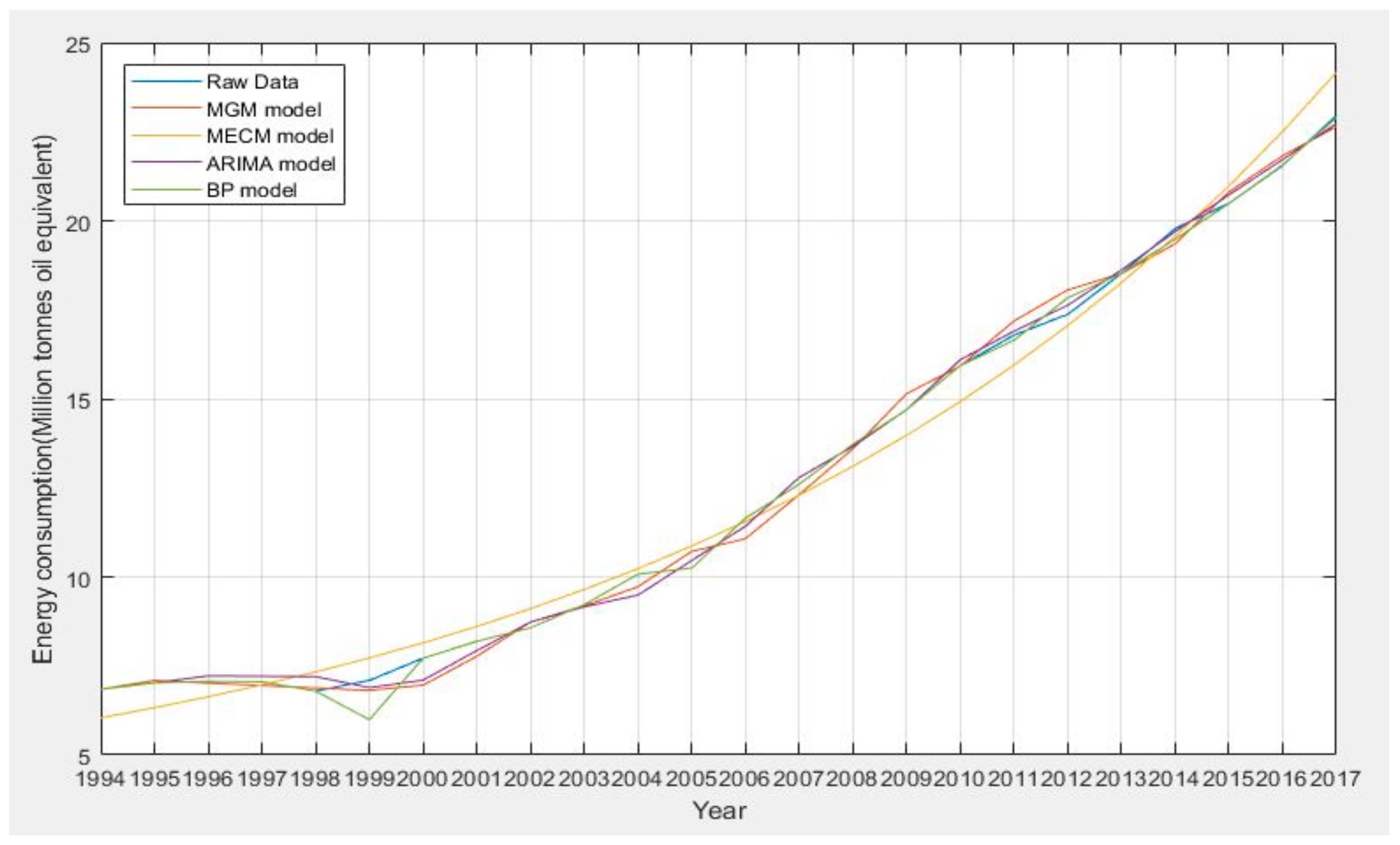
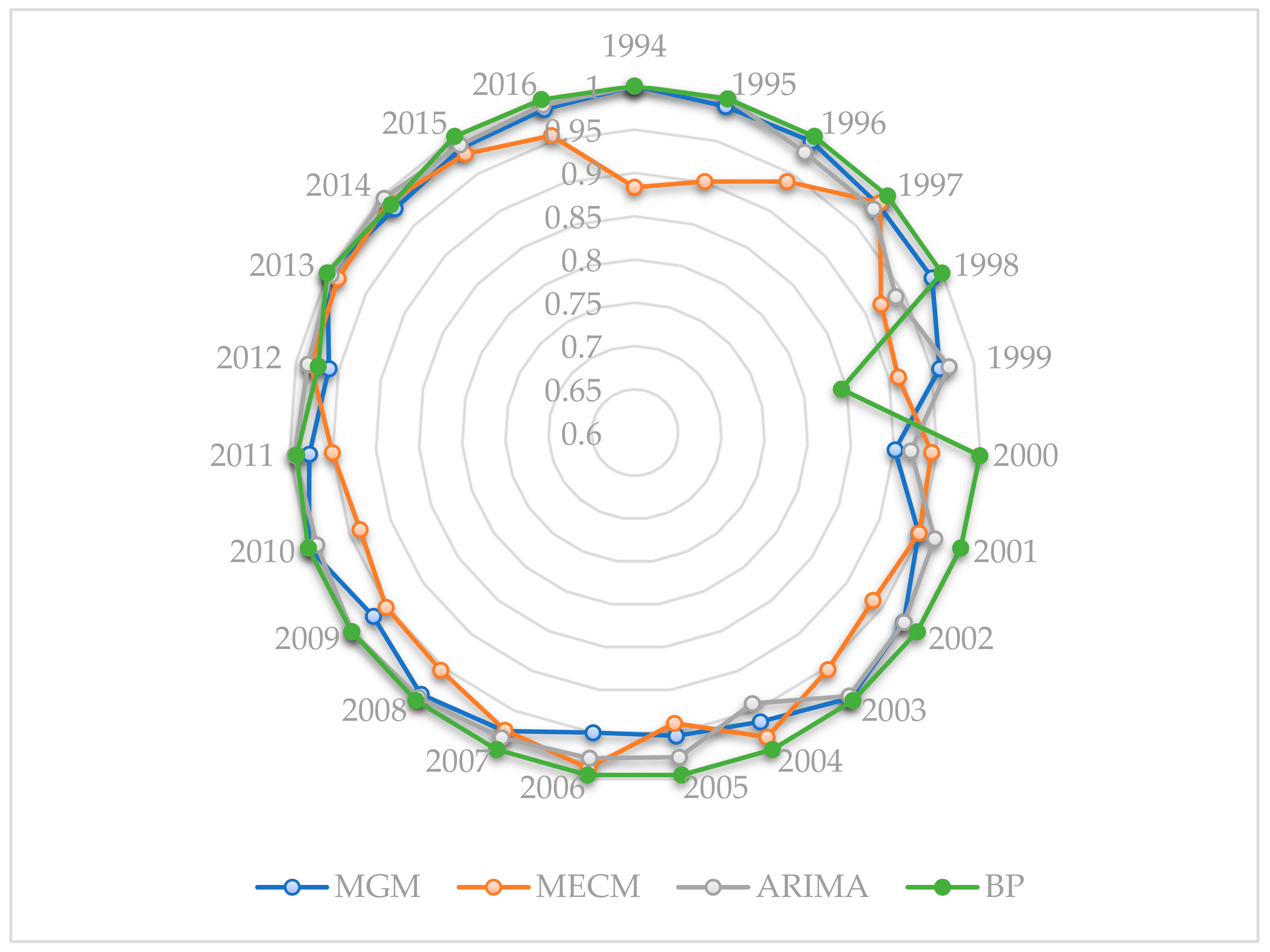
4.5. Evaluation and Comparison of Four Models
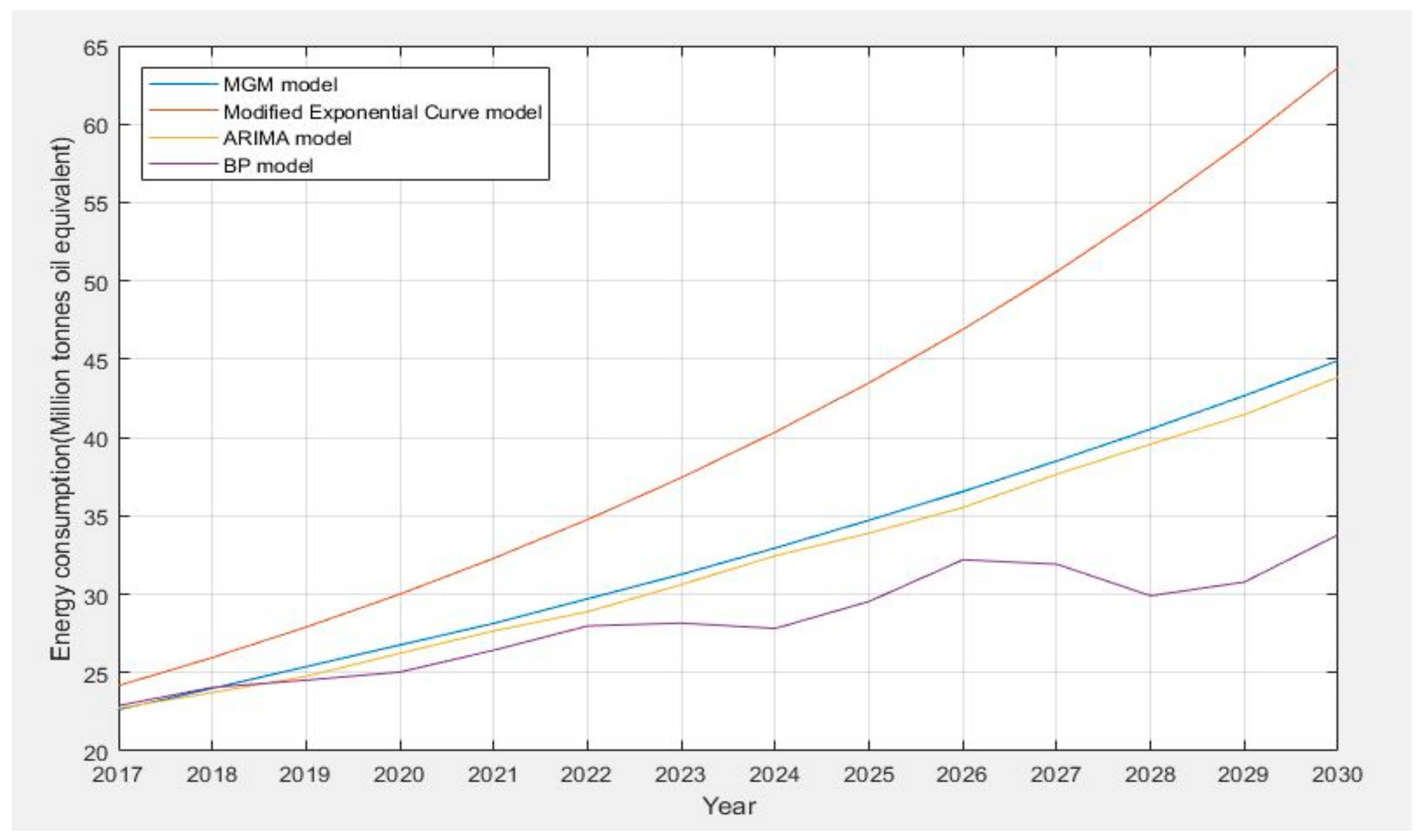
4.6. Forecast Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Year | Raw Data | MGM | Goodness of MGM | MECM | Goodness of MECM | ARIMA | Goodness of ARIMA | BP | Goodness of BP |
|---|---|---|---|---|---|---|---|---|---|
| 1994 | 6.8429 | 6.8429 | 100.00% | 6.0418 | 88.29% | 6.8429 | 100.00% | 6.8429 | 100.00% |
| 1995 | 7.0243 | 7.0900 | 99.07% | 6.3265 | 90.07% | 7.0243 | 100.00% | 7.0243 | 100.00% |
| 1996 | 7.0666 | 7.0194 | 99.33% | 6.6349 | 93.89% | 7.2200 | 97.83% | 7.0666 | 100.00% |
| 1997 | 7.0529 | 6.9496 | 98.54% | 6.9691 | 98.81% | 7.2100 | 97.77% | 7.0529 | 100.00% |
| 1998 | 6.7935 | 6.8804 | 98.72% | 7.3310 | 92.09% | 7.2000 | 94.02% | 6.7935 | 100.00% |
| 1999 | 7.0945 | 6.8120 | 96.02% | 7.7232 | 91.14% | 6.8900 | 97.12% | 5.9888 | 84.42% |
| 2000 | 7.7170 | 6.9589 | 90.18% | 8.1481 | 94.41% | 7.1000 | 92.00% | 7.7170 | 100.00% |
| 2001 | 8.1911 | 7.7703 | 94.86% | 8.6084 | 94.91% | 7.9300 | 96.81% | 8.1911 | 100.00% |
| 2002 | 8.5702 | 8.7348 | 98.08% | 9.1070 | 93.74% | 8.7300 | 98.14% | 8.5702 | 100.00% |
| 2003 | 9.2227 | 9.1859 | 99.60% | 9.6472 | 95.40% | 9.1600 | 99.32% | 9.2227 | 100.00% |
| 2004 | 10.0752 | 9.7228 | 96.50% | 10.2325 | 98.44% | 9.4900 | 94.19% | 10.0752 | 100.00% |
| 2005 | 10.2485 | 10.7156 | 95.44% | 10.8665 | 93.97% | 10.4600 | 97.94% | 10.2485 | 100.00% |
| 2006 | 11.6470 | 11.0722 | 95.06% | 11.5534 | 99.20% | 11.4200 | 98.05% | 11.6470 | 100.00% |
| 2007 | 12.6035 | 12.3112 | 97.68% | 12.2976 | 97.57% | 12.7900 | 98.52% | 12.6035 | 100.00% |
| 2008 | 13.7240 | 13.5969 | 99.07% | 13.1037 | 95.48% | 13.6600 | 99.53% | 13.7240 | 100.00% |
| 2009 | 14.6939 | 15.1453 | 96.93% | 13.9771 | 95.12% | 14.7000 | 99.96% | 14.6939 | 100.00% |
| 2010 | 15.9344 | 15.9225 | 99.93% | 14.9233 | 93.65% | 16.1000 | 98.96% | 15.9344 | 100.00% |
| 2011 | 16.7902 | 17.1864 | 97.64% | 15.9484 | 94.99% | 16.9000 | 99.35% | 16.6433 | 99.12% |
| 2012 | 17.3739 | 18.0613 | 96.04% | 17.0589 | 98.19% | 17.6300 | 98.53% | 17.8403 | 97.32% |
| 2013 | 18.5253 | 18.5168 | 99.95% | 18.2619 | 98.58% | 18.6200 | 99.49% | 18.5253 | 100.00% |
| 2014 | 19.7821 | 19.3561 | 97.85% | 19.5653 | 98.90% | 19.7000 | 99.58% | 19.4856 | 98.50% |
| 2015 | 20.4878 | 20.8098 | 98.43% | 20.9773 | 97.61% | 20.7300 | 98.82% | 20.4878 | 100.00% |
| 2016 | 21.5524 | 21.8259 | 98.73% | 22.5071 | 95.57% | 21.7200 | 99.22% | 21.5717 | 99.91% |
| 2017 | 22.9603 | 22.6431 | 98.62% | 24.1643 | 94.76% | 22.7300 | 99.00% | 22.8956 | 99.72% |
| Year | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
|---|---|---|---|---|---|---|---|
| 0.01 | 0.0025 | −0.0328 | −0.0649 | −0.0617 | −0.0583 | −0.0706 | |
| 7.1939 | 7.0552 | 6.472 | 6.0637 | 6.5386 | 7.0645 | 7.2526 | |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| −0.0611 | −0.073 | −0.0816 | −0.0938 | −0.0778 | −0.077 | −0.0681 | |
| 7.9088 | 8.2365 | 8.663 | 8.9816 | 10.4191 | 11.2537 | 12.4333 | |
| Year | 2013 | 2014 | 2015 | 2016 | |||
| −0.0544 | −0.0489 | −0.0563 | −0.0554 | ||||
| 13.7477 | 14.8128 | 15.2532 | 16.0776 |
| Year | MGM | MECM | ARIMA | BP | ||||
|---|---|---|---|---|---|---|---|---|
| 2018 | 23.9908 | 5.95% | 25.9597 | 7.43% | 23.7300 | 4.40% | 24.0539 | 5.06% |
| 2019 | 25.3784 | 5.78% | 27.9047 | 7.49% | 24.7600 | 4.34% | 24.5187 | 1.93% |
| 2020 | 26.7649 | 5.46% | 30.0119 | 7.55% | 26.2400 | 5.98% | 25.0354 | 2.11% |
| 2021 | 28.1450 | 5.16% | 32.2947 | 7.61% | 27.6600 | 5.41% | 26.4296 | 5.57% |
| 2022 | 29.7117 | 5.57% | 34.7679 | 7.66% | 28.8900 | 4.45% | 27.9783 | 5.86% |
| 2023 | 31.2769 | 5.27% | 37.4472 | 7.71% | 30.6200 | 5.99% | 28.1606 | 0.65% |
| 2024 | 32.9530 | 5.36% | 40.3498 | 7.75% | 32.4600 | 6.01% | 27.8203 | −1.21% |
| 2025 | 34.7258 | 5.38% | 43.4944 | 7.79% | 33.9000 | 4.44% | 29.5435 | 6.19% |
| 2026 | 36.5601 | 5.28% | 46.9012 | 7.83% | 35.5400 | 4.84% | 32.2001 | 8.99% |
| 2027 | 38.5033 | 5.32% | 50.5919 | 7.87% | 37.6600 | 5.97% | 31.9195 | −0.87% |
| 2028 | 40.5386 | 5.29% | 54.5903 | 7.90% | 39.5800 | 5.10% | 29.9038 | −6.31% |
| 2029 | 42.6751 | 5.27% | 58.9219 | 7.93% | 41.4600 | 4.75% | 30.7826 | 2.94% |
| 2030 | 44.9170 | 5.25% | 63.6147 | 7.96% | 43.8700 | 5.81% | 33.8041 | 9.82% |
References
- Oladiran, M.T.; Meyer, J.P. Energy and exergy analyses of energy consumptions in the industrial sector in South Africa. Appl. Energy 2007, 84, 1056–1067. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Wei, L. Brief Analysis of Energy Development in Africa. China’s Collect. Econ. 2010, 25, 199–200. [Google Scholar]
- Kebede, E.; Kagochi, J.; Jolly, C.M. Energy consumption and economic development in Sub−Sahara Africa. Energy Econ. 2010, 32, 532–537. [Google Scholar] [CrossRef]
- Mohammed, Y.S.; Mustafa, M.W.; Bashir, N. Status of renewable energy consumption and developmental challenges in Sub–Sahara Africa. Renew. Sustain. Energy Rev. 2013, 27, 453–463. [Google Scholar] [CrossRef]
- Szabó, S.; Bódis, K.; Huld, T.; Moner-Girona, M. Sustainable energy planning: Leapfrogging the energy poverty gap in Africa. Renew. Sustain. Energy Rev. 2013, 28, 500–509. [Google Scholar]
- Wang, Q.; Chen, X. Energy policies for managing China’s carbon emission. Renew. Sustain. Energy Rev. 2015, 50, 470–479. [Google Scholar] [CrossRef]
- Lin, B.; Wesseh, P.K. Energy consumption and economic growth in South Africa reexamined: A nonparametric testing apporach. Renew. Sustain. Energy Rev. 2014, 40, 840–850. [Google Scholar] [CrossRef]
- Wang, Q. Effective policies for renewable energy—the example of China’s wind power—lessons for China’s photovoltaic power. Renew. Sustain. Energy Rev. 2010, 14, 702–712. [Google Scholar] [CrossRef]
- Wang, Q.; Li, R. Drivers for energy consumption: A comparative analysis of China and India. Renew. Sustain. Energy Rev. 2016, 62, 954–962. [Google Scholar] [CrossRef]
- British Petroleum. Statistical Review of World Energy; British Petroleum: London, UK, 2017. [Google Scholar]
- Landman, W.A.; Goddard, L. Statistical Recalibration of GCM Forecasts over Southern Africa Using Model Output Statistics. J. Clim. 2001, 15, 2038–2055. [Google Scholar] [CrossRef]
- Landman, W.A.; Beraki, A. Multi–model forecast skill for mid–summer rainfall over southern Africa. Int. J. Climatol. 2012, 32, 303–314. [Google Scholar] [CrossRef]
- Collins, D.C.; Reason, C.J.; Hewitson, B. An analysis of the output of the Hadley Centre Unified Model forecast for Southern Africa using Nonlinear Primary Component Analysis (NLPCA) for feature recognition. In Proceedings of the Agu Spring Meeting, Boston, MA, USA, 1 May 2001. [Google Scholar]
- Singh, A.; Kumar, S.; George, J.P. Dust forecast over North Africa: Verification with satellite- and ground-based observations. In Proceedings of the Remote Sensing of the Atmosphere, Clouds, & Precipitation VI, New Delhi, India, 9 May 2016. [Google Scholar]
- Darwish, A.S.; Shaaban, S. Solar and Wind Energy–Present and Future Energy Prospects in the Middle East and North Africa; Sayigh, A., Ed.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Jebli, M.B.; Youssef, S.B. The role of renewable energy and agriculture in reducing CO2 emissions: Evidence for North Africa countries. Ecol. Indic. 2017, 74, 295–301. [Google Scholar] [CrossRef]
- Ramanathan, R. An analysis of energy consumption and carbon dioxide emissions in countries of the Middle East and North Africa. Energy 2005, 30, 2831–2842. [Google Scholar] [CrossRef]
- Inglesi, R. Aggregate electricity demand in South Africa: Conditional forecasts to 2030. Appl. Energy 2010, 87, 197–204. [Google Scholar] [CrossRef]
- Deng, J. Grey System Fundamental Method; Huazhong University of Science and Technology: Wuhan, China, 1982. [Google Scholar]
- Wu, S.J.; Wu, X.J.; Liu, X.M. GM (1, 1) Grey Forecasting and Analysis on Energy Production and Supply in Shandong Province. In Proceedings of the International Conference on Management & Service Science, Wuhan, China, 12 August 2011. [Google Scholar]
- Kumar, U.; Jain, V.K. Time series models (Grey–Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy 2010, 35, 1709–1716. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. Forecasting energy demand in China and India: Using single–linear, hybrid–linear, and non–linear time series forecast techniques. Energy 2018, 161, 821–831. [Google Scholar] [CrossRef]
- Chun-Hui, S.U.; Zhou, J.; Pan, H.Z. The Applied Analysis on Taylor Expansion Modified Exponential Curve Method for Subgrade Settlement Prediction; Construction & Design for Project: Changsha, China, 2013. [Google Scholar]
- Wang, Q.; Song, X.; Li, R. A novel hybridization of nonlinear grey model and linear ARIMA residual correction for forecasting U.S. shale oil production. Energy 2018, 165, 1320–1331. [Google Scholar] [CrossRef]
- Muriana, C.; Tommaso, P.; Giovanni, V. An expert system for financial performance assessment of health care structures based on fuzzy sets and KPIs. Knowl. Based Syst. 2016, 97, 1–10. [Google Scholar] [CrossRef]
- Aiello, G.; Cannizzaro, L.; La Scalia, G.; Muriana, C. An expert system for vineyard management based upon ubiquitous network technologies. Int. J. Serv. Oper. Inform. 2011, 6, 230–247. [Google Scholar] [CrossRef]
- Liu, J.H. Application of ARIMA model in predicting the incidence of HFMD in Yichang city. China Trop. Med. 2014, 14, 956–958. [Google Scholar]
- Yue-Hua, H.U. Application of multiple seasonal autoregressive integrated moving average model in prediction of incidence of hand foot and mouth disease in China. Dis. Surveill. 2014, 64, 1801–1808. [Google Scholar]
- Wang, Q.; Li, S.; Li, R.; Ma, M. Forecasting U.S. shale gas monthly production using a hybrid ARIMA and metabolic nonlinear grey model. Energy 2018, 160, 378–387. [Google Scholar] [CrossRef]
- Bhutto, A.W.; Bazmi, A.A.; Qureshi, K.; Harijan, K.; Karim, S.; Ahmad, M.S. Forecasting the consumption of gasoline in transport sector in pakistan based on ARIMA model. Environ. Prog. Sustain. Energy 2017, 36, 1490–1497. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. China’s dependency on foreign oil will exceed 80% by 2030: Developing a novel NMGM–ARIMA to forecast China’s foreign oil dependence from two dimensions. Energy 2018, 163, 151–167. [Google Scholar] [CrossRef]
- Wang, L.; Wang, A.; Qu, H.; Liu, S. Optimal Forecast Combination Based on Neural Networks for Time Series Forecasting. Appl. Soft Comput. 2018, 66, 1–17. [Google Scholar] [CrossRef]
- Modarresi, M.S.; Huang, T.; Ming, H.; Xie, L. Robust Phase Detection in Distribution Systems. In Proceedings of the 2017 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 9 February 2018. [Google Scholar]
- Modarresi, M.S.; Xie, L.; Campi, M.; Garatti, S.; Carè, A.; Thatte, A.; Kumar, P.R. Scenario−Based Economic Dispatch with Tunable Risk Levels in High−renewable Power Systems. In Proceedings of the IEEE Transactions on Power System, College Station, TX, USA, 18 October 2018. [Google Scholar]
- Yuan, C.; Liu, S.; Fang, Z. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM(1,1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Nichiforov, C.; Stamatescu, L.; Făgărăşan, L.; Stamatescu, G. Energy consumption forecasting using ARIMA and neural network models. In Proceedings of the International Symposium on Electrical & Electronics Engineering, Galati, Romania, 20–22 October 2017. [Google Scholar]
- Akbari-Zadeh, M.R. A hybrid method based on wavelet, ANN and ARIMA model for short-term load forecasting. J. Exp. Theor. Artif. Intell. 2014, 26, 167–182. [Google Scholar]
- Wang, Q.; Li, S.; Li, R. Will Trump’s coal revival plan work?—Comparison of results based on the optimal combined forecasting technique and an extended IPAT forecasting technique. Energy 2019, 169, 762–775. [Google Scholar] [CrossRef]
- Mengxue, S. Application of Modified Exponential Curve Method in Settlement Prediction of Soft Soil Subgrade. Transp. Technol. 2014, 21, 61–64. [Google Scholar]
- Wei, W.; Qiang, C.W.; Liu, P. Prediction of Stock Market Rise and Drop by BP Neural Network. J. Dalian Univ. Technol. 2001, 41, 9–15. [Google Scholar]
- Shi, L.; Liu, S.; Yan, G.; Mu, H. Temperature prediction of the molten salt collector tube using BP neural network. Renew. Power Gener. IET 2016, 10, 212–220. [Google Scholar]
- Sadeghi, B.H.M. A BP-neural network predictor model for plastic injection molding process. J. Mater. Process. Technol. 2000, 103, 411–416. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wang, Y.; Wu, L. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA–BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
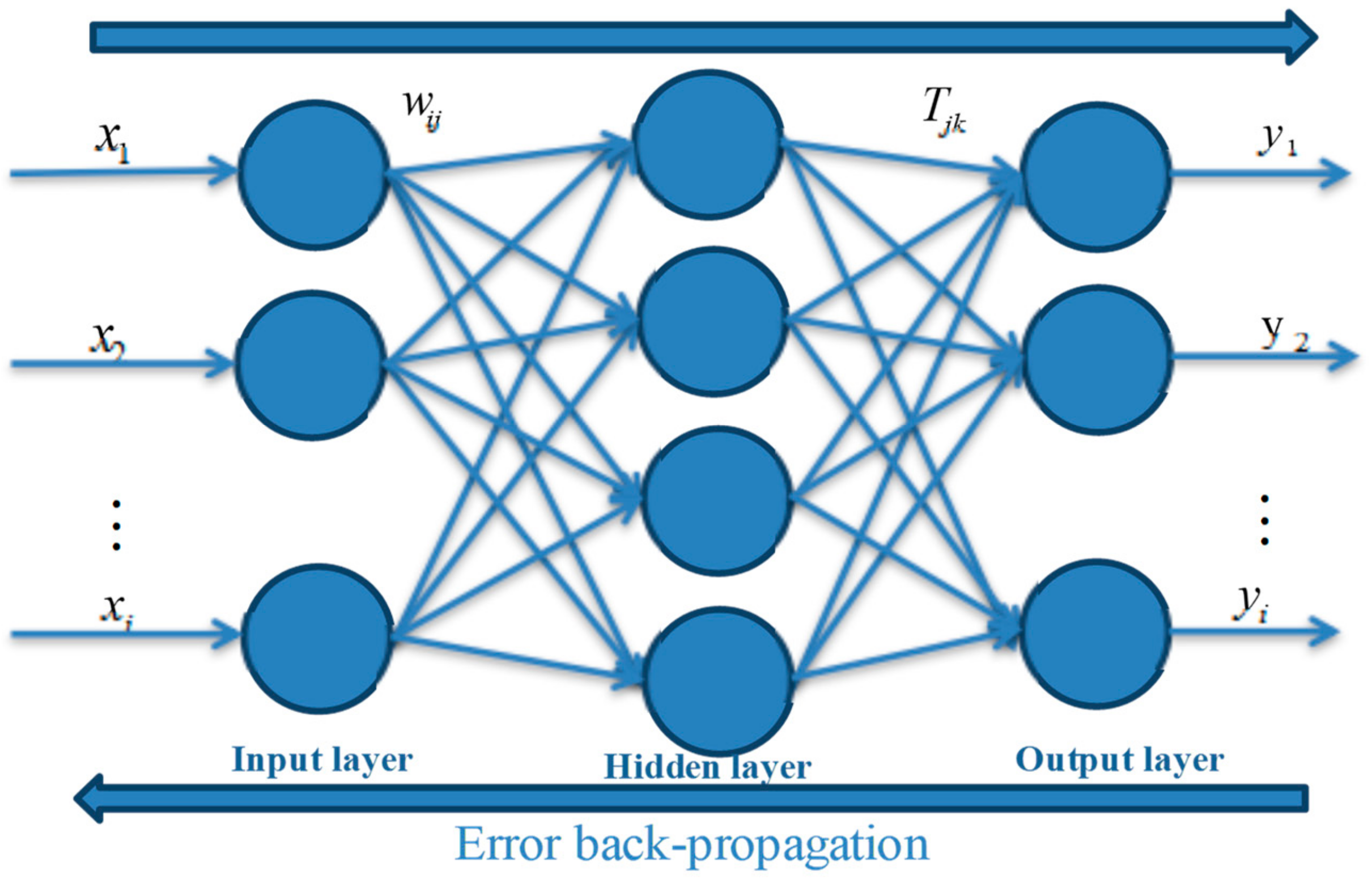

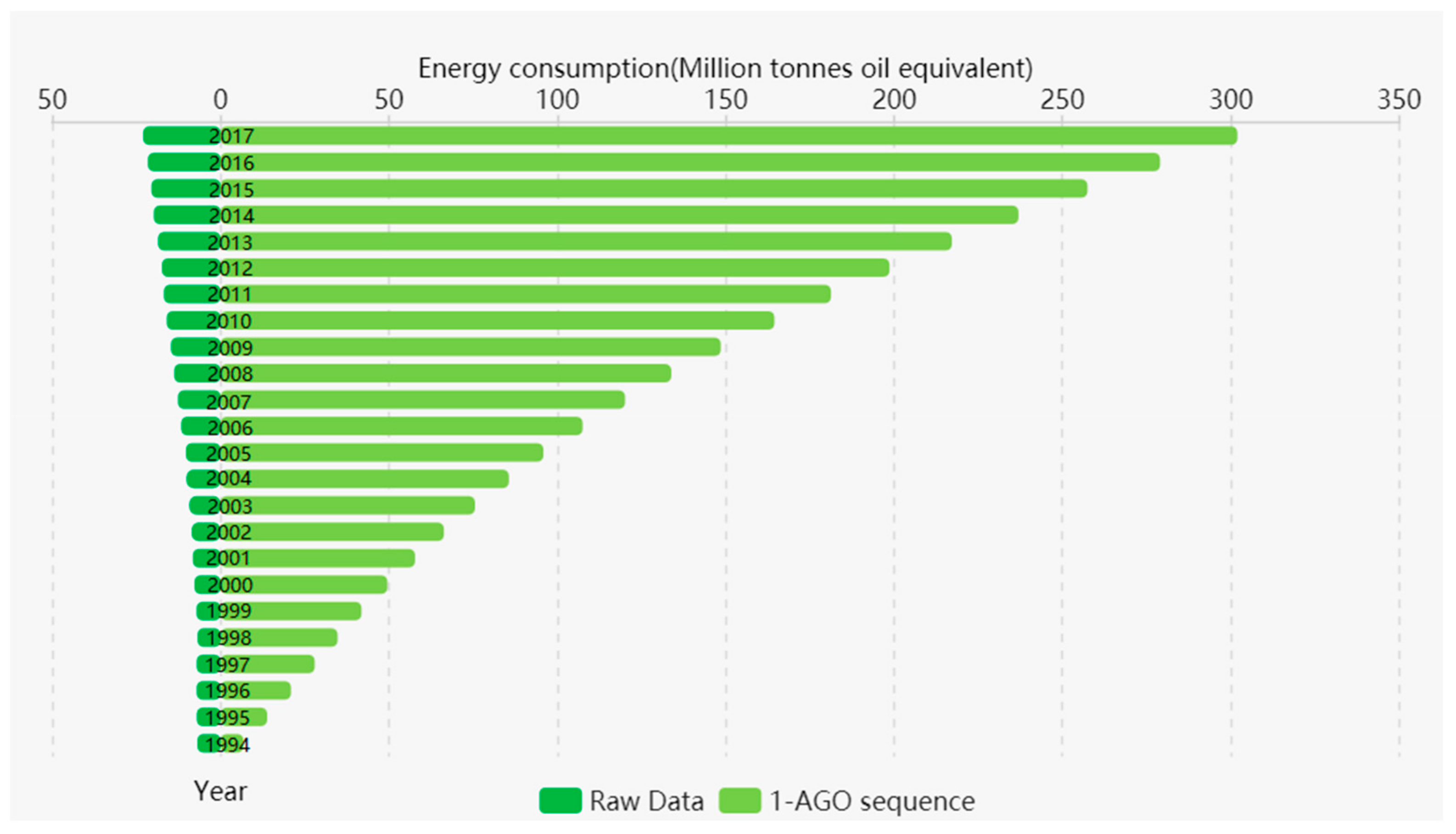
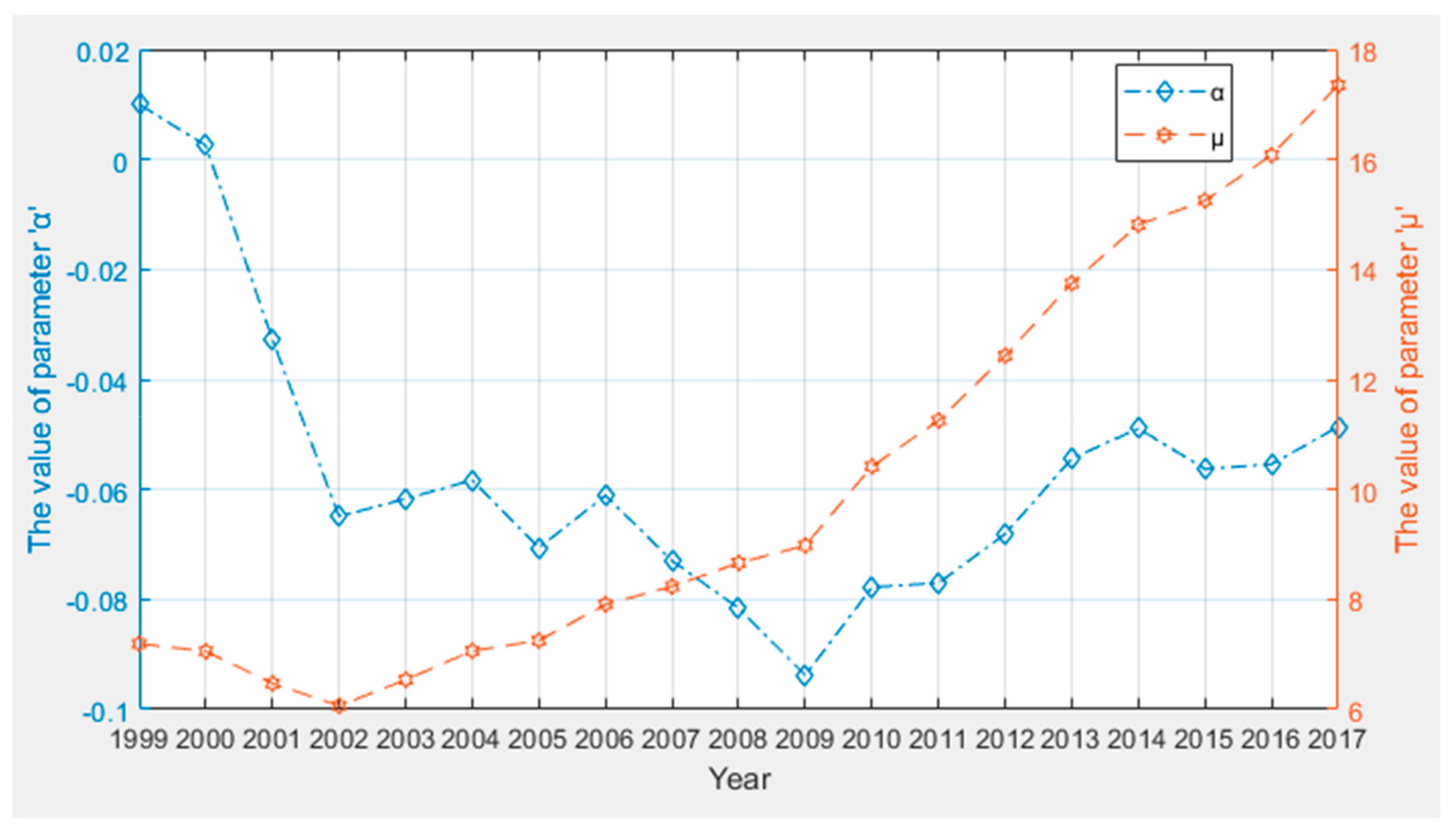
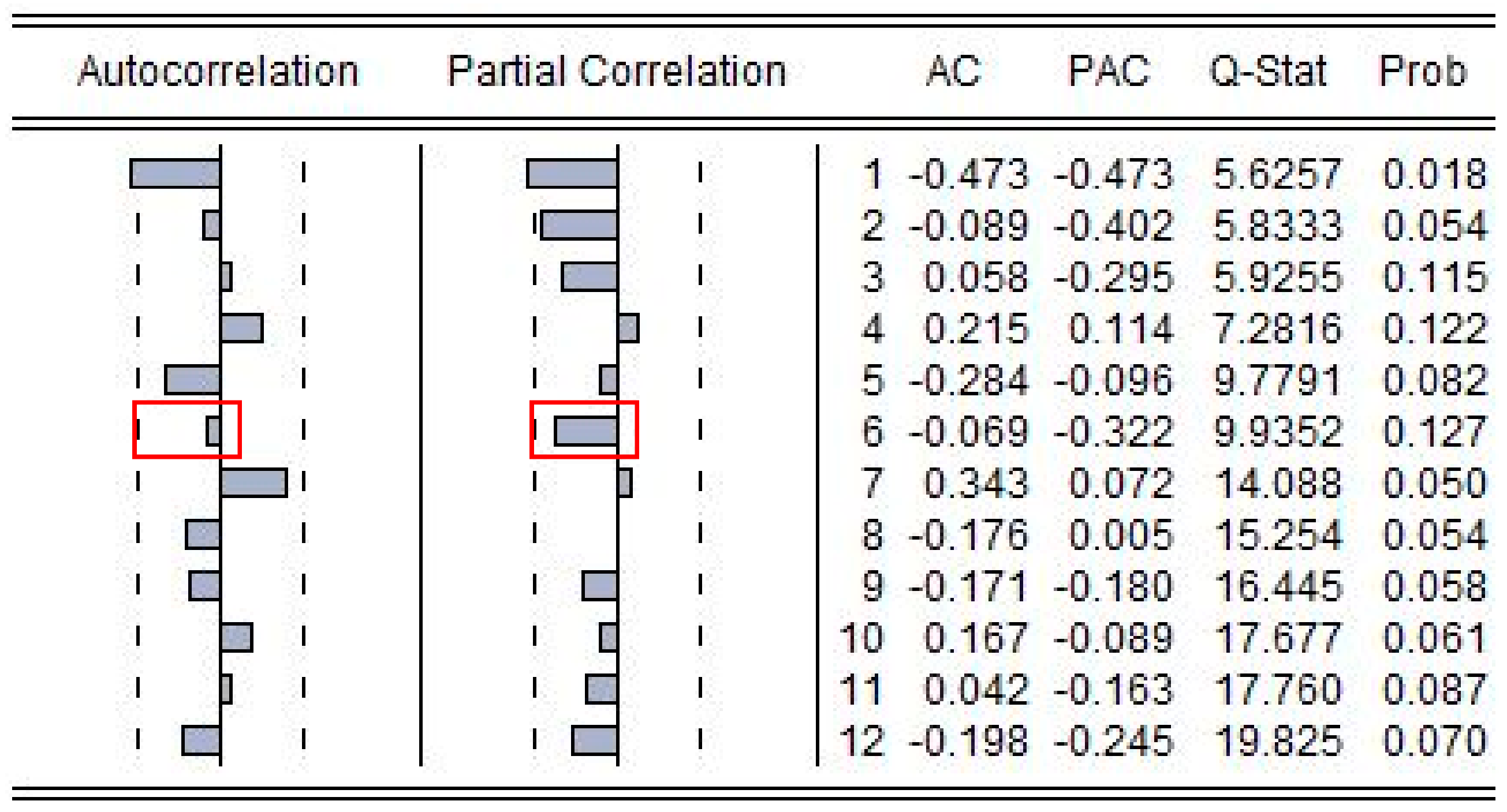
| t | Raw Data | Predicted Values of MECM | Residuals |
|---|---|---|---|
| 1 | 6.8429 | 6.0418 | −0.8012 |
| 2 | 7.0243 | 6.3265 | −0.6979 |
| 3 | 7.0666 | 6.6349 | −0.4317 |
| 4 | 7.0529 | 6.9691 | −0.0838 |
| 5 | 6.7935 | 7.3310 | 0.5376 |
| 6 | 7.0945 | 7.7232 | 0.6287 |
| 7 | 7.7170 | 8.1481 | 0.4311 |
| 8 | 8.1911 | 8.6084 | 0.4172 |
| 9 | 8.5702 | 9.1070 | 0.5368 |
| 10 | 9.2227 | 9.6472 | 0.4246 |
| 11 | 10.0752 | 10.2325 | 0.1573 |
| 12 | 10.2485 | 10.8665 | 0.6180 |
| 13 | 11.6470 | 11.5534 | −0.0936 |
| 14 | 12.6035 | 12.2976 | −0.3060 |
| 15 | 13.7240 | 13.1037 | −0.6203 |
| 16 | 14.6939 | 13.9771 | −0.7168 |
| 17 | 15.9344 | 14.9233 | −1.0111 |
| 18 | 16.7902 | 15.9484 | −0.8419 |
| 19 | 17.3739 | 17.0589 | −0.3150 |
| 20 | 18.5253 | 18.2619 | −0.2633 |
| 21 | 19.7821 | 19.5653 | −0.2168 |
| 22 | 20.4878 | 20.9773 | 0.4895 |
| 23 | 21.5524 | 22.5071 | 0.9546 |
| 24 | 22.9603 | 24.1643 | 1.2040 |
| Sequence | ADF Statistic | Critical Value | Value of p | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| Q | 4.375982 | 3.752946 | 2.998064 | 2.638752 | 0.0000 |
| Q * | −2.195891 | 3.831511 | 3.029970 | 2.655194 | 0.0000 |
| Q ** | −5.033266 | 3.831511 | 3.029970 | 2.655194 | 0.0000 |
| MGM | MECM | ARIMA | BP | |
|---|---|---|---|---|
| RMSE | 35.08% | 60.52% | 24.76% | 25.45% |
| MAPE | 2.41% | 4.80% | 1.91% | 0.88% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhan, L.; Li, R. Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models. Sustainability 2019, 11, 2436. https://doi.org/10.3390/su11082436
Wang L, Zhan L, Li R. Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models. Sustainability. 2019; 11(8):2436. https://doi.org/10.3390/su11082436
Chicago/Turabian StyleWang, Lili, Lina Zhan, and Rongrong Li. 2019. "Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models" Sustainability 11, no. 8: 2436. https://doi.org/10.3390/su11082436
APA StyleWang, L., Zhan, L., & Li, R. (2019). Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models. Sustainability, 11(8), 2436. https://doi.org/10.3390/su11082436





