Modeling Co-Movement among Different Agricultural Commodity Markets: A Copula-GARCH Approach

Abstract

The aim of this research is to explore the volatility contagion among different agricultural commodity markets. For this purpose, this research make use of the copula-GARCH (Generalized Autoregressive Conditional Heteroskedasticity) model for the daily spot prices of six major agriculture grain commodities including corn, wheat, soybeans, soya oil, cotton, and oat over the period from 2000 to 2019. Our results provide evidence that significant contagion effects and risk transmissions exist among different agricultural grain commodity markets, suggesting that potential speculation effects on one agricultural market could be contagious for another agricultural market and result an increase in volatility in agricultural product markets. Second, agricultural commodities appears to co-move symmetrically. We also find substantial extreme co-movements among agricultural commodity markets. This indicates that agricultural commodity markets tend to crash (boom) together during extreme events. Moreover, after the food crisis, contagion effects and risk transmissions among different agricultural commodity markets increased substantially. Fourth, we find that the strongest contagion effects and risk transmissions are between corn and soybeans, and the weakest contagion effects and risk transmissions are between soya oil cotton and between cotton and oat. Last, we document that the co-movement varies over time. Our findings hold important implications for modeling the co-movement by the copula-GARCH approach.

1. Introduction

With recent surges in agricultural commodity prices and price volatilities, academics, policymakers, investors, farmers, and consumers have been paying more attention to agricultural commodity markets. Moreover, since 2000, the prices of agricultural commodities have experienced long-term and sharp fluctuations. In particular, from 2006 onward, the international price of major agricultural commodities has exhibited a substantial tendency to rise. The prices of agricultural commodity surged and experienced sharp fluctuations in 2013 and 2014. Thereafter, the price of agricultural products showed a downward trend in 2015–2016, and then there was a significant stagnation. The observed fluctuations in agricultural commodity prices could be interpreted by some external factors such as macroeconomic uncertainties, agricultural production, financial crises, huge and persistent demand, biofuels demand, different stock market phases, and climate warming. In addition, it can be explained by the interaction and contagion among agricultural commodity markets, as studied in this paper.

Several research studies have been done on using external factors and applying GARCH models to study agricultural commodity markets. For example, applying both GARCH models to research volatility in agricultural commodity markets, Giot [1] employs stochastic volatility models to analyze the spillover of speculation and volatility between agricultural commodity and crude oil markets. Du et al. [2] researched volatility spillover among the corn, crude oil, and wheat in late 2016. Gardebroek and Hernandez [3] find a cross-volatility effect from ethanol corn to markets by a multivariate GARCH approach. Employing a VAR-GARCH model to research relationship and volatility spillovers between the Standard and Poor (S&P) 500 and commodity (beverage, wheat, gold, and crude oil) prices, Mensi et al. [4] document a significant interaction between the S&P 500 and commodity markets. Applying both EGARCH (Exponential GARCH, is also Exponential Generalized Autoregressive Conditional Heteroskedasticity) and BEKK-MVGARCH (Baba, Engle, Kraft and Kroner-Multivariate GARCH) models to investigate spillovers of volatility among corn, crude oil, and fuel ethanol markets in China, Haixia and Shiping find volatility spillovers between corn and fuel ethanol markets [5]. Mensi et al. [6] find dynamic spillovers between the energy and cereal markets. Wang and McPhail [7] find an energy price shock and an agricultural productivity shock account for U.S. agricultural commodity price volatility employing a SVAR model. Algieri [8] finds that the Standard and Poor (S&P) 500 has a positive impact on the increase of the commodity returns, while the US/Euro exchange rates negatively affect commodity prices. Bonato [9] applies the Beta GARCH model to find that agriculture commodities increase correlation with oil. Shahzad et al. [10] provide the evidence that there exists tail dependence between oil prices and the price of agricultural commodities. Ji et al. [11] also finds the risk spillover between energy and agricultural commodity markets by a GARCH-CoVaR-copula model (Conditional Value at Risk copula model). Yahya et al. found the temporal and spectral dependence between crude oil and 10 major agricultural commodities [12]. Shiferaw [13] applies Bayesian multivariate DCC-GARCH (Dynamic Conditional Correlation GARCH) models to research the correlation between prices of agricultural commodities and energy, finding that agricultural commodity and energy markets exhibit strong co-movement. Nicola et al. [14] use a multivariate GARCH model to investigate co-movement among energy, agricultural, and food commodity markets, finding high correlation among major energy, agricultural, and food commodity price returns.

However, there has been very little work done to study dependence or co-movement between agricultural commodity markets. The copula-GARCH approach has been found to be useful in investigating the dependence or the co-movement of different series; thus, it has become popular. For example, Garcia and Tsafack [15] use the model to analyze international equity and bond markets and find that there are strong dependencies among different international assets of the same type but weak dependence between equities and bonds. Using the model, Yang and Hamori [16] imply gold prices and exchange rates have asymmetric dependence and that tail dependence is stronger in a normal period than during a period of financial turmoil. Benlaghab [17] points out that four French nominal and index-linked bonds possess dynamic correlation and asymmetric dependence. Chebbi and Hedhli [18] find strong dependence in Tunisian–French and American–French markets. Tang et al. [19] examine the co-movement between tourism demand and the exchange rate using copula-GARCH models, finding that the tail dependence and dynamic dependence improve the model’s explanatory ability. Aloui and Jammazi [20] apply a wavelet-based approach to analyze dependence between crude oil and the exchange rate, and Shahzad et al. [21] examine the risk contagion of Greece stock markets and other European country stock markets. Moreover, using time-varying copula models, Han et al. [22] find dependence among a mixed-asset portfolio. Boubaker and Raza [23] find a strong and asymmetric dependence between USA equity markets and CEE equity markets (three Central and Eastern Europe equity markets). Koirala et al. [24] find that agricultural commodity and energy future prices exhibit strong dependence.

There are very few research studies on the application of the copula-GARCH approach in agricultural commodity markets. Among them, Reboredo [25] investigates the dependence between agricultural commodity prices and oil price. Delatte and Lopez [26] identify the co-movement structure between commodity and stock markets, while Sriboonchitta et al. [27] document dependence between agricultural prices and production indices in Thailand. As far as we know, there is no previous study that applies the copula-GARCH approach to analyze the nature of agricultural commodity markets. To bridge the gap in the literature, we employ the copula-GARCH approach to investigate dependence and asymmetric co-movements among different agricultural commodity markets in this paper. To do so, we first specify a model of the marginal distribution of the return on each main agricultural commodity and a joint model for co-movement (The methodology we applied in this paper is to analyze the co-movement between variables, which is also called dependence. We use both terms in this paper.). We the first employ the ARMA-GJRGARCH (Autoregressive moving average-Glosten, Jagannathan and Runkel’s GARCH) model to estimate the heteroscedasticity and other features of the marginal distribution for the return on each agricultural commodity. Thereafter, we employ several static copulas to examine dependence structures and tail dependence and use the dynamic copulas to capture time-varying dependence. Employing daily data from 3 January 2000 to 30 September 2019, we find significant dependence among different agricultural commodity markets. More interestingly, we notice that there are symmetric extreme co-movements among different agricultural commodity returns, indicating that the agricultural commodity markets being studied in this paper boom and crash together. In addition, we document that the co-movement and extreme co-movement are stronger after the food crisis than before the crisis, which imply a contagion effect enhancement after food crises. Finally, the empirical results show that the dependence changes over time. Our findings hold important implications for modeling the co-movement by the copula-GARCH approach.

The organization of this research is as follows. The data and the copula-GARCH approach are presented in Section 2. Section 3 describes the empirical study, and Section 4 presents drawn inferences on policy making from our findings. The last section provide some concluding remarks.

2. Data and Methodology

2.1. Data

In this paper, we investigate whether there is any contagion effect between any pair of the six agriculture grain commodities, namely, corn (No. 2 Yellow US), wheat (No. 2 Soft Red), soybean (No. 1 Yellow US), soya oil (Crude Decatur), oats (No. 2 Milling Minneapolis), and cotton( Low -Midl). We choose the daily closing spot price ${\mathrm{P}}_{\mathrm{t}}$ at time t for any of the six agriculture commodities in our study. The data being used in our study are from 1 January 2000 to 30 September 2018, which were obtained from Thomson Reuters. In this paper, we will analyze the behaviors of the log-return ${\mathrm{r}}_{\mathrm{t}}=\ln \left({\mathrm{P}}_{\mathrm{t}}/{\mathrm{P}}_{\mathrm{t}-1}\right)$ of the daily closing spot price ${\mathrm{P}}_{\mathrm{t}}$ for any of the agriculture grain commodities.

2.2. Copula Function

A copula is a multivariate cumulative distribution function (CDF) of several random variables with uniform marginal distributions to capture the dependence or co-movement among the variables. Since our paper only studies the relationship between two variables, we only discuss the bivariate case in this paper as follows: we let ${\mathrm{r}}_1{\mathrm{and}\mathrm{r}}_2$ be the log-returns of daily agriculture prices in two different markets with marginal distributions ${\mathrm{F}}_1{\mathrm{and}\mathrm{F}}_2$ with joint distribution ${\mathrm{F}}_{12}$ (Sklar [28]). Then, there exists a copula $\mathrm{C}$: ${\left[0,1\right]}^2\to \left[0,1\right]$ such that

$${\mathrm{F}}_{12}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)=\mathrm{C}\left({\mathrm{F}}_1\left({\mathrm{r}}_1\right),{\mathrm{F}}_2\left({\mathrm{r}}_2\right)\right).$$

(1)

Copula $\mathrm{C}$ that could be used to measure the dependence between the variables ${\mathrm{r}}_1$ and ${\mathrm{r}}_2$. In addition, the copula could be used to characterize the tail dependence such that it can measure the probability of the variables to be jointly in the lower (left) or upper (right) tails. We call the dependence measures of the two tails the lower (left) or upper (right) dependence parameters, denoted by ${\mathsf{\lambda }}_{\mathrm{U}}$ and ${\mathsf{\lambda }}_{\mathrm{L}}$ such that

$${\mathsf{\lambda }}_{\mathrm{U}}={\lim }_{\mathrm{u}\to 1}\mathrm{Pr}\left[{\mathrm{r}}_2\ge {\mathrm{F}}_2^{-1}\left({\mathrm{r}}_2\right)|{\mathrm{r}}_1\ge {\mathrm{F}}_1^{-1}\left({\mathrm{r}}_1\right)\right]$$

(2)

$${\mathsf{\lambda }}_{\mathrm{L}}={\lim }_{\mathrm{u}\to 0}\mathrm{Pr}\left[{\mathrm{r}}_2<{\mathrm{F}}_2^{-1}\left({\mathrm{r}}_2\right)|{\mathrm{r}}_1<{\mathrm{F}}_1^{-1}\left({\mathrm{r}}_1\right)\right].$$

${\mathsf{\lambda }}_{\mathrm{L}}>0$ implies that the random variables have lower tail dependence, while ${\mathsf{\lambda }}_{\mathrm{U}}>0$ shows that variables have upper tail dependence. These suggest that a non-zero probability of observing an extremely low (large) return of one series is associated with an extremely low (large) volatility of the other series in this research. Moreover, tail dependence is called symmetric if the lower tail dependence is equal to the upper tail dependence parameter; otherwise, it is asymmetric.

2.3. Marginal Distribution of Agricultural Commodity Returns

Daily agricultural commodity returns have a tendency to show the characteristics of heteroskedastic, clustered, fat-tailed, and asymmetric leverage volatility. As a result, the (log) return of agricultural commodity ${\mathrm{r}}_{\mathrm{t}}$ can be estimated by the following ARMA ($\mathrm{k},\mathrm{r})$–GJRGARCH ($1,1$) model:

$${\mathrm{r}}_{\mathrm{s},\mathrm{t}} = {\mathrm{c}}_{\mathrm{s},0}+{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{k}}{\mathsf{\varphi }}_{\mathrm{s},\mathrm{i}}{\mathrm{r}}_{\mathrm{s},\mathrm{t}-\mathrm{i}}+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{r}}{\mathsf{\theta }}_{\mathrm{s},\mathrm{j}}{\mathrm{e}}_{\mathrm{s},\mathrm{t}-\mathrm{j}}+{\mathrm{e}}_{\mathrm{s},\mathrm{t}}$$

$${\mathrm{e}}_{\mathrm{s},\mathrm{t}}=\sqrt{\frac{{\mathrm{h}}_{\mathrm{s},\mathrm{t}}\left({\mathrm{df}}_{\mathrm{s}}-2\right)}{{\mathrm{df}}_{\mathrm{s}}}}{\mathrm{z}}_{\mathrm{s},\mathrm{t}},{\mathrm{z}}_{\mathrm{s},\mathrm{t}}~\mathrm{Skt}\left({\mathrm{z}}_{\mathrm{s},\mathrm{t}}/{\mathsf{\xi }}_{\mathrm{s}},{\mathsf{\lambda }}_{\mathrm{s}}\right){\mathrm{t}}_{{\mathrm{df}}_{\mathrm{s}}}$$

(3)

$${\mathrm{h}}_{\mathrm{s},\mathrm{t}} = {\mathsf{\omega }}_{\mathrm{s}}+{\mathsf{\alpha }}_{\mathrm{s}}{\mathrm{e}}_{\mathrm{s},\mathrm{t}-1}^2+{\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{s},\mathrm{t}-1}{\mathrm{e}}_{\mathrm{s},\mathrm{t}-1}^2+{\mathsf{\beta }}_{\mathrm{s}}{\mathrm{h}}_{\mathrm{s},\mathrm{t}-1}$$

where ${\mathrm{e}}_{\mathrm{s},\mathrm{t}}$ denotes the random error, ${\mathrm{h}}_{\mathrm{s},\mathrm{t}}$ is the conditional variance of volatility ${\mathrm{of}\mathrm{e}}_{\mathrm{s},\mathrm{t}}$, ${\mathsf{\varphi }}_{\mathrm{s},\mathrm{i}}$ stands for the ith lag autoregressive (AR) parameter, ${\mathsf{\alpha }}_{\mathrm{s}}$ denotse the ARCH parameter associated with ${\mathrm{e}}_{\mathrm{s},\mathrm{t}-1}^2$, and ${\mathsf{\beta }}_{\mathrm{s}}$ denotes the GARCH parameter associated with ${\mathrm{h}}_{\mathrm{s},\mathrm{t}-1}.$ The asymmetric effect is captured by the coefficient ${\mathsf{\gamma }}_{\mathrm{s}},$ and ${\mathsf{{\rm I}}}_{\mathrm{s},\mathrm{t}-1}$ is an indicator function taking the value of one if ${\mathrm{e}}_{\mathrm{s},\mathrm{t}-1}< 0$ and zero otherwise. In addition, we assume that ${\mathsf{\omega }}_{\mathrm{s}}> 0$, ${\mathsf{\alpha }}_{\mathrm{s}},{\mathsf{\beta }}_{\mathrm{s}}\ge 0,\mathsf{\alpha }$+$\mathsf{\gamma }\ge 0$, and ${\mathsf{\alpha }}_{\mathrm{s}}+{\mathsf{\beta }}_{\mathrm{s}}+{\mathsf{\gamma }}_{\mathrm{s}}/2< 1$ to ensure that variance process is positive and stationary. Moreover, the standardized residual ${\mathrm{z}}_{\mathrm{s},\mathrm{t}}$ is skewed t-distribution with ${\mathsf{\lambda }}_{\mathrm{s}}$ degrees of freedom.

2.4. The Static Copulas

This paper adopts static Gaussian copula, Student-t copula, Clayton copula, and Gumbel copula to investigate the dependence and tail dependence between any two agriculture markets. The different copula models are briefly shown as follows.

The Gaussian copula (Embrechts et al. [29]) is

$${\mathrm{C}}_{\mathsf{\rho }}^{\mathrm{Gau}}\left(\mathrm{u},\mathrm{v}|\mathsf{\rho }\right)={\mathsf{\Phi }}_{\mathsf{\rho }}\left({\mathsf{\Phi }}^{-1}\left(\mathrm{u}\right),{\mathsf{\Phi }}^{-1}\left(\mathrm{v}\right)\right)$$

(4)

where $\mathrm{u}$ and $\mathrm{v}$ stand for the CDFs of the standardized residuals from the marginal models discussed in Section 2.3, in which the values of both $\mathrm{u}$ and $\mathrm{v}$ in [0,1] ${\mathsf{\Phi }}_{\mathsf{\rho }}$ are the bivariate standard normal distribution function with correlation $\mathsf{\rho }\in \left(-1,1\right)$.

The Student-t copula (Embrechts et al. [29]) is

$${\mathrm{C}}_{\mathsf{\rho }}^{\mathrm{Stu}}\left(\mathrm{u},\mathrm{v}|\mathsf{\rho },\mathrm{n}\right)={\mathrm{t}}_{\mathsf{\rho },\mathrm{n}}\left[{\mathrm{t}}_{\mathrm{n}}^{-1}\left(\mathrm{u}\right),{\mathrm{t}}_{\mathrm{n}}^{-1}\left(\mathrm{v}\right)\right]$$

(5)

where ${\mathrm{t}}_{\mathrm{n}}$ is the univariate Student-t distribution with $\mathrm{n}$ degrees of freedom (DoF), and ${\mathrm{t}}_{\mathsf{\rho },\mathrm{n}}$ is the bivariate Student-t distribution with $\mathrm{n}$ DoF and correlation $\mathsf{\rho }\in \left(-1,1\right).$ The parameters of $\mathrm{n}$ and $\mathsf{\rho }$ determine the extent of the symmetric extreme dependence by the upper and lower tail dependencies, ${\mathsf{\lambda }}_{\mathrm{L}}{\mathrm{and}\mathsf{\lambda }}_{\mathrm{R}},$ such that ${\mathsf{\lambda }}_{\mathrm{L}}={\mathsf{\lambda }}_{\mathrm{R}}=2{\mathrm{t}}_{\mathrm{n}+1} \left(-\frac{\sqrt{\mathrm{n}+1}\sqrt{1-\mathsf{\rho }}}{\sqrt{1+\mathsf{\rho }}}\right)> 0$.

The Gumbel copula (Gumbel [30]) is asymmetric and is defined as

$${\mathrm{C}}_{\mathsf{\tau }}^{\mathrm{Gum}}\left(\mathrm{u},\mathrm{v}|\mathsf{\tau }\right)=\exp \left\{-{\left({\tilde{\mathrm{u}}}^{\mathsf{\tau }}+{\tilde{\mathrm{v}}}^{\mathsf{\tau }}\right)}^{1/\mathsf{\tau }}\right\}$$

(6)

where $\tilde{\mathrm{u}}=-\ln \left(\mathrm{u}\right)$, $\tilde{\mathrm{v}}=-\ln \left(\mathrm{v}\right)$, and $\mathsf{\tau }\in \left[1,+\infty \right)$ measures the dependence between $\mathrm{u}\mathrm{and}\mathrm{v}.$ It has a higher probability concentration in the upper tail with dependence ${\mathsf{\lambda }}_{\mathrm{U}}=2-2^{\frac{1}{\mathsf{\tau }}}>0$, while the probability of dependence in the lower tail is zero; that is, ${\mathsf{\lambda }}_{\mathrm{L}}=0$.

The Clayton copula (Clayton [31]) is also asymmetric and it is defined as

$${\mathrm{C}}_{\mathsf{\tau }}^{\mathrm{Clay}}\left(\mathrm{u},\mathrm{v}|\mathsf{\tau }\right)=\left({\mathrm{u}}^{-\mathsf{\tau }}+{\mathrm{v}}^{-\mathsf{\tau }}-1\right){}^{-1/\mathsf{\tau }}$$

(7)

where $\mathsf{\tau }\in \left[0,+\infty \right)$ measures the dependence between $\mathrm{u}\mathrm{and}\mathrm{v}.$ Different from the Gumbel copula, it has a higher probability concentration in the lower tail with lower tail dependence ${\mathsf{\lambda }}_{\mathrm{L}}=2^{-1/\mathsf{\tau }}$>0. Moreover, the probability of dependence in the upper tail is zero; that is, ${\mathsf{\lambda }}_{\mathrm{U}}=0$.

2.5. The Time-Varying Copula

In order to get the dynamic dependence, this research use Equation (8) to do, which as follow:

$${\mathsf{\rho }}_{\mathrm{t}}=\mathsf{\Lambda }\left({\mathsf{\alpha }}_{\mathrm{c}}+{\mathsf{\beta }}_{\mathrm{c}}{\mathsf{\rho }}_{\mathrm{t}-1}+{\mathsf{\gamma }}_{\mathrm{c}}\left({\mathsf{\mu }}_{\mathrm{t}-1}-0.5\right)\left({\mathrm{v}}_{\mathrm{t}-1}-0.5\right)\right)$$

(8)

where $\mathsf{\Lambda }\left({\mathrm{x}}_{\mathrm{t}}\right)=-\ln \left[\left(1-{\mathrm{x}}_{\mathrm{t}}\right)/\left(1+{\mathrm{x}}_{\mathrm{t}}\right)\right]$ is to ensure that the dynamic dependence parameter, ${\mathsf{\rho }}_{\mathrm{t}}$, falls within the interval (–1, 1), $0\le {\mathsf{\beta }}_{\mathrm{c}}<1$, captures the persistence effect from ${\mathsf{\rho }}_{\mathrm{t}-1}$, ${\mathsf{\alpha }}_{\mathrm{c}}$ is a constant term such that ${\mathsf{\alpha }}_{\mathrm{c}}>0$ indicating that there is a significant positive copula, and ${\mathsf{\gamma }}_{\mathrm{c}}$ is a latent parameter that displays whether the return information from the previous period contributes to the copula.

2.6. Estimation and Calibration of the Copula

The canonical maximum likelihood (CML) method is adopted to obtain the CML estimate ${\hat{\mathsf{\theta }}}_{\mathrm{CML}}$ of the parameter $\mathsf{\theta }$ for different copulas in our study. To do so, we first obtain the estimates ${\hat{\mathrm{F}}}_1$ and ${\hat{\mathrm{F}}}_2$ for the CDFs, ${\mathrm{F}}_1$ and ${\mathrm{F}}_2$, from the observations ${\mathrm{x}}_1$ and ${\mathrm{x}}_2$. We denote them as $\hat{\mathrm{u}}$ and $\hat{\mathrm{v}}$ such that:

$$\hat{\mathrm{u}}={\hat{\mathrm{F}}}_1\left({\mathrm{x}}_1\right)=\frac{1}{\mathrm{T}+1}{{\displaystyle \sum }}_{\mathrm{s}=1}^{\mathrm{T}}{\mathrm{I}}_{{\mathrm{x}}_{\mathrm{s}}\le {\mathrm{x}}_1}\mathrm{and}\hat{\mathrm{v}}={\hat{\mathrm{F}}}_2\left({\mathrm{x}}_2\right)=\frac{1}{\mathrm{T}+1}{{\displaystyle \sum }}_{\mathrm{s}=1}^{\mathrm{T}}{\mathrm{I}}_{{\mathrm{x}}_{\mathrm{s}}\le {\mathrm{x}}_2}$$

(9)

where T is the number of observations and $\mathrm{I}$ is the indicator function with

$$\mathrm{I}\left(\mathrm{expression}\right)= \{\begin{array}{c}1 \mathrm{if} \mathrm{expression} \mathrm{is} \mathrm{true}\\ 0 \mathrm{if} \mathrm{expression} \mathrm{is} \mathrm{false}.\end{array}$$

Thereafter, we apply the following equation to obtain the CML estimate ${\hat{\mathsf{\theta }}}_{\mathrm{CML}}$ of the parameter, $\mathsf{\theta }$, for the copulas discussed in Section 2.5 and Section 2.6:

$${\hat{\mathsf{\theta }}}_{\mathrm{CML}}=\arg \max {{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}\mathrm{lnc}(\hat{\mathrm{u}},\hat{\mathrm{v}};\mathsf{\theta })$$

(10)

where $\mathsf{\theta }$ is an unknown copula parameter, including the dependence ${\mathsf{\rho }}_{\mathrm{t}}$, ${\mathsf{\tau }}_{\mathrm{t}}$ and $\mathrm{n}$ degrees of freedom for the copulas discussed in Section 2.5.

3. Empirical Results

3.1. Preliminary Study

Before we apply the approaches we described in the methodology section to the data, we first conduct some simple analysis to explore the nature of the data. To do so, Figure 1 show the plot of the daily prices of corn, wheat, soybeans, and oats. From the figure, we obtain the following observations: first, the price movements of corn, wheat, soybeans, and soya oil are similar and highly correlated. Second, prices spike in both 2008 and 2011. For example, we note that academics such as Abbott et al. ([32]) believe that the major drivers of the spikes in agricultural commodity prices in both 2008 and 2011 are the persistent shocks stemming from demand for biofuels, Chinese soybean imports, weather conditions, and stock levels. Third, the prices of the four agricultural commodities start to rise in 2006. This is due to the food price crisis during 2006–2008. In order to account for the impact of the food crisis on the prices of the commodities, we divide the full sample into two parts: the pre-crisis period, which is from 3 January 2000 to 31 December 2005, and the crisis and post-crisis period, which is from 1 January 2006 to 30 September 2019. To avoid confusion, we will refer to the crisis and post-crisis period as the post-crisis period.

This paper will analyze the behaviors of the log-return, ${\mathrm{r}}_{\mathrm{t}},$ of the price of an agricultural commodity at day t. We exhibit the descriptive statistics in

Table 1. Descriptive Statistics for agriculture commodity price returns.

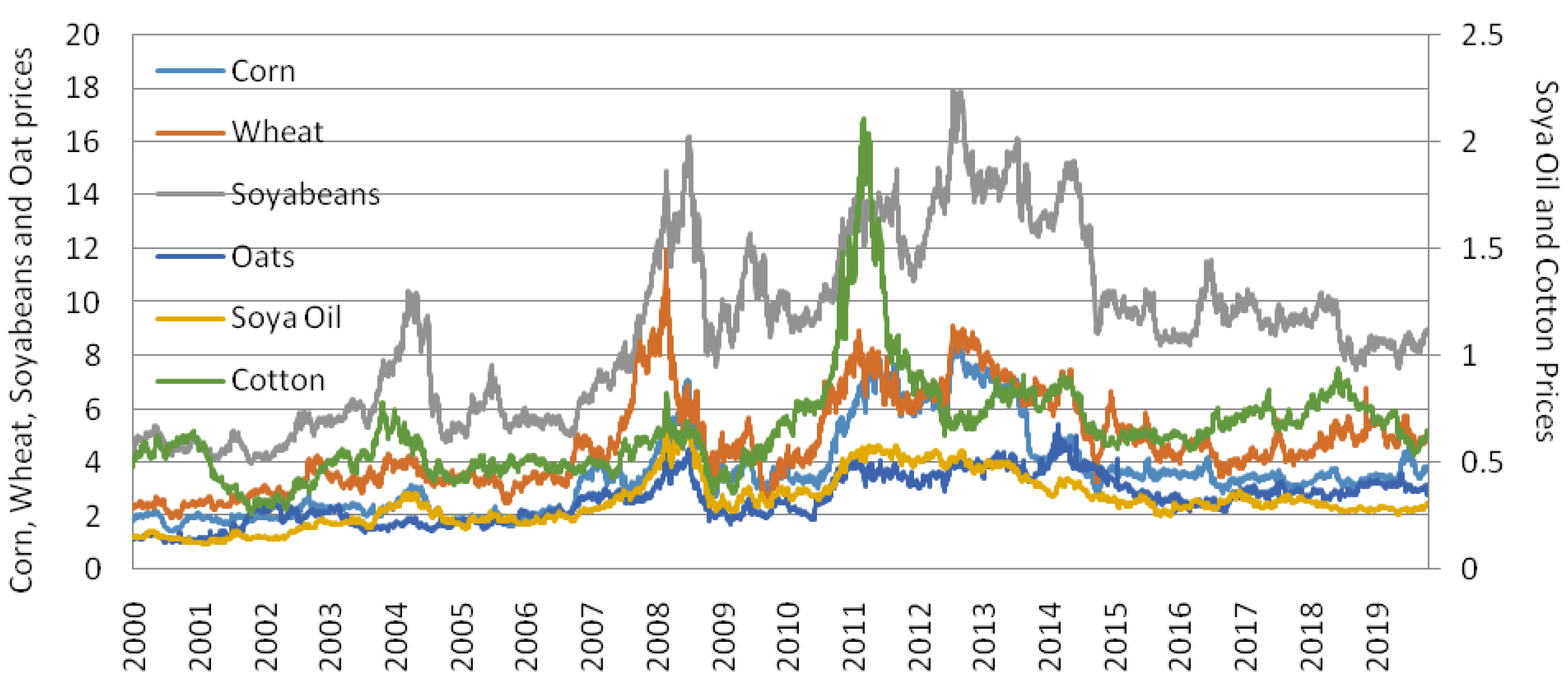
	Corn	Wheat	Soybeans	Soya Oil	Oat	Cotton
Panel A: pre-crisis
Mean	$2.32\times {10}^{-5}$	$1.01\times {10}^{-4}$	$7.80\times {10}^{-5}$	$9.34\times {10}^{-5}$	$1.74\times {10}^{-4}$	$1.11\times {10}^{-5}$
Maximum	0.0305	0.0438	0.0261	0.0348	0.1034	0.0414
Minimum	−0.0320	−0.0401	−0.0727	−0.0348	−0.1033	−0.0414
Std. Dev.	0.0069	0.0087	0.0071	0.01205	0.0104	0.0097
Skewness	−0.0081	0.2165 **	−1.0887 **	−0.0045	−0.1344 *	0.1193 *
Kurtosis	4.7120 **	5.4847 **	13.839 **	5.4201 **	23.499 **	4.6313 **
JB	191.0211 **	414.5361 **	7965.4680 **	381.6715 **	27387.5100 **	177.1336 **
ADF	−39.9734 **	−40.9156 **	−42.1857 **	−27.6548 **	−42.4205 **	−23.9698 **
KPSS	0.0679	0.0548	0.0810	0.1145	0.0784	0.0918
ARCH (10)	74.7720 **	71.4740 **	57.4640 **	32.8610	170.5200 **	22.7650 *
LB (10)	0.0908	0,0126	0.0235	0.0000	0.0016	0.0004
Panel B: post-crisis
Mean	$7.65\times {10}^{-5}$	$4.65\times {10}^{-5}$	$4.67\times {10}^{-5}$	$3.91\times {10}^{-5}$	$4.13\times {10}^{-5}$	$2.17\times {10}^{-5}$
Maximum	0.0473	0.1037	0.0329	0.0414	0.1099	0.0395
Minimum	−0.0527	−0.1071	−0.0556	−0.0367	−0.1112	−0.0452
Std. Dev.	0.0084	0.0115	0.0068	0.0082	0.0104	0.0081
Skewness	−0.1833 **	−0.2507 **	−0.5861 **	0.0907 **	−0.2322 **	−0.0497 **
Kurtosis	6.2765 **	12.1069 **	8.0658 **	4.2983 **	25.6142 **	4.8712 **
JB	1624.2230 **	12429.6500 **	4039.7430 **	256.7899 **	76444.8100 **	524.6991 **
ADF	−59.9848 **	−66.2518 **	−61.0212 **	−70.52158 **	−29.8184 **	−62.11608 **
KPSS	0.2087	0.0848	0.2167	0.2093	0.0596	0.1021
ARCH (10)	106.7805 **	387.6200 **	296.9900	157.3300 **	618.0300 **	407.9600 **
LB (10)	0.0251	0.0000	0.0387	0.0000	0.0000	0.0181

Note: Both D’Agostino and Anscombe–Glynn tests are used to test for no skewness (${\mathrm{H}}_0$: skewness = 0) and no kurtosis (${\mathrm{H}}_0$: kurtosis = 3), respectively. JB is Jarque Bera, which is ${\chi }^2$ statistics for the test of normality. ADF and KPSS are augmented Dickey–Fuller test and Kwiatkowski–Phillips–Schmidt–Shin test for test of stationary. ARCH (q) is Engel’s LM test for heteroskedasticity, conducted using q lags. ** and * denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively. This table reports the p-values of the Ljung–Box (LB) statistic to test whether there is any serial dependence in the series.

. Comparing the descriptive statistics of the returns for the agricultural commodity prices in the two periods, we have the following observations: (1) The mean returns of both soya oil and oat (but not significantly higher) in the post-crisis period. On the other hand, the mean returns of both cotton and soya oil are smaller (but not significantly smaller) in the post-crisis period. The results of the t test lead us to conclude that the mean returns of all the commodity prices being studied in the paper in both the pre- and the post-crisis periods are not rejected to be the same. (2) The estimates of the skewness for the returns of all the commodities are significant in both the pre- and post-crisis the periods except for corn in the pre-crisis period. (3) The returns of all the commodities in both periods have significantly large kurtosis, indicating that all distributions are fat-tailed. (4) The results of the Jarque–Bera test strongly reject the assumption of normal distribution for the returns of all the commodities in both periods. (5) There are significant ARCH (Autoregressive conditional heteroskedasticity) effects in all agricultural commodity returns in both periods. (6) Finally, both ADF (Dickey and Fuller [33]) and KPSS (Kwiatkowski et al. [34]) tests suggest that the returns of all the commodities in both periods are stationary.

3.2. Correlation Analysis

We turn to studying correlations for any pair of returns from the four agricultural commodities being studied in this paper. The results are presented in

Table 2. Unconditional correlation measures.

	Pearson Correlation	Kendall’s Tau	Spearman’s Rho	Pearson Correlation	Kendall’’s Tau	Spearman’s Rho
Panel A: Pre-Crisis				Panel B: Post-Crisis
Corn and Wheat	0.4176 **	0.3151 **	0.4431 **	0.5080 **	0.3810 **	0.5253 **
Corn and Soybeans	0.5003 **	0.3756 **	0.5141 **	0.5695 **	0.3887 **	0.5345 **
Corn and Soya oil	0.2801 **	0.2331 **	0.2955 **	0.3275 **	0.2232 **	0.2917 **
Corn and Oat	0.2424 **	0.2386 **	0.3328 **	0.3108 **	0.2855 **	0.4023 **
Corn and Cotton	0.1098 **	0.0931 **	0.1253 **	0.2320 **	0.1490 **	0.2043 **
Wheat and Soybeans	0.3103 **	0.2343 **	0.3361 **	0.3720 **	0.2566 **	0.3643 **
Wheat and Soya oil	0.1803 **	0.1526 **	0.1967 **	0.2569 **	0.1852 **	0.2430 **
Wheat and Oat	0.1585 **	0.1672 **	0.2378 **	0.2151 **	0.2195 **	0.3117 **
Wheat and Cotton	0.0818 **	0.0620 **	0.0862 **	0.2012 **	0.1304 **	0.1786 **
Soybeans and Soya oil	0.4098 **	0.3320 **	0.4227 **	0.5075 **	0.3808 **	0.4895 **
Soybeans and Oat	0.2135 **	0.2107 **	0.2976 **	0.2329 **	0.2034 **	0.2921 **
Soybeans and Cotton	0.1356 **	0.1117 **	0.1539 **	0.2538 **	0.1535 **	0.2104 **
Soya oil and Oat	0.0704 **	0.1016 **	0.1277 **	0.1220 **	0.1239 **	0.1623 **
Soya oil and Cotton	0.0809 **	0.0892 **	0.1068 **	0.2015 **	0.1426 **	0.1782 **
Oat and Cotton	0.0163	0.0124	0.0167	0.1196 **	0.1048 **	0.1436 **

Note: * and ** denote rejection of the null hypothesis at the 1% and 5%significance levels, respectively.

show that all the correlations are significantly positive except for the correlations between oat and cotton in pre-crisis period. The positive Kendall’s tau implies that the probability of concordance is significant among returns of six agricultural commodities. Likewise, there exist strong rank correlations between agricultural commodity markets. Moreover, the table shows that the conclusions drawn from all the correlations are consistent. It shows that corn and soybeans have the strongest dependence, followed by corn and wheat, while wheat and oats have the least dependence. Last, we find that the relationship between agriculture commodities has strengthened since the advent of the food crisis from 2006 onward.

3.3. Marginal Models

We apply the ARMA ($\mathrm{k},\mathrm{r})$–GJRGARCH ($1,1$) model discussed in Section 2.4 to estimate the marginal distribution of the return for each of the agriculture commodities in the two periods by employing maximum likelihood estimation. We consider different combinations of $\mathrm{k}\mathrm{and}\mathrm{r}$ in the estimation and use the AIC (Akaike information criterion) to select the best model and present the results in

Table 3. Estimated parameter of the agriculture commodity returns for the marginal model.

	Corn	Wheat	Soybeans	Soya Oil	Oat	Cotton
Panel A: Pre-Crisis
${\mathit{c}}_{\mathit{s},\mathit{o}}$	0.0002 (0.0002)	0.0000 (0.0002)	0.0002 (0.0001)	0.0000 (0.0001)	0.0002 (0.0002)	−0.0000 (0.0002)
${\mathit{\varphi }}_{s,1}$			−0.0083 ** (0.0237)			−0.0985 (0.0230)
${\mathit{\omega }}_{\mathit{s}}$	0.0000 (0.0000)	0.0000 ** (0.0000)	0.0000 (0.0000)	0.0000 ** (0.0000)	0.0000 (0.0000)	0.0000 (0.0000)
${\mathit{\alpha }}_{\mathit{s}}$	0.0871 ** (0.0023)	0.0197 (0.0131)	0.0493 ** (0.0076)	0.0301 ** (0.003)	0.2139 ** (0.0876)	0.0006 (0.0045)
${\mathit{\beta }}_{\mathit{s}}$	0.9197 ** (0.0633)	0.9385 ** (0.0118)	0.9686 ** (0.0059)	0.8680 ** (0.0101)	0.6923 ** (0.0821)	0.9872 ** (0.0006)
${\gamma }_{\mathit{s}}$	−0.0462* (0.0231)	0.0349 ** (0.0106)	−0.0420 ** (0.0071)	−0.0590 ** (0.0004)	−0.0791 (0.0835)	0.0195* (0.0085)
${\mathbf{\lambda }}_{\mathit{s}}$	5.8032 ** (0.8049)	5.5625 ** (0.8116)	6.3826 ** (0.3490)	2.0100 ** (0.0007)	2.6437 ** (0.2259)	4.1356 ** (1.6566)
${\xi }_s$	1.0357 ** (0.0309)	1.0401 ** (0.0348)	0.9852 ** (0.0330)	1.0120 ** (0.0258)	0.9883 ** (0.0287)	1.0018 ** (0.0240)
LL	5664.544	5293.8270	5718.1430	6462.4430	5315.5800	5108.4490
AIC	−7.2334	−6.7594	−7.3020	−8.2550	−6.7885	−6.5223
ARCH(7)	1.9660	2.8910	2.3150	0.0075	6.0684	5.7310
Panel B: Post-Crisis
${\mathit{c}}_{\mathit{s},\mathit{o}}$	0.0001 (0.0001)	0.0000 (0.0001)	0.0001 (0.0000)	0.0000 ** (0.0000)	0.0001 (0.0001)	0.0000 (0.0001)
${\mathit{\varphi }}_{s,1}$		−0.0368 * (0.0162)	−0.0265 * (0.1290)	0.11199 (0.0002)		−0.0703 ** (0.0165)
${\mathit{\omega }}_{\mathit{s}}$.	0.0000 (0.0000)	0.0000 (0.0000)	0.0000 (0.0000)	0.0000 (0.0005)	0.0000 ** (0.0000)	0.0000 (0.0000)
${\mathit{\alpha }}_{\mathit{s}}$	0.0499 ** (0.0045)	0.0901 ** (0.0247)	0.0554 ** (0.0043)	0.0312 ** (0.0051)	0.2315 ** (0.0534)	0.0444 ** (0.0048)
${\mathit{\beta }}_{\mathit{s}}$	0.9436 ** (0.0034)	0.8995 ** (0.0274)	0.9433 ** (0.0035)	0.9989 ** (0.0484)	0.6413 ** (0.0770)	0.9558 ** (0.0049)
${\gamma }_{\mathit{s}}$	0.0066 (0.0118)	−0.0057 (0.0175)	−0.0114 (0.0119)	−0.0725 ** (0.0100)	−0.0920* (0.0452)	−0.0089 (0.0097)
${\mathit{\lambda }}_{\mathit{s}}$.	4.6349 ** (0.3483)	4.3717 ** (0.2987)	4.5251 ** (0.3266)	2.0111 ** (0.1679)	3.1413 ** (0.1944)	5.9549 ** (1.1136)
${\xi }_s$	1.0052 ** (0.0201)	1.0134 ** (0.0204)	0.9745 ** (0.0198)	1.0048 ** (0.2402)	1.0135 ** (0.0196)	1.0020 ** (0.0164)
LL	12444.4800	11499.3500	13278.9600	12995.0600	12027.3100	12491.0400
AIC	−6.9367	−6.4090	−7.4015	−7.2426	−6.7040	−6.9621
ARCH(7)	1.3576	2.1008	0.9391	0.9036	0.8553	2.4167

Notes: The table shows the estimates and their standard errors of the parameters for the marginal distribution model defined in Equations (3) and (4). ** and * denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively. ARCH (7) is an Engel’s LM test for the ARCH effect in the residuals up to seventh orders.

. For the pre-crisis period, we find that the ARMA ($0,0)$–GJRGARCH ($1,1$) specification is the best model for corn, wheat, soya oil, and oats, and the ARMA ($1,0)$–GJRGARCH ($1,1$) is the best model for soybeans and cotton. For the post-crisis period, the best model for corn and oats is ARMA ($0,0)$ GJRGARCH ($1,1$), and the best model for wheat, soybeans, soya oil, and cotton is ARMA ($1,0)$–GJRGARCH ($1,1$). In both periods, the estimates of the GARCH parameter ${\mathsf{\beta }}_{\mathrm{s}}$ are highly significant in all series, suggesting that the volatility at time t depends on the volatility at time t-1. On the other hand, the estimates of the ARCH parameter ${\mathsf{\alpha }}_{\mathrm{s}}$ are significant in all series, except for wheat and corn in the pre-crisis period, indicating that the volatility of the returns on all of the series except for wheat and corn in the pre-crisis period at time t depends on the innovation at time t-1. In the pre-crisis period, volatility asymmetry ${\mathsf{\gamma }}_{\mathrm{s}}$ is negative significant in the returns of corn, soybeans, and soya oil, showing that corn, soybeans, and soya oil have a significant leverage effect whereby in general, good news has a greater impact on the conditional variance than bad news. Meanwhile, volatility asymmetry ${\mathsf{\gamma }}_{\mathrm{s}}$ is positive significant only in the returns of wheat and cotton, showing that both wheat and cotton have the significant leverage effect whereby in general, bad news has a greater impact on the conditional variance than good news. In the Post-Crisis, volatility asymmetry ${\mathsf{\gamma }}_{\mathrm{s}}$ is negative significant only in the returns of soya oil and oat, showing that both soya oil and oat have a significant leverage effect whereby in general, good news has a greater impact on the conditional variance than bad news. Last, the ARCH (10) statistic suggests that an ARCH effect does not exist in the residuals of the returns of all the agriculture commodities being studied in this paper.

After fitting various ARMA-GARCH models for the returns of the agriculture commodities, we obtain the corresponding standardized residual ${\mathrm{z}}_{\mathrm{s},\mathrm{t}}$, which is then transformed into the variates ${\hat{\mathrm{u}}}_{\mathrm{s},\mathrm{t}}$, using the CDF. Patton [35] points out that the probability integral transform of variates ${\hat{\mathrm{u}}}_{\mathrm{s},\mathrm{t}}$ must be an independently and identically distributed (iid) uniform random variable of range [0,1]. If the probability integral transform of variate ${\hat{\mathrm{u}}}_{\mathrm{s},\mathrm{t}}$ is not iid uniform (0,1), then the copula models cannot be used to model the residuals. Thus, to ensure that copula models can be used, the Ljung–Box (LB) test is used to examine the serial correlation under the null hypothesis of serial independence; then, we apply the Kolmogorow–Smirnov (KS) test to test the null hypothesis that ${\hat{\mathrm{u}}}_{\mathrm{s},\mathrm{t}}$ is distributed as uniform (0,1).

Table 4. Results of the goodness-of-fit for the marginal distributions.

	Corn	Wheat	Soybean	Soya Oil	Oat	Cotton
Panel A: Pre-Crisis
LB test: First moment	0.3222	0.1262	0.1545	0.1361	0.3307	0.1156
LB test: Second moment	0.9992	0.0826	0.0796	0.0923	0.0657	0.1856
LB test: Third moment	0.1975	0.4731	0.1811	0.5612	0.3312	0.3957
LB test: Fourth moment	0.9595	0.1566	0.2487	0.3817	0.1911	0.2114
KS test	0.9585	0.9971	0.9971	0.9381	0.9182	0.9971
Panel B: Post-Crisis
LB test: First moment	0.5335	0.2909	0.6270	0.4518	0.1556	0.1121
LB test: Second moment	0.1079	0.3819	0.1076	0.6661	0.0938	0.3210
LB test: Third moment	0.2482	0.0705	0.6173	0.3917	0.1151	0.2106
LB test: Fourth moment	0.0826	0.5218	0.0618	01429	0.3819	0.1082
KS test	0.9971	0.9381	0.9971	0.0.9971	0.9178	0.9971

Note: This table reports the p-values of the Ljung–Box (LB) statistic to test whether there is any serial dependence in the first four moments of the variables ${\widehat{u}}_{i,t}$. To perform the test, we regress ${\left(u_{i,t}-{\overline{u}}_i\right)}^k$ on the first 20 lags of the variables and apply the LB statistic to test whether there is any serial dependence in the residual. In addition, we present the p-values of the Kolmogorow–Smirnov (KS) statistic to test for the adequacy of the distribution model.

reports these two test’s P-values. The results of the LB tests imply that all of the first four moments are serially independent, while the results of the KS test indicate that all the series are distributed as uniform (0,1). The results imply that the copula method could be applied to capture the tail dependence and dependence for each pair of agricultural commodity returns.

3.4. The Static Copulas

Table 5. Estimates of the static copula models.

	Corn Wheat	Corn Soybeans	Corn Soya Oil	Corn Oat	Corn Cotton	Wheat Soybeans	Wheat Soya Oil	Wheat Oat	Wheat Cotton	Soybeans Soya Oil	Soybeans Oat	Soybeans Cotton	Soya Oil Oat	Soya Oil Cotton	Oat Cotton
Panel A: Pre-Crisis
Gaussian Copula
$\mathit{\rho }$	0.4586 ** (0.0182)	0.5141 ** (0.0166)	0.263 ** (0.0229)	0.3256 ** (0.0216)	0.107 ** (0.0250)	0.3464 ** (0.0211)	0.1640 ** (0.0244)	0.2277 ** (0.0235)	0.1040 ** (0.0250)	0.3912 ** (0.0200)	0.2964 ** (0.0222)	0.1514 ** (0.0246)	0.1221 ** (0.0249)	0.0894 ** (0.0251)	0.0196 (0.0254)
AIC	−363.0443	−473.1398	−108.5808	−170.9899	−16.0302	−195.4400	−40.0453	−80.1386	−14.7818	−254.6856	−139.9072	−33.7538	−21.1522	−10.3637	1.4032
Student-t Copula
$\mathit{\rho }$	0.4667 ** (0.0196)	0.5275 ** (0.0190)	0.2620 ** (0.0236)	0.3359 ** (0.0231)	0.1128 ** (0.0262)	0.3507 ** (0.0233)	0.1644 ** (0.0250)	0.2441 ** (0.0252)	0.1045 ** (0.0257)	0.3924 ** (0.0216)	0.3110 ** (0.0244)	0.1539 ** (0.0255)	0.1274 ** (0.0263)	0.0980 ** (0.0265)	0.0208 (0.0264)
$\mathit{n}$	11.1613 ** (3.0730)	5.8577 ** (1.0490)	30.0000 ** (3.4682)	10.8025 ** (3.2826)	17.2431 * (8.8803)	15.4217 ** (6.5390)	30.0000 ** (7.2839)	9.4587 ** (2.5542)	29.0201 ** (7.4319)	12.7673 ** (4.6443)	7.1996 ** (1.5855)	22.6982* (11.5193)	13.8409 ** (5.8014)	16.0064 ** (7.5918)	22.9956 (15.9424)
AIC	−378.9014	−517.0141	−169.3174	−182.4128	−18.1465	−199.9978	−45.3890	−94.3274	−15.5722	−261.4485	−163.6914	−34.0894	−25.6425	−13.3224	1.1391
Clayton Copula
$\mathit{\theta }$	0.5983 ** (0.0418)	0.7211 ** (0.0446)	0.2938 ** (0.0359)	0.3843 ** (0.0382)	0.1208 ** (0.0319)	0.3926 ** (0.0381)	0.1597 ** (0.0327)	0.2637 ** (0.0362)	0.1169 ** (0.0310)	0.5039 ** (0.0401)	0.3482 ** (0.0376)	0.1418 ** (0.0331)	0.1044 ** (0.0319)	0.0882 ** (0.0307)	0.0338 (0.0271)
AIC	−268.956	−358.5201	−84.5244	−128.4241	−15.1220	−134.1780	−26.8542	−64.3549	−15.0358	−210.9440	−108.0008	−19.7274	−10.5102	−7.5200	0.3126
Gumbel Copula
$\mathit{\theta }$	1.3987 ** (0.0272)	1.5106 ** (0.0302)	1.1694 ** (0.0211)	1.2496 ** (0.0236)	1.0607 ** (0.0177)	1.2639 ** (0.02380)	1.0962 ** (0.0189)	1.1628 ** (0.0213)	1.0577 ** (0.0174)	1.3055 ** (0.0248)	1.2326 ** (0.0232)	1.0967 ** (0.0186)	1.0839 ** (0.0181)	1.0587 ** (0.0177)	1.008 ** (0.0146)
AIC	−342.7825	−484.4547	−85.8350	−163.0900	−12.4766	−184.5592	−29.9470	−78.9915	−11.5462	−228.4602	−146.3674	−34.8705	−27.0259	−11.0662	1.6726
Panel B: Post-Crisis
Gaussian Copula
$\mathit{\rho }$	0.5388 ** (0.0140)	0.5660 ** (0.0098)	0.3402 ** (0.0148)	0.3956 ** (0.0131)	0.2315 ** (0.0157)	0.3829 ** (0.0133)	0.2813 ** (0.0158)	0.2943 ** (0.0146)	0.2023 ** (0.0160)	0.5334 ** (0.0109)	0.2924 ** (0.0147)	0.2452 ** (0.0155)	0.1659 ** (0.0173)	0.2232 ** (0.0170)	0.1455 ** (0.0165)
AIC	−1220.820	−1375.3860	−379.8913	−603.4096	−186.1636	−562.7014	−251.9902	−320.1962	−140.7194	−1072.9660	−315.9051	−209.9698	−82.7970	−147.0226	−70.9275
Student-t Copula
$\mathit{\rho }$	0.5569 ** (0.0124)	0.5717 ** (0.0125)	0.3317 ** (0.0168)	0.4215 ** (0.0460)	0.2252 ** (0.0178)	0.3918 ** (0.0157)	0.2749 ** (0.0178)	0.3295 ** (0.0629)	0.1973 ** (0.0183)	0.5326 ** (0.0123)	0.3091 ** (0.0162)	0.2338 ** (0.0179)	0.1764 ** (0.0187)	0.2127 ** (0.0189)	0.1523 ** (0.0180)
$\mathit{n}$	4.3864 **(0.3989)	3.7298 **(0.3207)	9.7162 **(1.8226)	5.8215 **(0.6343)	6.9595 **(0.9816)	4.5028 **(0.4308)	8.5044 **(1.3429)	5.3549 **(0.5610)	5.9040 **(0.7237)	10.5790 **(1.9751)	6.8157 **(0.9220)	6.2214 **(0.7987)	9.8464 **(1.7714)	10.6802 **(2.1107)	8.9171 **(1.5773)
AIC	−1409.5730	−821.5779	−412.1649	−725.5759	−217.6517	−713.3069	−299.7956	−437.5038	−219.1754	−1109.7270	−385.2677	−283.9827	−117.5111	−176.2976	−105.9034
Clayton Copula
$\mathit{\theta }$	0.8310 ** (0.0311)	0.8927 ** (0.0431)	0.3781 ** (0.0257)	0.5396 ** (0.0274)	0.2670 ** (0.0234)	0.5035 ** (0.0271)	0.3003 ** (0.0246)	0.3675 ** (0.0258)	0.2205 ** (0.0229)	0.7299 (0.0303)	0.3541 ** (0.0251)	0.2900 ** (0.0238)	0.1635 ** (0.0228)	0.2241 ** (0.0231)	0.1582 ** (0.0218)
AIC	−1000.1410	−608.6376	−292.7633	−513.0657	−172.7686	−466.1734	−196.9280	−262.6091	−121.2844	−809.7473	−257.6510	−199.9438	−61.3437	−122.4880	−63.7072
Gumbel Copula
$\mathit{\theta }$	1.5610 ** (0.0207)	1.5884 ** (0.0284)	1.2423 ** (0.0161)	1.3449 ** (0.0173)	1.1594 ** (0.0139)	1.3300 ** (0.0169)	1.1934 ** (0.0152)	1.2433 ** (0.0156)	1.1435 ** (0.0135)	1.4849 ** (0.0201)	1.2274 ** (0.0152)	1.1689 ** (0.0140)	1.1108 ** (0.0135)	1.1391 ** (0.0142)	1.0950 ** (0.0126)
AIC	−1262.5670	−747.0330	−351.3830	−615.2037	−189.8232	−614.2285	−248.7963	−354.2732	−166.6553	−974.2636	−330.3811	−216.2131	−88.6602	−141.5636	−74.7373

Note: This table reports the estimates of static copula parameters defined in Equations (5)–(8) and their corresponding standard errors (in brackets) for several copula specifications for each pair of agriculture commodity return. ** and * denote rejections of the null hypothesis at the 1% and 5% significance levels, respectively.

exhibits the copula models’ results. The table show that the parameters of dependence for the four copulas are positively and strongly significant for all the pairs of the agriculture commodities in all periods, excluding the pairs of oat and cotton in the pre-crisis period. This result concludes that a strong positive dependence exists between any pair of agricultural commodity prices, except for the pairs of oat and cotton in the pre-crisis period. This, in turn, implies that there is a strong contagion effect among the agricultural commodity markets such that an increase in volatility in one agricultural market is likely to lead to an increase in volatility in other agricultural markets. Moreover, we can observe that the values of the estimates of the dependence parameters among different agricultural commodity markets increased substantially after the food crisis in 2006. This results show that contagious effects among agricultural products boost after the food crisis in 2006. In addition, the results of the copula models studied in this paper indicate that the static dependence is highest between soybeans and corn, followed by corn and wheat, wheat and soybeans, and then soybeans and soya oil. The main reason is that corn, wheat, and soybeans are the main agriculture products, and they have high substitution among them. The least dependence is between cotton and oat, which suggests that there is little correlation and a weak transmission effect between oat and cotton.

The smallest values of the AIC among all of the pairs are those of the Student-t copula. This implies that the Student-t copula is the best model for capturing the dependence. This result indicates that dependence among agricultural commodities is governed by symmetry; that is to say, agricultural commodities appears to co-move symmetrically. The DoF of the Student-t copula range from 5.8557 (corn and soybeans) to 30 (corn and soya oil, wheat, and soya oil) in the pre-crisis period and from 3.7298 (corn and soybeans) to 10.6802 (soya oil and cotton) in the post-crisis period. The values of the tail dependence between agricultural commodity markets reported in

Table 6. Dependence values of the best fitting copula.

Best Fitting Copula	Panel A: Pre-Crisis	${\mathit{\lambda }}_{\mathit{L}}$	${\mathit{\lambda }}_{\mathit{U}}$	Panel B: Post-Crisis	${\mathit{\lambda }}_{\mathit{L}}$	${\mathit{\lambda }}_{\mathit{U}}$
Student-t copula	Corn and Wheat	0.0569	0.0569	Corn and Wheat	0.2669	0.2669
Student-t copula	Corn and Soybeans	0.1894	0.1894	Corn and Soybeans	0.3105	0.3105
Student-t copula	Corn and Soya Oil	0.0001	0.0001	Corn and Soya oil	0.0412	0.0412
Student-t copula	Corn and Oat	0.0324	0.0324	Corn and Oat	0.1407	0.1407
Student-t copula	Corn and Cotton	0.0012	0.0012	Corn and Cotton	0.0552	0.0552
Student-t copula	Wheat and Soybeans	0.0123	0.0123	Wheat and Soybeans	0.1764	0.1764
Student-t copula	Wheat and Soya Oil	0.0001	0.0001	Wheat and Soya Oil	0.0436	0.0436
Student-t copula	Wheat and Oat	0.0294	0.0294	Wheat and Oat	0.1208	0.1208
Student-t copula	Wheat and Cotton	0.0000	0.0000	Wheat and Cotton	0.0690	0.0690
Student-t copula	Soybeans and Soya Oil	0.0282	0.0282	Soybeans and Soya Oil	0.0856	0.0856
Student-t copula	Soybeans and Oat	0.0707	0.0707	Soybeans and Oat	0.0775	0.0775
Student-t copula	Soybeans and Cotton	0.0003	0.0003	Soybeans and Cotton	0.0708	0.0708
Student-t copula	Soya Oil and Oat	0.0041	0.0041	Soya Oil and Oat	0.0189	0.0189
Student-t copula	Soya Oil and Cotton	0.0016	0.0016	Soya Oil and Cotton	0.0179	0.0179
Student-t copula	Oat and Cotton	0.0001	0.0001	Oat and Cotton	0.0224	0.0224

Notes: The table presents the lower and upper tail dependence coefficients estimated from the copula that provide the best fit.

yield clear evidence that extreme co-movement exists in each pair of agricultural commodity prices being studied in this paper, except the pairs of cotton with corn, wheat, soybeans, soya oil, and oat in the pre-crisis period. Thus, we conclude that the agricultural commodity markets, except cotton, tend to boom and crash at the same time; that is, when one agricultural commodity market has a high positive return, another agricultural commodity market tends to have a high positive return and vice versa. We also compare the dependence of the pre-crisis and post-crisis periods and find that the tail dependence among agricultural commodity markets is higher after the food crisis. This implies that after the food crisis, agricultural commodity returns move together more closely. Thus, we conclude that the food crisis increased the dependence among agricultural commodity markets. We also observe that the tail dependence reaches the highest level between corn and soybeans, followed by corn and wheat, wheat and soybeans, and then corn and oat. The least dependence is between wheat and oats. The results are consistent with those for unconditional correlation (reported in Table 2) and conditional dependence (reported in Table 5). Taken together, these results strongly support the argument that the strongest co-movement is found in the pair of corn and soybeans, followed by corn and wheat, and the lowest degree of extreme co-movement is between soya oil and cotton. A possible reason for the strong co-movement between corn and soybeans could be the demand for biofuels, since corn and soybeans are the main crops that are used in the production of biofuels (biodiesel and ethanol).

3.5. The Time-Varying Copula

The dependence obtained from the static copulas as discussed above is under the assumption that the dependence is time invariant, but in reality, the dependence could be time varying. To circumvent this limitation, we employ the dynamic Student-t copula as stated in Equation (8) in the analysis and exhibit the results in

Table 7. Estimation parameters for dynamic copula models.

	Corn Wheat	Corn Soybeans	Corn Soya Oil	Corn Oat	Corn Cotton	Wheat Soybeans	Wheat Soya Oil	Wheat Oat	Wheat Cotton	Soybeans Soya Oil	Soybeans Oat	Soybeans Cotton	Soya Oil Oat	Soya Oil Cotton	Oat Cotton
Panel A: Pre-Crisis
${\mathit{\alpha }}_{\mathit{c}}$	0.3740 ** (0.1260)	0.09154 (0.0686)	0.7131 ** (0.2177)	0.0133 (0.0086)	0.0013 (0.0017)	0.0489 (0.4905)	0.6677 ** (0.1025)	0.7115 ** (0.2604)	0.0913 (0.1004)	0.4387 ** (0.2097)	0.0116 (0.0067)	0.3499 (0.1994)	0.0033 (0.0030)	0.0003 (0.0005)	0.0485 (0.0669)
${\mathit{\beta }}_{\mathit{c}}$	0.5840 ** (0.1247)	0.8940 ** (0.0682)	0.3676 (0.3650)	0.9615 ** (0.0161)	0.9877 ** (0.0102)	0.8055 * (0.3687)	0.9746 ** (0.0321)	0.3792 (0.4966)	0.5641 (0.4586)	0.7186 ** (0.2347)	0.9650 ** (0.0130)	0.1169 (0.5959)	0.9732 ** (0.0145)	0.9951 ** (0.0405)	0.1401 (0.6240)
${\mathit{\gamma }}_{\mathit{c}}$	1.6561 ** (0.5182)	0.8605 (0.4498)	1.6475 ** (0.5665)	0.4957 ** (0.1867)	0.1622 (0.1177)	0.8130 (0.6911)	0.1981 (0.1690)	0.5716 (0.5942)	0.3676 (0.4869)	0.6844 (0.4576)	0.4327 ** (0.1659)	0.4289 (0.6261)	0.2932* (0.1390	0.0954 (0.0598)	0.4794 (0.5906)
$n$	12.9271 ** (0.6502)	5.7568 ** (0.4930)	53.9531 ** (0.2121)	9.9681 ** (1.3829)	18.3019 ** (0.2758)	15.4850 ** (0.3671)	8.7251 ** (2.9170)	9.5712 ** (0.3481)	37.4290 ** (10.2901)	12.9185 ** (0.2665)	7.1660 ** (2.3901)	22.0127 ** (0.2289)	14.3228 ** (0.4018)	18.1200* (0.5917)	22.7434 ** (0.1373)
AIC	−388.4608	−523.0586	−111.4026	−194.69250	−19.4123	−197.7442	−36.6833	−91.1857	−10.2340	−259.4488	−172.0219	−30.9602	−32.4385	−16.7575	4.4635
Panel B: Post–Crisis
${\mathit{\alpha }}_{\mathit{c}}$	0.0511 (0.0279)	0.0043 (0.0011)	0.0130 (0.0100)	0.0386 ** (0.0147)	0.1539 (0.1219)	0.2331 (0.2188)	0.0865 (0.0065)	0.0148* (0.0065)	0.1184 (0.0922)	0.0140 (0.0082)	0.0255 (0.0144)	0.2317 (0.1751)	0.0001 (0.0003)	0.5798 ** (0.1554)	0.0048 (0.0029)
${\mathit{\beta }}_{\mathit{c}}$	0.9675 ** (0.0184)	0.8434 ** (0.0104)	0.9772 ** (0.0173)	0.9336 ** (0.0210)	0.6884 ** (0.2538)	0.7128 ** (0.2631)	0.6975 ** (0.2299)	0.9638 ** (0.0121)	0.7296 ** (0.2162)	0.9845 ** (0.0089)	0.9428 ** (0.0274)	0.5367 (0.3541)	0.9966 ** (0.0152)	0.3590 (0.3209)	0.9766 ** (0.0112)
${\mathit{\gamma }}_{\mathit{c}}$	−0.1928 (0.1090)	−0.6739* (0.3277)	0.1221 (0.0949)	0.6232 ** (0.1722)	−0.3561 (0.2902)	0.2806 (0.2620)	−0.4035 (0.3211)	0.3819 ** (0.1098)	−0.3738 (0.3042)	0.1254 (0.0708)	0.4618 ** (0.1772)	−0.2630 (0.3275)	0.0866 ** (0.0300)	1.0048 (0.06259	0.1668* (0.0726)
$n$	4.4678 ** (1.1156)	3.7447 ** (0.2778)	9.8585 ** (0.8598)	6.2679 ** (0.1824)	7.0565 ** (0.3950)	4.5155 ** (0.3937)	8.6108 ** (0.7172	5.5387 ** (0.5020)	5.9539 ** (0.1857)	10.3843 ** (0.5962)	7.1546 ** (0.4096)	6.2717 ** (0.3105)	10.5600 ** (0.0274)	10.8886 ** (1.8445)	8.9563 ** (0.3663)
AIC	−1413.5360	−1596.7140	−416.5988	−764.4676	−245.0743	−368.1865	−297.5022	−464.3449	−216.8226	−1135.8380	−406.7658	−280.3931	−144.0980	−127.3910	−112.6110

Note: This table reports the estimates of static copula parameters defined in Equations (5)–(8) and their corresponding standard errors (in brackets) for dynamic Student-t copula specifications for each pair of agriculture commodity return. ** and * denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively.

. From the table, we notice that most estimates of the autoregressive parameter ${\mathsf{\beta }}_{\mathrm{c}}$ are significant and close to one, which indicates a high degree of persistence pertaining to the dependence structure in the agricultural commodity markets that the correlation at time t depends strongly on the correlation at time t-1.${\mathsf{\gamma }}_{\mathrm{c}}$ is the latent parameter that displays the latest return information. The dynamic dependence parameter estimates between agricultural commodity markets generated from the dynamic Student-t copula are plotted in Figure 2. Figure 2 also provides evidence that the contagion effect increases after food crises.

4. Implications and Suggestions

We turn to a discussion of some of the implications for policy and investment of our empirical analysis of dependence and co-movements among the agricultural commodity markets studied in this research. First, the dependence analysis shows strong contagion effects exist among different agricultural commodity markets. This implies that the agricultural commodity markets have been integrated, with prices booming and crashing together during extreme events, and an increase in volatility in one agricultural commodity will lead to an increase in volatility and price fluctuations in other agricultural commodities. Our findings suggest that policy makers should set up agricultural policies that reduce the probability of an unreasonable increase in agricultural commodity prices as well as any unreasonable large price fluctuations for any major agricultural commodity market. Policy makers should also establish a warning mechanism for any unreasonable multi-market price fluctuations in agricultural commodities. Third, policy makers should design a ‘road map’ of tail dependence and systemic risk among agricultural markets to protect against spillover risk contagion effects and foster market stability. Fourth, agricultural commodity are not independent; hence, policy makers ought to make one kind of agricultural price support or stabilization policy and should pay attention to the effect of other agriculture prices on this kind of agricultural price.

Moreover, our findings show that there are stronger contagion effects, risk transmissions, and asymmetric tail dependencies among agricultural commodity markets after the food crisis. This suggests that policy makers should pay more attention to setting up policies to stabilize price fluctuations and price increases after the food crisis. They should also set up policies that offer more food subsidies to reduce the negative impact of a rise in agricultural commodity prices on the poor. The finding is consistent with the argument by Reboredo [36] that a rise in agricultural commodity prices would greatly affect the poor’s standard of living. On the other hand, a drop in the price of a particular agricultural commodity would cause a drop in the prices of other agricultural commodities, which is a situation that would affect farmers’ income. Thus, policy makers should also provide agricultural commodity subsidies to farmers during a period when prices in agricultural commodities drop. Moreover, governments should also consider implementing price controls and trade barriers to stabilize the prices of agriculture commodities and reduce price fluctuations.

In addition, our findings have potentially important implications for investors in their decisions regarding the selection of stocks in their portfolios, as well as on their international diversification and risk management. Our findings show that all the markets are more tail-dependent in the post-crisis than in the pre-crisis, and the distributions are fat-tailed. This information could give hints to investors that risk in one agricultural commodity will likely be dependent on risk in other agricultural commodity markets. Thus, investors and speculators should be portfolio diversification and hedging purposes, thus avoiding the risk of investment in the agricultural commodity market.

5. Conclusions

This study investigates the co-movement of spot prices of four agricultural commodities (corn, wheat, soybeans, and oats) by using a copula-GARCH approach. We first apply the marginal ARMA ($\mathrm{k},\mathrm{r})$-GJRGARCH ($1,1$) distribution model to examine the marginal distribution for each agricultural commodity studied in our paper. We document the existence of the heteroskedastic effect in all the return series in both the pre-crisis and the post-crisis periods. Moreover, we find an asymmetric volatility effect in wheat and soybean in the pre-crisis period. Then, we apply several copulas to examine the standardized residuals from the marginal models. We find that there are both contagion and risk transmission effects between any pair of agricultural commodity markets, implying that an increase in price and volatility in one agricultural market is likely to lead to an increase in price and volatility in other agricultural markets. Second, agricultural commodities appears to co-move symmetrically. We also observe substantial extreme positive co-movements among different agricultural commodity markets, indicating that when one agricultural commodity market has a high positive or negative return, other agricultural commodity markets tend to have a high positive or negative return. We also find that the co-movements among different agricultural commodity markets increase substantially after the food crisis, and the co-movement varies over time. Moreover, we find that among different agricultural commodity markets, the strongest co-movement is between soybeans and corn, while the weakest is between wheat and oats. Our findings hold implications for policy makers, investors, farmers, and consumers in their policy making, integration, risk management, and asset pricing decisions for agricultural commodity markets.