Cluster Analysis of Haze Episodes Based on Topological Features
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Preparation
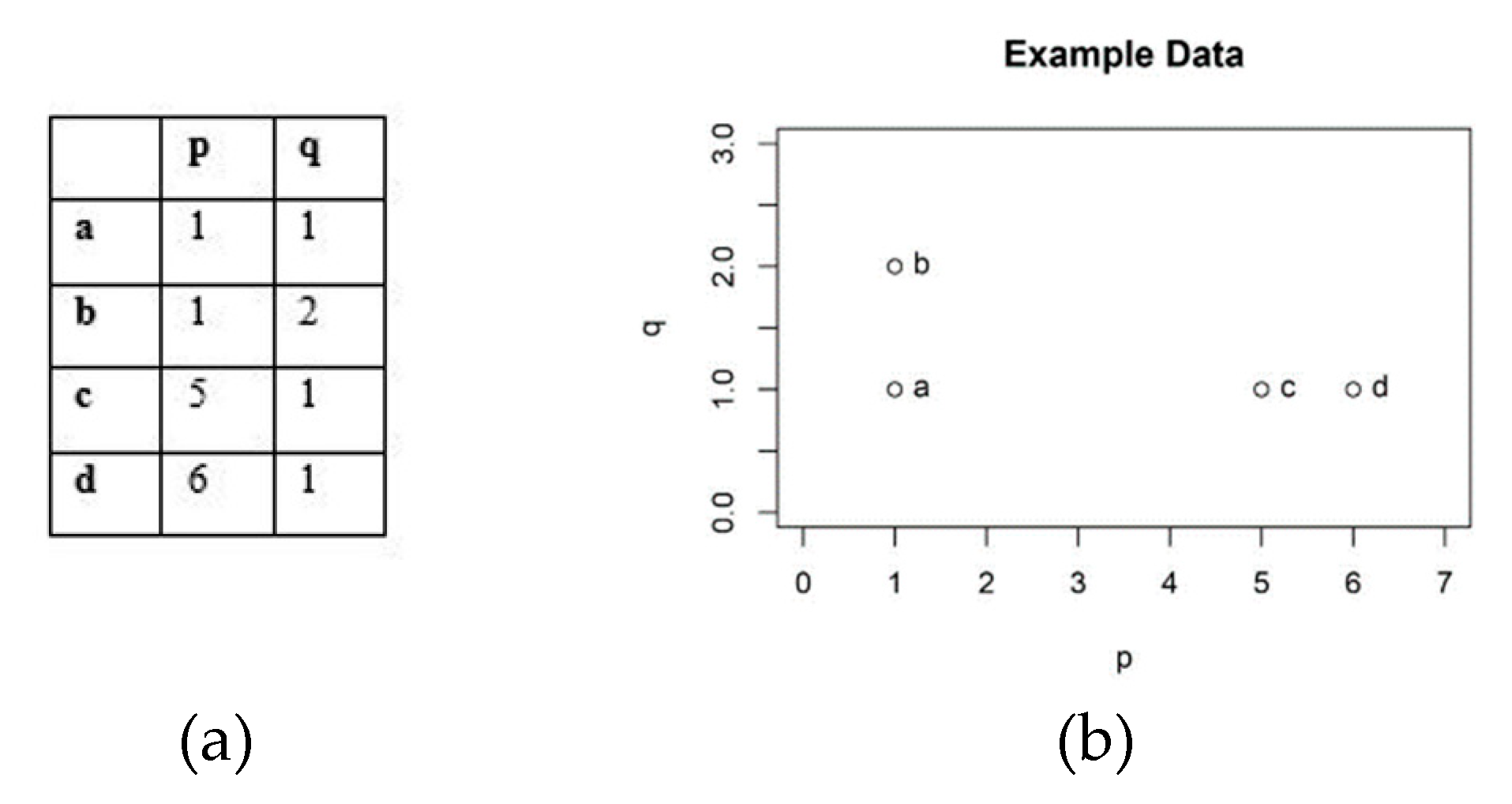
2.2. Hierarchical Agglomerative Clustering Analysis (HACA)
2.3. Persistent Homology
2.4. Analysis of Topological Features
2.5. HACA with Persistent Homology
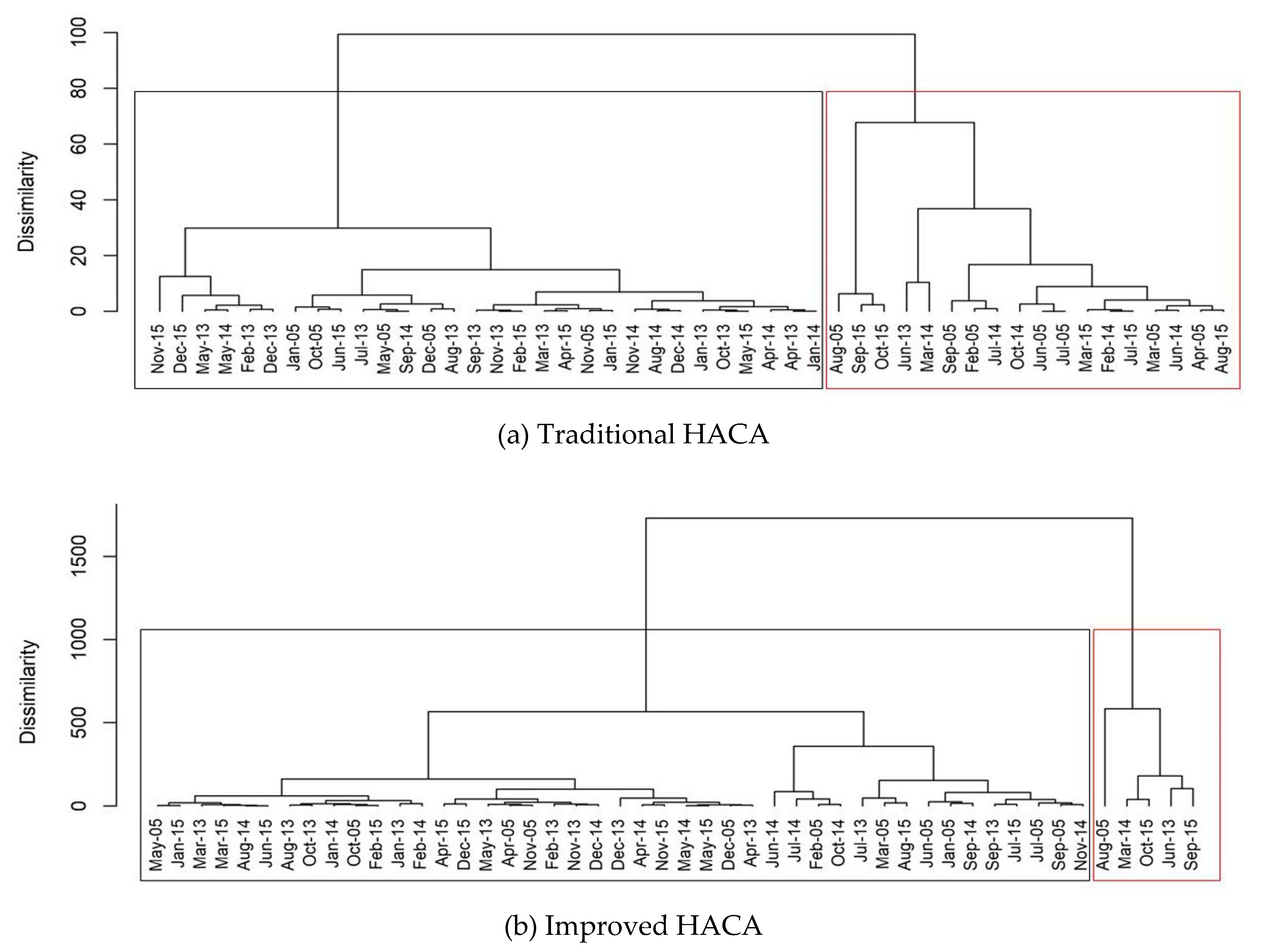
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Pretto, L.; Acreman, S.; Ashfold, M.J.; Mohankumar, S.K.; Campos-Arceiz, A. The link between knowledge, attitudes and practices in relation to atmospheric haze pollution in Peninsular Malaysia. PLoS ONE 2015, 10, e0143655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sulong, N.A.; Latif, M.T.; Khan, M.F.; Amil, N.; Ashfold, M.J.; Wahab, M.I.A.; Chan, K.M.; Sahani, M. Source apportionment and health risk assessment among specific age groups during haze and non-haze episodes in Kuala Lumpur, Malaysia. Sci. Total Environ. 2017, 601, 556–570. [Google Scholar] [CrossRef] [PubMed]
- Afroz, R.; Hassan, M.N.; Ibrahim, N.A. Review of air pollution and health impacts in Malaysia. Environ. Res. 2003, 92, 71–77. [Google Scholar] [CrossRef]
- Payus, C.; Abdullah, N.; Sulaiman, N. Airborne particulate matter and meteorological interactions during the haze period in Malaysia. Int. J. Environ. Sci. Dev. 2013, 4, 398–402. [Google Scholar] [CrossRef] [Green Version]
- Dotse, S.Q.; Dagar, L.; Petra, M.I.; De Silva, L.C. Influence of Southeast Asian Haze episodes on high PM10 concentrations across Brunei Darussalam. Environ. Pollut. 2016, 219, 337–352. [Google Scholar] [CrossRef]
- Department of Environment (DOE), Chronology of Haze Episodes in Malaysia. Available online: https://www.doe.gov.my/portalv1/en/info-umum/info-kualiti-udara/kronologi-episod-jerebu-di-malaysia/319123 (accessed on 25 November 2018).
- Latif, M.T.; Othman, M.; Idris, N.; Juneng, L.; Abdullah, A.M.; Hamzah, W.P.; Khan, M.F.; Sulaiman, N.M.N.; Jewaratnam, J.; Aghamohammadi, N.; et al. Impact of regional haze towards air quality in Malaysia: A review. Atmos. Environ. 2018, 177, 28–44. [Google Scholar] [CrossRef]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis; John Wiley & Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Liu, J.; Li, W.; Wu, J. A framework for delineating the regional boundaries of PM 2.5 pollution: A case study of China. Environ. Pollut. 2018, 235, 642–651. [Google Scholar] [CrossRef]
- Müllner, D. Modern Hierarchical, Agglomerative Clustering Algorithms. 2011. Available online: https://arxiv.org/abs/1109.2378 (accessed on 27 November 2018).
- Pires, J.C.M.; Sousa, S.I.V.; Pereira, M.C.; Alvim-Ferraz, M.C.M.; Martins, F.G. Management of air quality monitoring using principal component and cluster analysis—Part I: SO2 and PM10. Atmos. Environ. 2008, 42, 1249–1260. [Google Scholar] [CrossRef]
- Lu, W.Z.; He, H.D.; Dong, L.Y. Performance assessment of air quality monitoring networks using principal component analysis and cluster analysis. Build. Environ. 2011, 46, 577–583. [Google Scholar] [CrossRef]
- Austin, E.; Coull, B.A.; Zanobetti, A.; Koutrakis, P.A. framework to spatially cluster air pollution monitoring sites in US based on the PM2. 5 composition. Environ. Int. 2013, 59, 244–254. [Google Scholar] [CrossRef]
- Azid, A.; Juahir, H.; Ezani, E.; Toriman, M.E.; Endut, A.; Rahman, M.N.A.; Yunus, K.; Kamarudin, M.K.A.; Hasnam, C.N.C.; Saudi, A.S.M.; et al. Identification source of variation on regional impact of air quality pattern using chemometric. Aerosol Air Qual. Res. 2015, 15, 1545–1558. [Google Scholar] [CrossRef] [Green Version]
- Isiyaka, H.A.; Azid, A. Air quality pattern assessment in Malaysia using multivariate techniques. Malays. J. Anal. Sci. 2015, 19, 966–978. [Google Scholar]
- Song, J.; Guang, W.; Li, L.; Xiang, R. Assessment of air quality status in Wuhan, China. Atmosphere 2016, 7, 56. [Google Scholar] [CrossRef] [Green Version]
- Beaver, S.; Palazoğlu, A. A cluster aggregation scheme for ozone episode selection in the San Francisco, CA Bay Area. Atmos. Environ. 2006, 40, 713–725. [Google Scholar] [CrossRef]
- Mutalib, S.N.S.A.; Juahir, H.; Azid, A.; Sharif, S.M.; Latif, M.T.; Aris, A.Z.; Zain, S.M.; Dominick, D. Spatial and temporal air quality pattern recognition using environmetric techniques: A case study in Malaysia. Environ. Sci. Process. Impacts 2013, 15, 1717–1728. [Google Scholar] [CrossRef]
- Ignaccolo, R.; Ghigo, S.; Giovenali, E. Analysis of air quality monitoring networks by functional clustering. Environmetrics 2008, 19, 672–686. [Google Scholar] [CrossRef]
- Qiao, Z.; Wu, F.; Xu, X.; Yang, J.; Liu, L. Mechanism of Spatiotemporal Air Quality Response to Meteorological Parameters: A National-Scale Analysis in China. Sustainability 2019, 11, 3957. [Google Scholar] [CrossRef] [Green Version]
- Carlsson, G. Topology and data. Bull. Amer. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef] [Green Version]
- Otter, N.; Porter, M.A.; Tillmann, U.; Grindrod, P.; Harrington, H.A. A roadmap for the computation of persistent homology. EPJ Data Sci. 2017, 6, 17. [Google Scholar] [CrossRef] [Green Version]
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Nicolau, M.; Levine, A.J.; Carlsson, G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc. Natl. Acad. Sci. USA 2011, 108, 7265–7270. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S.; Ghrist, R.; Kumar, V. Persistent homology for path planning in uncertain environments. IEEE Trans. Robot. 2015, 31, 578–590. [Google Scholar] [CrossRef]
- Petri, G.; Expert, P.; Turkheimer, F.; Carhart-Harris, R.; Nutt, D.; Hellyer, P.J.; Vaccarino, F. Homological scaffolds of brain functional networks. J. R. Soc. Interface 2014, 11, 20140873. [Google Scholar] [CrossRef] [Green Version]
- Zomorodian, A.J. Topology for Computing; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Pereira, C.M.; de Mello, R.F. Persistent homology for time series and spatial data clustering. Expert Syst. Appl. 2015, 42, 6026–6038. [Google Scholar] [CrossRef]
- Wubie, B.A.; Andres, A.; Greiner, R.; Hoehn, B.; Montano-Loza, A.; Kneteman, N.; Heo, G. Cluster Identification via Persistent Homology and Other Clustering Techniques, with Application to Liver Transplant Data; Springer International Publishing: Cham, Switzerland, 2018; pp. 145–177. [Google Scholar]
- Islambekov, U.; Gel, Y.R. Unsupervised space–time clustering using persistent homology. Environmetrics 2019, 30, e2539. [Google Scholar] [CrossRef] [Green Version]
- Takens, F. Detecting strange attractors in turbulence. In Lecture Notes in Mathematics Dynamical Systems and Turbulence, Warwick; Springer: Berlin/Heidelberg, Germany, 1980; pp. 366–381. [Google Scholar]
- Umeda, Y. Time series classification via topological data analysis. Trans. Jpn. Soc. Artif. Intell. 2017, 32, D-G72_1-12. [Google Scholar] [CrossRef] [Green Version]
- Khasawneh, F.A.; Munch, E. Stability determination in turning using persistent homology and time series analysis. In Proceedings of the ASME 2014 International Mechanical Engineering Congress Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V04BT04A038. [Google Scholar]
- Khasawneh, F.A.; Munch, E.; Perea, J.A. Chatter Classification in Turning Using Machine Learning and Topological Data Analysis. IFAC-PapersOnLine 2018, 51, 195–200. [Google Scholar] [CrossRef]
- Enviro Knowledge Centre. Malaysia Environmental Quality Report 2015. Available online: https://enviro.doe.gov.my/ (accessed on 25 November 2018).
- Enviro Knowledge Centre. Malaysia Environmental Quality Report 2013. Available online: https://enviro.doe.gov.my/ (accessed on 25 November 2018).
- Enviro Knowledge Centre. Malaysia Environmental Quality Report 2014. Available online: https://enviro.doe.gov.my/ (accessed on 25 November 2018).
- Enviro Knowledge Centre. Malaysia Environmental Quality Report 2005. Available online: https://enviro.doe.gov.my/ (accessed on 25 November 2018).
- Abdullah, A.M.; Samah, M.A.A.; Jun, T.Y. An overview of the air pollution trend in Klang Valley, Malaysia. Open Environ. Sci. 2012, 6, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Pigott, T.D. A review of methods for missing data. Educ. Res. Eval. 2001, 7, 353–383. [Google Scholar] [CrossRef] [Green Version]
- McKenna, J.E., Jr. An enhanced cluster analysis program with bootstrap significance testing for ecological community analysis. Environ. Model. Softw. 2003, 18, 205–220. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Amer. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef] [Green Version]
- Kerber, M.; Morozov, D.; Nigmetov, A. Geometry helps to compare persistence diagrams. J. Exp. Algorithmics 2017, 22, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Zulkepli, N.F.S.; Noorani, M.S.M.; Razak, F.A.; Ismail, M.; Alias, M.A. Topological characterization of haze episodes using persistent homology. Aerosol Air Qual. Res. 2019, 19, 1614–1624. [Google Scholar] [CrossRef] [Green Version]
- Mittal, K.; Gupta, S. Topological characterization and early detection of bifurcations and chaos in complex systems using persistent homology. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 051102. [Google Scholar] [CrossRef]
- R Core Team. R: A language and Environment for Statistical Computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 25 January 2017).
- Fasy, B.T.; Kim, J.; Lecci, F.; Maria, C.; Rouvreau, V. Statistical Tools for Topological Data Analysis. 2017. Available online: https://cran.rproject.org/web/packages/TDA/TDA.pdf (accessed on 25 January 2017).
- Wong, C.L.; Venneker, R.; Uhlenbrook, S.; Jamil, A.B.M.; Zhou, Y. Variability of rainfall in Peninsular Malaysia. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 5471–5503. [Google Scholar] [CrossRef] [Green Version]
- Soleiman, A.; Othman, M.; Samah, A.A.; Sulaiman, N.M.; Radojevic, M. The occurrence of haze in Malaysia: A case study in an urban industrial area. Pure Appl. Geophys. 2003, 160, 221–238. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 167, 664–681. [Google Scholar] [CrossRef] [Green Version]









| Month | Statistic | Station | ||
|---|---|---|---|---|
| Klang | Petaling Jaya | Shah Alam | ||
| Aug-05 | Max | 590 | 482 | 587 |
| Min | 36 | 43 | 26 | |
| Mean | 140 | 119 | 115 | |
| Jun-13 | Max | 581 | 370 | 362 |
| Min | 36 | 20 | 21 | |
| Mean | 122 | 84 | 83 | |
| Mar-14 | Max | 448 | 303 | 279 |
| Min | 47 | 33 | 36 | |
| Mean | 138 | 95 | 95 | |
| Sep-15 | Max | 337 | 295 | 301 |
| Min | 59 | 49 | 49 | |
| Mean | 141 | 123 | 135 | |
| Oct-15 | Max | 326 | 320 | 346 |
| Min | 52 | 24 | 42 | |
| Mean | 159 | 126 | 147 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zulkepli, N.F.S.; Noorani, M.S.M.; Razak, F.A.; Ismail, M.; Alias, M.A. Cluster Analysis of Haze Episodes Based on Topological Features. Sustainability 2020, 12, 3985. https://doi.org/10.3390/su12103985
Zulkepli NFS, Noorani MSM, Razak FA, Ismail M, Alias MA. Cluster Analysis of Haze Episodes Based on Topological Features. Sustainability. 2020; 12(10):3985. https://doi.org/10.3390/su12103985
Chicago/Turabian StyleZulkepli, Nur Fariha Syaqina, Mohd Salmi Md Noorani, Fatimah Abdul Razak, Munira Ismail, and Mohd Almie Alias. 2020. "Cluster Analysis of Haze Episodes Based on Topological Features" Sustainability 12, no. 10: 3985. https://doi.org/10.3390/su12103985
APA StyleZulkepli, N. F. S., Noorani, M. S. M., Razak, F. A., Ismail, M., & Alias, M. A. (2020). Cluster Analysis of Haze Episodes Based on Topological Features. Sustainability, 12(10), 3985. https://doi.org/10.3390/su12103985





