The Strategies of the Poverty-Alleviation Supply Chain with Government Subsidies and Cost Sharing: Government-Led or Market-Oriented?
Abstract
:1. Introduction
- What are the impacts of CSR cost sharing and/or government subsidies on poverty alleviation? Is it true that the higher the government subsidies or CSR cost sharing, the more effective poverty alleviation becomes?
- Which poverty alleviation mechanisms among the four are more effective?
- Is poverty alleviation reconcilable with profit maximization and social welfare improvement?
2. Literature Review
2.1. Sustainable Supply Chain Management and Poverty Alleviation
2.2. Sustainable Supply Chain Management and CSR
2.3. Sustainable Supply Chain Management with Government Policies and/or Cost Sharing
2.4. Our Contributions
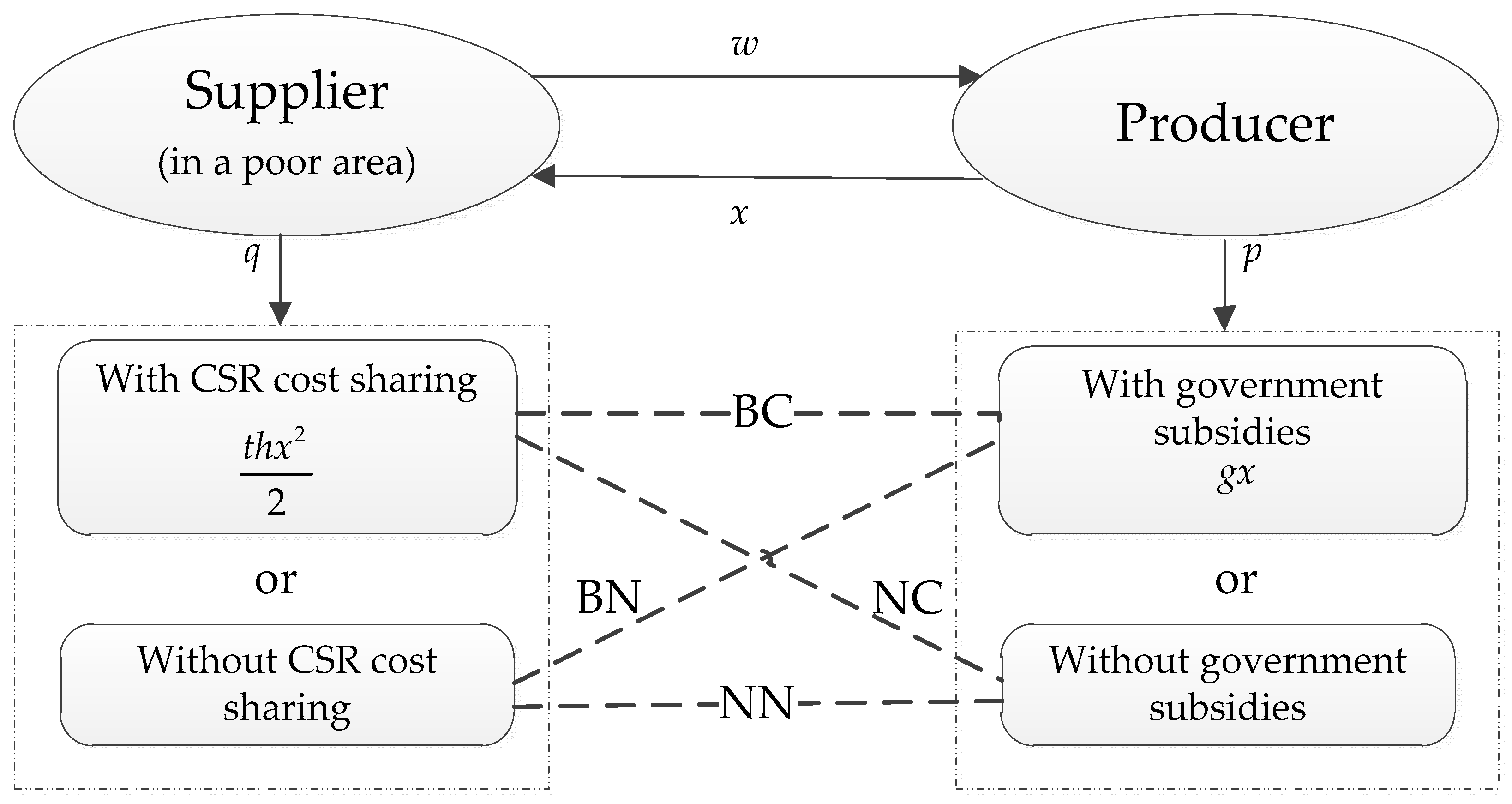
3. The Models
3.1. Model Settings and Notations
3.2. NN Model
3.3. NC Model
3.4. BN Model
3.5. BC Model
4. Analysis and Comparison
4.1. Comparison of the CSR Level, Wholesale Price, Output of the Supplier and Retail Price
4.2. Numerical Analysis of the Profits of the Supplier and the Producer and Social Welfare
4.3. Numerical Analysis of the Effects of Government Subsidies
4.4. Numerical Analysis of the CSR Level, Wholesale Price, Output of the Supplier and Retail Price
5. Managerial Insights
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Organisation for Economic Co-operation and Development. Public Expenditure on Income Maintenance Programmes; Organisation for Economic Co-operation and Development: Paris, France; OECD: Paris, France; Washington, DC, USA, 1976; p. 69. [Google Scholar]
- Tang, L. The Evolution of China’s Poverty Alleviation and Development Policy (2001–2015), 1st ed.; Zuo, C., Ed.; Springer Nature Singapore Pte Ltd.: Singapore, 2019; pp. 65–111. [Google Scholar]
- Sun, J. China’s Poverty Alleviation Strategy and the Delineation of the Relative Poverty Line after 2020: An Analysis Based on Theory, Policy and Empirical Data. Chin. Rural Econ. 2020, 10, 98–113. [Google Scholar]
- Wanh, C. The research context and theme content of Chinese industrial poverty alleviation since 21st century. China Popul. Environ. 2017, 27, 145–154. [Google Scholar] [CrossRef]
- Burke, L.; Logsdon, J.M. How corporate social responsibility pays off. Long Range Plan. 1996, 29, 495–502. [Google Scholar] [CrossRef]
- Porter, M.E.; Kramer, M.R. The competitive advantage of corporate philanthropy. Harv. Bus. Rev. 2002, 80, 57. [Google Scholar]
- Kramer, M.R.; Porter, M.E. Strategy and society: The link between competitive advantage and corporate social responsibility. Strat. Dir. 2007, 23, 78–92. [Google Scholar] [CrossRef]
- Lee, H.L. Don’t tweak your supply chain-rethink it end to end. Harv. Bus. Rev. 2010, 88, 9. [Google Scholar]
- Lee, H.L.; Tang, C.S. Socially and Environmentally Responsible Value Chain Innovations: New Operations Management Research Opportunities. Manag. Sci. 2018, 64, 983–996. [Google Scholar] [CrossRef]
- Tang, C.S. Socially responsible supply chains in emerging markets: Some research opportunities. J. Oper. Manag. 2018, 57, 1–10. [Google Scholar] [CrossRef]
- Sen, A. Poverty: An Ordinal Approach to Measurement. Econometrica 1976, 44, 219. [Google Scholar] [CrossRef]
- Ansari, S.S.; Munir, K.; Gregg, T. Impact at the ‘Bottom of the Pyramid’: The Role of Social Capital in Capability Development and Community Empowerment. J. Manag. Stud. 2012, 49, 813–842. [Google Scholar] [CrossRef]
- Elkington, J. Partnerships from Cannibals with Forks: The Triple iottom line of 2 1 st-Century Business. Environ. Qual. Manag. 1998, 8, 37–51. [Google Scholar] [CrossRef]
- Govindan, K.; Cheng, T. Sustainable supply chain management: Advances in operations research perspective. Comput. Oper. Res. 2015, 54, 177–179. [Google Scholar] [CrossRef]
- Brandenburg, M.; Govindan, K.; Sarkis, J.; Seuring, S. Quantitative models for sustainable supply chain management: Developments and directions. Eur. J. Oper. Res. 2014, 233, 299–312. [Google Scholar] [CrossRef]
- Brandenburg, M.; Gruchmann, T.; Oelze, N. Sustainable Supply Chain Management—A Conceptual Framework and Future Research Perspectives. Sustainability 2019, 11, 7239. [Google Scholar] [CrossRef] [Green Version]
- Ahi, P.; Searcy, C. A comparative literature analysis of definitions for green and sustainable supply chain management. J. Clean. Prod. 2013, 52, 329–341. [Google Scholar] [CrossRef]
- Georgiadis, P.; Besiou, M. Environmental and economical sustainability of WEEE closed-loop supply chains with recycling: A system dynamics analysis. Int. J. Adv. Manuf. Technol. 2009, 47, 475–493. [Google Scholar] [CrossRef]
- Kleindorfer, P.; Singhal, J.; Van Wassenhove, L.N. Sustainable Operations Management. Prod. Oper. Manag. 2009, 14, 482–492. [Google Scholar] [CrossRef]
- Sarkis, J.; Zhu, Q.; Lai, K.-H. An organizational theoretic review of green supply chain management literature. Int. J. Prod. Econ. 2011, 130, 1–15. [Google Scholar] [CrossRef]
- Seuring, S.; Sarkis, J.; Müller, M.; Rao, P. Sustainability and supply chain management–An introduction to the special issue. J. Clean. Prod. 2008, 16, 1545–1551. [Google Scholar] [CrossRef]
- Sodhi, M.S.; Tang, C.S. Corporate social sustainability in supply chains: A thematic analysis of the literature. Int. J. Prod. Res. 2017, 56, 882–901. [Google Scholar] [CrossRef]
- Tang, C.S.; Zhou, S.X. Research advances in environmentally and socially sustainable operations. Eur. J. Oper. Res. 2012, 223, 585–594. [Google Scholar] [CrossRef]
- Malik, M.; Abdallah, S. Sustainability Initiatives in Emerging Economies: A Socio-Cultural Perspective. Sustainability 2019, 11, 4893. [Google Scholar] [CrossRef] [Green Version]
- Silvestre, B.S.; Ţîrcă, D.M. Innovations for sustainable development: Moving toward a sustainable future. J. Clean. Prod. 2019, 208, 325–332. [Google Scholar] [CrossRef]
- Hall, J.; Matos, S. Incorporating impoverished communities in sustainable supply chains. Int. J. Phys. Distrib. Logist. Manag. 2010, 40, 124–147. [Google Scholar] [CrossRef]
- Bendul, J.C.; Rosca, E.; Pivovarova, D. Sustainable supply chain models for base of the pyramid. J. Clean. Prod. 2017, 162, S107–S120. [Google Scholar] [CrossRef]
- Yawar, S.A.; Seuring, S. The role of supplier development in managing social and societal issues in supply chains. J. Clean. Prod. 2018, 182, 227–237. [Google Scholar] [CrossRef]
- Sodhi, M.S.; Tang, C.S. Supply-Chain Research Opportunities with the Poor as Suppliers or Distributors in Developing Countries. Prod. Oper. Manag. 2013, 23, 1483–1494. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Tang, C.S. The Economic Value of Market Information for Farmers in Developing Economies. Prod. Oper. Manag. 2015, 24, 1441–1452. [Google Scholar] [CrossRef]
- Kang, K.; Zhao, Y.; Ma, Y.; Li, Z. Green supply chain poverty alleviation through microfinance game model and cooperative analysis. J. Clean. Prod. 2019, 226, 1022–1041. [Google Scholar] [CrossRef]
- Shan, H.; Yang, J. Sustainability of photovoltaic poverty alleviation in China: An evolutionary game between stakeholders. Energy 2019, 181, 264–280. [Google Scholar] [CrossRef]
- Smith, N.C. Corporate Social Responsibility: Whether or How? Calif. Manag. Rev. 2003, 45, 52–76. [Google Scholar] [CrossRef]
- Hoejmose, S.U.; Roehrich, J.K.; Grosvold, J. Is doing more doing better? The relationship between responsible supply chain management and corporate reputation. Ind. Mark. Manag. 2014, 43, 77–90. [Google Scholar] [CrossRef]
- Roberts, S. Supply Chain Specific? Understanding the Patchy Success of Ethical Sourcing Initiatives. J. Bus. Ethic 2003, 44, 159–170. [Google Scholar] [CrossRef]
- Klassen, R.; Vereecke, A. Social issues in supply chains: Capabilities link responsibility, risk (opportunity), and performance. Int. J. Prod. Econ. 2012, 140, 103–115. [Google Scholar] [CrossRef]
- Schinckus, C.; Akbari, M.; Clarke, S. Corporate Social Responsibility in Sustainable Supply Chain Management: An Econo-Bibliometric Perspective. Theor. Econ. Lett. 2019, 9, 247–270. [Google Scholar] [CrossRef] [Green Version]
- Panda, S. Coordination of a socially responsible supply chain using revenue sharing contract. Transp. Res. Part E 2014, 67, 92–104. [Google Scholar] [CrossRef]
- Panda, S.; Modak, N.M.; Basu, M.; Goyal, S. Channel coordination and profit distribution in a social responsible three-layer supply chain. Int. J. Prod. Econ. 2015, 168, 224–233. [Google Scholar] [CrossRef]
- Modak, N.M.; Panda, S.; Mishra, R.; Sana, S. A three-layer supply chain coordination in socially responsible distribution system. Tékhne 2016, 14, 75–87. [Google Scholar] [CrossRef]
- Ni, D.; Li, K.W. A game-theoretic analysis of social responsibility conduct in two-echelon supply chains. Int. J. Prod. Econ. 2012, 138, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Hsueh, C.-F. Improving corporate social responsibility in a supply chain through a new revenue sharing contract. Int. J. Prod. Econ. 2014, 151, 214–222. [Google Scholar] [CrossRef]
- Hsueh, C.-F. A bilevel programming model for corporate social responsibility collaboration in sustainable supply chain management. Transp. Res. Part E 2015, 73, 84–95. [Google Scholar] [CrossRef]
- Liu, Y.; Quan, B.-T.; Xu, Q.; Forrest, J.Y.-L. Corporate social responsibility and decision analysis in a supply chain through government subsidy. J. Clean. Prod. 2019, 208, 436–447. [Google Scholar] [CrossRef]
- Raj, A.; Biswas, I.; Srivastava, S. Designing supply contracts for the sustainable supply chain using game theory. J. Clean. Prod. 2018, 185, 275–284. [Google Scholar] [CrossRef]
- Cheng, W.; Appolloni, A.; Zhu, Q.; D’Amato, A. Green Public Procurement, missing concepts and future trends–A critical review. J. Clean. Prod. 2018, 176, 770–784. [Google Scholar] [CrossRef]
- Hou, G.; Wang, Y.; Xin, B. A coordinated strategy for sustainable supply chain management with product sustainability, environmental effect and social reputation. J. Clean. Prod. 2019, 228, 1143–1156. [Google Scholar] [CrossRef]
- Madani, S.R.; Rasti-Barzoki, M. Sustainable supply chain management with pricing, greening and governmental tariffs determining strategies: A game-theoretic approach. Comput. Ind. Eng. 2017, 105, 287–298. [Google Scholar] [CrossRef]
- Niu, B.; Jin, D.; Pu, X. Coordination of channel members’ efforts and utilities in contract farming operations. Eur. J. Oper. Res. 2016, 255, 869–883. [Google Scholar] [CrossRef]
- Sodhi, M.S. Conceptualizing Social Responsibility in Operations Via Stakeholder Resource-Based View. Prod. Oper. Manag. 2015, 24, 1375–1389. [Google Scholar] [CrossRef]
- Ni, D.; Li, K.W.; Tang, X. Social responsibility allocation in two-echelon supply chains: Insights from wholesale price contracts. Eur. J. Oper. Res. 2010, 207, 1269–1279. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.S.; Wang, Y. The Impact of Input-vs. Output-Based Farm Subsidies on Farmer Welfare and Income Inequality in Developing Economies. Available online: https://ssrn.com/abstract=3182548 (accessed on 21 May 2018).
- Li, X.; Li, Y. Chain-to-chain competition on product sustainability. J. Clean. Prod. 2016, 112, 2058–2065. [Google Scholar] [CrossRef]
- Phillips, D.Z. Does It Pay to Be Good? Interv. Ethics 1992, 110–124. [Google Scholar] [CrossRef]
- Sinayi, M.; Rasti-Barzoki, M. A game theoretic approach for pricing, greening, and social welfare policies in a supply chain with government intervention. J. Clean. Prod. 2018, 196, 1443–1458. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Nielsen, I.; Majumder, S.; Sana, S.S.; Saha, S. Comparative analysis of government incentives and game structures on single and two-period green supply chain. J. Clean. Prod. 2019, 235, 1371–1398. [Google Scholar] [CrossRef]








| Reference | Sustainable Supply Chain | Dimensions of Sustainability | CSR | Government Subsidies | Cost Sharing | |
|---|---|---|---|---|---|---|
| Economic | Social (Poverty) | |||||
| Hall and Matos, 2010 [26] | √ | √ | √ | × | × | × |
| Bendul et al., 2017 [27] | √ | √ | √ | √ | × | × |
| Sodhi and Tang, 2013 [29] | √ | √ | √ | × | × | × |
| Chen and Tang, 2015 [30] | × | × | √ | × | × | × |
| Kang et al., 2019 [31] | √ | √ | √ | √ | × | × |
| Shan and Yang, 2019 [32] | √ | √ | √ | × | √ | √ |
| Liu et al., 2019 [44] | √ | √ | × | √ | √ | × |
| Raj et al., 2018 [45] | √ | √ | √ | √ | × | √ |
| Hou et al., 2019 [47] | √ | √ | × | × | √ | × |
| Madani and Rasti-Barzoki, 2017 [48] | √ | √ | × | × | √ | × |
| Niu et al., 2016 [49] | × | √ | × | × | × | √ |
| Our work | √ | √ | √ | √ | √ | √ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, K.; Luan, X.; Shen, W.; Ma, Y.; Wei, X. The Strategies of the Poverty-Alleviation Supply Chain with Government Subsidies and Cost Sharing: Government-Led or Market-Oriented? Sustainability 2020, 12, 4050. https://doi.org/10.3390/su12104050
Kang K, Luan X, Shen W, Ma Y, Wei X. The Strategies of the Poverty-Alleviation Supply Chain with Government Subsidies and Cost Sharing: Government-Led or Market-Oriented? Sustainability. 2020; 12(10):4050. https://doi.org/10.3390/su12104050
Chicago/Turabian StyleKang, Kai, Xinfeng Luan, Wenjing Shen, Yanfang Ma, and Xuguang Wei. 2020. "The Strategies of the Poverty-Alleviation Supply Chain with Government Subsidies and Cost Sharing: Government-Led or Market-Oriented?" Sustainability 12, no. 10: 4050. https://doi.org/10.3390/su12104050





