First Train Timetabling for Urban Rail Transit Networks with Maximum Passenger Transfer Satisfaction
Abstract
1. Introduction
- Public transit service is first described as an interval service in this paper, in contrast to a no-interval service, e.g., services in retailing stores, hospitals and banks. The distinct characteristics of people’s waiting behavior and psychology in interval services are deeply analyzed.
- A reference-based waiting time satisfaction function is firstly proposed, in which passengers’ expectations, tolerances and dissatisfaction on “just miss” were taken into account.
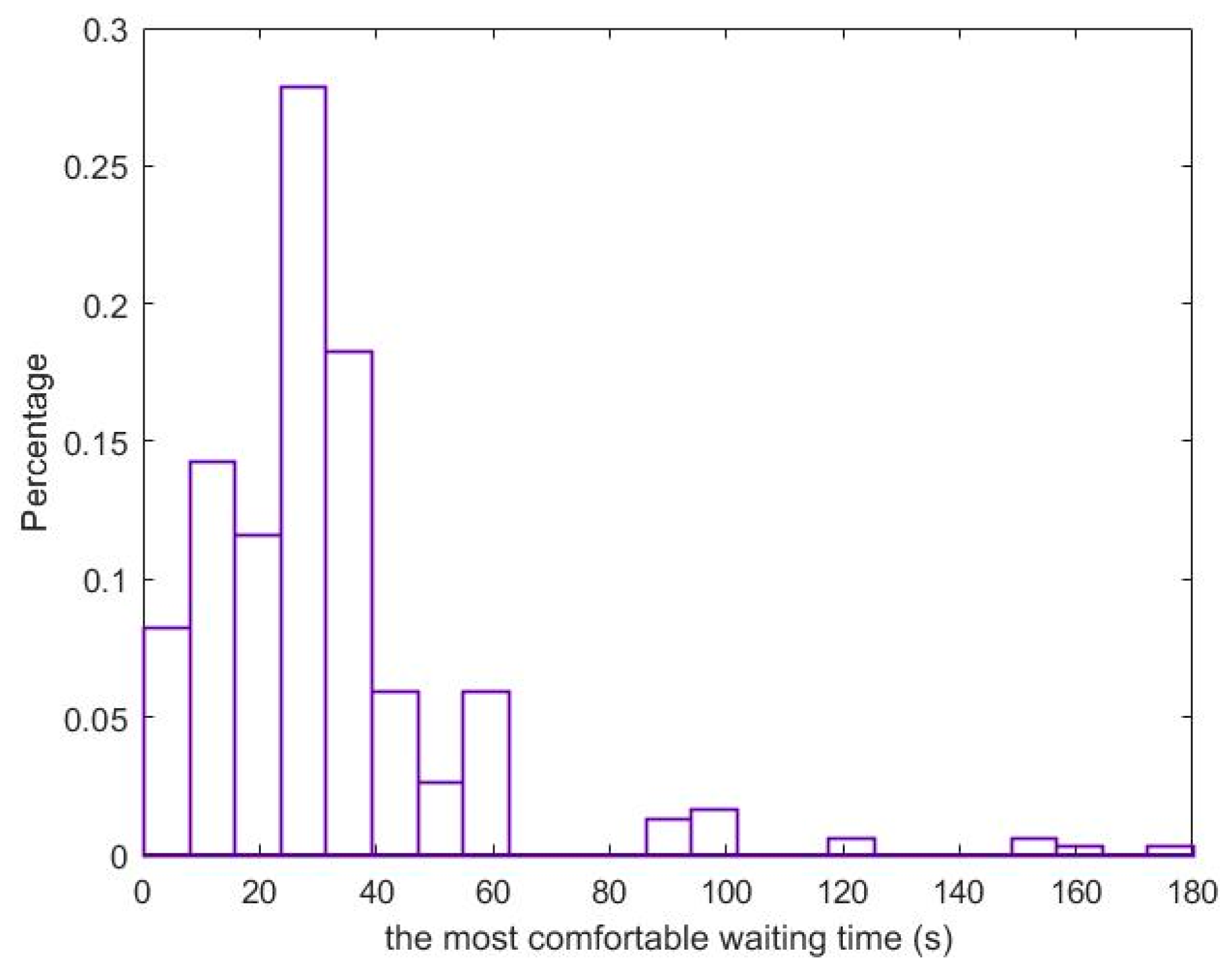
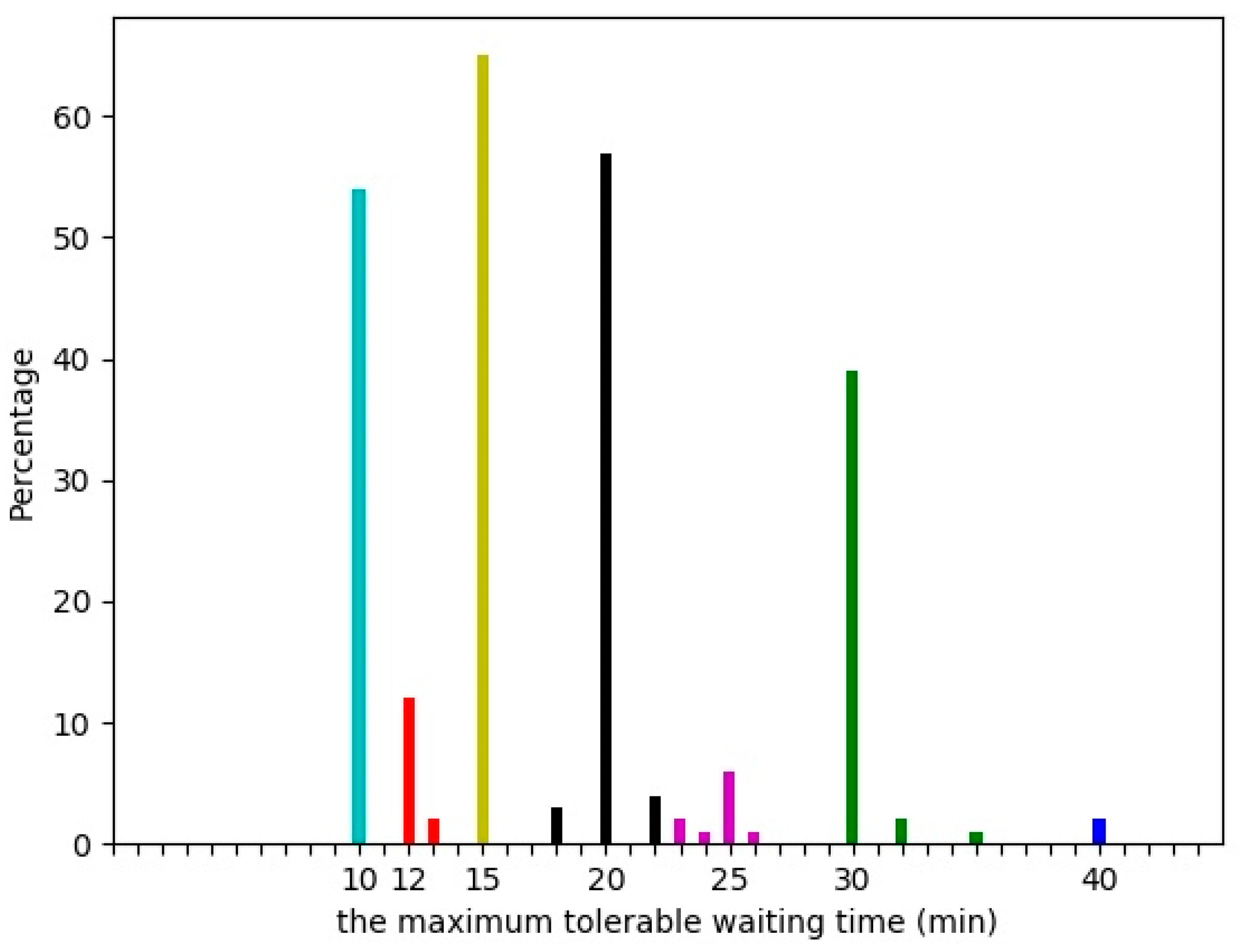
- A stated preference survey is conducted to obtain first-hand information about passengers’ response to zero waiting, the most comfortable waiting time and the maximum tolerable waiting time.
- A novel model is developed to optimize the first train timetables for urban rail transit networks, with the goal of maximizing passengers’ transfer waiting time satisfaction. The first train originating times, train running times, train dwell times and train headways are optimized simultaneously in the model.
2. Transfer Waiting Time Satisfaction Evaluation
2.1. The Changing Rules of Waiting Time Satisfaction
2.2. Waiting Time Satisfaction Function
2.3. A Stated Preference Survey on , and
3. The First Train Timetabling Model
3.1. Assumptions
3.2. Notations
- : set of operating lines in the urban rail transit network. , where denotes the total number of lines in the network. and represent the up and down directions of , respectively.
- : set of operating stations on line . , where m is the total number of stations on line .
- : set of the transfer stations in the urban rail transit network. , where is the total number of transfer stations in the network.
- : set of the transfer relationships at transfer station . , where is the total number of transfer relationships at . Here, a transfer relationship means a transfer at station from line direction () to line direction ().
- : set of passenger clusters. .
- : the minimum train running time from station to station for line direction ().
- : the maximum train running time from station to station for line direction ().
- : the minimum train dwell time at station for line direction ().
- : the maximum train dwell time at station for line direction ().
- : the minimum train headway.
- : the maximum train headway.
- : the maximum changing range of the first train originating time compared to the original timetable.
- : the transfer walking time at transfer station for transfer relationship .
- : the passenger transfer demand at transfer station for transfer relationship .
- : the maximum tolerable waiting time for passengers in cluster .
- : the number of transfer passengers in cluster at transfer station for transfer relationship .
- : the upper bound of the transfer waiting time among all transfer relationships in the first train timetables.
- : the first train originating time from the depot for line direction ().
- : the first train departure time from station for line direction ().
- : the first train arrival time at station for line direction ().
- : the train running time from station to station for line direction ().
- : the train dwell time at station for line direction ().
- : the train headway for line direction ().
- : the transfer waiting time at transfer station for transfer relationship .
3.3. Model Formulations
4. Solution Algorithm
4.1. Artificial Bee Colony Algorithm
4.2. A Sample Test
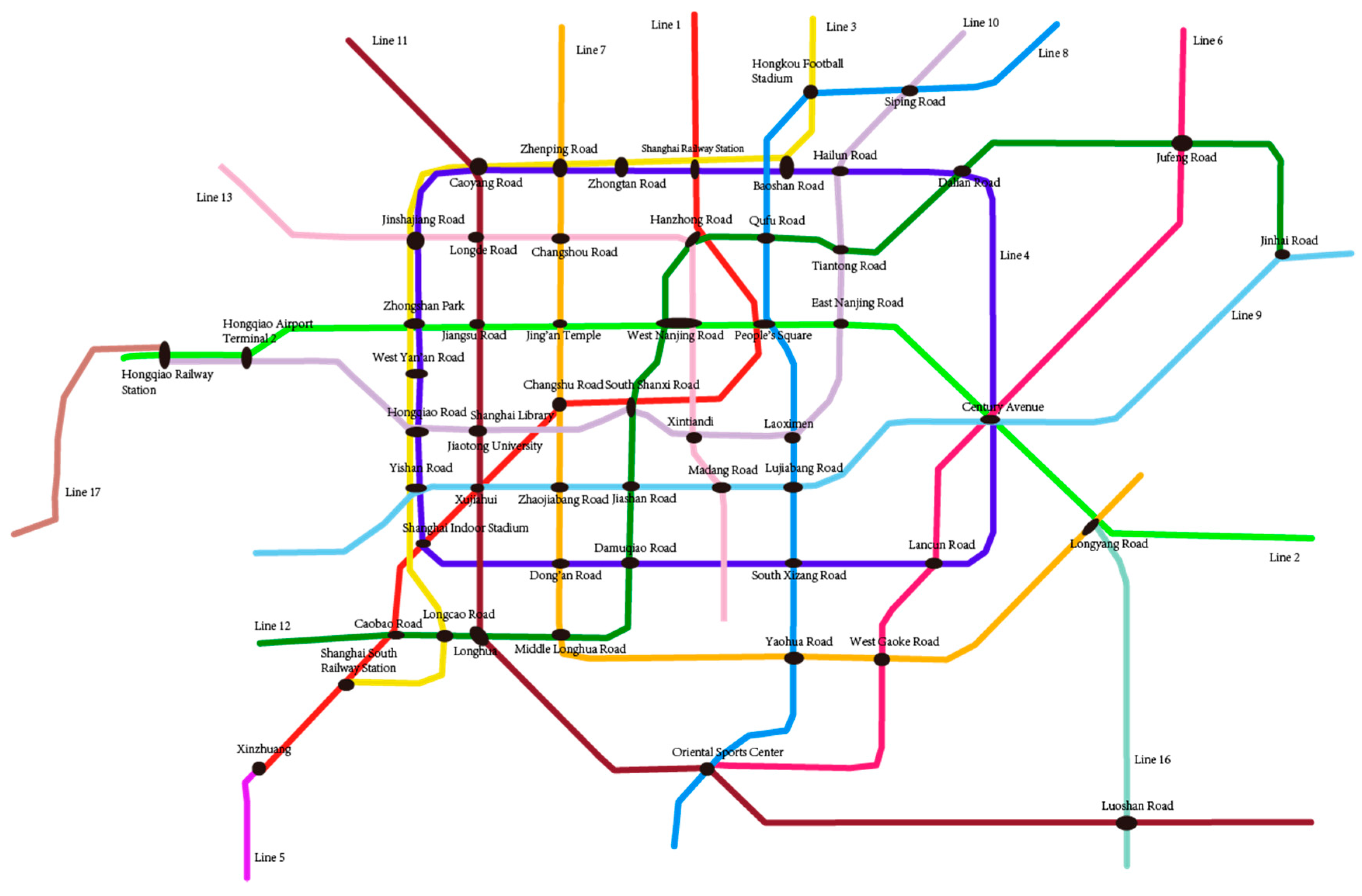
5. Case Study
5.1. Optimization Results
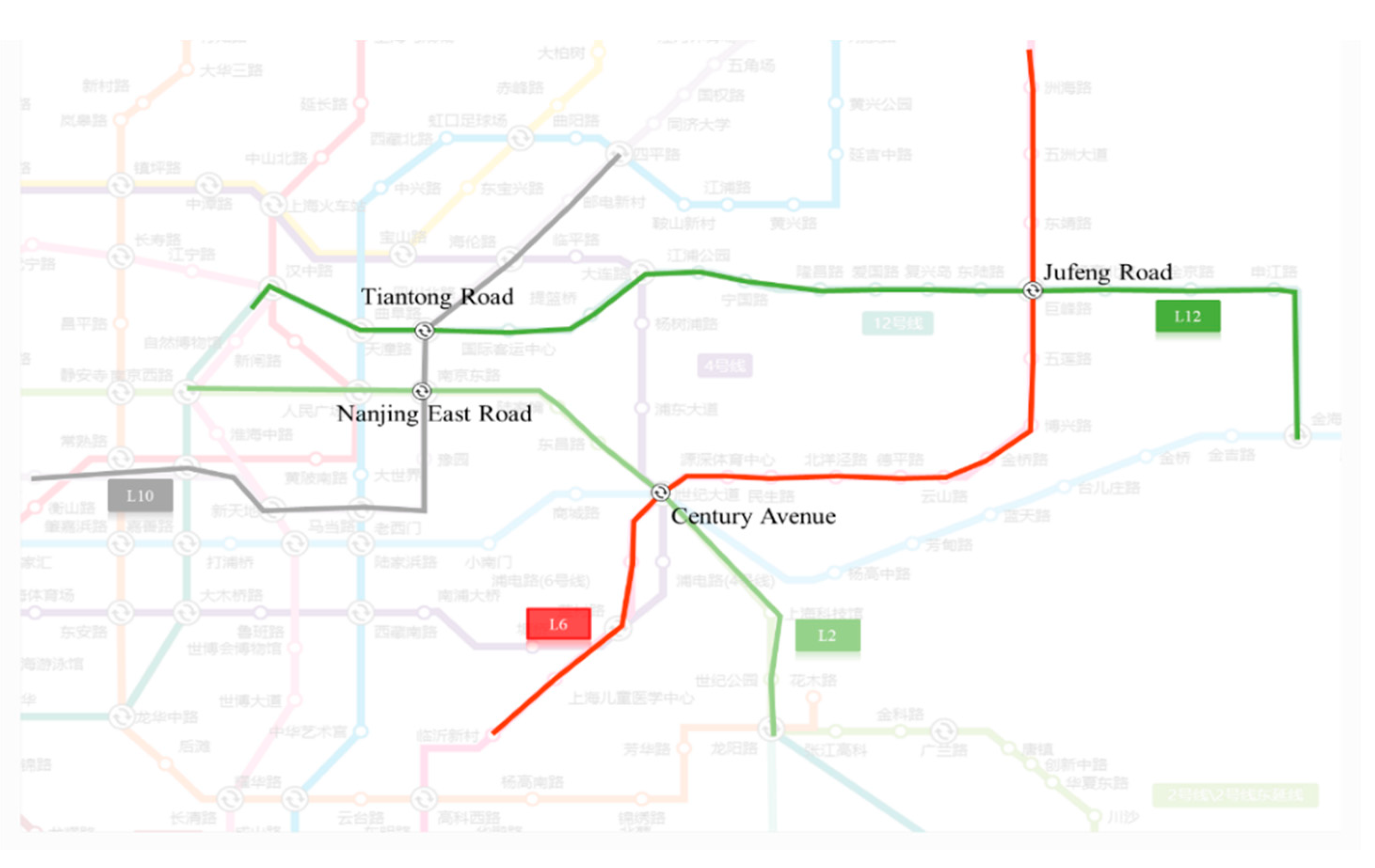
5.2. Analysis of the Results of Publishing Timetables
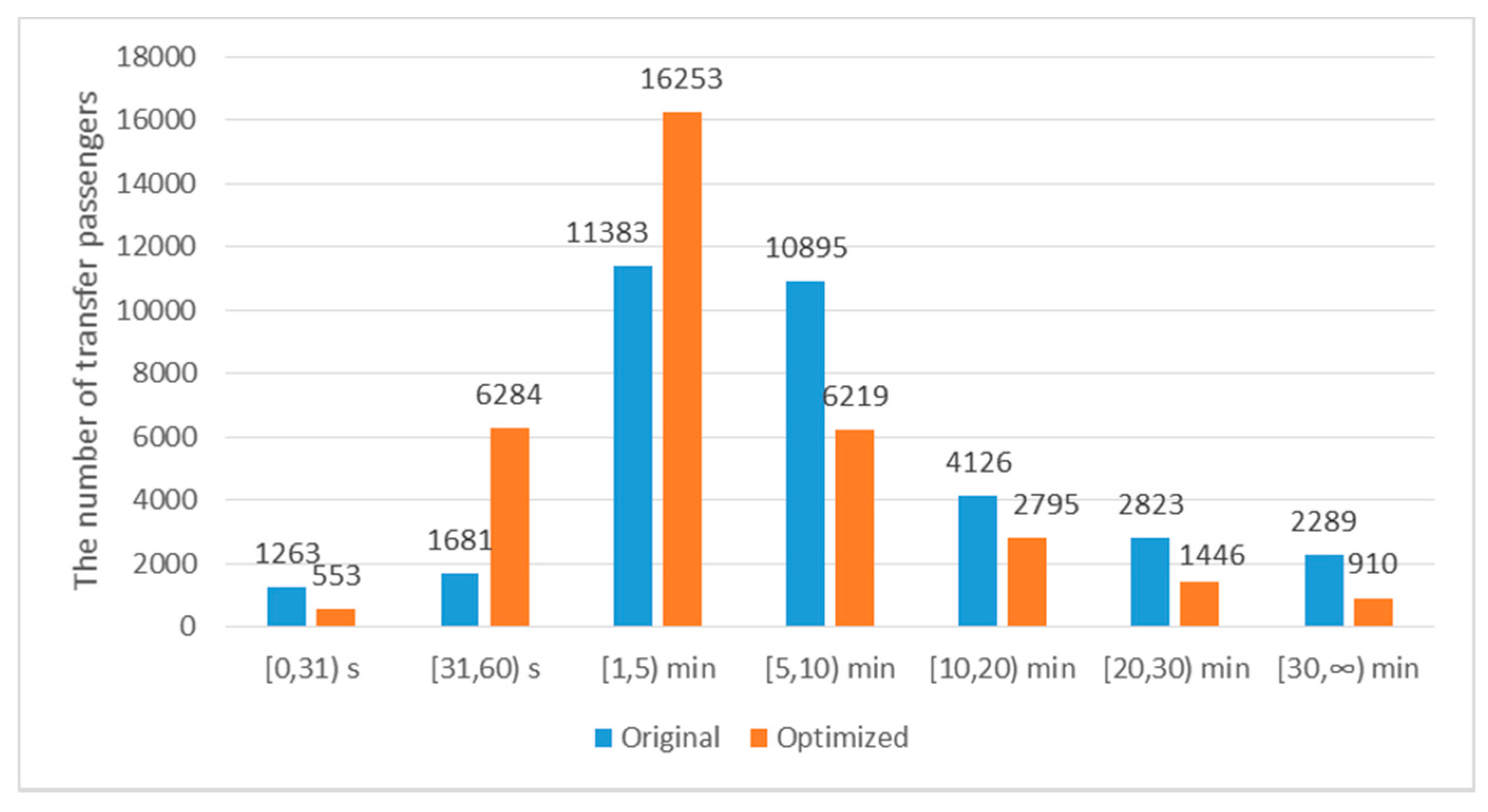
5.3. Comparison with the Results of Minimizing the Transfer Waiting Time
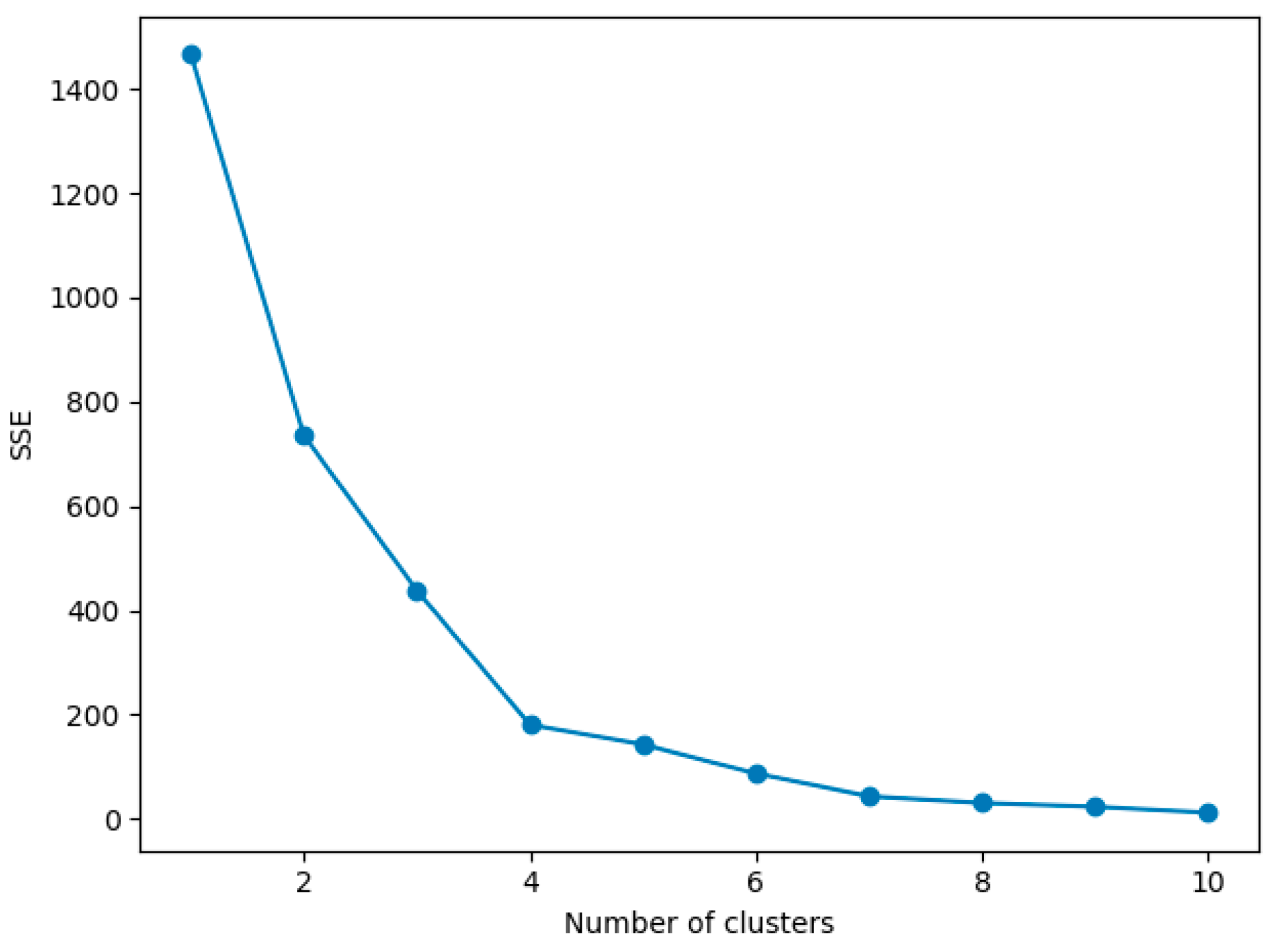
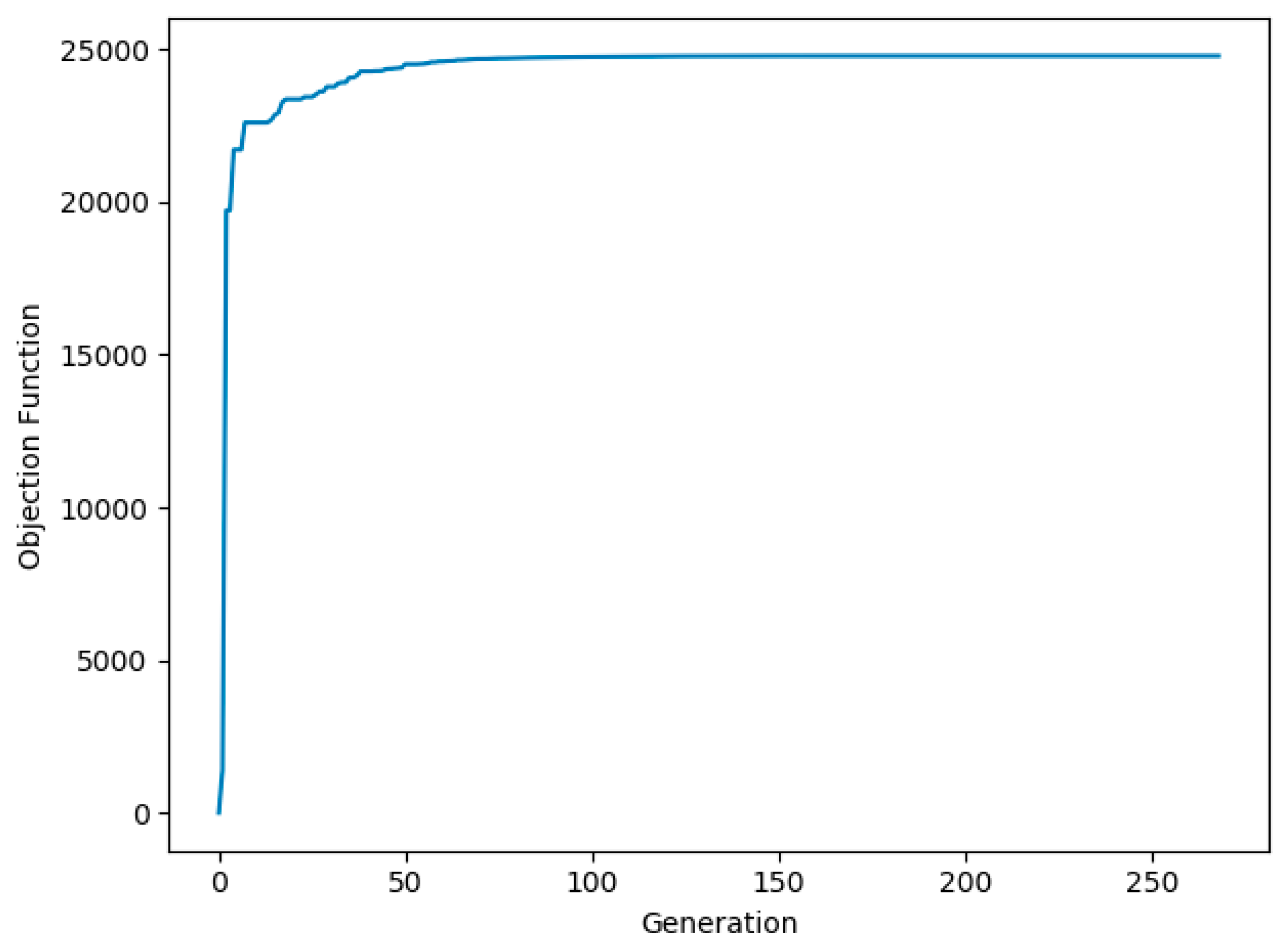
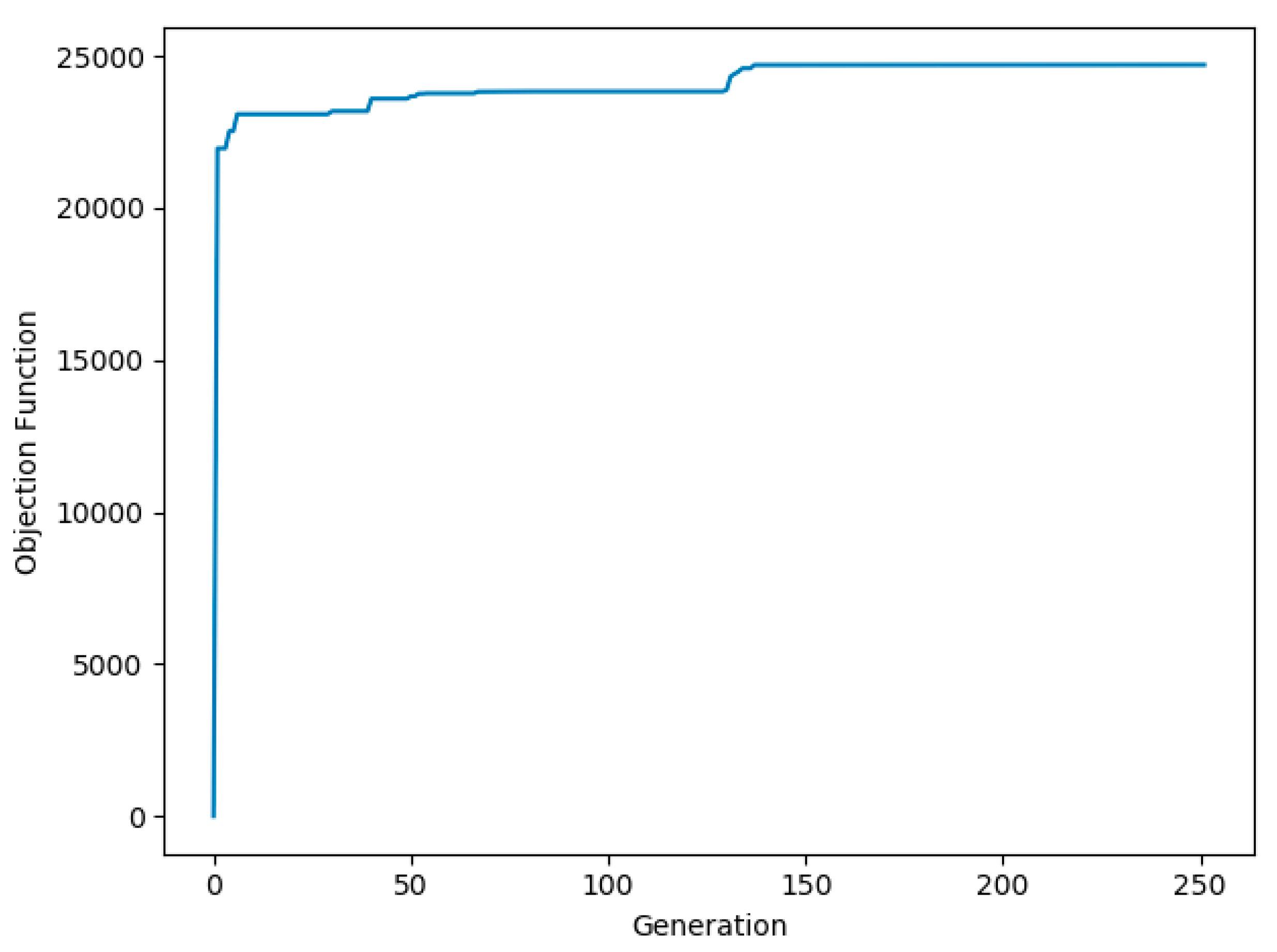
5.4. Convergence Test
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Variable | Categories | Amounts | Percentage |
|---|---|---|---|
| Gender | Male | 121 | 48.17% |
| Female | 130 | 51.83% | |
| Age | Under 25 | 66 | 26.25% |
| 26~35 | 141 | 56.48% | |
| 36~45 | 31 | 12.29% | |
| 46~55 | 11 | 4.32% | |
| 56 or more | 2 | 0.66% | |
| Occupation | Office workers | 201 | 80.07% |
| Students | 40 | 15.95% | |
| Retired | 8 | 3.32% | |
| Other | 2 | 0.66% |
Appendix B
| Original | Optimized | ||||
|---|---|---|---|---|---|
| Time Satisfaction | Time Satisfaction | ||||
| Tiantong Road | line12Down→line10Down | 0′41″ | 77.14 | 2′19″ | 68.83 |
| line10Down→line12Down | 12′41″ | 1.11 | 11′19″ | 1.33 | |
| line12Down→line10Up | 2′41″ | 50.49 | 1′7″ | 56.71 | |
| line10Up→line12Down | 3′41″ | 83.84 | 4′37″ | 77.39 | |
| line10Down→line12Up | 17′41″ | 10.22 | 1′9″ | 93.05 | |
| line12Up→line10Down | 3′41″ | 56.27 | 4′27″ | 52.76 | |
| line10Up→line12Up | 8′41″ | 2.9 | 3′27″ | 4.89 | |
| line12Up→line10Up | 5′41″ | 12.52 | 3′15″ | 15.59 | |
| Century Avenue | line2Up→line6Down | 2′51″ | 13.6 | 4′33″ | 11.87 |
| line6Down→line2Down | 4′51″ | 234.94 | 0′32″ | 329 | |
| line6Down→line2Up | 0′51″ | 109.54 | 0′32″ | 113 | |
| line6Up→line2Down | 7′51″ | 57.28 | 2′31″ | 96.45 | |
| line2Down→line6Up | 27′51″ | −4.74 | 2′24″ | 78.96 | |
| line2Down→line6Down | 38′51″ | −5.24 | 13′25″ | 6.33 | |
| line6Up→line2Up | 11′51″ | 3.14 | 11′31″ | 3.32 | |
| line2Up→line6Up | 7′51″ | 30.82 | 0′32″ | 62 | |
| Nanjing East Road | line2Down→line10Up | 24′27″ | -0.98 | 5′51″ | 66.77 |
| line10Up→line2Up | 5′27″ | 57.35 | 0′32″ | 85 | |
| line10Up→line2Down | 0′27″ | 16.94 | 5′17″ | 13.04 | |
| line2Up→line10Down | 6′27″ | 25.59 | 4′20″ | 31.47 | |
| line10Down→line2Down | 5′27″ | 60.12 | 0′33″ | 88.9 | |
| line10Down→line2Up | 10′27″ | 26.29 | 4′48″ | 53.16 | |
| line2Down→line10Down | 11′27″ | 14.44 | 1′39″ | 43.52 | |
| line2Up→line10Up | 3′27″ | 66.91 | 0′32″ | 82 | |
| Jufeng Road | line12Down→line6Up | 6′58″ | 44.87 | 0′32″ | 79 |
| line6Up→line12Up | 6′58″ | 47.31 | 0′33″ | 81.91 | |
| line12Down→line6Down | 0′58″ | 22.32 | 3′24″ | 18.66 | |
| line12Up→line6Down | 3′58″ | 26.91 | 4′35″ | 25.49 | |
| line12Up→line6Up | 33′58″ | −1.42 | 22′43″ | 0.1 | |
| line6Down→line12Down | 34′58″ | −1.01 | 37′53″ | −1.26 | |
| line6Up→line12Down | 4′58″ | 4.84 | 19′46″ | 0.23 | |
| line6Down→line12Up | 0′58″ | 210.55 | 0′40″ | 215.09 | |
| Original Headway | Optimized Headway | |||
|---|---|---|---|---|
| 5:30 | 5:27 | 6 | 7 | |
| 5:30 | 5:25 | 4 | 8 | |
| 5:28 | 5:25 | 8 | 9 | |
| 5:10 | 5:10 | 8 | 8 | |
| 5:25 | 5:25 | 7 | 8 | |
| 5:25 | 5:23 | 7 | 9 | |
| 5:27 | 5:21 | 7 | 7 | |
| 5:34 | 5:29 | 7 | 8 | |
| 5:50 | 5:45 | 8 | 8 | |
| 5:42 | 5:39 | 8 | 8 | |
| 5:30 | 5:24 | 8 | 7 | |
| 5:30 | 5:26 | 8 | 9 | |
| 5:30 | 5:23 | 10 | 9 | |
| 5:30 | 5:25 | 10 | 8 | |
| 5:30 | 5:26 | 9 | 9 | |
| 5:30 | 5:25 | 9 | 8 | |
| 5:40 | 5:31 | 9 | 9 | |
| 5:30 | 5:21 | 9 | 8 | |
| 5:30 | 5:23 | 8 | 7 | |
| 5:25 | 5:24 | 8 | 7 | |
| 5:40 | 5:35 | 11 | 9 | |
| 5:20 | 5:12 | 11 | 8 | |
| 5:30 | 5:23 | 9 | 7 | |
| 5:30 | 5:21 | 9 | 7 | |
| 5:30 | 5:28 | 8 | 7 | |
| 5:30 | 5:21 | 8 | 8 | |
| 5:50 | 5:45 | 10 | 8 | |
| 6:00 | 5:55 | 10 | 8 | |
| 6:00 | 5:54 | 9 | 8 | |
| 5:40 | 5:35 | 9 | 9 |
References
- Szpigel, B. Optimal train scheduling on a single track railway. Oper. Res. 1973, 34, 343–352. [Google Scholar]
- Lee, K.K.T.; Schonfeld, P. Optimal slack time for timed transfers at a transit terminal. J. Adv. Transp. 1991, 25, 281–308. [Google Scholar] [CrossRef]
- Chien, F.; Schonfeld, P. Joint optimization of a rail transit line and its feeder bus system. J. Adv. Transp. 1998, 32, 253–284. [Google Scholar] [CrossRef]
- Chowdhury, S.M.; Chien, S.I. Intermodal transit system coordination. Transp. Plan. Technol. 2002, 25, 257–287. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Oudheusden, D.V. Decreasing the passenger waiting time for an intercity rail network. Transp. Res. Part B 2007, 41, 478–492. [Google Scholar] [CrossRef]
- Li, S.J.; Xu, R.H.; Han, K. Demand-oriented train services optimization for a congested urban rail line: Integrating short turning and heterogeneous headways. Transp. A Transp. Sci. 2019, 15, 1459–1486. [Google Scholar] [CrossRef]
- Xue, Q.C.; Yang, X.; Wu, J.J.; Sun, H.J.; Yin, H.D.; Qu, Y.C. Urban rail timetable optimization to improve operational efficiency with flexible routing plans: A nonlinear integer programming model. Sustainability 2019, 11, 3701. [Google Scholar] [CrossRef]
- Wang, Y.H.; Tang, T.; Ning, B.; Boom, T.J.J.; Schutter, B.D. Passenger-demands-oriented train scheduling for an urban rail transit network. Transp. Res. Part C 2015, 60, 1–23. [Google Scholar] [CrossRef]
- Zhou, W.L.; Fan, W.Z.; You, X.R.; Deng, L.B. Demand-oriented train timetabling integrated with passenger train-booking decisions. Sustainability 2019, 11, 4932. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Gao, Z.; Wang, H.; Tang, T. A cooperative scheduling model for timetable optimization in subway systems. IEEE Trans. Intell. Transp. Syst. 2013, 14, 438–447. [Google Scholar] [CrossRef]
- Chakroborty, P.; Deb, K.; Subrahmanyam, P.S. Optimal scheduling of urban transit systems using genetic algorithms. J. Transp. Eng. 1995, 121, 544–553. [Google Scholar] [CrossRef]
- Goverde, R.M.P. Optimal Scheduling of Connections in Railway Systems; Technical Report No. 929; Delft University of Technology: Delft, The Netherlands, 1998. [Google Scholar]
- Kwan, C.M.; Chang, C.S. Timetable synchronization of mass rapid transit system using multiobjective evolutionary approach. IEEE Trans. Syst. 2008, 38, 636–648. [Google Scholar] [CrossRef]
- Zhou, W.L.; Deng, L.B.; Xie, M.Q.; Yang, X. Coordination optimization of the first and last trains’ departure time on urban rail transit network. Adv. Mech. Eng. 2013, 5, 848292. [Google Scholar] [CrossRef]
- Wu, J.J.; Liu, M.H.; Sun, H.J.; Li, T.F.; Gao, Z.Y.; Wang, D.Z.W. Equity-based timetable synchronization optimization in urban subway network. Transp. Res. Part C 2015, 51, 1–18. [Google Scholar] [CrossRef]
- Shi, R.J.; Mao, B.H.; Ding, Y.; Bai, Y.; Chen, Y. Timetable optimization of rail transit loop line with transfer coordination. Discret. Dyn. Nat. Soc. 2016, 2016, 4627094. [Google Scholar] [CrossRef]
- Shang, P.; Li, R.; Liu, Z.; Xian, K.; Guo, J. Timetable synchronization and optimization considering time-dependent passenger demand in an urban subway network. Transp. Res. Rec. 2018, 2672, 243–254. [Google Scholar] [CrossRef]
- Chen, Y.; Mao, B.H.; Bai, Y.; Ho, T.K.; Li, Z.J. Timetable synchronization of last trains for urban rail networks with maximum accessibility. Transp. Res. Part C 2019, 99, 110–129. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Yang, H.; Yan, X.D. Last train scheduling for maximizing passenger destination reachability in urban rail transit networks. Transp. Res. Part B 2019, 129, 79–95. [Google Scholar] [CrossRef]
- Kang, L.J.; Zhu, X.N. A simulated annealing algorithm for first train transfer problem in urban railway networks. Appl. Math. Model. J. 2016, 40, 419–435. [Google Scholar] [CrossRef]
- Kang, L.J.; Zhu, X.N.; Sun, H.J.; Puchinger, J.; Ruthmair, M.; Hu, B. Modeling the first train timetabling problem with minimal missed trains and synchronization time differences in subway networks. Transp. Res. Part B 2016, 93, 17–36. [Google Scholar] [CrossRef]
- Guo, X.; Wu, J.J.; Sun, H.J.; Liu, R.H.; Gao, Z.Y. Timetable coordination of first trains in urban railway network: A case study of Beijing. Appl. Math. Model. 2016, 40, 8048–8066. [Google Scholar] [CrossRef]
- Ning, L.Q.; Zhao, P.; Xu, W.K.; Qiao, K. Transfer Coordination for Metro Networks during the Start- or End-of-Service Period. Math. Probl. Eng. 2018, 2018, 3835270. [Google Scholar] [CrossRef]
- Schroder, M.; Solchenbach, I. Optimization of Transfer Quality in Regional Public Transit; Technical Report No. 84; Berichte des Fraunhofer Instituts for Techno-und Wirtschafts: Munich, Germany, 2006. [Google Scholar]
- Wang, Y.B.; Guo, J.Q.; Ceder, A.; Currie, G.; Dong, W.; Yuan, H. Waiting for public transport services: Queueing analysis with balking and reneging behaviors of impatient passengers. Transp. Res. Part B 2014, 63, 53–76. [Google Scholar] [CrossRef]
- Barrer, D.Y. Queuing with impatient customers and indifferent clerks. Oper. Res. 1957, 5, 644–649. [Google Scholar] [CrossRef]
- Maister, D. The Psychology of Waiting Lines. In The Service Encounter; Lexington Books: Lexington, KY, USA, 1985; pp. 13–23. [Google Scholar]
- Davis, M.M.; Maggard, M.J. An analysis of customer satisfaction with waiting times in a two-stage service. J. Oper. Manag. 1990, 9, 324–334. [Google Scholar] [CrossRef]
- Carmon, Z.; Shanthikumar, J.G.; Freed, T. A psychological perspective on service segmentation models: The significance of accounting for consumers’ perceptions of waiting and service. Manag. Sci. 1995, 41, 1806–1815. [Google Scholar] [CrossRef]
- Durrande-Moreau, A. Waiting for service: Ten years of empirical research. Int. J. Serv. Ind. Manag. 1999, 10, 171–194. [Google Scholar] [CrossRef]
- Wong, R.C.W.; Yuen, T.W.Y.; Fung, K.W.; Leung, J.M.Y. Optimizing timetable synchronization for rail mass transit. Transp. Sci. 2008, 42, 57–69. [Google Scholar] [CrossRef]
- Miller, J.A. Studying satisfaction, modifying models, eliciting expectations, posing problems, and making meaningful measurements. In Conceptualization and Measurement of Consumer Satisfaction and Dissatisfaction; Hunt, H.K., Ed.; Marketing Science Institute (May): Cambridge, MA, USA, 1977; pp. 72–91. [Google Scholar]
- Churchill, G.A.; Surprenant, C. An investigation into the determinants of customer satisfaction. J. Mark. Res. 1982, 19, 491–504. [Google Scholar] [CrossRef]
- Palawatta, T.M.B. Waiting Times and Defining Customer Satisfaction. Vidyojaya J. Manag. 2015, 1, 15–24. [Google Scholar] [CrossRef]
- Shang, H.Y.; Huang, H.J.; Wu, W.X. Bus timetabling considering passenger satisfaction: An empirical study in Beijing. Comput. Ind. Eng. 2019, 135, 1155–1166. [Google Scholar] [CrossRef]
- Gao, Y.N.; Rasouli, S.; Timmermans, H.; Wang, Y.Q. Trip stage satisfaction of public transport users: A reference-based model incorporating trip attributes, perceived service quality, psychological disposition and difference tolerance. Transp. Res. Part A 2018, 118, 759–775. [Google Scholar] [CrossRef]
- Cats, O. Dynamic Modelling of Transit Operations and Passenger Decisions. Ph.D. Thesis, KTH, School of Architecture and the Built Environment (ABE), Transport Science, Traffic and Logistics, Stockholm, Sweden, 2011. [Google Scholar]
- Abenoza, R.F.; Cats, O.; Susilo, Y.O. Travel satisfaction with public transport: Determinants, user classes, regional disparities and their evolution. Transp. Res. Part A 2017, 95, 64–84. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. A Subjective Optimal Strategy for Transit Simulation Models. J. Adv. Transp. 2018, 2018, 8797328. [Google Scholar] [CrossRef]
- Wang, J.; Peeta, S.; He, S. Multiclass traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles. Transp. Res. Part B Methodol. 2019, 126, 139–168. [Google Scholar] [CrossRef]
- Schmöcker, J.D.; Fonzone, A.; Shimamoto, H.; Kurauchi, F. Frequency-based transit assignment considering seat capacities. Transp. Res. Part A 2011, 45, 392–408. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]




| Authors | Objective | Model | Highlights |
|---|---|---|---|
| Zhou et al. [14] | minimize passengers’ total originating waiting time and transfer waiting time for the first trains | MIP 1 | consider passenger OD and passenger travel route choice |
| Kang et al. [21] | minimize train arrival time differences and the number of missed trains | MIP | consider the number of missed trains and transfer waiting time |
| Kang & Zhu [20] | minimize the total passenger transfer waiting time of first trains | MILP 2 | develop a simulated annealing algorithm |
| Guo et al. [22] | minimize the connection time between first trains | MILP | apply the importance of lines and transfer stations |
| Ning et al. [23] | minimize the total transfer waiting time of first trains | MIP | consider the penalty of transfer failure |
| Clusters | Number of Respondents | Percentage | |
|---|---|---|---|
| 1 | 10 | 54 | 21.51% |
| 2 | 12 | 14 | 5.58% |
| 3 | 15 | 65 | 25.90% |
| 4 | 20 | 64 | 25.50% |
| 5 | 25 | 10 | 3.98% |
| 6 | 30 | 42 | 16.73% |
| 7 | 40 | 2 | 0.80% |
| Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Assigned value | 7 min | 11 min | ±15 min | 80 min | 50 | 1000 | 100 | 100 |
| Original Headway | Optimized Headway | |||
|---|---|---|---|---|
| 5:28:00 | 5:21:00 | 8 | 8 | |
| 5:10:00 | 5:23:00 | 8 | 9 | |
| 5:30:00 | 5:22:00 | 8 | 8 | |
| 5:30:00 | 5:24:00 | 8 | 9 | |
| 5:30:00 | 5:15:00 | 8 | 8 | |
| 5:25:00 | 5:30:00 | 8 | 8 | |
| 5:30:00 | 5:24:00 | 9 | 9 | |
| 5:30:00 | 5:24:00 | 9 | 7 |
| Original | Optimized | Change | Percentage | |
|---|---|---|---|---|
| The total time satisfaction | 1354 | 1954 | 600 | +44.31% |
| The number of transfer passengers within the maximum tolerable waiting time | 1921 | 2170 | 249 | +12.96% |
| The total transfer waiting time (min·person) | 17065 | 5242 | −11,823 | −69.28% |
| The average transfer waiting time (min/person) | 7.75 | 2.38 | −5.37 | −69.29% |
| Original | Optimized | Change | Percentage | |
|---|---|---|---|---|
| The total time satisfaction | 18,555 | 24,636 | 6081 | +32.77% |
| The number of transfer passengers within the maximum tolerable waiting time | 28,341 | 31,351 | 3010 | +10.62% |
| The total transfer waiting time (min· person) | 324,831 | 209,340 | −115,491 | −35.55% |
| The average transfer waiting time (min/person) | 9.43 | 6.07 | −3.36 | −35.63% |
| Before | After | Change | Percentage | |
|---|---|---|---|---|
| The total time satisfaction | 24,636 | 286,72 | 4036 | +16.38% |
| The number of transfer passengers within the maximum tolerable waiting time | 31,351 | 34,457 | 3106 | +9.91% |
| The total transfer waiting time (min· person) | 209,340 | 101,767 | −107,573 | −51.39% |
| The average transfer waiting time (min/ person) | 6.07 | 2.95 | −3.12 | −51.40% |
| Transfer Waiting Time | |||
|---|---|---|---|
| Before Publication | After Publication | ||
| Jiangsu Road | Line2Down→line11Up | 59′15″ | 3′15″ |
| Line2Up→line11Up | 52′18″ | 7′18″ | |
| Longde Road | Line13Up→line11Up | 55′38″ | 6′38″ |
| Line13Down→line11Up | 37′19″ | 5′19″ | |
| Caoyang Road | Line3Down→line11Up | 33′2″ | 6′2″ |
| West gaoke Road | Line6Up→line7Up | 35′24″ | 0′24″ |
| Jiashang Road | Line12Down→line9Up | 32′52″ | 4′52″ |
| Century Avenue | Line6Up→line9Up | 39′54″ | 7′54″ |
| Longhua Road | Line12Up→line11Up | 41′9″ | 6′9″ |
| Minimize Transfer Waiting Time | Maximize Waiting Time Satisfaction | Difference | Percentage | |
|---|---|---|---|---|
| The total time satisfaction | 22,748 | 24,636 | 1888 | +8.30% |
| The number of transfer passengers within the maximum tolerable waiting time | 31,418 | 31,351 | −67 | −0.21% |
| The total transfer waiting time (min· person) | 201,863 | 209,340 | 7477 | +3.70% |
| The average transfer waiting time (min/person) | 5.86 | 6.07 | 0.21 | +3.58% |
| Algorithm | Objective Function Value | Number of Iterations | CPU Time |
|---|---|---|---|
| ABC algorithm | 24,636 | 266 | 8′41″ |
| GA | 22,960 | 249 | 22′46″ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yamamoto, T.; Yan, T.; Lu, L.; Ye, X. First Train Timetabling for Urban Rail Transit Networks with Maximum Passenger Transfer Satisfaction. Sustainability 2020, 12, 4166. https://doi.org/10.3390/su12104166
Li X, Yamamoto T, Yan T, Lu L, Ye X. First Train Timetabling for Urban Rail Transit Networks with Maximum Passenger Transfer Satisfaction. Sustainability. 2020; 12(10):4166. https://doi.org/10.3390/su12104166
Chicago/Turabian StyleLi, Xuan, Toshiyuki Yamamoto, Tao Yan, Lili Lu, and Xiaofei Ye. 2020. "First Train Timetabling for Urban Rail Transit Networks with Maximum Passenger Transfer Satisfaction" Sustainability 12, no. 10: 4166. https://doi.org/10.3390/su12104166
APA StyleLi, X., Yamamoto, T., Yan, T., Lu, L., & Ye, X. (2020). First Train Timetabling for Urban Rail Transit Networks with Maximum Passenger Transfer Satisfaction. Sustainability, 12(10), 4166. https://doi.org/10.3390/su12104166






