A Multi-Item Replenishment Problem with Carbon Cap-and-Trade under Uncertainty
Abstract
:1. Introduction
2. Literature Review
3. Notation, Assumptions, and Problem Definitions
3.1. Notation
| item, |
| period, |
| binary variable indicating the order during period |
| inventory level of item at the end of period |
| on-hand inventory of item at the end of period |
| backorder level of item at the end of period |
| order amount for item in period |
| the order-up-to level of item in period |
| if drops below , then , otherwise |
| if drops below , then , otherwise |
| if drops below and at least one item is ordered in period , then , otherwise |
| if minor setup is done for item during period t, then , otherwise |
| amount of buying carbon credit in period t |
| amount of selling carbon credit in period t |
| major ordering cost in period ($/order) |
| minor ordering cost of item in period ($/order) |
| per unit backorder cost of item in period ($/unit) |
| per period holding cost of item in period ($/unit) |
| carbon tax ($/ton) |
| carbon cap for entire planning horizon |
| amount of carbon emissions when a buyer holds inventory of item in period |
| amount of carbon emissions when a buyer orders inventory of item in period |
| demand for item during period |
| volume of item |
| storage capacity during period |
| purchase price of item |
| amount of budget during period |
| can-order level of item |
| reorder level of item |
| big M, very big number |
3.2. Assumptions
- A single buyer orders multiple items from a single supplier and simultaneously considers carbon cap-and-trade under limited storage capacity and budget.
- The system considers a periodic review can-order policy to obtain the order-up to level. The supplier can utilize limited transportation, so the review period is dependent on the contract period between the buyer and the supplier.
- Both the buyer and the supplier share the demand information of the items in real time. Thus, the supplier can deliver multiple items with no lead time. Also, the demand for each item is known.
- The reorder level and the can-order level are assumed as constant.
- The storage capacity and budget are assumed as constant in the deterministic model and fuzzy numbers in the fuzzy model.
- The buyer’s carbon emissions occur throughout the ordering item and holding inventory. A buyer has a carbon cap and could buy or sell its own carbon credit to other company depending on the carbon emissions.
3.3. Problem Definition
4. Deterministic Model
5. Fuzzy Model
6. Numerical Experiments
6.1. Efficiency Test
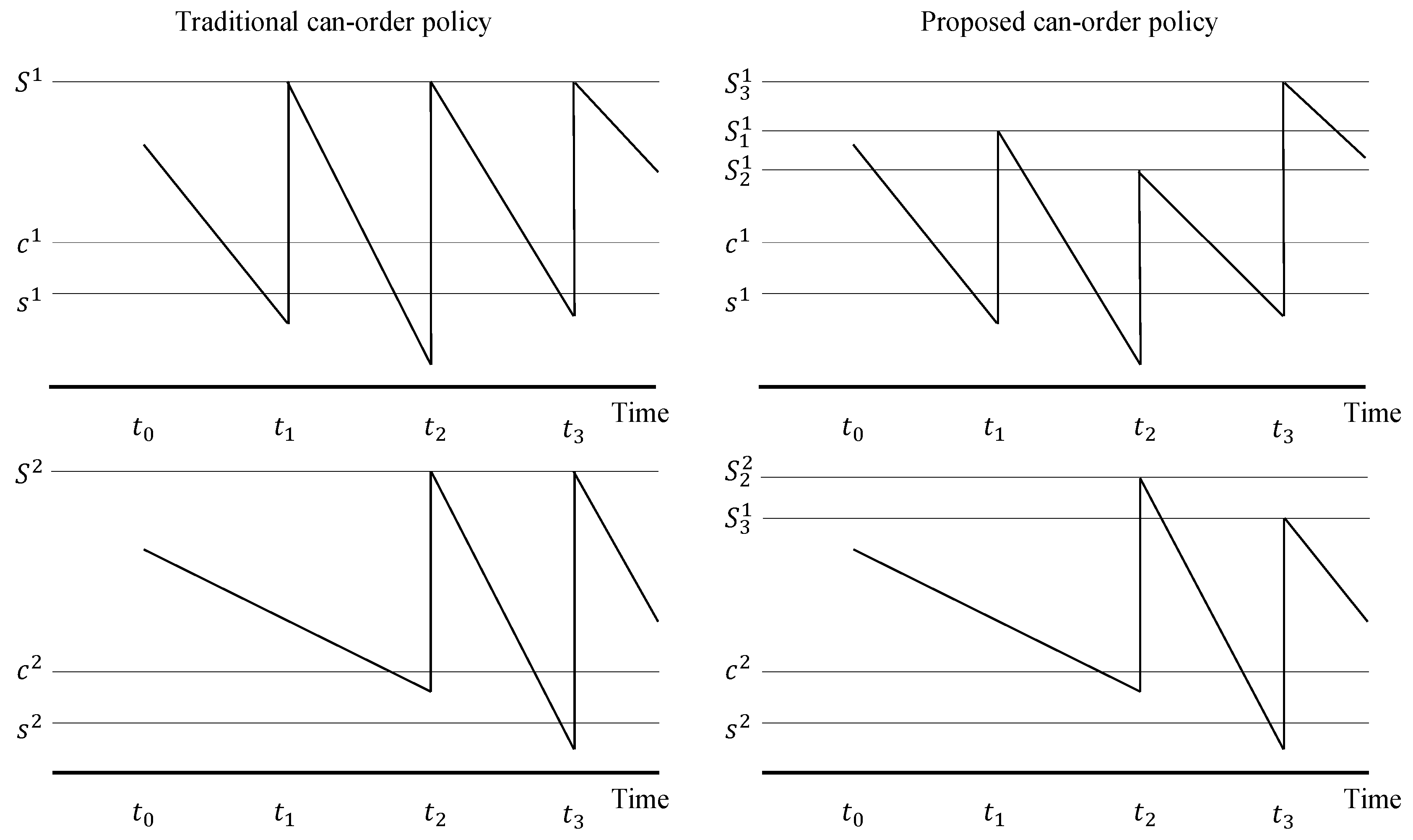
6.2. Comparison Test between the Proposed Can-Order Policy and the Traditional can-order Policy
6.3. Fuzzy Model Test
7. Academic, Managerial, and Environmental Insights
7.1. Academic Insights
7.2. Managerial Insights
7.3. Environmental Insights
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Noh, J.; Kim, J.S. Cooperative green supply chain management with greenhouse gas emissions and fuzzy demand. J. Clean. Prod. 2019, 208, 1421–1435. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Bai, Q. A two-echelon sustainable supply chain coordination under cap-and-trade regulation. J. Clean. Prod. 2016, 135, 42–56. [Google Scholar] [CrossRef]
- Cao, K.; Xu, X.; Wu, Q.; Zhang, Q. Optimal production and carbon emission reduction level under cap-and-trade and low carbon subsidy policies. J. Clean. Prod. 2017, 167, 505–513. [Google Scholar] [CrossRef]
- Hua, G.; Cheng, T.; Wang, S. Managing carbon footprints in inventory management. Int. J. Prod. Econ. 2011, 132, 178–185. [Google Scholar] [CrossRef]
- Hintermann, B. Allowance price drivers in the first phase of the eu ets. J. Environ. Econ. Manag. 2010, 59, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Shen, B.; Chow, P.-S.; Yang, L.; Ng, C.T. Sustainability investment under cap-and-trade regulation. Ann. Oper. Res. 2016, 240, 509–531. [Google Scholar] [CrossRef]
- Ramanathan, U.; Bentley, Y.; Pang, G. The role of collaboration in the uk green supply chains: An exploratory study of the perspectives of suppliers, logistics and retailers. J. Clean. Prod. 2014, 70, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Nia, A.R.; Far, M.H.; Niaki, S. A hybrid genetic and imperialist competitive algorithm for green vendor managed inventory of multi-item multi-constraint eoq model under shortage. Appl. Soft Comput. 2015, 30, 353–364. [Google Scholar]
- Dimitrova, M.; Schlee, E.E. Monopoly, competition and information acquisition. Int. J. Ind. Organ. 2003, 21, 1623–1642. [Google Scholar] [CrossRef]
- Roy, A.; Kar, S.; Maiti, M. A deteriorating multi-item inventory model with fuzzy costs and resources based on two different defuzzification techniques. Appl. Math. Model. 2008, 32, 208–223. [Google Scholar] [CrossRef]
- Konur, D. Carbon constrained integrated inventory control and truckload transportation with heterogeneous freight trucks. Int. J. Prod. Econ. 2014, 153, 268–279. [Google Scholar] [CrossRef]
- Mokhtari, H.; Rezvan, M.T. A single-supplier, multi-buyer, multi-product vmi production-inventory system under partial backordering. Oper. Res. 2020, 20, 37–57. [Google Scholar] [CrossRef]
- Cui, L.; Deng, J.; Zhang, Y.; Tang, G.; Xu, M. Hybrid differential artificial bee colony algorithm for multi-item replenishment-distribution problem with stochastic lead-time and demands. J. Clean. Prod. 2020, 119873. [Google Scholar] [CrossRef]
- Balintfy, J.L. On a basic class of multi-item inventory problems. Manag. Sci. 1964, 10, 287–297. [Google Scholar] [CrossRef]
- Silver, E.A. A control system for coordinated inventory replenishment. Int. J. Prod. Res. 1974, 12, 647–671. [Google Scholar] [CrossRef]
- Liu, L.; Yuan, X.-M. Coordinated replenishments in inventory systems with correlated demands. Eur. J. Oper. Res. 2000, 123, 490–503. [Google Scholar] [CrossRef]
- Kayiş, E.; Bilgic, T.; Karabulut, D. A note on the can-order policy for the two-item stochastic joint-replenishment problem. IIE Trans. 2008, 40, 84–92. [Google Scholar]
- Tsai, C.-Y.; Tsai, C.-Y.; Huang, P.-W. An association clustering algorithm for can-order policies in the joint replenishment problem. Int. J. Prod. Econ. 2009, 117, 30–41. [Google Scholar] [CrossRef]
- Kouki, C.; Babai, M.Z.; Jemai, Z.; Minner, S. A coordinated multi-item inventory system for perishables with random lifetime. Int. J. Prod. Econ. 2016, 181, 226–237. [Google Scholar] [CrossRef]
- Johansen, S.; Melchiors, P. Can-order policy for the periodic-review joint replenishment problem. J. Res. Soc. 2003, 54, 283–290. [Google Scholar] [CrossRef]
- Nagasawa, K.; Irohara, T.; Matoba, Y.; Liu, S. Applying genetic algorithm for can-order policies in the joint replenishment problem. Ind. Eng. Manag. Syst. 2015, 14, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, H.-J. Fuzzy set Theory—And its Applications; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Sadeghi, J.; Sadeghi, S.; Niaki, S.T.A. Optimizing a hybrid vendor-managed inventory and transportation problem with fuzzy demand: An improved particle swarm optimization algorithm. Inf. Sci. 2014, 272, 126–144. [Google Scholar] [CrossRef]
- Nia, A.R.; Far, M.H.; Niaki, S. A fuzzy vendor managed inventory of multi-item economic order quantity model under shortage: An ant colony optimization algorithm. Int. J. Prod. Econ. 2014, 155, 259–271. [Google Scholar]
- Sadeghi, J.; Mousavi, S.M.; Niaki, S. Optimizing an inventory model with fuzzy demand, backordering, and discount using a hybrid imperialist competitive algorithm. Appl. Math. Model. 2016, 40, 7318–7335. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2012, 10, 99–116. [Google Scholar] [CrossRef]
| Item | 1 | 2 | 3 |
|---|---|---|---|
| Item | |||
|---|---|---|---|
| 1 | 0 | 50 | 80 |
| 2 | 0 | 70 | 100 |
| 3 | 0 | 10 | 20 |
| Traditional Can-Order Policy with Predetermined Values ($) | Proposed Model ($) |
|---|---|
| 1,107,962.00 | 757,120.50 |
| Test Number | Percent of the Highest Demand | Order-Up-to Level | Total Cost of The Traditional Can-Order Policy with Predetermined Values ($) | ||
|---|---|---|---|---|---|
| 1 | 95% | 662 | 561 | 175 | 928,417.00 |
| 2 | 90% | 627 | 531 | 166 | 935,320.50 |
| 3 | 85% | 592 | 502 | 157 | 940,683.00 |
| 4 | 80% | 558 | 472 | 148 | 1,045,999.00 |
| 5 | 75% | 523 | 443 | 138 | 1,155,508.00 |
| Item Number | ||||||
|---|---|---|---|---|---|---|
| 1 | 1 | 13 | 1 | 0.1 | 1 | |
| 2 | 2 | 14 | 2 | 0.5 | 0.1 | |
| 3 | 1 | 10 | 1 | 1 | 0.2 | |
| 4 | 1 | 15 | 3 | 0.8 | 1 | |
| 5 | 2 | 8 | 1 | 1.1 | 2 | |
| 6 | 2 | 9 | 2 | 2 | 0.2 | |
| 7 | 1 | 6 | 1 | 1 | 0.1 | |
| 8 | 1 | 10 | 1 | 0.9 | 0.3 | |
| 9 | 2 | 11 | 2 | 1.5 | 2 | |
| 10 | 1 | 13 | 1 | 1.3 | 0.1 |
| Number of Items | Periods | Total Cost ($) | |
|---|---|---|---|
| Traditional Can-Order Policy | Proposed Can-Order Policy | ||
| 6 | 5 | −5599.80 | −7264.20 |
| 10 | 8800.40 | 5471.60 | |
| 15 | 23,200.60 | 18,207.40 | |
| 20 | 37,600.80 | 30,943.20 | |
| 8 | 5 | −895.60 | −4021.20 |
| 10 | 18,208.80 | 11,957.60 | |
| 15 | 37,313.20 | 27,936.40 | |
| 20 | 56,417.60 | 43,915.20 | |
| 10 | 5 | 987.80 | −2448.60 |
| 10 | 21,975.60 | 15,102.80 | |
| 15 | 42,963.40 | 32,654.20 | |
| 20 | 63,951.20 | 50,205.60 | |
| Test Number | ||
|---|---|---|
| 1 | 300 | 3000 |
| 2 | 300 | 4000 |
| 3 | 400 | 2000 |
| 4 | 400 | 4500 |
| 5 | 450 | 2500 |
| Test Number | Fuzzy Total Cost ($) | |||||
|---|---|---|---|---|---|---|
| 1 | 907,298.50 | 1,039,618.0 | 0.73 | 1081 | 8810 | 1,400,277.0 |
| 2 | 884,448.50 | 1,011,266.0 | 0.75 | 1075 | 9000 | |
| 3 | 930,148.50 | 1,078,992.0 | 0.68 | 1128 | 8640 | |
| 4 | 881,762.50 | 1,002,462.0 | 0.77 | 1092 | 9035 | |
| 5 | 918,723.50 | 1,062,622.0 | 0.72 | 1126 | 8700 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, J.; Kim, J.S.; Hwang, S.-J. A Multi-Item Replenishment Problem with Carbon Cap-and-Trade under Uncertainty. Sustainability 2020, 12, 4877. https://doi.org/10.3390/su12124877
Noh J, Kim JS, Hwang S-J. A Multi-Item Replenishment Problem with Carbon Cap-and-Trade under Uncertainty. Sustainability. 2020; 12(12):4877. https://doi.org/10.3390/su12124877
Chicago/Turabian StyleNoh, Jiseong, Jong Soo Kim, and Seung-June Hwang. 2020. "A Multi-Item Replenishment Problem with Carbon Cap-and-Trade under Uncertainty" Sustainability 12, no. 12: 4877. https://doi.org/10.3390/su12124877





