Foreign-Funded Enterprises and Pollution Halo Hypothesis: A Spatial Econometric Analysis of Thirty Chinese Regions

Abstract

China is one of the world’s major environmental polluters, therefore, Chinese environmental efficiency is an issue of global importance. In this study, we aim to identify economic factors affecting environmental efficiency scores in different regions of China from a spatial econometric perspective. We measure environmental efficiency scores, relative to the theoretically consistent production possibilities frontier estimated, according to a novel iterative methodology. As expected, we find that environmental efficiency scores are negatively affected by the prevalence of heavy industry sector in the economy, with a higher share of coal as a source of energy exacerbating the problem. We also find evidence that strongly support the pollution halo hypothesis, which credits foreign-funded enterprises with producing in a more environmentally-friendly way. Surprisingly, we find a negative association between the share of tertiary sectors in a regional economy and environmental efficiency—emphasizing the need to address the indirect effects produced on the environment by the seemingly innocuous sectors, such as the hotel sector. We encourage the creation of foreign-funded enterprises, and support formulating environmental protection policies that consider the indirect effects various economic sectors have on the environment.

1. Introduction

As environmental concerns grow around the globe, the role of the world’s major polluters, such as China, in affecting the environment increases in importance. China has surpassed the US as a single largest global emitter of CO₂ in 2006 [1]. As a result of the Chinese government’s awareness of the environmental problems associated with China’s industrial growth, comprehensive pollution reduction targets were formulated in the Twelfth Five-Year Energy Saving and Emissions Reduction Comprehensive Plan [2]. An important feature of this plan is its formulation in terms of reducing the levels of harmful emissions by a specific amount, e.g., 8% for SO₂.

Several studies [3] have shown, however, that a substantial reduction of pollution is possible by increasing the environmental efficiency of the polluting technologies used in industry. Environmental (in)efficiency is often defined in terms of the distance between the actually observed combination of a good and bad output, and their projection on the best-practice frontier—which is a textbook definition of productive efficiency applied to the environmental context. The best-practice, or production possibilities frontier (PPF), is defined as a locus of combinations of a good (steel) output y and bad (CO₂) output b such that for each possible b the value of y on the frontier is the maximum possible amount of good output for that particular level of pollution b.

In this study, we apply a novel methodology developed by Reference [4] to the estimation of the parameters of an environmentally efficient frontier based on the estimation of the parameters of the directional output distance functions (DODF) popularized by Reference [5]. This approach, for instance, was used by Reference [6] in order to estimate marginal abatement costs of reducing CO₂ emissions in the Chinese regions. By employing the estimation methodology developed by Reference [4], we arrive at the theoretically consistent estimates of environmental efficiency scores based on a parametric PPF. While the traditional DODF approach to the estimation of environmental efficiency scores allows for the estimation of environmental efficiency scores, e.g., Reference [7], the DODF values, as shown in Reference [4], do not necessarily correspond to a theoretically consistent concave PPF.

Our second contribution is to recognize the phenomenon of spatial clustering of the regional environmental efficiencies, which has hardly been done before. Such recognition is important since, as shown in Reference [8], ignoring spatial autocorrelation in the dependent variable in general results in biased and inefficient estimates of the estimated model’s coefficients. We avoid this shortcoming by applying spatial econometric models to our data and demonstrate that, even though their geographical location explains a substantial part of the variation in environmental efficiency scores in the Chinese regions, socio-economic factors play an important role.

For policy-making purposes, it appears important to identify economic factors affecting the level of environmental efficiency. The effect produced on the latter by the Chinese foreign-funded enterprises (FFEs) appears to be particularly interesting to study as an increasingly larger share of the Chinese exports, the key driver of China’s economic growth, has been recently coming from the FFEs, see Reference [9]. The Chinese National Bureau of Statistics (NBS) defines several categories of the enterprises jointly classified as the FFEs, such as joint venture and cooperative enterprises with foreign investment, enterprises with the sole foreign investment, and share-holding corporations with foreign investment. The exact definitions of these FFE types can be found on the website of China’s National Bureau of Statistics, see Reference [10]. According to Reference [11], enterprises with the sole foreign investment and joint venture and cooperative enterprises with foreign investment accounted for 92% of the total FDI in China in 2016. Depending on whether it is the pollution haven or pollution halo hypothesis that is valid, the environmental effect of the FFEs on the Chinese environmental efficiency will be different. According to the pollution haven hypothesis, e.g., Reference [12], more developed economies will try to transfer their polluting production facilities to the less developed ones in order to benefit from their lax environmental regulation. According to the pollution halo hypothesis, however, the FFEs will use more advanced technologies that are more environmentally-friendly. While most related studies [13] appear to be identifying the effects of the international trade on environmental efficiency or those of the FDI, see Reference [14], we specifically measure the influence of the foreign-funded firms in the Chinese regions on their environmental efficiency by looking at the FFEs’ export intensity and the importance of international FFEs to the regions’ international trade in general. By performing our analysis at the level of the FFEs rather than the aggregate FDI flows, we are able to capture the structural idiosyncracies in these flows, e.g., the difference between FFEs with a high or low share of foreign capital that cannot be analyzed at an aggregate FDI level.

By means of a spatial panel econometric analysis, we examine the importance of several factors potentially influencing environmental efficiency levels in the Chinese regions using theoretically consistent estimates of the environmental efficiency scores, and derive policy implications in the concluding section.

2. Literature Review

2.1. Environmental Efficiency

While the Chinese government realizes the importance of controlling the impact produced by polluting production processes on the environment, in terms of policy measures, the emphasis appears to have been mostly on energy intensity. Thus, in its Eleventh Five-Year Plan, the Chinese government set the goal of decreasing energy intensity measured as the energy used per unit of GDP by 20% compared to the level of 2005 [15]. Reference [3] found that savings of 2.6 billion tons of coal equivalent of energy consumption can be saved in China in 2030. However, Reference [16] suggests that, while most Chinese provinces have achieved a significant reduction of energy intensity during the Eleventh Five-Year Plan, in some provinces this reduction is due to inaccurately measured regional GDP rather than actual improvements in the use of energy. The authors conclude that a single-factor measure of energy intensity should be amended with other indicators, e.g., environmental efficiency.

In recent years, several methodologies were developed to measure the extent of environmental efficiency. Thus, Reference [17] developed an environmental performance index (EPI) that aggregates twenty-four environmental indicators to gauge the extent to which countries are close to the achievement of the established environmental policy objectives. The life-cycle assessment (LCA) approach consists of tracing the environmental impact associated with all stages of a product’s lifetime beginning with the extraction of raw materials necessary for its production, all the way through the intermediate stages of its production, and ending with its disposal, e.g., Reference [18].

One way to define environmental efficiency, which is firmly rooted in economic theory is to compute it as a function of distance to the best-practice frontier in the space of a good and bad output. The directional output distance function (DODF) methodology developed by Reference [19] fits especially well with this purpose since it is based on the simultaneous contraction of bad, and the expansion of good outputs in the process of moving towards the best-practice, or production possibilities frontier (PPF). Reference [5] employ a quadratic approximation to the directional output distance function in order to estimate the PPF slope at the efficient projections of the actually observed combinations of a good and bad output taken along a particular, e.g., 45-degree, directional output vector. The authors demonstrate that both data envelopment analysis (DEA) and stochastic frontier analysis (SFA) can be used in order to estimate the quadratic approximation to the DODF. Reference [4] took this a further step, and suggests an iterative methodology to estimate a parametric-form PPF for a polluting technology. While the original DODF estimation is based on an arbitrary choice of a single directional output vector, Reference [4] suggests using a large number of such vectors in the iterative process which results in a parametric PPF consistent with economic theory. In case the directional output vectors are normalized to unity, the Euclidean distance between an actually observed combination of a good and bad output and the PPF is equal to the value of the DODF for that combination of outputs, and environmental efficiency scores can be computed as an exponent of the negative of the DODF value at the observed combination of outputs, e.g., Reference [7].

Several recent studies attempted to evaluate environmental efficiency scores in China. Reference [20], for instance, evaluate environmental efficiency scores in thirty-one Chinese provinces using a combination of DEA approach and spatial econometrics. Reference [21] examines the determinants of environmental efficiency in thirty Chinese provinces and found a Kuznets-type U-shaped relationship between the levels of foreign direct investment and environmental efficiency. Reference [22] computes environmental efficiency scores for 192 thermal power plants in the delta of Yangtze river and found that environmental efficiency follows an ambiguous trend, being negatively affected by the share of coal in the plants’ energy input mix.

2.2. Pollution Haven Versus Pollution Halo Hypothesis

An important part of research efforts has been directed towards the role foreign capital plays in forming the Chinese environmental landscape through foreign-funded enterprises, particularly in the context of pollution haven/halo hypotheses. The pollution haven hypothesis implies that the foreign-funded enterprises will be used as a means to transfer polluting technologies to the countries or regions with lax environmental regulation, in this way obviating the need to comply with the more stringent, and financially burdensome, regulations at home, e.g., Reference [12]. The pollution haven hypothesis would imply, however, that international trade and FDI in the less developed economies would produce a negative impact on the environment. Some studies [23] confirm that who argue that China has recently increased its pollution-intensive exports to the rest of the world, thus, becoming the world’s pollution haven. Yet, Reference [13] concluded that the net effect of free international trade produced on the environment is positive in terms of reducing pollution concentration. Reference [24] cites several empirical studies that found that FDI had a positive impact on the environment, and thus, foreign-funded enterprises—confirming the pollution halo, as opposed to the pollution haven, hypothesis.

2.3. Spatial Econometric Studies

The seminal contribution [8] demonstrated that ignoring the fact that the values of dependent and independent variables, along with the estimated model’s errors, can be spatially autocorrelated will in general result in biased and inefficient estimates. A plethora of spatial econometric models and their estimation methods have been developed since then, Reference [25] provides a comprehensive summary in the spatial panel econometric context. Since polluted air moves freely between different geographical regions, due to air circulation, regional environmental efficiency scores and measures of regional environmental pollution are more likely than not to be spatially autocorrelated. Indeed, Reference [1] found evidence of spatial correlation among levels of CO₂ intensity in the Chinese provinces while examining the determinants of regional pollution levels. Reference [26] estimates spatial panel data models to found evidence of an inverted N-shaped relationship between regional GDP per capita and the level of CO₂ emissions. Reference [15] found significant autocorrelation in the CO₂ emissions in Chinese cities. Reference [27] measured urban eco-efficiency levels in China and found evidence of spatial autocorrelation as well.

3. Research Method and Data

3.1. Data Sources and Summary

We obtained the data on China’s regional GDP and the economic determinants of the environmental efficiency scores from the National Bureau of Statistics of China [28]. The regional labor force data are gathered from Reference [29]. The regional capital stock is obtained from the authors of Reference [30], who use the Chinese regional capital stock estimates as a starting point [31]. The data on fuel consumption in the Chinese regions are provided by Reference [32]. Since the regional data on CO₂ emissions are not directly available for China, we follow Reference [30] to impute their level by using the data in Reference [32] on the regional consumption of several types of energy and the conversion factors suggested by the Intergovernmental Panel on Climate Change (see their Emission Factor Database [33]) and reported in

Table 1. Definitions of variables used in this study.

Variable	Definition	Unit of Measurement
Production Technology
RGDP	Regional GDP	100 million yuan
B	CO2 emissions	10,000 ton
K	Physical capital	100 million yuan
L	Labor force	10,000 persons
F	Fuel	10,000 tons of coal equivalent
Determinants of Environmental Efficiency
Pollution-Related Determinants
COALRATE	Coal share in total energy consumption	%
HEAVY	Share of heavy industry enterprises in regional GDP	%
TERTIARY	Share of tertiary sector in regional GDP	%
ENVINVSH	Share of investment in environmental quality in regional GDP	%
Determinants Related to Pollution Haven- and Halo-Hypotheses
FKSHARE	Share of foreign capital in foreign-funded enterprises	%
FEXPINT	Share of exports of foreign-funded enterprises in the total volume of their international trade	%
TROPEN	Share of the international trade by foreign-funded enterprises in regional GDP	%
Economic Affluence Determinant
RGDPL	Regional GDP per capita	10,000 yuan

[30]. All data were collected for the period between 2005 and 2014. Table 1 below provides definitions of the variables used in this study along with their names we later use for empirical estimation.

Table 2. Summary statistics.

Variable	Mean	Standard Deviation	Min	Max	Mean	Standard Deviation	Min	Max
	Original Data				Rescaled Data
Production Technology
RGDP	10,293.22	8934.07	465.52	49,707.92	0.999	0.868	0.045	4.829
B	9798.01	6903.14	445.25	35,300.93	1.000	0.705	0.043	3.603
K	22,284.39	18,992.48	1228.80	104,840.40	1.000	0.852	0.055	4.705
L	2555.14	1698.98	291.04	6614.00	1.000	0.665	0.114	2.589
F	15,451.58	10,585.14	845.90	55,598.92	1.000	0.685	0.055	3.598
Determinants of Environmental Efficiency
Pollution-Related Determinants
COALRATE	61.45	16.06	14.16	97.48	1.000	0.261	0.230	1.586
HEAVY	75.07	10.39	4.20	95.40	1.000	0.138	0.056	1.271
TERTIARY	40.92	8.34	28.30	77.90	1.000	0.204	0.692	1.904
ENVINVSH	0.24	0.22	0.01	2.04	1.000	0.907	0.045	8.509
Determinants Related to Pollution Haven- and Halo- Hypotheses
FKSHARE	73.85	8.12	44.39	88.40	1.000	0.110	0.601	1.197
FEXPINT	49.57	14.52	1.87	86.92	1.000	0.293	0.038	1.753
TROPEN	2.97	4.41	0.001	19.13	0.999	1.483	0.003	6.434
Economic Affluence Determinant
RGDPL	2.38	1.47	0.45	7.80	1.000	0.616	0.188	3.274

Note: for coding of variables in the first column, see Table 1.

reports summary statistics for all the variables employed in this study. The data on regional GDP and physical capital stock are in constant prices of 2000. For the estimation purposes, all data were rescaled by dividing the value of each observation by the mean of the respective variable.

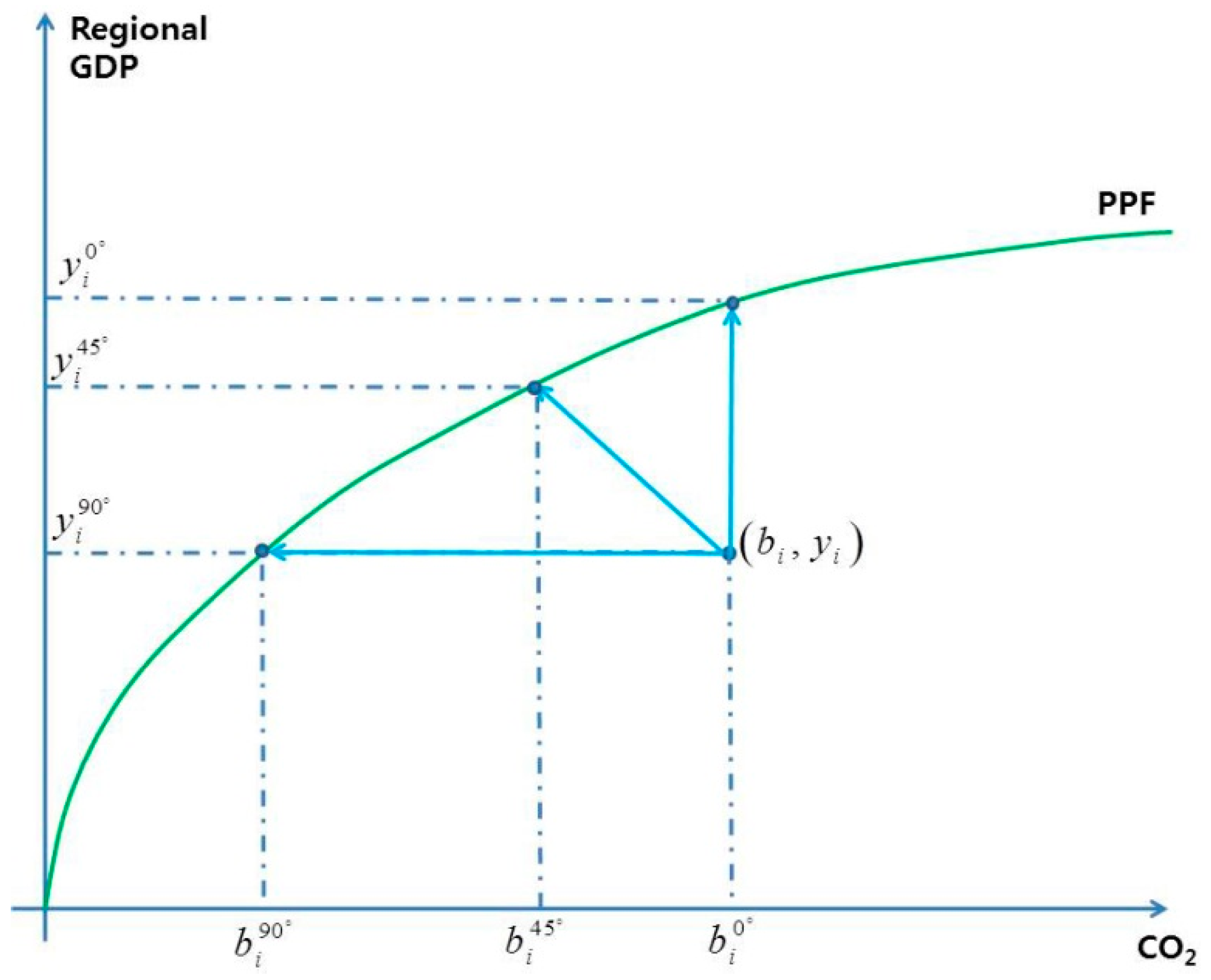
3.2. Directional Output Distance Functions and Production Possibilities Frontier

Figure 1 below displays an efficient boundary of the production possibilities set (PPS) for a polluting technology whereby a set of production inputs produces a feasible combination of a bad output, i.e., CO₂, and a good output, regional GDP. The production possibility frontier of this PPS is defined as a curve containing the maximally possible level of regional GDP for a given level of CO₂. Reference [5] provide theoretical foundations for the fact that the production possibilities set for a polluting technology is open, and that its PPF as a function $y=f\left(b\right)$ is increasing in the level of pollution b and is concave. Figure 1 below illustrates the idea.

Region $i=1\dots N$ emits the amount of CO₂ equal to $b_i$, while $y_i$ is the level of regional GDP in that region, N being the total number of regions in the sample. The output mix $\left(b_i,y_i\right)$ in Figure 1 is environmentally inefficient since it is located below the production possibilities frontier. As illustrated, the distance between $\left(b_i,y_i\right)$ and the PPF depends on the choice of a directional output distance vector $\overrightarrow{d}$ that maps the observed combination of outputs $\left(b_i,y_i\right)$ to its efficient projection $\left(b_i^{\overrightarrow{d}},y_i^{\overrightarrow{d}}\right)$. In Figure 1 vector $\overrightarrow{d}$ is taken to be equal to 45° with the output mix $\left(b_i^{45°},y_i^{45°}\right)$ being an efficient projection of $\left(b_i,y_i\right)$ taken along that vector.

The meaning of moving from the actual output mix $\left(b_i,y_i\right)$ along a directional output distance vector $\overrightarrow{d}$ towards a point on the efficient PPF is to make a more efficient use of the available inputs [34] in his seminal treatise makes an essential point that it is impossible to study economic production processes without taking heed of the physical laws, such as the first and the second laws of thermodynamics. Since according to these laws matter and energy cannot appear from nowhere a movement towards the efficient PPF is only possible if the production process resulting in $\left(b_i,y_i\right)$ is technically inefficient in the sense that either more good output can be produced while keeping pollution levels intact, or pollution can be reduced while preserving a particular level of a good output. Consequently, a simultaneous reduction of pollution levels together with an expansion of a good output is also possible if production is technically inefficient. The choice of a particular directional output distance vector $\overrightarrow{d}$ is thus completely at a policymakers’ discretion provided the production process is technically inefficient, and the two laws of thermodynamics are observed.

Reference [5] develops a procedure to measure the distance between $\left(b_i,y_i\right)$ and $\left(b_i^{\overrightarrow{d}},y_i^{\overrightarrow{d}}\right)$ by estimating the value of a directional output distance function (DODF) defined as follows:

$${\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)=\max \left\{\xi :\left(b_i-\xi g_b,y_i+\xi g_y\right)\in P\left(\overrightarrow{x}\right)\right\}$$

(1)

where ${\overrightarrow{x}}_i$ is a vector of inputs used by unit I to produce $\left(b_i,y_i\right)$, $P\left({\overrightarrow{x}}_i\right)$ is the production possibilities set of ${\overrightarrow{x}}_i$, and $\overrightarrow{d}=\left(-g_b,g_y\right)$. In Figure 1 the Euclidean distance between an observed output mix $\left(b_i,y_i\right)$ and its efficient projection $\left(b_i^{45°},y_i^{45°}\right)$ is exactly equal to the value of the DODF at $\left(b_i,y_i\right)$ conditioned on the directional output vector $\overrightarrow{d}$.

Most empirical studies appear to be following Reference [5], and choose a 45-degree unit vector $\overrightarrow{d}=\left(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$, in which case the value of a directional output distance function ${\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|45°\right)$ is equal to a Euclidean distance between the actually produced output mix $\left(b_i,y_i\right)$ and its efficient projection $\left(b_i^{45°},y_i^{45°}\right)$, as illustrated in Figure 1. We refer to a particular directional output distance vector by the angle it is forming with the vertical axis.

Environmental efficiency score for region i can then be defined as $e^{-{\overrightarrow{D}}_0\left(b_i,y_i|45°\right)}$, as is done, e.g., Reference [7]. Depending on the choice of the directional output distance vector $\overrightarrow{d}$, the value of the environmental efficiency score will be different, since the Euclidean distance between $\left(b_i,y_i\right)$ and $\left(b_i^{45°},y_i^{45°}\right)$ is obviously different from that between $\left(b_i,y_i\right)$ and $\left(b_i^{0°},y_i^{0°}\right)$ corresponding to a vertical $\overrightarrow{d}$.

Depending on the choice of vector $\overrightarrow{d}$ the values of both the DODF and the associated environmental efficiency scores are going to be different. Thus, if vector $\overrightarrow{d}$ is vertical the associated DODF value is the lowest corresponding to the highest environmental efficiency score, while the lowest score will be obtained in case of opting for the horizontal directional output vector, as can be inferred from Figure 1.

As noted by Reference [15], the choice of vector $\overrightarrow{d}$ depends on the objectives of an underlying environmental policy. The 45-degree vector, for instance, serves the purpose of a simultaneous increase of the amount of good, and the reduction of a bad output. A policy aiming at reducing pollution as much as possible while keeping the level of good output intact corresponds to the horizontal vector. Finally, if environmental policymakers aim at increasing good output while keeping pollution at the same level, the vertical vector is appropriate.

Reference [5] suggests estimating the values of a quadratic approximation to ${\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)$ in a stochastic framework where for each observation the value of ${\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)$ is assumed to be a random variable with mean $E\left[{\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)\right]=v_i+u_i$ where $v_i~N\left(0,{\sigma }_v^2\right)$ are independently distributed symmetric shocks, and $u_i~\left|N\left({\mu }_u,{\sigma }_u^2\right)\right|$ are half-normally distributed random values. Reference [5] suggests evaluating the coefficients of a quadratic approximation to ${\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)$ by maximizing a likelihood function subject to the constraints ensuring the properties of translation, representation, monotonicity, and symmetry.

The translation property makes sure that if the amount of good output increases by $\alpha g_y$ while the amount of bad output reduces by $\alpha g_b$, the distance to PPF reduces by $\alpha$. In other words, this property guarantees that the estimated quadratic form approximating the DODF defined in Equation (1) is satisfies the definition of the directional output distance function. The representation property ensures that the DODF values are only positive for those output combinations that belong to the set of feasible production bundles, i.e., the production possibilities set. The monotonicity property ensures that the DODF be non-increasing in good output, and non-decreasing in bad output. Finally, the symmetry property is a technical requirement related to the fact that we are aproximating the true DODF by a quadratic form.

Efficient projection $\left(b_i^{\overrightarrow{d}},y_i^{\overrightarrow{d}}\right)$ on the PPF for any observed combination of outputs $\left(b_i,y_i\right)$ and a directional output distance vector $\overrightarrow{d}$ can then be computed as $\left(b_i^{\overrightarrow{d}}-{\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)\times g_b,y_i^{\overrightarrow{d}}+{\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)\times g_y\right)$ where $\sqrt{g_b^2+g_y^2}=1$.

3.3. Iterated PPF and Environmental Efficiency Scores

Reference [4] demonstrate that the PPF implied by the estimated projection values of the observed output combinations does not satisfy the theoretical requirement of concavity. The latter property says that pollution abatement costs in terms of the forgone GDP decrease with more pollution. Alternatively, decreasing pollution becomes increasingly costly with increases environmental quality. In case higher pollution levels are associated with higher marginal abatement costs, the underlying PPF is not consistent. In order to compute environmental efficiency scores based on the theoretically consistent PPF, we apply an iterative procedure suggested by the authors in order to estimate a parametric form of the PPF based on the DODF values for a large number of the directional output distance vectors.

Figure 2 below illustrates the idea behind an iteration procedure used in Reference [4], in order to estimate a theoretically consistent PPF.

To avoid clutter, we only consider two observed combinations of output, namely, $\left(b_1,y_1\right)$ and $\left(b_2,y_2\right)$. In case of using just one directional, 45-degree output vector the methodology in Reference [5] identifies two efficient projections denoted $P_1^{45°}$ and $P_2^{45°}$ in Figure 2, in which case our best estimate of the PPF corresponding to these efficient projections would be a straight line $PP{F}_1$ passing through $P_1^{45°}$ and $P_2^{45°}$. However, by adding two more directional output vectors, namely, the thirty- and sixty-degree ones, one comes up with six efficient projections even as the number of the observed combinations of outputs stays the same at two. Thus, with three directional output vectors we have efficient projections $P_1^{30°},P_1^{45°},P_1^{60°},P_2^{30°},P_2^{45°},\mathrm{and}{P}_2^{60°}$ so that the PPF obtained at this second iteration, i.e., $PP{F}_2$, is more theoretically consistent compared to $PP{F}_1$. Two iterations are not enough in this hypothetical example as the two approximations to the true PPF, i.e., $PP{F}_1$ and $PP{F}_2$ are too different from each other in the sense, e.g., of the sum of the squared vertical differences between the two at the observed output mixes. By consistently adding more directional output vectors we increase the number of the efficient projection estimates up to the point where the difference between two consecutive PPF estimates becomes negligible. In other words, we stop at iteration number N if $\Vert PP{F}_N-PP{F}_{N-1}\Vert <\epsilon$ where $PP{F}_N$ is a PPF estimate at iteration N, and $\epsilon$ is a small number of our choice.

The iteration procedure is formalized as follows. Define $S_k,k\in \mathbb{N}$ to be the set of directional output vectors at iteration k. For k = 1 one can employ $S_1=\left\{0^{°},{45}^{°},{90}^{°}\right\}$. For each $\overrightarrow{d}\in S_k$ applying the procedure in Reference [5] to estimate the DODF parameters results in a set of efficient projections $\left({\widehat{b}}_i^{\overrightarrow{d}},{\widehat{y}}_i^{\overrightarrow{d}}\right)$ for each observed combination of outputs $\left(b_i,y_i\right),i=1\dots N$. At the initial iteration, for instance, there result $3\times N$ such projections since there are three directional output vectors in $S_1$.

At iteration step k we estimate the following stochastic model:

$$\{\begin{array}{l}{\eta }_i={\widehat{y}}_i^{\overrightarrow{d}}-{\alpha }_k{\left({\widehat{b}}_i^{\overrightarrow{d}}\right)}^{{\beta }_k}~N\left(0,{\sigma }_{\eta }^2\right),i\in 1\dots N,\overrightarrow{d}\in S_1\\ {\alpha }_k>0,0<{\beta }_k<1\\ E\left[{\eta }_i\right]=0,Var\left[{\eta }_i\right]={\sigma }_{\eta }^2\end{array}$$

(2)

where $\left({\widehat{b}}_i^{\overrightarrow{d}},{\widehat{y}}_i^{\overrightarrow{d}}\right)$ are the estimated efficient projections of the observed combinations of outputs $\left(b_i,y_i\right)$ on the iterated PPF taken along the directional output vectors $\overrightarrow{d}\in S_k$, while ${\alpha }_k$ and ${\beta }_k$ are estimated parameters of the iterated PPF at iteration k. The PPF parameters in Equation (2) are constrained to be such that the PPF $y=f\left(b\right)$ be increasing, concave, and satisfy the property of null-jointness, i.e., the impossibility of producing any amount of good output without polluting the environment.

At the next step, the estimation in Equation (2) is repeated for $S_{k+1}\supset S_k$, i.e., the parameters of a PPF at iteration k + 1 are estimated on the basis of a broader set of the directional output vectors that includes all such vectors employed at the previous iteration. We follow Repkine and Min (2018) to form $S_{k+1}\supset S_k$ for iteration k + 1 by adding to $S_k$ the odd multiples $s\Delta ,s=1,3,5,7,\dots$ where $\Delta$ is the minimum angle formed with the vertical axis by any of the directional output vectors in $S_k$, provided that all $s\Delta <{90}^0$. In other words, the vectors at iteration k + 1 include all vectors at the iteration k, plus the additional vectors that split the angle between adjacent vectors at iteration k in half.

The iterative process stops when the norm of the vector of proportionate changes between coefficients of the two consecutive iterations is smaller than a predefined small number $\epsilon$, i.e., if $\sqrt{{\left(\frac{{\alpha }_k-{\alpha }_{k-1}}{{\alpha }_{k-1}}\right)}^2+{\left(\frac{{\beta }_k-{\beta }_{k-1}}{{\beta }_{k-1}}\right)}^2}\le \epsilon$ where $\epsilon$ is a predefined small number.

Assuming the iterations stop at some step K, we follow [7] to measure environmental efficiency score for a particular directional output vector $\overrightarrow{d}$ as an exponent of the negative of the Euclidean distance between the observed combination of outputs $\left(b_i,y_i\right)$ and its efficient projection $\left({\tilde{b}}_i^{\overrightarrow{d}},{\tilde{y}}_i^{\overrightarrow{d}}\right)$ on the iterated PPF. It is important to notice that $\left({\tilde{b}}_i^{\overrightarrow{d}},{\tilde{y}}_i^{\overrightarrow{d}}\right)\ne \left(b_i^{\overrightarrow{d}},y_i^{\overrightarrow{d}}\right)$ since $\left({\tilde{b}}_i^{\overrightarrow{d}},{\tilde{y}}_i^{\overrightarrow{d}}\right)$ is located on the iterated PPF, while $\left(b_i^{\overrightarrow{d}},y_i^{\overrightarrow{d}}\right)$ in general is not. Formally, we compute environmental efficiency scores as follows:

$$\{\begin{array}{l}ENVEF{F}_i=e^{-{\overrightarrow{D}}_0{\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)}_i},i=1\dots N\\ {\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)=\sqrt{{\left({\tilde{b}}_i^{\overrightarrow{d}}-b_i^{\overrightarrow{d}}\right)}^2+{\left({\tilde{y}}_i^{\overrightarrow{d}}-y_i^{\overrightarrow{d}}\right)}^2}\end{array}$$

(3)

where $\left({\tilde{b}}_i^{\overrightarrow{d}},{\tilde{y}}_i^{\overrightarrow{d}}\right)$ are projections of the observed $\left(b_i,y_i\right)$ obtained on the iterated PPF at the last step K along a unit vector $\overrightarrow{d}=\left(-g_b,g_y\right)$.

3.4. Model Specification and the Choice of Environmental Efficiency Determinants

We estimate the following empirical specification:

$$\begin{array}{l}\ln \left(ENVEF{F}_{it}\right)={\alpha }_0+{\alpha }_{1}COALRAT{E}_{it}+{\alpha }_{2}HEAV{Y}_{it}+{\alpha }_{3}TER{T}_{it}+{\alpha }_{4}GDP{C}_{it}+\\ +{\alpha }_{5}GDP{C}_{it}^2+{\alpha }_{6}FKS{H}_{it}+{\alpha }_{7}EXPIN{T}_{it}+{\alpha }_{8}TROPE{N}_{it}+{\alpha }_{9}ENVINVS{H}_{it}+{\epsilon }_{it}\end{array}$$

(4)

where $ENVEF{F}_{it}$ denotes a score of environmental efficiency computed according to Equation (3) for some directional output vector in province i and year t. Environmental efficiency scores are computed under the assumption of a year-specific PPF that we estimated by an iterative procedure described in Section 3.2. We define the dependent variable in Equation (4) as a natural log of the environmental efficiency score $ENVEF{F}_{it}$. Since the latter is an exponential transformation in Equation (3) of the value of the directional distance function, $\ln \left(ENVEF{F}_{it}\right)$ is equal to the negative of the DODF value, i.e., $-{\overrightarrow{D}}_0\left({\overrightarrow{x}}_i,b_i,y_i|\overrightarrow{d}\right)$, which makes $\ln \left(ENVEF{F}_{it}\right)$ an increasing function of any factor contributing to higher environmental efficiency. Specification Equation (4) does not include any regional or time controls since these will be added in the context of spatial panel econometrics models discussed in Section 3.5.

$COALRAT{E}_{it}$ is the share of coal in total energy consumption by the industrial enterprises, also known as coal intensity. Using coal as a source of energy presents a major environmental problem as, for instance, combustion of coal is responsible for the creation of nearly one-half of all CO₂ emissions on the planet, e.g., Reference [35]. In addition, coal-intensive enterprises are shown to be less environmentally efficient compared to their less coal-intensive counterparts, as documented in Reference [22]. COALRATE for each region and year is calculated as a ratio of the coal consumption as a source of energy in a particular region measured in 10,000 tons to the total energy consumption measured in 10,000 tons of standard coal equivalent (SCE).

$HEAV{Y}_{it}$ is the share of heavy industry enterprises, e.g., steel and energy production in regional GDP, both measured in one hundred million yuan. Besides being major polluters, enterprises in the heavy industry sector are also the ones needing most improvements in terms of environmental efficiency. Thus, Reference [36] estimated a weighted slacks-based model for the Chinese industrial sectors to separate them into three clusters according to the level of their environmental efficiency. According to their analysis, most enterprises operating in the heavy industry sector are also the ones characterized by the lowest environmental efficiency scores. As the tertiary sector industries are less likely to produce harmful emissions into the ambient environment, we also include the share of tertiary sector $TER{T}_{it}$ in regional GDP measured as a ratio of the tertiary sector’s output measured in one hundred million yuan to the regional GDP.

While higher per-capita incomes are typically associated with higher levels of CO₂ emissions as found, among others, by Reference [37], their impact on environmental efficiency is likely non-linear as suggested by the environmental Kuznets curve (EKC) theory developed in Reference [38]. The theory says that in a low-income economy, the priority is given to growth, while environmental issues acquire more weight with more economic affluence. Since the existence of the environmental Kuznets curve has been confirmed for the Chinese regions in several studies, e.g., References [26] or [39], we include both regional GDP per capita level $GDP{C}_{it}$ and its square $GDP{C}_{it}^2$ in our specification.

The following three determinants, namely, $FKS{H}_{it}$, $FEXPIN{T}_{it}$, and $TROPE{N}_{it}$ account for the effects of foreign investment and international trade on environmental efficiency. Ever since 1979, when the Chinese government promulgated regulations for foreign investment, the foreign-funded enterprises (FFEs) have played an increasingly important role in an export-driven Chinese economy. Thus, in 2017 the FFEs accounted for 43% of the total Chinese exports, see Reference [40]). We include the share of foreign capital $FKS{H}_{it}$ in the foreign-funded enterprises to control for the implications of the pollution haven/halo hypotheses discussed in Section 2. We measure foreign capital share as a ratio of the value of the FFE’s registered foreign capital to the total value of registered capital in the foreign-funded enterprises, both measured in million USD. In case the pollution haven hypothesis is correct, the FFEs engage in polluting and environmentally inefficient production activities in China, due to her lax environmental regulation. On the other hand, according to the pollution halo hypothesis, foreign participation brings in clean and environmentally efficient production technologies, implying a positive sign of the $FKS{H}_{it}$ coefficient.

In this study, we aim to examine whether active engagement in the international trade in general, and in exporting activities in particular, on the side of the FFEs is beneficial for environmental efficiency. The effect of international trade by the foreign-funded Chinese enterprises on environmental efficiency is captured by the share $FEXPIN{T}_{it}$ of a region’s exports by foreign-funded enterprises to the volume of their international trade, both measured in 10,000 USD, and trade openness $TROPE{N}_{it}$ measured as the ratio of the international trade volume by the foreign-funded enterprises to regional GDP, both measured in one hundred million yuan. Reference [13] argues that, while international trade produces both positive and negative effects on the environment, the overall effect is positive. On the other hand, Reference [21] uses a slacks-based efficiency measure to analyze environmental efficiency in thirty Chinese provinces and conclude that more exports are associated with lower environmental efficiency. Neither study, however, has taken into account the inter-regional spatial spillover effects that, as shown by Reference [8], may seriously affect the estimated coefficients. In addition, the above-mentioned studies, among others, analyze the effect of international trade by all, not necessarily foreign-funded, firms. Our study is different in that it analyzes the relationship between international trade and environmental efficiency from a spatial econometrics perspective focusing on the foreign-funded enterprises.

In line with the global efforts to limit the CO₂ emissions, the Chinese government in 2018 formulated an action plan that requires, for instance, the steel production plans to meet “ultra-low emission” standards by 2020, and the power generating plants to take measures to produce more energy with less coal. The Chinese statistical yearbooks report the total amount of regional investment in improving the environment. We compute $ENVINVS{H}_{it}$ as the share of such investment in the regional GDP, both measured in one hundred million yan, to account for the effects of the government policy on environmental efficiency. Table 1 presents summary statistics for the variables in the specification Equation (1).

3.5. Taxonomy of the Spatial Panel Models

Since all observations in our dataset are linked to a particular geographical region, it is highly likely that these observations are not spatially independent. Spatial dependence I when values observed in one region depend in some way on the values observed in the neighboring regions. For instance, environmental efficiency scores in a particular region are likely to be a function of these scores in the neighboring regions. Indeed, it is more likely than not that in any particular region environmental efficiency scores will be more or less close to those of the neighboring regions. This is the case of spatial lag in the terminology of Reference [41]. Spatial lags can be present in the determinants of the dependent variable as well. For instance, not only the environmental efficiency scores are correlated across the neighboring regions, but the values of regional GDP per capita in the neighboring regions may be correlated as well. Finally, neighboring regions are more likely than not to experience correlated shocks, in which case spatial autocorrelation is present. A detailed description of various types of spatial correlation in the geographical data can be found in Reference [41].

Reference [25] suggests the following portmanteau model capturing the three basic ways in which spatial correlation can be present in the data:

$$\{\begin{array}{l}{Y}_{it}=\rho {\displaystyle \sum _{j=1}^N{W}_{ij}{Y}_{jt}+X_{it}\beta +{\displaystyle \sum _{j=1}^N{W}_{ij}{X}_{jt}\gamma +{\mu }_i+{\eta }_t+{\phi }_{it}}},i=1\dots N,t=1\dots T\\ {\phi }_{it}=\lambda {\displaystyle \sum _{j=1}^N{W}_{ij}{\phi }_{jt}+{\epsilon }_{it}},{\epsilon }_{it}~i.i.d.\end{array}$$

(5)

where $Y_{it}$ is the value of the dependent variable, i.e., environmental efficiency scores in our case, in reIion i at time t, X is an $NT\times M$ matrix of the determinants of $Y_{it}$, and W is a $N\times N$ spatial weights matrix whose elements $w_{ij}\ne 0$ if reIions i and j are neighbors according to some criterion. We chose for queen contiguity to define W where two regions are neighbors if polygons representing them on a map share either a common edge or vertex. If the elements of W are row-standardized, i.e., if the sum of the elements of W in each row is equal to unity, ${\displaystyle \sum _{j=1}^N{W}_{ij}{Y}_{jt}}$ for a particular Iegion i is equal to the average value of the variable Y computed across the adjacent regions.

Specification Equation (5) becomes the spatial lag model (SLM) if the only type of spatial dependence in the data is that between the values of the dependent variable in the neighboring regions, i.e., if $\rho \ne 0,\gamma =\lambda =0$ where $\gamma$ is a vector of coefficients for the spatial lag of the independent variables in the right-hand side of Equation (4). If it is only the errors ${\phi }_{it}$ that are correlated across the adjacent regions, but not the dependent variable values, the parameter constraints on Equation (5) are $\rho =\gamma =0$ and $\lambda \ne 0$, and the model is referred to as the spatial error model (SEM). The model of Kelejian and Prucha [42] results if $\gamma =0,\rho \ne 0$ and $\lambda \ne 0$, hence (KP). In case $\lambda =0$ but $\rho \ne 0$ and $\gamma \ne 0$, the values of both dependent and the independent variables are correlated across the neighboring regions, resulting in the spatial Durbin model (SDM). In case there is no spatial autocorrelation in the dependent variable, i.e., if $\gamma \ne 0,\lambda \ne 0$, but $\rho =0$, Equation (5) becomes the spatial Durbin error model (SDEM). Finally, if all three types of spatial correlation are allowed, i.e., if $\rho \ne 0,\gamma \ne 0\mathrm{and}\lambda \ne 0$, one ends up with the most comprehensive Durbin model with spatial lag and error, or Manski model, that can be traced back to Reference [43]. As noted by Reference [41], if the benchmark specification Equation (4) is estimated with conventional panel data estimation techniques instead of one of the three models in Equation (5), the resulting estimates are likely to be biased and inefficient.

4. Results

4.1. Environmental Efficiency Scores

Figure 3 below is a quantile map of the estimated efficiency scores in the first and the last year of our sample for the 45-degree directional output vector. Darker regions correspond to higher scores of environmental efficiency.

Figure 3 suggests that while industrially the most developed regions in China’s North-East are expectedly also the least environmentally efficient, they remain to be so in the course of ten years between 2005 and 2014. In

Table 3. Estimated average environmental efficiency levels in China, 2005–2014.

	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Directional Output Vector	Average Environmental Efficiency Score
$0°$	53.78	49.97	47.80	44.76	42.60	41.02	34.03	33.11	29.41	27.26
$45°$	51.95	48.23	46.23	43.31	41.18	39.64	32.80	31.99	28.47	26.42
$90°$	49.77	46.22	44.49	41.81	39.75	38.26	31.66	31.00	27.74	25.81

we report average environmental efficiency scores in each year of our sample for the three directional output vectors, namely, $0°,45°$, and $90°$. In

Table A1. Estimated average environmental efficiency levels in the Chinese regions, 2005–2014. Directional output vector $0°$.

	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Region	Environmental Efficiency Scores
Beijing	82.57%	83.94%	88.84%	87.58%	88.66%	95.46%	99.87%	98.07%	99.83%	92.12%
Tianjin	64.39%	62.35%	63.41%	63.43%	61.48%	55.46%	48.91%	48.44%	41.50%	40.66%
Hebei	14.73%	11.98%	7.70%	5.93%	4.81%	3.85%	1.75%	1.58%	1.00%	1.12%
Shanghai	63.71%	66.71%	71.75%	66.53%	69.13%	67.95%	61.81%	62.71%	49.79%	55.40%
Jiangsu	43.95%	40.81%	34.76%	35.30%	37.51%	33.83%	19.00%	20.07%	14.86%	16.18%
Zhejiang	61.97%	56.16%	50.21%	47.98%	47.14%	47.78%	38.95%	42.85%	35.34%	34.57%
Fujian	82.75%	80.23%	80.53%	78.85%	69.19%	69.37%	56.60%	58.95%	56.30%	41.84%
Shandong	17.09%	12.05%	7.11%	5.26%	5.21%	3.75%	2.34%	1.93%	1.64%	1.09%
Guangdong	100.00%	100.00%	100.00%	99.98%	100.00%	99.71%	81.68%	100.00%	93.58%	99.83%
Hainan	94.81%	89.91%	81.90%	79.53%	77.07%	76.60%	69.55%	65.44%	63.13%	55.10%
Shanxi	9.03%	6.33%	4.37%	4.11%	3.91%	3.09%	1.63%	1.21%	1.20%	0.48%
Inner Mongolia	26.84%	11.33%	14.87%	8.99%	7.19%	5.57%	1.97%	1.54%	1.10%	0.80%
Anhui	52.10%	48.95%	45.06%	36.19%	31.73%	31.48%	25.71%	23.01%	15.57%	12.75%
Jiangxi	67.82%	64.64%	64.15%	62.35%	60.79%	56.32%	48.30%	46.77%	37.02%	32.76%
Henan	27.75%	22.14%	16.33%	14.12%	13.94%	12.28%	7.68%	9.84%	7.84%	6.90%
Hubei	46.49%	40.79%	36.52%	36.59%	33.82%	29.21%	20.50%	20.25%	24.01%	21.62%
Hunan	52.49%	49.77%	43.55%	43.60%	42.34%	43.35%	34.03%	35.20%	32.40%	32.23%
Liaoning	20.07%	16.91%	12.73%	10.47%	9.99%	8.30%	5.58%	4.74%	4.06%	3.44%
Jilin	49.93%	47.59%	47.12%	39.72%	38.81%	35.61%	26.56%	26.07%	22.97%	20.23%
Heilongjiang	42.85%	39.66%	36.28%	31.45%	29.56%	27.53%	21.79%	18.77%	17.24%	14.21%
Guangxi	74.61%	72.30%	70.42%	68.81%	64.65%	57.92%	43.31%	36.74%	31.88%	28.80%
Chongqing	68.51%	65.52%	66.04%	63.04%	60.38%	59.92%	51.32%	51.81%	56.41%	48.64%
Sichuan	54.01%	49.66%	44.94%	40.42%	35.18%	38.37%	37.20%	35.37%	28.41%	24.10%
Guizhou	44.63%	38.45%	35.77%	32.34%	27.85%	28.18%	21.81%	17.29%	12.79%	11.74%
Yunnan	48.40%	43.82%	42.76%	39.14%	34.97%	34.04%	30.04%	27.09%	23.29%	24.87%
Shaanxi	48.37%	39.38%	36.30%	30.08%	26.31%	20.63%	14.84%	9.97%	6.34%	4.57%
Gansu	54.10%	50.91%	48.02%	44.69%	44.08%	40.68%	31.60%	28.46%	22.57%	19.32%
Qinghai	84.71%	81.81%	81.45%	78.17%	76.54%	77.75%	71.56%	64.00%	56.02%	53.72%
Ningxia	64.15%	60.66%	59.27%	53.17%	48.34%	43.00%	29.61%	24.87%	18.66%	15.36%
Xinjiang	50.49%	44.48%	41.75%	34.91%	27.44%	23.65%	15.35%	10.26%	5.43%	3.27%

,

Table A2. Estimated average environmental efficiency levels in the Chinese regions, 2005–2014. Directional output vector $45°$.

	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Region	Environmental Efficiency Scores
Beijing	81.59%	83.08%	88.26%	86.99%	88.13%	95.25%	99.86%	97.99%	100.00%	91.89%
Tianjin	62.72%	60.69%	61.85%	62.00%	60.04%	53.87%	47.37%	46.99%	40.20%	39.48%
Hebei	12.61%	10.16%	6.50%	4.97%	3.98%	3.16%	1.39%	1.25%	0.80%	0.90%
Shanghai	61.74%	64.95%	70.34%	65.05%	67.78%	66.57%	60.40%	61.39%	48.43%	54.22%
Jiangsu	41.14%	38.06%	32.42%	33.10%	35.31%	31.67%	17.30%	18.34%	13.49%	14.77%
Zhejiang	59.82%	53.89%	48.09%	45.96%	45.13%	45.82%	37.09%	41.07%	33.75%	33.05%
Fujian	81.77%	79.16%	79.54%	77.87%	67.89%	68.08%	55.10%	57.57%	55.06%	40.51%
Shandong	14.69%	10.11%	5.93%	4.34%	4.29%	3.04%	1.88%	1.52%	1.31%	0.85%
Guangdong	100.00%	100.00%	100.00%	99.98%	100.00%	99.76%	80.76%	100.00%	93.28%	99.99%
Hainan	94.62%	89.53%	81.15%	78.78%	76.30%	75.80%	68.66%	64.57%	62.40%	54.39%
Shanxi	7.46%	5.12%	3.56%	3.39%	3.23%	2.52%	1.31%	0.96%	0.98%	0.37%
Inner Mongolia	24.45%	9.66%	13.21%	7.80%	6.16%	4.72%	1.60%	1.24%	0.89%	0.65%
Anhui	49.90%	46.78%	43.02%	34.23%	29.83%	29.61%	24.08%	21.49%	14.43%	11.77%
Jiangxi	66.27%	63.04%	62.61%	60.90%	59.34%	54.77%	46.78%	45.32%	35.73%	31.59%
Henan	25.14%	19.78%	14.53%	12.54%	12.39%	10.86%	6.69%	8.72%	6.96%	6.12%
Hubei	44.10%	38.42%	34.38%	34.61%	31.88%	27.32%	18.93%	18.75%	22.65%	20.37%
Hunan	50.25%	47.57%	41.45%	41.66%	40.44%	41.47%	32.30%	33.54%	30.97%	30.90%
Liaoning	17.69%	14.79%	11.14%	9.13%	8.69%	7.17%	4.76%	4.03%	3.48%	2.95%
Jilin	47.78%	45.48%	45.15%	37.83%	36.98%	33.79%	24.96%	24.56%	21.73%	19.14%
Heilongjiang	40.42%	37.31%	34.15%	29.49%	27.66%	25.69%	20.22%	17.35%	16.05%	13.19%
Guangxi	73.36%	71.00%	69.10%	67.55%	63.31%	56.39%	41.72%	35.21%	30.58%	27.63%
Chongqing	67.02%	63.99%	64.57%	61.62%	58.94%	58.46%	49.85%	50.44%	55.34%	47.57%
Sichuan	51.77%	47.41%	42.84%	38.42%	33.20%	36.42%	35.43%	33.67%	26.96%	22.77%
Guizhou	42.46%	36.31%	33.76%	30.51%	26.12%	26.47%	20.37%	16.03%	11.85%	10.92%
Yunnan	46.21%	41.66%	40.75%	37.26%	33.15%	32.24%	28.45%	25.61%	22.08%	23.75%
Shaanxi	46.18%	37.14%	34.23%	28.20%	24.52%	18.97%	13.53%	8.94%	5.65%	4.04%
Gansu	52.18%	49.01%	46.14%	42.94%	42.41%	38.98%	30.07%	27.05%	21.44%	18.36%
Qinghai	84.14%	81.15%	80.71%	77.40%	75.79%	77.02%	70.77%	63.15%	55.22%	53.04%
Ningxia	62.71%	59.19%	57.74%	51.65%	46.83%	41.41%	28.16%	23.56%	17.66%	14.54%
Xinjiang	48.42%	42.40%	39.77%	33.06%	25.69%	21.98%	14.07%	9.25%	4.83%	2.86%

and

Table A3. Estimated average environmental efficiency levels in the Chinese regions, 2005–2014. Directional output vector $90°$.

	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Region	Environmental Efficiency Scores
Beijing	80.39%	82.04%	87.58%	86.35%	87.58%	95.02%	99.86%	97.92%	100.00%	91.73%
Tianjin	60.81%	58.85%	60.13%	60.54%	58.62%	52.28%	45.96%	45.72%	39.21%	38.64%
Hebei	10.02%	8.02%	5.22%	4.01%	3.17%	2.49%	1.08%	0.98%	0.64%	0.74%
Shanghai	59.09%	62.65%	68.63%	63.36%	66.25%	65.03%	58.95%	60.09%	47.25%	53.26%
Jiangsu	36.99%	34.16%	29.48%	30.45%	32.64%	29.12%	15.47%	16.51%	12.16%	13.43%
Zhejiang	56.76%	50.79%	45.44%	43.58%	42.81%	43.57%	35.13%	39.24%	32.29%	31.71%
Fujian	80.52%	77.85%	78.36%	76.77%	66.46%	66.65%	53.60%	56.24%	54.00%	39.45%
Shandong	11.48%	7.65%	4.61%	3.37%	3.33%	2.32%	1.44%	1.15%	1.03%	0.65%
Guangdong	100.00%	100.00%	100.00%	100.00%	100.00%	99.76%	79.67%	100.00%	92.95%	100.00%
Hainan	94.45%	89.22%	80.42%	78.12%	75.66%	75.12%	67.99%	63.97%	61.99%	54.05%
Shanxi	5.77%	3.89%	2.77%	2.72%	2.61%	2.02%	1.05%	0.77%	0.83%	0.31%
Inner Mongolia	21.74%	7.89%	11.47%	6.65%	5.20%	3.93%	1.28%	0.99%	0.74%	0.54%
Anhui	47.25%	44.26%	40.70%	32.18%	27.90%	27.69%	22.55%	20.14%	13.53%	11.05%
Jiangxi	64.49%	61.28%	60.91%	59.40%	57.91%	53.22%	45.39%	44.08%	34.77%	30.79%
Henan	21.78%	16.88%	12.49%	10.87%	10.76%	9.39%	5.74%	7.66%	6.22%	5.49%
Hubei	41.13%	35.60%	31.93%	32.48%	29.84%	25.35%	17.45%	17.38%	21.53%	19.42%
Hunan	47.45%	44.92%	39.04%	39.57%	38.42%	39.48%	30.62%	31.99%	29.79%	29.86%
Liaoning	14.74%	12.27%	9.38%	7.73%	7.37%	6.02%	4.01%	3.39%	3.02%	2.56%
Jilin	45.33%	43.18%	43.00%	35.91%	35.18%	31.98%	23.53%	23.28%	20.81%	18.40%
Heilongjiang	37.46%	34.55%	31.76%	27.44%	25.74%	23.82%	18.77%	16.09%	15.12%	12.46%
Guangxi	71.93%	69.57%	67.61%	66.23%	61.97%	54.87%	40.27%	33.89%	29.60%	26.82%
Chongqing	65.36%	62.34%	62.98%	60.18%	57.54%	57.02%	48.52%	49.27%	54.53%	46.84%
Sichuan	48.90%	44.63%	40.38%	36.25%	31.10%	34.34%	33.67%	32.03%	25.72%	21.71%
Guizhou	40.21%	34.16%	31.69%	28.77%	24.55%	24.91%	19.17%	15.07%	11.22%	10.43%
Yunnan	43.75%	39.31%	38.57%	35.39%	31.39%	30.50%	27.04%	24.37%	21.19%	23.02%
Shaanxi	43.71%	34.72%	32.00%	26.30%	22.78%	17.37%	12.37%	8.08%	5.14%	3.68%
Gansu	50.19%	47.12%	44.20%	41.28%	40.90%	37.43%	28.80%	25.98%	20.71%	17.80%
Qinghai	83.68%	80.64%	80.02%	76.77%	75.22%	76.45%	70.21%	62.61%	54.80%	52.75%
Ningxia	61.46%	57.95%	56.29%	50.35%	45.62%	40.10%	27.07%	22.69%	17.09%	14.14%
Xinjiang	46.21%	40.25%	37.68%	31.27%	24.08%	20.43%	12.99%	8.47%	4.42%	2.61%

of the Appendix A, we report the environmental efficiency scores for the same years and directional output distance vectors by thirty Chinese regions.

Environmental efficiency of the Chinese regions appears to have been deteriorating between 2005 and 2014 irrespectively of what directional output vector we use in order to compute these scores. While not attempting to explain this decline, we will instead explore the factors contributing to environmental inefficiency in the Chinese regions.

4.2. Non-Spatial Estimation Results and the Analysis of Fixed Effects

In specification Equation (5), spatial and time-period fixed effects are accounted for by the terms ${\mu }_i$ and ${\eta }_t$, respectively. We employ the likelihood ratio tests to determine which type of fixed effects are present in the data. We found that the null hypothesis of joint insignificance of the spatial fixed effects can be rejected at a 0.01% significance level with the test statistic of 572.62 and twenty-nine degrees of freedom. However, the test statistic of 6.61 is statistically insignificant, with nine degrees of freedom for the null hypothesis of the joint insignificance of the time-period fixed effects. Finally, for a model with two-way fixed effects, i.e., the one that includes both spatial and time-period fixed effects, the test statistic of 22.37 with nine degrees of freedom is statistically significant at a 0.01% level for the comparison between a two-way fixed effects model, and the one that includes only spatial fixed effects. Similarly, the test statistic of 588.38 is statistically significant at a 0.01% level with twenty-nine degrees of freedom for a comparison between the two-way fixed effects model against the one with the time-period fixed effects only. We conclude that both space- and time-specific fixed effects are present in our data with the two-way fixed effects specification outperforming the ones containing only space- or time-period specific fixed effects in case of the non-spatial estimation.

We report estimation results for the non-spatial specifications in

Table 4. Estimation results of non-spatial panel model specifications.

	Fixed Effects
	None	Spatial	Time-Period	Spatial and Time-Period
COALRATE	−2.121 (−5.902) ***	−1.556 (−3.231) ***	−2.128 (−5.842) ***	−1.764 (−3.662) ***
HEAVY	−2.548 (−4.825) ***	−0.321 (−0.764)	−2.760 (−5.064) ***	−0.586 (−1.390)
TERT	4.370 (6.006) ***	−1.325 (−1.496)	4.401 (5.974) ***	−0.738 (−0.746)
GDPC	−1.287 (−11.033) ***	−1.136 (−16.074) ***	−1.191 (−8.738) ***	−0.923 (−5.344) ***
GDPC2	0.107 (6.383) ***	0.097 (9.118) ***	0.103 (5.849) ***	0.088 (5.998) ***
FKSH	1.932 (2.654) ***	0.373 (0.765)	1.887 (2.531) **	−0.038 (−0.076)
FEXPINT	−1.312 (−4.065) ***	0.801 (3.349) ***	−1.359 (−4.140) ***	0.905 (3.670) ***
TROPEN	10.244 (6.512) ***	3.077 (1.273)	8.680 (4.850) ***	5.139 (2.031) **
ENVINVSH	−41.897 (−1.709) *	−32.452 (−2.441) **	−28.749 (−1.118)	−17.249 (−1.212)
CONST	1.327 (1.516)	1.423 (2.026) **	1.388 (1.546)	1.603 (2.246) **
Adjusted R2	0.560	0.928	0.582	0.930
No. Obs.	300	300	300	300
LM Spatial Lag	22.877 ***	24.94 ***	21.277 ***	18.566 ***
Robust LM Spatial Lag	18.373 ***	1.862	16.411 ***	1.108
LM Spatial Error	7.020 ***	25.053 ***	7.557 ***	17.557 ***
Robust LM Spatial Error	2.515	1.975	2.692	0.098

Note: t-statistic in parentheses. *** stands for a 1%, ** for 5%, and * for a 10% statistical significance levels.

below corresponding to the benchmark model Equation (4), and a 45-degree directional output distance vector used to measure the dependent variable, i.e., logged environmental efficiency. In the lower part of Table 4, we report the results of Lagrange multiplier tests for the presence of spatial lag and error effects in the data.

While the Lagrange multiplier test confirms the presence of both spatial lag and spatial error in all four non-spatial specifications, its robust version suggests the absence of spatial errors in the data, while the spatial lag is confirmed in the specification with time fixed effects, and the one with no fixed effects at all. We conclude that the presence of either spatial lag or spatial error can be excluded on statistical grounds, and the usage of spatial panel model specifications is justified.

4.3. Spatial Panel Model Specification Tests

In order to select one of the spatial panel model specifications contained in Equation (5), we follow [26] to perform a series of the likelihood-ratio tests. Since the likelihood-ratio test can only be meaningfully conducted for the two nested specifications, one cannot apply this test in case two models contain the same set of the independent variables, e.g., the SLM and SEM.

Table 5. Log-likelihood ratio test results for the spatial panel model specification.

	Type of Fixed Effects
	Spatial	Time-Period	Spatial and Time-Period
Manski vs. SDM	169.309 ***	171.260 ***	172.733 ***
SDM vs. SLM	35.359 ***	108.181 ***	26.964 **
Manski vs. SDEM	169.009 ***	169.489 ***	170.118 ***
Manski vs. KP	97.525 ***	118.499 ***	70.491 ***
KP vs. SEM	203.44 ***	178.2 ***	170.02 ***

Note: The likelihood ratio test statistic follows a chi-squared distribution with k degrees of freedom where k is the number of restrictions in the restricted model. *** stands for a 0.1% significance level, ** denotes a 1% significance level. SDM, spatial Durbin model; SDEM, spatial Durbin error model; SLM, spatial lag model.

below details the spatial model specification tests for the three types of fixed effects.

The results of the likelihood ratio tests in Table 5 suggest that the comprehensive Manski model is outperforming all spatial alternatives, namely, the spatial Dubrin, spatial lag, Kelejian–Prucha, spatial error, and the spatial error Durbin models at a one percent significance level for all the three types of fixed effects.

4.4. Estimation Results of the Spatial Panel Models

In

Table 6. Estimation results of Manski and SDEM Models, $45°$ directional output vector.

	Spatial Panel Model
	Manski			SDEM
Fixed Effects	Spatial	Time-Period	Spatial and Time-Period	Spatial	Time-Period	Spatial and Time-Period
COALRATE	−1.564 (−3.363) ***	−1.867 (−4.515) ***	−1.869 (−3.979) ***	−1.507 (−3.423) ***	−1.964 (−5.526)	−1.661 (−3.755) ***
HEAVY	−0.600 (−1.581)	−4.374 (−7.845) ***	−0.636 (−1.691) *	−0.617 (−1.693) *	−4.350 (−7.772) ***	−0.688 (−1.861) *
TERT	−2.017 (−2.311) **	5.355 (7.083) ***	−2.617 (−2.477) **	−1.892 (−2.272) **	5.424 (7.316) ***	−2.271 (−2.227) **
GDPC	−1.204 (−9.248) ***	−1.112 (−8.376) ***	−0.971 (−5.798) ***	−1.199 (−9.023) ***	−1.129 (−8.734) ***	−1.021 (−6.310) ***
GDPC2	0.114 (8.987) ***	0.103 (6.302) ***	0.104 (7.426) ***	0.113 (8.818) ***	0.104 (6.307) ***	0.105 (7.522) ***
FKSH	0.064 (0.145)	1.440 (2.106) **	0.116 (0.261)	0.024 (0.055)	1.557 (2.416) **	−0.022 (−0.051)
FEXPINT	1.121 (5.068) ***	−0.521 (−1.757) *	1.079 (4.454) ***	1.096 (5.098) ***	−0.479 (−1.710) **	1.014 (4.414) ***
TROPEN	3.770 (1.548)	5.155 (2.683) ***	5.018 (2.069) **	3.957 (1.761) *	5.120 (2.640) ***	5.168 (2.226) **
ENVINVSH	−19.270 (−1.473)	−57.217 (−2.678) ***	−13.046 (−0.915)	−18.612 (−1.533)	−58.519 (−2.754) ***	−12.662 (−0.922)
W*COALRATE	−3.160 (−2.786) ***	−6.177 (−5.981) ***	−4.237 (−3.697) ***	−2.974 (−2.957) ***	−6.415 (−7.305) ***	−3.627 (−3.494) ***
W*HEAVY	0.987 (1.095)	−0.323 (−0.230)	0.529 (0.547)	1.025 (1.168)	−0.640 (−0.509)	0.642 (0.702)
W*TERT	−3.690 (−1.664) *	4.252 (2.294) **	−5.739 (−1.969) **	−3.197 (−1.581)	4.654 (2.913) ***	−4.336 (−1.567)
W*GDPC	0.031 (0.373)	0.057 (0.147)	0.541 (1.160)	0.126 (0.666)	−0.070 (−0.258)	0.753 (1.950) *
W*GDPC2	−0.015 (−0.387)	−0.025 (−0.569)	−0.026 (−0.609)	−0.027 (−1.057)	−0.013 (−0.338)	−0.062 (−1.773) *
W*FKSH	1.281 (1.277)	4.871 (3.694) ***	1.194 (1.134)	1.232 (1.242)	4.916 (3.682) ***	1.022 (0.990)
W*FEXPINT	0.553 (0.952)	3.435 (4.716) ***	0.852 (1.356)	0.417 (0.858)	3.399 (4.569) ***	0.448 (0.840)
W*TROPEN	−16.170 (−3.042) ***	−14.557 (−3.135) ***	−9.559 (−1.548)	−16.825 (−3.261) ***	−13.899 (−3.190) ***	−13.078 (−2.252) **
W*ENVINVSH	−44.595 (−1.208)	34.258 (0.522)	−23.858 (−0.571)	−44.246 (−1.306)	24.159 (0.385)	−25.935 (−0.646)
$\rho$	−0.068 (−0.245)	0.088 (0.948)	−0.251 (−1.205)	NA	NA	NA
$\lambda$	0.436 (2.029) **	0.201 (0.419)	0.570 (4.294) ***	0.372 (5.601) ***	0.269 (3.755) ***	0.364 (5.461) ***
Log-Likelihood	−366.2377	−612.386	−360.655	−450.742	−697.13	−445.714
No. Observations	300	300	300	300	300	300

Note: t-statistic in parentheses. *** stands for a 1%, ** for 5%, and * for a 10% statistical significance levels.

below we report the results of the Manski and SDEM specifications with space-, time-, and two-way fixed effects for a 45-degree directional output vector used to compute environmental efficiency scores. While the likelihood ratio tests indicate that the Manski specification outperforms the SDEM, the Wald test on the spatial lag parameter suggests that most spatial correlation in our data is revealed in the error terms, and in the explanatory variables. Therefore, we find it informative to include the results of estimating the SDEM as well.

According to our estimates, the more intensively coal used as a source of energy in a region (COALRATE) and in the neighboring regions (W*COALRATE), the less environmentally efficient the region in question is likely to be. The share of heavy industries also appears to be producing downward pressure on environmental efficiency.

The coefficient on the share of the tertiary sector TERT is estimated to be statistically significant and negative in the Manski and SDEM specifications with the spatial and two-way fixed effects, which at first seems surprising since, e.g., the service sector is not readily associated with environmental pollution. However, some studies [44] have argued that service sector businesses are affecting the environment through the infrastructure they require for their operations. The tourism industry, for instance, exploits hotel buildings that require heating which is often provided by local energy producers. In case these producers are polluting the environment, tourism industry becomes indirectly responsible for the increased $\mathrm{C}{\mathrm{O}}_2$ emissions. A study of the Spanish input-output tables by Reference [45] revealed that the indirect effects on the $\mathrm{C}{\mathrm{O}}_2$ emissions by the seemingly innocuous sectors, such as the wholesale and retail trade, real estate, or hotels and restaurants, far exceeds their direct contribution to the generation of harmful emissions. Similarly, in Reference [46] the authors found that commercial trade and hotel business sectors in Spain contribute to pollution by buying their inputs from “very polluting” sectors, e.g., producers of energy that heavily rely on coal. Since environmental regulations around the world, including the Chinese one, tend to be targeting the direct rather than the indirect sources of environmental pollution, it is not surprising to find a negative association between the economic importance of the tertiary sector and environmental efficiency scores.

Our results also strongly suggest the existence of a U-shaped relationship between the level of regional per-capita income, and the level of environmental efficiency since the coefficient on the square of regional per-capita GDP is estimated to be statistically significant and positive in all specifications in Table 6. This finding is in agreement with the idea of an environmental Kuznets curve. Namely, while the issues of environmental quality are of relatively little concern in the poorer regions, these issues grow in importance once a specific income level has been reached. Our empirical findings are, thus, confirming the environmental Kuznets curve hypothesis in the context of environmental efficiency.

The coefficient on FEXPINT, or the share of exports in total international trade by the foreign-funded enterprises in a particular region, is estimated to be positive and statistically significant in the Manski and SDEM specifications with space and two-way fixed effects, supporting the pollution halo, as opposed to the pollution haven, hypothesis. Indeed, if foreign-funded firms were exploiting lax environmental regulation in the Chinese regions to create an international comparative advantage by saving on the environmentally clean production technologies, a higher exports share of such firms would be associated with lower environmental efficiency scores. In addition, the coefficient on TROPEN measuring the extent to which international trade in the Chinese regions is important in comparison with the regional GDP, is also estimated to be positive in both Manski and SDEM for all the three types of fixed effects, being only statistically insignificant in the Manski specification with spatial fixed effects. We conclude that international trade by the foreign-funded enterprises in China is conducive to a higher level of environmental efficiency.

The coefficient on ENVINVSH, the share in the regional GDP of the region’s investment into the environmental improvement, is estimated to be statistically insignificant in all but two specifications. This finding probably reflects the fact that since 1973 when China held its first national conference on environmental protection, the emphasis of the government policies directed at cleaner environment has been on the wastewater treatment rather than on the CO₂ emissions [47]. The breakdown of the environmental investments in Reference [48] demonstrates that in the period between 2012 and 2017 about 60% of the total amount directed at protecting the environment were investments in the existing urban infrastructure whose most important component appears to be gardening and greening. Another 30% of the total environmental investments is accounted for by the “projects of environmental protection” of unspecified nature. We infer that the CO₂ emissions per se have not been among major targets of the Chinese government’s policy aimed at improving the environment, so it is not surprising that we do not find a statistically significant relationship between ENVINVSH and the environmental efficiency scores.

In general, the estimation results of both Manski and SDEM specifications with space and two-way fixed effects differ markedly from the coefficient estimates in Manski and SDEM specifications with time fixed effects. We observe at the same time that the values of the log-likelihood function for the latter specifications are significantly lower compared to the other two specifications. While the likelihood ratio test is not applicable to the comparison of the Manski specification with space and time fixed effects, the likelihood ratio test statistic of 503.463 for the comparison between Manski specification with two-way fixed effects, and the one with the time fixed effects is statistically significant at a 0.001% level. A similar conclusion obtains if we test SDEM with two-way fixed effects against SDEM with the time fixed effects. Therefore, we choose to base our inference on the estimation results of Manski specification with space and two-way fixed effects.

4.5. Robustness of Empirical Results with Respect to the Choice of Directional Output Vectors

To test the robustness of our findings with respect to the choice of a directional output distance vector, in

Table 7. Estimation results of Manski model, $0°$ and $90°$ directional output vectors.

	$\mathbf{Directional}\mathbf{Output}\mathbf{Vector}0°$		$\mathbf{Directional}\mathbf{Output}\mathbf{Vector}90°$
	Fixed Effects		Fixed Effects
	Spatial	Spatial and Time-Period	Spatial	Spatial and Time-Period
COALRATE	−1.501 (−3.341) ***	−1.818 (−4.006) ***	−1.599 (−3.401) ***	−1.872 (−3.939) ***
HEAVY	−0.577 (−1.569)	−0.607 (−1.672) *	−0.614 (−1.601)	−0.657 (−1.727) *
TERT	−1.940 (−2.299) **	−2.548 (−2.496) **	−1.974 (−2.236) **	−2.542 (−2.380) **
GDPC	−1.161 (−9.174) ***	−0.934 (−5.770) ***	−1.224 (−9.380) ***	−0.990 (−5.846) ***
GDPC2	0.110 (8.953) ***	0.100 (7.430) ***	0.115 (9.030) ***	0.105 (7.402) ***
FKSH	0.062 (0.145)	0.132 (0.309)	0.040 (0.089)	0.062 (0.138)
FEXPINT	1.078 (5.051) ***	1.045 (4.467) ***	1.150 (5.120) ***	1.089 (4.453) ***
TROPEN	3.685 (1.557)	4.829 (2.061) **	3.735 (1.524)	5.082 (2.072) **
ENVINVSH	−18.369 (−1.444)	−12.180 (−0.884)	−21.290 (−1.619)	−15.370 (−1.065)
W*COALRATE	−2.965 (−2.684) ***	−4.085 (−3.687) ***	−3.322 (−2.921) ***	−4.290 (−3.708) ***
W*HEAVY	0.969 (1.124)	0.509 (0.545)	0.982 (1.062)	0.540 (0.552)
W*TERT	−3.517 (−1.644)	−5.627 (−1.998) **	−3.726 (−1.658) *	−5.598 (−1.902) *
W*GDPC	0.058 (0.154)	0.527 (1.170)	−0.014 (−0.038)	0.550 (1.164)
W*GDPC2	−0.018 (−0.456)	−0.025 (−0.590)	−0.0111 (−0.290)	−0.029 (−0.669)
W*FKSH	1.225 (1.269)	1.181 (1.162)	1.285 (1.258)	1.133 (1.063)
W*FEXPINT	0.477 (0.845)	0.816 (1.343)	0.650 (1.112)	0.869 (1.371)
W*TROPEN	−15.862 (−3.124) ***	−9.187 (−1.541)	−16.042 (−2.934) ***	−9.847 (−1.577)
W*ENVINVSH	−42.954 (−1.200)	−21.745 (−0.539)	−46.819 (−1.254)	−28.024 (−0.663)
$\rho$	−0.035 (−0.119)	−0.246 (0.237)	−0.127 (0.258)	−0.269 (−1.292)
$\lambda$	0.414 (1.776) *	0.575 (4.365) ***	0.467 (2.461) **	0.562 (4.182) ***
Log-Likelihood	−355.546	−349.971	−370.549	−364.778
No. Observations	300	300	300	300

Note: t-statistic in parentheses. *** stands for a 1%, ** for 5%, and * for a 10% statistical significance levels.

and

Table 8. Estimation results of SDEM, $0°$ and $90°$ directional output vectors.

	$\mathbf{Directional}\mathbf{Output}\mathbf{Vector}0°$		$\mathbf{Directional}\mathbf{Output}\mathbf{Vector}90°$
	Fixed Effects		Fixed Effects
	Spatial	Spatial and Time-Period	Spatial	Spatial and Time-Period
COALRATE	−1.473 (−3.463) ***	−1.624 (−3.797) ***	−1.492 (−3.348) ***	−1.644 (−3.676) ***
HEAVY	−0.585 (−1.663) *	−0.655 (−1.836) *	−0.646 (−1.750) *	−0.716 (−1.917) *
TERT	−1.879 (−2.335) **	−2.221 (−2.252) **	−1.743 (−2.071) **	−2.166 (−2.106) **
GDPC	−1.159 (−9.066) ***	−0.981 (−6.276) ***	−1.216 (−8.953) ***	−1.045 (−6.392) ***
GDPC2	0.109 (8.867) ***	0.101 (7.521) ***	0.114 (8.719) ***	0.106 (7.522) ***
FKSH	0.042 (0.101)	0.001 (0.002)	−0.034 (−0.079)	−0.086 (−0.195)
FEXPINT	1.065 (5.127) ***	0.985 (4.432) ***	1.103 (5.069) ***	1.021 (4.402) ***
TROPEN	3.781 (1.742) *	4.960 (2.210) **	4.076 (1.796) *	5.280 (2.254) **
ENVINVSH	−18.038 (−1.538)	−11.865 (−0.894)	−20.044 (−1.633)	−14.772 (−1.067)
W*COALRATE	−2.872 (−2.951) ***	−3.513 (−3.497) ***	−2.974 (−2.938) ***	−3.619 (−3.465) ***
W*HEAVY	0.986 (1.160)	0.618 (0.698)	1.060 (1.202)	0.655 (0.711)
W*TERT	−3.273 (−1.669) *	−4.311 (−1.609)	−2.825 (−1.393)	−4.059 (−1.458)
W*GDPC	0.105 (0.573)	0.724 (1.936) *	0.165 (0.857)	0.783 (2.017) **
W*GDPC2	−0.024 (−0.956)	−0.059 (−1.723) *	−0.033 (−1.282)	−0.068 (−1.922) *
W*FKSH	1.198 (1.250)	1.016 (1.019)	1.207 (1.204)	0.950 (0.911)
W*EXPINT	0.410 (0.870)	0.434 (0.839)	0.394 (0.807)	0.436 (0.815)
W*TROPEN	−16.176 (−3.237) ***	−12.511 (−2.227) **	−17.300 (−3.337) ***	−13.657 (−2.334) **
W*ENVINVSH	−42.795 (−1.305)	−23.725 (−0.611)	−45.812 (−1.343)	−29.744 (−0.735)
$\lambda$	0.381 (5.784) ***	0.375 (5.670) ***	0.348 (5.141) ***	0.336 (4.930) ***
Log-Likelihood	−440.046	−435.0247	−455.068	−449.8664
No. Observations	300	300	300	300

Note: t-statistic in parentheses. *** stands for a 1%, ** for 5%, and * for a 10% statistical significance levels.

we present estimation results of the Manski and SDEM specifications, respectively, reported in Table 6 for the $0°$ and $90°$ directional output vectors. The coefficient estimates reported in Table 7 and Table 8 largely confirm the conclusions we derived by examining the results in Table 6. We obtain similar findings for the other values of the directional output vector, namely, for vectors $0°,1°,\dots ,89°,$ and $90°$ (results not reported here, but available from the authors immediately upon request). We conclude that our empirical findings are robust with respect to the direction along which the distance to the production possibilities frontiers is measured.

5. Discussion

Our estimates of environmental efficiency scores and their determinants imply that there is a large scope of government policy that could be used to decrease the level of harmful emissions without necessarily sacrificing good output. Simultaneously, several policy measures can help improve environmental efficiency. First, and most obviously, coal should be substituted with the more environmentally-friendly sources of energy. Second, economic restructuring away from the heavy industry and towards the tertiary sector should be initiated. Third, given the environmental danger posed by the developed tertiary sector (inducing demand for energy, that may not be produced in the environmentally efficient way), industrial restructuring should proceed with due regard for the indirect effect produced on the environment by the seemingly innocuous sectors, e.g., hotel sector. In other words, while the tertiary sector may look innocuous in terms of its ability to damage the environment, the indirect effects it is producing on the pollution generation through, e.g., purchases of energy from heavy polluters should be seriously addressed when formulating policies of environmental protection. To that end, more research needs to be done in the area of input-output analysis in order to duly account for such indirect effects.

One limitation of our research is that environmental efficiency is understood in the sense of technical efficiency alone, i.e., in terms of the potential ability to increase the amount of good output while decreasing the level of the bad output without changing the input mix. Analyzing allocative efficiency in this context appears to be highly desirable as it would expand the scope of the available policy options by exploiting the possibility of substituting for the pollution-intensive inputs with the ones whose usage is not associated with harm to the environment. Another caveat in our research is that we implicitly assume that the production of both good and bad outputs is statistically independent, while it makes sense talking about joint production of the two outputs in the sense of Reference [49], in which case the estimation framework has to be modified to account for the possible statistical dependence between the two outputs.

Finally, given the strong evidence that supports the pollution halo hypothesis, encouraging the creation of foreign-funded enterprises and providing for their smooth functioning is a policy measure that would contribute to a higher level of environmental efficiency.

6. Conclusions

In this study, we conducted a spatial panel econometric analysis of the determinants of environmental efficiency scores in thirty Chinese provinces for the period between 2005 and 2014. Differently from similar studies, we measured environmental efficiency scores with respect to the theoretically consistent parametric production possibilities frontier estimates, according to the iterative methodology of Reference [4].

Our data exhibit strong spatial autocorrelation patterns, warranting the use of spatial panel econometric models. The estimated environmental efficiency scores in the Chinese regions are found to be following a downward trend. In terms of the determinants of environmental efficiency, we found that, expectedly, a higher share of coal in the energy consumption mix and a higher share of heavy industry in the regional industrial structure reduce environmental efficiency. We also identified a variant of the environmental Kuznets curve, and discovered a U-shaped relationship between the environmental efficiency scores and the regional GDP per capita levels. Our estimates strongly support the pollution halo hypothesis, rather than haven hypothesis, since we found that both the export intensity of the foreign-funded enterprises and the contribution of their international trade to the regional GDP are associated with higher scores of environmental efficiency.

We did not find strong evidence to support a statistically significant relationship between the investments aimed at environmental improvement, and environmental efficiency scores. More surprisingly, we found that a higher share of the tertiary sector in a region’s economy tends to be associated with lower levels of environmental efficiency. We interpret the latter finding to be indicative of a serious problem that appears to be frequently overlooked—namely, the problem of a seemingly non-polluting sector contributing to pollution by inducing demand for energy from the polluting sectors of the economy.