Application of Lateral Transshipment in Cost Reduction of Decentralized Systems
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Basic Model Settings
- First, each store determines the replenishment level. and before realization of demand.
- Second, the local demands are realized respectively, with the realization of and , without loss of generality, say Store has excess stock, while Store runs out of stock, i.e., and .
- Third, Store requests transshipment from Store .
- Fourth, surplus Store determines the transshipment quantity to be shipped to Store before the observation of potential demand from unmet customers.
- Fifth, unsatisfied customers of Store switch to Store .
- Sixth, both stores collect revenue.
- ;
- ;
- ;
3.2. Optimal Transshipment Quantity
- (1)
- If, then.
- (2)
- Otherwise, there are two thresholds:andsuch that, and. The optimal transshipment quantity is determined based howcompares to the two thresholds. Specifically, (2a) if, we have; (2b); and (2c) if.
3.3. Optimal Replenishment Quantity
4. Results and Discussion
4.1. Benchmarks
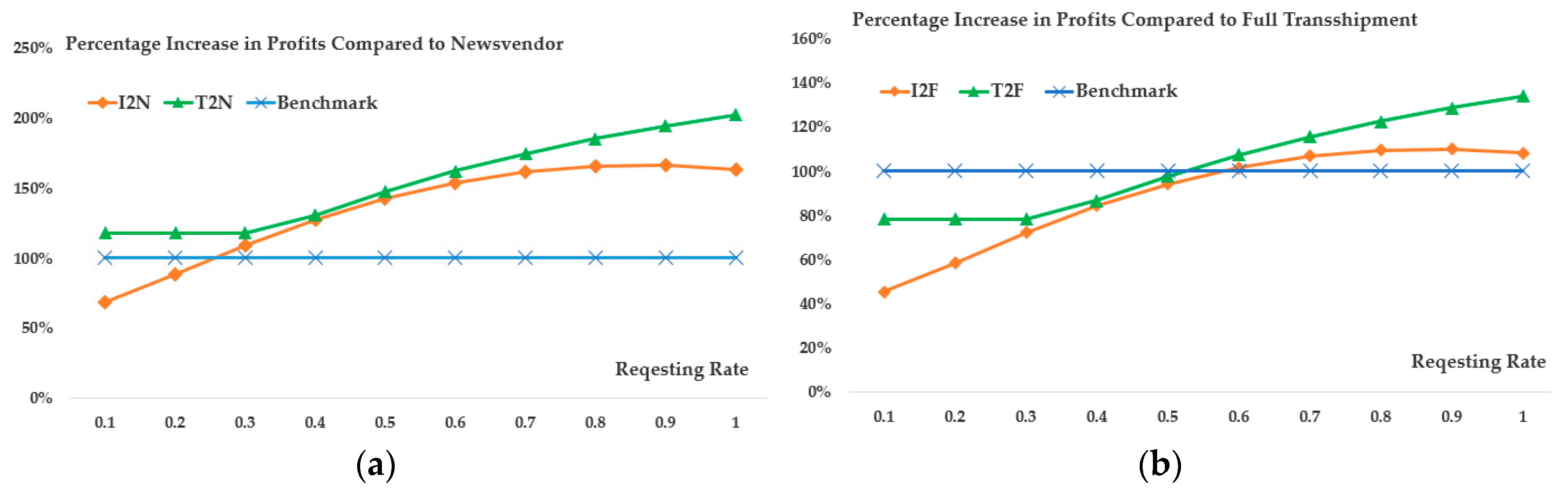
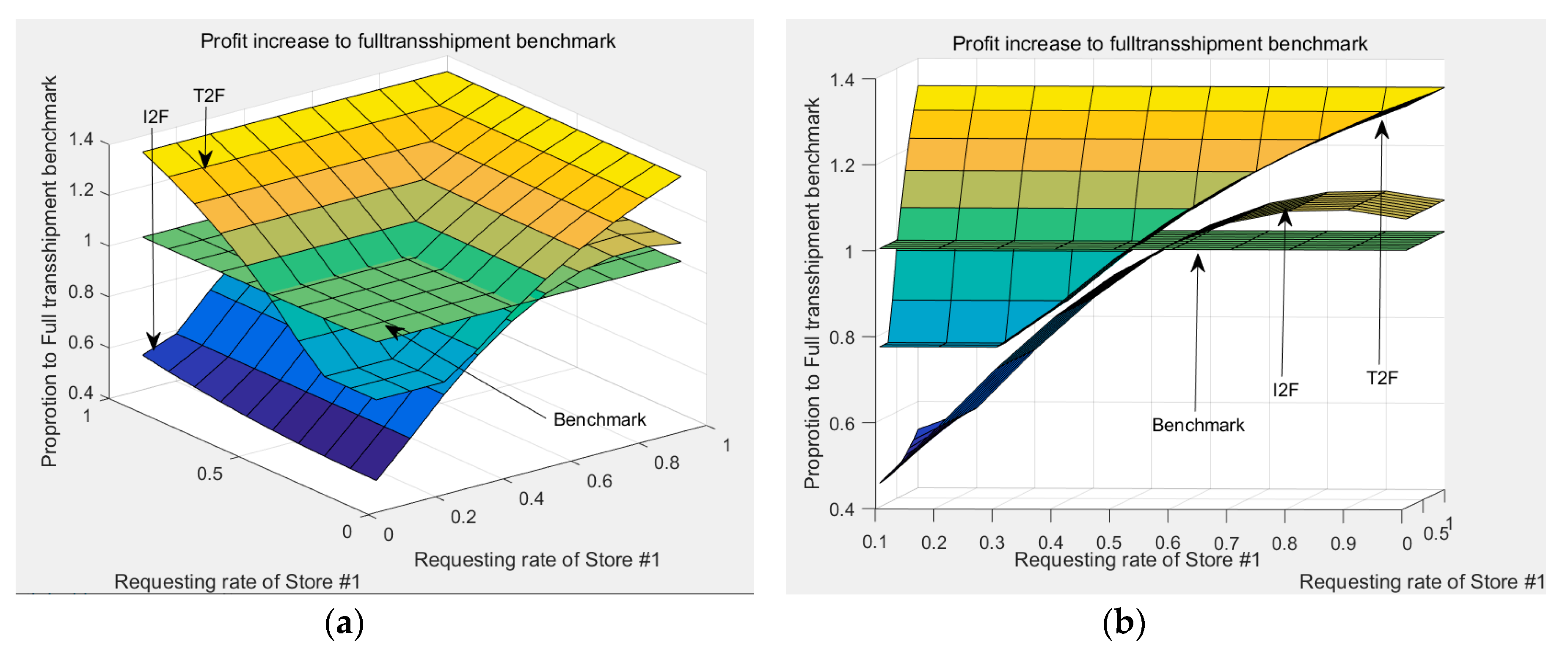
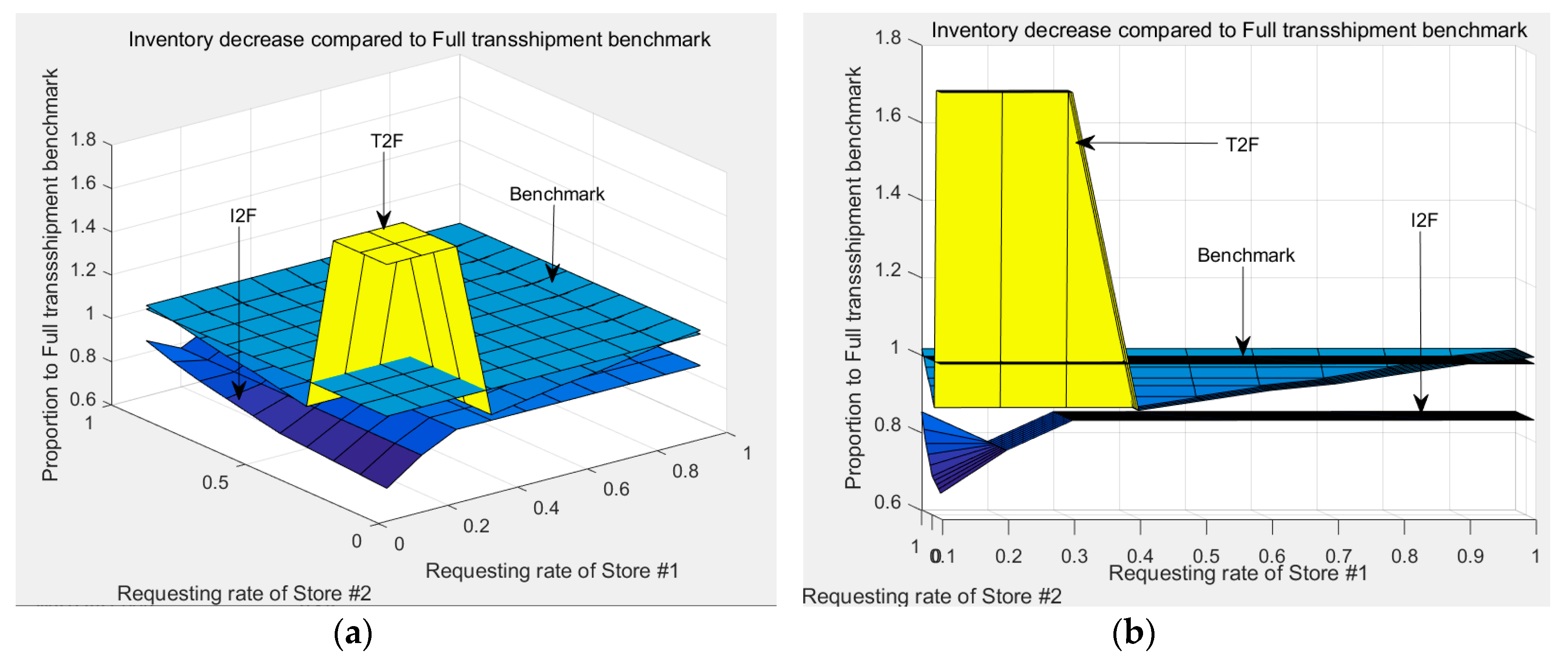
4.2. Impact of Request Rate
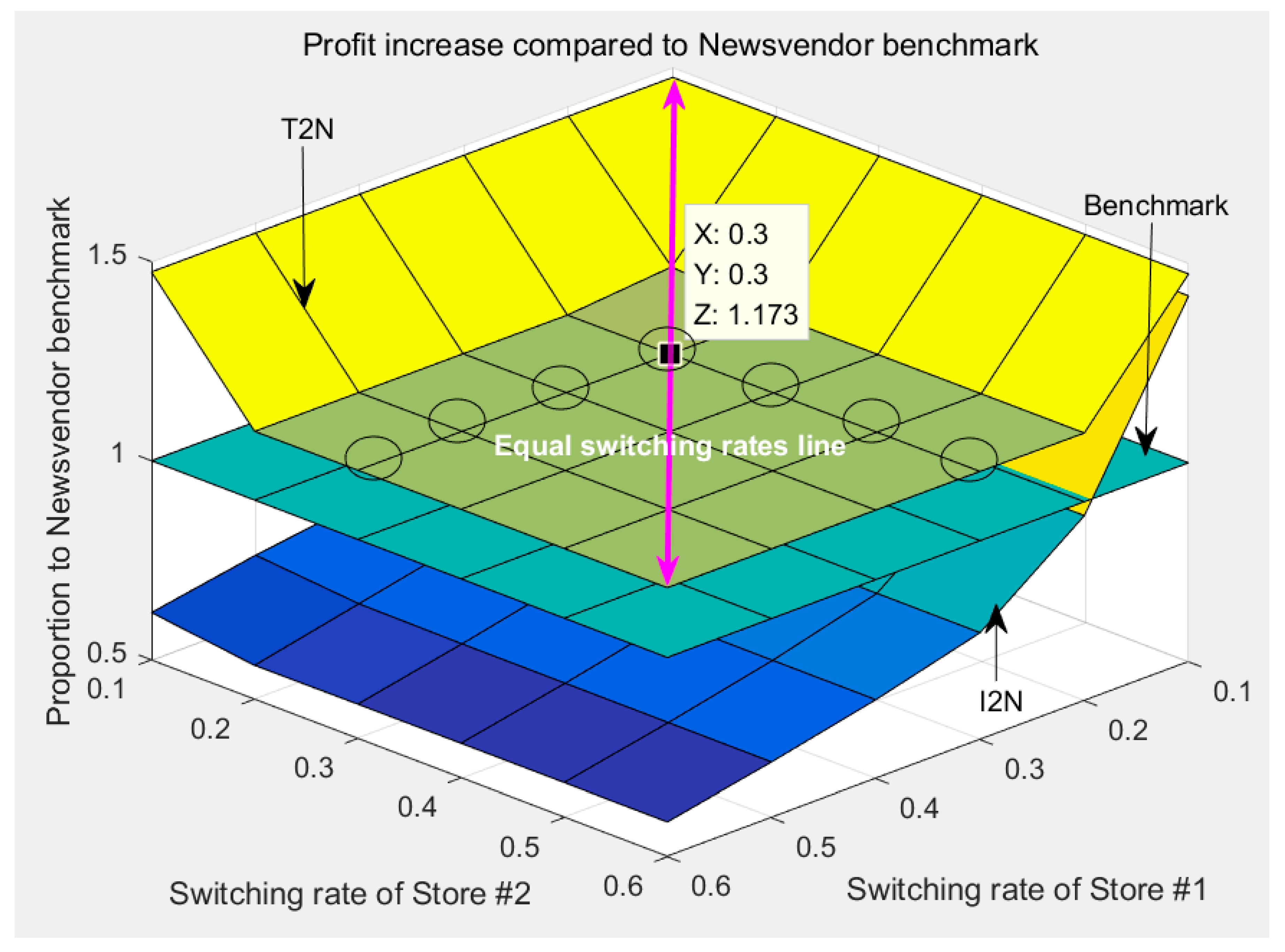
4.3. Impact of Random Switching Rate
4.4. Managerial Insights
5. Conclusions
5.1. Concluding Remarks
5.2. Theoretical Contributions
5.3. Research Limitations and Future Directions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- If , for any , we have ,
- If , denote and decreases in , we have and . Therefore, a unique optimal and . Specifically, (i) if , then ; (ii) if , then .
References
- Galanakis, C.M. The Food Systems in the Era of the Coronavirus (COVID-19) Pandemic Crisis. Foods 2020, 9, 523. [Google Scholar] [CrossRef] [PubMed]
- Martin, W.; Glauber, J.B. Trade policy and food security. In COVID-19 and Trade Policy: Why Turning Inward Won’t Work, 1st ed.; Richard, E.B., Simon, J.E., Eds.; Centre for Economic Policy Research: 33 Great Sutton Street, London, UK, 2020; pp. 89–101. [Google Scholar]
- Heiland, I.; Ulltveit-Moe, K.H. An Unintended Crisis in Sea Transportation due to COVID-19 Restrictions. In COVID-19 and Trade Policy: Why Turning Inward Won’t Work, 1st ed.; Richard, E.B., Simon, J.E., Eds.; Centre for Economic Policy Research: 33 Great Sutton Street, London, UK, 2020; pp. 151–163. [Google Scholar]
- Sanchez-Caballero, S.; Selles, M.A. An Efficient COVID-19 Prediction Model Validated with the Cases of China, Italy, and Spain: Total or Partial Lockdowns? J. Clin. Med. 2020, 9, 1547. [Google Scholar] [CrossRef] [PubMed]
- Pirouz, B.; Haghshenas, S.S.; Haghshenas, S.S.; Piro, P. Investigating a serious challenge in the sustainable development process: Analysis of confirmed cases of COVID-19 (new type of Coronavirus) through a binary classification using artificial intelligence and regression analysis. Sustainability 2020, 12, 2427. [Google Scholar] [CrossRef] [Green Version]
- Clemente-Suárez, V.J.; Hormeño-Holgado, V.; Jiménez, M.; Benitez-Agudelo, J.C.; Navarro-Jiménez, E.; Perez-Palencia, N.; Maestre-Serrano, R.; Laborde-Cárdenas, C.C.; Tornero-Aguilera, J.F. Dynamics of Population Immunity Due to the Herd Effect in the COVID-19 Pandemic. Vaccines 2020, 8, 236. [Google Scholar]
- Kot, S. Sustainable supply chain management in small and medium enterprises. Sustainability 2018, 10, 1058. [Google Scholar] [CrossRef] [Green Version]
- Rezaee, Z. Supply chain management and business sustainability synergy: A theoretical and integrated perspective. Sustainability 2018, 10, 275. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Zhang, X.; Zhang, M.; Li, W. How to Coordinate Economic, Logistics and Ecological Environment? Evidences from 30 Provinces and Cities in China. Sustainability 2020, 12, 1058. [Google Scholar] [CrossRef] [Green Version]
- Bian, J.; Liao, Y.; Wang, Y.; Tao, F. Analysis of Firm CSR Strategies. Eur. J. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Koberg, E.; Longoni, A. A systematic review of sustainable supply chain management in global supply chains. J. Clean. Prod. 2019, 207, 1084–1098. [Google Scholar] [CrossRef]
- Yawar, S.; Seuring, S. Management of Social Issues in Supply Chains: A Literature Review Exploring Social Issues, Actions and Performance Outcomes. J. Bus. Ethics. 2017, 141, 621–643. [Google Scholar] [CrossRef]
- Kot, S.; Haque, A.U.; Kozlovski, E. Strategic SCM’s Mediating Effect on the Sustainable Operations: Multinational Perspective. Organizacija 2019, 52, 219–235. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liao, Y.; Shi, V.; Chen, X. Supplier encroachment strategy in the presence of retail strategic inventory: Centralization or decentralization? Omega. (forthcoming). [CrossRef]
- Cheng, W.; Appolloni, A.; D’Amato, A.; Zhu, Q. Green Public Procurement, missing concepts and future trends—A critical review. J. Clean. Prod. 2018, 176, 1084–1098. [Google Scholar] [CrossRef]
- Brammer, S.; Walker, H. Sustainable procurement in the public sector: An international comparative study. Int. J. Operations Prod. Manag. 2011, 31, 309–316. [Google Scholar] [CrossRef]
- Paterson, C.; Kiesmüller, G.; Teunter, R.; Glazebrook, K. Inventory models with lateral transshipments: A review. Eur. J. Oper. Res. 2010, 210, 125–136. [Google Scholar] [CrossRef] [Green Version]
- Huang, X. A Review on Policies and Supply Chain Relationships under Inventory Transshipment. Bull. Stat. Oper. Res. 2013, 29, 21–42. [Google Scholar]
- Rudi, N.; Kapur, S.; Pyke, D.F. A Two-Location Inventory Model with Transshipment and Local Decision Making. Manag. Sci. 2001, 47, 1668–1680. [Google Scholar] [CrossRef] [Green Version]
- Anupindi, R.; Bassok, Y.; Zemel, E. A General Framework for the Study of Decentralized Distribution Systems *. M&Som-Manuf. Serv. Op. 2001, 3, 349–368. [Google Scholar]
- Granot, D.; Sosic, G. A three-stage model for a decentralized distribution system of retailers. Oper. Res. 2003, 51, 771–784. [Google Scholar] [CrossRef]
- Sosic, G. Transshipment of inventories among retailers: Myopic vs. farsighted stability. Manag. Sci. 2006, 52, 1493–1508. [Google Scholar] [CrossRef] [Green Version]
- Rong, Y.; Lawrence, V.; Sun, Y. Inventory sharing under decentralized preventive transshipments. Nav. Res. Log. 2010, 57, 540–562. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, D.; Liang, L.; Dolgui, A. Lateral inventory transshipment problem in online-to-offline supply chain. Int. J. Prod. Res. 2016, 54, 1951–1963. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, H. Decentralized inventory sharing with asymmetric information. Oper. Res. 2011, 59, 1528–1538. [Google Scholar] [CrossRef]
- Krishnan, K.; Rao, V. Inventory control in N warehouses. J. Ind. Eng. 1965, 16, 212–215. [Google Scholar]
- Robinson, L.W. Optimal and Approximate Policies in Multiperiod, Multilocation Inventory Models with Transshipments. Oper. Res. 1990, 38, 278–295. [Google Scholar] [CrossRef]
- Herer, Y.; Rashit, A. Lateral stock transshipment in a two-location inventory system with fixed or joint replenishment costs. Nav. Res. Log. 1999, 46, 525–548. [Google Scholar] [CrossRef]
- Wee, K.; Dada, M. Optimal policies for transshipping inventory in a retail network. Manag. Sci. 2005, 51, 1519–1533. [Google Scholar] [CrossRef]
- Hu, X.; Duenyas, I.; Kapuscinski, R. Optimal joint inventory and transshipment under uncertain capacity. Oper. Res. 2008, 56, 881–897. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Ryan, J.; Deshpande, V. Optimal dynamic production and inventory transshipment policies for a two-location make-to-stock system. Oper. Res. 2008, 56, 400–410. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Hu, X.; Shen, W. Lateral transshipment with partial request and random switching. Omega 2019, 102134. [Google Scholar] [CrossRef]
- Lippman, P.; McCardle, K. The Competitive Newsboy. Oper. Res. 1997, 45, 54–56. [Google Scholar] [CrossRef]
- Anupindi, R.; Bassok, Y. Centralization of stocks: Retailers vs. Manufacturer. Manag. Sci. 1999, 45, 178–191. [Google Scholar] [CrossRef]
- Zhao, X.; Atkins, D. Transshipment between competing retailers. IIE Trans. 2009, 41, 665–676. [Google Scholar] [CrossRef]
- Jiang, L.; Anupindi, R. Customer-driven vs. retailer-driven search: Channel performance and implications. M&Som-Manuf. Serv. Op. 2010, 12, 102–119. [Google Scholar]
- Comez, N.; Stecke, K.; Cakanyildirim, M. In-season transshipments among competitive retailers. M&Som-Manuf. Serv. Op. 2012, 14, 290–300. [Google Scholar]
- Liao, Y.; Shen, W.; Hu, X.; Yang, S. Optimal responses to stockouts: Lateral transshipment versus emergency order policies. Omega 2014, 49, 79–92. [Google Scholar] [CrossRef]
- Corsten, D.; Gruen, T. Stock-outs cause walkouts. Harvard Bus. Rev. 2004, 82, 26–28. [Google Scholar]
- Hu, X.; Duenyas, I.; Kapuscinski, R. Existence of coordinating transshipment prices in a two-location inventory model. Manag. Sci. 2007, 53, 1289–1302. [Google Scholar] [CrossRef]











| Decision Variables | |
| replenishment inventory level at Store ; | |
| transshipment quantity from Store to Store ; | |
| Model Parameters | |
| unit procurement at Store ; | |
| unit revenue at Store in local markets; | |
| unit salvage value at Store ; | |
| unit transshipment cost from Store to Store ; | |
| unit revenue at Store for transshipment; | |
| request rate at Store ; | |
| local demand with a realization of , a cdf of and a pdf of | |
| switch rate at Store percentage of Store ’s ultimately unmet demand that is switched to Store with a realization of , a cdf of and a pdf of ; | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Li, J.; Hu, X.; Li, Y.; Shen, W. Application of Lateral Transshipment in Cost Reduction of Decentralized Systems. Sustainability 2020, 12, 5081. https://doi.org/10.3390/su12125081
Liao Y, Li J, Hu X, Li Y, Shen W. Application of Lateral Transshipment in Cost Reduction of Decentralized Systems. Sustainability. 2020; 12(12):5081. https://doi.org/10.3390/su12125081
Chicago/Turabian StyleLiao, Yi, Jun Li, Xinxin Hu, Ying Li, and Wenjing Shen. 2020. "Application of Lateral Transshipment in Cost Reduction of Decentralized Systems" Sustainability 12, no. 12: 5081. https://doi.org/10.3390/su12125081
APA StyleLiao, Y., Li, J., Hu, X., Li, Y., & Shen, W. (2020). Application of Lateral Transshipment in Cost Reduction of Decentralized Systems. Sustainability, 12(12), 5081. https://doi.org/10.3390/su12125081





