Cooperative Strategies in Two-Echelon Rescue Delivery Environment with Accessibility Uncertainty
Abstract
:1. Introduction
2. Literature Review
3. Problem Formulation
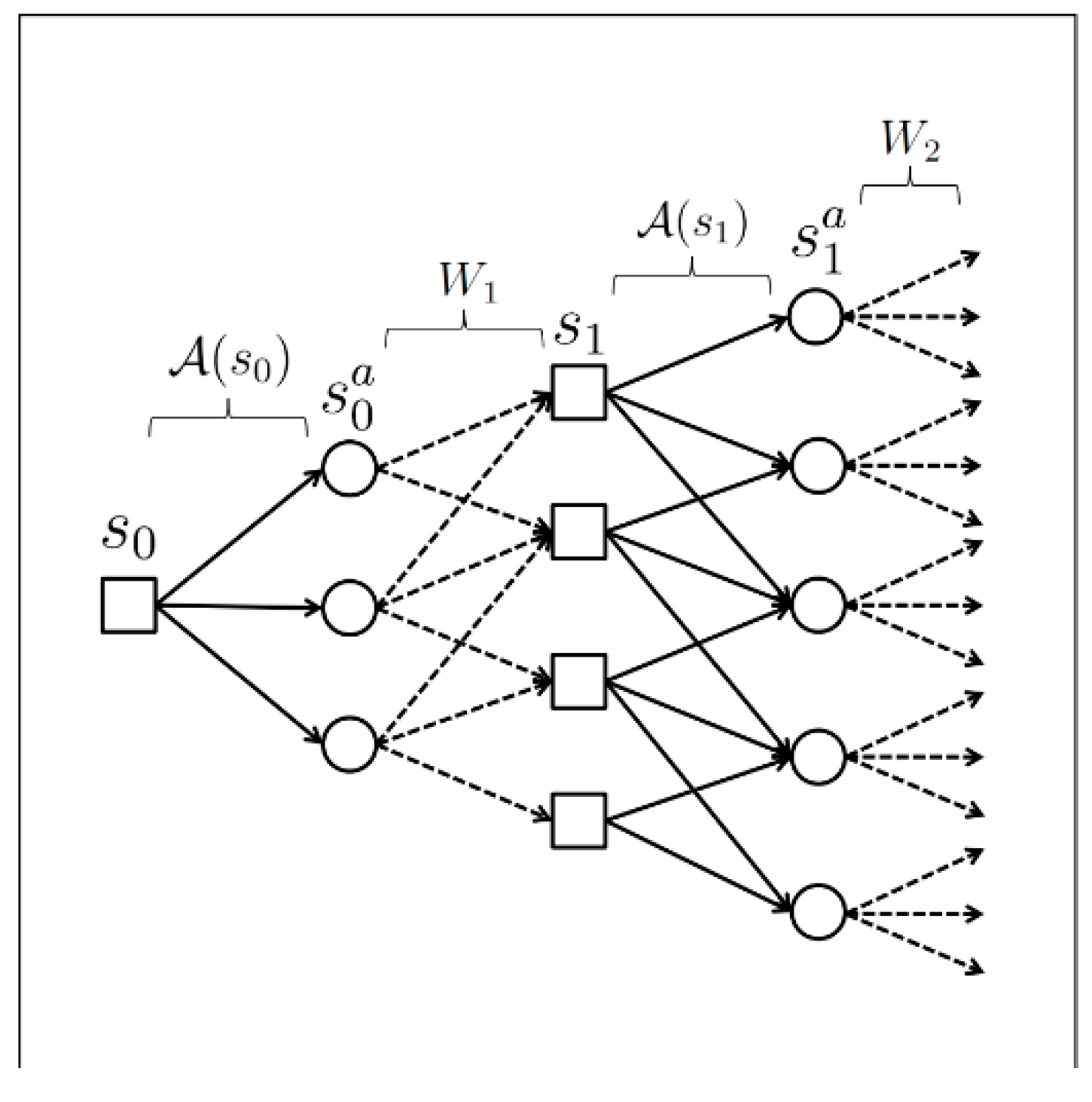
3.1. Basic Background
- There are LDCs and disaster victims in the isolated islands.
- Each LDC is only served by one rescue team’s vehicle.
- When the vehicle of any rescue team is on the way from one LDC to the next LDC, which is determined by a cooperative strategy, it is not allowed to take another new LDC as the next destination during transportation.
- The demand for each disaster victim is known and cannot be split between the vehicles of different LDCs.
- The demands of disaster victims cannot be delivered by direct shipping from the rescue team but must be consolidated in one of the LDC.
- Each disaster victim is served by one LDC vehicle.
- All LDC vehicles have the same capacity limitations.
- The amount delivered by each vehicle cannot exceed its capacity.
- Each LDC vehicle must begin and end at the same LDC.
- The rescue resources received by an LDC are completely delivered to the disaster victims.
- The overall capacity of all LDCs can fulfill the total demand.
- is the time in which interrupted road A is restored to its original status.
- is the time in which interrupted road B is restored to its original status.
- a binary variable of the first-level routing that equals 0 if LDC k is visited before LDC l.
- a binary variable of the second-level routing that equals 1 if a second-level vehicle starts from LDC k and goes from disaster victim i to disaster victim j.
- is a disaster victim set that is assigned to LDC k.
- is an LDC set that is assigned to the rescue team
- Rescue team.
- Set of local distribution centers; number of LDCs.
- Set of disaster victims; number of disaster victims.
- Relief time from interrupted road to victims through LDC k.
- Travel time from interrupted road to victims through LDC k.
- Travel time from interrupted road A to LDC l directly.
- Travel time from interrupted road B to LDC l directly.
- Travel time from interrupted road A to LDC k (through l).
- Travel time from interrupted road B to LDC k (through l).
- Travel time from LDC k to victims.
- Travel time from disaster victim i to disaster victim j by vehicle k.
- Travel time from LDC k to LDC l.
- Demands of disaster victim j.
- q Vehicle capacity.
- Maximum rescue resource delivery time.
- Rescue resource delivery time through LDC k.
- Stochastic restored time combination scenarios.
- Probability of time combination scenario .
- Expected maximum rescue resource delivery time.
- Travel time from rescue team to victims.
3.2. Research Question
4. Non-Cooperation, Cooperation Strategies and Method
4.1. Non-Cooperation Situation
4.2. Cooperation Strategies
4.3. Method for Anticipatory Cooperative Strategy
5. Test Set and Results
5.1. Test Set
- The demand quantity of each disaster victim is 1.
- The capacity of vehicles at the second level is 15.
5.2. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| No. | x | y | No. | x | y | No. | x | y |
|---|---|---|---|---|---|---|---|---|
| 1 | 22 | 22 | 26 | 41 | 46 | 51 | 29 | 39 |
| 2 | 36 | 26 | 27 | 55 | 34 | 52 | 54 | 38 |
| 3 | 21 | 45 | 28 | 35 | 16 | 53 | 55 | 57 |
| 4 | 45 | 35 | 29 | 52 | 26 | 54 | 67 | 41 |
| 5 | 55 | 20 | 30 | 43 | 26 | 55 | 10 | 70 |
| 6 | 33 | 34 | 31 | 31 | 76 | 56 | 6 | 25 |
| 7 | 50 | 50 | 32 | 22 | 53 | 57 | 65 | 27 |
| 8 | 55 | 45 | 33 | 26 | 29 | 58 | 40 | 60 |
| 9 | 26 | 59 | 34 | 50 | 40 | 59 | 70 | 64 |
| 10 | 40 | 66 | 35 | 55 | 50 | 60 | 64 | 4 |
| 11 | 55 | 65 | 36 | 54 | 10 | 61 | 36 | 6 |
| 12 | 35 | 51 | 37 | 60 | 15 | 62 | 30 | 20 |
| 13 | 62 | 35 | 38 | 47 | 66 | 63 | 20 | 30 |
| 14 | 62 | 57 | 39 | 30 | 60 | 64 | 15 | 5 |
| 15 | 62 | 24 | 40 | 30 | 50 | 65 | 50 | 70 |
| 16 | 21 | 36 | 41 | 12 | 17 | 66 | 57 | 72 |
| 17 | 33 | 44 | 42 | 15 | 14 | 67 | 45 | 42 |
| 18 | 9 | 56 | 43 | 16 | 19 | 68 | 38 | 33 |
| 19 | 62 | 48 | 44 | 21 | 48 | 69 | 50 | 4 |
| 20 | 66 | 14 | 45 | 50 | 30 | 70 | 66 | 8 |
| 21 | 44 | 13 | 46 | 51 | 42 | 71 | 59 | 5 |
| 22 | 26 | 13 | 47 | 50 | 15 | 72 | 35 | 60 |
| 23 | 11 | 28 | 48 | 48 | 21 | 73 | 27 | 24 |
| 24 | 7 | 43 | 49 | 12 | 38 | 74 | 40 | 20 |
| 25 | 17 | 64 | 50 | 15 | 56 | 75 | 40 | 37 |
Appendix D
| Instances | Rescue Teams | LDCs | Victims |
|---|---|---|---|
| instance1 | (0, 0) (50, 70) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Appendix C |
| instance2 | (0, 0) (50, 70) | Randomly within range (x: 0–50, y: 0–70); | Appendix C |
| instance3 | (−20, −20) (70, 90) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Randomly within range (x: 0–50, y: 0–60) |
| instance4 | (−10, −10) (60, 80) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Appendix C |
| instance5 | (−10, −10) (60, 80) | Randomly within range (x: 0–50, y: 0–70); | Appendix C |
| instance6 | (−10, −10) (60, 80) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Randomly within range (x: 0–50, y: 0–60) |
| instance7 | (−30, 30) (90, 30) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Appendix C |
| instance8 | (−30, 30) (90, 30) | (30, 40), (40, 20), (25, 50), (40, 40) and (78, 30) | Appendix C |
| instance9 | (−30, 30) (90, 30) | (20, 23), (60, 10), (18, 45), (45, 50) and (75, 40) | Randomly within range (x: 0–50, y: 0–60) |
References
- Zhu, L.; Rousseau, L.M.; Rei, W.; Li, B. Paired cooperative reoptimization strategy for the vehicle routing problem with stochastic demands. Comput. Oper. Res. 2014, 50, 1–13. [Google Scholar] [CrossRef]
- Gansterer, M.; Hartl, R.F. Collaborative vehicle routing: A survey. Eur. J. Oper. Res. 2018, 268, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Crainic, T.G.; Gajpal, Y.; Gendreau, M. Multi-Zone Multi-Trip Vehicle Routing Problem with Time Windows. Infor: Inf. Syst. Oper. Res. 2015, 53, 49–67. [Google Scholar] [CrossRef] [Green Version]
- Noyan, N.; Balcik, B.; Atakan, S. A Stochastic Optimization Model for Designing Last Mile Relief Networks. Transp. Sci. 2016, 50, 1092–1113. [Google Scholar] [CrossRef]
- Cruijssen, F.; Bräysy, O.; Dullaert, W.; Fleuren, H.; Salomon, M. Joint route planning under varying market conditions. Int. J. Phys. Distrib. Logist. Manag. 2007, 37, 287–304. [Google Scholar] [CrossRef] [Green Version]
- Cruijssen, F.; Cools, M.; Dullaert, W. Horizontal cooperation in logistics: Opportunities and impediments. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 129–142. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Bernabeu, E.; Juan, A.A.; Faulin, J.; Barrios, B.B. Horizontal cooperation in road transportation: A case illustrating savings in distances and greenhouse gas emissions. Int. Trans. Oper. Res. 2014, 22, 585–606. [Google Scholar] [CrossRef]
- Defryn, C.; Sörensen, K.; Cornelissens, T. The selective vehicle routing problem in a collaborative environment. Eur. J. Oper. Res. 2016, 250, 400–411. [Google Scholar] [CrossRef] [Green Version]
- Dudek, G.; Stadtler, H. Negotiation-based collaborative planning between supply chains partners. Eur. J. Oper. Res. 2007, 163, 668–687. [Google Scholar] [CrossRef]
- Vanovermeire, C.; Sörensen, K. Measuring and rewarding flexibility in collaborative distribution, including two-partner coalitions. Eur. J. Oper. Res. 2014, 239, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Zibaei, S.; Hafezalkotob, A.; Ghashami, S.S. Cooperative vehicle routing problem: An opportunity for cost saving. J. Ind. Eng. Int. 2016, 12, 271–286. [Google Scholar] [CrossRef] [Green Version]
- Speranza, M.G.; Fernàndez, E.; Roca-Riu, M. The Shared Customer Collaboration Vehicle Routing Problem. Eur. J. Oper. Res. 2018, 265, 1078–1093. [Google Scholar]
- Chinh, N.Q.; Kim, H.C.; Jiang, S.; Zhang, N.S. Collaborative vehicle routing problem for urban last-mile logistics. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 1531–1536. [Google Scholar]
- Sprenger, R.; Mönch, L. A methodology to solve large-scale cooperative transportation planning problems. Eur. J. Oper. Res. 2012, 223, 626–636. [Google Scholar] [CrossRef]
- Quintero-Araujo, C.L.; Gruler, A.; Juan, A.A. Quantifying Potential Benefits of Horizontal Cooperation in Urban Transportation Under Uncertainty: A Simheuristic Approach. Lect. Notes Comput. Sci. 2016, 9868, 280–289. [Google Scholar]
- Perboli, G.; Tadei, R.; Vigo, D. The two-echelon capacitated vehicle routing problem: Models and math-based heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Ma, X.; Xu, M.; Liu, Y.; Wang, Y. Two-echelon logistics distribution region partitioning problem based on a hybrid particle swarm optimization-genetic algorithm. Expert Syst. Appl. 2015, 42, 5019–5031. [Google Scholar]
- Hemmelmayr, V.C.; Cordeau, J.-F.-O.; Crainic, T.G. An adaptive large neighborhood search heuristic forTwo-EchelonVehicle Routing Problems arising in city logistics. Comput. Oper. Res. 2012, 39, 3215–3228. [Google Scholar] [CrossRef] [Green Version]
- Breunig, U.; Schmid, V.; Hartl, R.F.; Vidal, T. A large neighbourhood based heuristic for two-echelon routing problems. Comput. Oper. Res. 2016, 76, 208–225. [Google Scholar] [CrossRef] [Green Version]
- Grangier, P.; Gendreau, M.; Lehuédé, F.; Rousseau, L.M. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization. Eur. J. Oper. Res. 2016, 254, 80–91. [Google Scholar] [CrossRef]
- Wang, K.; Shao, Y.; Zhou, W. Matheuristic for a two-echelon capacitated vehicle routing problem with environmental considerations in city logistics service. Transp. Res. Part D Transp. Environ. 2017, 57, 262–276. [Google Scholar] [CrossRef]
- Liu, T.; Luo, Z.; Qin, H.; Lim, A. A branch-and-cut algorithm for the two-echelon capacitated vehicle routing problem with grouping constraints. Eur. J. Oper. Res. 2018, 266, 487–497. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; Bektaş, T. The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations. Int. J. Prod. Econ. 2015, 164, 366–378. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Lv, T.; Chang, X. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems. Transp. Res. Part B Methodol. 2016, 94, 169–188. [Google Scholar] [CrossRef]
- Belgin, O.; Karaoglan, I.; Altiparmak, F. Two-echelon vehicle routing problem with simultaneous pickup and delivery: Mathematical model and heuristic approach. Comput. Ind. Eng. 2018, 115, 1–16. [Google Scholar] [CrossRef]
- Cuda, R.; Guastaroba, G.; Speranza, M.G. A survey on two-echelon routing problems. Comput. Oper. Res. 2015, 55, 185–199. [Google Scholar] [CrossRef]
- Bian, J.; Liao, Y.; Wang, Y.Y.; Tao, F. Analysis of Firm CSR Strategies. Eur. J. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Li, J.; Yi, L.; Shi, V.; Chen, X. Supplier encroachment strategy in the presence of retail strategic inventory: Centralization or decentralization? Omega 2020, 102213. [Google Scholar] [CrossRef]
- Ritzinger, U.; Puchinger, J.; Hartl, R.F. A survey on dynamic and stochastic vehicle routing problems. Int. J. Prod. Res. 2016, 54, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Novoa, C.; Storer, R. An approximate dynamic programming approach for the vehicle routing problem with stochastic demands. Eur. J. Oper. Res. 2009, 196, 509–515. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Voß, S. Risk-Averse Anticipation for Dynamic Vehicle Routing. In International Conference on Learning and Intelligent Optimization; Springer: Cham, Switzerland, 2016; pp. 274–279. [Google Scholar]
- Ulmer, M.W.; Goodson, J.C.; Mattfeld, D.C.; Hennig, M. Offline-Online Approximate Dynamic Programming for Dynamic Vehicle Routing with Stochastic Requests. Transp. Sci. 2018, 53, 185–202. [Google Scholar] [CrossRef] [Green Version]
- Goodson, J.C.; Thomas, B.W.; Ohlmann, J.W. A Rollout Algorithm Framework for Heuristic Solutions to Finite-Horizon Stochastic Dynamic Programs. Eur. J. Oper. Res. 2017, 258, 216–229. [Google Scholar] [CrossRef]
- Arena, F.; Ticali, D. The development of autonomous driving vehicles in tomorrow’s smart cities mobility. AIP Conf. Proc. 2018, 2040, 140007. [Google Scholar]
- Arena, F.; Pau, G.; Mario Collotta, M. A survey on driverless vehicles: From their diffusion to security features. J. Internet Serv. Inf. Secur. 2018, 8, 1–19. [Google Scholar]

| Problem Type | Stochastic Variable | Non-Cooperative Scenarios | Cooperative Scenarios | Cooperative Mechanisms (Strategies) | Authors |
|---|---|---|---|---|---|
| PCVRP (Periodic Capacitated Vehicle Routing Problem) | The partner relaxes its constraints, such as delivery dates, order sizes, and order splitting rules, in a coalition. | Cooperative mechanisms based on how to share the gained benefits. Especially, persuading companies to relax their delivery terms by rewarding flexibility. | Vanovermeire (2014) | ||
| Multi-depot VRP | Each player minimizes the total transportation cost of all their vehicles. | The players cooperate using each other’s vehicles in order to minimize their transportation costs. | Cooperative mechanisms based on how to assign the coalition cost. Especially, allocation depends on the amount that each player adds to a coalition, and they receive a percentage of cost-saving. | Zibaei (2016) | |
| Selective VRP | Serving the customers of all partners in one single logistic operation to minimize compensation for non-delivery. | Cooperative mechanisms based on how to assign the coalition cost. Especially, partners that consistently set high compensation for non-delivery cost values for their customers should be penalized by being assigned a relatively large share of the total coalition cost. | Defryn, Sörensen, and Cornelissens (2016) | ||
| Shared customer CVRP | Consumers demand from every carrier only delivered by the carrier. | The demand for each shared customer can be delivered by more than one company. | Cooperative mechanisms based on how to reduce coalition costs compared with the scenario without collaboration. | Fernández (2018) | |
| Multi-VRP | Strategy 1: LSPs (logistics service providers) fully collaborate with each other. Strategy 2: an LSP’s vehicle can serve customers from other LSPs only after they finish serving their customers. | Chinh et al. (2017) | |||
| VRPSD (Vehicle Routing Problem with Split Deliveries) | demands | A single pair of vehicles cooperates to serve a set of customer demands. | PCR (paired cooperative reoptimization): multiple customers are dynamically assigned when each vehicle completes the current assignment, and trigger a sharing of information. PLC (paired locally coordinated): each pair of vehicles serve customers sequentially in opposite directions, following a fixed route, and if one vehicle fails, the remaining customers are assigned to its partner. | Zhu (2014) | |
| MDVRPSD (MDVRP with Stochastic Demands) | Vehicle breakdowns; traveling, loading, and unloading times | Each manufacturer distributes its own products with its own car | Each manufacturer’s products can be distributed through vehicles of other manufacturers or third-party logistics companies | Sprenger (2012) | |
| MDVRPSD (MDVRP with Stochastic Demands) | Stochastic demands | Each company plans the optimal routing plans. | Companies are involved in the cooperation agreement, which includes the sharing of storage areas and vehicle capacities. | Quintero-Araujo (2016) | |
| Two-echelon VRP | Accessibility | The vehicles of team 0 and team 1 work together to deliver supplies to LDCs, and the vehicles of LDCs work together to deliver supplies to victims. | This paper |
| Instances | Non-Cooperation (NC) | Reactive Cooperation Strategy (RCS) | Anticipatory Cooperation Strategy (ACS) | RCS/NC | RCS Saving (1-RCS/NC) | ACS/NC | ACS Saving (1-RCS/NC) | ACS/RCS |
|---|---|---|---|---|---|---|---|---|
| Instance 1 | 611.82 | 298.09 | 277.21 | 0.49 | 0.51 | 0.45 | 0.55 | 0.93 |
| Instance 2 | 892.78 | 279.02 | 258.06 | 0.31 | 0.69 | 0.29 | 0.71 | 0.92 |
| Instance 3 | 1010.82 | 354.81 | 312.93 | 0.35 | 0.65 | 0.31 | 0.69 | 0.88 |
| Instance 4 | 657.58 | 335.07 | 325.93 | 0.51 | 0.49 | 0.50 | 0.50 | 0.97 |
| Instance 5 | 822.61 | 338.57 | 327.73 | 0.41 | 0.59 | 0.40 | 0.60 | 0.97 |
| Instance 6 | 1135.63 | 361.51 | 342.78 | 0.32 | 0.68 | 0.30 | 0.70 | 0.95 |
| Instance 7 | 465.00 | 293.12 | 272.57 | 0.63 | 0.37 | 0.59 | 0.41 | 0.93 |
| Instance 8 | 505.19 | 283.66 | 256.06 | 0.56 | 0.44 | 0.51 | 0.49 | 0.90 |
| Instance 9 | 483.74 | 274.28 | 263.23 | 0.57 | 0.43 | 0.54 | 0.46 | 0.96 |
| Instance | Description | Non-Cooperation (NC) | Reactive Cooperation Strategy (RCS) | Anticipatory Cooperation Strategy (ACS) | RCS/NC | RCS Saving (1-RCS/NC) | ACS/NC | ACS Saving (1-RCS/NC) |
|---|---|---|---|---|---|---|---|---|
| 1 | [50, 50] | 561.97 | 250.36 | 236.72 | 0.45 | 0.55 | 0.42 | 0.58 |
| 2 | [100, 100] | 570.12 | 279.55 | 275.56 | 0.49 | 0.51 | 0.48 | 0.52 |
| 3 | [150, 150] | 636.04 | 298.09 | 286.99 | 0.47 | 0.53 | 0.45 | 0.55 |
| 4 | [250, 250] | 660.18 | 299.42 | 292.55 | 0.45 | 0.55 | 0.44 | 0.56 |
| 5 | [300, 300] | 682.33 | 328.67 | 319.98 | 0.48 | 0.52 | 0.47 | 0.53 |
| 6 | [350, 350] | 681.05 | 313.58 | 310.33 | 0.46 | 0.54 | 0.46 | 0.54 |
| 7 | [400, 400] | 735.98 | 353.52 | 320.40 | 0.43 | 0.57 | 0.42 | 0.58 |
| 8 | [450, 450] | 729.70 | 356.87 | 338.48 | 0.49 | 0.51 | 0.46 | 0.54 |
| 9 | [500, 500] | 739.77 | 372.38 | 344.70 | 0.50 | 0.5 | 0.47 | 0.53 |
| Average | 0.53 | 0.55 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wu, Y.; Liao, Y.; Gajpal, Y. Cooperative Strategies in Two-Echelon Rescue Delivery Environment with Accessibility Uncertainty. Sustainability 2020, 12, 5333. https://doi.org/10.3390/su12135333
Zhang H, Wu Y, Liao Y, Gajpal Y. Cooperative Strategies in Two-Echelon Rescue Delivery Environment with Accessibility Uncertainty. Sustainability. 2020; 12(13):5333. https://doi.org/10.3390/su12135333
Chicago/Turabian StyleZhang, Hanpeng, Yuxin Wu, Yi Liao, and Yuvraj Gajpal. 2020. "Cooperative Strategies in Two-Echelon Rescue Delivery Environment with Accessibility Uncertainty" Sustainability 12, no. 13: 5333. https://doi.org/10.3390/su12135333
APA StyleZhang, H., Wu, Y., Liao, Y., & Gajpal, Y. (2020). Cooperative Strategies in Two-Echelon Rescue Delivery Environment with Accessibility Uncertainty. Sustainability, 12(13), 5333. https://doi.org/10.3390/su12135333






