Emulating Rotational Inertia of Synchronous Machines by a New Control Technique in Grid-Interactive Converters
Abstract
:1. Introduction
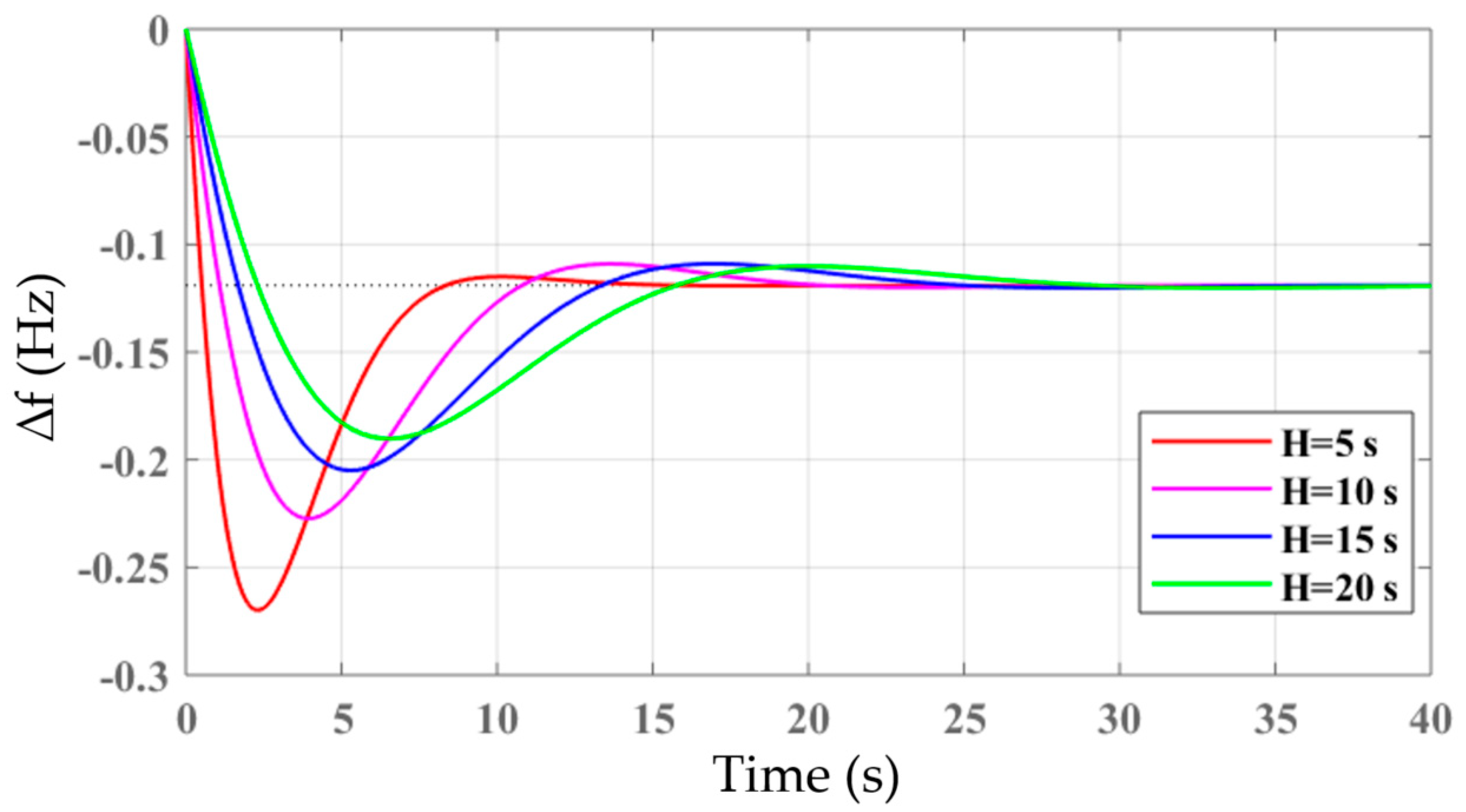
2. Inertial Response of Synchronous Machines
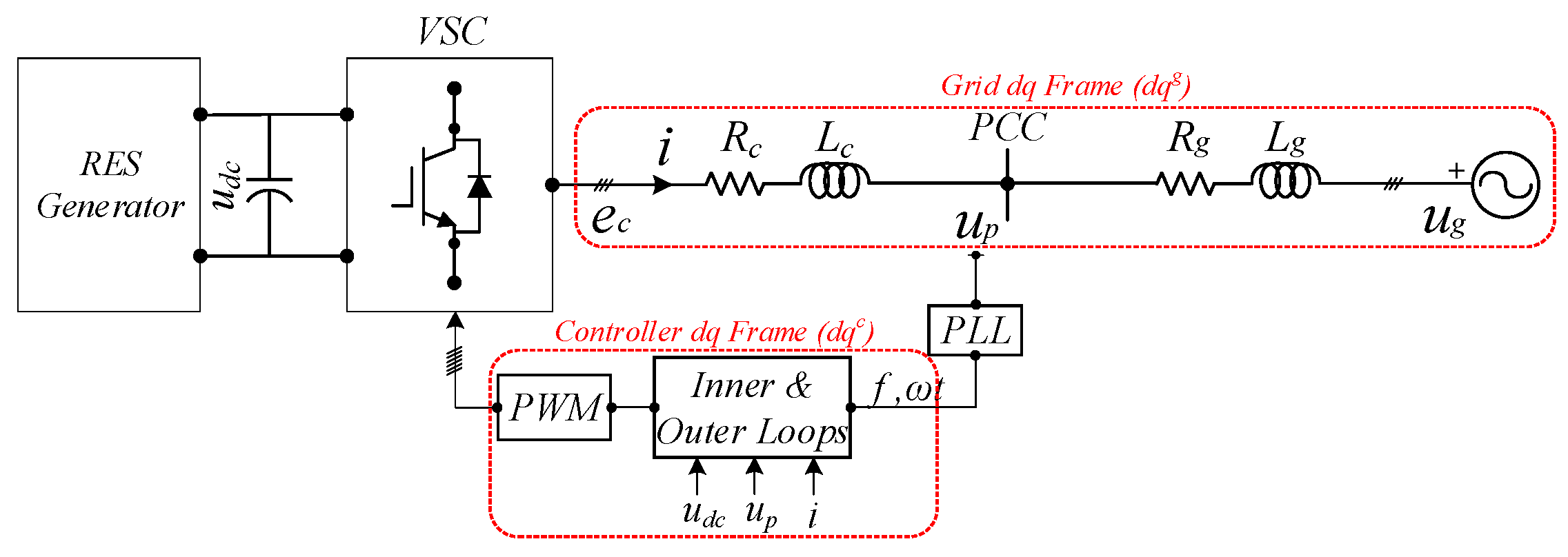
3. The Proposed Converter Control Scheme
3.1. Analysis of the Interfaced Converter Under Dynamic Operating Condition
3.2. Dynamic Analysis of the Phase-Locked Loop
3.3. Fast Grid Frequency Support
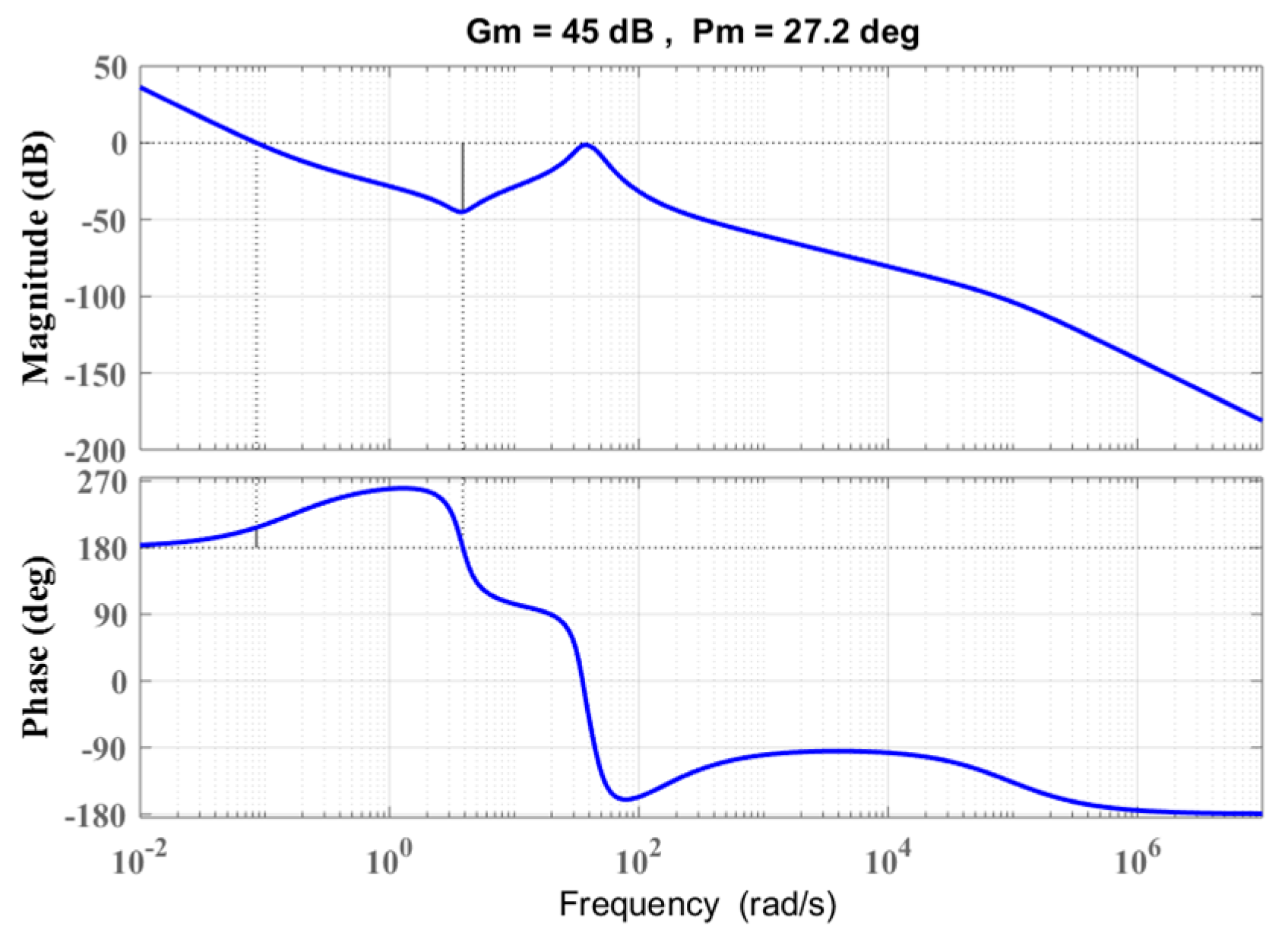
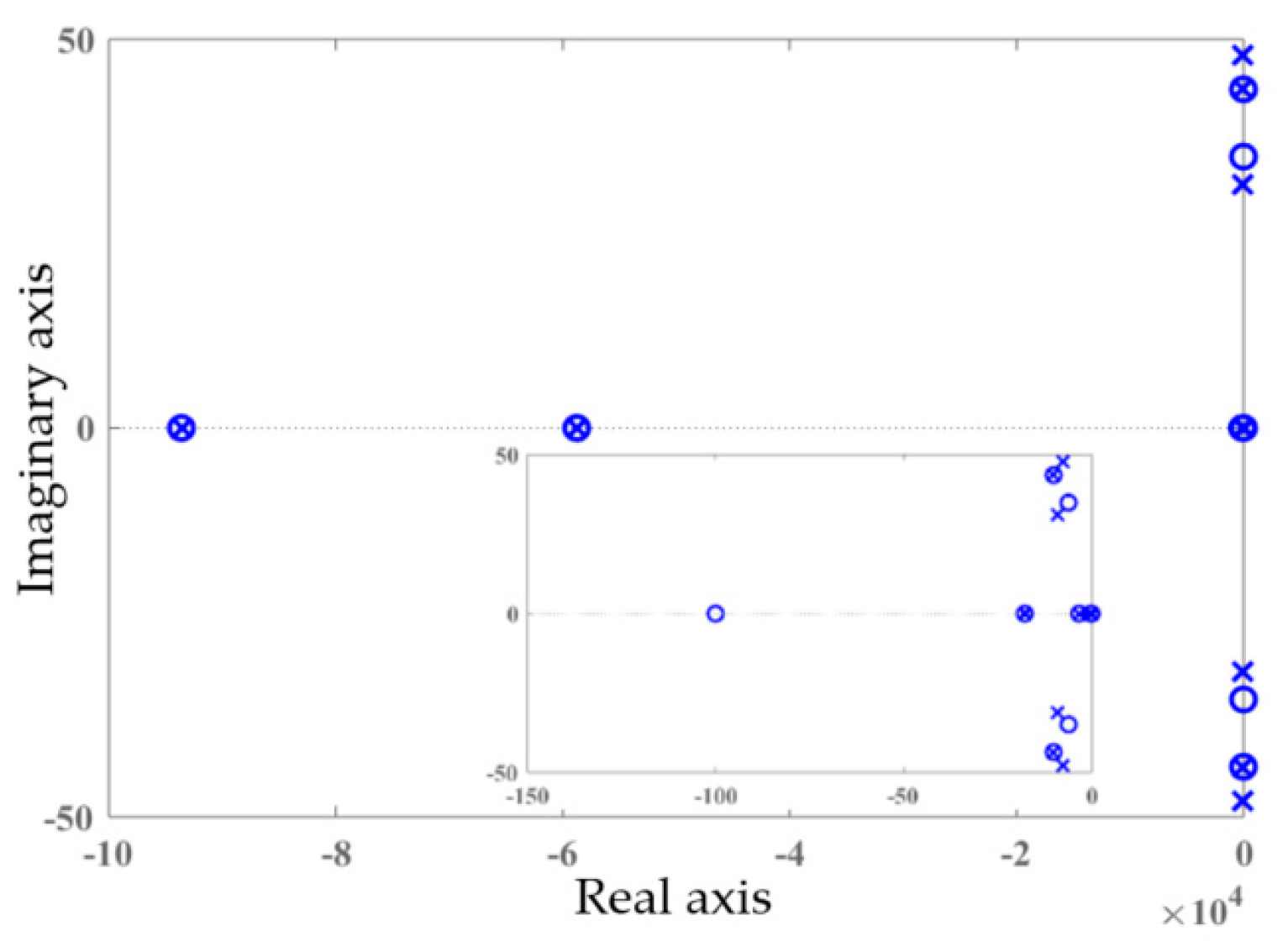
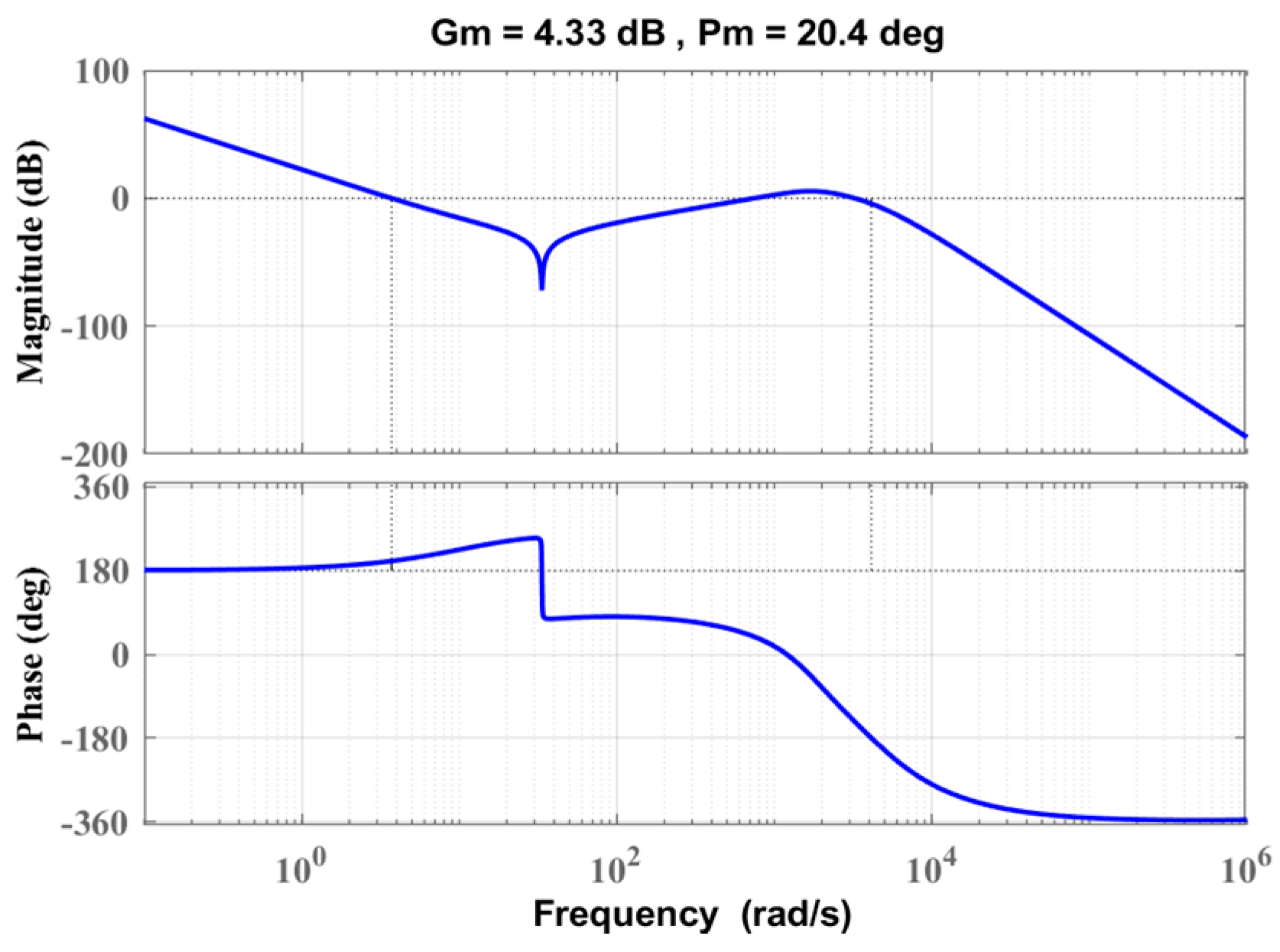
4. Dynamics Assessment of the Proposed Control Technique
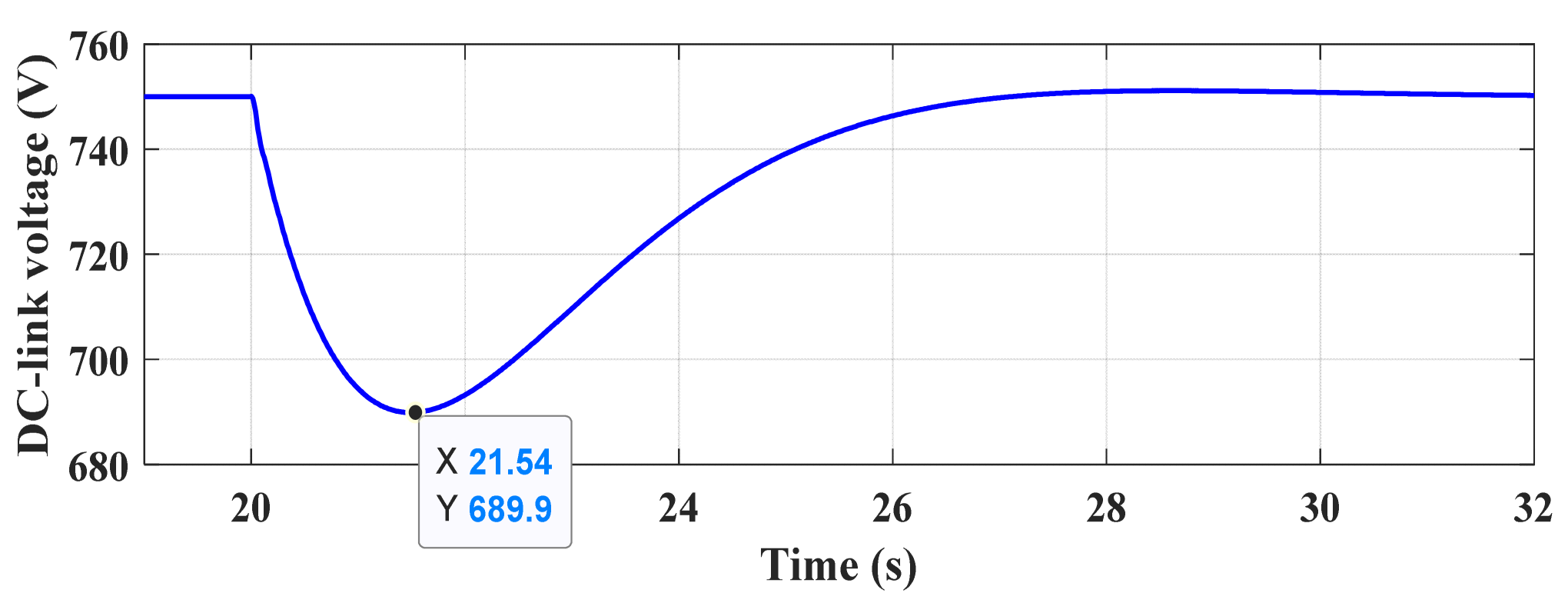
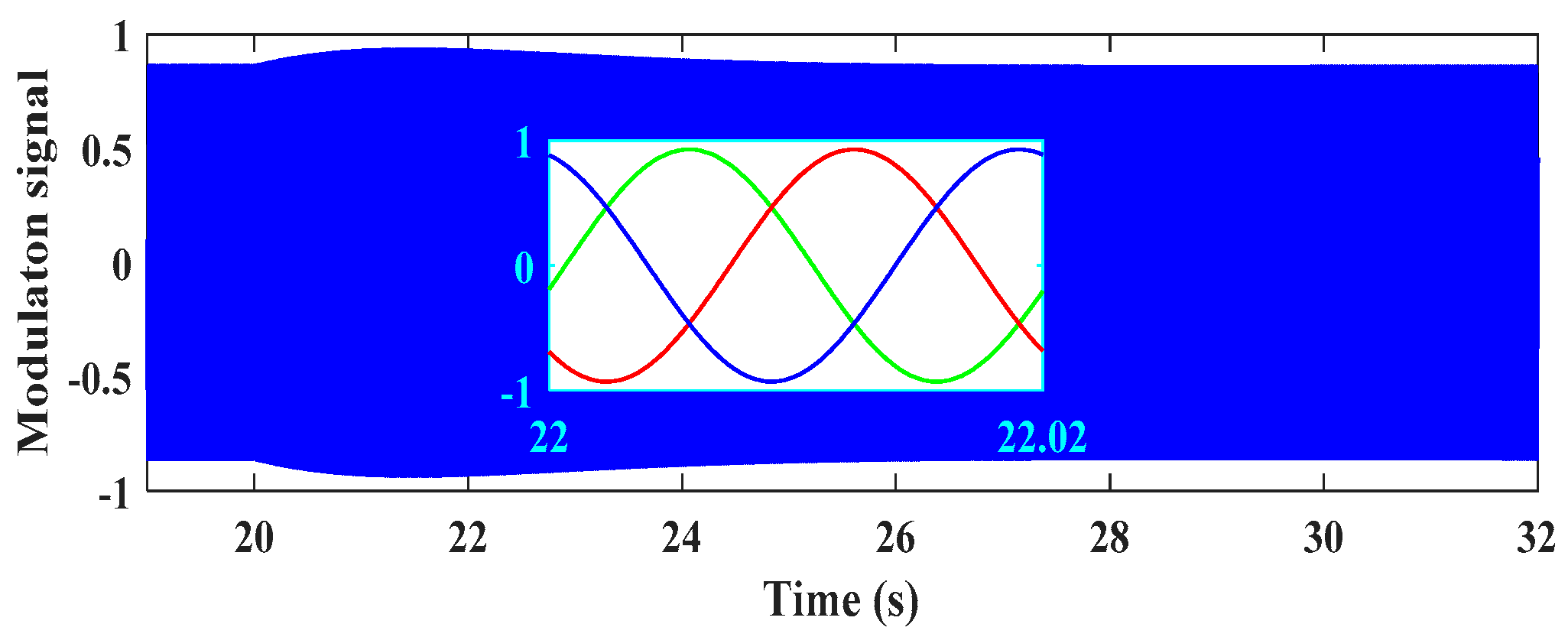
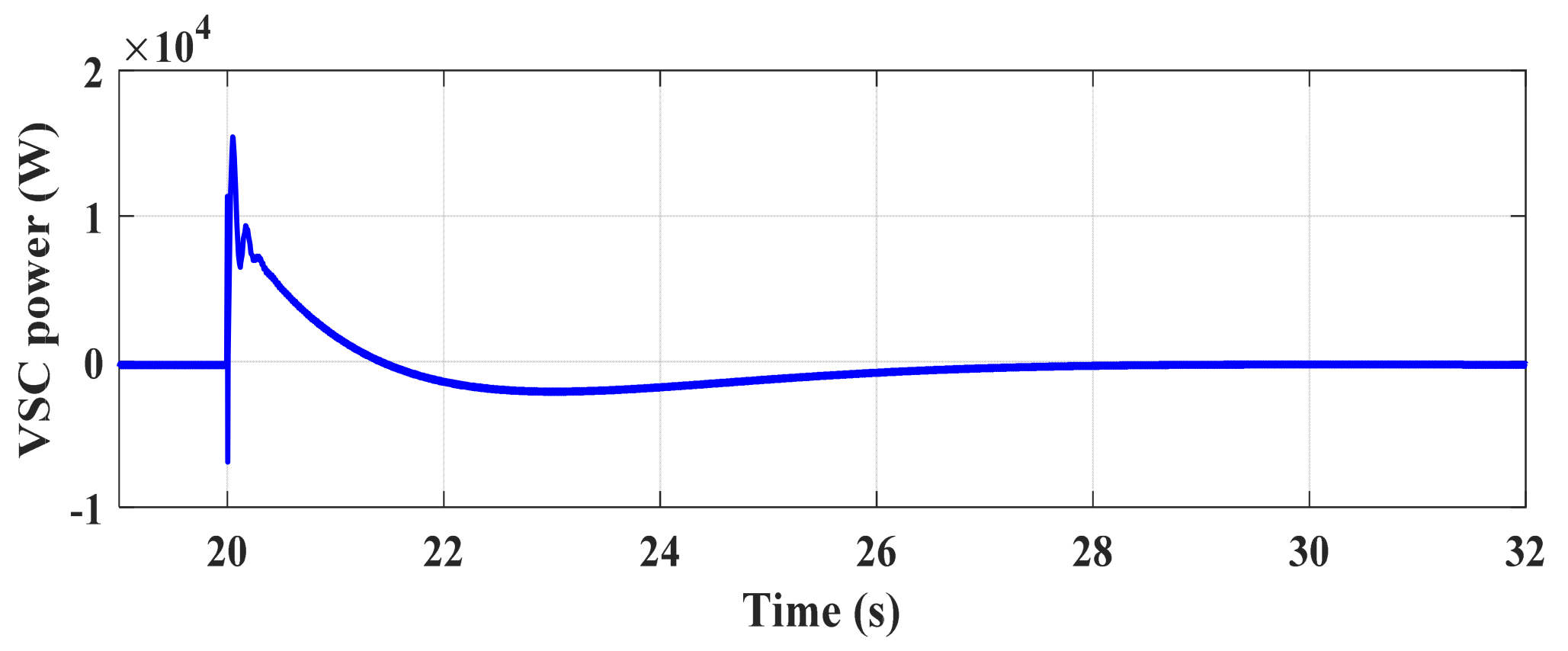
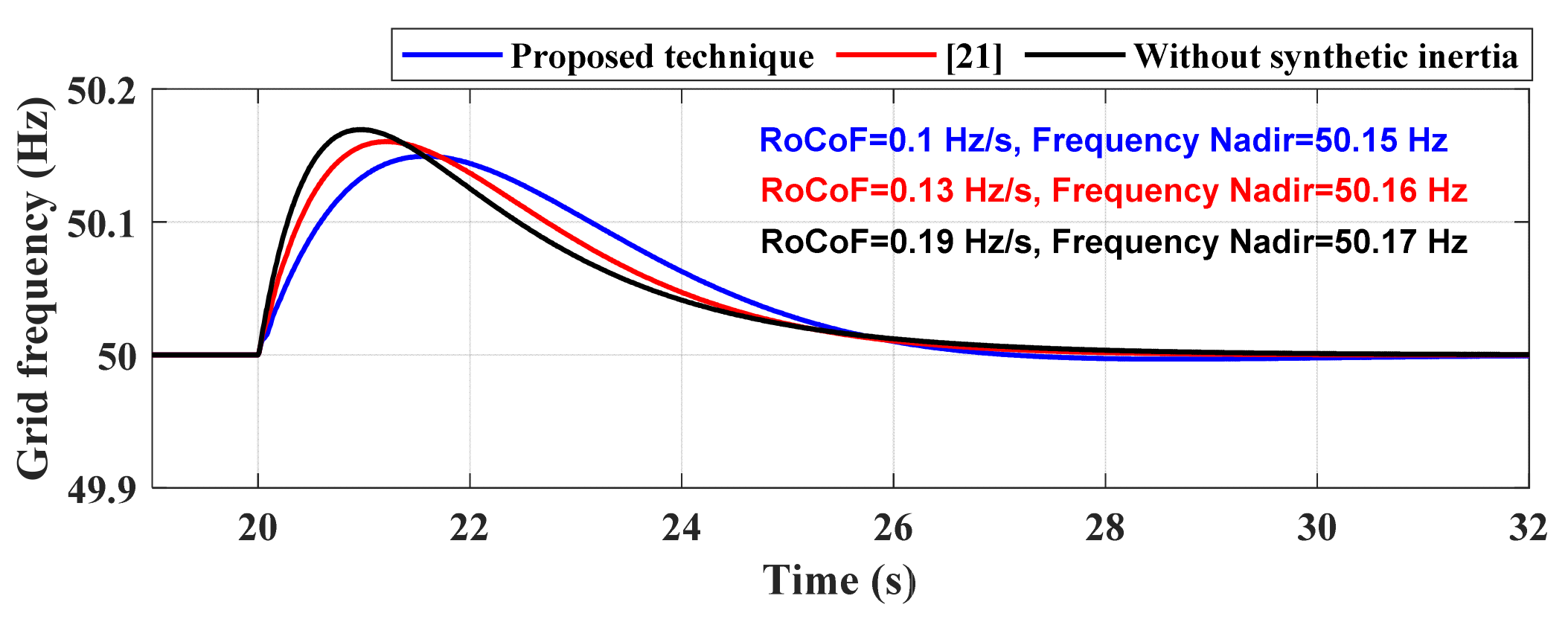
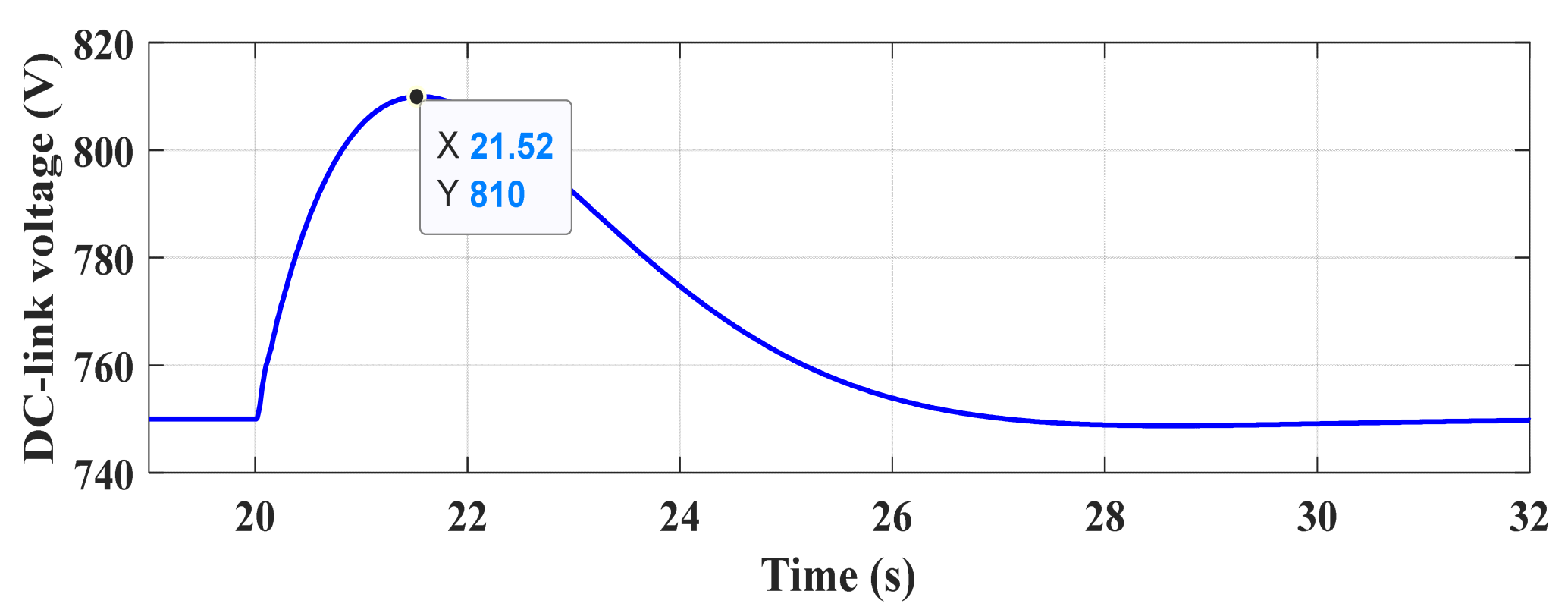
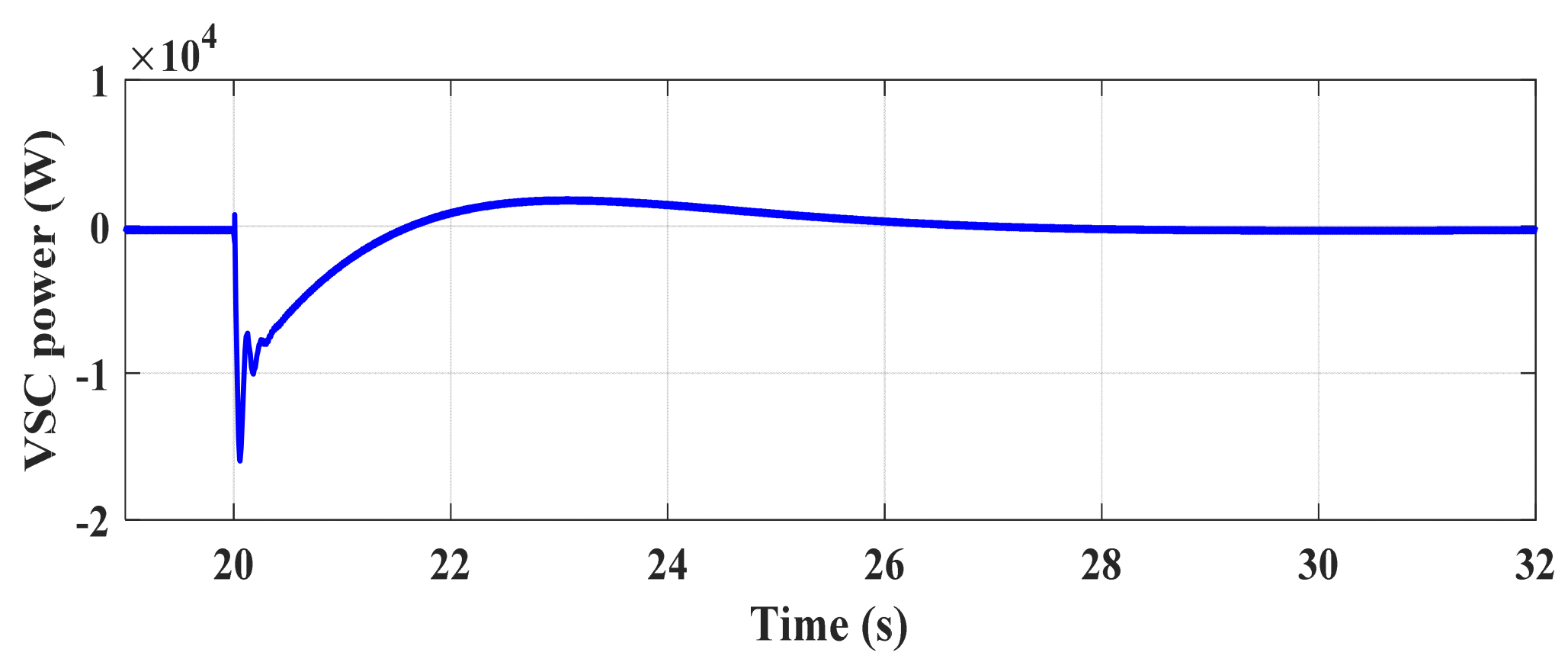
5. Simulation Results and Discussions
5.1. Scenario 1
5.2. Scenario 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations: | |
| dqg, dqc | Synchronous reference frames corresponding to the grid and the controller |
| ESS | Energy storage system |
| PLL | Phase-locked loop |
| PCC | Point of common coupling |
| RESs | Renewable energy sources |
| RoCoF | Rate of change of frequency |
| SGs | Synchronous generators |
| VSC | Voltage source converter |
| VSG | Virtual synchronous generator |
| Variables: | |
| i | Current flowing into the grid |
| ma | Modulation Index |
| Pm | Input mechanical power of SG |
| Pe | Electromagnetic power of SG |
| udc, ec, up, ug | DC-link capacitor voltage, converter voltage, PCC voltage, grid voltage |
| upg, upc | PCC voltage vectors in the grid frame and the controller frame |
| ω | Angular velocity/frequency of the rotor/grid |
| Δ | The difference angle between the converter voltage and the PCC voltage |
| Parameters: | |
| C | DC-link capacitance |
| D, Dp | Damping coefficient, virtual damping coefficient |
| FHP | Turbine coefficient |
| fs | Sampling frequency |
| H, Hp | Inertia constant, virtual inertia constant |
| Id | Rated value of the current i in the d-axis |
| J | Moment of inertia of the turbine and the generator |
| kcp, kci | Proportional and integral gains of the current controller |
| kup, kui | Proportional and integral gains of the voltage controller |
| kppll, kipll | Proportional and integral gains of the PLL |
| Lc, Lg | Inductance of the filter and the grid |
| Rc, Rg | Resistance of the filter and the grid |
| R | Droop coefficient |
| TG | Governor time constant |
| TCH | Inlet volume time constant |
| TRH | Re-heater time constant |
| Udc,ref | DC-link voltage reference |
| Upd | Nominal PCC voltage in the d-axis |
| ωr | Reference angular velocity/frequency of the rotor/grid |
References
- Kundur, P. Power System Stability and Control, 1st ed.; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator with Alternating Moment of Inertia. J. Emerg. Sel.Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Saeedian, M.; Eskandari, B.; Taheri, S.; Hinkkanen, M.; Pouresmaeil, E. A Control Technique Based on Distributed Virtual Inertia for High Penetration of Renewable Energies Under Weak Grid Conditions. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. J. Emerg. Sel.Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia Response and Frequency Control Techniques for Renewable Energy Sources: A Review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Vorobev, P.; Greenwood, D.M.; Bell, J.H.; Bialek, J.; Taylor, P.; Turitsyn, K. Deadbands, Droop, and Inertia Impact on Power System Frequency Distribution. IEEE Trans. Power Syst. 2019, 34, 3098–3108. [Google Scholar] [CrossRef] [Green Version]
- Mehrasa, M.; Pouresmaeil, E.; Sepehr, A.; Pournazarian, B.; Catalão, J.P.S. Control of Power Electronics-Based Synchronous Generator for the Integration of Renewable Energies into the Power Grid. Int. J. Electr. Power Energy Syst. 2019, 111, 300–314. [Google Scholar] [CrossRef]
- Golpîra, H.; Messina, A.R.; Bevrani, H. Emulation of Virtual Inertia to Accommodate Higher Penetration Levels of Distributed Generation in Power Grids. IEEE Trans. Power Syst. 2019, 34, 3384–3394. [Google Scholar] [CrossRef]
- EirGrid/SONI. RoCoF Modification Proposal—TSOs’ Recommendations; EirGrid/SONI: Dublin, Ireland, 2012. [Google Scholar]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Højgaard Jensen, P. Combination of Synchronous Condenser and Synthetic Inertia for Frequency Stability Enhancement in Low-Inertia Systems. IEEE Trans. Sustain. Energy 2019, 10, 997–1005. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.-P.; Hesse, R. Virtual Synchronous Machine. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters with Auto-Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016, 7, 1660–1674. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.-P. Improving the Grid Power Quality Using Virtual Synchronous Machines. In Proceedings of the International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Wang, S.; Tomsovic, K. Fast Frequency Support From Wind Turbine Generators With Auxiliary Dynamic Demand Control. IEEE Trans. Power Syst. 2019, 34, 3340–3348. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Kim, J.; Gevorgian, V.; Luo, Y.; Mohanpurkar, M.; Koritarov, V.; Hovsapian, R.O.; Muljadi, E. Supercapacitor to Provide Ancillary Services with Control Coordination. IEEE Trans. Ind. Appl. 2019, 55, 5119–5127. [Google Scholar] [CrossRef]
- Namor, E.; Sossan, F.; Cherkaoui, R.; Paolone, M. Control of Battery Storage Systems for the Simultaneous Provision of Multiple Services. IEEE Trans. Smart Grid 2019, 10, 2799–2808. [Google Scholar] [CrossRef] [Green Version]
- Gollenstede, J.; Beushausen, L.; Benger, R.; Beck, H.-P.; Schael, M.; Kruschel, W.; Ulbrich, T.; Schmies, S. Design of a High-Performance Battery Converter System for Providing Synthetic Inertia at Distribution Network Level. In Proceedings of the 20th European Conference on Power Electronics and Applications, Riga, Latvia, 17–21 September 2018; pp. 1–10. [Google Scholar]
- Duckwitz, D.; Fischer, B. Modeling and Design of df/dt-Based Inertia Control for Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1553–1564. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef] [Green Version]
- Marković, U.; Früh, N.; Aristidou, P.; Hug, G. Interval-Based Adaptive Inertia and Damping Control of a Virtual Synchronous Machine. In Proceedings of the 2019 IEEE PowerTech conference IEEE, Milano, Italy, 23–27 June 2019. [Google Scholar]
- Wu, W.; Chen, Y.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L.; Dong, Y.; Guerrero, J.M. A Virtual Inertia Control Strategy for DC Microgrids Analogized With Virtual Synchronous Machines. IEEE Trans. Ind. Electron. 2017, 64, 6005–6016. [Google Scholar] [CrossRef] [Green Version]
- Pournazarian, B.; Pouresmaeil, E.; Saeedian, M.; Lehtonen, M.; Chan, R.; Taheri, S. Microgrid Frequency & Voltage Adjustment Applying Virtual Synchronous Generator. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.; Boroyevich, D. Decoupled Double Synchronous Reference Frame PLL for Power Converters Control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.; Hansen, T.; Tonkoski, R. Virtual Inertia: Current Trends and Future Directions. J. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Governor time constant (TG) | 0.1 s |
| Inlet volume time constant (TCH) | 0.2 s |
| Re-heater time constant (TRH) | 7 s |
| Turbine coefficient (FHP) | 0.3 s |
| Droop coefficient (R) | 0.05 |
| Inertia constant (H) | 5–20 s |
| Damping coefficient (D) | 1 |
| System Parameters | Values | Controllers Parameters | Values |
|---|---|---|---|
| SG nominal power | 100 kW | H, D | 3, 1 |
| VSC nominal power | 15 kW | Hp, Dp | 50, 100 |
| Lg | 0.003 H | kcp | 0.1 |
| Lc | 0.002 H | kci | 10 |
| r | 0.001 Ω | kup | 0.006 |
| Upd | 326.59 V | kui | 0.001 |
| Udc,ref | 750 V | kppll | 180 |
| C | 0.1 F | kipll | 3200 |
| ωr | 100π rad/s | Tj | 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeedian, M.; Pournazarian, B.; Seyedalipour, S.S.; Eskandari, B.; Pouresmaeil, E. Emulating Rotational Inertia of Synchronous Machines by a New Control Technique in Grid-Interactive Converters. Sustainability 2020, 12, 5346. https://doi.org/10.3390/su12135346
Saeedian M, Pournazarian B, Seyedalipour SS, Eskandari B, Pouresmaeil E. Emulating Rotational Inertia of Synchronous Machines by a New Control Technique in Grid-Interactive Converters. Sustainability. 2020; 12(13):5346. https://doi.org/10.3390/su12135346
Chicago/Turabian StyleSaeedian, Meysam, Bahram Pournazarian, S. Sajjad Seyedalipour, Bahman Eskandari, and Edris Pouresmaeil. 2020. "Emulating Rotational Inertia of Synchronous Machines by a New Control Technique in Grid-Interactive Converters" Sustainability 12, no. 13: 5346. https://doi.org/10.3390/su12135346
APA StyleSaeedian, M., Pournazarian, B., Seyedalipour, S. S., Eskandari, B., & Pouresmaeil, E. (2020). Emulating Rotational Inertia of Synchronous Machines by a New Control Technique in Grid-Interactive Converters. Sustainability, 12(13), 5346. https://doi.org/10.3390/su12135346






