A Fuzzy Analytic Hierarchy Process-Based Analysis of the Dynamic Sustainable Management Index in Leisure Agriculture
Abstract
:1. Introduction
2. Literature Review
2.1. Leisure Agriculture
2.2. FAHP Method
2.3. Dynamic Management Index
2.4. The Evolution of FAHP Theory
3. Research Method
3.1. Framework and Definition of Study
3.1.1. Framework
3.1.2. Definition of Study
3.2. Samples and Surveys
3.3. Fuzzy Pair Comparison
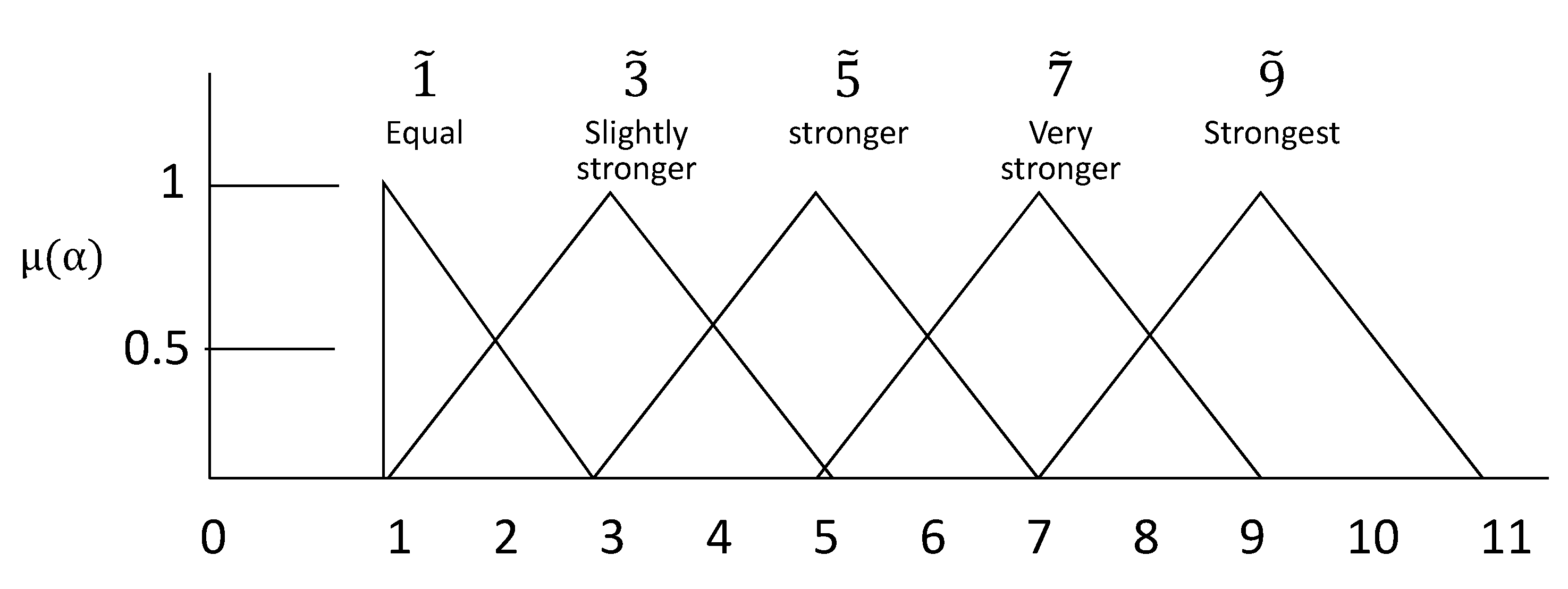
3.3.1. Triangular Fuzzy Number
3.3.2. Algebra Calculation
3.4. FAHP Algorithm
- Step 1.
- Establish a hierarchical analysis framework and define comparative performance values. Establish a hierarchical framework of consumer experience value, and then calculate Equation (2) according to the algebraic operation of Equation (3) to obtain triangular fuzzy numbers.
- Step 2.
- Establish a fuzzy pair comparison matrix. Use the average value of triangular fuzzy numbers, and establish a fuzzy discriminant matrix, which is defined as follows:
- Step 3.
- Calculates the fuzzy eigenvalue. Assuming that ~ is a fuzzy number, the formula for solving fuzzy eigenvalues is as follows:where A is an n x n fuzzy matrix composed of the non-zero fuzzy vectors of , , and n × 1, and the fuzzy number . The fuzzy multiplication and addition are shown, and the interval algorithm and αα-cut must be used. Equation (5) is equal to:wherewhere i and j, i = 1, 2, …, n; j = 1, 2, …, n.
- Step 4.
- According to the hierarchical relationship between principles and subprinciples, the preference importance of consumer experience value is calculated with α of different values.
- Step 5.
- Susceptibility analysis and discussion.
4. Case Analysis
- Step 1.
- Five evaluation aspects of FAHP algorithm as explained in Section 3.2 were formulated, namely organization and operation, leisure agricultural resources, environmental maintenance management, public facility maintenance management, and operational performance. Thereafter, according to the five evaluation aspects, 21 subprojects were further divided at the second level according to different attributes; thus, the third level of the hierarchical structure was established. The 21 subprojects were classified into five subprojects under the structure of organizational operation, four subprojects under the structure of leisure agricultural resources, and three subprojects under the structure of environmental maintenance management and public facilities maintenance management. Moreover, three and six subprojects were classified into the face and operational performance face, respectively. This three-level structure comprised the research framework required for this research.A hierarchical analysis framework to define comparative performance values was established. This study uses the manager experience value hierarchical framework proposed by this study to Charla Mathwick et al. [57] to classify consumer experience perception value into four principles and eight subprinciples with 17 attributes, and adopts a four-level hierarchical framework, as shown in Appendix A. The triangular fuzzy number is defined as equivalent, slightly strong, strong, very strong, and extremely strong, and Equation (2) was used to calculate the triangular fuzzy number.
- Step 2.
- After consolidating the opinions of relevant scholars through a literature review and providing a theoretical basis, this paper constructs the Delphi method index questionnaire data, covering a total of five aspects and 21 evaluation indicators. The questionnaire was issued in November 2019 and was used to assess the production of leisure agriculture-related fields. Questionnaires were administered to five experts, scholars, and officials, and five responses were received. Hence, the recovery rate was 100%. The average work experience of the experts was 20.6 years.
- Step 3.
- After performing the screening using the Delphi method, five major evaluation aspects and 21 evaluation criteria passed the test. Therefore, all the evaluation aspects and evaluation criteria were retained, and the hierarchical architecture diagram remained unchanged.
- Step 4.
- Establish a fuzzy pair comparison matrix.
- Step 5.
- Calculate the fuzzy eigenvalue.
- Step 6.
- Calculate the preference value of each factor
- Step 7.
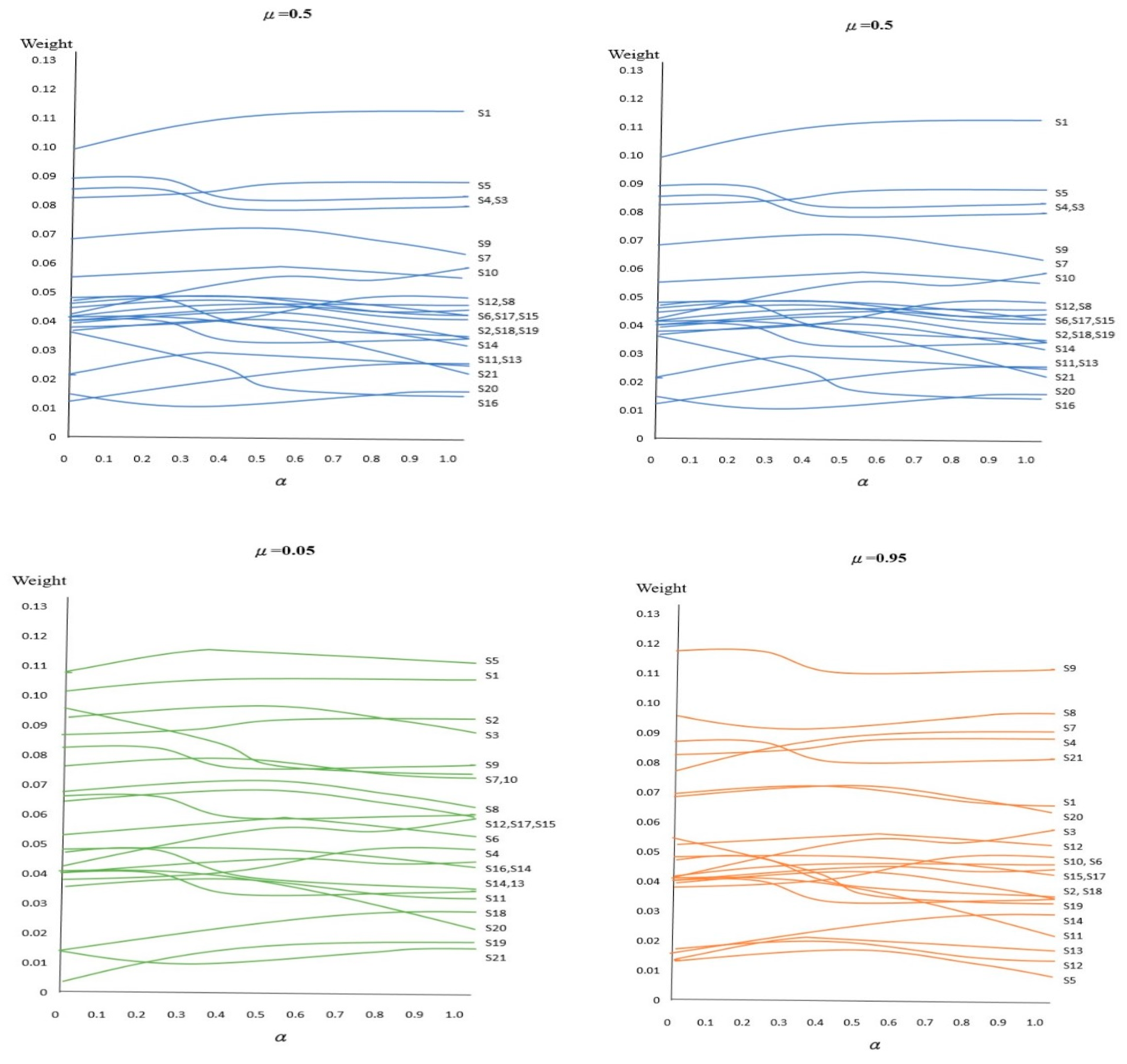
- Susceptibility analysis
5. Conclusions and Suggestions
5.1. Conclusions
- The most important aspects of active management attitude toward leisure agriculture entail the following: S9: channel connection and cooperation between different industries, S8: leisure agriculture-related fields, S7: use of local industrial resources, S4: self; five items such as improvement and function enhancement, and S20: internet usage situation. Active managers’ management attitude toward leisure agriculture is biased toward the integration of marketing and local resources. They attach importance to the improvement of self-management capabilities. Therefore, managers’ attitudes toward leisure agriculture tend to be active, and the indicators they value tend to be related to the market. The positive management attitude of this type can improve enterprises’ competitive advantage in the market for the operation of leisure agriculture. Management attitude is more meaningful in management practice.
- The most important aspects of moderate managers’ management attitudes toward leisure agriculture entail the following: S1: enterprise structure and implementation of division of labor, S5: enterprise self-sufficiency, S4: self-improvement and function enhancement, S3: enterprise operation goals, S9: channel connection and inter-industry cooperation, and other five items. These items focus on strengthening and improving the company’s operating capacity and survival goals, improving the company’s operating competitiveness, and then expanding external marketing channels. Therefore, managers’ attitudes toward leisure agriculture usually tend to be moderate. Moreover, the management indicators they value mainly strengthen the competitiveness of the enterprise. In practice, the management performance of enterprises has the most important consideration by managers.
- Conservative managers and moderate managers have almost the same attitude toward leisure agriculture. However, they differ in order due to the following: S5: enterprise self-sufficiency, S1: enterprise structure and division of labor implementation, S2: enterprise growth situation, S3: business operation target and S9: channel connection and inter-industry cooperation. The conservative focus is placed on the survival of the company, and the internal business performance indicators of the company tend to be used. Therefore, managers who tend to have conservative management attitudes toward leisure agriculture value management indicators that focus on strengthening the survival of the enterprise. Moreover, in practice, implementing the enterprise’s management system is the most important consideration.
- Leisure farms should pay attention to the internal operation and the integrity and fluency of critical processes, and attention to the efficiency of resource use and the resource base of agriculture. This has a relationship with the establishment of the competitive advantages of corporate operations. Therefore, leisure farms should pay attention to the implementation of corporate structure and division of labor. In the maintenance of the operating environment, attention should be paid to the overall environmental creation.
5.2. Research Contribution
- Applying the FAHP algorithm proposed by Kwong and Bai [20] to evaluate the relative importance of manager dynamic management index, which is easy to understand and use, and is close to the real management of managers’ value. Using this method to strengthen the preference value of high relative importance can support managers’ intentions of management; hence, this method benefits the formulation of management strategies.
- In susceptibility analysis, we found that the ranking of the management value preferences of managers vary with different management tendencies. Manager or strategy-makers should pay attention to the performance of managers and changes in their attitudes toward increasing the competitive advantage of enterprises.
5.3. Management Significance
- In terms of managers, recreational agriculture managers should strengthen training in order to enhance the professional competence and quality of management skills, while managerial tendencies must be more aligned with a positive attitude with the right choice, enterprise architecture and professional and clear explanation of travel market.
- With regard to strategy-makers, finding managers who are suitable to the role of managing leisure agriculture is very important for leisure agriculture enterprises. Managers with different business tendencies place different degrees of emphasis on enterprise management. Different strategic combinations are utilized for the shaping of enterprise organizations, resource allocation, personnel assignment, and market judgment—all of which affects the overall competitiveness of leisure agricultural enterprises. Therefore, the choice of managers with different business preferences is the most important consideration for decision-makers.
- With regard to enterprise competitiveness, the business of leisure farms is different from other general leisure businesses because the farms involve the production of agricultural products. However, companies are still competing in the leisure business in a broad sense; hence, managers must thoroughly analyze environmental changes and the resource advantages of the company. Appointing managers with appropriate attitudes, continuously improving the company’s operating efficiency, and creating a competitive advantage for the company can bring sustainable business value to the company.
Funding
Conflicts of Interest
Appendix A. Analysis of the Relative Importance of Experience Value Preference
References
- Zhao-Lin, D. Leisure Agriculture-Experience View; Huadu Culture Co., Ltd.: Taipei City, Taiwan, 2019. [Google Scholar]
- Bryant, C.R.; Chahine, G. Action Research and Reducing the Vulnerability of Peri-Urban Agriculture: A Case Study from the Montreal Region. Geogr. Res. 2016, 54, 165–175. [Google Scholar] [CrossRef]
- Tsaur, S.-H.; Yen, C.-H.; Ku, P.-S. An Evaluation Framework for the Sustainable Operation of Leisure Farms. Leis. Stud. 2017, 36, 739–751. [Google Scholar] [CrossRef]
- Pinckney, H.P.; Mowatt, R.A.; Outley, C.; Brown, A.; Floyd, M.F.; Black, K.L. Black Spaces/White Spaces: Black Lives, Leisure, And Life Politics. Leis. Sci. 2018, 40, 267–287. [Google Scholar] [CrossRef]
- Winslow, M. Cultivating Leisure: Tourism, Progressive Agriculture, And Technologies of Landscape at Pinehurst, North Carolina, 1895–1935. Agric. Hist. 2020, 94, 61–83. [Google Scholar] [CrossRef]
- Liu, D. Development and Utilization of Rural Idle Homesteads in the Context of Rural Revitalization—A Case Study of Leisure Agriculture. Asian Agric. Res. 2019, 11, 53–56. [Google Scholar]
- Fan, W.; Fu, H.; Chen, X. Development of Leisure Agriculture in Hainan. Agric. Sci. Technol. 2014, 15, 1977–1980. [Google Scholar]
- Afuah, A.; Tucci, C. Internet Business Models and Strategies; Mcgraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Lunner-Kolstrup, C.; Hörndahl, T.; Karttunen, J.P. Farm Operators’ Experiences of Advanced Technology and Automation in Swedish Agriculture: A Pilot Study. J. Agromed. 2018, 23, 215–226. [Google Scholar] [CrossRef] [PubMed]
- Seguí, A.E.; Maćkiewicz, B.; Rosol, M. From Leisure to Necessity: Urban Allotments in Alicante Province, Spain in Times of Crisis. ACME Int. J. Crit. Geogr. 2017, 16, 276–304. [Google Scholar]
- Rzekęć, A.; Vial, C.; Bigot, G. Green Assets of Equines in the European Context of the Ecological Transition of Agriculture. Animals 2020, 10, 106. [Google Scholar] [CrossRef] [Green Version]
- Jinzhu, H.; Zebin, C.; Yajun, S.; Jia’Ni, L.; Liyuan, Y.; Yuyu, Z.; Jingxiang, H.; Haotian, W.; Zhiwei, Z. Leisure Agriculture Based on Cultural Resources of Sani People in Yunnan. Asian Agric. Res. 2017, 9, 45–50. [Google Scholar]
- Farmer, J. Leisure in Living Local Through Food And Farming. Leis. Sci. 2012, 34, 490–495. [Google Scholar] [CrossRef]
- Essen, E.; Tickle, L. Leisure or Labour: An Identity Crisis for Modern Hunting? Sociol. Rural. 2020, 60, 174–197. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J. Research on Performance Evaluation of Leisure Agriculture Supply-Side Structural Reform With interval-Valued Dual Hesitant Fuzzy Linguistic information. J. Intell. Fuzzy Syst. 2019, 37, 1801–1808. [Google Scholar] [CrossRef]
- Lin, C.-N.; Hung, T.-A.; Li, H.-H. Construction of Evaluation indexes for the integrated Development of Leisure Agriculture Management: The Application of Delphi Technology. Open Access Libr. J. 2020, 7, 99744. [Google Scholar] [CrossRef]
- Satty, T.L. The Analytic Hierarchy Process; Mcgraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Abbasimehr, H.; Tarokh, M. A Combined Approach Based on Fuzzy Ahp And Fuzzy inference System to Rank Reviewers in online Communities. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 862–876. [Google Scholar] [CrossRef]
- Singh, P.K.; Sarkar, P. A Framework Based on Fuzzy Ahp-topsis for Prioritizing Solutions to Overcome the Barriers in the Implementation of Ecodesign Practices in Smes. Int. J. Sustain. Dev. World Ecol. 2019, 26, 506–521. [Google Scholar] [CrossRef]
- Kwong, C.K.; Bai, H. A Fuzzy Ahp Approach to the Determination of Importance Weights of Customer Requirements in Quality Function Deployment. J. Intell. Manuf. 2002, 13, 367–377. [Google Scholar] [CrossRef]
- Jian-Hung, C.; Jian-Jing, L.; Xing-Chen, C. A System Dynamics Approach to the Business Model of Cultural Creativity Based industries: A Case of the Bunun Tribe. J. Taiwan Enterp. Perform. 2013, 7, 25–40. [Google Scholar]
- Tsung-Min, W. A Study on the Relationships between Business Development Stages, Dynamic Capabilities and Innovation Business Model. Master’s Thesis, Institute of International Business Management, Qingyun University of Science and Technology, Hefei, China, 2009; pp. 1–2. [Google Scholar]
- Jovčić, S.; Průša, P.; Samson, J.; Lazarević, D. A Fuzzy—Ahp Approach to Evaluate the Criteria of Third-Party Logistics (3pl) Service Provider. Int. J. Traffic Transp. Eng. 2019, 9, 280–289. [Google Scholar]
- Venkatesh, V.G.; Zhang, A.; Deakins, E.; Luthra, S.; Mangla, S. A Fuzzy Ahp-topsis Approach to Supply Partner Selection in Continuous Aid Humanitarian Supply Chains. Ann. Oper. Res. 2019, 283, 1517–1550. [Google Scholar] [CrossRef]
- Buckley, J.J. The Multiple Judge, Multiplecriteria Ranking Problem: A Fuzzy Set Approach. Fuzzy Set Syst. 1984, 17, 233–247. [Google Scholar] [CrossRef]
- Mirhedayatian, M.; Jelodar, M.; Adnani, S.; Akbarnejad, M.; Saen, R. A New Approach for Prioritization in Fuzzy Ahp with an Application for Selecting the Best Tunnel Ventilation System. Int. J. Adv. Manuf. Technol. 2013, 68, 2589–2599. [Google Scholar] [CrossRef]
- Samanlioglu, F.; Ayağ, Z. A Fuzzy Ahp-Vikor Approach for Evaluation of Educational Use Simulation Software Packages. J. Intell. Fuzzy Syst. 2019, 37, 7699–7710. [Google Scholar] [CrossRef]
- Godoy, D.L.P. Application of the Fuzzy-Ahp Method in the Optimization of Production of Concrete Blocks with Addition of Casting Sand. J. Intell. Fuzzy Syst. 2018, 35, 3477–3491. [Google Scholar] [CrossRef]
- Ocampo, L.A.; Himang, C.M.; Kumar, A.; Brezocnik, M. A Novel Multiple Criteria Decision-Making Approach Based on Fuzzy Dematel, Fuzzy Anp And Fuzzy Ahp for Mapping Collection and Distribution Centers in Reverse Logistics. Adv. Prod. Eng. Manag. 2019, 14, 297–322. [Google Scholar] [CrossRef] [Green Version]
- Onar, S.C.; Oztaysi, B.; Kahraman, C.; Ozturk, E. Evaluation of Legal Debt Collection Services by Using Hesitant Pythagorean (intuitionistic Type 2) Fuzzy Ahp. J. Intell. Fuzzy Syst. 2020, 38, 883–894. [Google Scholar] [CrossRef]
- Hapsari, M.A.; Subiyanto, S. Fuzzy Ahp Based Optimal Design Building-Attached Photovoltaic System for Academic Campus. Int. J. Photoenergy 2020, 2020. [Google Scholar] [CrossRef] [Green Version]
- Kutlu Gündoğdu, F.; Kahraman, C. A Novel Spherical Fuzzy Analytic Hierarchy Process and its Renewable Energy Application. Soft Comput. Fusion Found. Methodol. Appl. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Sultana, I.; Ahmed, I.; Azeem, A. An integrated Approach for Multiple Criteria Supplier Selection Combining Fuzzy Delphi, Fuzzy Ahp & Fuzzy topsis. J. Intell. Fuzzy Syst. 2015, 29, 1273–1287. [Google Scholar]
- Nguyen, H.-T.; Dawal, S.Z.M.; Nukman, Y.; Aoyama, H.; Case, K. An integrated Approach of Fuzzy Linguistic Preference Based Ahp And Fuzzy Copras for Machine tool Evaluation. PLoS ONE 2015, 10, e0133599. [Google Scholar] [CrossRef] [Green Version]
- Pandey, P.; Litoriya, R. Fuzzy Ahp Based Identification Model for Efficient Application Development. J. Intell. Fuzzy Syst. 2020, 38, 3359–3370. [Google Scholar] [CrossRef]
- Beskese, A.; Camci, A.; Temur, G.T.; Erturk, E.; Kahraman, C. Wind Turbine Evaluation Using the Hesitant Fuzzy Ahp-topsis Method with A Case in Turkey. J. Intell. Fuzzy Syst. 2020, 38, 997–1011. [Google Scholar] [CrossRef]
- Naderzadeh, M.; Arabalibeik, H.; Monazzam, M.R.; Ghasemi, I. Comparative Analysis of Ahp-topsis And Fuzzy Ahp Models in Selecting Appropriate Nanocomposites for Environmental Noise Barrier Applications. Fluct. Noise Lett. 2017, 16, 1750038. [Google Scholar] [CrossRef]
- Meshram, S.G.; Alvandi, E.; Singh, V.P.; Meshram, C. Comparison of Ahp And Fuzzy Ahp Models for Prioritization of Watersheds. Soft Comput. Fusion Found. Methodol. Appl. 2019, 23, 13615–13625. [Google Scholar] [CrossRef]
- Singh, D.K.; Kaushik, P. Framework for Fuzzy Rule Based Automatic intrusion Response Selection System (Frairss) Using Fuzzy Analytic Hierarchy Process And Fuzzy topsis. J. Intell. Fuzzy Syst. 2018, 35, 2559–2571. [Google Scholar] [CrossRef]
- Tadic, D.; Gumus, A.T.; Arsovski, S.; Aleksic, A.; Stefanovic, M. An Evaluation of Quality Goals by Using Fuzzy Ahp And Fuzzy topsis Methodology. J. Intell. Fuzzy Syst. 2013, 25, 547–556. [Google Scholar] [CrossRef]
- Singh, M.P.; Singh, P.; Singh, P. Fuzzy Ahp-Based Multi-Criteria Decision-Making Analysis for Route Alignment Planning Using Geographic information System (Gis). J. Geogr. Syst. 2019, 21, 395–432. [Google Scholar] [CrossRef]
- Behera, S.; Panigrahi, M.K.; Pradhan, A. Identification of Geochemical Anomaly and Gold Potential Mapping in the Sonakhan Greenstone Belt, Central india: An integrated Concentration-Area Fractal And Fuzzy Ahp Approach. Appl. Geochem. 2019, 107, 45–57. [Google Scholar] [CrossRef]
- Yucesan, M.; Gul, M. Hospital Service Quality Evaluation: An integrated Model Based on Pythagorean Fuzzy Ahp And Fuzzy topsis. Soft Comput. Fusion Found. Methodol. Appl. 2020, 24, 3237–3255. [Google Scholar] [CrossRef]
- Roy, T.; Dutta, R.K. Integrated Fuzzy Ahp And Fuzzy topsis Methods for Multi-Objective Optimization of Electro Discharge Machining Process. Soft Comput. Fusion Found. Methodol. Appl. 2019, 23, 5053–5063. [Google Scholar] [CrossRef]
- Prasad, R.V.; Rajesh, R.; Thirumalaikumarasamy, D. Selection of Coating Material for Magnesium Alloy Using Fuzzy Ahp-topsis. Sadhana 2020, 45, 23. [Google Scholar] [CrossRef]
- Kaya, A.; Çiçekalan, B.; Çebi, F.; Kahraman, C. Location Selection for Weee Recycling Plant by Using Pythagorean Fuzzy Ahp. J. Intell. Fuzzy Syst. 2020, 38, 1097–1106. [Google Scholar] [CrossRef]
- Serrano-Gomez, L.; Munoz-Hernandez, J.I. Monte Carlo Approach to Fuzzy Ahp Risk Analysis in Renewable Energy Construction Projects. PLoS ONE 2019, 14, e0215943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Yuan, G.; Zhuang, Q.; Tian, G. Multi-Objective Low-Carbon Disassembly Line Balancing for Agricultural Machinery Using Mdfoa And Fuzzy Ahp. J. Clean. Prod. 2019, 233, 1465–1474. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Zhang, X.; Liu, H. Optimization of Subsidy Policy for New Energy Automobile industry in China Based on an integrated Fuzzy-Ahp-topsis Methodology. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Moktadir, A.; Rahman, T.; Jabbour, C.J.C.; Ali, S.M.; Kabir, G. Prioritization of Drivers of Corporate Social Responsibility in the Footwear industry in An Emerging Economy: A Fuzzy Ahp Approach. J. Clean. Prod. 2018, 201, 369–381. [Google Scholar] [CrossRef]
- Li, M.; Wang, H.; Wang, D.; Shao, Z.; He, S. Risk Assessment of Gas Explosion in Coal Mines Based on Fuzzy Ahp And Bayesian Network. Process Saf. Environ. Prot. Trans. Inst. Chem. Eng. Part B 2020, 135, 207–218. [Google Scholar] [CrossRef]
- Hassaninia, M.; Ajalloeian, R.; Habibi, M.R. Seismic Microzonation And Building Vulnerability Assessment Based on Site Characteristic and Geotechnical Parameters By Use of Fuzzy-Ahp Model (A Case Study for Kermanshah City). Civ. Eng. Environ. Syst. 2019, 36, 172–198. [Google Scholar] [CrossRef]
- Wang, D.; Yu, H.; Wu, J.; Meng, Q.; Lin, Q. Integrating Fuzzy Based Qfd And Ahp for the Design And Implementation of A Hand Training Device. J. Intell. Fuzzy Syst. 2019, 36, 3317–3331. [Google Scholar] [CrossRef]
- Tuljak-Suban, D.; Bajec, P. The influence of Defuzzification Methods to Decision Support Systems Based on Fuzzy Ahp With Scattered Comparison Matrix: Application to 3plp Selection as A Case Study. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26, 475–491. [Google Scholar] [CrossRef]
- Jain, V.; Sangaiah, A.K.; Sakhuja, S.; Thoduka, N.; Aggarwal, R. Supplier Selection Using Fuzzy Ahp and topsis: A Case Study in the indian Automotive industry. Neural Comput. Appl. 2018, 29, 555–564. [Google Scholar] [CrossRef]
- Ding, J.F.; Kuo, J.F.; Tai, W.H. Using Fuzzy Ahp Method to Evaluate Key Competency and Capabilities of Selecting Middle Managers for Global Shipping Logistics Service Providers. Sci. J. Marit. Res. 2019, 33, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Mathwick, C.; Malhotra, N.K.; Rigdon, E. The Effect of Dynamic Retail Experiences on Experiential Perceptions of Value: On internet and Catalog Comparison. J. Retail. 2002, 78, 51–66. [Google Scholar] [CrossRef]
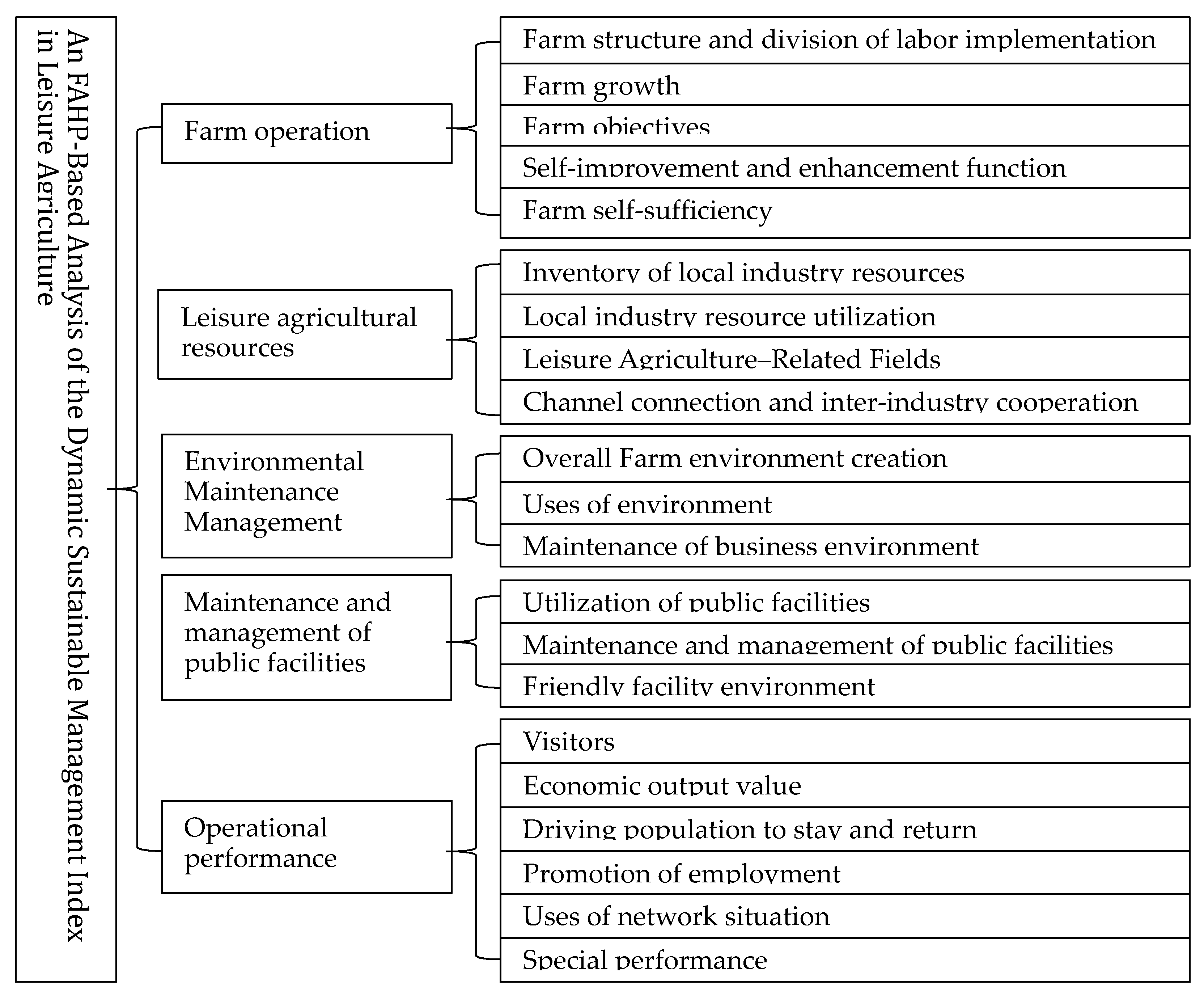
| Indicator Facet | Subindicator Facet | Description |
|---|---|---|
| C1 Farm operation | S1: Farm structure and division of labor implementation | Refers to the organizational structure and projects that an farm must have when operating |
| S2: Farm growth | ||
| S3: Farm objectives | ||
| S4: Self-improvement and enhancement function | ||
| S5: Farm self-sufficiency | ||
| C2 Leisure agricultural resources | S6: Inventory of local industry resources | The degree of cooperation between various resources and industries outside of leisure agriculture |
| S7: Local industry resource utilization | ||
| S8: Leisure Agriculture–Related Fields | ||
| S9: Channel connection and inter-industry cooperation | ||
| C3 Environmental Maintenance Management | S10: Overall Farm environment creation | Refers to the environmental maintenance during leisure farm operations |
| S11: Use of environment | ||
| S12: Maintenance of Farm environment | ||
| C4 Maintenance and management of public facilities | S13: Utilization of public facilities | The establishment and maintenance of various facilities related to leisure farm operations |
| S14: Maintenance and management of public facilities | ||
| S15: Friendly facility environment | ||
| C5 Operational performance | S16: Visitors | Operational performance refers to the basis for the performance of leisure farm in operation |
| S17: Economic output value | ||
| S18: Driving population to stay and return | ||
| S19: Promotion of employment | ||
| S20: Use of network situation | ||
| S21: Special performance |
| Region | Farms | Title | Working Years |
|---|---|---|---|
| Northern | Flying Cow Ranch | Special Assistant to the Chairman | 15 |
| Central | Dongshi Forest Farm | Commissioner | 9 |
| Hualu Leisure Farm | General manager | 18 | |
| Southern | Fairy Lake Leisure Farm | Manager | 25 |
| Eastern | Shangrila Leisure Farm | Manager | 12 |
| Region | Farms | Title | Working Years |
|---|---|---|---|
| Northern | Flying Cow Ranch | Special Assistant to the Chairman | 15 |
| Green World Leisure Farm | Manger | 6 | |
| Jiudou Village Leisure Farm | General manager | 24 | |
| Jinyong Tourism Farm | General manager | 20 | |
| Futianyuan Leisure Farm | Manager | 5 | |
| Central | Dongshi Forest Farm | Commissioner | 9 |
| Hualu Leisure Farm | General manager | 18 | |
| Taiyi Educational Leisure Farm | Manager | 10 | |
| Lavender Forest Leisure Farm | Manager | 10 | |
| Mogu Tribe Leisure Farm | Manager | 10 | |
| Southern | Fairy Lake Leisure Farm | Manager | 25 |
| Tsou Ma Lai Farm | Commissioner | 10 | |
| Dakeng Leisure Farm | Manager | 15 | |
| Angel Garden Leisure Farm | General manager | 10 | |
| Fuwan Leisure Farm | Chairman | 21 | |
| Eastern | Shangrila Leisure Farm | Manager | 12 |
| Toucheng Leisure Farm | Manager | 5 | |
| Lichuan Fishing Leisure Farm | Chairman | 10 | |
| Xinguang Zhaofeng Leisure Farm | Manager | 6 | |
| Chulu Ranch | Manager | 2 | |
| Toyugi Leisure Farm | Manager | 3 |
| Criterion | Weight | Subcriteria | Weight | Total Weight |
|---|---|---|---|---|
| C1 Business operation | 0.39953 | S1: Enterprise structure and division of labor implementation | 0.29623 | 0.118353 |
| S2: Business growth | 0.09255 | 0.036977 | ||
| S3: Business objectives | 0.17926 | 0.07162 | ||
| S4: Self-improvement and enhancement function | 0.20788 | 0.083054 | ||
| S5: Enterprise self-sufficiency | 0.22409 | 0.089531 | ||
| C2 Leisure agricultural resources | 0.20887 | S6: Inventory of local industry resources | 0.213823 | 0.044661 |
| S7: Local industry resource utilization | 0.274575 | 0.05735 | ||
| S8: Leisure Agriculture–Related Fields | 0.224256 | 0.04684 | ||
| S9: Channel connection and inter-industry cooperation | 0.287346 | 0.060018 | ||
| C3 Environmental Maintenance Management | 0.13149 | S10: Overall business environment creation | 0.430296 | 0.05658 |
| S11: Use of environment | 0.203544 | 0.026764 | ||
| S12: Maintenance of business environment | 0.36616 | 0.048146 | ||
| C4 Maintenance and management of public facilities | 0.09789 | S13: Utilization of public facilities | 0.244312 | 0.023916 |
| S14: Maintenance and management of public facilities | 0.33890 | 0.033175 | ||
| S15: Friendly facility environment | 0.416788 | 0.040799 | ||
| C5 Operational performance | 0.16222 | S16: Visitors | 0.08295 | 0.013456 |
| S17: Economic output value | 0.25433 | 0.041257 | ||
| S18: Driving population to stay and return | 0.22762 | 0.036925 | ||
| S19: Promotion of employment | 0.21181 | 0.03436 | ||
| S20: Use of network situation | 0.08940 | 0.014502 | ||
| S21: Special performance | 0.13388 | 0.021718 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-N. A Fuzzy Analytic Hierarchy Process-Based Analysis of the Dynamic Sustainable Management Index in Leisure Agriculture. Sustainability 2020, 12, 5395. https://doi.org/10.3390/su12135395
Lin C-N. A Fuzzy Analytic Hierarchy Process-Based Analysis of the Dynamic Sustainable Management Index in Leisure Agriculture. Sustainability. 2020; 12(13):5395. https://doi.org/10.3390/su12135395
Chicago/Turabian StyleLin, Chun-Nan. 2020. "A Fuzzy Analytic Hierarchy Process-Based Analysis of the Dynamic Sustainable Management Index in Leisure Agriculture" Sustainability 12, no. 13: 5395. https://doi.org/10.3390/su12135395
APA StyleLin, C. -N. (2020). A Fuzzy Analytic Hierarchy Process-Based Analysis of the Dynamic Sustainable Management Index in Leisure Agriculture. Sustainability, 12(13), 5395. https://doi.org/10.3390/su12135395





