Optimal Distribution of Renewable Energy Systems Considering Aging and Long-Term Weather Effect in Net-Zero Energy Building Design
Abstract
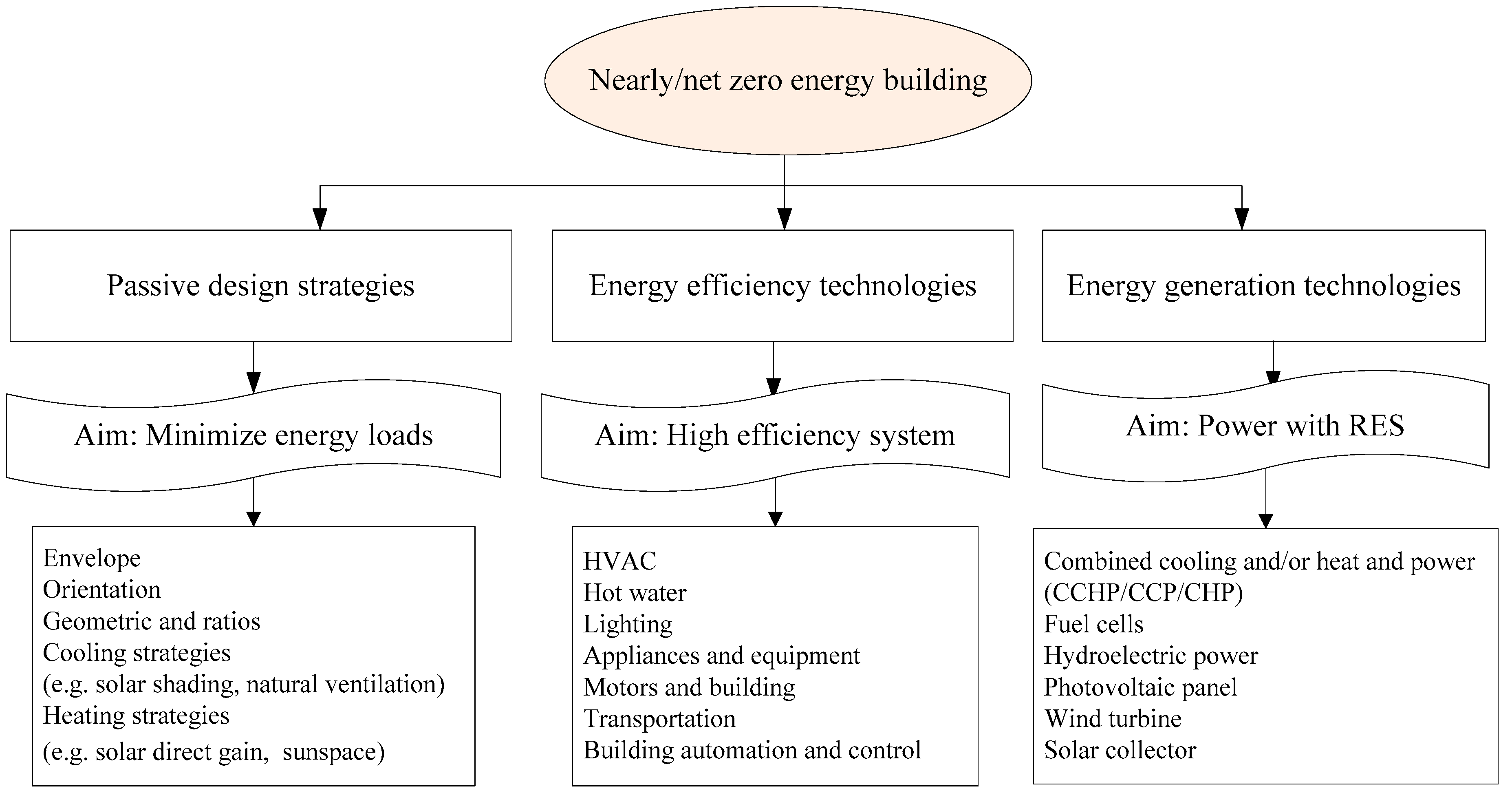
:1. Introduction
2. Problem Identification
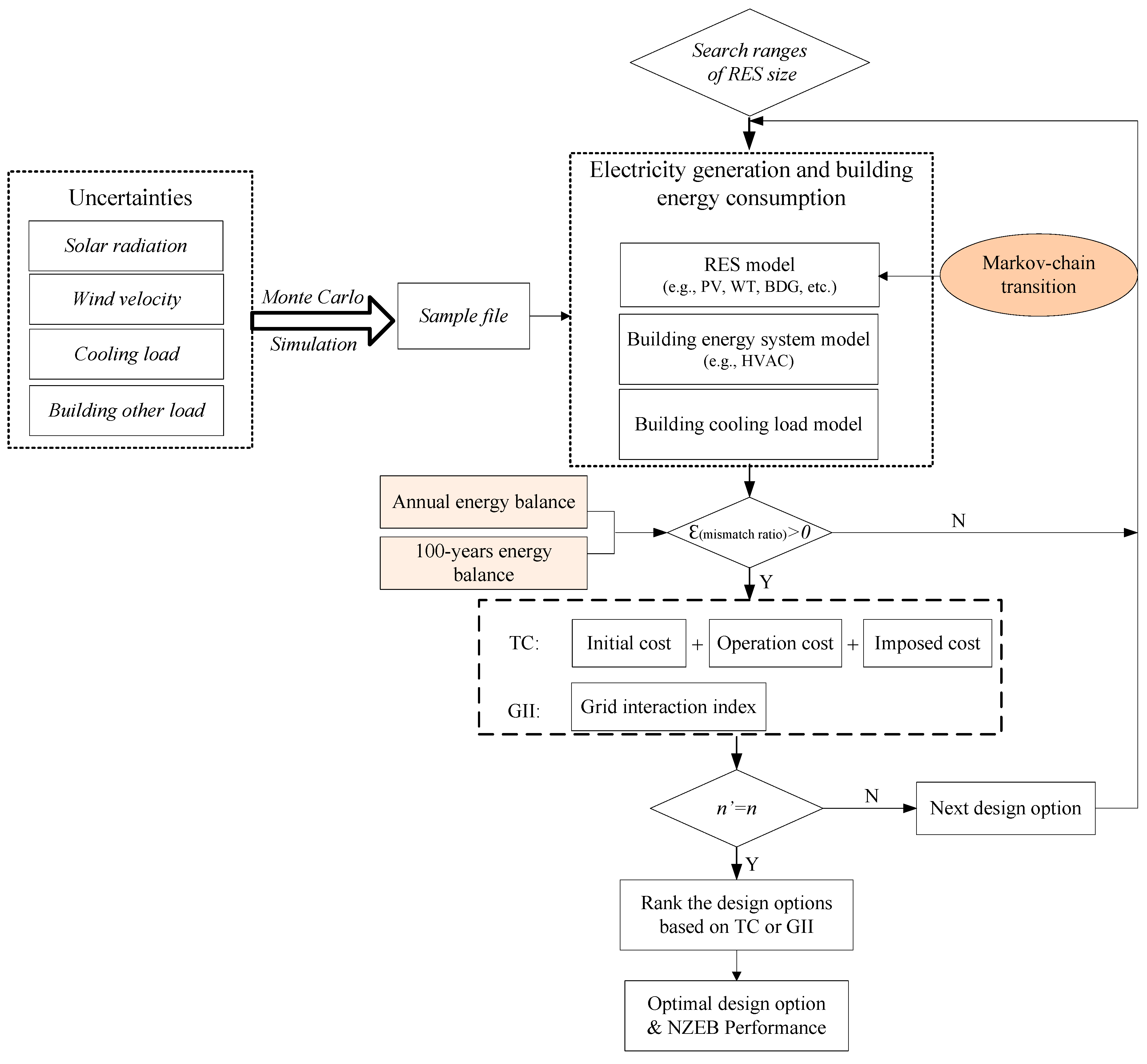
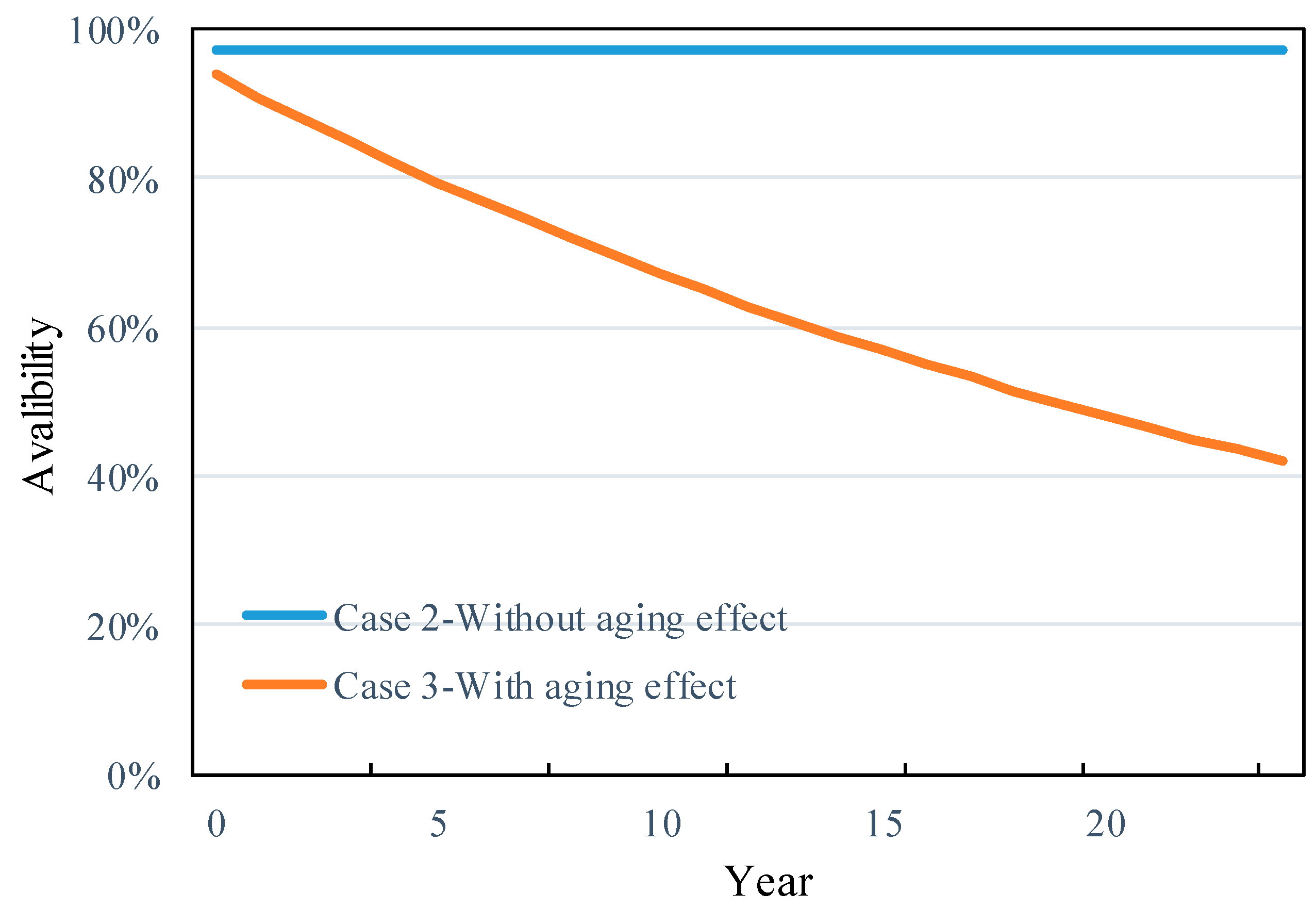
3. System Generation Reliability Model
4. Evaluation Indicator
5. Building Features
6. Results and Discussion
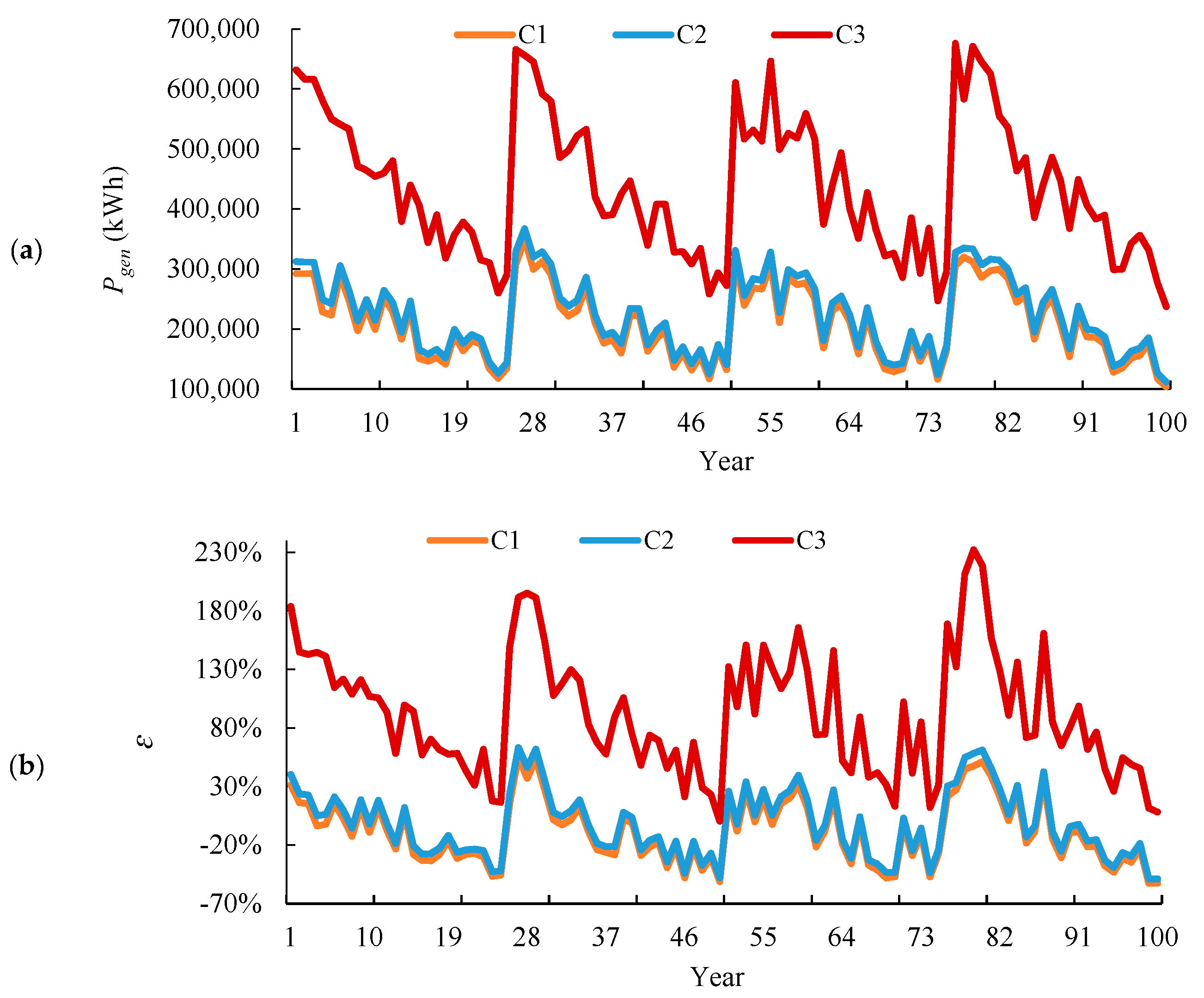
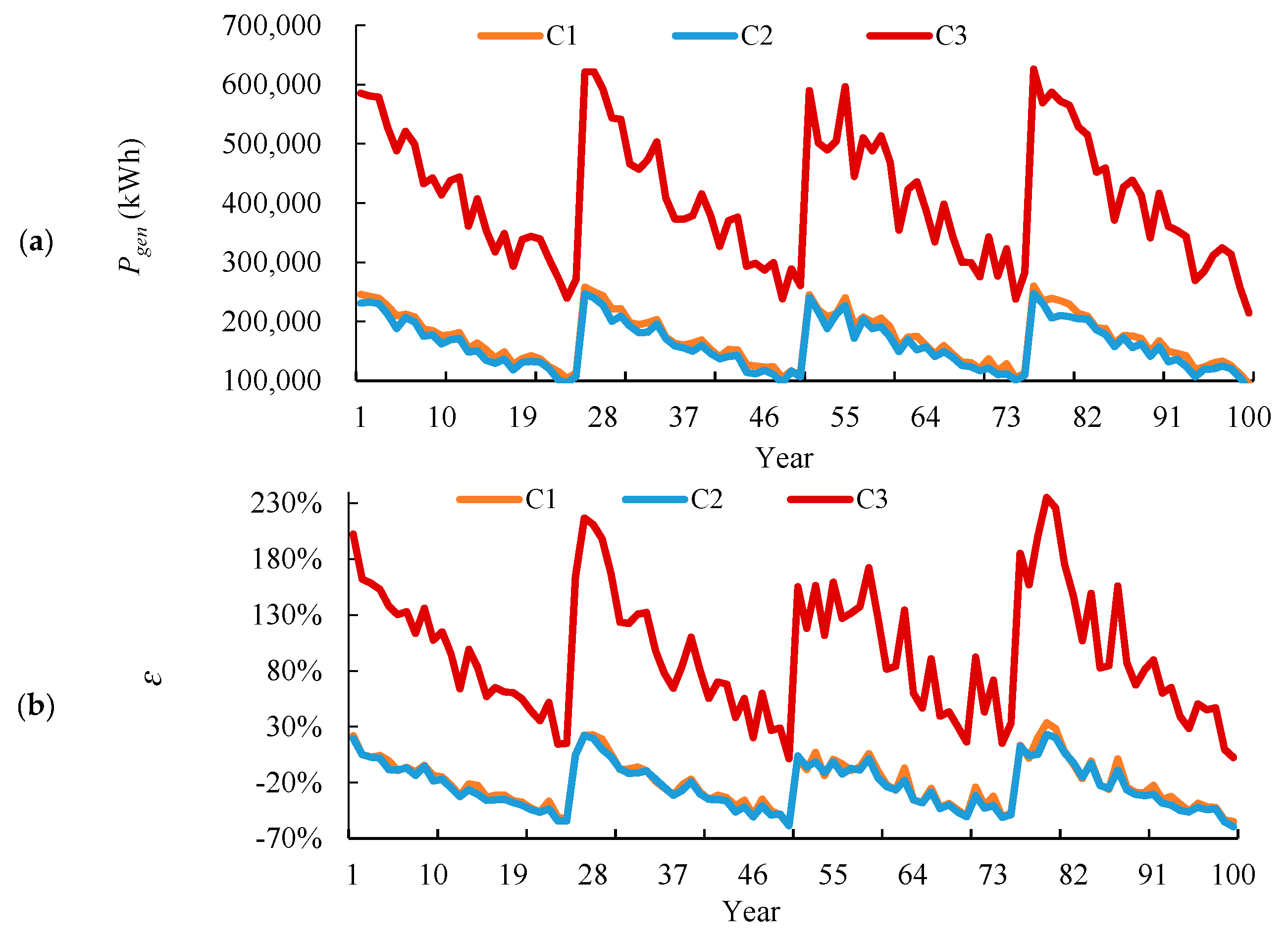
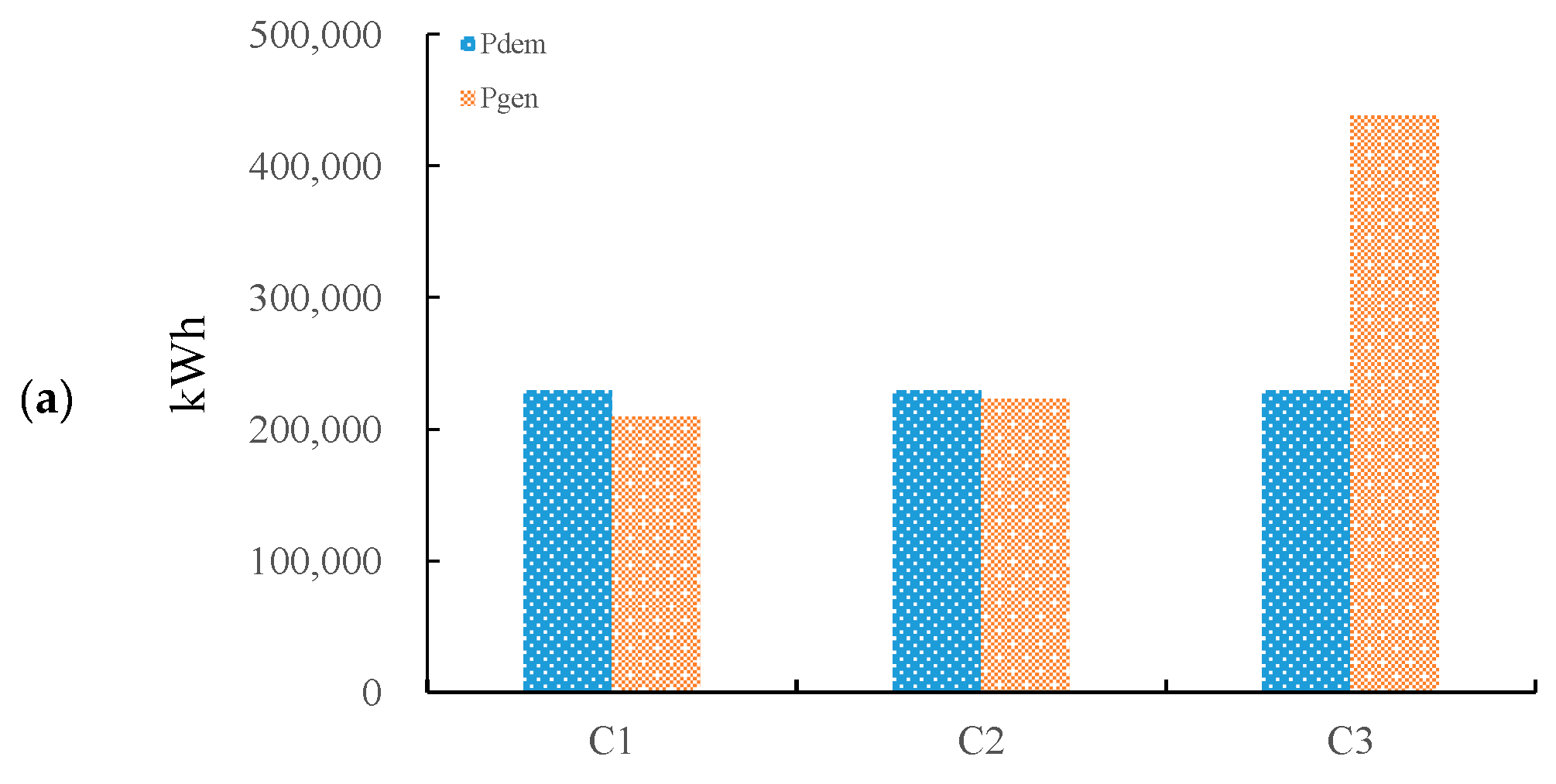
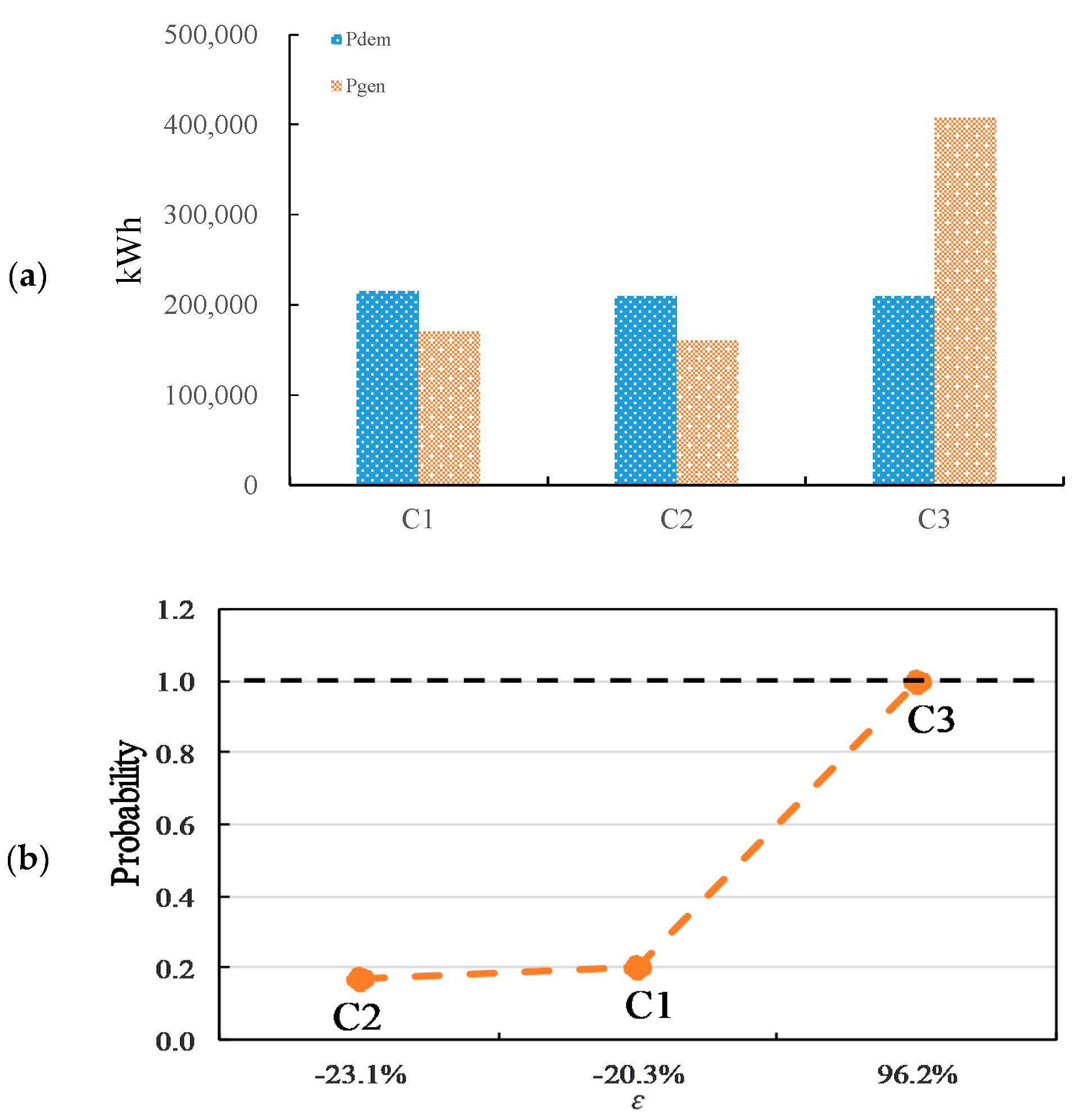
6.1. Performance Evaluation: Annual Energy Balance
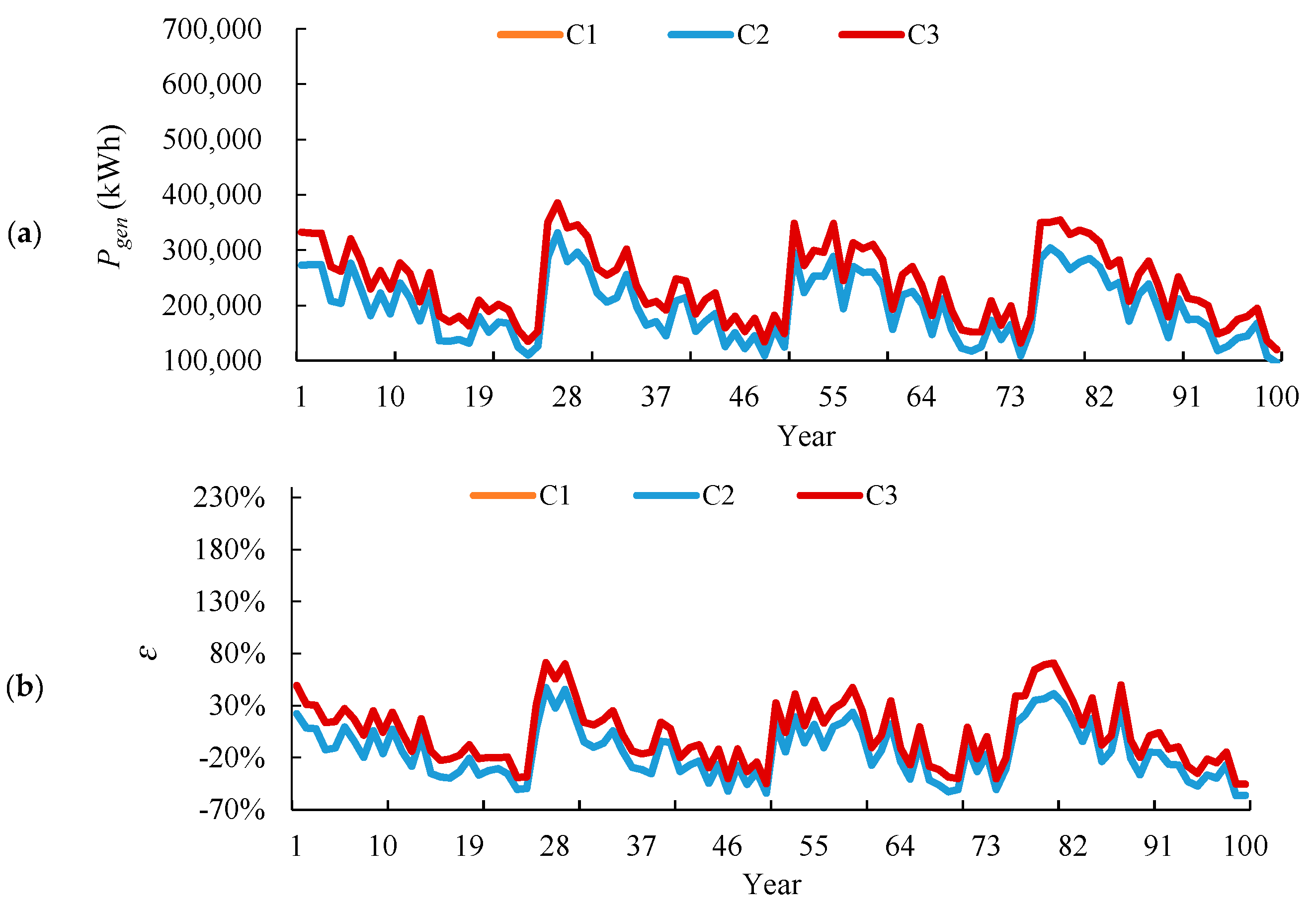
6.2. Performance Evaluation: 100-Years Energy Balance
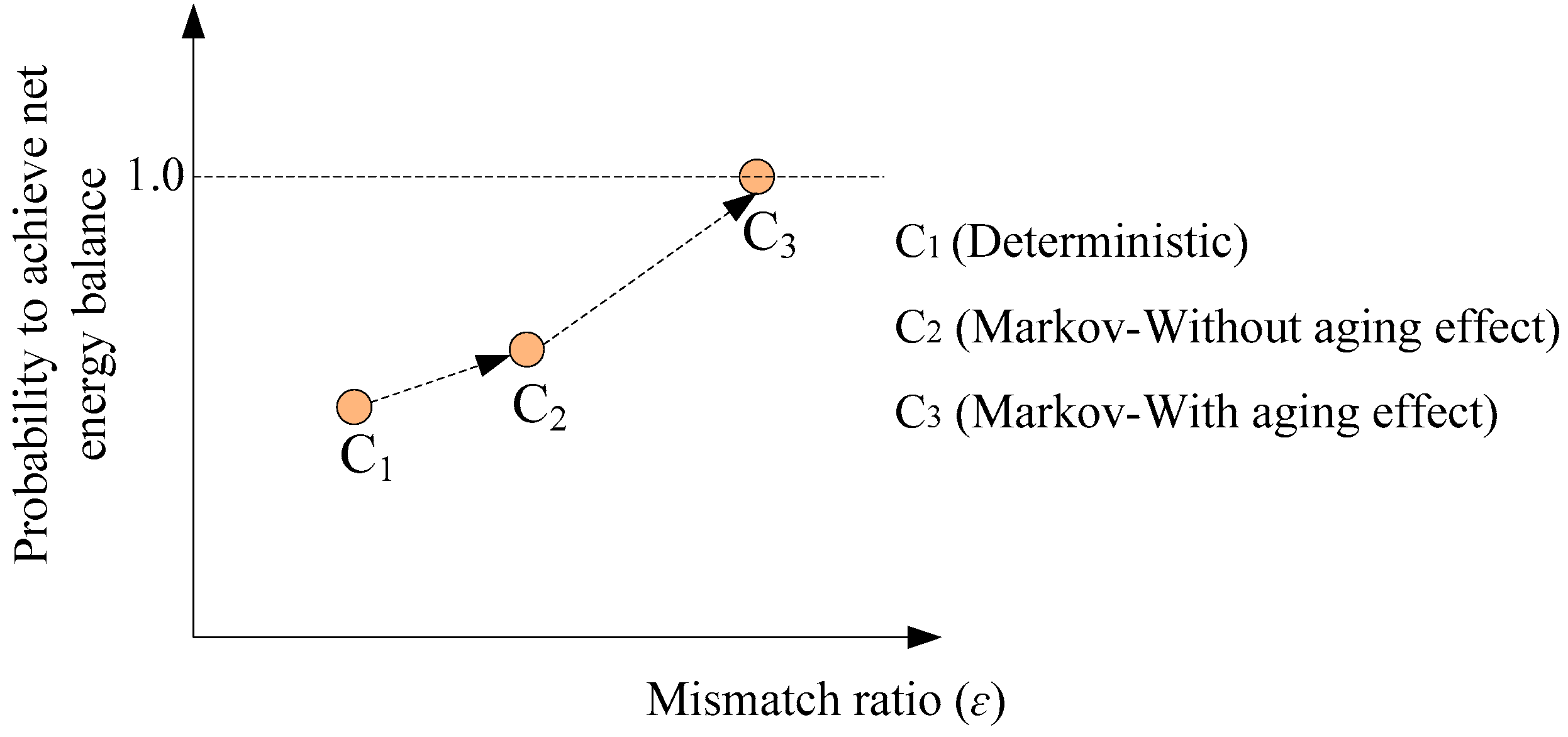
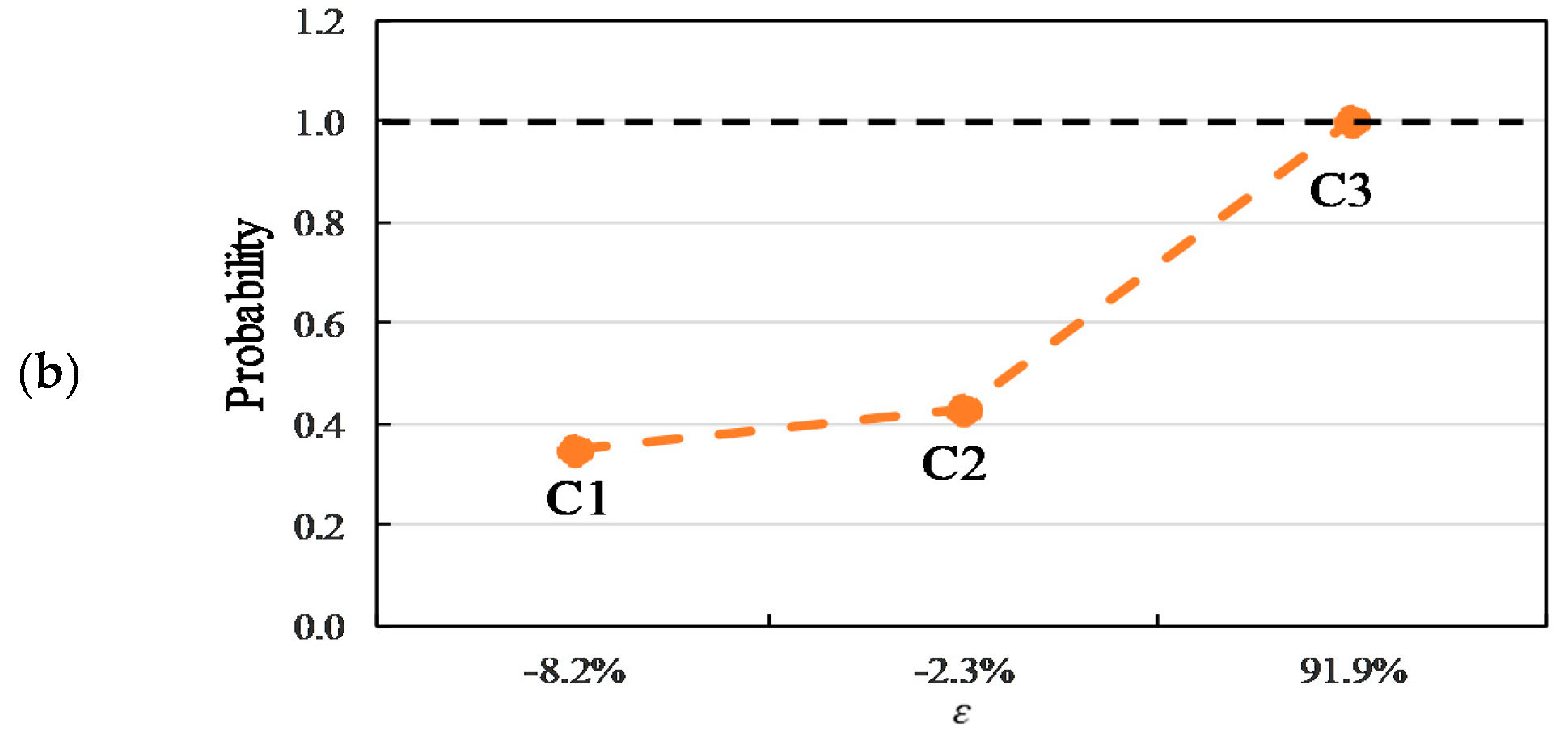
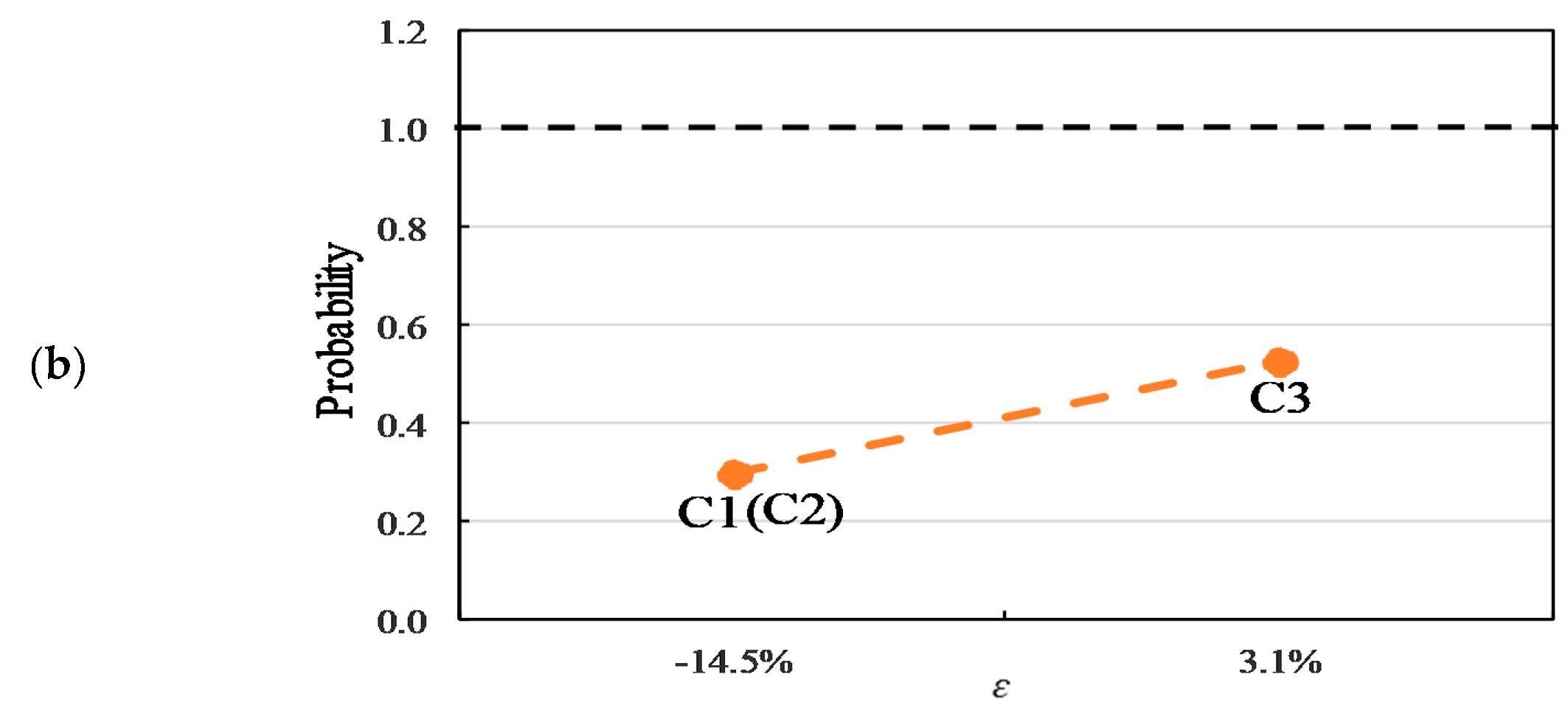
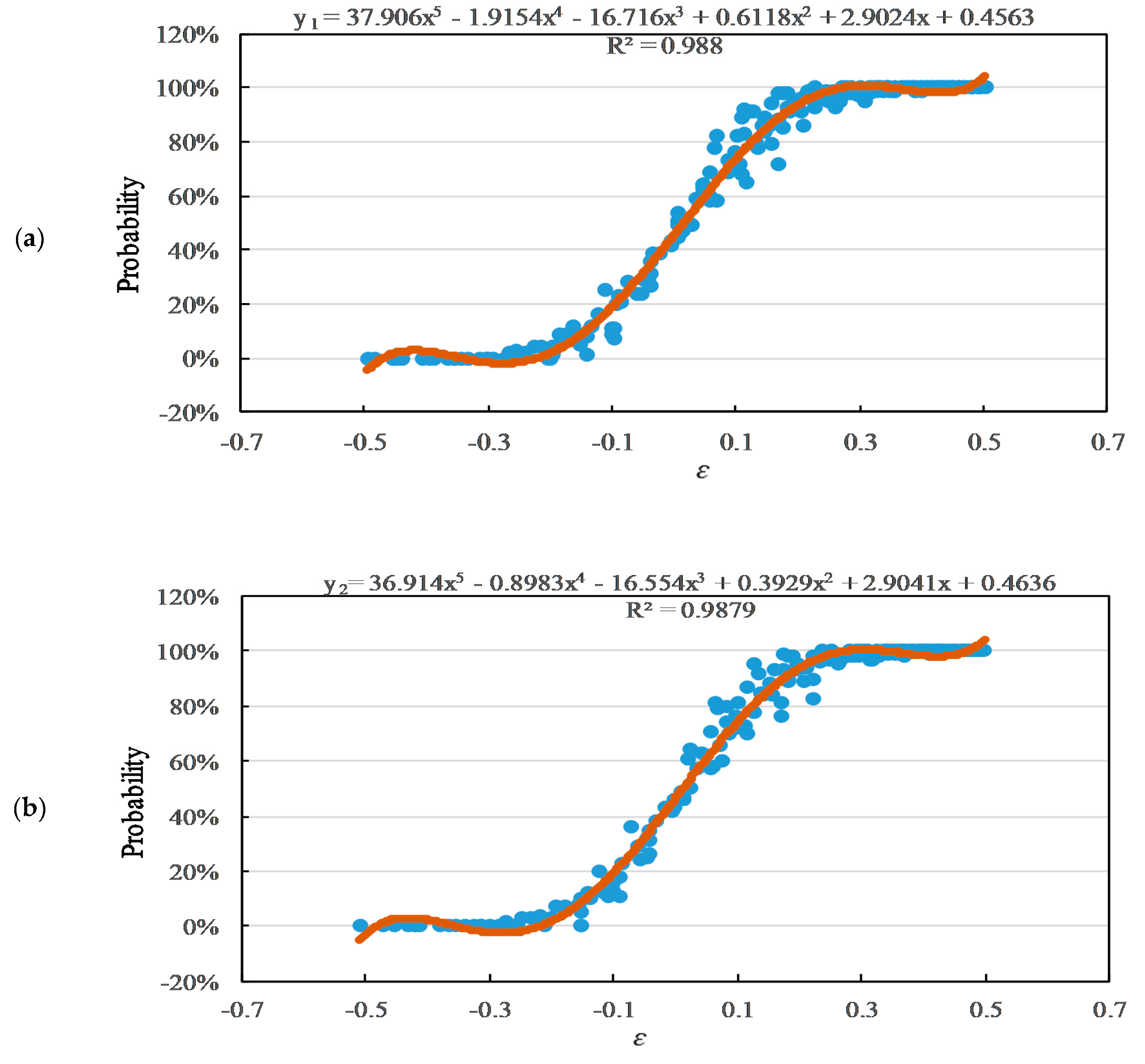
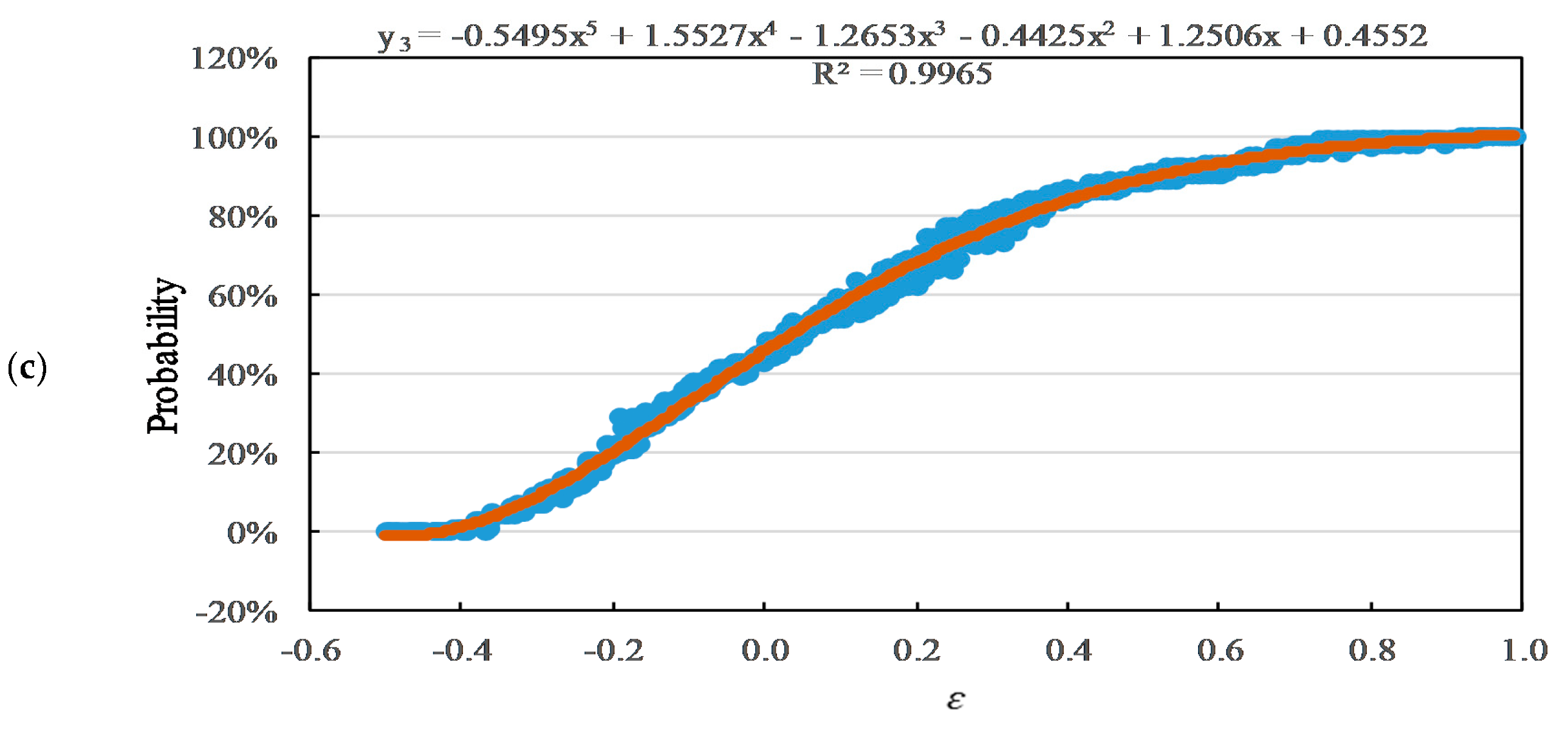
6.3. Relationship between Probabilities and Mismatch Ratio
- Case 1: y1 = 36.914x5 − 0.8983x4 − 16.554x3 + 0.3929x2 + 2.9041x + 0.4636; −0.5 < x < 0.5 (R² = 0.988);
- Case 2: y2 = 37.906x5 − 1.9154x4 − 16.716x3 + 0.6118x2 + 2.9024x + 0.4563; −0.5 < x < 0.5 (R² = 0.988);
- Case 3: y3 = -0.5495x5 + 1.5527x4 − 1.2653x3 − 0.4425x2 + 1.2506x + 0.4552; −0.5 < x < 1.0 (R² = 0.997).
7. Conclusions
- (1)
- In terms of the annual energy balance, the optimal size of RES in Case 3 (i.e., mismatch ratio of above 90%) was much larger than that in Case 1 and Case 2 (i.e., mismatch ratio of below 50%). Meanwhile, the aging effect of the generation system was identified to be a vital factor in system selection and the expected target for NZEB.
- (2)
- In terms of the 100-years energy balance, a much smaller RES size was required, especially in Case 3, where a remarkable reduction of mismatch ratio was found from 92% to 3%. Meanwhile, the number of years for net-zero energy balance was also identified to be an essential factor in system selection and expected target for NZEB.
- (3)
- The fitting formula with a good coefficient of determination was obtained to describe the relationship between the mismatch ratio and the probabilities for each case. In all cases, the probability to be NZEB was 0% under a mismatch ratio of below −0.4 and was around 45% under a mismatch ratio of 0.0. In addition, a mismatch ratio of over 1.0 was required to ensure a 100% NZEB in Case 3 when considering the aging effect, and it was over 0.6 that required for a 100% NZEB in Case 1 and Case 2.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| total area of PV [m2] | |
| blade area of wind turbine [m2] | |
| imposed cost | |
| BDG | biodiesel generator |
| CCHP | combined heating, cooling, and power |
| coefficient of performance of electric chiller | |
| coefficient of the wind turbine performance | |
| Pother | load |
| fuel consumption of the biodiesel generator | |
| grid interaction index | |
| normalized grid interaction index | |
| HVAC | heating, ventilation, and air conditioning |
| hourly irradiance [kWh/m2] | |
| initial cost | |
| water flow rate (m3/s) | |
| number of years satisfying NZEB requirement | |
| number of simulations [year] | |
| operation cost | |
| PV | photovoltaic |
| power generation of generator [kW] | |
| power generation of generator [kW] | |
| imported/exported electricity from/to the grid [kW] | |
| imported electricity to the building/exported electricity to the grid [kW] | |
| power consumption from other appliances [kW] | |
| power generation of photovoltaic [kW] | |
| power generation of wind turbine [kW] | |
| power consumption of electric chillers [kW] | |
| power consumption of cooling water pumps and chiller water pumps [kW] | |
| power consumption of cooling tower fans [kW] | |
| power consumption of AHU fans [kW] | |
| power consumption from equipment [kW] | |
| electrical supply [kW] | |
| electrical demand [kW] | |
| power generation from renewable energy system [kW] | |
| building cooling demand [kW] | |
| cooling provided by the absorption chiller [kW] | |
| cooling capacity of the absorption chiller [kW] | |
| cooling provided by electric chillers [kW] | |
| cooling capacity of the cooling tower [kW] | |
| RES | renewable energy system |
| annual total cost including initial cost, operation cost, and imposed cost [USD/year] | |
| normalized annual total cost including initial cost, operation cost, and imposed cost | |
| wind speed [m/s] | |
| ZCB | zero-carbon building |
| ZEB/NZEB | net-zero energy building |
| pump efficiency | |
| fan efficiency | |
| BDG efficiency | |
| heat recovery system efficiency | |
| PV module efficiency | |
| power conditioning efficiency | |
| combined efficiency of the generator and wind turbine | |
| air density [kg/m3] | |
| air flow rate [m3/s] | |
| mismatch ratio | |
| failure rate [1/h] | |
| repair rate [1/h] | |
| degradation rate of the component [1/h] | |
| lifetime of the component [years] |
References
- Recast, E.P.B.D. Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance Of Buildings (Recast). Available online: https://eur-lex.europa.eu/legal-content/en/TXT/?uri=CELEX%3A32010L0031 (accessed on 25 May 2020).
- Crawley, D.; Pless, S.; Torcellini, P. Getting to Net Zero; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009.
- Thalfeldt, M.; Pikas, E.; Kurnitski, J.; Voll, H. Facade design principles for nearly zero energy buildings in a cold climate. Energy Build. 2013, 67, 309–321. [Google Scholar] [CrossRef]
- Rabani, M.; Madessa, H.B.; Nord, N. A state-of-art review of retrofit interventions in buildings towards nearly zero energy level. Energy Procedia 2017, 134, 317–326. [Google Scholar] [CrossRef]
- Wu, W.; Skye, H.M.; Domanski, P.A. Selecting HVAC systems to achieve comfortable and cost-effective residential net-zero energy buildings. Appl. Energy 2018, 212, 577–591. [Google Scholar] [CrossRef] [PubMed]
- Costanzo, G.T.; Zhu, G.; Anjos, M.F.; Savard, G. A system architecture for autonomous demand side load management in smart buildings. IEEE Trans. Smart Grid 2012, 3, 2157–2165. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, S.; Zhao, Y.; Yan, C. Renewable energy system optimization of low/zero energy buildings using single-objective and multi-objective optimization methods. Energy Build. 2015, 89, 61–75. [Google Scholar] [CrossRef]
- Huang, Z.; Lu, Y.; Wei, M.; Liu, J. Performance analysis of optimal designed hybrid energy systems for grid-connected nearly/net zero energy buildings. Energy 2017, 141, 1795–1809. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Y.; Cheng, Y.; Huang, P.; Oladokun, M.O.; Lin, Z. Response-surface-model-based system sizing for Nearly/Net zero energy buildings under uncertainty. Appl. Energy 2018, 228, 1020–1031. [Google Scholar] [CrossRef] [Green Version]
- Maheri, A. Multi-objective design optimisation of standalone hybrid wind-PV-diesel systems under uncertainties. Renew. Energy 2014, 66, 650–661. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Zhang, X.-P.; Huang, Z.; Lu, J.; Wang, D. Impact of introducing penalty-cost on optimal design of renewable energy systems for net zero energy buildings. Appl. Energy 2019, 235, 106–116. [Google Scholar] [CrossRef]
- Yu, Z.J.; Chen, J.; Sun, Y.; Zhang, G. A GA-based system sizing method for net-zero energy buildings considering multi-criteria performance requirements under parameter uncertainties. Energy Build. 2016, 129, 524–534. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, P.; Huang, G. A multi-criteria system design optimization for net zero energy buildings under uncertainties. Energy Build. 2015, 97, 196–204. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, S.; Yan, C.; Huang, Z. Robust optimal design of renewable energy system in nearly/net zero energy buildings under uncertainties. Appl. Energy 2017, 187, 62–71. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. A feasibility study of a stand-alone hybrid solar–wind–battery system for a remote island. Appl. Energy 2014, 121, 149–158. [Google Scholar] [CrossRef]
- Huang, P.; Huang, G.; Sun, Y. A robust design of nearly zero energy building systems considering performance degradation and maintenance. Energy 2018, 163, 905–919. [Google Scholar] [CrossRef]
- Maleki, A.; Khajeh, M.G.; Ameri, M. Optimal sizing of a grid independent hybrid renewable energy system incorporating resource uncertainty, and load uncertainty. Int. J. Electr. Power Energy Syst. 2016, 83, 514–524. [Google Scholar] [CrossRef]
- Bekele, G.; Tadesse, G. Feasibility study of small Hydro/PV/Wind hybrid system for off-grid rural electrification in Ethiopia. Appl. Energy 2012, 97, 5–15. [Google Scholar] [CrossRef]
- Hassoun, A.; Dincer, I. Development of power system designs for a net zero energy house. Energy Build. 2014, 73, 120–129. [Google Scholar] [CrossRef]
- Ekren, O.; Ekren, B.Y. Size optimization of a PV/wind hybrid energy conversion system with battery storage using simulated annealing. Appl. Energy 2010, 87, 592–598. [Google Scholar] [CrossRef]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-objective optimal design of stand-alone hybrid energy system using entropy weight method based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef] [Green Version]
- Harkouss, F.; Fardoun, F.; Biwole, P.H. Multi-objective optimization methodology for net zero energy buildings. J. Build. Eng. 2018, 16, 57–71. [Google Scholar] [CrossRef]
- Karki, R.; Billinton, R.; Verma, A.K. Reliability Modeling and Analysis of Smart Power Systems; Springer Science & Business Media: New York, NY, USA, 2014; ISBN 8132217985. [Google Scholar]
- Alvarez-Alvarado, M.S.; Jayaweera, D. Aging Reliability Model for Generation Adequacy. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Alvarez-Alvarado, M.S.; Jayaweera, D. Reliability model for a Static Var Compensator. In Proceedings of the 2017 IEEE Second Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; pp. 1–6. [Google Scholar]
- Alvarez-Alvarado, M.S.; Jayaweera, D. A New Approach for Reliability Assessment of a Static V ar Compensator Integrated Smart Grid. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; pp. 1–7. [Google Scholar]
- Gen, B. Reliability and Cost/Worth Evaluation of Generating Systems Utilizing Wind and Solar Energy. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]


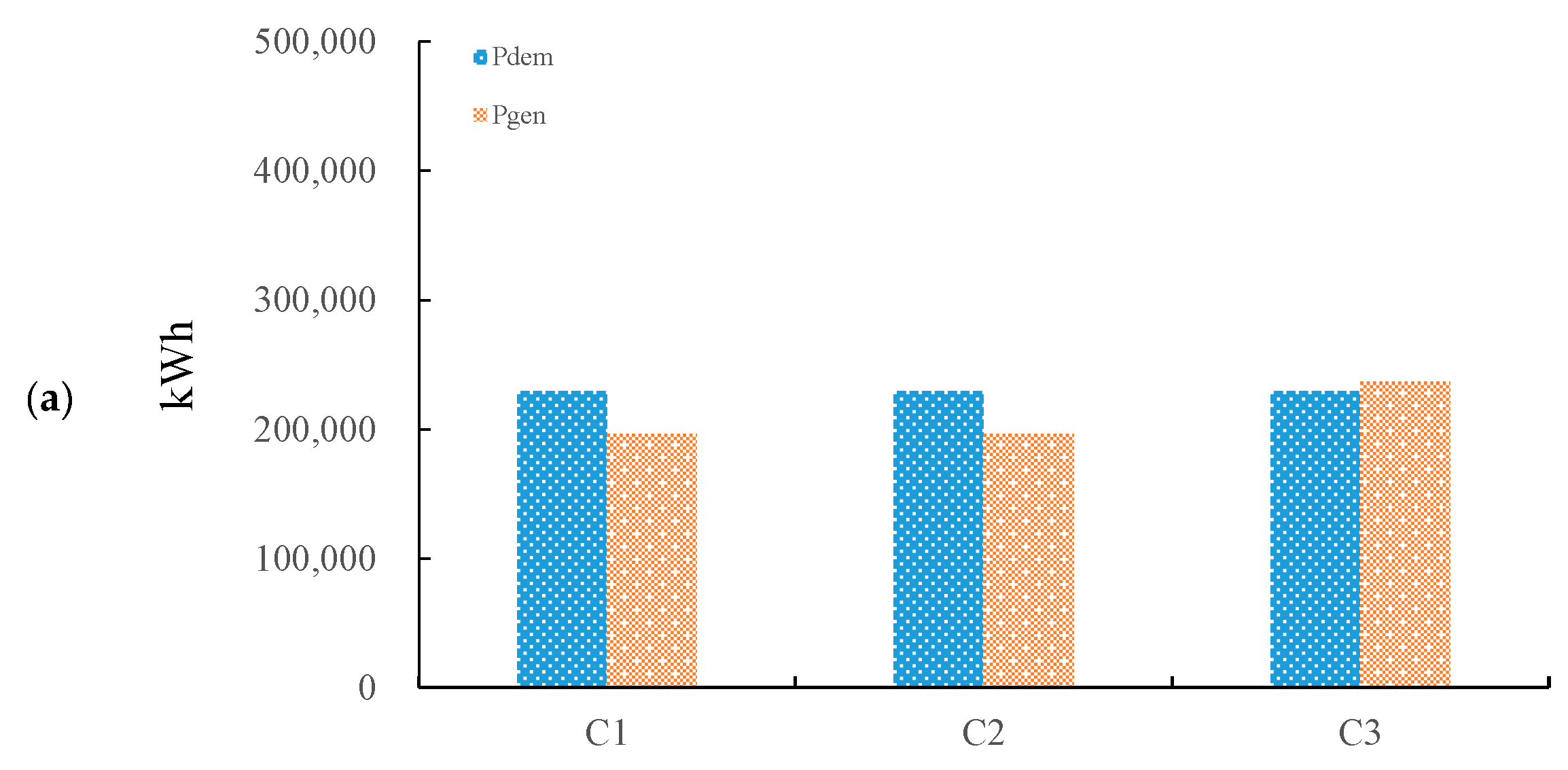

| Ref. | Energy Production System | Uncertainty/Reliability Analysis | Factors Considered for Reliability Analysis |
|---|---|---|---|
| [7] | PV/WT/BDG | N | None |
| [8] | PV/WT, PV/BDG, WT/BDG, PV/WT/BDG | Y | Solar radiation, wind velocity, cooling load, other electricity load. |
| [9] | PV/WT/Battery | Y | Physical parameters (e.g., U value of window, shading coefficient), design parameters (e.g., occupant number, light ratio), scenario parameters (e.g., ambient temperature, ambient relative humidity). |
| [10] | PV/WT/BDG | Y | Solar radiation, wind speed, demand load, wind turbine power coefficient model, PV array efficiency. |
| [11] | PV/WT/BDG | Y | Solar radiation, wind velocity, cooling load, other electricity load. |
| [12] | PV/WT/TES/EES | Y | Ambient temperature, relative humidity, solar radiation, and wind speed. |
| [13] | PV/WT | Y | Physical parameters (e.g., U value of window, shading coefficient), design parameters (e.g., occupant number, light ratio), scenario parameters (e.g., ambient temperature, ambient relative humidity). |
| [14] | PV/WT/BDG | Y | Solar radiation, wind velocity, cooling load, other electricity load. |
| [15] | PV/WT/Battery | Y | Solar radiation, wind speed, and demand load. |
| [16] | PV/WT/Battery | Y | 18 scenario parameters (e.g., occupant density, infiltration rate, solar radiation), 5 design parameters (e.g., window/wall thermal resistance, chiller capacity, and COP), degradation parameters of HVAC system, PV array, WT, energy storage system. |
| [17] | PV/WT/Battery | Y | Solar radiation, wind speed, and load. |
| [18] | PV/WT/Hydro | Y | Diesel cost, PV capital, and replacement cost. |
| [19] | PV/WT/BDG/Battery | Y | Different parameters of the house, e.g., the area of the house. |
| [20] | PV/WT/Battery | N | None. |
| [21] | PV/WT/BDG/Battery | Y | Cost of PV panel, wind turbine, as well as fossil fuel. |
| [22] | PV/SDHW | N | None. |
| Generation | |||
|---|---|---|---|
| PV | 3 | 90 | 25 |
| WT | 4.6 | 80 | 25 |
| BDG | 9.2 | 50 | 25 |
| Generation | Availability | ||
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| PV | 1.00 | 0.97 | 0.42–0.94 |
| WT | 1.00 | 0.96 | 0.41–0.93 |
| BDG | 1.00 | 0.95 | 0.41–0.92 |
| Items | Parameters | Conditions |
|---|---|---|
| Design variables | WT [kW] | 0:20:160 |
| BDG [kW] | 20:20:100 | |
| PV [m2] | 0:200:4000 | |
| Energy system | Heat recovery system efficiency [%] | 80 |
| Biodiesel generator efficiency [%] | 30 | |
| Chiller coefficient of absorption [%] | 70 | |
| Lifetime for biodiesel generator [year] | 25 | |
| Lifetime for photovoltaic [year] | 25 | |
| Lifetime for wind turbine [year] | 25 | |
| Rated power of electric chillers [kW] | 70 × 3 | |
| Rated power of absorption chillers [kW] | 70 × 1 | |
| Price | Unit price of biodiesel generator [USD/kW] | 205.53 |
| Unit price for photovoltaic [USD/m2] | 378.17 | |
| Unit price for wind turbine [USD/kW] | 714.29 | |
| Oil price [USD/l] | 1.3 | |
| Delivered/Exported price [USD/kWh] | 0.13/0.065 | |
| Uncertain parameters | Solar radiation () | Uniform () |
| Wind velocity () | Uniform () | |
| Cooling load () | Uniform () | |
| Other load () | Uniform () |
| Case | Indicator (Objective) | WT (kW) | BDG (kW) | PV (m2) | F [–] | ɛ [%] |
|---|---|---|---|---|---|---|
| 1: Deterministic | 160 | 20 | 200 | 0.71 | 46.4 | |
| 40 | 60 | 800 | 0.76 | 32.5 | ||
| 2: Markov—No aging effect | 160 | 20 | 400 | 0.74 | 49.1 | |
| 40 | 80 | 400 | 0.77 | 22.8 | ||
| 3: Markov—aging effect | 160 | 20 | 3600 | 1.52 | 91.2 | |
| 160 | 80 | 2200 | 2.37 | 96.2 |
| Case | Indicator (Objective) | WT (kW) | BDG (kW) | PV (m2) | F [–] | ɛ [%] |
|---|---|---|---|---|---|---|
| 1: Deterministic | 160 | 20 | 0 | 0.69 | 36.0 | |
| 40 | 60 | 200 | 0.57 | 0.52 | ||
| 2: Markov—No aging effect | 160 | 20 | 0 | 0.69 | 29.9 | |
| 40 | 60 | 400 | 0.60 | 5.05 | ||
| 3: Markov—aging effect | 160 | 20 | 600 | 0.78 | 3.05 | |
| 60 | 60 | 1200 | 1.03 | 1.34 |
| ɛ. | C1 | C2 | C3 |
|---|---|---|---|
| <−0.4 | 0.0% | 0.0% | 0.0% |
| −0.4 | 2.7% | 2.3% | 1.1% |
| −0.2 | 1.9% | 1.8% | 20.0% |
| 0.0 | 45.6% | 46.4% | 45.5% |
| 0.2 | 93.7% | 93.8% | 68.0% |
| 0.4 | 98.6% | 98.4% | 83.8% |
| 0.6 | 100.0% | 100.0% | 93.1% |
| 0.8 | 100.0% | 100.0% | 98.1% |
| ≥1 | 100.0% | 100.0% | 100.0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Alghassab, M.; Alvarez-Alvarado, M.S.; Gunduz, H.; Khan, Z.A.; Imran, M. Optimal Distribution of Renewable Energy Systems Considering Aging and Long-Term Weather Effect in Net-Zero Energy Building Design. Sustainability 2020, 12, 5570. https://doi.org/10.3390/su12145570
Lu Y, Alghassab M, Alvarez-Alvarado MS, Gunduz H, Khan ZA, Imran M. Optimal Distribution of Renewable Energy Systems Considering Aging and Long-Term Weather Effect in Net-Zero Energy Building Design. Sustainability. 2020; 12(14):5570. https://doi.org/10.3390/su12145570
Chicago/Turabian StyleLu, Yuehong, Mohammed Alghassab, Manuel S. Alvarez-Alvarado, Hasan Gunduz, Zafar A. Khan, and Muhammad Imran. 2020. "Optimal Distribution of Renewable Energy Systems Considering Aging and Long-Term Weather Effect in Net-Zero Energy Building Design" Sustainability 12, no. 14: 5570. https://doi.org/10.3390/su12145570
APA StyleLu, Y., Alghassab, M., Alvarez-Alvarado, M. S., Gunduz, H., Khan, Z. A., & Imran, M. (2020). Optimal Distribution of Renewable Energy Systems Considering Aging and Long-Term Weather Effect in Net-Zero Energy Building Design. Sustainability, 12(14), 5570. https://doi.org/10.3390/su12145570








