Strengthening the Statistical Summaries of Economic Output Areas for Urban Planning Support Systems

Abstract

Despite efforts to research the transformation of urban structures, difficulties remain in estimating credible statistical information in the existing census output areas. This research proposes two alternatives to construct new economic output areas by considering the socioeconomic homogeneities where economic activities occur. In particular, we developed an algorithm to aggregate new economic zones into the existing census output areas. For this purpose, we utilized matrix systems that consider population sizes, the number of workers and workplaces, and a combination of these factors in the two alternatives. Urban planners need to provide credible statistical summaries at the census output areas. Our findings contribute to this research by suggesting that it is essential to consider the population and the number of workplaces with socioeconomic homogeneity. These findings will also help other researchers who study the transformation of urban structures because they can use more reliable statistical information for their simulation model that predicts an urban structure. Furthermore, it will help improve the national statistics office’s roles for public and urban planners and provide an important source for the national statistical geographic information services.

1. Introduction

As stressed by many speakers at the United Nations 2030 Agenda for Sustainable Development in 2015 and 2019, realistic and robust statistical data are seen as critical [1,2]. Without reliable and robust measurements of where economic activities particularly occur, it would not be easy to successfully achieve sustainable development goals and monitor sustainable transformations of urban environments. The economy is one of the three pillars (economy, society, and the environment) of sustainability. An economic factor is often used for assessing the performances of cities. Consequently, statistical information in an urban area is seen as more important than ever to accurately monitor sustainable transformations of urban environments and as one of the important indicators of urban sustainability. However, each country has used different types of theories or issues that determine economic zones or census output areas in a hierarchy of census geographic units because transformations of urban structures are complex and depend on a variety of factors.

Normally, the transformations have been affected by the different types of sectors [3,4,5], the size of sub-centers [6,7], the population [8,9], employment densities [10,11,12,13], transportation costs [14,15], agglomeration patterns of the commercial establishment [16,17], and land-use planning and regulations [18]. As a result, many researchers have paid attention to the structure of urban transformation, but few papers have discussed statistical information in the small census output areas or economic zones. Credible statistical summaries in economic zones can be one of the important factors supporting the right policy-making systems or planning support systems [17,19]. As noted above, there are a variety of theories or computational approaches that construct smaller sub-zones that are spatially aggregated. The approaches help resolve spatial location concerns and validate statistical information in a small economic zone [20,21,22]. Because each country has used a different hierarchy of census geographic units, different statistical summaries in the same economic zones may result [22]. As a result, statistical summaries can often be overestimated or underestimated. Thus, urban planners need to construct an optimal economic district with the proper homogeneity of the geographic area.

In response to the reliable and robust statistical data in the existing census output areas, this research raised the following questions: (1) Do the existing census output areas that are aggregated guarantee the homogeneity of the geographic area? (2) What are the scientifically defensible approaches to accurately estimate statistical information about where economic activity occurs in the census output areas? and (3) What types of social and economic factors should be considered to maintain the consistency of the statistical information in the census output areas? With respect to these considerations, this study proposes two main alternatives to constructing new census output areas within the current basic unit districts. We are particularly interested in a central business district where economic activities frequently occur.

In this study, we developed a new algorithm to delimit new census output areas that contain reasonable statistical summaries of the number of workers resulting from the basic unit districts. Note that a basic unit district is the smallest unit (i.e., zone) in the current hierarchy of census geographic units of the study area [23]. The smallest districts are delimited through physical characteristics such as roads, creeks, railroads, and mountain ranges. Districts are also determined through a block unit or the smallest administrative boundaries in an urban area [23]. The existing census output areas are determined by the population size (at least 300, proper 500, and a max of 1000), type of residency and property values, shapes of census output areas, and more. One census output area includes multiple basic unit districts and is an upper-level unit of the basic unit districts and a lower-level unit to administrative boundaries [22]. This study used matrix systems that consider population sizes, the number of workers and workplaces, and a combination of these factors in two main alternatives. The factors are quantitatively assessed through descriptive statistics and used as weighted values in a matrix that computationally creates new economic census zones. Accordingly, this research constructs new economic census zones that satisfy the reliable statistical summaries of where economic activities highly occur. The economic zones include the existing basic unit districts. The following show the key contributions of this work:

• Through this research, we expect that the resultant outputs will be used for a new method to determine business districts or economic census zones in a country. It is important for urban planners to use scenario-based approaches that directly apply a new policy to reality.
• On the research side, urban scientists can statistically monitor how the economic zones have been transformed over time and consider the social and economic homogeneities that contain a combination of populations, workers, and workplaces.
• Furthermore, this approach will contribute to individuals who would like to use reliable statistical summaries for general data analysis.
• Additionally, due to the issues related to maps’ aerial unit problem, statistical summaries for the same location can be overestimated or underestimated. However, the outputs of this work will be used for urban planners to provide more accurate national services associated with statistical geographic information services.

Accordingly, this research assists in estimating reliable and accurate statistical information that is used for the development of a sustainable economy and high-quality spatial data. This paper is structured as follows. In Section 2, we describe the previous studies related to the automated zoning program (AZP) and the existing small census output areas used in multiple countries. Furthermore, modifiable areal unit problems are addressed in the existing census output areas. In Section 3, we address the primary research approaches. Section 4 provides the results obtained from the primary approaches. Finally, in Section 5, we discuss the significant contribution of this research, and then provide our conclusions in Section 6.

2. Related Studies

2.1. Literature Review

This research focuses on previous studies in two ways. First, this research determines the factors needed to analyze urban structures, and second, the research methods construct a smaller geographic unit (i.e., census output area) in an urban area or a city.

First, a plethora of studies have focused on transforming urban structures in terms of urban sprawl and re-agglomeration. Unquestionably, spatial transformations of urban structures have become increasingly decentralized over time in contemporary cities. It is a major characteristic of cities with particularly rapid economic growth. The urban structure has transformed monocentric, mixed, or polycentric structures over time [13,24,25,26,27,28].

During the nighttime, a city center with a business district becomes “hollowed-out” because the economically active population has left the city—commonly known as a “doughnut effect” [29]. The doughnut phenomenon occurs often because businesses and people move into the outskirts of the city [29]. Even though most jobs were historically located in the city center [11,13], McMillen pointed out that employment in large metropolitan areas has become increasingly decentralized, and the percentage of suburban residents working in the city has declined [10,11,13]. In addition, large sub-centers can look similar to a traditional central business district. Thus, the contemporary city is seen as a polycentric city that forms a metropolitan area with a strong central business district and large sub-centers [24,25,26,27]. In general, the processes of sprawl or decentralization have heavily relied on people, transportation, land use planning and its regulations, and employment opportunities [13,18]. Accordingly, credible statistical summaries in central business districts are an important factor for understanding how an urban structure has been transformed. However, each of the countries uses a different theory to delimit urban structures or economic places. Below, we discuss how other countries use various criteria for economic census places or small statistic areas.

The United States uses an economic census place that expands or contracts over time as the population and commercial activity increase or decrease [30]. The Economic Census is the U.S. Government’s official five-year measure of American businesses and the economy. However, the economic census place is used to provide detailed information about employers and businesses from the Economic Census and the Survey of Business Owners. The economic census place is composed of incorporated places, census-designated places, minor civil divisions, and balances of minor civil divisions or counties [31]. Some of the economic places are legally defined boundaries, and the economic places cannot be over the county boundaries. In general, the US follows the following three criteria: (1) the economic place must have at least 2500 people; (2) according to the results of the American Community Survey obtained between 2016 and 2010, the economic place must include at least 2500 jobs; and (3) after the 2010 Census Survey, there are new places with a population of at least 2500 people [30]. When these requirements are met, without aggregating procedures of existing boundaries of economic places, the new places can be defined as new economic places.

England uses output areas to represent the geographical distributions of residents and residences; however, these distributions are different from those of workplaces and workers. Thus, the government uses workplace zones that are based on data from the 2011 Census of England and Wales to better represent the distributions of the working population [32]. Using automated zone-design techniques, workplace zones are delimited via splitting, merging, or retaining the 2011 output areas. Moreover, workplace zones are determined by the number of workers and industrial factors at the small area level, i.e., the automated processes consider similar characteristics of the workers and workplaces [32,33,34].

The design criteria of the workplace zones are that all zones must be “above,” “within,” or “below” thresholds, which are homogeneous in population size and as compact in shape as possible [33]. The abovementioned threshold zones need to be split and must include over three postal codes. The below-threshold zones need to be merged into one or more zones with fewer than three postal codes. For example, the below-threshold zones are only allowed to merge with other below-threshold zones or within-threshold zones. Within-threshold zones must include at least three postal codes and be above the lower threshold (greater than 200 people) and below the upper threshold (fewer than 625 people). England inputted criteria into an AZTool, which is an automated zone design tool developed by David Martin and Samantha Cockings. The AZTool is able to make a spatial unit of workplace zones bigger, the same, or smaller compared to the spatial scale of the output areas using delimitation processes with splitting, merging, or retaining. Based on the new workplace zones, England compared descriptive statistics (mean and standard deviation (SD)) of the middle layer super output areas with those of the workplace zones. When comparing SDs in a district, the middle layer super output areas are basically higher than the workplace zones; thus the mean of the SD was used to compare them. Consequently, the outputs of the workplace zones showed better results. Using the algorithm in the AZTool, 48 census variables were selected to differentiate different types of workers and workplaces. The 48 variables were grouped by four domains: (1) composition of the workplace population; (2) composition of the built environment; (3) socioeconomic characteristics of the workplace population; and (4) employment characteristics of the workplace population [35]. Furthermore, K-means clustering was used to generate seven sub-groups: (1) retail, (2) top jobs, (3) metro suburbs, (4) suburban services, (5) manufacturing and distribution, (6) rural, and (7) servants of society.

Note that other countries such as Norway or Canada use similar concepts for determining economic regions. Norway is divided into 90 economic regions that are designed for three data sets: commuting data, wholesale and retail trade statistics, and population data [36]. Furthermore, Canada uses economic regions that maximize social and economic homogeneities in the same area and minimize social and economic homogeneity between the regions.

To summarize, the economic census place in the United States was not determined by a complex algorithm or an automated process. Norway defined the economic regions to explain economic activities rather than to delimit a spatial unit of the economic place. Canada designed its economic regions after considering social and economic homogeneity [37]. England considered the workers and workplaces and used a clustering technique to generate social and economic variables. Furthermore, based on the AZ-based algorithm, their small census areas were automatically merged and split.

Regarding the research methods needed to construct a smaller geographic unit, many researchers have used a raster-based model with a certain cell size. The cell sizes (i.e., zones) are determined by complex computational approaches and are statically aggregated through the homogeneity or variables of each cell. In their most recent research, Yang et al. pointed out that urban planners have dealt with issues such as the jobs–housing balance [38] and the ecological capacity of the city center [39]. They proposed a new method by considering the preference of emerging economic sectors and their associated workers to forecast agglomeration patterns for the formation of newer employment sub-centers [16]. The statistical information in a city or a suburb is essential to managing the land use and to predicting the transformation process of an urban structure. In general, current census output areas rely heavily on geographic features [40], and their boundaries in multiple scales are determined by computational algorithms or various criteria. Based on a preferred algorithm, it may generate a different size of the smallest geographic unit.

The process of aggregation makes it difficult to assess the spatial location and geographic accuracy of the simulation because of the size of the cell. It means that the smaller a scale, the more accurate the simulation result or representation of an urban structure [17,41]. Thus, others have applied alternative approaches using a fine spatial scale, which helps to more precisely assess the urban structure or processes of sprawl and aggregation for planning purposes. Examples include a confusion matrix [42,43,44], fitness regression [45], or a receiver operating characteristic curve [46]. Other researchers proposed a zonal aggregation approach to generate smaller cells with discrete subdivisions that improve the validation process of how urban areas are transformed [21,22]. The models indicate that the approaches in the large-scale regional models are useful for long-term planning.

However, when compared with reality, a small cell size is still not enough to validate a small zone because an area represented by one cell can be off. Pan and Deal pointed out that a smaller cell at a fine scale is useful for a large region, but there are still limitations of the models. To overcome these limitations, Pan and Deal proposed the use of a multi-resolution fitting process for improving the objectiveness and reasonableness of the planning support system’s spatial model applications [17]. Dean and Lit also used machine learning methods to forecast the transformation of future urban development [19,44]. However, the models are not proper for providing existing statistical information in a small census output area for general purposes.

Consequently, although many researchers have focused on investigating urban structures and developing algorithms for zonal aggregation methods, few researchers have focused on statistical information in the urban structure, particularly at census output areas or where economic activity occurs. In other words, the existing census output areas in a hierarchy of census geographic units do not reflect the reality of the current spatial urban structure. It may cause underestimated or overestimated statistical summaries, particularly in areas where economic activities occur. Thus, to fill this gap and strengthen the existing economic census output areas, this study proposes two alternatives using a combination of factors—population, workers, and workplaces—and develops an algorithm to newly construct census output areas, including the smallest basic unit districts with national statistical information. Accordingly, this research assists in estimating reliable and accurate statistical information, which is used for the development of a sustainable economy and high-quality spatial data.

2.2. Problem Statement

As stated in Section 2.1, there are gaps between previous research on urban structures and the statistical information in small census economic areas (i.e., COAs). To provide reliable statistical information about COAs, it is essential to reevaluate and re-aggregate the statistical summaries in existing COAs. Figure 1 shows how the current COAs produce different statistical summaries in the study area. The area of interest in this study is the Gangnam district (yellow boundary in Figure 1a), which is one of the 25 districts in the city of Seoul, South Korea, and a central business district (Figure 1a). According to the 2018 census data, the total population of the Gangnam district is 544,257. The area of interest is the third-largest district in Seoul, with an area of 39.5 km². The district consists of a mix of many businesses and residential areas with extremely expensive real estate [47]. Figure 1b illustrates a population density map describing how many individuals are in a given area, and Figure 1c shows the number of workers in the current basic unit districts (BUDs).

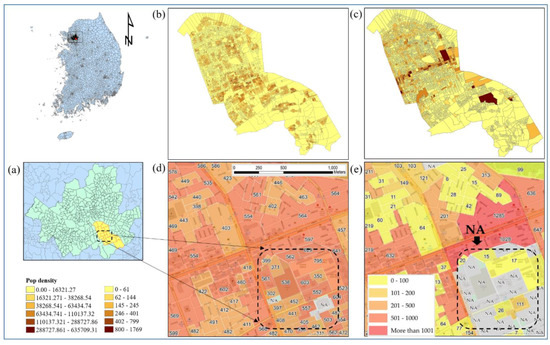
Figure 1. Study area: (a) Gangnam district of Seoul City, (b) the size of the population in basic unit districts (BUDs), (c) the number of workers in BUDs, (d) the size of the population in census economic areas (COAs), and (e) the actual number of employees in COAs.

The population is slightly spatially dispersed but mostly centralized in the study area. Most workers are clustered at the center but are slightly dispersed. The COAs were delimited through AZP algorithms, which consider the statistical homogeneity and heterogeneity of the geographic feature and industry-related factors such as the number of employees and workplaces. The AZP has a computationally intensive procedure, which seeks to optimize areas such as zonal compactness or social homogeneity and recombine a large set of block polygons into a smaller set of output areas [35]. The algorithm uses iterative processes to split, merge, and recombine objects until a smaller set of census output areas are determined. Moreover, the algorithm optimizes COAs that are delimited by considering population sizes (population of more than 500) and indices of social and economic homogeneity. Therefore, COAs have been consistently updated over the past 10 years; consequently, the existing number of COAs increased from 390,000 to 460,000 [48].

Despite these efforts, there are still various problems in the analysis of community development and business districts, particularly regarding the use of statistical summaries associated with the number of workers and workplaces in the existing COAs. For example, when using statistical summaries in the existing COAs, the number of summaries can often be overestimated or underestimated because of the doughnut phenomenon, which occurs as businesses and people move into the outskirts of the city [29]. Furthermore, if the number of workers in the smallest geographic unit is small (e.g., a few employees in an economic zone), the number cannot be published publicly because of privacy issues. Thus, it is necessary to improve the existing AZP algorithms by considering the number of employees and workplaces.

As shown in Figure 1d,e, when referring to the existing COAs (Figure 1e), the number of employees in the dashed line is estimated as “Not available” (NA), but the population size in Figure 1d is approximately 8800, which is large enough. The total number was summed from the population size in the BUD, which is the smallest geographic unit officially used in South Korea [23,49]. However, the statistical summaries of employees are not available because the numbers are so low that it will be easy for the public to determine. Consequently, they have underestimated values. Furthermore, when considering different homogeneities, the sizes of the census output areas may vary, but they will also cause overestimated or underestimated statistical summaries.

The geography field has addressed this modifiable areal unit problem (MAUP), which affects aggregated geographical boundaries [50,51]. The MAUP refers to the fact that the observed values will vary depending on how the census output areas are delimited. Note that the MAUP is composed of a scale and a zoning effect. The scale effect refers to the size of the aerial units, whereas the zoning effect occurs when the number of spatial units of the measure remains the same; however, there are changes in the boundaries and shapes [52]. The zoning effect can lead to differences in the analytical results of the same input data [53,54]. The problem presented in Figure 1 is associated with the zoning effect. The delimitation of the census output area plays a key role in estimating the exact statistical information, particularly for business analysis. Although the AZP algorithm considered the statistical homogeneity and heterogeneity, industry-related factors are more important for analyzing the area of trade happening in economic places. The existing aggregated districts cannot guarantee the homogeneity of the geographic areas because there are many differences between the total population and the number of workers in the existing COAs; therefore, the numbers of workers or workplaces can be overestimated or underestimated. The current criteria used in the hierarchy of census geographic units are uncertain.

3. Methods

3.1. Schematic Diagram

This study proposes two main alternatives that help construct new census output areas where economic activities heavily happen. The following shows a schematic diagram developed in this research.

As shown in Figure 2, the first alternative considered population, the number of workers, and the number of workplaces in a matrix (Figure 2(A1)). The second alternative considered only the number of workers and the number of workplaces in a matrix (Figure 2(A2)). The first alternative had three scenarios: population (Scenario 1.1), number of workplaces (Scenario 1.2), and a combination of the population and the number of workplaces (Scenario 1.3). This approach integrated information of the workspace into the information of the existing COAs, which is beneficial for individuals using the workplace-centered statistical information. The second alternative only considered new economic zones without considering the existing COAs. It also had three scenarios: the number of workers (Scenario 2.1), the number of workplaces (Scenario 2.2), and a combination of the number of workers and workplaces (Scenario 2.3). The second alternative was designed for applications of business information.

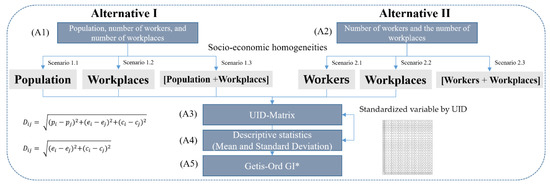
Figure 2. Schematic diagram of this research: Two main alternatives to identify an optimized small economic zone.

Next, we classified all types of land into two main classes: urbanized and non-urbanized areas. The sub-classes (Table 1) in the two main classes were used to quantitatively assess all scenarios. We used unique identifiers (UIDs) to represent all types of land classes, which we inserted into a matrix to determine a weighted value for the newly determined economic zones (Figure 2(A3)). Finally, to examine how homogeneity improved, this study computed means and standard deviation (SD) of both the existing small census output areas and new economic zones (Figure 2(A4)). Furthermore, the study explored spatial patterns of the economic zones using hot spot analysis that used Getis-Ord Gi*, which can determine statistically significant hot or cold spots and reveal spatial trends in the clustering of polygon features, i.e., it assesses where high values in the economic zones spatially cluster [55]. The following sub-sections in Section 3.2 address detailed analysis procedures to delimit new economic zones.

Table 1. Classes of unique identifiers (UIDs) in the basic statistics areas.

Urbanized/Non-Urbanized Areas		Types of Residences		Land Use Classification	UIDs
Urbanized areas	Building area is greater than 10% in the basic statistical zone.	Residential area	Over 70%	Single-family housing districts	11
				Apartment areas	12
				Multiunit dwellings	13
				Mixed housing districts	14
		Semi-residential area	Between 30% and 70%	Single-Family housing and downtown areas	21
				Multiunit dwelling and downtown areas	22
				Single-Family housing and factory complex areas	23
				Factory complex area	24
				Other complex areas	25
		Non-residential area	Less than 30%	Shopping center concentrated areas	31
				Public facility areas	32
				Cultural facility areas	33
				Factory concentrated areas	34
				Shopping center and factory congested areas	35
				Other non-residential areas	36
Non-urbanized areas	Building area is less than 10% in the basic statistical zone.	Farming and fishing areas		Plane areas	41
				Semi plane areas	42
				Forestlands	43
				Coastal areas	44
				Islands	51
Others				Others	00

3.2. Analysis Procedures for Delimiting New Economic Places

In this study, we considered social and economic homogeneities in the analysis procedures. To quantitatively assess these homogeneities, we classified unique identifiers (UIDs) by areas of building types, land use, and urbanized and non-urbanized areas (Figure 2(A3)). For example, if a building area was greater than 10% in the area of interest, we classified it as an urbanized area; however, if it was less than 10%, we classified it as a non-urbanized area. If the areas of residence were greater than 70% in the area of interest, we classified them as residences (e.g., single-family housing districts, apartment areas, multiunit dwellings, and mixed housing districts); however, if they were less than 30%, we classified them as non-residences (See Table 1). In the case of non-urbanized areas, we divided them into farmlands, forest lands, and rivers. The classes and sub-classes in Table 1 are pre-defined land-use classes determined by Statistics Korea [49].

When considering population, workers, and workplaces, the unit of the value is different from the others; thus, the values in UIDs must be standardized. This study used a z-value that standardized the three different measurement units. Using this standardization process, this research explained the similarities between factors (Figure 2(A4)). The formula of the z-value is calculated as follows:

$$Z=\frac{X-m}{\sigma }.$$

Here, Z is a standardized variable, x denotes the raw data value, m denotes the mean, and $\sigma$ denotes the standard deviation (SD).

Social and economic homogeneity between UIDs can be represented as a distance in a matrix (UID-Matrix). Based on the standardized values (Table 2), we computed the means of each of the standardized UIDs and then, we calculated the geometric distance in a matrix (e.g., in the case of Alternative 1, we considered three factors: population, workers, and workplaces). We computed the three factors using the following formula:

$$D_{ij}=\sqrt{{\left(p_i-p_j\right)}^2+{\left(e_i-e_j\right)}^2+{\left(c_i-c_j\right)}^2}–\mathrm{Alternative} 1.$$

$$D_{ij}=\sqrt{{\left(e_i-e_j\right)}^2+{\left(c_i-c_j\right)}^2}–\mathrm{Alternative} 2.$$

Table 2. Mean of standardized values per UID.

UIDs	Population	Workers	Workplaces	UIDs	Population	Workers	Workplaces
0	−0.399	−0.106	−0.125	32	−0.581	0.334	−0.125
11	−0.155	−0.13	−0.12	33	−0.717	0.126	0.077
12	0.746	−0.162	−0.242	34	−0.659	1.333	0.816
13	0.293	−0.158	−0.227	35	−0.469	0.325	0.571
14	0.474	−0.101	−0.058	36	−0.514	0.125	0.083
21	−0.234	0.026	0.273	41	−0.489	−0.111	−0.181
22	0.342	0.082	0.265	45	−0.31	−0.053	−0.097
23	−0.379	−0.012	−0.003	42	−0.482	−0.075	−0.147
24	0.418	0.001	−0.037	43	−0.227	−0.023	−0.017
25	0.113	0.216	0.517	44	−0.803	−0.181	−0.291
31	−0.498	0.551	0.982	51	−0.399	−0.106	−0.125

p = population;

e = number of workers;

c = number of workplaces.

Here, $D_{ij}$ represents degrees of social and economic homogeneity between UIDs i and j in a matrix. Thus, as $D_{ij}$ decreases, the levels of social and economic homogeneity increase.

We used the AZTool, developed by Statistics Korea, in this study. In the AZTool, the above matrix was used to determine a weighted value after considering each of the alternatives (Table 3). It automatically merges, splits, and retains economic zones in a COA. In addition to the matrix, this study provided the following criteria (Table 4) to delimit new economic zones (i.e., census output areas).

Table 3. UID Matrix for Alternative 1.

	00	11	12	13	14	21	22	23	24	25	31	32	33	34	35	36	41	42	43	44	51
00	0.0	0.2	1.2	0.7	0.9	0.5	0.9	0.2	0.8	0.9	1.3	0.5	0.4	1.7	0.8	0.3	0.1	0.1	0.1	0.2	0.4
11	0.2	0.0	0.9	0.5	0.6	0.4	0.7	0.3	0.6	0.8	1.3	0.6	0.6	1.8	0.9	0.5	0.3	0.2	0.3	0.2	0.7
12	1.2	0.9	0.0	0.5	0.3	1.1	0.7	1.2	0.4	1.1	1.9	1.4	1.5	2.3	1.5	1.3	1.2	1.1	1.2	1.0	1.5
13	0.7	0.5	0.5	0.0	0.3	0.7	0.5	0.7	0.3	0.9	1.6	1.0	1.1	2.1	1.2	0.9	0.8	0.6	0.8	0.6	1.1
14	0.9	0.6	0.3	0.3	0.0	0.8	0.4	0.9	0.1	0.7	1.6	1.1	1.2	2.0	1.2	1.0	1.0	0.8	1.0	0.7	1.3
21	0.5	0.4	1.1	0.7	0.8	0.0	0.6	0.3	0.7	0.5	0.9	0.6	0.5	1.5	0.5	0.4	0.5	0.4	0.5	0.3	0.8
22	0.9	0.7	0.7	0.5	0.4	0.6	0.0	0.8	0.3	0.4	1.2	1.0	1.1	1.7	0.9	0.9	1.0	0.8	0.9	0.6	1.3
23	0.2	0.3	1.2	0.7	0.9	0.3	0.8	0.0	0.8	0.8	1.1	0.4	0.4	1.6	0.7	0.2	0.2	0.1	0.2	0.2	0.5
24	0.8	0.6	0.4	0.3	0.1	0.7	0.3	0.8	0.0	0.7	1.5	1.1	1.1	1.9	1.1	0.9	0.9	0.7	0.9	0.6	1.3
25	0.9	0.8	1.1	0.9	0.7	0.5	0.4	0.8	0.7	0.0	0.8	1.0	0.9	1.4	0.6	0.8	1.0	0.8	0.9	0.7	1.3
31	1.3	1.3	1.9	1.6	1.6	0.9	1.2	1.1	1.5	0.8	0.0	1.1	1.0	0.8	0.5	1.0	1.3	1.3	1.3	1.2	1.5
32	0.5	0.6	1.4	1.0	1.1	0.6	1.0	0.4	1.1	1.0	1.1	0.0	0.3	1.4	0.7	0.3	0.5	0.5	0.4	0.5	0.6
33	0.4	0.6	1.5	1.1	1.2	0.5	1.1	0.4	1.1	0.9	1.0	0.3	0.0	1.4	0.6	0.2	0.4	0.5	0.4	0.5	0.5
34	1.7	1.8	2.3	2.1	2.0	1.5	1.7	1.6	1.9	1.4	0.8	1.4	1.4	0.0	1.1	1.4	1.8	1.7	1.7	1.6	1.9
35	0.8	0.9	1.5	1.2	1.2	0.5	0.9	0.7	1.1	0.6	0.5	0.7	0.6	1.1	0.0	0.5	0.9	0.8	0.8	0.7	1.1
36	0.3	0.5	1.3	0.9	1.0	0.4	0.9	0.2	0.9	0.8	1.0	0.3	0.2	1.4	0.5	0.0	0.4	0.3	0.3	0.3	0.6
41	0.1	0.3	1.2	0.8	1.0	0.5	1.0	0.2	0.9	1.0	1.3	0.5	0.4	1.8	0.9	0.4	0.0	0.2	0.1	0.3	0.3
42	0.1	0.2	1.1	0.6	0.8	0.4	0.8	0.1	0.7	0.8	1.3	0.5	0.5	1.7	0.8	0.3	0.2	0.0	0.2	0.1	0.5
43	0.1	0.3	1.2	0.8	1.0	0.5	0.9	0.2	0.9	0.9	1.3	0.4	0.4	1.7	0.8	0.3	0.1	0.2	0.0	0.3	0.4
44	0.2	0.2	1.0	0.6	0.7	0.3	0.6	0.2	0.6	0.7	1.2	0.5	0.5	1.6	0.7	0.3	0.3	0.1	0.3	0.0	0.7
51	0.4	0.7	1.5	1.1	1.3	0.8	1.3	0.5	1.3	1.3	1.5	0.6	0.5	1.9	1.1	0.6	0.3	0.5	0.4	0.7	0.0

Table 4. Indices and weighted values for six scenarios (“S” stands for scenario).

Division	S1.1		S1.2		S1.3		S2.1		S2.2		S2.3
Factors	Population + Worker + Workplace						Worker + Workplace
UID-Matrix	Matrix 1						Matrix 2
Criteria	Population		Worker + Workplace		Population + Workplace		Worker		Workplace		Worker + Workplace
Weighted	Optimal	500	Optimal	10	Optimal	65	Optimal	200	Optimal	30	Optimal	10
	Least	300	Least	4	Least	15	Least	100	Least	10	Least	4
	Tolerance	100	Tolerance	2	Tolerance	3	Tolerance	40	Tolerance	7	Tolerance	2

In Scenario 1.1, new economic zones were delimited by computing standardized population values in the above matrix. The given criteria in Scenario 1 were that the optimized population was 500, the lowest population was 300, and the tolerance of the population was 100. The tolerance value was used to protect overestimated values. Note that Scenarios 1.2 and 1.3 used log values, whereas Scenario 1.2 used log (number of workers + 1) × log (number of workplaces + 1). Note that the optimal value was 10 (approximate values to the mean of the new economic statistics zone), the least was 4 (close to the mean of the basic statistic zones), and the tolerance value was 2 (because there were two factors, the least value was divided by 2 [1/2]).

Scenario 1.3 computed log (population + 1) × log (number of worker + 1) × log (number of workplace + 1); thus, the optimal value was 65 (approximate values to the mean of the new economic statistics zone), the least was 15 (close to mean of the basic statistic zones), and the tolerance value was 5 (because there were three factors, the least value was divided by 2 [1/3]). Scenario 2.1 considered 200 as the optimal number of workers, 100 as the minimum number of workers, and 40 as the tolerance value. Scenario 2.2 considered 30 as the optimal number of workplaces, 10 as the minimum number of workplaces, and 7 as the tolerance value. Scenario 2.3 computed log (number of worker + 1) × log (number of workplace + 1); thus, the optimal value was 10 (approximate values to mean of the new economic statistics zone), the least was 4 (close to mean of the basic statistic zones), and the tolerance value was 2 (because there were two factors, the least value was divided by 2 [1/2]). It was important to assess social and economic homogeneity between UIDs in the matrix. To examine how homogeneity improved, this study computed the means and SDs of both the existing small census output areas and new economic zones. Furthermore, the study explored spatial patterns of the economic zones using hot spot analysis that used Getis-Ord GI*, which can determine statistically significant hot or cold spots and reveal spatial trends in the clustering of polygon features, i.e., it assesses where high values in the economic zones spatially cluster [55].

$$G_i^{*}=\frac{{{\displaystyle \sum }}_{j=1}^n{w}_{ij}{x}_j-\underset{\_}{X}{{\displaystyle \sum }}_{j=1}^n{w}_{ij}}{\sqrt{\frac{{{\displaystyle \sum }}_{j=1}^n{x}_j^2}{n}-{\left(\underset{\_}{X}\right)}^2}\times \sqrt{\frac{\left[n{{\displaystyle \sum }}_{j=1}^n{w}_{ij}^2-{\left({{\displaystyle \sum }}_{j=1}^n{w}_{ij}\right)}^2\right]}{n-1}}}$$

$$\underset{\_}{X}=\frac{{{\displaystyle \sum }}_{j=1}^n{x}_j}{n}$$

-

Getis-Ord $G_i^{*}.$

When using Getis-Ord GI*, we visualized highly overcrowded areas as hot spots in a red color. The spatial trends were used to determine an optimal scenario by observing the increase or decrease of hot spots in areas of interest. This research used one method that is the default weight for Self-Potential in the Hot Spot Analysis tool in ArcMap.

4. Results

4.1. Means and SDs for Population, Workers and Workplaces.

The total number of COAs was 1085, the average population size in each of the COAs was 477.09, the SD of each COA was 145.74, and the average number of workers in each COA was 616.19. Note that the SD of the number of workers was 1824, and the mean and SD of workplaces were 62.75 and 149.16, respectively. The following table shows the mean and SD of population, workers, and workplaces.

As shown in Table 5 and Figure 3a, the mean (477.09) of the population in the existing COA was similar to the mean (465.20) in Scenario 1.1; however, this confirmed that the mean of other scenarios was lower than the mean of the existing COA and all COAs. As for the SDs, except for Scenario 1.1, all of the SDs of the other scenarios showed big differences with the mean of all of the COAs. Regarding workers (Figure 3b), the means of Scenarios 2.2 and 2.3 were lower than others. When comparing the SD of Scenario 1.1, the SDs of other scenarios were much lower than the others. As for workplaces (Figure 3c), the trend of the differences was similar to those shown in Figure 3b, i.e., the SDs of other scenarios were much lower than the means of the existing COA and Scenario 1.1. The above differences meant that the extent of social and economic homogeneity was different, and it depended on the situation.

Table 5. Means and SDs of population, workers, and workplaces in the Gangnam district.

	Population (#)		Workers (#)	Workplaces (#)
ExistingCOA	Mean	477.09	616.19	62.75
	SD	145.74	1824.18	149.16
S1.1	Mean	465.20	601.44	61.24
	SD	172.53	1931.09	155.79
S1.2	Mean	252.47	326.41	33.24
	SD	662.26	720.19	50.60
S1.3	Mean	335.69	434.00	44.19
	SD	756.11	1056.40	66.17
S2.1	Mean	358.24	463.17	47.16
	SD	876.66	826.24	57.72
S2.2	Mean	334.18	432.06	43.99
	SD	815.75	817.71	55.59
S2.3	Mean	251.85	325.62	33.16
	SD	659.16	720.75	50.61

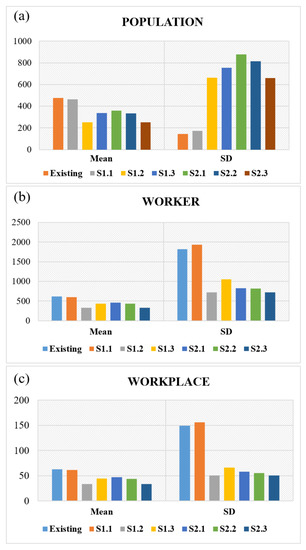
Figure 3. Means and standard deviations (SDs) of the (a) population, (b) workers, and (c) workplaces in the Gangnam district.

4.2. Spatial Distributions of Hot Spots and Second SD

This study used hot spot analysis to explore highly overcrowded populations, workers, and workplaces of the economic zones used in the two alternatives. It was important to investigate the general spatial trend of the variables in a place. The spatial trend of the pattern was used to select an optimal scenario among the proposed alternatives. Figure 4 shows hot and cold spot trends of the population in the existing and new economic zones.

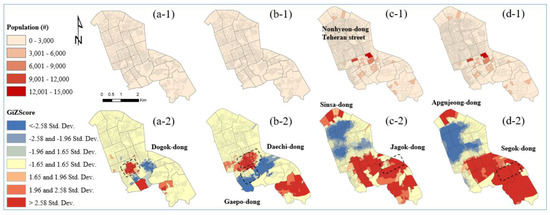
Figure 4. Choropleth maps of the population size in the existing COAs (a-1) and Scenarios 1.1 (b-1), 1.2 (c-1), and 1.3 (d-1). Hot and cold spot trends of the population size in the existing COAs (a-2), Scenarios 1.1 (b-2), 1.2 (c-2), and 1.3 (d-2).

Figure 5 shows hot and cold spot trends of the population size in Alternative 2. In the case of Scenario 2.1, the spatial trend was similar to that of Scenario 1.3, whereas Scenario 2.2 was similar to Scenario 2.1. As for Scenario 2.3, the hot spot trends occurring in Gaepo-dong, Segok-dong, and Irwon-dong (c-2) were moderated (i.e., disseminated).

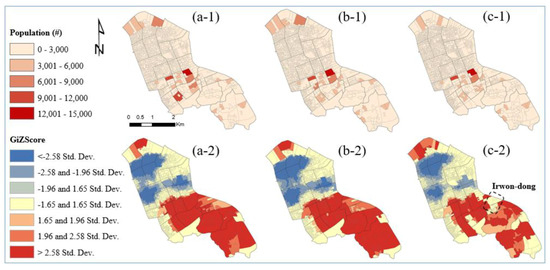
Figure 5. Choropleth maps of the population size in Scenarios 2.1 (a-1), 2.2 (b-1), and 2.3 (c-1). Hot and cold spot trends of the population size in Scenarios 2.1 (a-2), 2.2 (b-2), and 2.3 (c-2).

Regarding the hot and cold spot trends of the number of workers, Alternative 1 showed that hot spot trends existed around Nonhyeon-dong and Teheran street (Figure 6(a-2)). Furthermore, the hot spot patterns expanded to Suseo station (Figure 6(d-2)), and cold spot trends were observed around Nonhyeon-dong, Dachi 4-dong, and Gaepo 4-dong. Alternative 2, associated with the number of workers, showed that hot spots occurred around Teheran street (Figure 6(d-2)) and expanded to Suseo station, whereas cold spots were observed around Cheongdam-dong, Yeoksam2-dong, Gaepo 1 and 4-dong, Teheran street, and Nohyeon 1-dong.

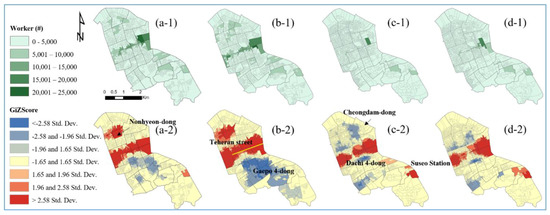
Figure 6. Choropleth maps of the number of workers in the existing COAs (a-1) and Scenarios 1.1 (b-1), 1.2 (c-1), and 1.3 (d-1). Hot and cold spot trends of the number of workers in the existing COAs (a-2), Scenario 1.1 (b-2), 1.2 (c-2), and 1.3 (d-2).

Alternative 2, associated with the number of workers, showed that hot spots occurred around Teheran street and expanded to Suseo station, whereas cold spots were observed around Cheongdam-dong, Yeoksam2-dong, Gaepo 1 and 4-dong, Teheran street, and Nohyeon 1-dong (Figure 7).

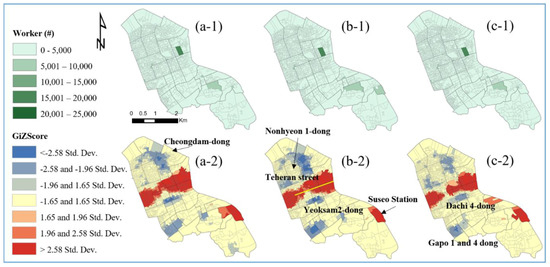
Figure 7. Choropleth maps of the number of workers in Scenarios 2.1 (a-1), 2.2 (b-1), and 2.3 (c-1). Hot and cold spot trends of the number of workers in Scenarios 2.1 (a-2), 2.2 (b-2), and 2.3 (c-2).

Regarding the hot and cold spot trends for the number of workplaces in the existing COAs (a-2), a high number of workplaces were clustered near Teheran street, Nohyeon-dong, and Suseo Stations (Figure 8). As for Scenario 1.1, it was obvious that a high number of workplaces were clustered in Teheran street, Nohyeon-dong, and Suseo Stations; however, cold spots were observed around Yeocksam 2-dong and Irwon-dong. Interestingly, hot spot patterns were fewer than in Scenarios 1.1 to 1.3, particularly on Teheran street; however, in Scenarios 1.2 and 1.3, hot spot zones were observed around Suseo station and the patterns were sporadic.

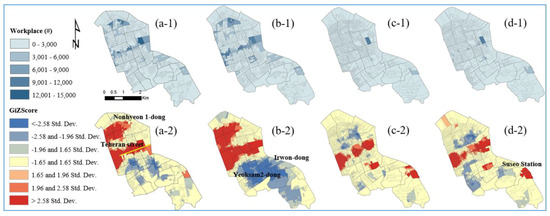
Figure 8. Choropleth maps of the number of workplaces in the existing COAs (a-1) and Scenarios 1.1 (b-1), 1.2 (c-1), and 1.3 (d-1). Hot and cold spot trends of the number of workplaces in the existing COAs (a-2), Scenarios 1.1 (b-2), 1.2 (c-2), and 1.3 (d-2).

Figure 9 shows hot spot trends still existed in areas near Teheran Street, Daechi 1-dong, and Suseo station, whereas cold spot trends were observed in Dogok-dong, Chungdam-dong, and Segok-dong. Overall, the hot spot trend decreased

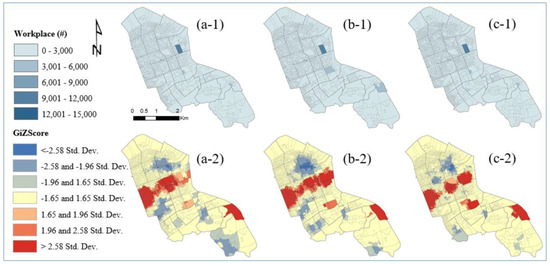
Figure 9. Choropleth maps of the number of workplaces in Scenarios 2.1 (a-1), 2.2 (b-1), and 2.3 (c-1). Hot and cold spot trends of the number of workplaces in Scenarios 2.1 (a-2), 2.2 (b-2), and 2.3 (c-2).

4.3. Second SDs of Population, Worker and Workplace

The following three tables show the means of the SDs for population, workers, and workplaces. The number from the existing census output areas (i.e., COAs) with the population was 59; however, the numbers were higher in the three scenarios. Scenario 1.3 had the highest value (1070.83) and Alternative 2 showed a similar pattern (Table 6); however, Scenario 2.1 showed the highest value (1164.98).

Table 6. Second SDs of the Gangnam district—Population.

Gangnam		Population (#)
Existing COAs	Census output areas	59	Existing COAs	Census output areas	59
	Mean of SD	606.37		Mean of SD	606.37
Scenario 1.1	Economic zones (#)	208	Scenario 2.1	Economic zones (#)	214
	Mean of SD	537.57		Mean of SD	1164.98
Scenario 1.2	Economic zones (#)	255	Scenario 2.2	Economic zones (#)	219
	Mean of SD	923.81		Mean of SD	1100.56
Scenario 1.3	Economic zones (#)	224	Scenario 2.3	Economic zones (#)	249
	Mean of SD	1070.83		Mean of SD	938.93

Regarding second SDs for workers, the number of the existing census output areas was 114, but the numbers increased in Scenarios 1 and 2 (Table 7). Scenario 1.2 showed the highest number of economic zones (369). As for Alternative 2, Scenario 2.1 had the highest number of economic zones (829.62).

Table 7. Second SDs of the Gangnam district—Workers.

Gangnam		Worker (#)
Existing COAs	Census output areas	114	Existing COAs	Census output areas	114
	Mean of SD	3199.46		Mean of SD	3199.46
Scenario 1.1	Economic zones (#)	182	Scenario 2.1	Economic zones (#)	365
	Mean of SD	2217.49		Mean of SD	829.62
Scenario 1.2	Economic zones (#)	369	Scenario 2.2	Economic zones (#)	355
	Mean of SD	739.25		Mean of SD	827.70
Scenario 1.3	Economic zones (#)	264	Scenario 2.3	Economic zones (#)	352
	Mean of SD	1007.54		Mean of SD	771.30

Regarding second SDs for workplaces, the number from the existing census output areas was 149, but the numbers increased in Scenarios 1 and 2 (Table 8). Scenario 2.2 showed the highest number of economic zones (320). As for Alternative 2, Scenario 2.2 had the highest number of economic zones (339).

Table 8. Second SDs of the Gangnam district—Workplaces.

Gangnam		Workplace (#)
Existing COAs	Census output areas	149	Existing COAs	Census output areas	149
	Mean of SD	250.24		Mean of SD	250.24
Scenario 1.1	Economic zones (#)	238	Scenario 2.1	Economic zones (#)	299
	Mean of SD	179.52		Mean of SD	70.25
Scenario 1.2	Economic zones (#)	320	Scenario 2.2	Economic zones (#)	339
	Mean of SD	63.43		Mean of SD	69.08
Scenario 1.3	Economic zones (#)	239	Scenario 2.3	Economic zones (#)	305
	Mean of SD	79.04		Mean of SD	66.13

4.4. Examples of the Number of Workplaces in the Existing COAs and Two Alternatives

Figure 10 shows an example of the number of workplaces in Nonhyeon-dong in the Gangnam district. As shown in Figure 10, there were 1105 workplaces in the existing basic statistic zone; however, there were 938 workplaces in Scenario 1.1. Both Scenarios 1.2 and 1.3 provided more segmented values. This protected the statistical information that might have been overestimated or underestimated in the same district or the economic zones.

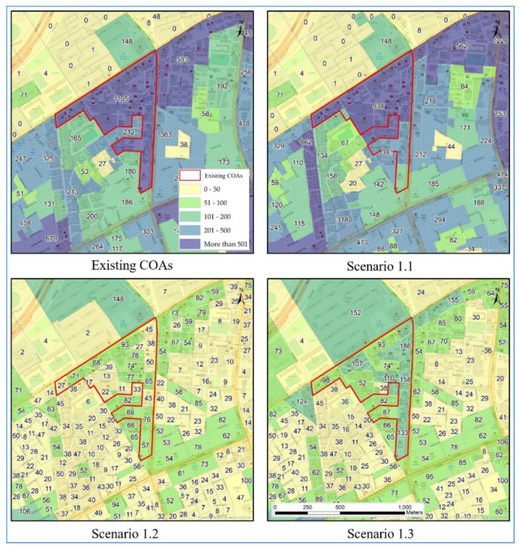
Figure 10. The number of workplaces in the existing COAs and Scenarios 1.1, 1.2, and 1.3.

In the case of Alternative 2 (Figure 11), the total number of the workplaces was similar; nevertheless, each of the outputs focused on just the number of workers, the number of workplaces, and a combination of workers and workplaces. Eventually, new economic zones were delimited through the algorithm proposed in this research.

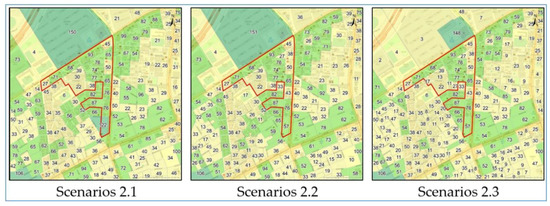
Figure 11. The number of workplaces in Scenarios 2.1, 2.2, and 2.3.

5. Discussion

Despite efforts to research the transformation of the urban structure, difficulties remain in estimating credible statistical information in the census output areas. Furthermore, there are a variety of theories and computational methods that delimitate a hierarchy of census geographic units or economic zones. Even though the methods consider the homogeneity of the geographic area to the aggregate zones, the size of the zones will vary [6,7]. Because each country used a different hierarchy of census geographic units and economic places or zones, it may result in different statistical summaries in the same geographic scale. As a result, the number of summaries can be often overestimated or underestimated. However, the existing census output areas in a hierarchy of census geographic units do not reflect the reality of the current spatial urban structure, particularly in providing business-relevant information. Thus, urban planners should consider all possible scenarios that estimate reliable statistical information in the existing census output areas and even create new economic census output areas.

As noted in this paper, we first evaluated the statistical summaries in the existing census output areas, and secondly, we considered social and economic homogeneities that contained a combination of populations, workers, and workplaces. Specifically, three scenarios in Alternative 1 considered population, number of workers, and number of workplaces in a matrix. Another three scenarios in Alternative 2 referred to only the number of workers and workplaces in a matrix. Each of the scenarios had three scenarios. Furthermore, this study assessed the degrees of social and economic homogeneity using the SDs (standard deviations) in the six scenarios. Because the means of different sizes of economic zones showed big differences, it was difficult to compare the differences of newly aggregated economic zones. Thus, we used SDs to investigate the degrees of social and economic homogeneity and monitor the trends of social and economic homogeneity at a given location.

Comparing the SDs of the existing census output areas with the SDs of new economic census zones, the results indicated that the extent of social and economic homogeneity was different, and it depended on the situation given. In other words, when the SD was lower than those of the other scenarios, it meant that the scenario with the lower value improved social and economic homogeneity. As a result, given an urban planning or a specific project, it meant that we could choose one of the scenarios with the lower SD values. We also developed an algorithm to newly aggregate new economic zones, including the existing basic unit districts. In addition to the UID matrix and AZP-based algorithms, new economic zones (census output areas) were delimited for central business districts. Consequently, we selected Scenarios 1.3 and 2.3 as the best working scenarios. Specifically, in the case of the Gangnam district, the SD of the population increased, whereas the SDs of workers and workplaces decreased, indicating that socioeconomic homogeneity improved.

When exploring the hot and cold spot trends, Scenarios 1.3 (a combination of the population and the number of workplaces) and 2.3 (a combination of the number of workers and workplaces) showed that hot and cold spot trends decreased compared with the spatial patterns of the existing census output areas, indicating that the overcrowded patterns (overestimated) in the existing census output areas were lesser in Scenarios 1.3 and 2.3. Therefore, Scenario 1.3 showed that the SDs for the number of workplaces were lesser, suggesting that the degree of homogeneity between economic zones of Scenarios 1.3 was high. Thus, we selected Scenario 1.3 as the optimal scenario to delimit new economic zones. In the case of Scenario 2.3, because the SDs for the number of workplaces were less, this scenario was suitable for areas with a high number of workplaces, such as Gangnam. Compared with the existing census output areas, the district should consider two factors (workers and workplaces) regarding the population (Scenarios 1.3 and 2.3). The two alternatives can make the results more meaningful. Accordingly, this work includes the following key contributions: (1) a new method can be used to determine new economic census zones through scenario-based approaches, and it is crucial for urban planners to directly apply this method to new urban planning; (2) researchers are able to scrutinize urban transformations over time where economic activities frequently occur; (3) even the general public can use reliable statistical summaries from the newly aggregated census output areas; and (4) eventually, policymakers or public officers can provide more accurate national statistical summaries, particularly those related to statistical geographic information services. After completing this research, the outputs of this research were validated by the research group at the Department of Geospatial Information Service Division of Statistics Korea [56]. Based on the outputs of this research, Statistics Koreas is currently working on developing new census output areas to serve the public with credible statistical summaries in economic zones.

Even though this research produces reliable statistical outputs in new economic zones, there are limitations to this research. The data used in this research are census output data including population, the number of workers and businesses, transportation, households, property values, and more that are officially surveyed by the National Statistics office in South Korea. For research purposes, we were able to use the smallest geographic unit, which is the BUD. However, the BUDs also need to be re-aggregated when an urban structure transforms over time. Additionally, statistical summaries in the BUD often provide very detailed information. For example, only one or two employees existed in the economic zone. However, the BUDs are not publicly available because many of the zones have lower numbers, even one or two employees. This will unintentionally share personal information with the public. Thus, we also need to consider ways to protect personal information at the smallest census output area (i.e., economic zone).

In sum, this research is significant for two reasons. First, our findings suggest that it is essential to consider the population and the number of workplaces and a combination of the number of workers and workplaces, particularly for central business districts. The numbers should be periodically recalculated when the urban structure has transformed. It will help other researchers who study the transformations of the urban structure because they can use more reliable statistical information for their simulation models that predict an urban structure. Second, as Pan and Deal suggested [17], it is important for the urban planner to use scenario-driven exercises. Through the analysis procedures and algorithms proposed in this research, we could easily apply a variety of combinations with socioeconomic homogeneity on purpose. Accordingly, Statistics Korea can use the results to serve reliable statistical information in an economic zone and for the development of a sustainable economy and high-quality spatial data.

6. Conclusions

In the era of big data, realistic and robust statistical data are seen as critical. This will help us gather more individualized and sophisticated data and applications for sustainable urban development. We note that this research was focused on proposing two main alternatives to find the best scenarios that can provide reliable statistical information where economic activity occurs. Moreover, we developed a model to aggregate new economic zones based on the proposed scenarios. Consequently, we identified Scenarios 1.3 and 2.3 as the best working scenarios for the study, and the National Statistical Offices can provide more accurate statistical information or summaries of workers and workplaces at central business districts. We contend that the resultant outputs can help urban planners to evaluate the existing economic zones that improve the usability of the national statistics data. Eventually, the results can be connected to the national geographic information service. As stated in the Discussion, we will next develop a masking tool that can reasonably hide or protect personal information in the smallest economic zones and maintain the consistency and accuracy of statistical information in the economic zone. Furthermore, we will also forecast changes in the urban structure using the credible statistical information in the new economic zones.