CO2 and Cost Optimization of Reinforced Concrete Cantilever Soldier Piles: A Parametric Study with Harmony Search Algorithm
Abstract
:1. Introduction
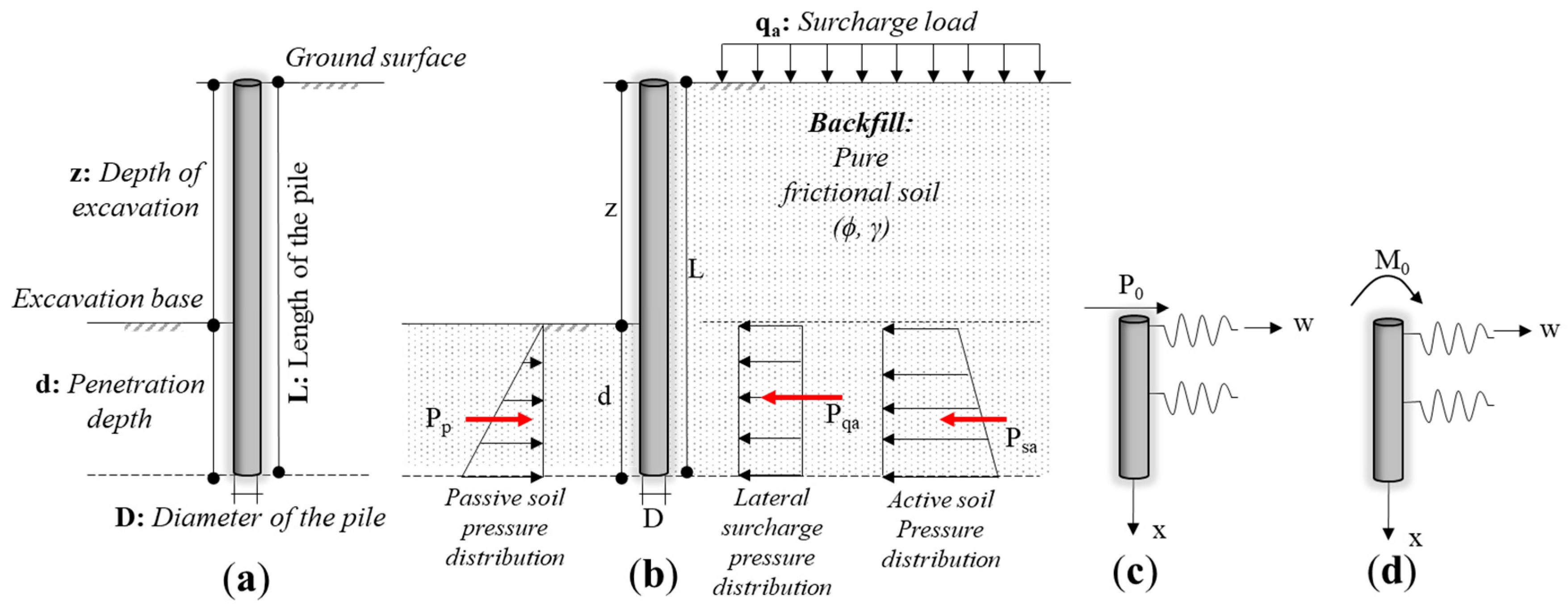
2. Design and Methodology
- The stable design of cantilever soldier pile walls;
- Cost minimization-based design of cantilever soldier piles;
- CO2 emission minimization-based design of cantilever soldier piles;
- Both cost and CO2 minimization-based design of cantilever soldier piles.
3. Parametrical Analyses
4. Result and Discussion
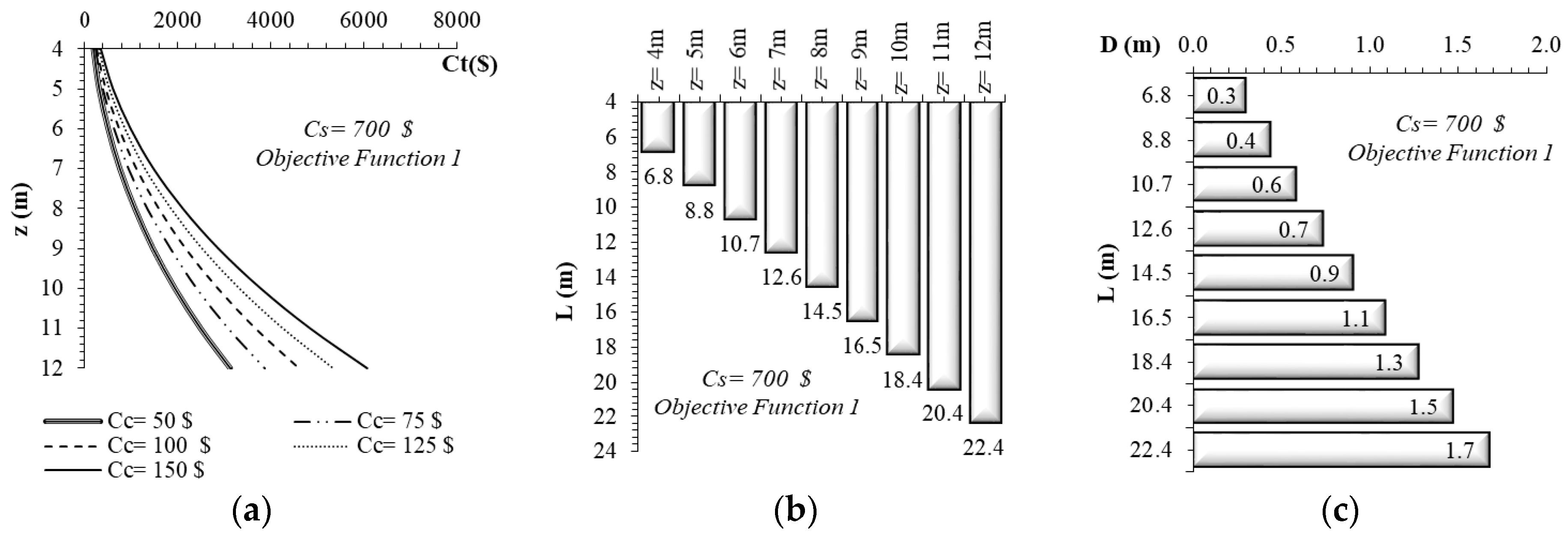
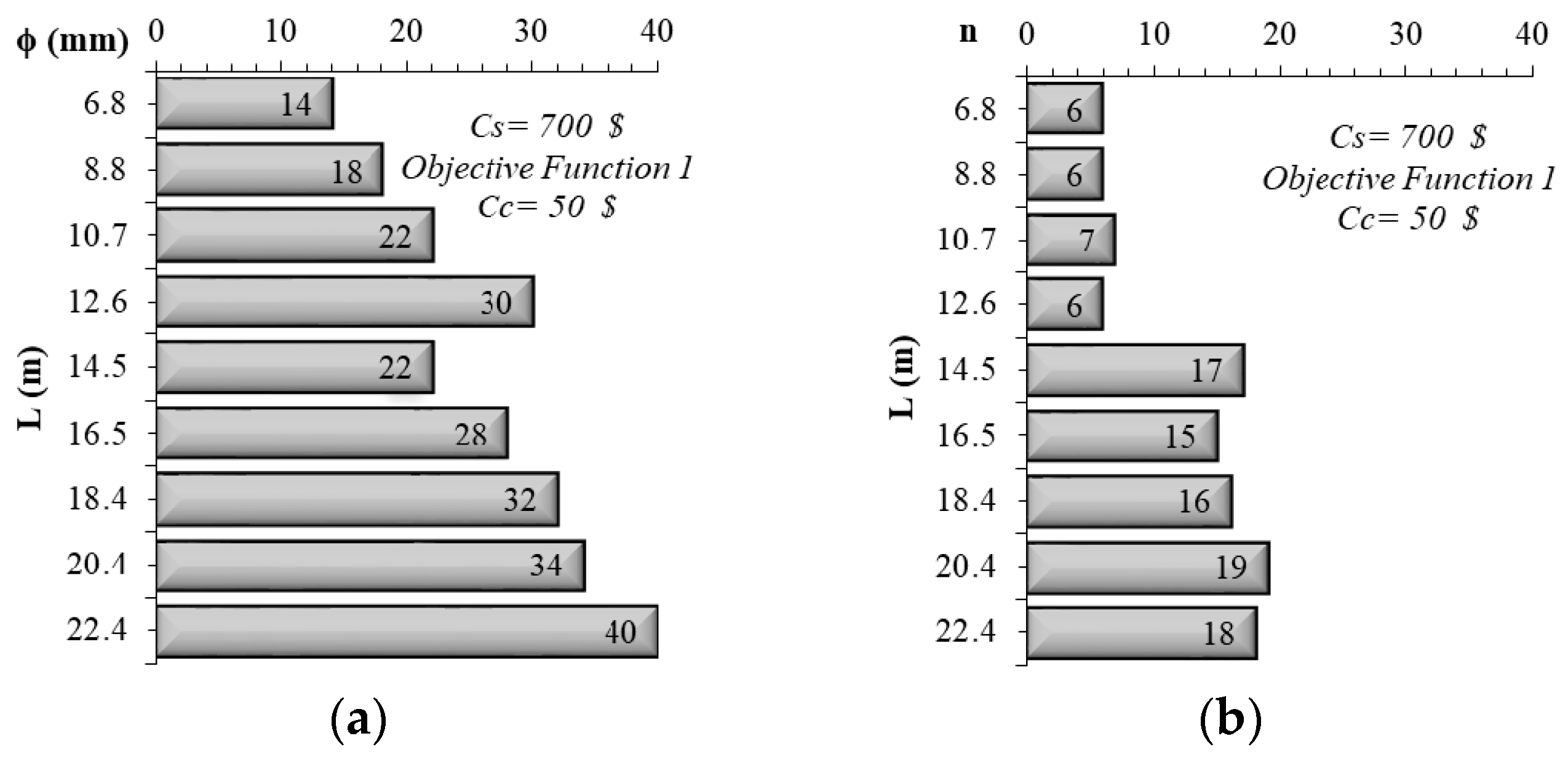
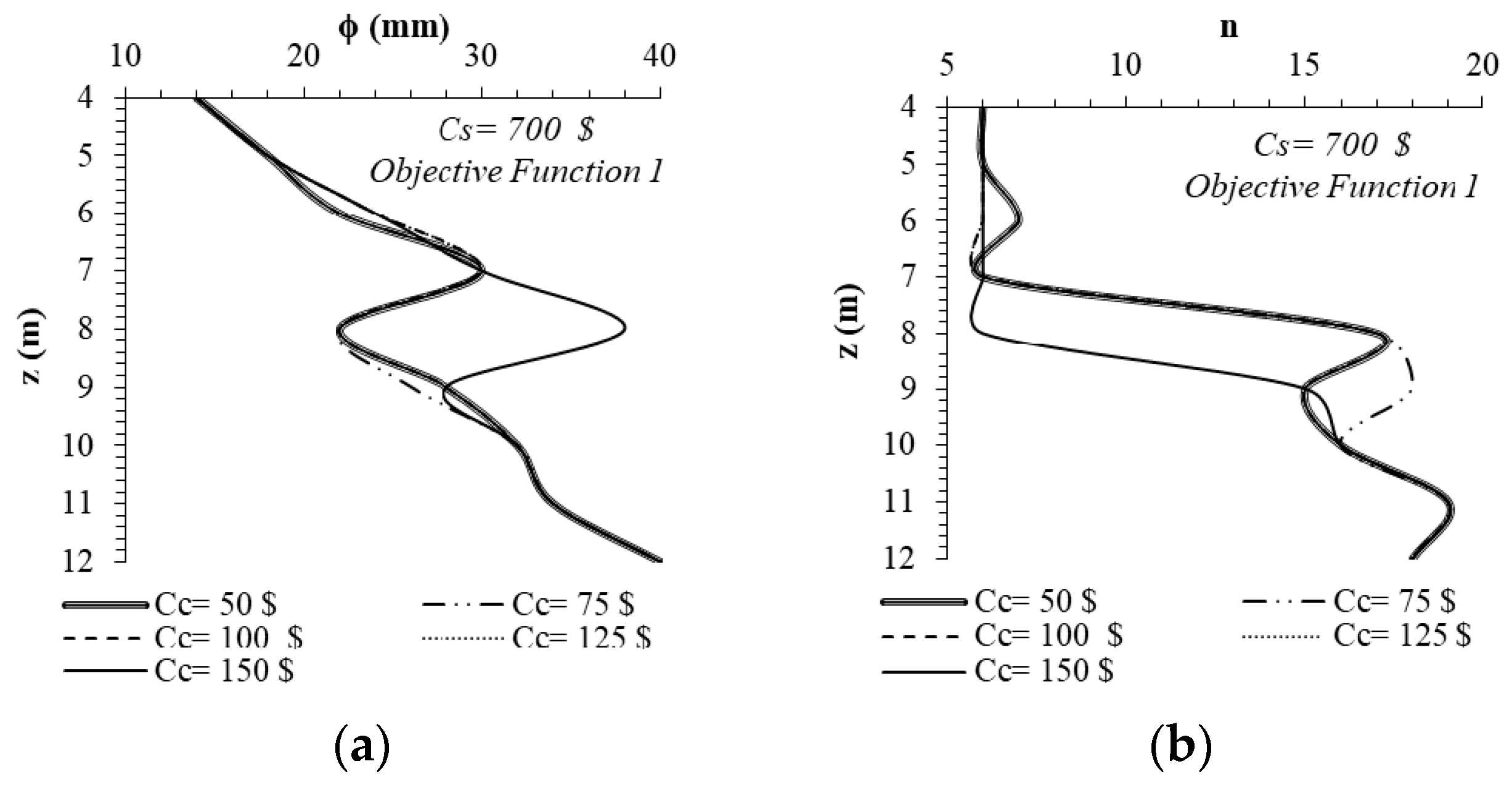
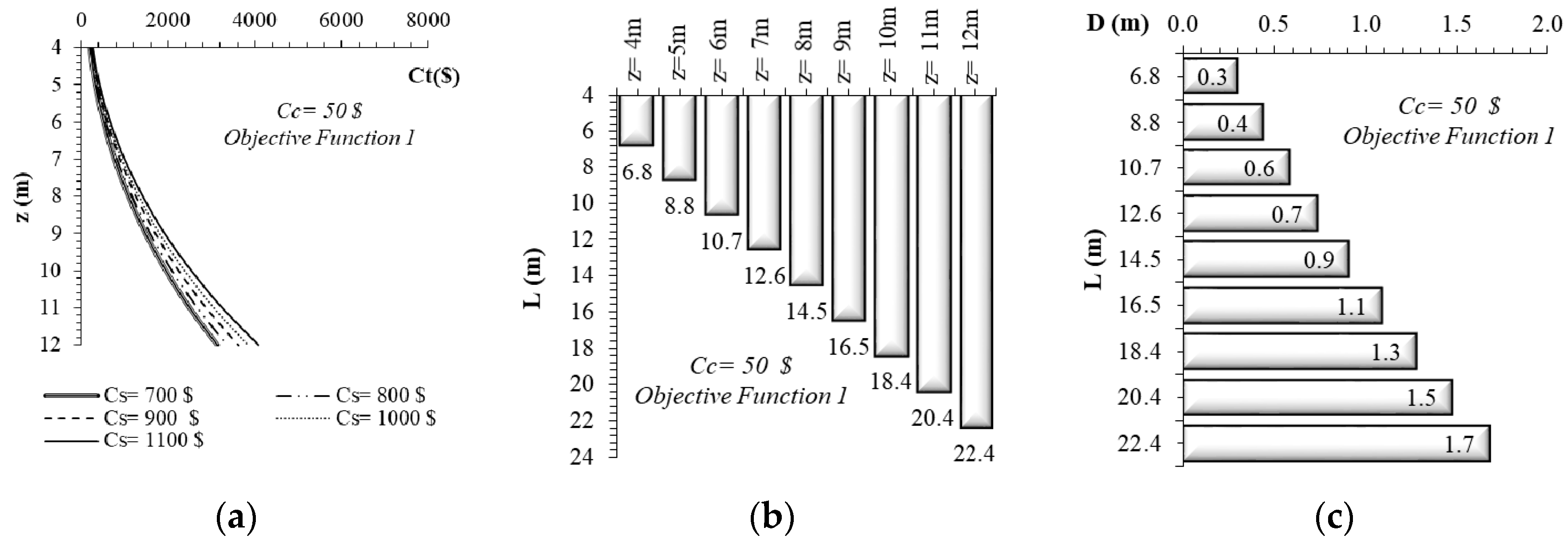
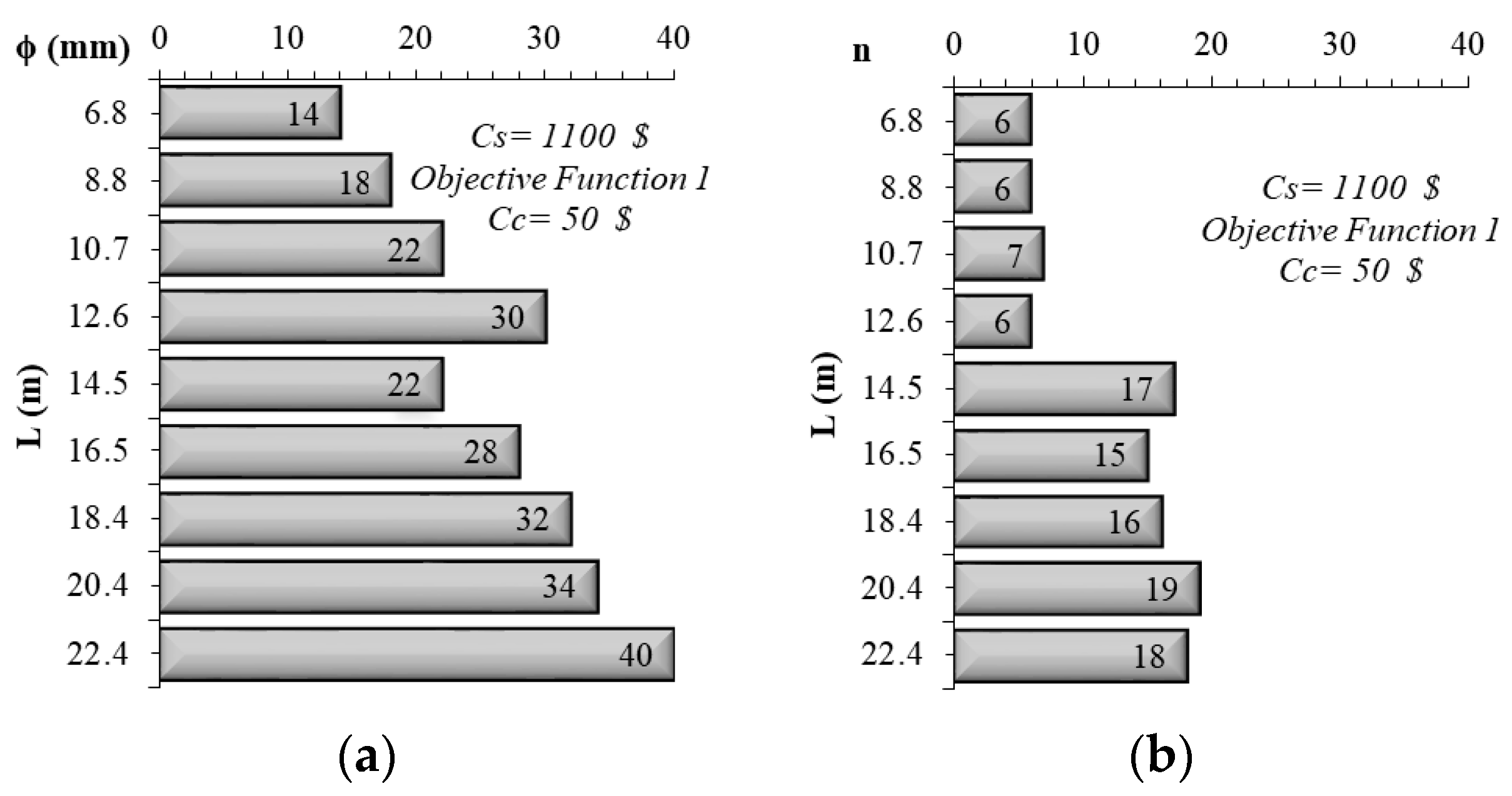
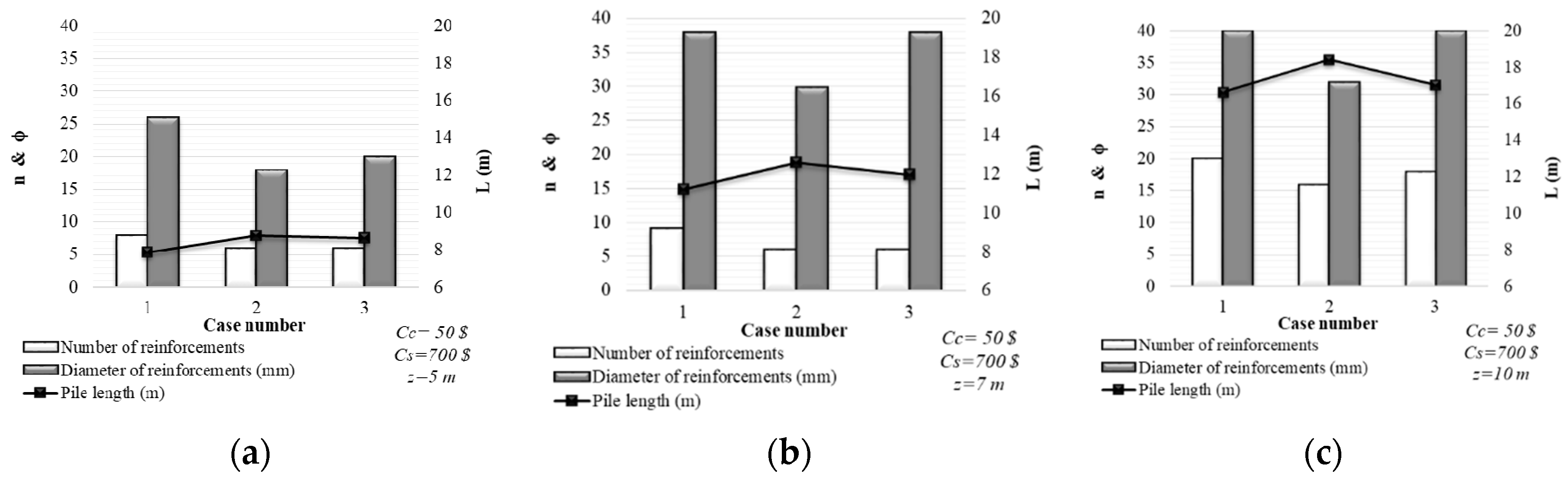
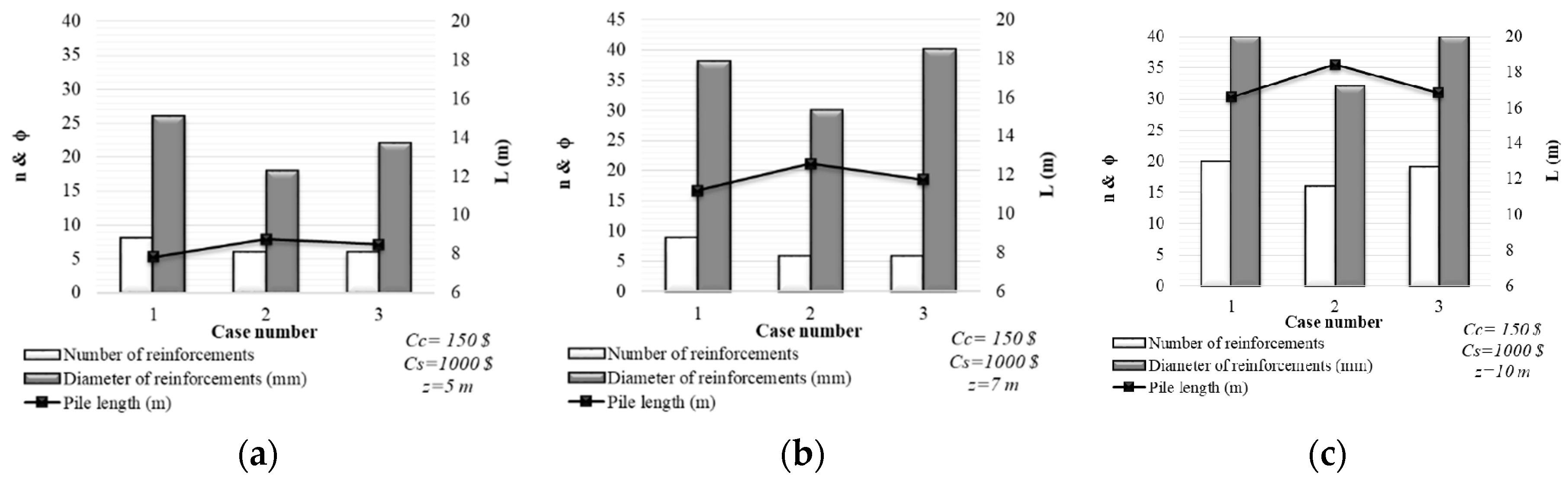
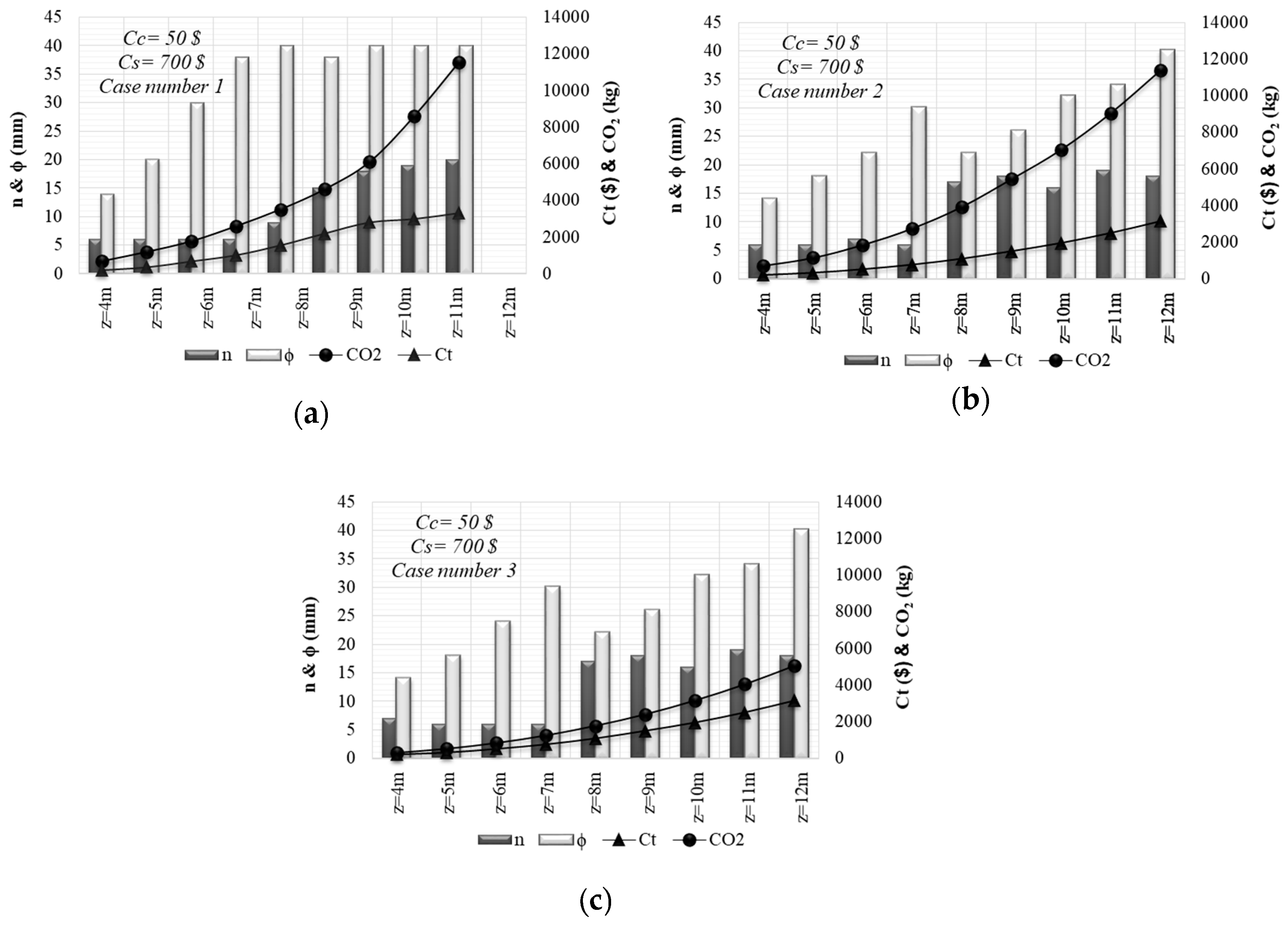
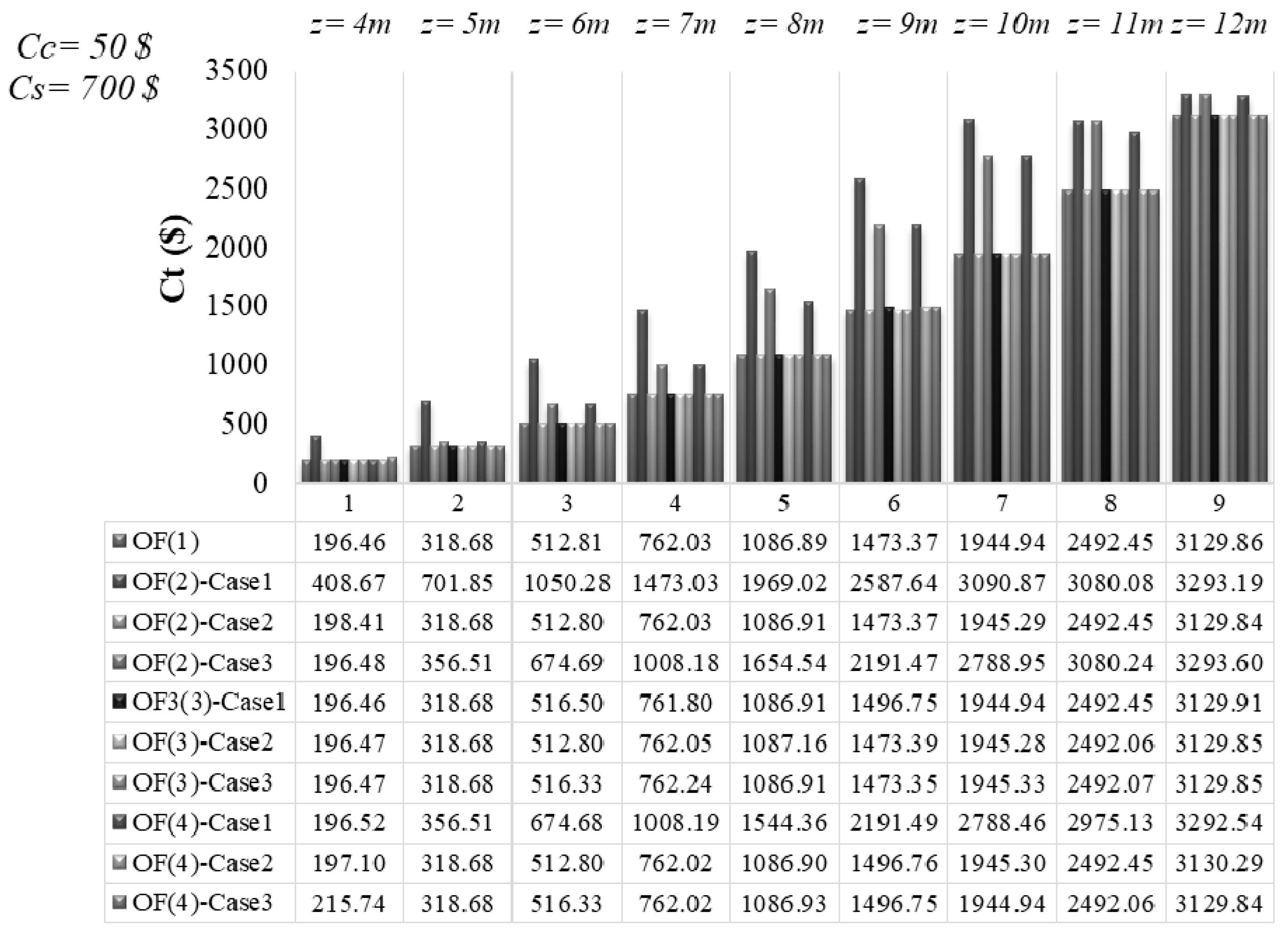
4.1. Design and Minimum Cost Relationship
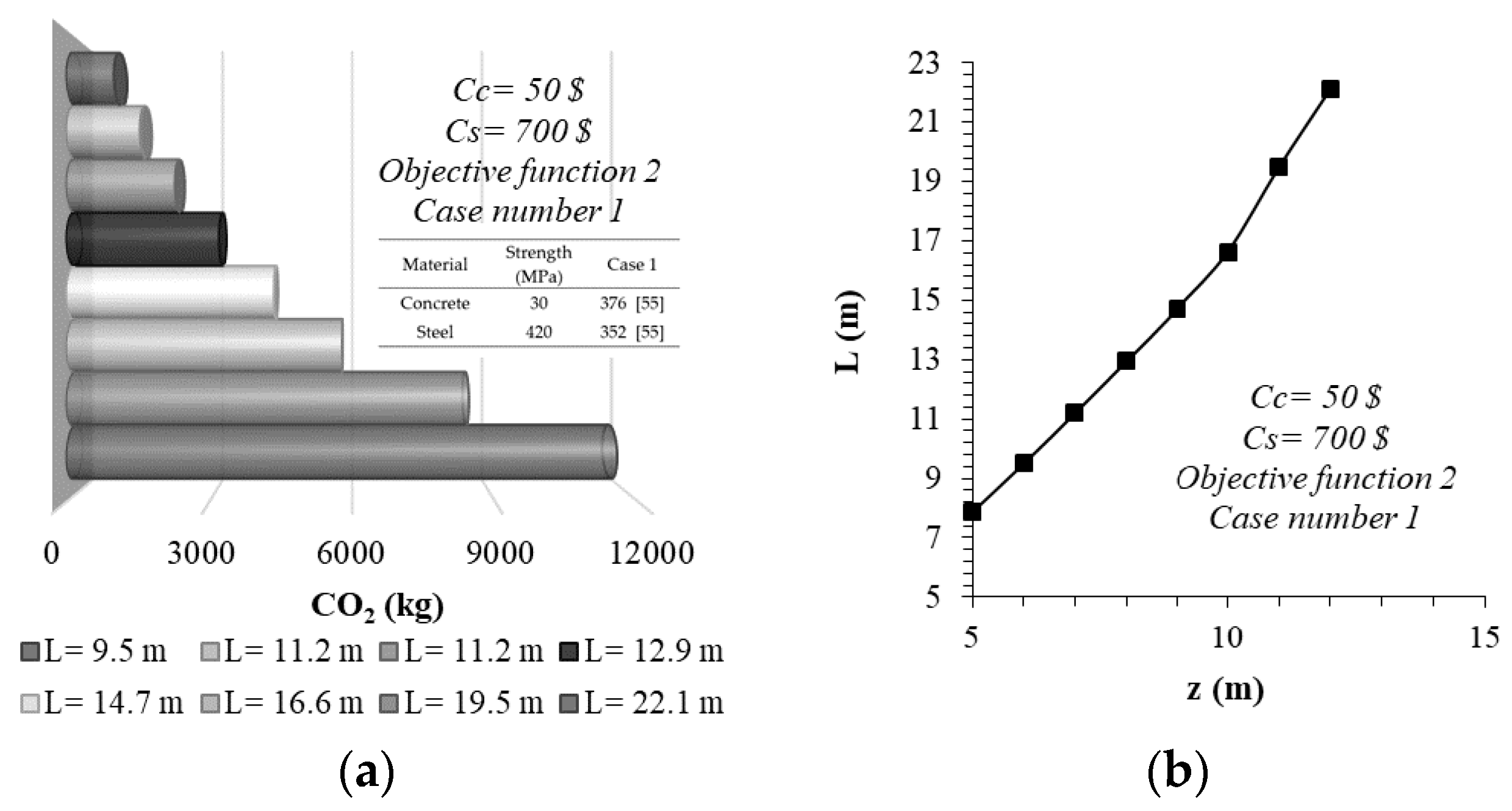
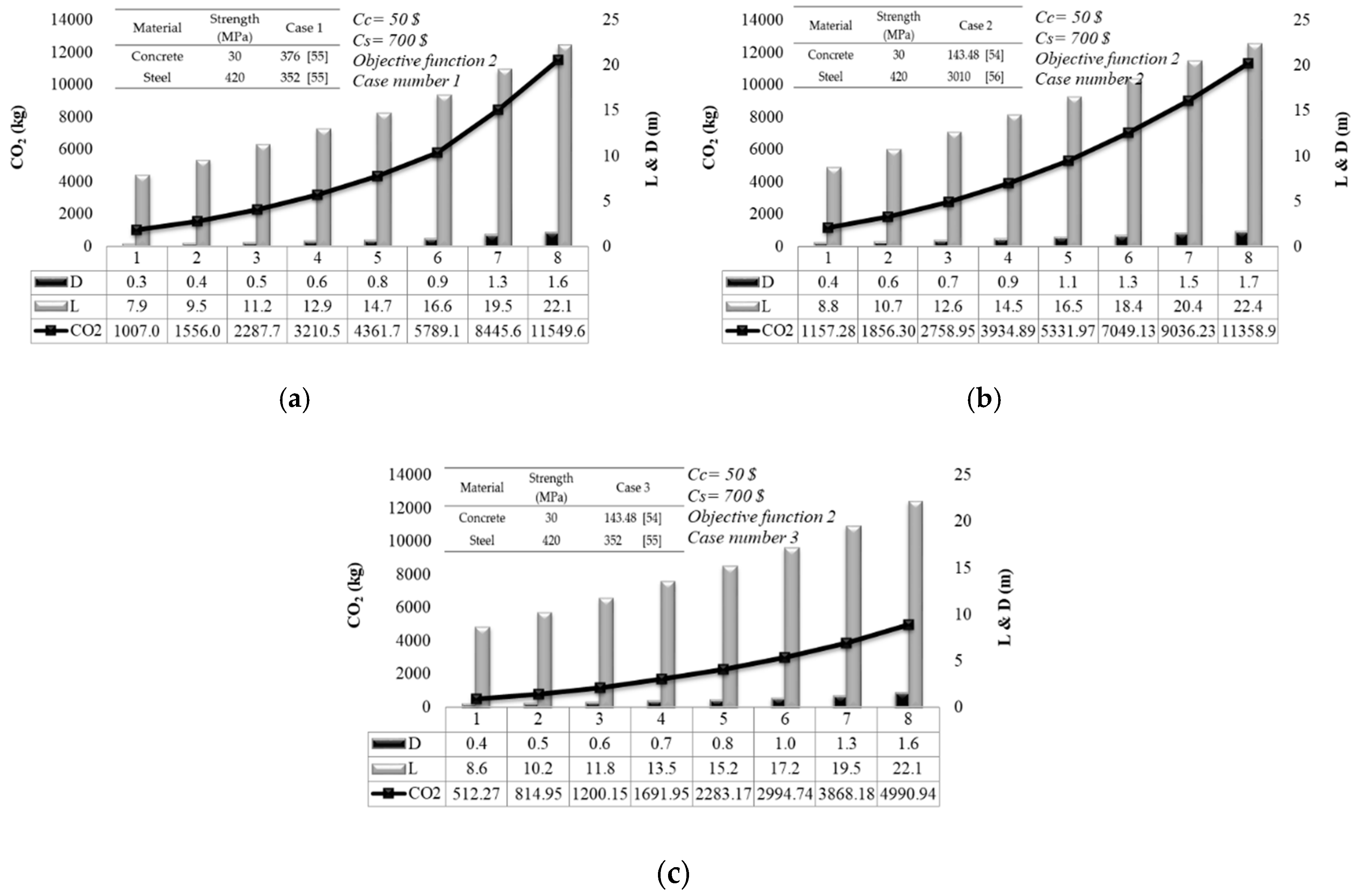
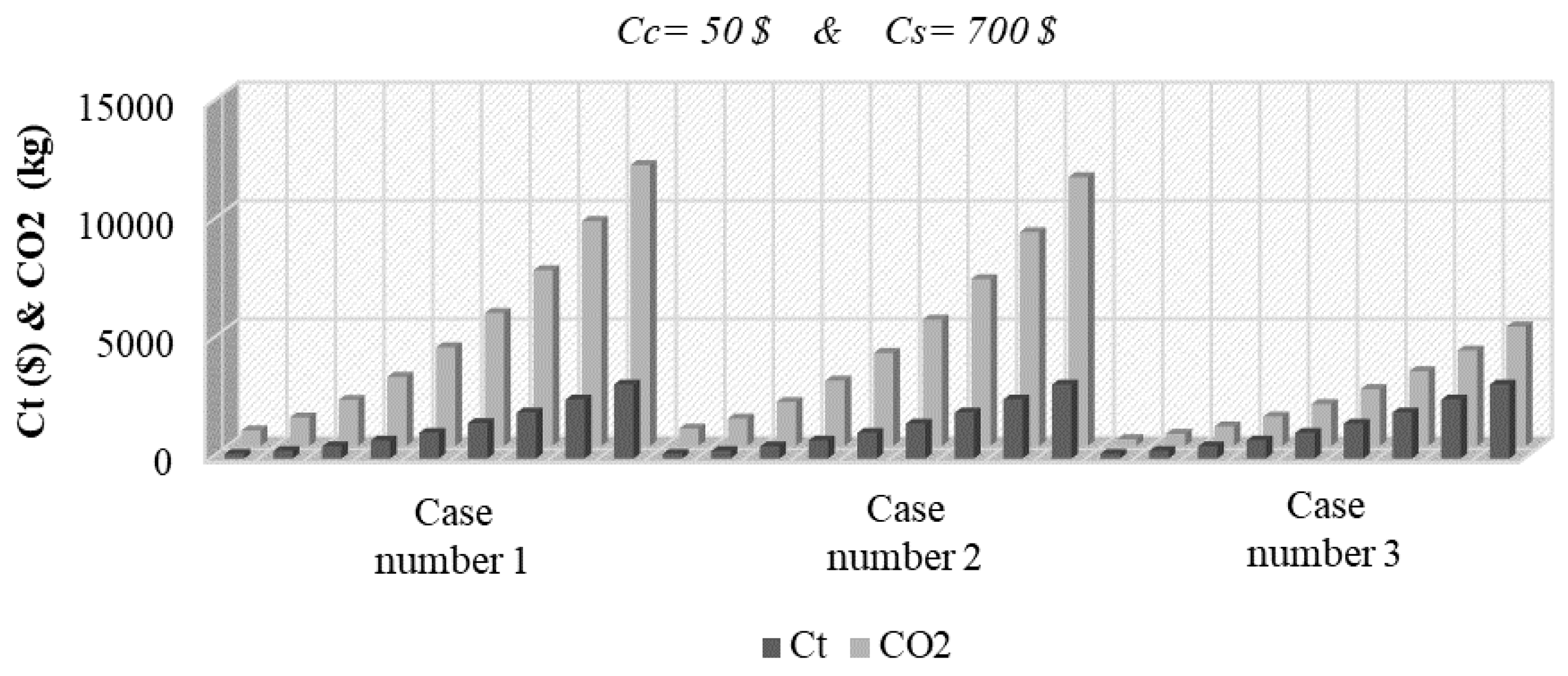
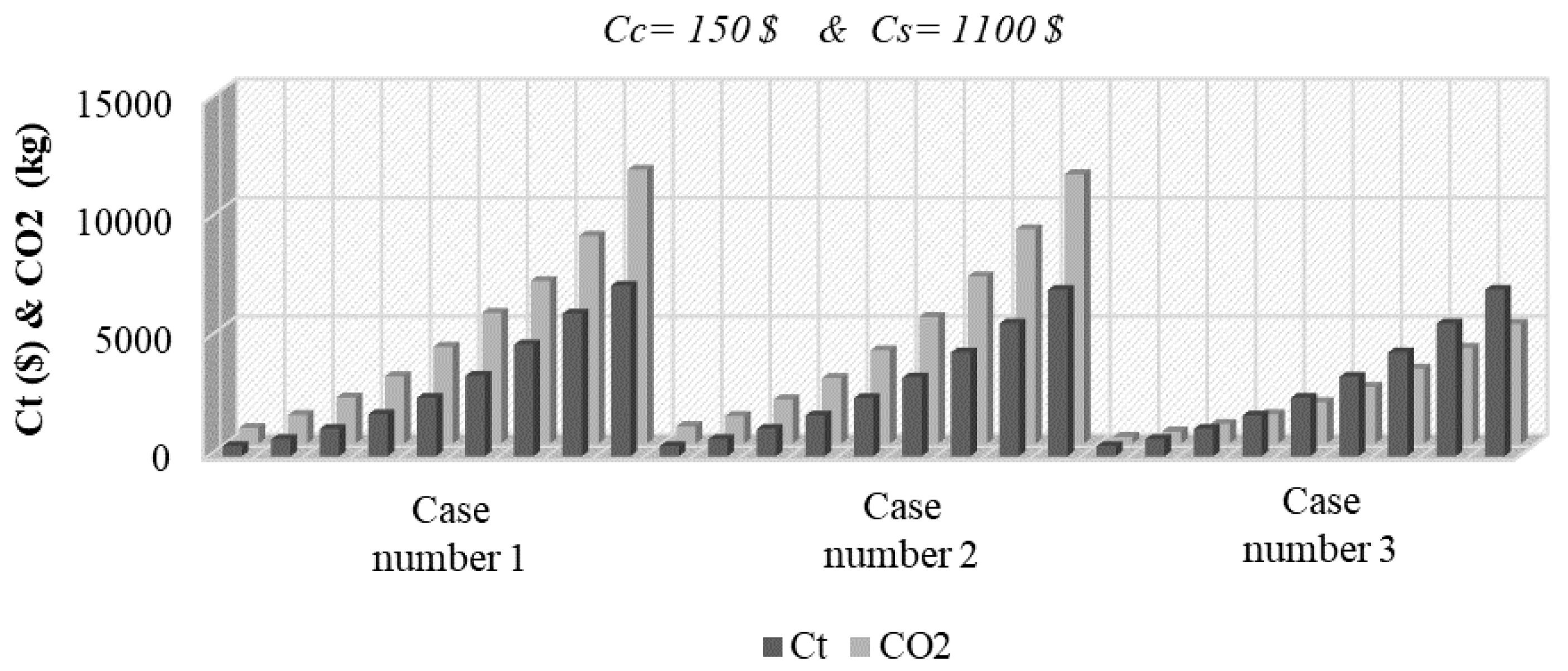
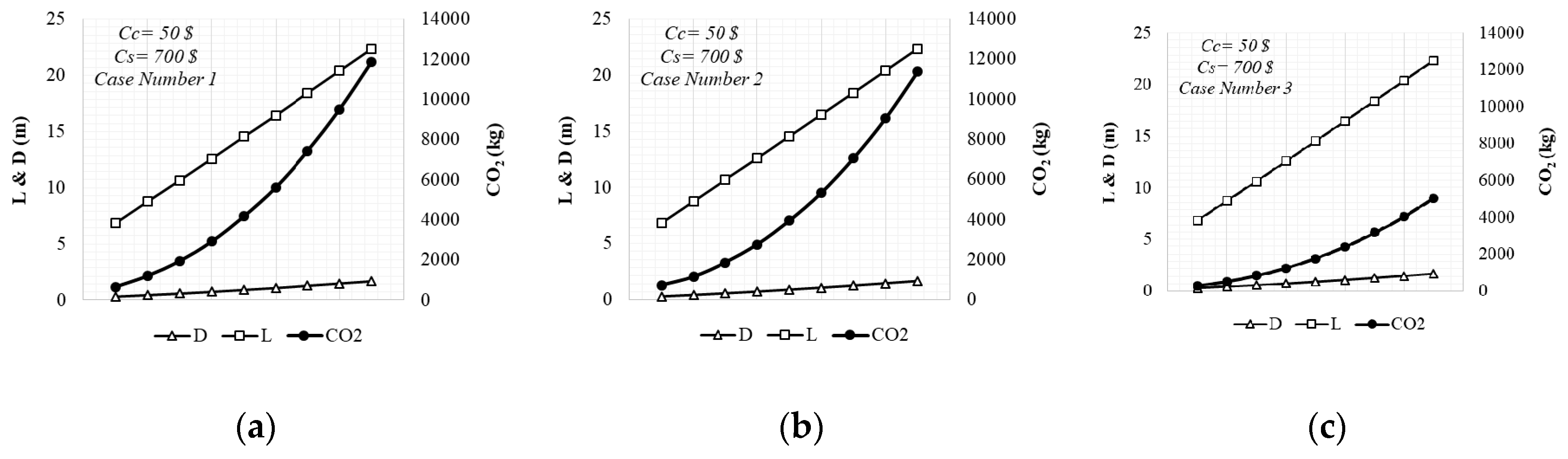
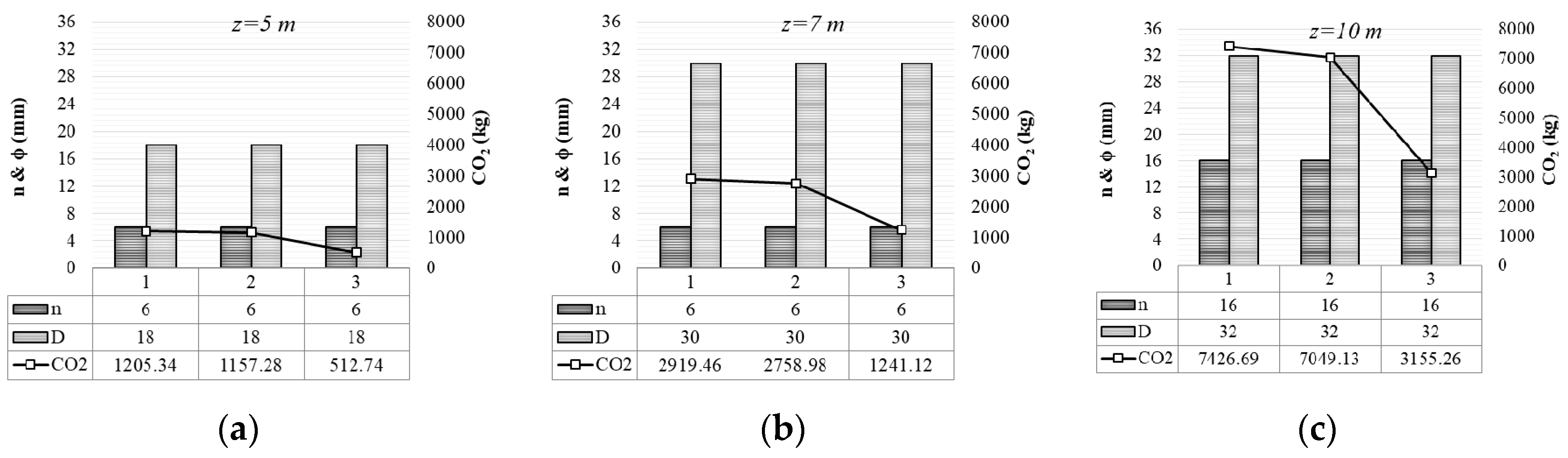
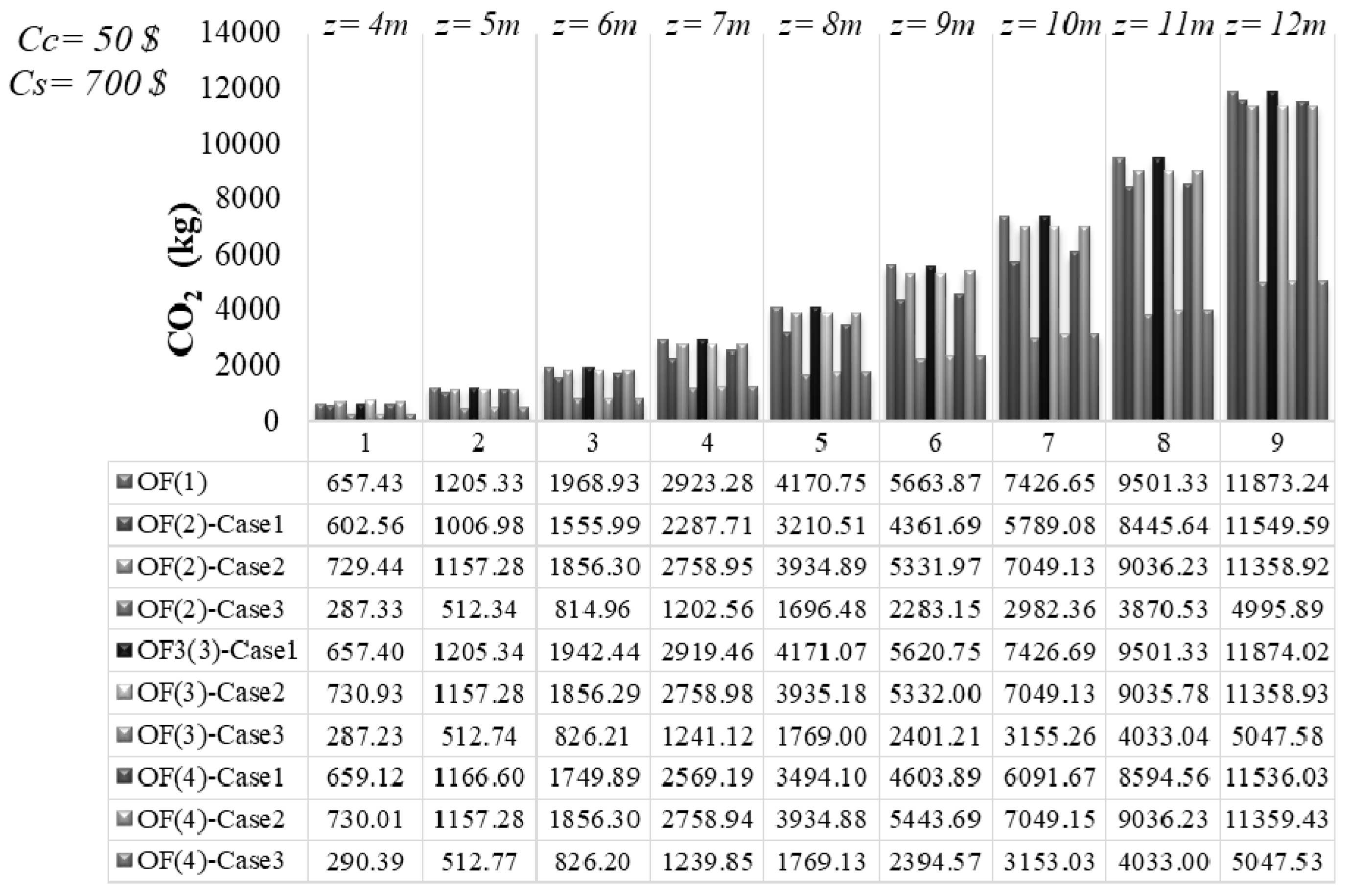
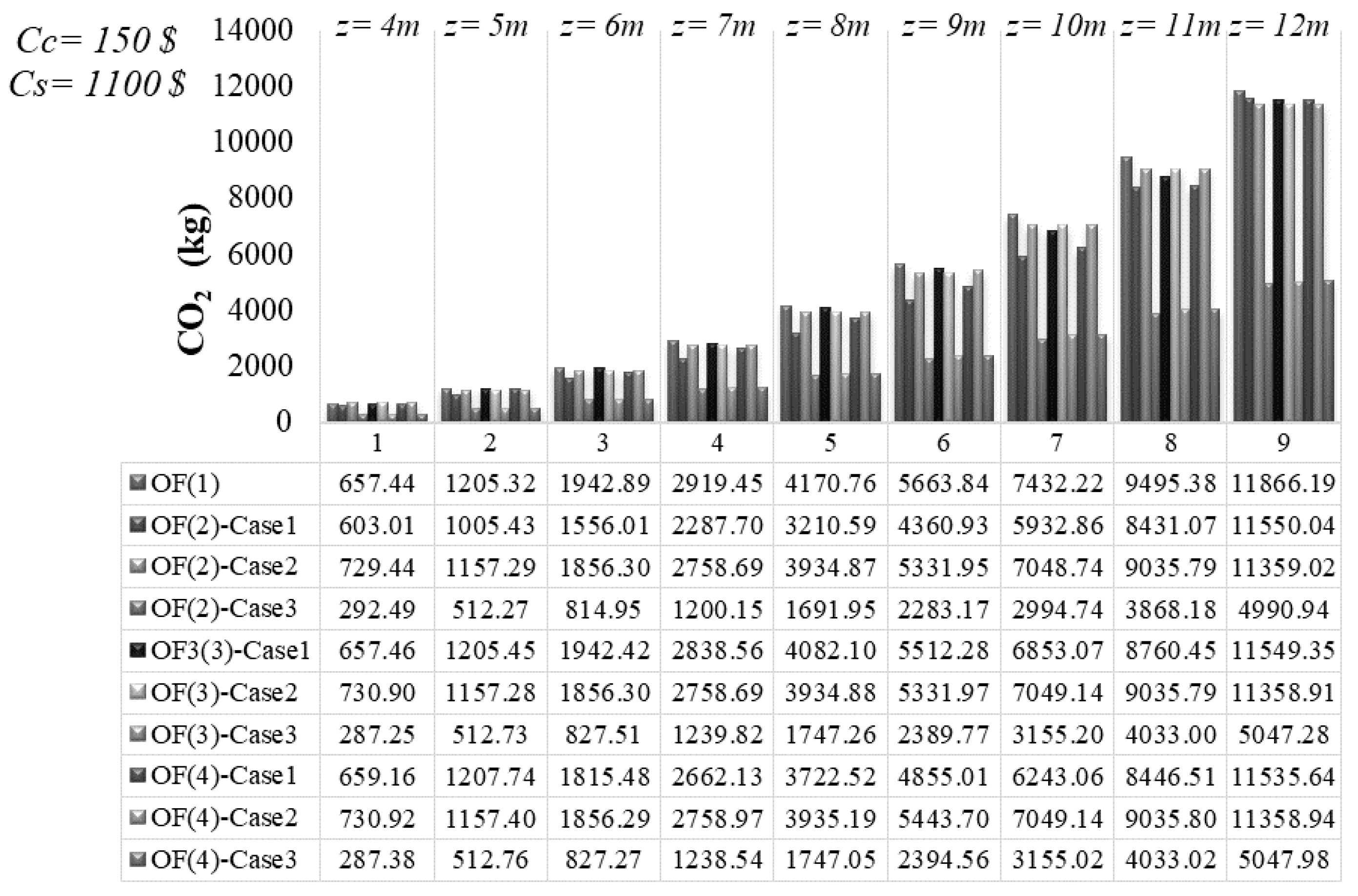
4.2. Design and Minimum CO2 Emission Relationship
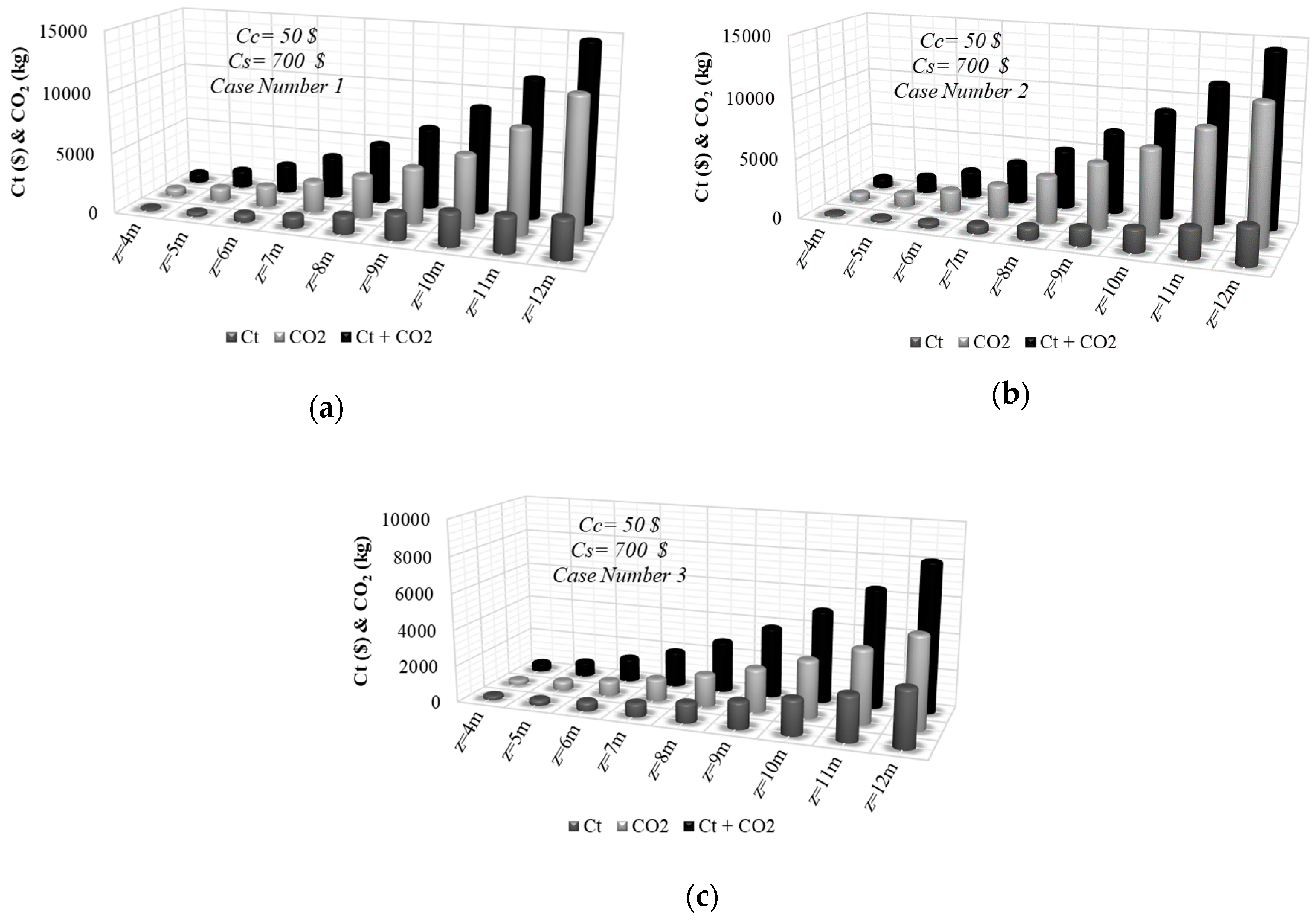
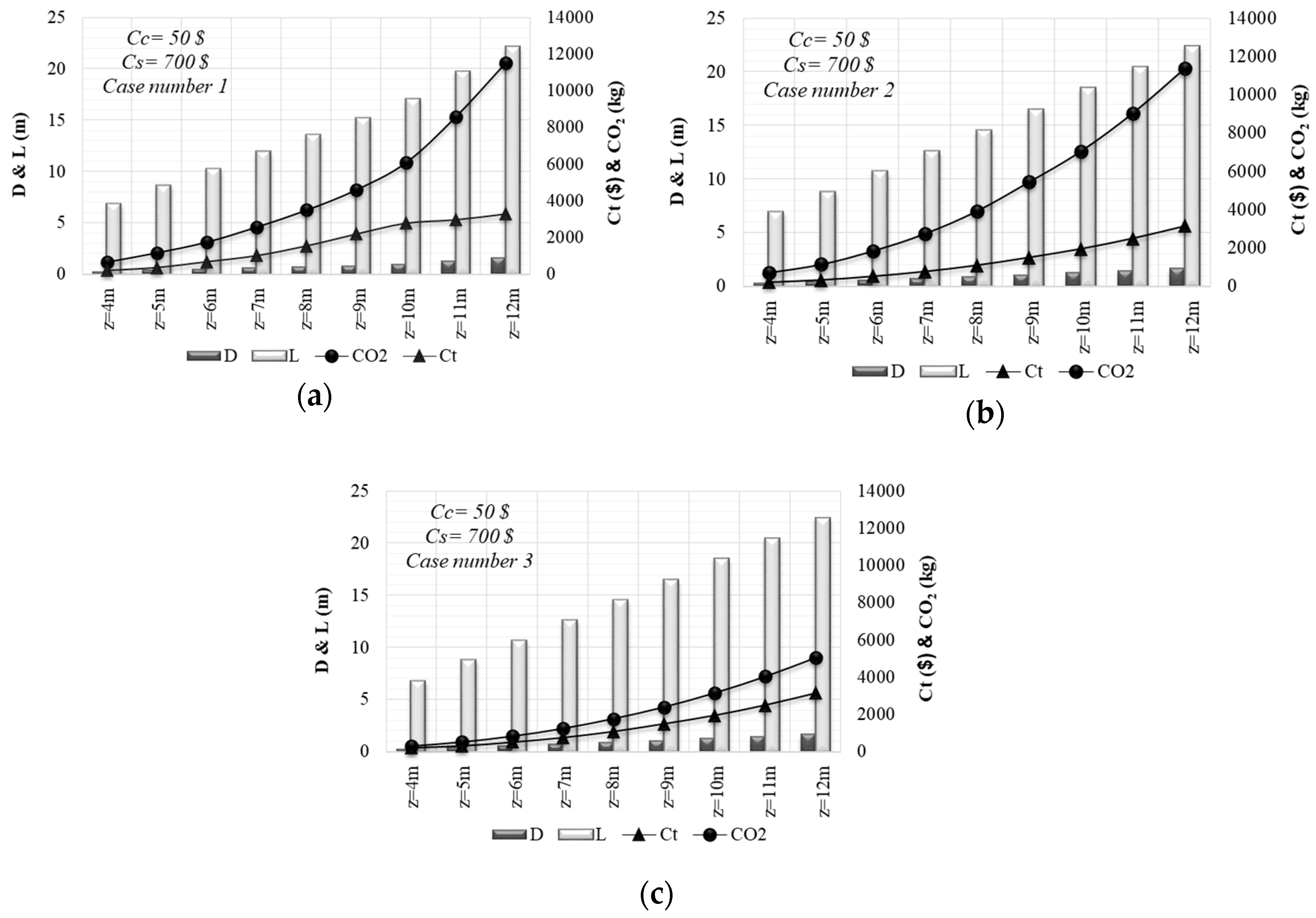
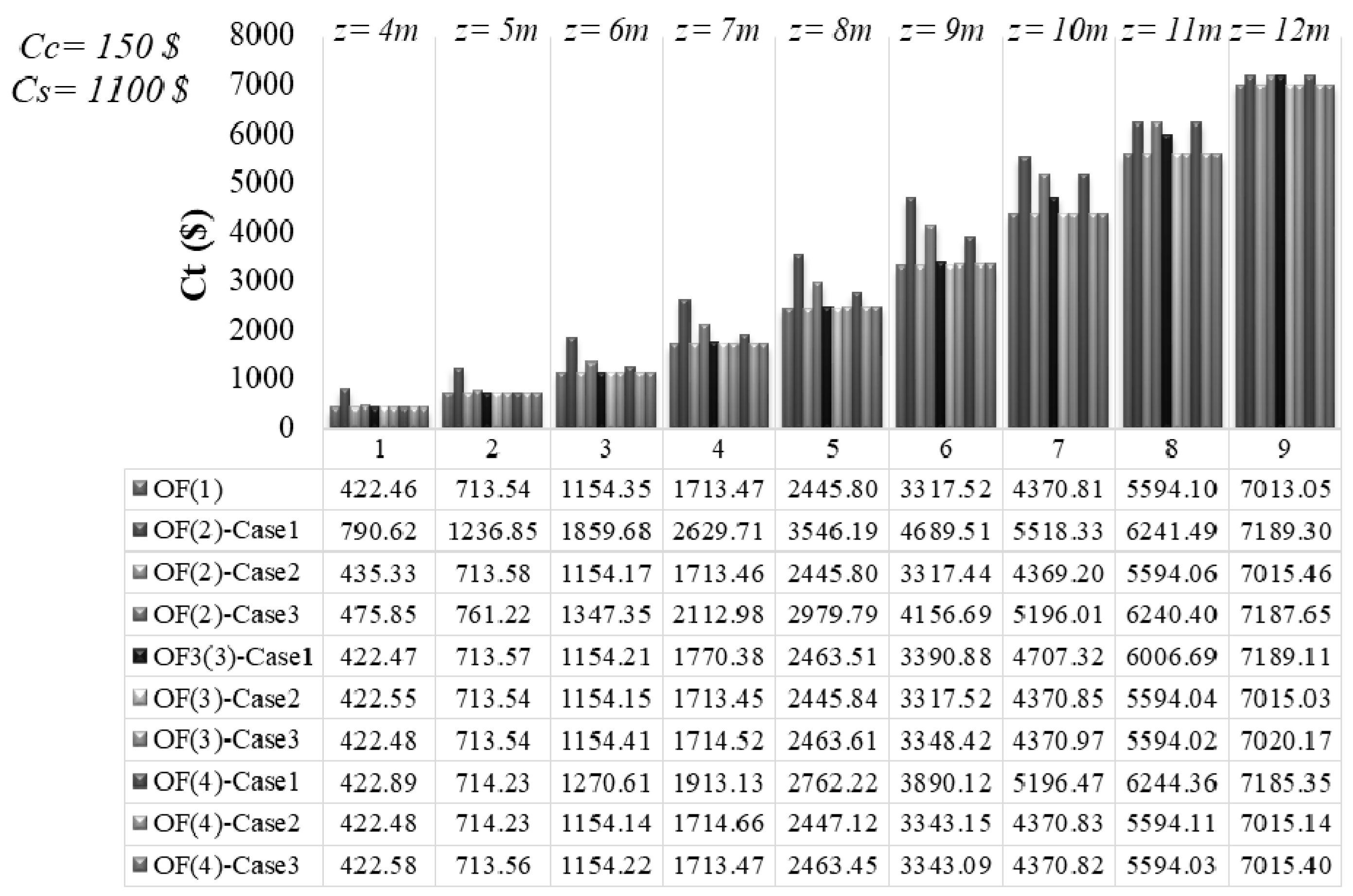
4.3. Design and Minimum Cost and Minimum CO2 Emission Relationship
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Azizi, F. Applied Analyses in Geotechnics; E & FN Spon: London, UK; Taylor and Francis Group: New York, NY, USA, 1999; ISBN 9780419253501. [Google Scholar]
- Das, B.M. Principles of Foundation Engineering, 6th ed.; Thomson: Toronto, ON, Canada, 2007; ISBN 9781305081567. [Google Scholar]
- Lee, C.J.; Wei, Y.C.; Chen, H.T.; Chang, Y.Y.; Lin, Y.C.; Huang, W.S. Stability analysis of cantilever double soldier-piled walls in sandy soil. J. Chin. Inst. Eng. 2011, 34, 449–465. [Google Scholar] [CrossRef]
- Macnab, A. Earth Retention Systems Handbook; McGraw-Hill: New York, NY, USA, 2002; pp. 319–322. ISBN 978-0071373319. [Google Scholar]
- Lyndon, A.; Pearson, R.A. Pressure distribution on a rigid retaining wall in cohesionless material. In Proceedings of the Symposium Application of Centrifuge Modeling to Geotechnical Design, Manchester, UK, 16–18 April 1984; pp. 271–280. [Google Scholar]
- Clayton, C.R.I.; Militisky, J. Earth Pressure and Earth Retaining Structures; Blackie Academic & Professional: New York, NY, USA, 1993; ISBN 9781138427297. [Google Scholar]
- Randolph, M.F. The response of flexible piles to lateral loading. Geotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Verruijt, A.; Kooijman, A.P. Laterally loaded piles in a layered elastic medium. Geotechnique 1989, 39, 39–49. [Google Scholar] [CrossRef]
- Konagai, K.; Yin, Y.; Murono, Y. Single beam analogy for describing soil–pile group interaction. Soil Dyn. Earthq. Eng. 2003, 23, 31–39. [Google Scholar] [CrossRef]
- Rashidi, F.; Shahir, H. Numerical investigation of anchored soldier pile wall performance in the presence of surcharge. Int. J. Geotech. Eng. 2019, 13, 162–171. [Google Scholar] [CrossRef]
- Aydoğdu, İ.; Akın, A. Biogeography Based CO2 and Cost Optimization of RC Cantilever Retaining Walls. World Acad. Sci. Eng. Technol. Int. J. Civil Environ. Eng. 2015. [Google Scholar] [CrossRef]
- Villalba, P.; Alcala, J.; Yepes, V.; Gonzales-Vidosa, F. CO2 optimization of reinforced concrete cantilever retaining walls. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Potugal, 6–9 September 2010. [Google Scholar]
- Sasidhar, T.; Neeraja, D.; Sudhindra, V.S.M. Application of genetic algorithm technique for optimizing design of reinforced concrete retaining wall. Int. J. Civ. Eng. Technol. 2017, 8, 999–1007. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison Wesley: Boston, MA, USA, 1989; ISBN 978-0201157673. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975; ISBN 9780262082136. [Google Scholar]
- Kaveh, A.; Kalateh-Ahani, M.; Fahimi-Farzam, M. Constructability optimal design of reinforced concrete retaining walls using a multi-objective genetic algorithm. Struct. Eng. Mech. 2013, 47, 227–245. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks No. IV, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Ahmadi-Nedushan, B.; Varaee, H. Optimal Design of Reinforced Concrete Retaining Walls using a Swarm Intelligence Technique. In Proceedings of the First International Conference on Soft Computing Technology in Civil, Structural and Environmental Engineering, Stirlingshire, Scotland, 1 September 2009. [Google Scholar]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization; InStochasticalgorithms: Foundations and applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Sheikholeslami, R.; Khalili, B.G.; Zahrai, S.M. Optimum Cost Design of Reinforced Concrete Retaining Walls Using Hybrid Firefly Algorithm. Int. J. Eng. Technol. 2014, 6, 465–470. [Google Scholar] [CrossRef] [Green Version]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Camp, C.V.; Akin, A. Design of Retaining Walls Using Big Bang-Big Crunch Optimization. J. Struct. Eng. ASCE 2012, 138, 438–448. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Kaveh, A.; Abadi, A.S.M. Harmony search based algorithms for the optimum cost design of reinforced concrete cantilever retaining walls. Int. J. Civ. Eng. 2011, 9, 1–8. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NISCO 2010); Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef] [Green Version]
- Talatahari, S.; Sheikholeslami, R. Optimum design of gravity and reinforced retaining walls using enhanced charged system search algorithm. KSCE J. Civ. Eng. 2014, 18, 1464–1469. [Google Scholar] [CrossRef]
- Ceranic, B.; Fryer, C.; Baines, R.W. An application of simulated annealing to the optimum design of reinforced concrete retaining structures. Comput. Struct. 2001, 79, 1569–1581. [Google Scholar] [CrossRef] [Green Version]
- Yepes, V.; Alcala, J.; Perea, C.; Gonzalez-Vidosa, F. A parametric study of optimum earth-retaining walls by simulated annealing. Eng. Struct. 2008, 30, 821–830. [Google Scholar] [CrossRef]
- Pei, Y.; Xia, Y. Design of cantilever retaining walls using heuristic optimization algorithms. Procedia Earth Planet. Sci. 2012, 5, 32–36. [Google Scholar] [CrossRef] [Green Version]
- Mergos, P.E.; Mantoglou, F. Optimum design of reinforced concrete retaining wall with the flower pollination algorithm. Struct. Multidiscip. Optim. 2019. [Google Scholar] [CrossRef]
- Yoo, D.G.; Kim, J.H.; Geem, Z.W. Overview of harmony search algorithm and its applications in civil engineering. Evol. Intell. 2014, 7, 3–16. [Google Scholar] [CrossRef]
- Geem, Z.W. State-of-the-Art in the Structure of Harmony Search Algorithm, Recent Advances in Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2010; Volume 270, pp. 1–10. [Google Scholar] [CrossRef]
- Akın, A.; Saka, M.P. Optimum Design of Concrete Cantilever Retaining Walls Using the Harmony Search Algorithm. In Proceedings of the Tenth International Conference on Computational Structures Technology; Topping, B.H.V., Adam, J.M., Pallarés, F.J., Bru, R., Romero, M.L., Eds.; Civil-Comp Press: Stirlingshire, UK, 2010; p. 130. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; José, V.M.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Yepes, V.; Marti, J.V.; Garcia, J. Black hole algorithm for sustainable design of counterfort retaining walls. Sustainability 2020, 12, 2767. [Google Scholar] [CrossRef] [Green Version]
- Aydoğdu, İ. Comparison of metaheuristics on multi objective (cost&CO2) optimization of RC cantilever retaining walls. Pamukkale Univ. Muh. Bilim. Derg. 2017, 23, 221–231. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Efficient gravitational search algorithm for optimum design of retaining walls. Struct. Eng. Mech. 2013, 45, 111–127. [Google Scholar] [CrossRef]
- Öztürk, H.T.; Türkeli, E. Optimum design of RC Retaining walls with key section using jaya algorithm. J. Polytech 2019, 22, 283–291. [Google Scholar] [CrossRef]
- King, G.J.W. Analysis of cantilever sheet-pile walls in cohesionless soil. J. Geotech. Eng. 1995, 121, 629–635. [Google Scholar] [CrossRef]
- Bica, A.V.D.; Clayton, C.R.I. Limit equilibrium design methods for free embedded cantilever walls in granular soils. Proc. Inst. Civ. Eng. 1989, 86, 879–898. [Google Scholar] [CrossRef]
- Banerjee, P.K.; Davies, T.G. The behaviour of axially and laterally loaded single piles embedded in nonhomogeneous soils. Géotechnique 1978, 28, 309–326. [Google Scholar] [CrossRef]
- Kay, S.; Griffiths, D.V.; Kolk, H.J. Application of pressuremeter testing to assess lateral pile response in clays. In Pressuremeter and Its Marine Applications: Second International Symposium; Briaud, J., Audibert, J., Eds.; ASTM International: West Conshohocken, PA, USA, 1985. [Google Scholar] [CrossRef]
- Geem, Z.W.; Lee, K.S.; Park, Y. Application of harmony search to vehicle routing. Am. J. Appl. Sci. 2005, 2, 1552–1557. [Google Scholar] [CrossRef] [Green Version]
- Ulusoy, S.; Kayabekir, A.E.; Bekdaş, G.; Niğdeli, S.M. Metaheuristic Algorithms in Optimum Design of Reinforced Concrete Beam by Investigating Strength of Concrete. Chall. J. Concr. Res. Lett. 2020, 11, 33–37. [Google Scholar] [CrossRef]
- Ulusoy, S.; Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M. Optimum Design of Reinforced Concrete Multi-Story Multi-Span Frame Structures under Static Loads. Int. J. Eng. Technol. 2018, 10, 403–407. [Google Scholar] [CrossRef] [Green Version]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary on Building Code Requirements for Structural Concrete (ACI 318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Gajan, S. Normalized relationships for depth of embedment of sheet pile walls and soldier pile walls in cohesionless soils. Soils Found 2011, 51, 559–564. [Google Scholar] [CrossRef] [Green Version]
- FHWA-IF-99-015. Geotechnical Engineering Circular No. 4 Ground Anchors and Anchored Systems; Federal Highway Administration: Washington, DC, USA, 1999.
- Kazı Çukurlarının Stabilitesi ve İksa Sistemi Etüt, Proje, Uygulama ve Kontrolleri Ile İlgili Uyulacak Esaslar hakkında Kazı Güvenliği ve Alınacak Önlemler; Çevre ve şehircilik Bakanlığı: Ankara, Turkey, 2018.
- British Standards Institution. Eurocode 7: Part 1, General Rules; British Standards Institution: London, UK, 1995. [Google Scholar]
- Yeo, D.; Potra, F.A. Sustainable design of reinforced concrete structures through CO2 emission optimization. J. Struct. Eng. 2015, 141, B4014002. [Google Scholar] [CrossRef] [Green Version]
- Paya-Zaforteza, I.; Yepes, V.; Hospitaler, A.; Gonzalez-Vidosa, F. CO2-optimization of reinforced concrete frames by simulated annealing. Eng. Struct. 2009, 31, 1501–1508. [Google Scholar] [CrossRef]
- Bekdaş, G.; Akbay Arama, Z.; Kayabekir, A.E.; Geem, Z.W. Optimal design of cantilever soldier pile retaining walls embedded in frictional soils with harmony search algorithm. Appl. Sci. 2020, 10, 3232. [Google Scholar] [CrossRef]

| Symbol | Description of Parameter | |
|---|---|---|
| Variables in relation to cross-section dimension | X1 | Diameter of soldier pile (D) |
| Variables in relation to reinforced concrete design | X2 | Diameter of reinforcing bars of soldier pile (ϕp) |
| X3 | Number of reinforcing bars of soldier pile |
| Description | Constraints |
|---|---|
| Flexural strength capacities of critical sections (Md) | g1(X): Md ≥ Mu |
| Shear strength capacities of critical sections (Vd) | g2(X): Vd ≥ Vu |
| Minimum reinforcement areas of critical sections (Asmin) | g3(X): As ≥ Asmin |
| Maximum reinforcement areas of critical sections (Asmax) | g4(X): As ≤ Asmax |
| Symbol | Definition | Value | Unit |
|---|---|---|---|
| h | Depth of excavation | 4 to12 | m |
| fy | Yield strength of steel | 420 | MPa |
| f’c | Compressive strength of concrete | 30 | MPa |
| cc | Concrete cover | 30 | mm |
| Esteel | Elasticity modulus of steel | 200 | GPa |
| Econcrete | Elasticity modulus of concrete | 23.5 | GPa |
| γsteel | Unit weight of steel | 7.85 | t/m3 |
| γconcrete | Unit weight of concrete | 25 | kN/m3 |
| Cc | Cost of concrete per m3 | 50, 75, 100, 125, 150 | $ |
| Cs | Cost of steel per ton | 700, 800, 900, 1000, 1100 | $ |
| q | Surcharge load located adjacent the top of the pile | 10 | kPa |
| β | Backfill slope angle | 0 | ° |
| ϕ | Shear strength angle | 30 | ° |
| γ | Unit weight of soil | 18 | kN/m3 |
| D | Diameter of pile | 0.3–2 | m |
| ϕp | Diameter of reinforcing bars of soldier pile | 14–40 | - |
| n | Number of reinforcing bars of soldier pile | 6–20 | - |
| Material | Class | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| Concrete | C30 | 376 | 143.48 | 143.48 |
| Steel | S420 | 352 | 3010 | 352 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arama, Z.A.; Kayabekir, A.E.; Bekdaş, G.; Geem, Z.W. CO2 and Cost Optimization of Reinforced Concrete Cantilever Soldier Piles: A Parametric Study with Harmony Search Algorithm. Sustainability 2020, 12, 5906. https://doi.org/10.3390/su12155906
Arama ZA, Kayabekir AE, Bekdaş G, Geem ZW. CO2 and Cost Optimization of Reinforced Concrete Cantilever Soldier Piles: A Parametric Study with Harmony Search Algorithm. Sustainability. 2020; 12(15):5906. https://doi.org/10.3390/su12155906
Chicago/Turabian StyleArama, Zülal Akbay, Aylin Ece Kayabekir, Gebrail Bekdaş, and Zong Woo Geem. 2020. "CO2 and Cost Optimization of Reinforced Concrete Cantilever Soldier Piles: A Parametric Study with Harmony Search Algorithm" Sustainability 12, no. 15: 5906. https://doi.org/10.3390/su12155906
APA StyleArama, Z. A., Kayabekir, A. E., Bekdaş, G., & Geem, Z. W. (2020). CO2 and Cost Optimization of Reinforced Concrete Cantilever Soldier Piles: A Parametric Study with Harmony Search Algorithm. Sustainability, 12(15), 5906. https://doi.org/10.3390/su12155906







