Renewable Energy Green Innovation, Fossil Energy Consumption, and Air Pollution—Spatial Empirical Analysis Based on China
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Variables and Data
3.1.1. Explained Variable
3.1.2. Explanatory Variables
Main Explanatory Variable
Control Variable
- (1)
- Environmental Regulation (ER): There are many ways to measure the intensity of environmental regulation, considering China’s environmental pollution control policies. This article refers to the practice of Zhu Y et al. (2019) [29] and selects the number of environmental punishment cases as a proxy variable for the intensity of environmental regulation. To a certain extent, environmental regulations will restrain the emission of micro-subjects.
- (2)
- Industrial Structure (IS): Select the proportion of the secondary industry as a proxy variable. The study of Hao et al. (2016) [37] shows that the correlation coefficient between the proportion of secondary industry and the amount of pollutant emissions is positive. Therefore, this article assumes that there is a positive correlation between industrial structure and air pollution.
- (3)
- Gross Domestic Product (GDP): Due to the difference between nominal GDP and real GDP, this article is based on the GDP of each province and municipality directly under the central government in 2000. By calculating the GDP deflator, the constant price GDP is calculated.
- (4)
- Population (POP): There is a direct link between population size and pollutant emissions. An increase in population will significantly increase energy consumption and pollutant emissions.
3.1.3. Variable Descriptive Statistics
3.1.4. Data Resources
3.2. Spatial Autocorrelation Test
3.2.1. Global Correlation Index
3.2.2. Local Correlation Index
- (1)
- H–H: area units with high observation values are surrounded by high-value areas.
- (2)
- H–L: area units with high observation values are surrounded by areas with low values.
- (3)
- L–L: area units with low observation values are surrounded by low-value areas.
- (4)
- L–H: area units with low observation values are surrounded by high-value areas.
3.3. Spatial Econometric Model
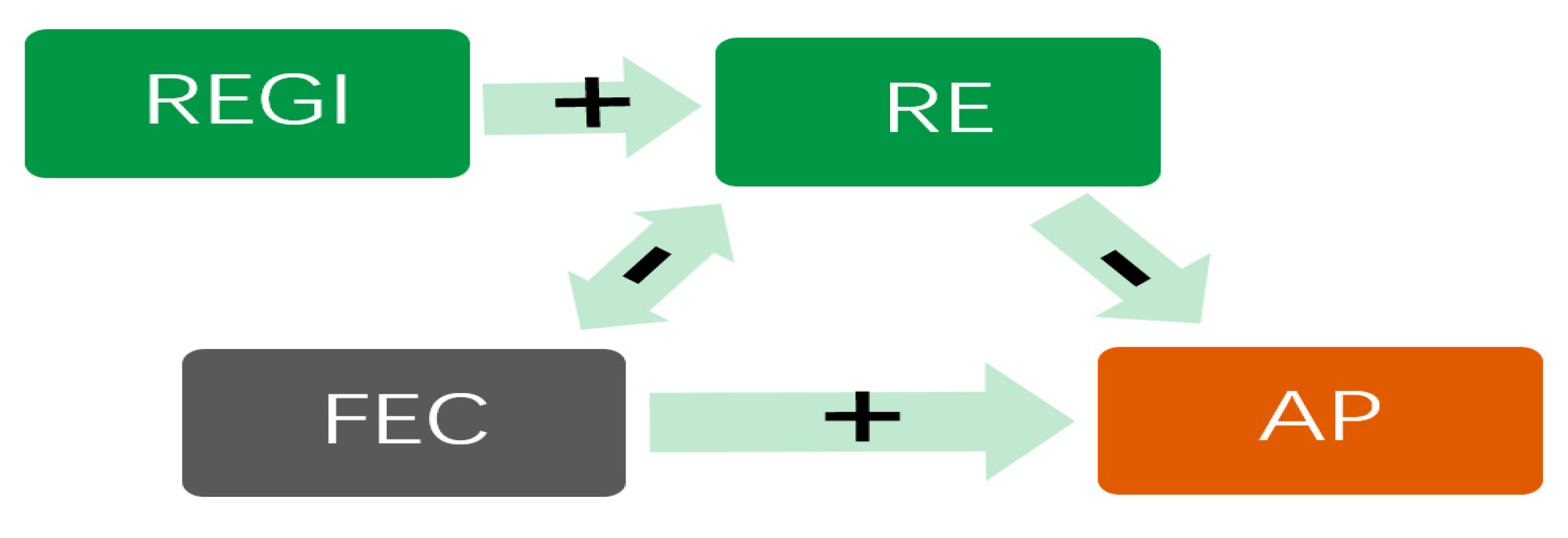
3.4. Direct and Indirect Spatial Impact
4. Exploratory Spatial Analysis Results and Discussion
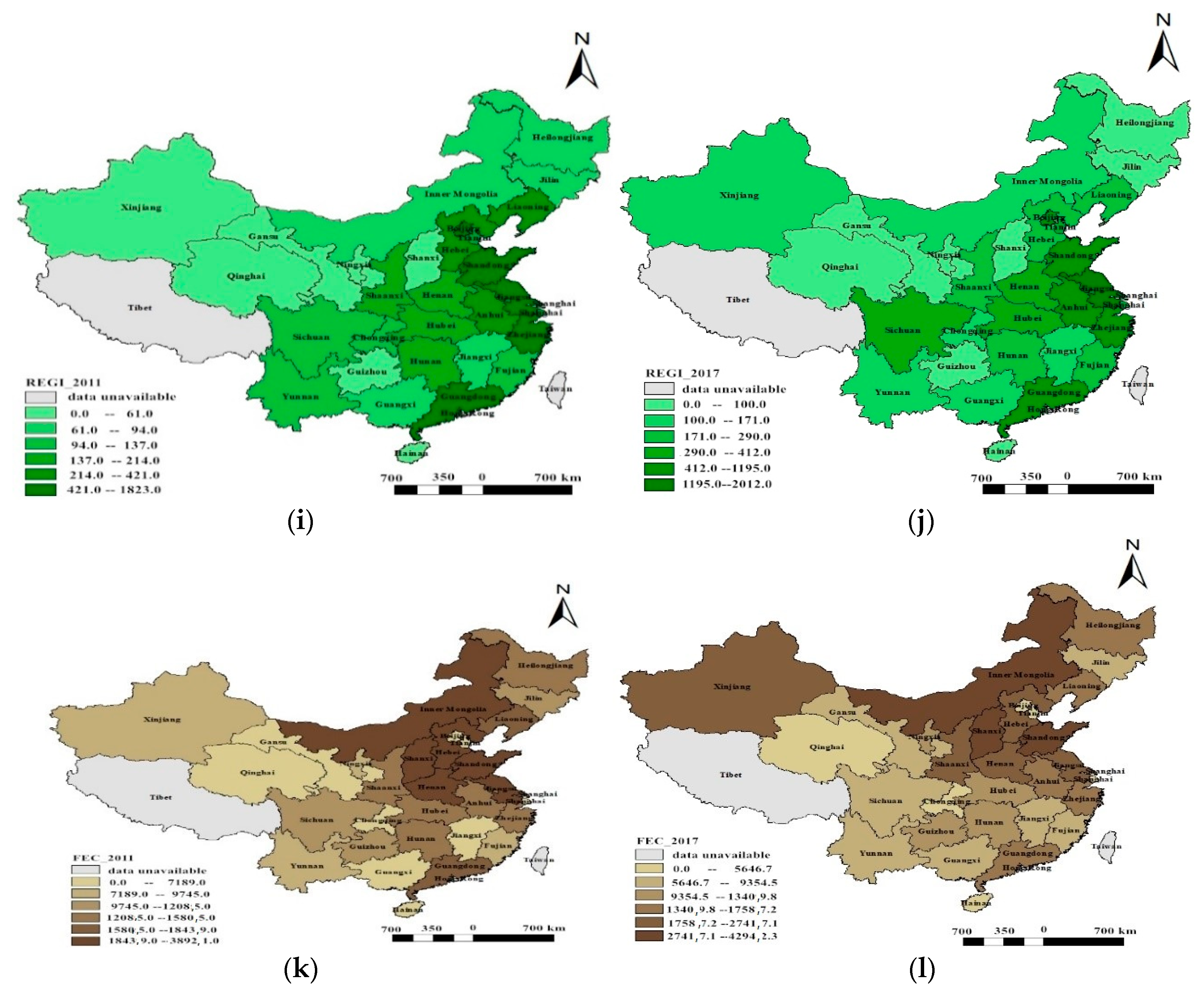
4.1. Temporal and Spatial Distribution Characteristics of Air Pollution, REGI, and Fossil Energy Consumption
4.2. Global Spatial Correlation Analysis
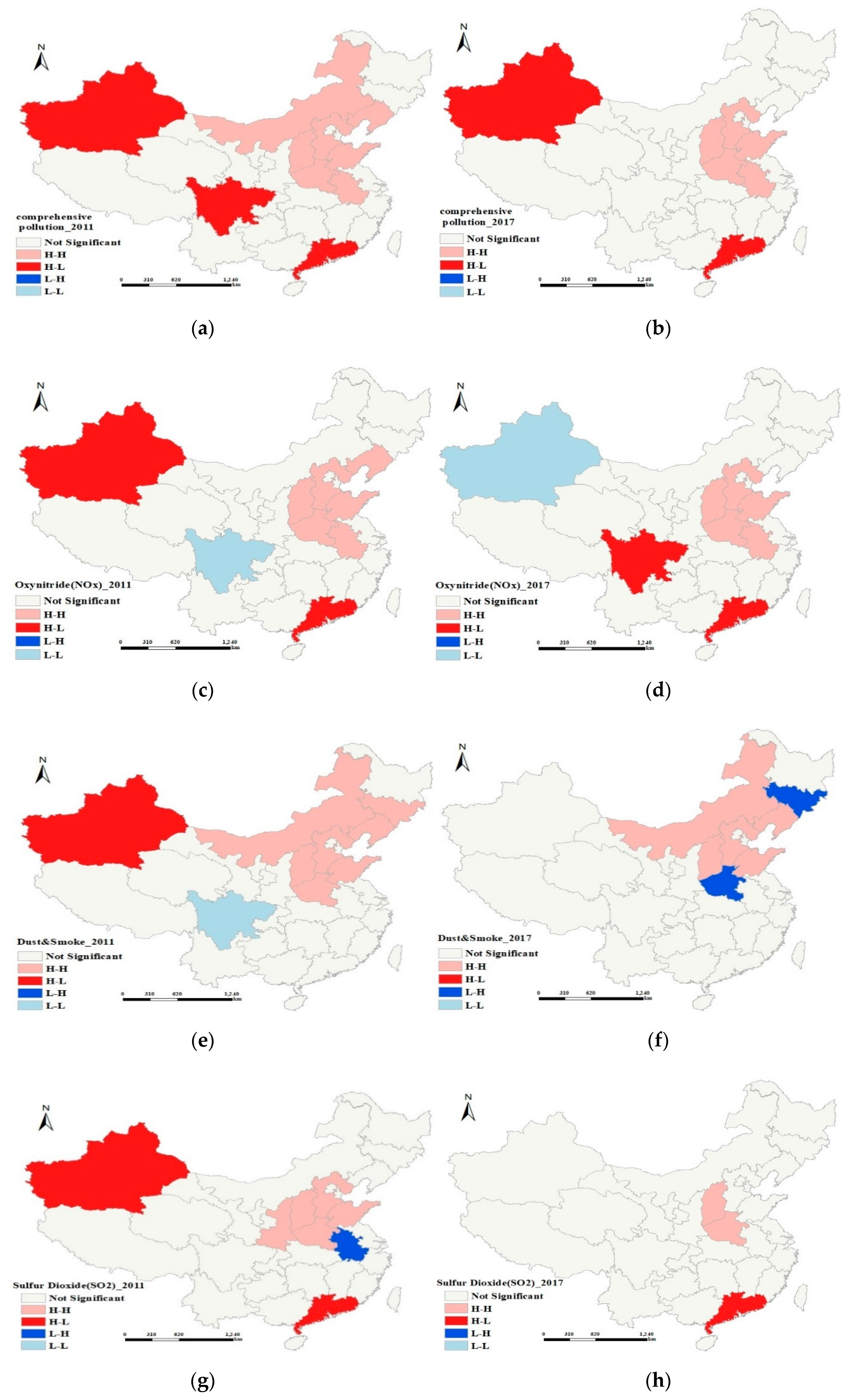
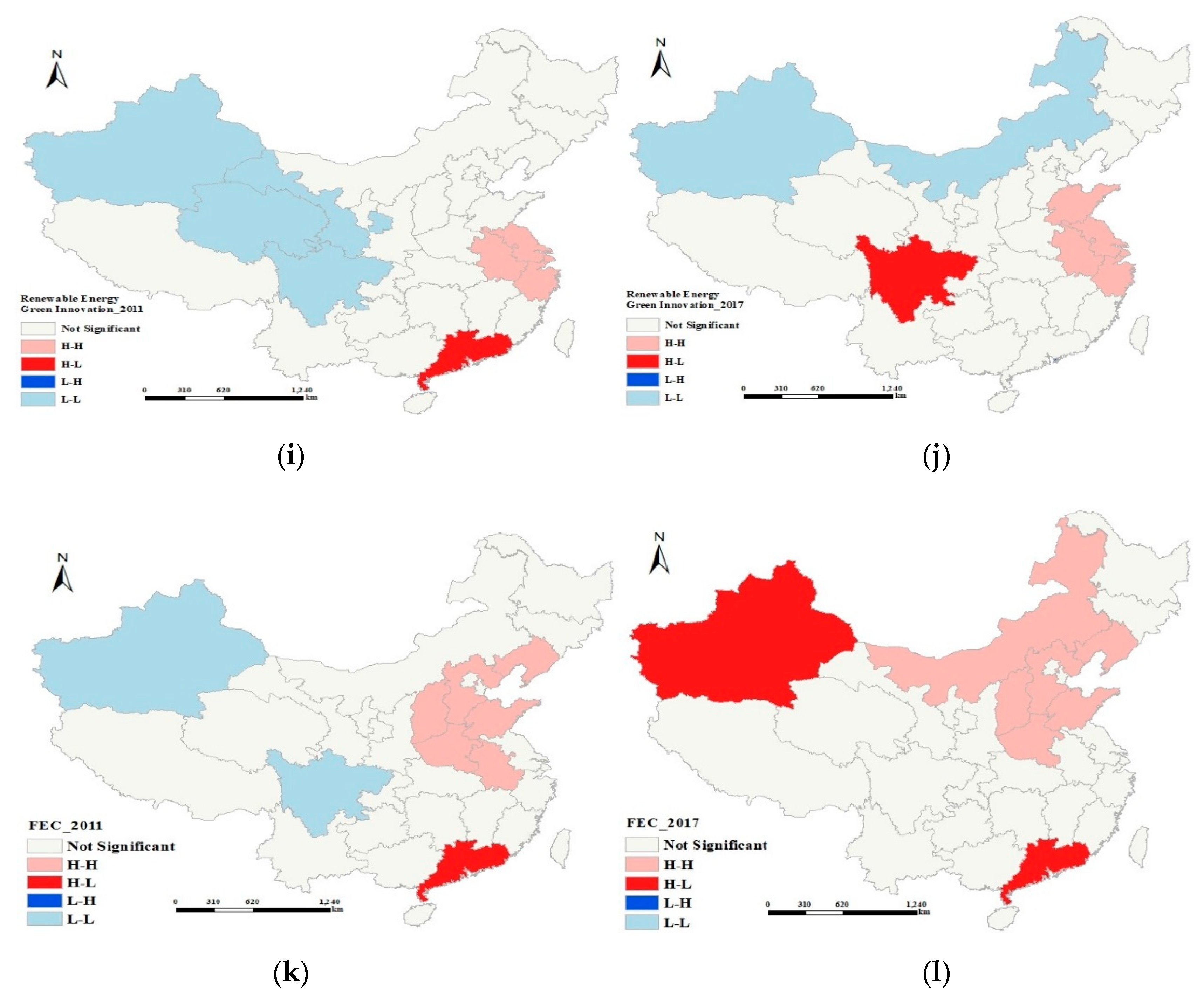
4.3. Local Indicators of Spatial Association (LISA) Analysis Results
5. Spatial Panel Estimate Results and Discussion
5.1. Analysis of Non-Spatial Panel Model Results
5.2. Analysis of Spatial Durbin Model Results
5.3. Direct Effect, Indirect Effect, and Total Effect
6. Conclusions and Policy Implication
- (1)
- The spatial distribution of air pollution in China is characterized by high in the east and low in the west, and high in the north and low in the south. The peaks of comprehensive pollutants, NOx, SO2, and dust and smoke (DS) are distributed in Shandong, Hebei, Shanxi, Henan, Inner Mongolia, and Guangdong. In addition, China’s air pollution has a strong spatial agglomeration effect. Shandong, Hebei, Shanxi, Henan, and Shaanxi are in the H–H cluster of comprehensive pollutants, NOx, SO2, and dust and smoke (DS) emissions.
- (2)
- Renewable energy green innovation and fossil energy consumption have shown increasingly significant spatial correlation. Renewable energy green innovation highland and low-lying land are becoming more and more prominent. The renewable energy green innovation H–H cluster gradually expanded to Shanghai, Jiangsu, Anhui, Zhejiang, and Shandong. The H–H cluster of fossil energy consumption gradually moved north to Henan, Shandong, Shanxi, Hebei, Liaoning, and Inner Mongolia.
- (3)
- Renewable energy green innovation and environmental regulations have a significant inhibitory effect on air pollution (SO2, NOx, DS). Renewable energy green innovations have curbed air pollution both locally and in neighboring provinces. The consumption of fossil energy, the increase in the proportion of the secondary industry in the industrial structure, and the increase in population size will all lead to an increase in air pollution.
- (1)
- It is recommended to establish a regional coordination mechanism for environmental governance. Neighboring regions should strengthen cooperation to jointly control pollution. When formulating environmental policies, coordination and communication should be emphasized.
- (2)
- It is recommended that while increasing investment in renewable energy innovation, the spatial diffusion of renewable energy green innovation should be strengthened. The government should build a platform for the backward provinces of renewable energy green innovation to introduce advanced renewable energy technologies. In this way, the green innovation of renewable energy can play the biggest role.
- (3)
- The consumption of infectious fossil energy should be controlled. Replacing traditional fossil energy with more renewable energy can effectively reduce air pollution. While upgrading the industrial structure, the government should reasonably control the proportion of industries with high fossil energy consumption and high pollution. Environmental regulations should be appropriately increased.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cozzi, L. World Energy Outlook Special Report 2016: Energy and Air Pollution; IEA: Paris, France, 2016. [Google Scholar]
- Ren, F.; Xia, L. Analysis of China’s Primary Energy Structure and Emissions Reduction Targets by 2030 Based on Multiobjective Programming. Math. Probl. Eng. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Gu, H.; Cao, Y.; Elahi, E.; Jha, S.K. Human health damages related to air pollution in China. Environ. Sci. Pollut. Res. 2019, 26, 13115–13125. [Google Scholar] [CrossRef] [PubMed]
- Khoshnevis Yazdi, S.K.; Khanalizadeh, B. Air pollution, economic growth and health care expenditure. Econ. Res. Ekon. Istraz. 2017, 30, 1181–1190. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Lin, B. Regional differences of pollution emissions in China: Contributing factors and mitigation strategies. J. Clean. Prod. 2016, 112, 1454–1463. [Google Scholar] [CrossRef]
- Liu, H.; Fang, C.; Zhang, X.; Wang, Z.; Bao, C.; Li, F. The effect of natural and anthropogenic factors on haze pollution in Chinese cities: A spatial econometrics approach. J. Clean. Prod. 2017, 165, 323–333. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Y. The influential factors of urban PM2.5 concentrations in China: A spatial econometric analysis. J. Clean. Prod. 2016, 112, 1443–1453. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, M.; Li, Y.; Pang, R.; Xiang, N. Correlating PM2.5 concentrations with air pollutant emissions: A longitudinal study of the Beijing-Tianjin-Hebei region. J. Clean. Prod. 2018, 179, 103–113. [Google Scholar] [CrossRef]
- Dong, N.; Prentice, I.C.; Evans, B.; Caddy-Retalic, S.; Lowe, A.J.; Caddy-Retalic, S. Leaf nitrogen from first principles: Field evidence for adaptive variation with climate. Biogeosciences 2017, 14, 481–495. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Worrell, E.; Crijns-Graus, W. Cutting air Pollution by Improving Energy Efficiency of China’s Cement Industry. Energy Procedia 2015, 83, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Gan, T.; Liang, W.; Yang, H.; Liao, X. The effect of Economic Development on haze pollution (PM2.5) based on a spatial perspective: Urbanization as a mediating variable. J. Clean. Prod. 2020, 266, 121880. [Google Scholar] [CrossRef]
- Zhao, X.; Burnett, J.W.; Fletcher, J.J. Spatial analysis of China province-level CO2 emission intensity. Renew. Sustain. Energy Rev. 2014, 33, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhou, C.; Wang, S.; Li, S. Impacts of energy consumption structure, energy intensity, economic growth, urbanization on PM2.5 concentrations in countries globally. Appl. Energy 2018, 230, 94–105. [Google Scholar] [CrossRef]
- Zhang, S.; Worrell, E.; Crijns-Graus, W.; Krol, M.; de Bruine, M.; Geng, G.; Wagner, F.; Cofala, J. Modeling energy efficiency to improve air quality and health effects of China’s cement industry. Appl. Energy 2016, 184, 574–593. [Google Scholar] [CrossRef] [Green Version]
- Tayanç, M. An assessment of spatial and temporal variation of sulfur dioxide levels over Istanbul, Turkey. Environ. Pollut. 2000, 107, 61–69. [Google Scholar] [CrossRef]
- Wang, X.; Klemes, J.J.; Dong, X.; Fan, W.; Xu, Z.; Wang, Y.; Varbanov, P.S. Air pollution terrain nexus: A review considering energy generation and consumption. Renew. Sustain. Energy Rev. 2019, 105, 71–85. [Google Scholar] [CrossRef]
- Lu, Y.; Shao, M.; Zheng, C.; Ji, H.; Gao, X.; Wang, Q. Air pollutant emissions from fossil fuel consumption in China: Current status and future predictions. Atmos. Environ. 2020, 231, 117536. [Google Scholar] [CrossRef]
- Kaneko, S.; Fujii, H.; Sawazu, N.; Fujikura, R. Financial allocation strategy for the regional pollution abatement cost of reducing sulfur dioxide emissions in the thermal power sector in China. Energy Policy 2010, 38, 2131–2141. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.J.; Cao, G.L.; Liu, J.H.; Barrie, L.A. Distribution of seasonal SO2 emissions from fuel combustion and industrial activities in Shanxi province, China, with 1/6° × 1/4° longitude/latitude resolution. Atmos. Environ. 1999, 33, 257–265. [Google Scholar] [CrossRef]
- Zhang, S.; Worrell, E.; Crijns-Graus, W. Mapping and modeling multiple benefits of energy efficiency and emission mitigation in China’s cement industry at the provincial level. Appl. Energy 2015, 155, 35–58. [Google Scholar] [CrossRef]
- Xie, Q.; Xu, X.; Liu, X. Is there an EKC between economic growth and smog pollution in China? New evidence from semiparametric spatial autoregressive models. J. Clean. Prod. 2019, 220, 873–883. [Google Scholar] [CrossRef]
- Yuan, J.; Yuan, Z.; Ou, X. Modelling of environmental benefit evaluation of energy transition to multi-energy complementary system. Energy Procedia 2019, 158, 4882–4888. [Google Scholar] [CrossRef]
- Bilgili, F.; Koçak, E.; Bulut, Ü. The dynamic impact of renewable energy consumption on CO2 emissions: A revisited Environmental Kuznets Curve approach. Renew. Sustain. Energy Rev. 2016, 54, 838–845. [Google Scholar] [CrossRef]
- Ito, K. CO2 emissions, renewable and non-renewable energy consumption, and economic growth: Evidence from panel data for developing countries. Int. Econ. 2017, 151, 1–6. [Google Scholar] [CrossRef]
- Shafiei, S.; Salim, R.A. Non-renewable and renewable energy consumption and CO2 emissions in OECD countries: A comparative analysis. Energy Policy 2014, 66, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Boudri, J.C.; Hordijk, L.; Kroeze, C.; Amann, M.; Cofala, J.; Bertok, I.; Junfeng, L.; Lin, D.; Shuang, Z.; Runquing, H.; et al. The potential contribution of renewable energy in air pollution abatement in China and India. Energy Policy 2002, 30, 409–424. [Google Scholar] [CrossRef]
- Alvarez-Herranz, A.; Balsalobre-Lorente, D.; Shahbaz, M.; Cantos, J.M. Energy innovation and renewable energy consumption in the correction of air pollution levels. Energy Policy 2017, 105, 386–397. [Google Scholar] [CrossRef]
- Xie, Y.; Dai, H.; Dong, H. Impacts of SO2 taxations and renewable energy development on CO2, NOx and SO2 emissions in Jing-Jin-Ji region. J. Clean. Prod. 2018, 171, 1386–1395. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Yang, J.; Zhu, L. Does renewable energy technological innovation control China’s air pollution? A spatial analysis. J. Clean. Prod. 2020, 250, 119515. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C. Renewable energy, non-renewable energy and economic growth in Brazil. Renew. Sustain. Energy Rev. 2013, 25, 381–392. [Google Scholar] [CrossRef]
- Zhao, D.; Chen, H.; Li, X.; Ma, X. Air pollution and its influential factors in China’s hot spots. J. Clean. Prod. 2018, 185, 619–627. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, T.; Feiock, R.; Li, F. The impacts of China’s provincial energy policies on major air pollutants: A spatial econometric analysis. Energy Policy 2019, 132, 392–403. [Google Scholar] [CrossRef]
- Li, L.; Hong, X.; Wang, J. Evaluating the impact of clean energy consumption and factor allocation on China’s air pollution: A spatial econometric approach. Energy 2020, 195, 116842. [Google Scholar] [CrossRef]
- Liu, X.; Li, S. Empirical Analysis of Energy Efficiency of Chinese Province Based on Unexpected Output SBM Model. Math. Pract. Underst. 2015, 45, 35–43. [Google Scholar]
- Wang, B.B.; Zhao, C. Green technology innovation in China: Patent statistics and influencing factors. Ind. Technol. Econ. 2019, 38, 53–66. [Google Scholar]
- General Office of the State Council of China. Strategic Action Plan for Energy Development (2014–2020); The Central People’s Government of the People’s Republic of China: Beijing, China, 2014.
- Hao, Y.; Liu, Y.; Weng, J.H.; Gao, Y. Does the Environmental Kuznets Curve for coal consumption in China exist? New evidence from spatial econometric analysis. Energy 2016, 114, 1214–1223. [Google Scholar] [CrossRef]
- Ehrlich, P.R.; Holdren, J.P. Impact of Population Growth. Science 1971, 171, 1212–1217. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Rethinking the Environmental Impacts of Population, Affluence and Technology. Hum. Ecol. Rev. 1994, 12, 277–300. [Google Scholar]
- Rosa, E.A.; York, R.; Dietz, T. Tracking the Anthropogenic Drivers of Ecological Impacts. Ambio J. Hum. Environ. 2004, 33, 279–512. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Effects of Population and Affluence on CO2 Emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Du, Q.; Geng, J.; Liu, B.; Huang, Y. An improved spatial error model for the mass appraisal of commercial real estate based on spatial analysis: Shenzhen as a case study. Habitat Int. 2015, 46, 196–205. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Panel Data Models. In Spatial Econometrics; Springer briefs in Regional Science: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Pace, R.K.; LeSage, J.P. A sampling approach to estimate the log determinant used in spatial likelihood problems. J. Geogr. Syst. 2009, 11, 209–225. [Google Scholar] [CrossRef]
- Xu, M.; Tu, Y.; Zeng, G.; Wang, Q.; Zhou, A.; Yang, W. Numerical study of further NOx emission reduction for coal MILD combustion by combining fuel-rich/lean technology. Int. J. Energy Res. 2019, 43. [Google Scholar] [CrossRef]
- Tang, X.; Jin, Y.; McLellan, B.C.; Wang, J.; Li, S. China’s coal consumption declining—Impermanent or permanent? Resour. Conserv. Recycl. 2018, 129, 307–313. [Google Scholar] [CrossRef]
- Zhu, L.; Gan, Q.; Liu, Y.; Yan, Z. The impact of foreign direct investment on SO2 emissions in the Beijing-Tianjin-Hebei region: A spatial econometric analysis. J. Clean. Prod. 2017, 166, 189–196. [Google Scholar] [CrossRef]
- Dong, L.; Liang, H. Spatial analysis on China’s regional air pollutants and CO2 emissions: Emission pattern and regional disparity. Atmos. Environ. 2014, 92, 280–291. [Google Scholar] [CrossRef]
- Zheng, Y.; Peng, J.; Xiao, J.; Su, P.; Li, S. Industrial Structure Transformation and Provincial Heterogeneity Characteristics Evolution of Air Pollution: Evidence of a Threshold Effect from China. Atmos. Pollut. Res. 2020, 11, 598–609. [Google Scholar] [CrossRef]
- Li, K.; Fang, L.; He, L. How population and energy price affect China’s environmental pollution? Energy Policy 2019, 129, 386–396. [Google Scholar] [CrossRef]





| Energy | IPC Codes |
|---|---|
| Wind | F03D |
| Solar | F03G6; F24J2; F26B3/28; H01L27/142; H01L31/042-058 |
| Marine | E02B9/08; F03B13/10-26; F03G7/05 |
| Biomass | C10L5/42-44; F02B43/08 |
| Storage | H01M10/06-18; H01M10/24-32; H01M10/34; H01M10/36-40 |
| Variables | Explanation | Units |
|---|---|---|
| Comprehensive pollution of i province in t year | 104 ton | |
| SO2 emission of i province in t year | 104 ton | |
| NOx emission of i province in t year | 104 ton | |
| Dust and smoke emission of i province in t year | 104 ton | |
| Number of renewable energy patents | Item | |
| Fossil energy consumption | 104 ton | |
| The proportion of secondary industry | % | |
| Environmental regulation | % | |
| Province gross domestic product | 108 yuan | |
| Province people | 104 people |
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|---|---|---|
| CP | 0.3386 *** | 0.3285 *** | 0.3153 *** | 0.2501 ** | 0.2719 ** | 0.2425 ** | 0.1980 ** |
| 3.337109 | 3.242872 | 3.125831 | 2.34488 | 2.527662 | 2.538885 | 2.119734 | |
| SO2 | 0.2397 ** | 0.2288 ** | 0.1641 * | 0.2152 ** | 0.2253 ** | 0.1460 * | 0.1242 |
| 2.454958 | 2.360465 | 1.63636 | 2.234856 | 2.330737 | 1.666974 | 1.424221 | |
| DS | 0.3589 *** | 0.3351 *** | 0.3131 *** | 0.3863 *** | 0.4104 *** | 0.3136 *** | 0.2230 ** |
| 3.645495 | 3.374994 | 3.194374 | 3.860736 | 4.095359 | 3.341564 | 2.354572 | |
| NOx | 0.3444 *** | 0.2565 ** | 0.3265 *** | 0.3248 *** | 0.3321 *** | 0.2351 ** | 0.2467 ** |
| 3.379879 | 2.390973 | 3.222591 | 3.208654 | 3.277173 | 2.440664 | 2.572206 | |
| REGI | 0.3100 *** | 0.3170 *** | 0.3243 *** | 0.2979 *** | 0.3426 *** | 0.3258 *** | 0.3090 *** |
| 3.302344 | 3.622955 | 3.61426 | 3.326746 | 3.390146 | 3.578343 | 3.445492 | |
| FEC | 0.3655 *** | 0.3496 *** | 0.3679 *** | 0.3564 *** | 0.3486 *** | 0.3277 *** | 0.3278 *** |
| 3.598077 | 3.468931 | 3.621565 | 3.533754 | 3.467786 | 3.272563 | 3.288949 |
| lnCP | lnNOx | lnSO2 | lnDS | |
|---|---|---|---|---|
| lnREGI | −0.1625 *** | −0.1056 ** | −0.2224 ** | −0.2993 *** |
| (0.0447) | (0.0415) | (0.0684) | (0.0726) | |
| lnFEC | −0.0370 | −0.1030 | 0.2434* | 0.2355 * |
| (0.0829) | (0.0769) | (0.1270) | (0.1347) | |
| lnPOP | 1.6969 | 0.7971 | 2.6985 | 4.6511 ** |
| (1.1027) | (1.0229) | (1.6881) | (1.7911) | |
| lnIS | 1.2855 *** | 1.2633 *** | 1.6842 *** | 0.8334 ** |
| (0.1733) | (0.1608) | (0.2653) | (0.2815) | |
| lnER | −0.1247 *** | −0.0948 *** | −0.1893 *** | −0.1253 *** |
| (0.0218) | (0.0203) | (0.0334) | (0.0355) | |
| lnGDP | 2.0521 ** | 0.5965 | 4.0354 *** | 2.8432 ** |
| (0.7251) | (0.6726) | (1.1100) | (1.1777) | |
| (lnGDP)2 | −0.1370 *** | −0.0630 * | −0.2577 *** | −0.1601 ** |
| (0.0375) | (0.0348) | (0.0574) | (0.0609) | |
| cons | −14.0485 | 0.6090 | −31.6856 ** | −46.1835 ** |
| (8.6659) | (8.0388) | (13.2663) | (14.0754) | |
| N | 210 | 210 | 210 | 210 |
| R-sq | 0.745 | 0.769 | 0.728 | 0.334 |
| lnCP | lnNOx | lnSO2 | lnDS | |
|---|---|---|---|---|
| Main | ||||
| lnREGI | −0.0258 | −0.0439 | −0.0401 | 0.0130 |
| (0.0263) | (0.0288) | (0.0431) | (0.0421) | |
| lnFEC | 0.0313 | 0.0050 | 0.4982 *** | 0.4350 *** |
| (0.0569) | (0.0655) | (0.0754) | (0.0750) | |
| lnPOP | 0.6722 *** | 0.6427 *** | 0.3229 ** | 0.7107 *** |
| (0.1882) | (0.1882) | (0.1587) | (0.2092) | |
| lnIS | 0.3281 ** | 0.2756 * | 0.5179 ** | 0.3524 * |
| (0.1296) | (0.1416) | (0.1696) | (0.1905) | |
| lnER | −0.0537 *** | −0.0490 *** | −0.0673 ** | −0.0088 |
| (0.0125) | (0.0138) | (0.0215) | (0.0202) | |
| lnGDP | 0.9549 ** | 0.2234 | 0.7882 | 0.3224 |
| (0.4424) | (0.4684) | (0.5982) | (0.6165) | |
| (lnGDP)2 | −0.0471 ** | −0.0030 | −0.0375 | −0.0369 |
| (0.0223) | (0.0238) | (0.0307) | (0.0320) | |
| _cons | −6.4776 * | −4.2013 | −14.0928 ** | −2.6661 |
| (3.4906) | (3.6056) | (4.6683) | (4.7041) | |
| Wx | ||||
| lnREGI | −0.1090 ** | −0.0371 | −0.0795 | −0.3228 *** |
| (0.0480) | (0.0507) | (0.0752) | (0.0761) | |
| lnFEC | 0.0988 | 0.1038 | −0.3217 ** | −0.2858 ** |
| (0.0937) | (0.1012) | (0.1188) | (0.1247) | |
| lnPOP | −0.6155 ** | −0.5392 ** | −0.0940 | −0.7550 ** |
| (0.2660) | (0.2676) | (0.2454) | (0.2959) | |
| lnIS | 0.3541 * | 0.8603 *** | 0.2420 | 0.0286 |
| (0.2053) | (0.2408) | (0.2822) | (0.2666) | |
| lnER | −0.0106 | −0.0084 | −0.0578 | −0.0923 ** |
| (0.0236) | (0.0253) | (0.0404) | (0.0368) | |
| lnGDP | 0.6716 | 1.0241 | 2.3489 ** | 0.4698 |
| (0.6865) | (0.7194) | (0.9698) | (0.9943) | |
| (lnGDP)2 | −0.0360 | −0.0617 * | −0.1337 ** | 0.0164 |
| (0.0349) | (0.0367) | (0.0495) | (0.0500) | |
| ρ | 0.6408 *** | 0.5248 *** | 0.6043 *** | 0.6320 *** |
| (0.0564) | (0.0680) | (0.0592) | (0.0543) | |
| LR-lag | 28.83 *** | 38.44 *** | 35.60 *** | 52.37 *** |
| LR-error | 44.43 *** | 56.55 *** | 39.14 *** | 34.72 *** |
| Wald-lag | 32.84 *** | 42.43 *** | 60.52 *** | 59.05 *** |
| Wald-error | 30.29 *** | 34.94 *** | 34.23 *** | 28.62 *** |
| lnCP | lnNOx | lnSO2 | lnDS | |
|---|---|---|---|---|
| LR_Direct | ||||
| lnREGI | −0.0531 * | −0.0520 * | −0.0586 | −0.0560 |
| (0.0300) | (0.0309) | (0.0467) | (0.0461) | |
| lnFEC | 0.0582 | 0.0208 | 0.4919 *** | 0.4301 *** |
| (0.0590) | (0.0641) | (0.0746) | (0.0798) | |
| lnPOP | 0.6462 *** | 0.6270 *** | 0.3592 ** | 0.6614 *** |
| (0.1811) | (0.1755) | (0.1488) | (0.2000) | |
| lnIS | 0.4631 *** | 0.4437 ** | 0.6371 *** | 0.4137 ** |
| (0.1351) | (0.1397) | (0.1832) | (0.2013) | |
| lnER | −0.0645 *** | −0.0550 *** | −0.0885 *** | −0.0315 |
| (0.0141) | (0.0143) | (0.0237) | (0.0226) | |
| lnGDP | 1.2637 ** | 0.4199 | 1.3969 ** | 0.4875 |
| (0.4962) | (0.4936) | (0.6635) | (0.6954) | |
| (lnGDP)2 | −0.0637 ** | −0.0146 | −0.0719 ** | −0.0400 |
| (0.0258) | (0.0258) | (0.0347) | (0.0368) | |
| LR_Indirect | ||||
| lnREGI | −0.3079 ** | −0.1075 | −0.2227 | −0.7686 *** |
| (0.1130) | (0.0928) | (0.1611) | (0.1664) | |
| lnFEC | 0.3183 | 0.2151 | −0.0372 | −0.0201 |
| (0.2389) | (0.1857) | (0.2544) | (0.3043) | |
| lnPOP | −0.5079 | −0.4269 | 0.2040 | −0.7953 |
| (0.5199) | (0.3953) | (0.4495) | (0.5858) | |
| lnIS | 1.4485 ** | 1.9555 *** | 1.2891 ** | 0.6552 |
| (0.4614) | (0.3751) | (0.6277) | (0.6728) | |
| lnER | −0.1183 ** | −0.0697 | −0.2332 ** | −0.2490 ** |
| (0.0568) | (0.0468) | (0.0904) | (0.0918) | |
| lnGDP | 3.3012 * | 2.2426 | 6.6331 ** | 1.6962 |
| (1.7082) | (1.3902) | (2.2782) | (2.5653) | |
| (lnGDP)2 | −0.1697 ** | −0.1236 * | −0.3671 ** | −0.0176 |
| (0.0859) | (0.0700) | (0.1154) | (0.1295) | |
| LR_Total | ||||
| lnREGI | −0.3610 ** | −0.1595 | −0.2813 | −0.8246 *** |
| (0.1292) | (0.1057) | (0.1817) | (0.1880) | |
| lnFEC | 0.3765 | 0.2359 | 0.4548 | 0.4101 |
| (0.2665) | (0.2070) | (0.2818) | (0.3460) | |
| lnPOP | 0.1383 | 0.2001 | 0.5632 | −0.1340 |
| (0.5753) | (0.4238) | (0.4806) | (0.6411) | |
| lnIS | 1.9115 *** | 2.3992 *** | 1.9262 ** | 1.0688 |
| (0.5200) | (0.4223) | (0.7281) | (0.7721) | |
| lnER | −0.1828 ** | −0.1247 ** | −0.3217 ** | −0.2806 ** |
| (0.0657) | (0.0545) | (0.1046) | (0.1059) | |
| lnGDP | 4.5650 ** | 2.6625 | 8.0300 ** | 2.1837 |
| (2.0213) | (1.6614) | (2.6918) | (2.9974) | |
| (lnGDP)2 | −0.2334 ** | −0.1382 | −0.4390 ** | −0.0575 |
| (0.1024) | (0.0846) | (0.1373) | (0.1526) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, N.; Wang, Y.; Peng, H.; Hou, Z. Renewable Energy Green Innovation, Fossil Energy Consumption, and Air Pollution—Spatial Empirical Analysis Based on China. Sustainability 2020, 12, 6397. https://doi.org/10.3390/su12166397
Shen N, Wang Y, Peng H, Hou Z. Renewable Energy Green Innovation, Fossil Energy Consumption, and Air Pollution—Spatial Empirical Analysis Based on China. Sustainability. 2020; 12(16):6397. https://doi.org/10.3390/su12166397
Chicago/Turabian StyleShen, Neng, Yifan Wang, Hui Peng, and Zhiping Hou. 2020. "Renewable Energy Green Innovation, Fossil Energy Consumption, and Air Pollution—Spatial Empirical Analysis Based on China" Sustainability 12, no. 16: 6397. https://doi.org/10.3390/su12166397
APA StyleShen, N., Wang, Y., Peng, H., & Hou, Z. (2020). Renewable Energy Green Innovation, Fossil Energy Consumption, and Air Pollution—Spatial Empirical Analysis Based on China. Sustainability, 12(16), 6397. https://doi.org/10.3390/su12166397




