Hybrid Stochastic-Grey Model to Forecast the Behavior of Metal Price in the Mining Industry
Abstract
:1. Introduction
2. Forecasting Model
2.1. Stochastic Grey Modeling
- k—coefficient which depends on time resolution of monitoring;
- —standard deviation of AGO series;
- —an increment to a standard Brownian motion.
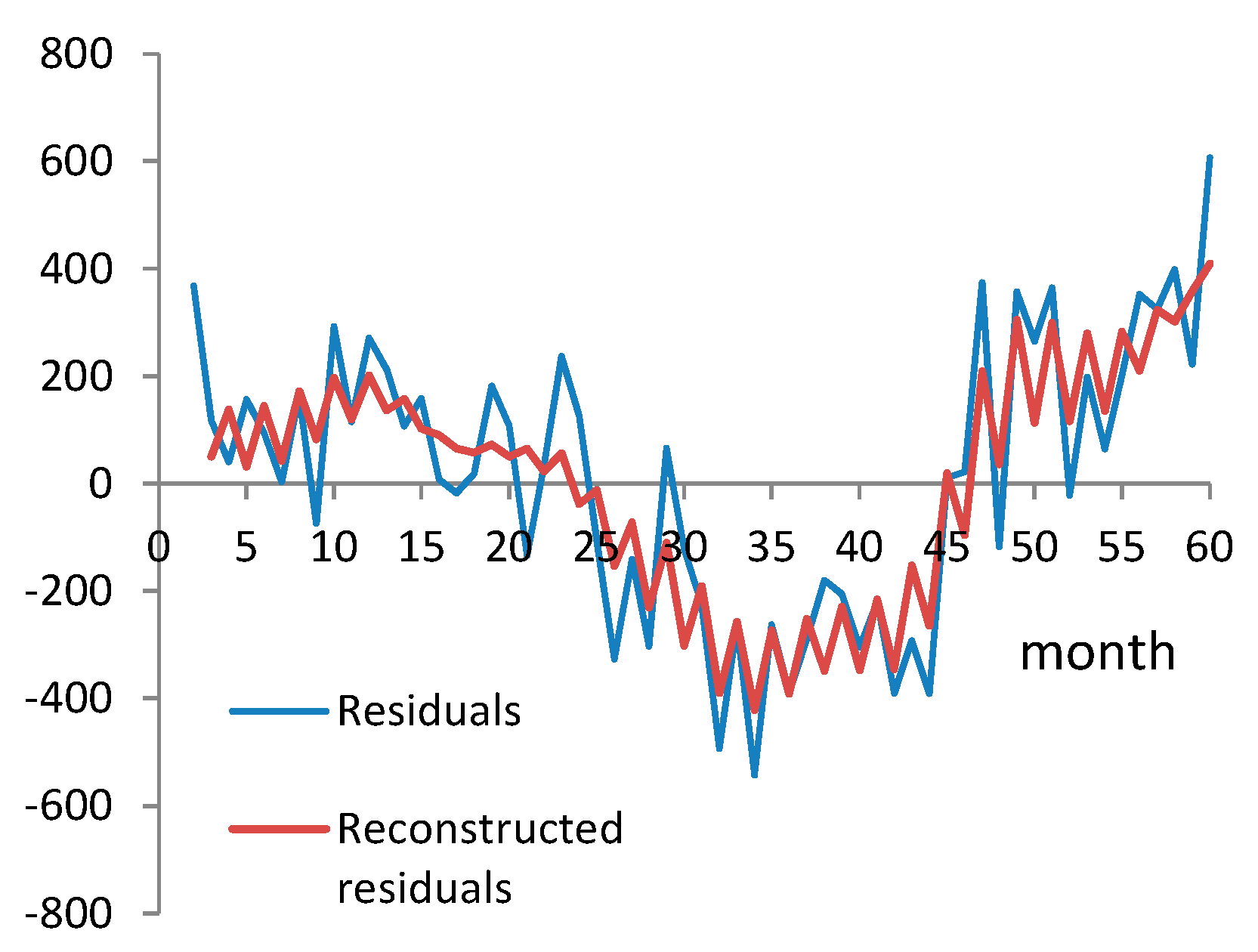
2.2. Improvement of the Model by Residual Error Correction
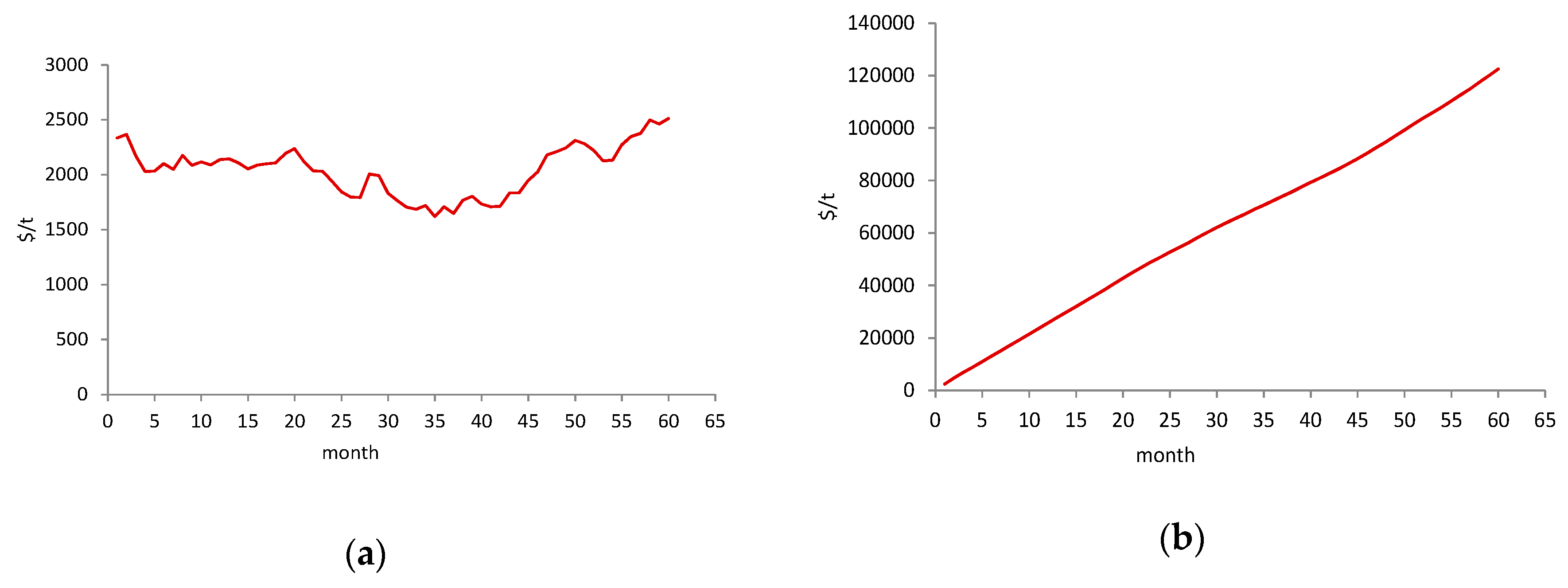
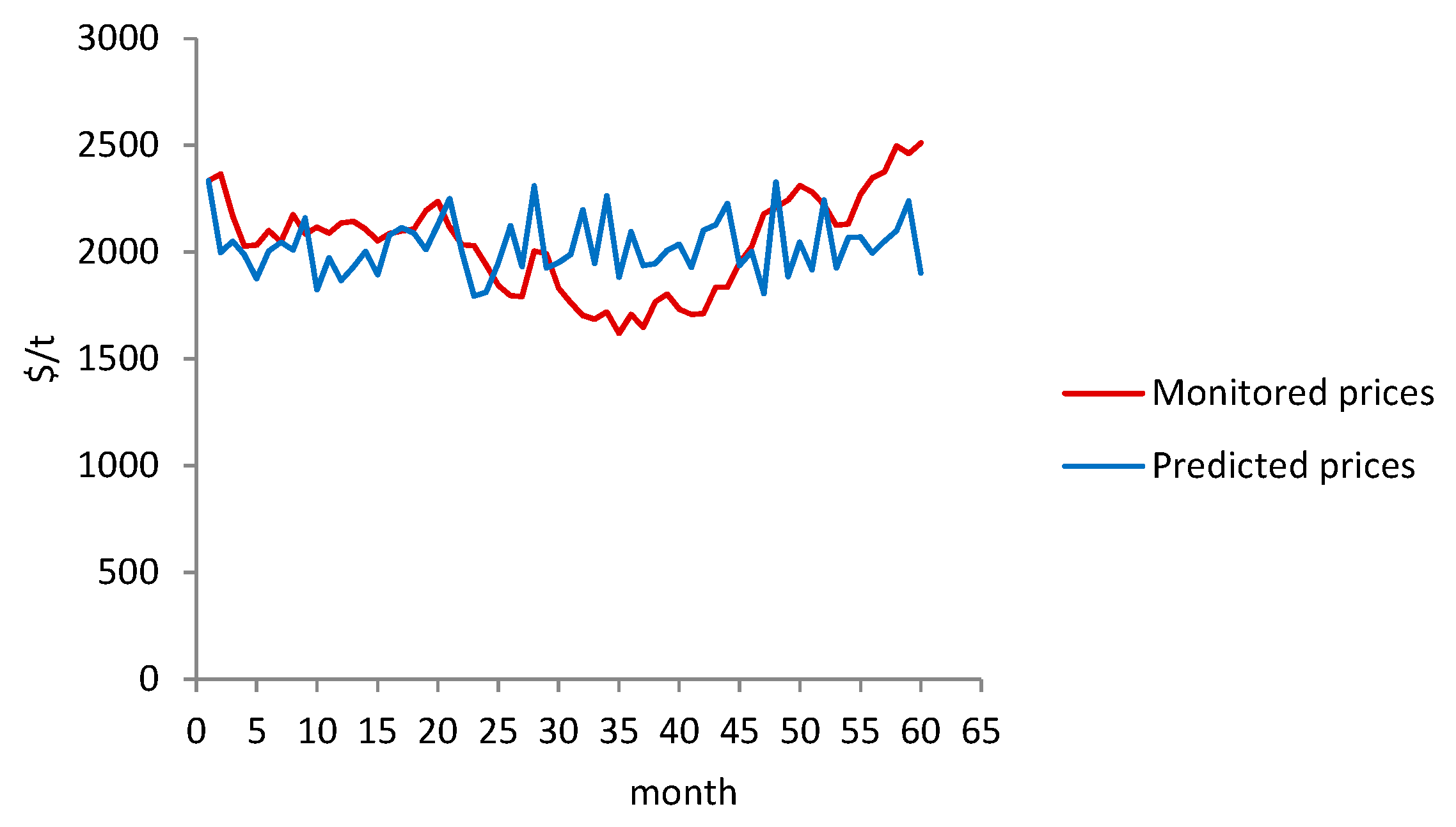
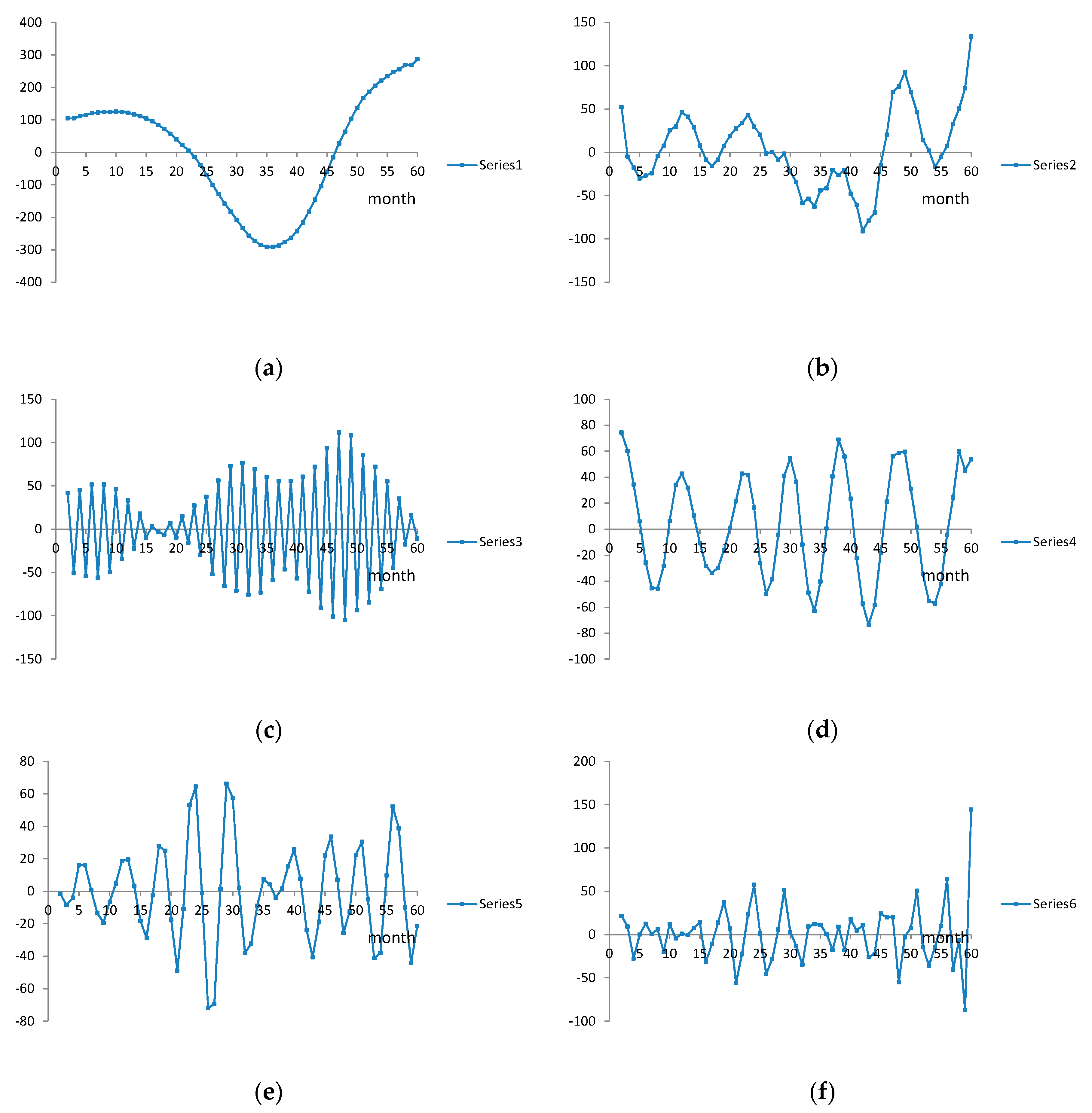
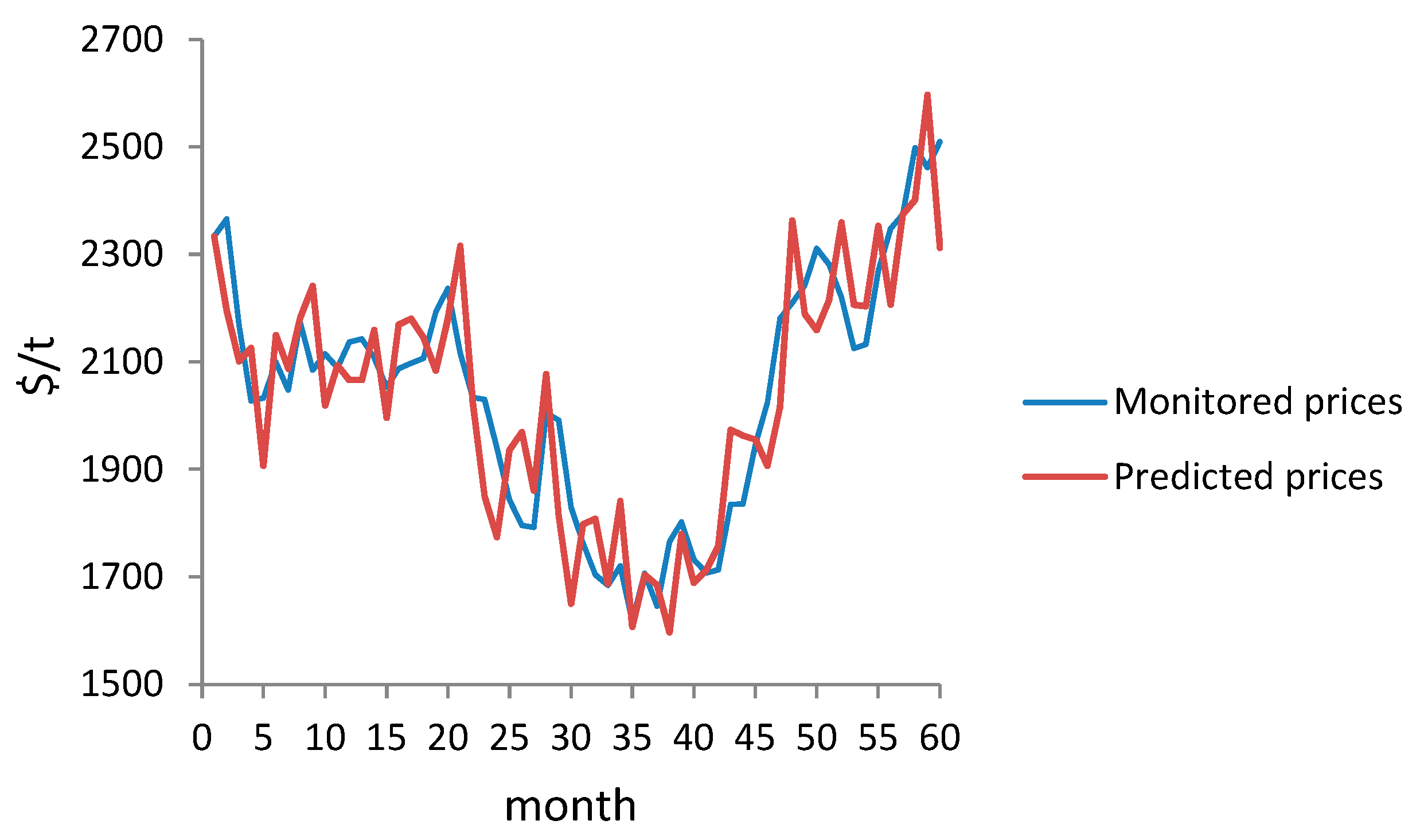
3. Numerical Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barczak, S. Gold Price Forecasting Using Grey Model GM(1,1) and Selected Classical Time Series Models. A Comparison of Methods. In Proceedings of the 8th International Days of Statistics and Economics, Prague, Czech Republic, 11–13 September 2014. [Google Scholar]
- Askari, M.; Askari, H. Time Series Grey System Prediction-based Models: Gold Price Forecasting. Trends Appl. Sci. Res. 2011, 6, 1287–1292. [Google Scholar] [CrossRef]
- Chang, C.J.; Li, D.C.; Chen, C.C.; Dai, W.L. A grey-based rolling procedure for short-term forecasting using limited time series data. Econ. Comput. Econ. Cybern. Stud. Res. 2013, 47, 75–90. [Google Scholar]
- Jalali, M.F.M.; Heidari, H. Forecasting Palladium Price Using GM(1,1). Glob. Anal. Discret. Math. 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Sous, S.; Thongjunthug, T.; Klongdee, W. Gold price forecasting based on the improved GM(1,1) model with Markov chain by average of middle points. KKU Sci. J. 2014, 42, 693–699. [Google Scholar]
- Yang, S.; Chen, J.H.; Guo, H.B.; Liao, G.S. Application of optimal unbiased grey-forecasting model in aluminum price quotation prediction. J. Hunan Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 2. [Google Scholar]
- Wang, K.G.; Zheng, Z.Q.; Yang, X.M. The Comparative Research of Mine Price Forecast Based on the Gray System GM(1,1) Model and the Model of Verhulst. J. Gansu Sci. 2014, 5. [Google Scholar]
- Li, D.; Moghaddam, M.R.; Monjezi, M.; Armaghani, D.J.; Mehrdanesh, A. Development of a Group Method of Data Handling Technique to Forecast Iron Ore Price. Appl. Sci. 2020, 10, 2364. [Google Scholar] [CrossRef] [Green Version]
- Alipour, A.; Khodaiari, A.A.; Jafari, A. Modeling and Prediction of Time-Series of Monthly Copper Prices. Int. J. Min. Geo-Eng. 2019, 53, 91–97. [Google Scholar] [CrossRef]
- Shafiee, S.; Topal, E. Introducing a new model to forecast mineral commodity price. In Proceedings of the First International Future Mining Conference and Exhibition, Sydney, Australia, 19–21 November 2008; pp. 243–250. [Google Scholar]
- Achireko, P.K.; Ansong, G. Stochastic model of mineral prices incorporating neural network and regression analysis. Min. Technol. 2000, 109, 49–54. [Google Scholar] [CrossRef]
- Tapia Cortez, C.A.; Saydam, S.; Coulton, J.; Sammut, C. Alternative techniques for forecasting mineral commodity prices. Int. J. Min. Sci. Technol. 2018, 28, 309–322. [Google Scholar] [CrossRef]
- Deng, J. Grey control system. J. Huazhong Univ. Sci. Technol. 1982, 10, 9–18. [Google Scholar]
- Deng, J.L. Control problems of grey systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Liu, S.F.; Zeng, B.; Liu, J.; Xie, N.M. Several basic models of GM(1,1) and their applicable bound. Syst. Eng. Electron. 2014, 36, 501–508. [Google Scholar]
- Dang, Y.; Liu, S.; Chen, K. The GM models that x(n) be taken as initial value. Kybernetes 2004, 33, 247–254. [Google Scholar]
- Evans, L.C. An Introduction to Stochastic Differential Equations—Version 1.2. Available online: http://ft-sipil.unila.ac.id/dbooks/AN%20INTRODUCTION%20TO%20STOCHASTIC%20DIFFERENTIAL%20EQUATIONS%20VERSION%201.2.pdf (accessed on 7 August 2020).
- Reis, M. Stochastic Differential Equation. Lecture Notes at Humboldt University Berlin and University of Heidelberg. 2007. Available online: https://www.math.uni-heidelberg.de/studinfo/reiss/sode-lecture.pdf (accessed on 7 August 2020).
- Bayram, M.; Partal, T.; Buyukoz, G.O. Numerical methods for simulation of stochastic differential equations. Adv. Differ. Equ. 2018, 17, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sauer, T. Numerical solution of stochastic differential equation in finance. In Handbook of Computational Finance; Springer: Berlin, Germany, 2012; pp. 529–550. [Google Scholar]
- Schwarz, E.S. The stochastic behavior of commodity prices: Implications for valuation and hedging. J. Financ. 1997, 52, 923–973. [Google Scholar] [CrossRef]
- Chapter 4, Brownian Motion and Stochastic Calculus, This Version. 15 January 2020. Available online: https://www.ntu.edu.sg/home/nprivault/indext.html (accessed on 9 February 2020).
- Hassani, H.; Mahmoudvand, R. Multivariate Singular Spectrum Analysis: A general view and new vector forecasting approach. Int. J. Energy Stat. 2013, 1, 55–83. [Google Scholar] [CrossRef]
- Hassani, H.; Zhigljavsky, A. Singular Spectrum Analysis: Methodology and Application to Economics Data. J. Syst. Sci. Complex. 2009, 22, 372–394. [Google Scholar] [CrossRef]
- Hassani, H. Singular Spectrum Analysis: Methodology and Comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar]
- Harris, T.J.; Yuan, H. Filtering and frequency interpretations of Singular Spectrum Analysis. Phys. D 2010, 239, 1958–1967. [Google Scholar] [CrossRef]
- Steel Success Strategies. 2020. Available online: https://www.indexmundi.com/commodities/?commodity=lead&months=120 (accessed on 14 April 2020).
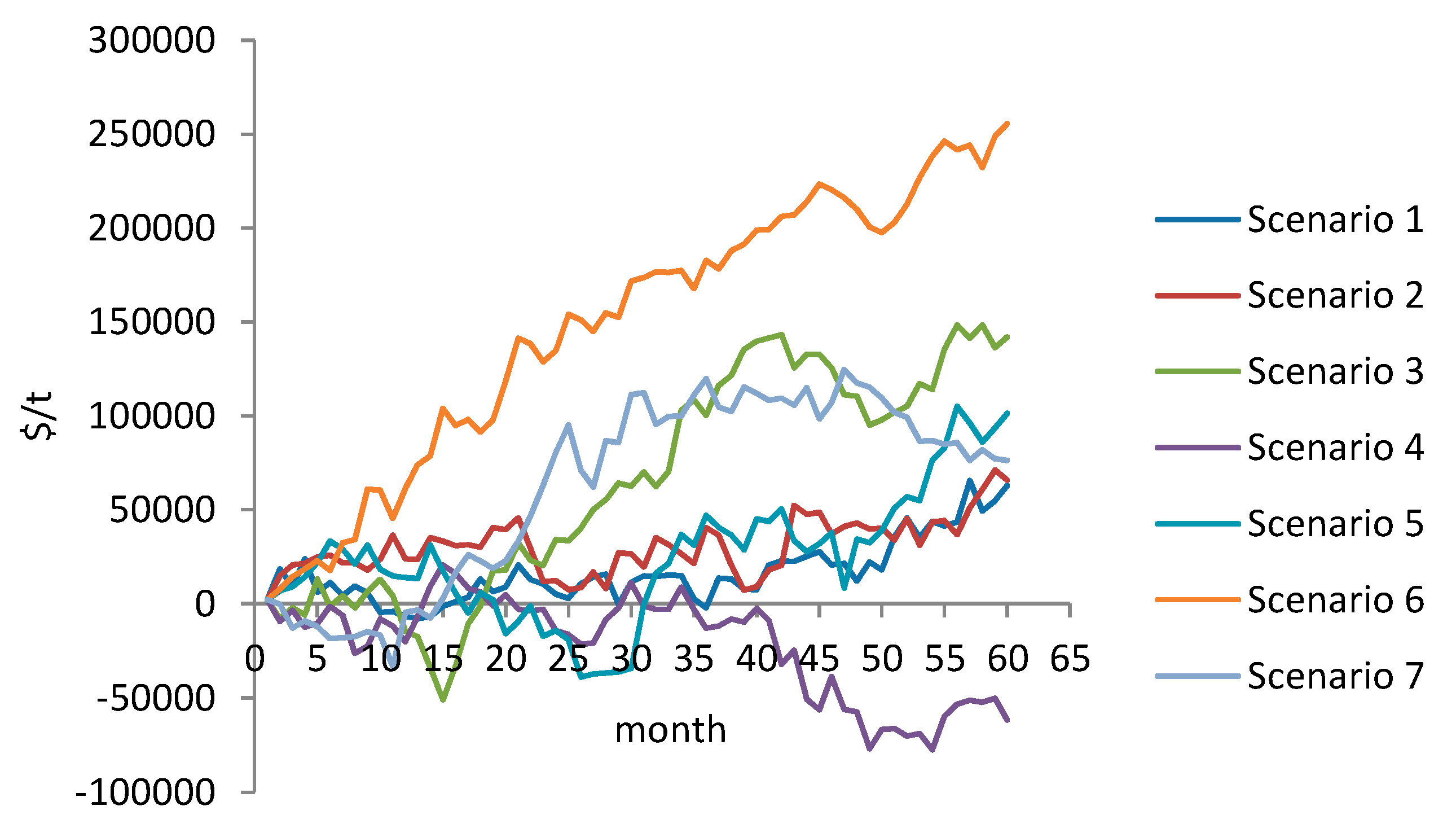



| Date | Price $/t | Date | Price $/t | Date | Price $/t | Date | Price $/t |
|---|---|---|---|---|---|---|---|
| Jan-2013 | 2334 | Jan-2015 | 1843 | Jan-2017 | 2243 | Jan-2019 | 1997 |
| Feb-2013 | 2366 | Feb-2015 | 1796 | Feb-2017 | 2312 | Feb-2019 | 2063 |
| Mar-2013 | 2169 | Mar-2015 | 1792 | Mar-2017 | 2281 | Mar-2019 | 2046 |
| Apr-2013 | 2027 | Apr-2015 | 2005 | Apr-2017 | 2221 | Apr-2019 | 1939 |
| May-2013 | 2033 | May-2015 | 1992 | May-2017 | 2125 | May-2019 | 1815 |
| Jun-2013 | 2100 | Jun-2015 | 1830 | Jun-2017 | 2133 | Jun-2019 | 1900 |
| Jul-2013 | 2048 | Jul-2015 | 1763 | Jul-2017 | 2270 | Jul-2019 | 1976 |
| Aug-2013 | 2174 | Aug-2015 | 1704 | Aug-2017 | 2348 | Aug-2019 | 2045 |
| Sep-2013 | 2085 | Sep-2015 | 1684 | Sep-2017 | 2374 | Sep-2019 | 2072 |
| Oct-2013 | 2115 | Oct-2015 | 1720 | Oct-2017 | 2498 | Oct-2019 | 2184 |
| Nov-2013 | 2090 | Nov-2015 | 1618 | Nov-2017 | 2461 | Nov-2019 | 2021 |
| Dec-2013 | 2137 | Dec-2015 | 1707 | Dec-2017 | 2510 | Dec-2019 | 1901 |
| Jan-2014 | 2143 | Jan-2016 | 1646 | Jan-2018 | 2584 | ||
| Feb-2014 | 2108 | Feb-2016 | 1766 | Feb-2018 | 2581 | ||
| Mar-2014 | 2053 | Mar-2016 | 1802 | Mar-2018 | 2390 | ||
| Apr-2014 | 2087 | Apr-2016 | 1732 | Apr-2018 | 2352 | ||
| May-2014 | 2097 | May-2016 | 1708 | May-2018 | 2361 | ||
| Jun-2014 | 2107 | Jun-2016 | 1713 | Jun-2018 | 2436 | ||
| Jul-2014 | 2193 | Jul-2016 | 1835 | Jul-2018 | 2207 | ||
| Aug-2014 | 2237 | Aug-2016 | 1836 | Aug−2018 | 2054 | ||
| Sep-2014 | 2117 | Sep-2016 | 1948 | Sep−2018 | 2023 | ||
| Oct-2014 | 2034 | Oct-2016 | 2024 | Oct−2018 | 1988 | ||
| Nov-2014 | 2030 | Nov-2016 | 2181 | Nov−2018 | 1937 | ||
| Dec-2014 | 1938 | Dec-2016 | 2210 | Dec−2018 | 1972 |
| Jan-2013 | Feb-2013 | Mar-2013 | Oct-2017 | Nov-2017 | Dec2017 | |
|---|---|---|---|---|---|---|
| Original value ($) | 2334 | 2366 | 2169 | 2498 | 2461 | 2510 |
| AGO ($) | 2334 | 4700 | 6869 | 117,481 | 119,942 | 122,452 |
| ($) | − | 3517 | 5784.5 | 116,232.2 | 118,711.5 | 121,197 |
| Date | AGO | Date | AGO | Date | AGO | Date | AGO | Date | AGO |
|---|---|---|---|---|---|---|---|---|---|
| Jan-2013 | 2334 | Jan-2014 | 26,059 | Jan-2015 | 50,183 | Jan-2016 | 74,732 | Jan-2017 | 99,065 |
| Feb-2013 | 4332 | Feb-2014 | 28,061 | Feb-2015 | 52,306 | Feb-2016 | 76,678 | Feb-2017 | 101,112 |
| Mar-2013 | 6383 | Mar-2014 | 29,955 | Mar-2015 | 54,239 | Mar-2016 | 78,685 | Mar-2017 | 103,027 |
| Apr-2013 | 8371 | Apr-2014 | 32,034 | Apr-2015 | 56,548 | Apr-2016 | 80,722 | Apr-2017 | 105,270 |
| May-2013 | 10,246 | May-2014 | 34,148 | May-2015 | 58,473 | May-2016 | 82,651 | May-2017 | 107,197 |
| Jun-2013 | 12,252 | Jun-2014 | 36,236 | Jun-2015 | 60,425 | Jun-2016 | 84,754 | Jun-2017 | 109,265 |
| Jul-2013 | 14,297 | Jul-2014 | 38,247 | Jul-2015 | 62,413 | Jul-2016 | 86,880 | Jul-2017 | 111,335 |
| Aug-2013 | 16,308 | Aug-2014 | 40,377 | Aug-2015 | 64,611 | Aug-2016 | 89,108 | Aug-2017 | 113,331 |
| Sep-2013 | 18,467 | Sep-2014 | 42,628 | Sep-2015 | 66,556 | Sep-2016 | 91,044 | Sep-2017 | 115,381 |
| Oct-2013 | 20,289 | Oct-2014 | 44,629 | Oct-2015 | 68,819 | Oct-2016 | 93,047 | Oct-2017 | 117,481 |
| Nov-2013 | 22,263 | Nov-2014 | 46,423 | Nov-2015 | 70,700 | Nov-2016 | 94,852 | Nov-2017 | 119,720 |
| Dec-2013 | 24,129 | Dec-2014 | 48,235 | Dec-2015 | 72,796 | Dec-2016 | 97,180 | Dec-2017 | 121,623 |
| Date | Price $/t | Date | Price $/t | Date | Price $/t | Date | Price $/t | Date | Price $/t |
|---|---|---|---|---|---|---|---|---|---|
| Jan-2013 | 2334 | Jan-2014 | 1930 | Jan-2015 | 1948 | Jan-2016 | 1936 | Jan-2017 | 1885 |
| Feb-2013 | 1998 | Feb-2014 | 2002 | Feb-2015 | 2123 | Feb-2016 | 1946 | Feb-2017 | 2046 |
| Mar-2013 | 2051 | Mar-2014 | 1894 | Mar-2015 | 1933 | Mar-2016 | 2008 | Mar-2017 | 1916 |
| Apr-2013 | 1988 | Apr-2014 | 2079 | Apr-2015 | 2309 | Apr-2016 | 2037 | Apr2017 | 2243 |
| May-2013 | 1876 | May-2014 | 2114 | May-2015 | 1925 | May-2016 | 1928 | May-2017 | 1926 |
| Jun-2013 | 2006 | Jun-2014 | 2088 | Jun-2015 | 1951 | Jun-2016 | 2103 | Jun-2017 | 2068 |
| Jul-2013 | 2045 | Jul-2014 | 2011 | Jul-2015 | 1988 | Jul-2016 | 2126 | Jul-2017 | 2070 |
| Aug-2013 | 2011 | Aug-2014 | 2130 | Aug-2015 | 2198 | Aug-2016 | 2227 | Aug-2017 | 1996 |
| Sep-2013 | 2159 | Sep-2014 | 2251 | Sep-2015 | 1945 | Sep-2016 | 1936 | Sep-2017 | 2050 |
| Oct-2013 | 1823 | Oct-2014 | 2001 | Oct-2015 | 2263 | Oct-2016 | 2003 | Oct-2017 | 2100 |
| Nov-2013 | 1974 | Nov-2014 | 1793 | Nov-2015 | 1881 | Nov-2016 | 1806 | Nov-2017 | 2240 |
| Dec-2013 | 1865 | Dec-2014 | 1812 | Dec-2015 | 2096 | Dec-2016 | 2328 | Dec-2017 | 1903 |
| Date | Error | Date | Error | Date | Error | Date | Error | Date | Error |
|---|---|---|---|---|---|---|---|---|---|
| Jan-2013 | 0 | Jan-2014 | 212.82 | Jan-2015 | −105.29 | Jan-2016 | −290.01 | Jan-2017 | 357.39 |
| Feb-2013 | 367.80 | Feb-2014 | 106.43 | Feb-2015 | −327.16 | Feb-2016 | −179.88 | Feb-2017 | 265.03 |
| Mar-2013 | 117.99 | Mar-2014 | 159.30 | Mar-2015 | −140.29 | Mar-2016 | −205.51 | Mar-2017 | 365.16 |
| Apr-2013 | 39.81 | Apr-2014 | 8.10 | Apr-2015 | −303.38 | Apr-2016 | −304.85 | Apr-2017 | −22.18 |
| May-2013 | 157.21 | May-2014 | −17.18 | May-2015 | 66.35 | May-2016 | −220.61 | May-2017 | 198.63 |
| Jun-2013 | 94.13 | Jun-2014 | 18.52 | Jun-2015 | −121.90 | Jun-2016 | −390.18 | Jun-2017 | 64.66 |
| Jul-2013 | 2.69 | Jul-2014 | 182.20 | Jul-2015 | −225.45 | Jul-2016 | −291.71 | Jul-2017 | 200.08 |
| Aug-2013 | 163.54 | Aug-2014 | 107.07 | Aug-2015 | −494.10 | Aug-2016 | −391.72 | Aug-2017 | 352.42 |
| Sep-2013 | −74.15 | Sep-2014 | −133.66 | Sep-2015 | −260.77 | Sep-2016 | 11.28 | Sep-2017 | 324.36 |
| Oct-2013 | 292.91 | Oct−2014 | 33.12 | Oct-2015 | −542.59 | Oct-2016 | 21.84 | Oct-2017 | 398.30 |
| Nov-2013 | 115.52 | Nov−2014 | 236.83 | Nov-2015 | −263.04 | Nov-2016 | 375.05 | Nov-2017 | 221.93 |
| Dec-2013 | 271.25 | Dec−2014 | 125.73 | Dec-2015 | −389.28 | Dec-2016 | −118.10 | Dec-2017 | 606.78 |
| Eigenvalue | 16852400.60 | 3998636.19 | 2460060.01 | 1802229.97 | 1332471.93 |
| 7.227 | 6.602 | 6.391 | 6.256 | 6.125 | |
| Contribution | 0.56197 | 0.13334 | 0.08203 | 0.06010 | 0.04443 |
| Eigenvector | |||||
| 1 | −0.2696 | −0.4300 | 0.2286 | 0.4210 | 0.2918 |
| 2 | −0.2767 | −0.3702 | −0.3707 | 0.2938 | 0.2496 |
| 3 | −0.3009 | −0.3767 | 0.2005 | 0.0958 | −0.2846 |
| 4 | −0.3086 | −0.2016 | −0.4298 | −0.1969 | −0.4163 |
| 5 | −0.3197 | −0.1666 | 0.2992 | −0.4384 | −0.3432 |
| 6 | −0.3336 | 0.0749 | −0.3571 | −0.4185 | 0.2514 |
| 7 | −0.3397 | 0.1139 | 0.3876 | −0.3197 | 0.4439 |
| 8 | −0.3442 | 0.3538 | −0.2147 | 0.0509 | 0.2956 |
| 9 | −0.3317 | 0.3311 | 0.3865 | 0.2241 | −0.1589 |
| 10 | −0.3280 | 0.4630 | −0.1502 | 0.4075 | −0.3280 |
| Eigenvalue | 1169850.94 | 841474.95 | 679539.923 | 451182.92 | 400094.859 |
| 6.068 | 5.925 | 5.832 | 5.654 | 5.602 | |
| Contribution | 0.03901 | 0.02806 | 0.02266 | 0.01505 | 0.01334 |
| Eigenvector | |||||
| 1 | 0.4615 | −0.0659 | 0.4139 | 0.1834 | −0.0744 |
| 2 | −0.2947 | −0.3348 | −0.3930 | −0.2625 | 0.2796 |
| 3 | −0.2062 | 0.6338 | −0.2718 | −0.1146 | −0.3254 |
| 4 | −0.2387 | −0.1172 | 0.3348 | 0.5331 | 0.0157 |
| 5 | 0.2606 | −0.1656 | 0.0905 | −0.4260 | 0.4307 |
| 6 | 0.3713 | −0.0910 | −0.1588 | −0.1483 | −0.5691 |
| 7 | −0.1663 | 0.0637 | −0.2896 | 0.5020 | 0.2334 |
| 8 | −0.2252 | 0.4277 | 0.4966 | −0.3136 | 0.2041 |
| 9 | −0.3645 | −0.4860 | 0.1112 | −0.1246 | −0.3981 |
| 10 | 0.4286 | 0.0960 | −0.3347 | 0.1753 | 0.2148 |
| Date | Price $/t | Date | Price $/t | Date | Price $/t | Date | Price $/t | Date | Price $/t |
|---|---|---|---|---|---|---|---|---|---|
| Jan-2013 | 2334 | Jan-2014 | 2066 | Jan-2015 | 1936 | Jan-2016 | 1684 | Jan-2017 | 2190 |
| Feb-2013 | 2197 | Feb-2014 | 2159 | Feb-2015 | 1969 | Feb-2016 | 1597 | Feb-2017 | 2159 |
| Mar-2013 | 2101 | Mar-2014 | 1996 | Mar-2015 | 1860 | Mar-2016 | 1779 | Mar-2017 | 2215 |
| Apr-2013 | 2126 | Apr-2014 | 2169 | Apr-2015 | 2077 | Apr-2016 | 1690 | Apr-2017 | 2359 |
| May-2013 | 1907 | May-2014 | 2180 | May-2015 | 1815 | May-2016 | 1712 | May-2017 | 2206 |
| Jun-2013 | 2150 | Jun-2014 | 2146 | Jun-2015 | 1650 | Jun-2016 | 1757 | Jun-2017 | 2203 |
| Jul-2013 | 2088 | Jul-2014 | 2084 | Jul-2015 | 1798 | Jul-2016 | 1974 | Jul-2017 | 2353 |
| Aug-2013 | 2182 | Aug-2014 | 2179 | Aug-2015 | 1808 | Aug-2016 | 1963 | Aug-2017 | 2206 |
| Sep-2013 | 2242 | Sep-2014 | 2316 | Sep-2015 | 1688 | Sep-2016 | 1955 | Sep-2017 | 2374 |
| Oct-2013 | 2020 | Oct-2014 | 2024 | Oct-2015 | 1841 | Oct-2016 | 1907 | Oct-2017 | 2402 |
| Nov-2013 | 2094 | Nov-2014 | 1849 | Nov-2015 | 1607 | Nov-2016 | 2014 | Nov-2017 | 2598 |
| Dec-2013 | 2067 | Dec-2014 | 1774 | Dec-2015 | 1704 | Dec-2016 | 2363 | Dec-2017 | 2312 |
| Date | Price $/t | Forecasted Price $/t | Error | Error % | |Error| % |
|---|---|---|---|---|---|
| Jan-2018 | 2584 | 2107 | −478 | −18.48 | 18.48 |
| Feb-2018 | 2581 | 2338 | −243 | −9.42 | 9.42 |
| Mar-2018 | 2390 | 2235 | −155 | −6.49 | 6.49 |
| Apr-2018 | 2352 | 2479 | 127 | 5.38 | 5.38 |
| May-2018 | 2361 | 2504 | 143 | 6.04 | 6.04 |
| Jun-2018 | 2436 | 2400 | −36 | −1.48 | 1.48 |
| Jul-2018 | 2207 | 2679 | 472 | 21.40 | 21.40 |
| Aug-2018 | 2054 | 2437 | 383 | 18.66 | 18.66 |
| Sep-2018 | 2023 | 2490 | 467 | 23.11 | 23.11 |
| Oct-2018 | 1988 | 2197 | 209 | 10.53 | 10.53 |
| Nov-2018 | 1937 | 2501 | 563 | 29.09 | 29.09 |
| Dec-2018 | 1972 | 2606 | 634 | 32.15 | 32.15 |
| Jan-2019 | 1997 | 1989 | −8 | −0.41 | 0.41 |
| Feb-2019 | 2063 | 2210 | 147 | 7.14 | 7.14 |
| Mar-2019 | 2046 | 2032 | −14 | −0.68 | 0.68 |
| Apr-2019 | 1939 | 2263 | 324 | 16.69 | 16.69 |
| May-2019 | 1815 | 2240 | 425 | 23.42 | 23.42 |
| Jun-2019 | 1900 | 2123 | 223 | 11.76 | 11.76 |
| Jul-2019 | 1976 | 2373 | 397 | 20.10 | 20.10 |
| Aug-2019 | 2045 | 2120 | 75 | 3.67 | 3.67 |
| Sep-2019 | 2072 | 2156 | 84 | 4.07 | 4.07 |
| Oct-2019 | 2184 | 1857 | −327 | −14.99 | 14.99 |
| Nov-2019 | 2021 | 2142 | 121 | 6.00 | 6.00 |
| Dec-2019 | 1901 | 2258 | 357 | 18.80 | 18.80 |
| Model | Phase | MAPE |
|---|---|---|
| SGDE+SSA | Prediction (Jan-2013 to Dec-2017) | 4.37% |
| Forecasting (Jan-2018 to Dec-2019) | 12.92% |
| Time | Price ($/t) | ARIMA (2,1,3) ($/t) | TGARCH (1,1) ($/t) | SDE ($/t) | SGDE+SSA ($/t) |
|---|---|---|---|---|---|
| Jan.2015 | 5830.54 | 6305.05 | 8227.29 | 5862.61 | 5830.54 |
| Feb.2015 | 5729.27 | 6319.53 | 8247.58 | 5862.49 | 5651.84 |
| March 2015 | 5939.67 | 6334.01 | 8267.89 | 5858.46 | 5919.15 |
| April.2015 | 6042.09 | 6348.48 | 8288.19 | 5870.12 | 6197.98 |
| May 2015 | 6294.78 | 6362.96 | 8308.50 | 5892.55 | 6188.28 |
| June 2015 | 5833.01 | 6377.43 | 8328.80 | 5919.63 | 5738.34 |
| July 2015 | 5456.75 | 6391.91 | 8349.11 | 5948.18 | 5555.65 |
| Aug. 2015 | 5127.30 | 6406.38 | 8369.41 | 5984.84 | 5247.37 |
| Sept. 2015 | 5217.25 | 6420.86 | 8389.72 | 6014.61 | 5159.78 |
| Oct. 2015 | 5216.09 | 6435.34 | 8410.01 | 6039.24 | 5022.23 |
| Nov. 2015 | 4799.90 | 6449.81 | 8430.33 | 6055.98 | 4952.51 |
| Dec. 2015 | 4638.83 | 6464.29 | 8450.62 | 6091.78 | 4551.01 |
| Jan. 2016 | 4471.79 | 6478.76 | 8470.93 | 6117.63 | 4595.83 |
| Feb. 2016 | 4598.62 | 6493.24 | 8491.23 | 6110.95 | 4627.92 |
| March 2016 | 4953.80 | 6507.72 | 8511.54 | 6129.23 | 4850.03 |
| April.2016 | 4872.74 | 6522.19 | 8531.84 | 6170.89 | 4876.21 |
| May 2016 | 4694.54 | 6536.67 | 8552.15 | 6206.12 | 4708.76 |
| June 2016 | 4641.97 | 6551.14 | 8572.45 | 6218.98 | 4629.30 |
| July 2016 | 4864.90 | 6565.62 | 8592.76 | 6243.33 | 4867.50 |
| Aug. 2016 | 4751.67 | 6580.10 | 8613.05 | 6263.15 | 4637.87 |
| Sept. 2016 | 4722.20 | 6594.57 | 8633.36 | 6291.74 | 4847.93 |
| Oct. 2016 | 4731.26 | 6609.05 | 8653.66 | 6313.25 | 4925.22 |
| Nov. 2016 | 5450.93 | 6623.52 | 8673.97 | 6336.70 | 5260.36 |
| Dec. 2016 | 5660.35 | 6638.00 | 8694.27 | 6341.77 | 5592.02 |
| Jan. 2017 | 5754.56 | 6652.48 | 8714.58 | 6362.59 | 5886.36 |
| Feb. 2017 | 5940.91 | 6666.95 | 8734.88 | 6361.37 | 5863.69 |
| March 2017 | 5824.63 | 6681.43 | 8755.19 | 6373.59 | 5742.58 |
| April.2017 | 5683.90 | 6695.90 | 8775.49 | 6382.08 | 5818.67 |
| May 2017 | 5599.56 | 6710.38 | 8795.80 | 6400.39 | 5463.98 |
| June 2017 | 5719.76 | 6724.86 | 8816.10 | 6412.17 | 5778.85 |
| July 2017 | 5699.48 | 6739.33 | 8836.40 | 6406.76 | 5976.38 |
| Aug. 2017 | 5978.60 | 6753.81 | 8856.70 | 6395.39 | 5839.70 |
| Sept. 2017 | 6478.35 | 6768.28 | 8877.01 | 6443.90 | 6125.46 |
| MAPE (%) | 20.90 | 54.36 | 15.61 | 2.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gligorić, Z.; Gligorić, M.; Halilović, D.; Beljić, Č.; Urošević, K. Hybrid Stochastic-Grey Model to Forecast the Behavior of Metal Price in the Mining Industry. Sustainability 2020, 12, 6533. https://doi.org/10.3390/su12166533
Gligorić Z, Gligorić M, Halilović D, Beljić Č, Urošević K. Hybrid Stochastic-Grey Model to Forecast the Behavior of Metal Price in the Mining Industry. Sustainability. 2020; 12(16):6533. https://doi.org/10.3390/su12166533
Chicago/Turabian StyleGligorić, Zoran, Miloš Gligorić, Dževdet Halilović, Čedomir Beljić, and Katarina Urošević. 2020. "Hybrid Stochastic-Grey Model to Forecast the Behavior of Metal Price in the Mining Industry" Sustainability 12, no. 16: 6533. https://doi.org/10.3390/su12166533





