User Equilibrium Analysis Considering Travelers’ Context-Dependent Route Choice Behavior on the Risky Traffic Network
Abstract
1. Introduction
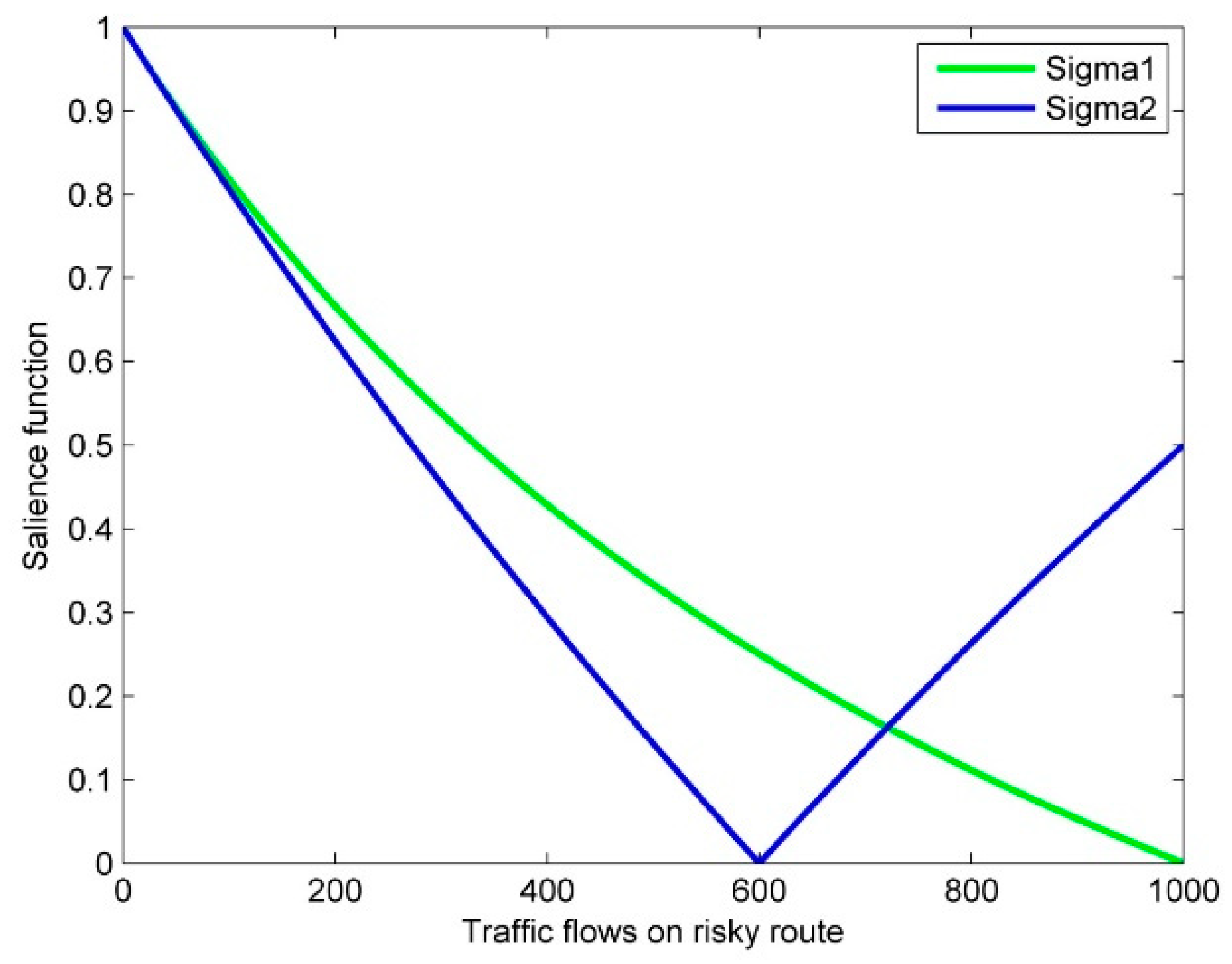
- We study travelers’ context-dependent route choice behavior in a risky traffic network. Particularly, we extend the salience theory to propose a flow-dependent salience theory for this study, where the flow denotes the traffic flows on the risky route. Three significant properties of the flow-dependent salience theory are ordering, diminishing sensitivity, and symmetry.
- Following the convention in [35], we propose a salient travel utility model with a discrete salience ranking, and further propose the salient user equilibrium based on this model. An analysis procedure is proposed to prove the existence and uniqueness of the salient user equilibrium, which consists of two parts, the flow-dependent salience ranking analysis and flow-dependent route preference analysis. The sufficient conditions for the existence and uniqueness of the salient user equilibrium are identified based on this analysis procedure.
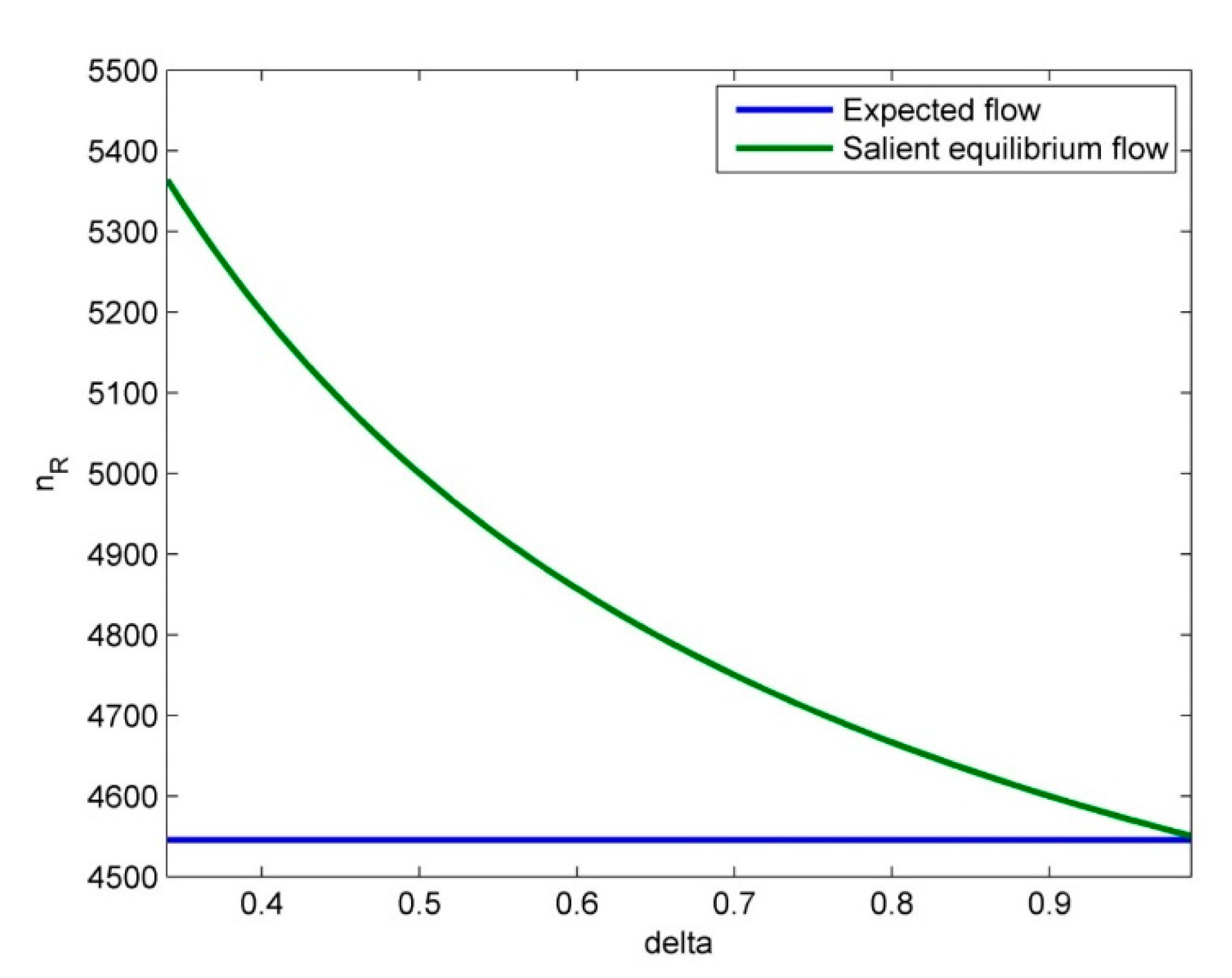
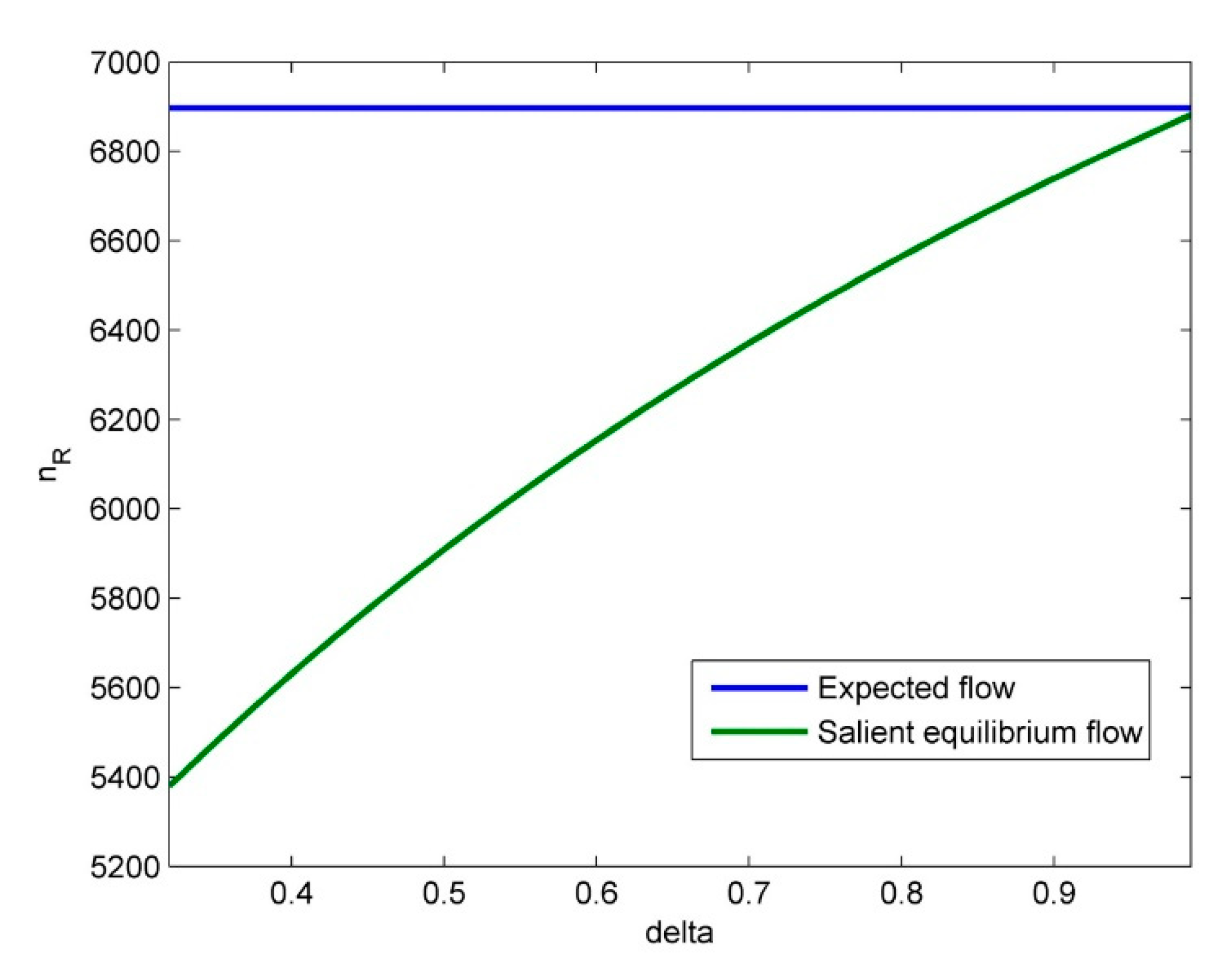
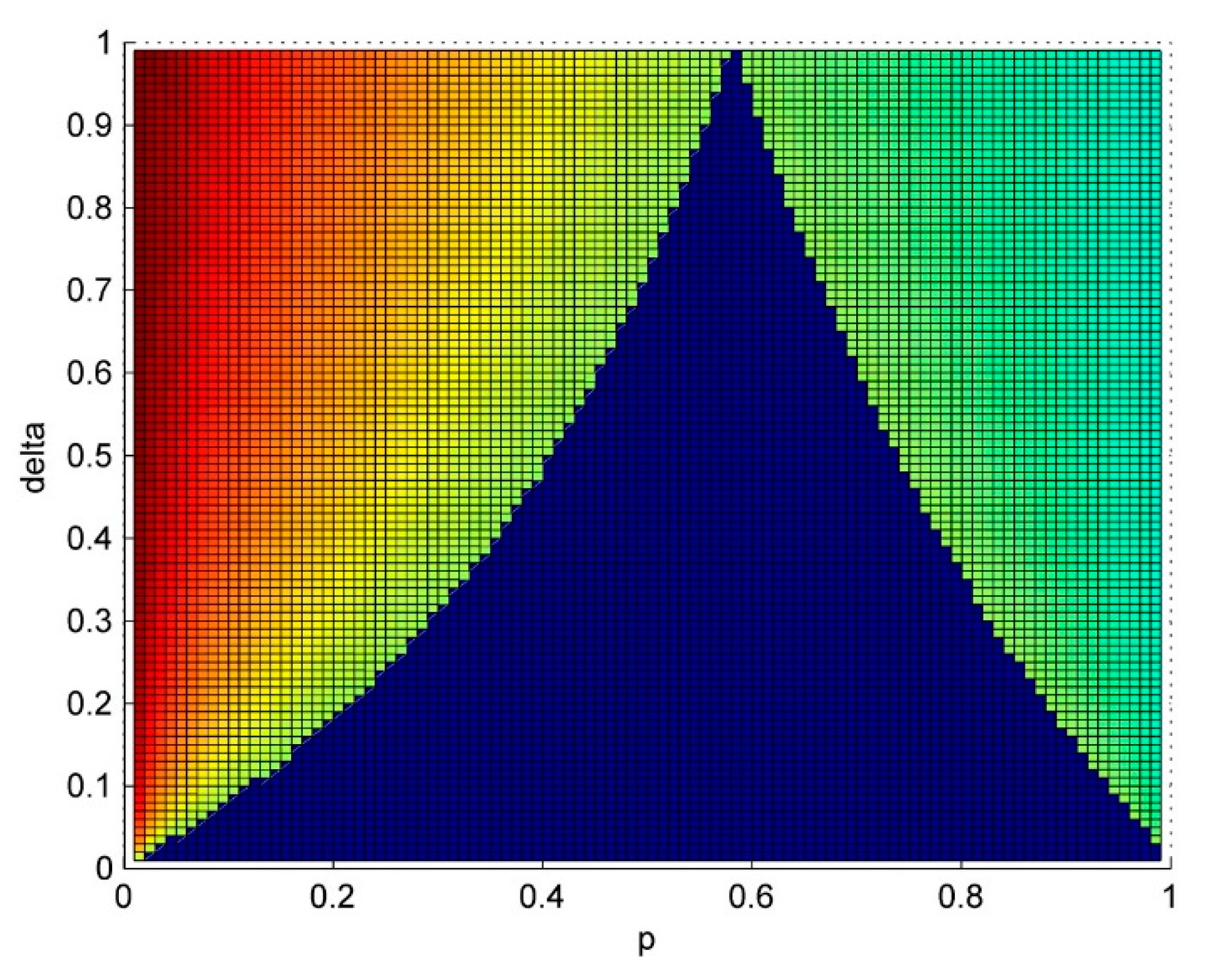
- Finally, numerical studies demonstrate our theoretical findings. The equilibrium results show non-intuitive insights into travelers’ route choice behavior. (a) Travelers can be risk-seeking (the travel utility of a risky route is small with a relatively high probability), risk-neutral (in special situations), or risk-averse (the travel utility of a risky route is large with a relatively high probability), which depends on the salient state. (b) The extent of travelers’ risk-seeking or risk-averse behavior depends on their extent of salience bias, while the risk-neutral behavior is irrelative to this salience bias. Our findings here can provide some new evidence about travelers’ risk attitudes to a risky traffic network (e.g., [7,11]).
2. Development of a General Salient Travel Utility Model
2.1. Review of Original Salience Theory
- Ordering. If for states, , we have thatis a subset of. Then:
- Diminishing sensitivity. Iffor, then for any:
- Reflection. For any two states, , such that. For, we have:
2.2. Salient Travel Utility Model
- Ordering. If for states, , we have thatis a subset of, then:
- Diminishing sensitivity. If, , then for any:
3. User Equilibrium Analysis with Salient Travel Utility Model
3.1. Definitions and Notations
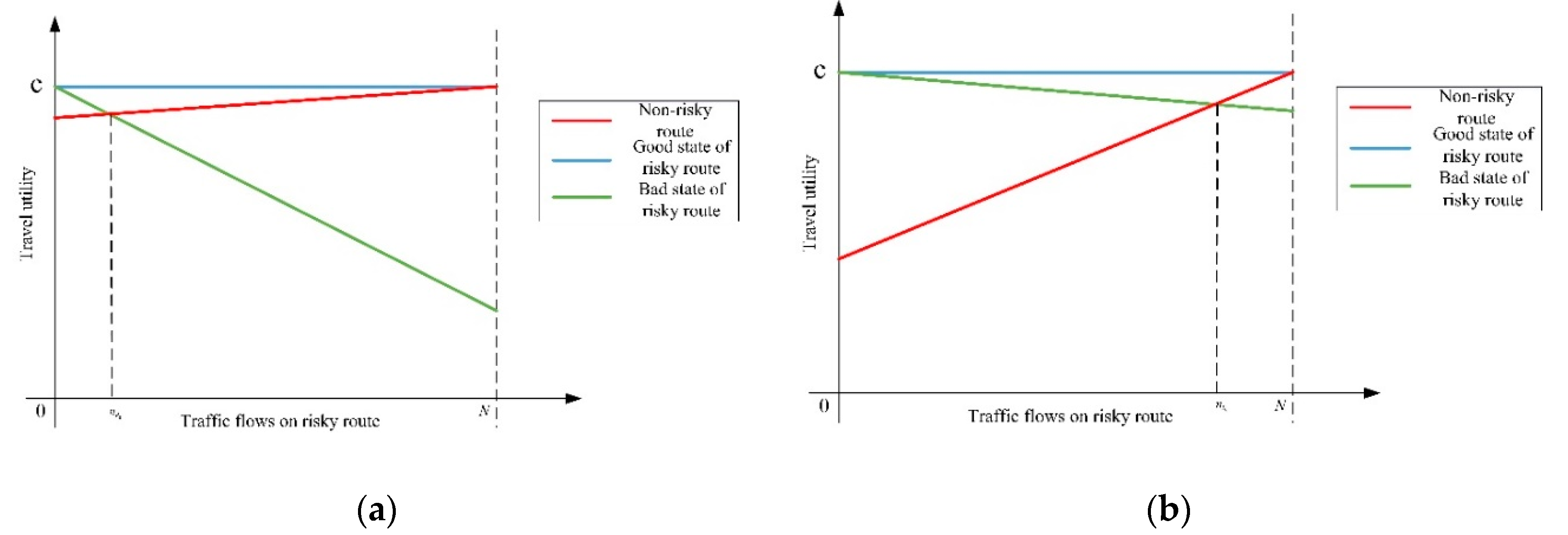
3.2. Trivial Equilibrium Analysis
- The case where or :
- (1)
- . In this case, one corner equilibrium solution can be obtained by solving —i.e., ;
- (2)
- . In this case, one equilibrium solution can be obtained by solving —i.e., .
- 2.
- The case where :
- (1)
- When , the salient travelers become the rational travelers as discussed before, and they make the route choice decision based on the expected utility theory. In this case, one equilibrium solution, termed the expected flow, can be obtained by solving:
- (2)
- When , we analyze the salient user equilibrium based on the salient travel utility model, which will be studied in the next section.
3.3. Salient User Equilibrium Analysis
3.3.1. Salience Ranking Analysis
- (1)
- Examination of monotonicity
- (2)
- Examination of salience ranking for special points
- When , we have that , , and . Furthermore, and . By ordering the property, we obtain .
- When , we have , and . By ordering the property, we obtain .
- When , we have , , and . Furthermore, and . By ordering the property, we obtain .
- (3)
- Examination of salience equivalence:
- Considering the interval , let , and we obtain:
- 2.
- Considering the interval , let , and we obtain:
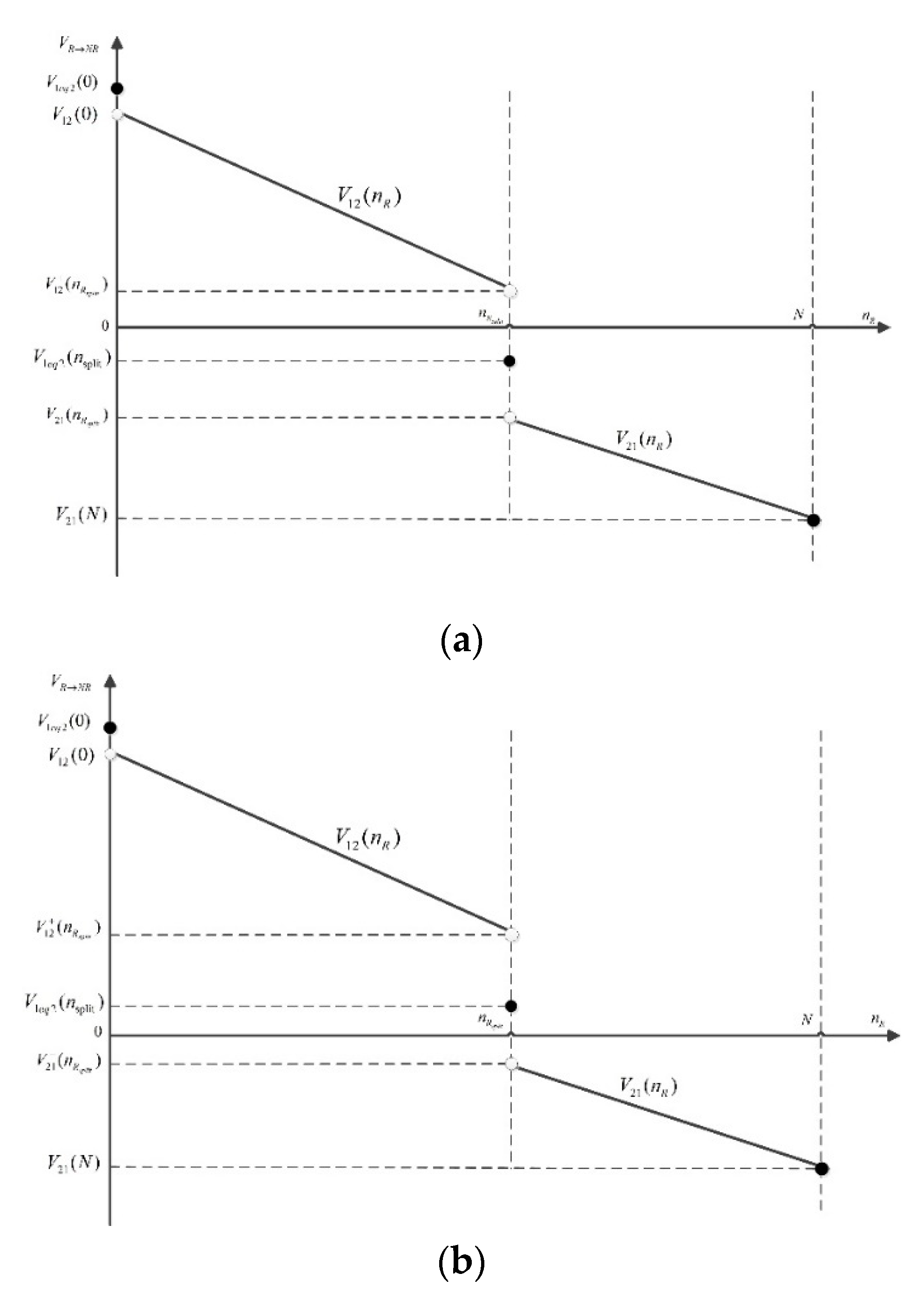
3.3.2. Equilibrium Analysis
- (1)
- When , we obtain —i.e., the salient travelers prefer the risky route to the non-risky route. Therefore, is not a salient user equilibrium.
- (2)
- Considering the interval , we have when . Besides this,. Therefore, we obtain —i.e., the salient travelers prefer the risky route to the non-risky route, and thus there is no salient user equilibrium in the considered interval. □
4. More Discussions on the Salient User Equilibrium
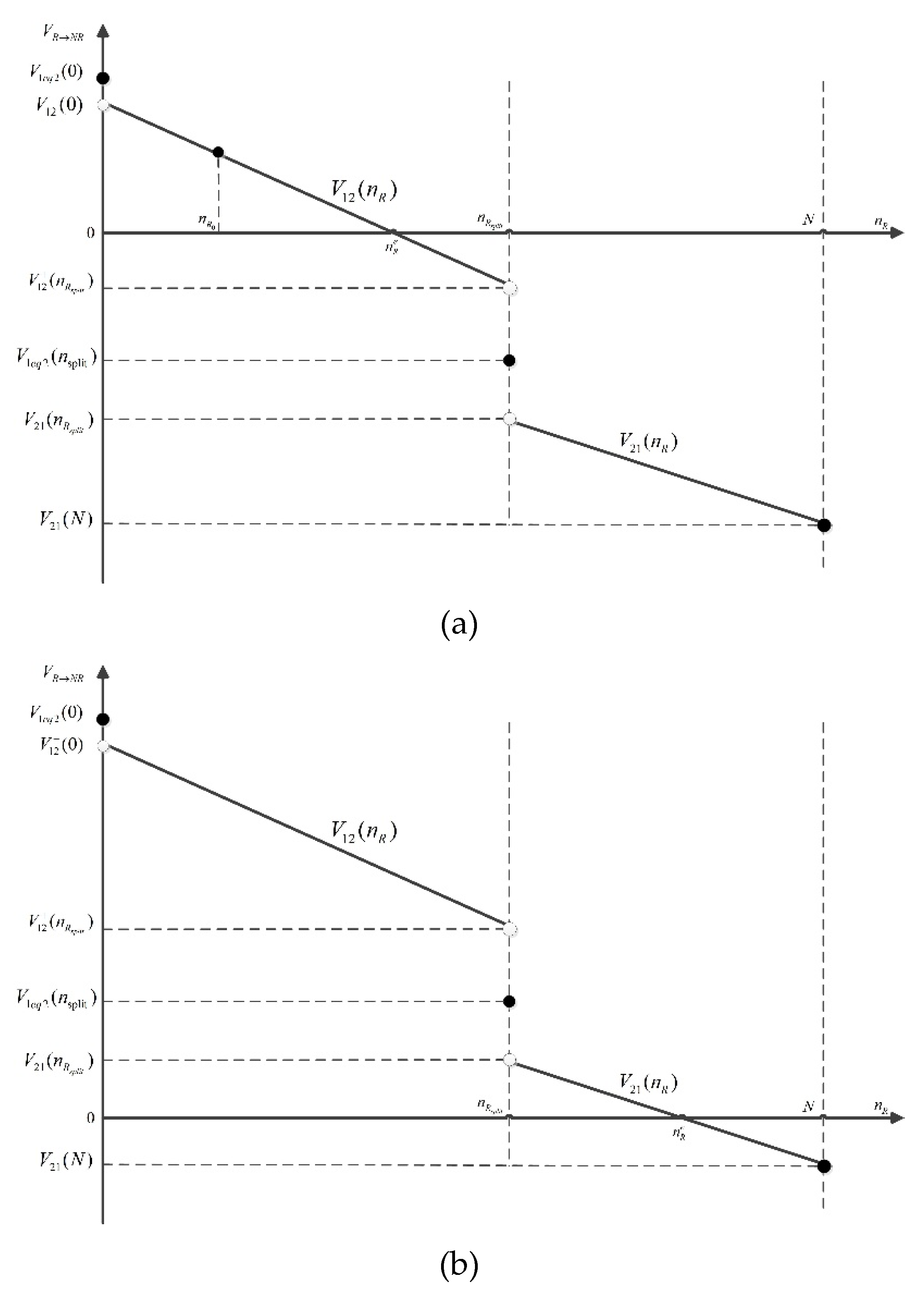
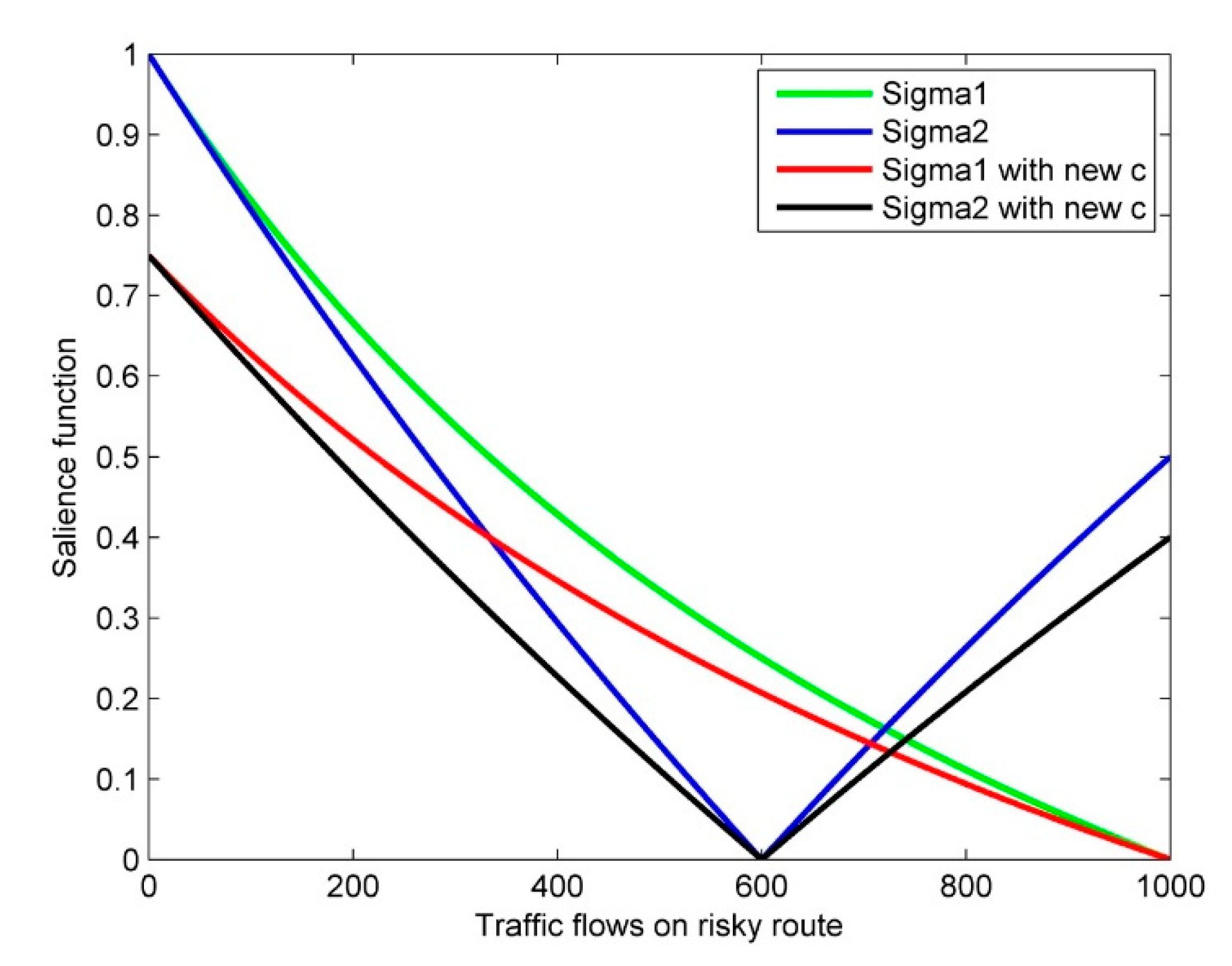
4.1. Diminishing Sensitivity
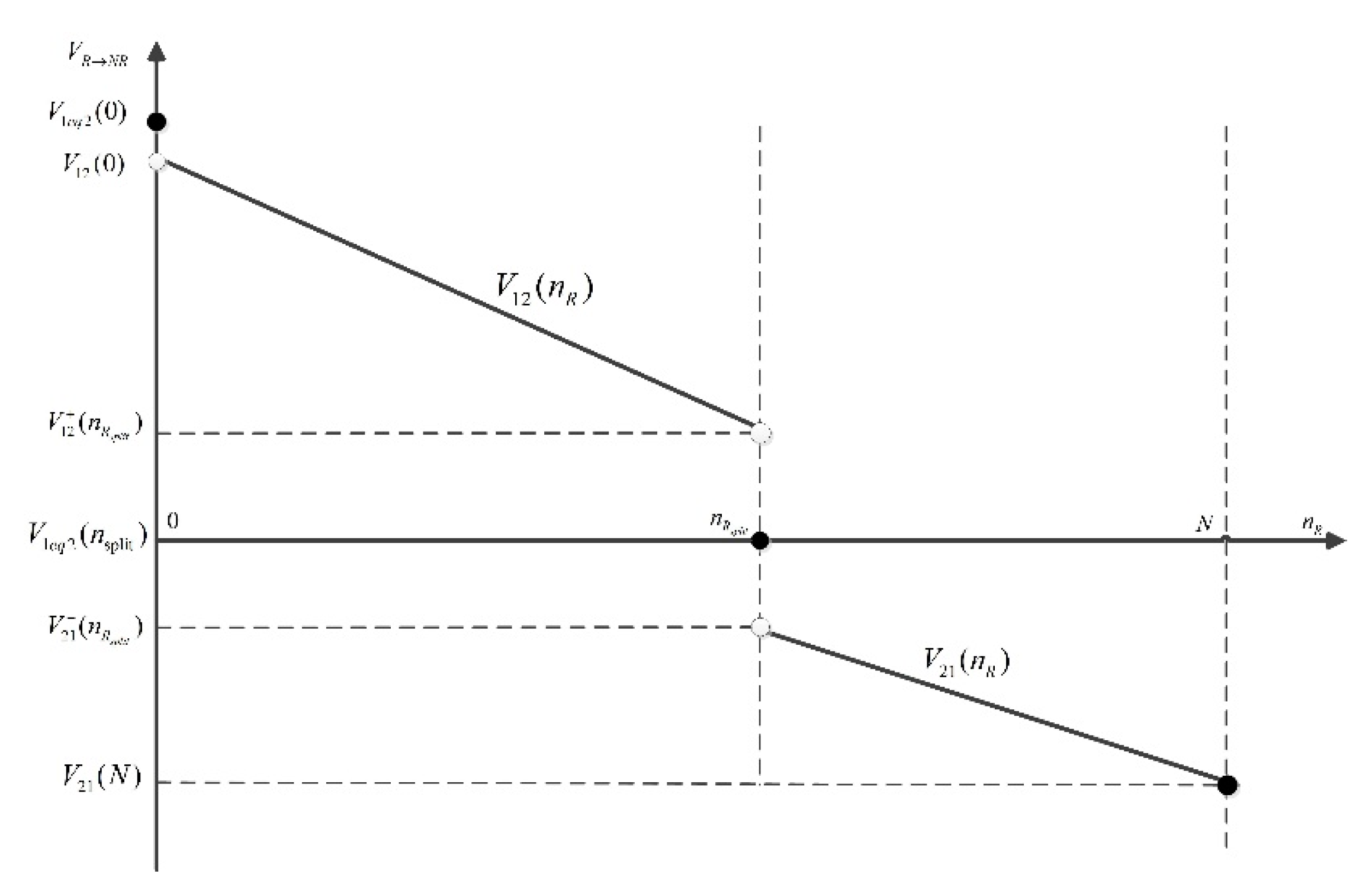
4.2. Relationship between and
5. Numerical Experiments
6. Conclusions and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wardrop, J.G. Some theoretical aspects of road traffic research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Beckmann, M.; McGuire, C.B.; Winsten, C.B. Studies in the Economics of Transportation; Yale University Press: New Haven, CT, USA, 1956. [Google Scholar]
- Gao, Z.; Wu, J.; Sun, H. Solution algorithm for the bi-level discrete network design problem. Transp. Res. Part B Methodol. 2005, 39, 479–495. [Google Scholar] [CrossRef]
- Wu, D.; Yin, Y.; Lawphongpanich, S.; Yang, H. Design of more equitable congestion pricing and tradable credit schemes for multimodal transportation networks. Transp. Res. Part B Methodol. 2012, 46, 1273–1287. [Google Scholar] [CrossRef]
- Sun, X.; Lu, H.P.; Chu, W.J. A low-carbon-based bilevel optimization model for public transit network. Math. Probl. Eng. 2013, 2013, 374826. [Google Scholar] [CrossRef]
- Umar, M.; Ji, X.; Kirikkaleli, D.; Xu, Q. COP21 Roadmap: Do innovation, financial development, and transportation infrastructure matter for environmental sustainability in China? J. Environ. Manag. 2020, 271, 111026. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z. The α-reliable mean-excess traffic equilibrium model with stochastic travel times. Transp. Res. Part B Methodol. 2010, 44, 493–513. [Google Scholar] [CrossRef]
- Ji, X.; Ban, X.; Zhang, J.; Ran, B. Moment-based travel time reliability assessment with lasserre’s relaxation. Transp. B Transp. Dyn. 2019, 7, 401–422. [Google Scholar] [CrossRef]
- Knight, F.H. Risk, Uncertainty and Profit; Houghton Mifflin: Boston, MA, USA, 1921. [Google Scholar]
- Chen, Z.; Sim, M.; Xu, H. Distributionally robust optimization with infinitely constrained ambiguity sets. Oper. Res. 2019, 67, 1328–1344. [Google Scholar] [CrossRef]
- Mirchandani, P.; Soroush, H. Generalized traffic equilibrium with probabilistic travel times and perceptions. Transp. Sci. 1987, 21, 133–152. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O.; Kuhn, H.W. Theory of Games and Economic Behavior (Commemorative Edition); Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Ban, X.J.; Ferris, M.C.; Tang, L.; Lu, S. Risk-neutral second best toll pricing. Transp. Res. Part B Methodol. 2013, 48, 67–87. [Google Scholar]
- Lo, H.K.; Luo, X.; Siu, B.W. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion. Transp. Res. Part B Methodol. 2006, 40, 792–806. [Google Scholar] [CrossRef]
- Watling, D. User equilibrium traffic network assignment with stochastic travel times and late arrival penalty. Eur. J. Oper. Res. 2006, 175, 1539–1556. [Google Scholar] [CrossRef]
- Ji, X.; Ban, X.J.; Li, M.; Zhang, J.; Ran, B. Non-expected route choice model under risk on stochastic traffic networks. Netw. Spat. Econ. 2017, 17, 777–807. [Google Scholar] [CrossRef]
- Ji, X.; Ban, X.; Zhang, J.; Ran, B. Subjective-utility travel time budget modeling in the stochastic traffic network assignment. J. Intell. Transp. Syst. 2017, 21, 439–451. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Bell, D.E. Regret in decision making under uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Xu, H.; Lou, Y.; Yin, Y.; Zhou, J. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing. Transp. Res. Part B Methodol. 2011, 45, 311–328. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.-L.; Huang, H.-J.; Chen, J. A cumulative prospect theory approach to commuters’ day-to-day route-choice modeling with friends’ travel information. Transp. Res. Part C Emerg. Technol. 2018, 86, 527–548. [Google Scholar] [CrossRef]
- Chorus, C.G.; Arentze, T.A.; Timmermans, H.J. A random regret-minimization model of travel choice. Transp. Res. Part B Methodol. 2008, 42, 1–18. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Sheffi, Y. On stochastic models of traffic assignment. Transp. Sci. 1977, 11, 253–274. [Google Scholar] [CrossRef]
- Mahmassani, H.S.; Chang, G.-L. On boundedly rational user equilibrium in transportation systems. Transp. Sci. 1987, 21, 89–99. [Google Scholar] [CrossRef]
- Ahipasaoglu, S.D.; Meskarian, R.; Magnanti, T.L.; Natarajan, K. Beyond normality: A cross moment-stochastic user equilibrium model. Transp. Res. Part B Methodol. 2015, 81, 333–354. [Google Scholar] [CrossRef]
- Yan, C.-Y.; Hu, M.-B.; Jiang, R.; Long, J.; Chen, J.-Y.; Liu, H.-X. Stochastic ridesharing user equilibrium in transport networks. Netw. Spat. Econ. 2019, 19, 1007–1030. [Google Scholar] [CrossRef]
- Xiao, F.; Shen, M.; Xu, Z.; Li, R.; Yang, H.; Yin, Y. Day-to-day flow dynamics for stochastic user equilibrium and a general lyapunov function. Transp. Sci. 2019, 53, 683–694. [Google Scholar] [CrossRef]
- Di, X.; Liu, H.X.; Ban, X.J. Second best toll pricing within the framework of bounded rationality. Transp. Res. Part B Methodol. 2016, 83, 74–90. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, X. Capacitated transit service network design with boundedly rational agents. Transp. Res. Part B Methodol. 2016, 93, 225–250. [Google Scholar] [CrossRef]
- Sun, L.; Karwan, M.H.; Kwon, C. Path-based approaches to robust network design problems considering boundedly rational network users. Transp. Res. Rec. 2019, 2673, 637–645. [Google Scholar] [CrossRef]
- Xu, H.; Yang, H.; Zhou, J.; Yin, Y. A route choice model with context-dependent value of time. Transp. Sci. 2017, 51, 536–548. [Google Scholar] [CrossRef]
- Finkelstein, A. E-ztax: Tax salience and tax rates. Q. J. Econ. 2009, 124, 969–1010. [Google Scholar] [CrossRef]
- Michel, A.; Zhao, J. Modeling saliency in transportation pricing: Optimal mixture of automobile management policies. In Proceedings of the Transportation Research Board 94th Annual Meeting, Washington, DC, USA, 11–15 January 2015. [Google Scholar]
- Bordalo, P.; Gennaioli, N.; Shleifer, A. Salience theory of choice under risk. Q. J. Econ. 2012, 127, 1243–1285. [Google Scholar] [CrossRef]
- Spitmaan, M.; Chu, E.; Soltani, A. Salience-driven value construction for adaptive choice under risk. J. Neurosci. 2019, 39, 5195–5209. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, C.S.; Sebald, A.C.; Sørensen, P.N. Testing for Salience Effects in Choices under Risk. Available online: http://web.econ.ku.dk/sorensen/papers/TestingForSalienceEffects.pdf (accessed on 17 May 2020).
- Frydman, C.; Wang, B. The impact of salience on investor behavior: Evidence from a natural experiment. J. Financ. Forthcom. 2020, 75, 229–276. [Google Scholar] [CrossRef]
- Bordalo, P.; Gennaioli, N.; Shleifer, A. Salience theory of judicial decisions. J. Leg. Stud. 2015, 44, S7–S33. [Google Scholar] [CrossRef]
- Dertwinkel-Kalt, M.; Köster, M. Salient compromises in the newsvendor game. J. Econ. Behav. Organ. 2017, 141, 301–315. [Google Scholar] [CrossRef]
- Fochmann, M.; Wolf, N. Framing and salience effects in tax evasion decisions-an experiment on underreporting and overdeducting. J. Econ. Psychol. 2019, 72, 260–277. [Google Scholar] [CrossRef]
- Bordalo, P.; Gennaioli, N.; Shleifer, A. Salience and consumer choice. J. Political Econ. 2013, 121, 803–843. [Google Scholar] [CrossRef]
- Taylor, S.E.; Thompson, S.C. Stalking the elusive “vividness” effect. Psychol. Rev. 1982, 89, 155. [Google Scholar] [CrossRef]
- Kontek, K. A critical note on salience theory of choice under risk. Econ. Lett. 2016, 149, 168–171. [Google Scholar] [CrossRef]
- Connors, R.D.; Sumalee, A. A network equilibrium model with travellers’ perception of stochastic travel times. Transp. Res. Part B Methodol. 2009, 43, 614–624. [Google Scholar] [CrossRef]
- Wu, X.; Nie, Y.M. Modeling heterogeneous risk-taking behavior in route choice: A stochastic dominance approach. Transp. Res. Part A Policy Pract. 2011, 45, 896–915. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Ji, X. User Equilibrium Analysis Considering Travelers’ Context-Dependent Route Choice Behavior on the Risky Traffic Network. Sustainability 2020, 12, 6706. https://doi.org/10.3390/su12176706
Xu Q, Ji X. User Equilibrium Analysis Considering Travelers’ Context-Dependent Route Choice Behavior on the Risky Traffic Network. Sustainability. 2020; 12(17):6706. https://doi.org/10.3390/su12176706
Chicago/Turabian StyleXu, Qinghui, and Xiangfeng Ji. 2020. "User Equilibrium Analysis Considering Travelers’ Context-Dependent Route Choice Behavior on the Risky Traffic Network" Sustainability 12, no. 17: 6706. https://doi.org/10.3390/su12176706
APA StyleXu, Q., & Ji, X. (2020). User Equilibrium Analysis Considering Travelers’ Context-Dependent Route Choice Behavior on the Risky Traffic Network. Sustainability, 12(17), 6706. https://doi.org/10.3390/su12176706





